Anatomical Prior-Based Automatic Segmentation for Cardiac Substructures from Computed Tomography Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source and Data Analysis
2.2. Cardiac Substructures and Their Anatomical Information
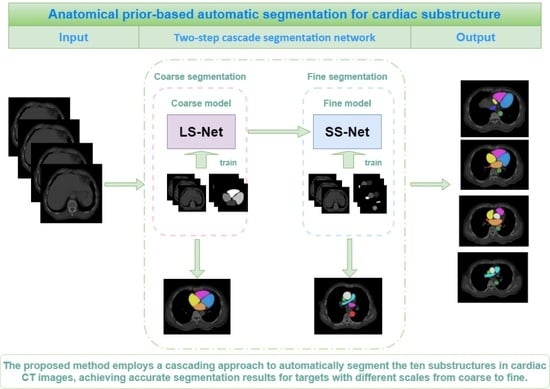
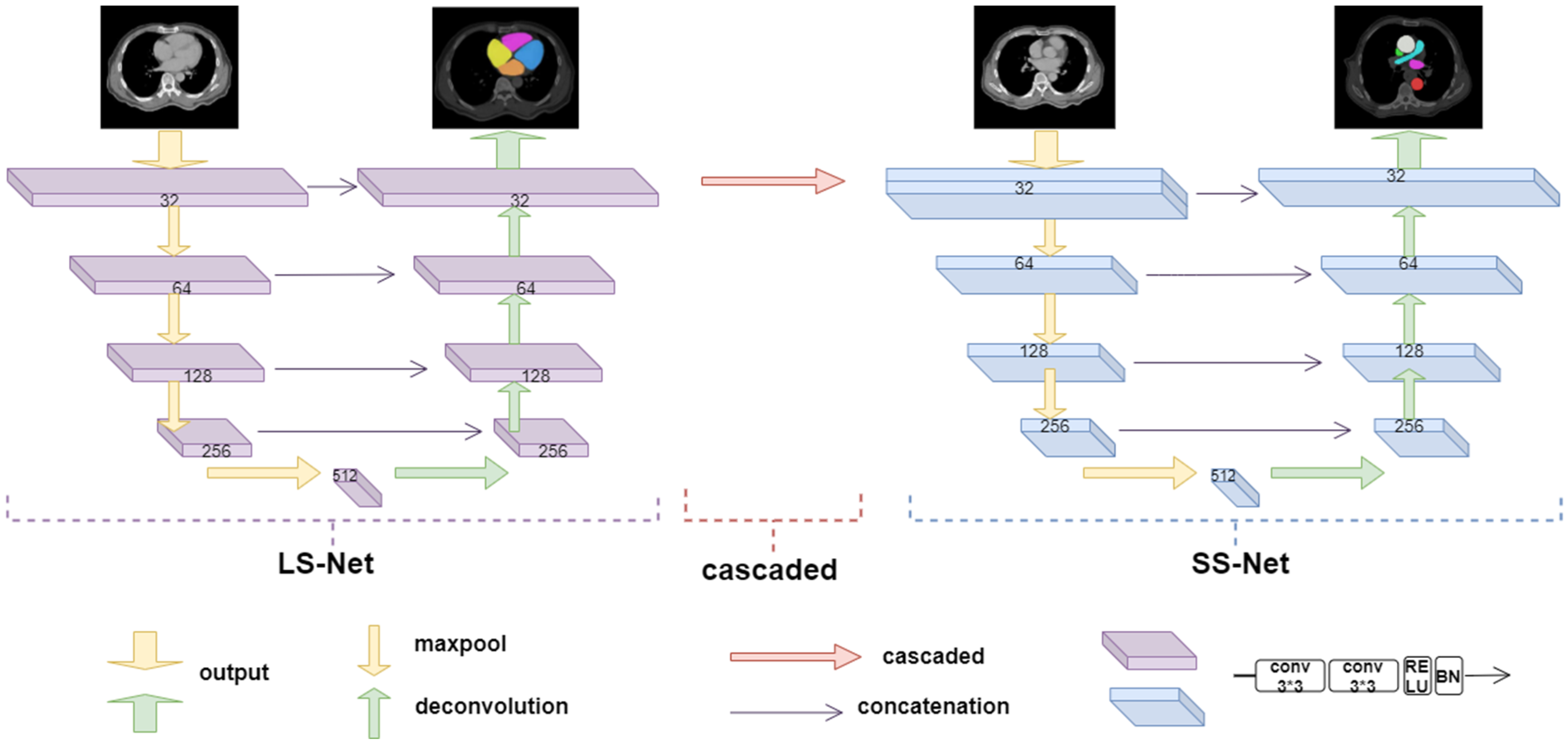
2.3. Anatomical Prior-Based Automatic Segmentation Framework
2.3.1. Large Substructure Segmentation Network (LS-Net)
2.3.2. Small Substructure Segmentation Network (SS-Net)
2.3.3. Grouping Strategy
2.4. Loss Function
3. Experiments and Results
3.1. Experimental Dataset
3.2. Image Preprocessing
3.3. Functionally Gradient Porous Mandibular Prosthesis
3.4. Evaluation Metrics
3.5. Experimental Results
3.5.1. Impact of Grouping Method for Cardiac Substructures on Segmentation Results
3.5.2. Segmentation Results
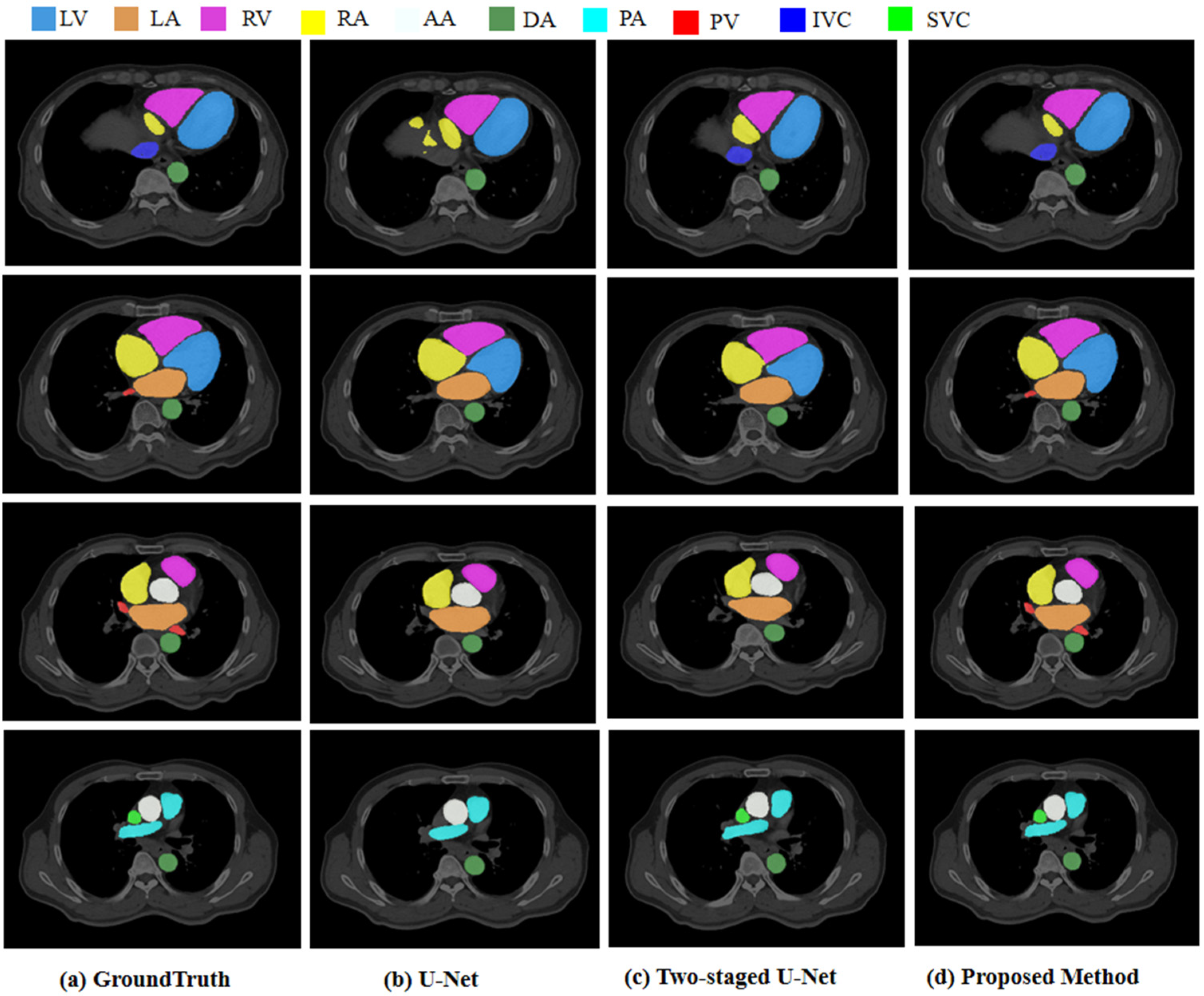
3.5.3. Comparison with Other Deep Learning Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- WHO. Cardiovascular Diseases (CVDs). Available online: https://www.who.int/zh/news/item/09-12-2020-who-reveals-leading-causes-of-death-and-disability-worldwide-2000-2019 (accessed on 11 June 2021).
- Roberts, W.T.; Bax, J.J.; Davies, L.C. Cardiac CT and CT coronary angiography: Technology and application. Heart 2008, 94, 781–792. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, X. Challenges and methodologies of fully automatic whole heart segmentation: A review. J. Healthc. Eng. 2013, 4, 371–408. [Google Scholar] [CrossRef] [PubMed]
- Peng, P.; Lekadir, K.; Gooya, A.; Shao, L.; Petersen, S.E.; Frangi, A.F. A review of heart chamber segmentation for structural and functional analysis using cardiac magnetic resonance imaging. Magn. Reson. Mater. Phy. 2016, 29, 155–195. [Google Scholar] [CrossRef] [PubMed]
- Auger, D.A.; Zhong, X.; Epstein, F.H.; Meintjes, E.M.; Spottiswoode, B.S. Semi-automated left ventricular segmentation based on a guide point model approach for 3D cine DENSE cardiovascular magnetic resonance. Cardiovasc. Magn. Reson. 2014, 16, 8. [Google Scholar] [CrossRef] [PubMed]
- Grosgeorge, D.; Petttjean, C.; Dacher, J.-N. Graph cut segmentation with a statistical shape model in cardiac MRI. Comput. Vis. Image Underst. 2013, 117, 1027–1035. [Google Scholar] [CrossRef]
- Ben Ayed, I.; Chen, H.M.; Punithakumar, K.; Ross, I.; Li, S. Max-flow segmentation of the left ventricle by recovering subject-specific distributions via a bound of the Bhattacharyya measure. Med. Image Anal. 2012, 16, 87–100. [Google Scholar] [CrossRef]
- Pednekar, A.; Kurkure, U.; Muthupillai, R.; Flamm, S.; Kakadiaris, I.A. Automated left ventricular segmentation in cardiac MRI. IEEE Trans. Biomed. Eng. 2006, 53, 1425–1428. [Google Scholar] [CrossRef]
- Hautvast, G.; Lobregt, S.; Breeuwer, M.; Gerritsen, F. Automatic contour propagation in cine cardiac magnetic resonance images. IEEE Trans. Med. Imaging 2006, 25, 1472–1482. [Google Scholar] [CrossRef]
- Billet, F.; Sermesant, M.; Delingette, H.; Ayache, N. Cardiac motion recovery and boundary conditions estimation by coupling an electromechanical model and cine-MRI data. In Proceedings of the International Conference on Functional Imaging and Modeling of Heart, Nice, France, 3–5 June 2009; pp. 376–385. [Google Scholar]
- Senegas, J.; Cocosco, C.A.; Netsch, T. Model-based segmentation of cardiac MRI cine sequences: A Bayesian formulation. In Medical Imaging 2004: Image Processing; International Society for Optics and Photonics: San Diego, CA, USA, 2004; pp. 432–443. [Google Scholar]
- Wang, J.; Xiaolei, D.; Zhou, P. Current Situation and Review of Image Segmentation. Recent Pat. Comput. Sci. 2017, 10, 70–79. [Google Scholar] [CrossRef]
- Payer, C.; Štern, D.; Bischof, H.; Urschler, M. Multilabel whole heart segmentation using cnns and anatomical label configurations. In International Workshop on Statistical Atlases and Computational Models of the Heart; Springer: Cham, Switzerland, 2017; pp. 190–198. [Google Scholar]
- Dangi, S.; Linte, C.A.; Yaniv, Z. A distance map regularized CNN for cardiac cine MR image segmentation. Med. Phys. 2019, 46, 5637–5651. [Google Scholar] [CrossRef]
- Bartoli, A.; Fournel, J.; Bentatou, Z.; Habib, G.; Lalande, A.; Bernard, M.; Boussel, L.; Pontana, F.; Dacher, J.-N.; Ghattas, B.; et al. Deep Learning-based Automated Segmentation of Left Ventricular Trabeculations and Myocardium on Cardiac MR Images: A Feasibility Study. Radiol. Artif. Intell. 2020, 3, e200021. [Google Scholar] [CrossRef]
- Wang, S.; Chauhan, D.; Patel, H.; Amir-Khalili, A.; da Silva, I.F.; Sojoudi, A.; Friedrich, S.; Singh, A.; Landeras, L.; Miller, T.; et al. Assessment of right ventricular size and function from cardiovascular magnetic resonance images using artificial intelligence. Cardiovasc. Magn. Reason. 2022, 24, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Huang, H.; Huang, J.; Wang, K.; Qin, H.; Wong, K.K.L. Deep learning-based medical segmentation of the aorta using XR-MSF-U-Net. Comput. Methods Programs Biomed. 2022, 225, 1070–1073. [Google Scholar] [CrossRef] [PubMed]
- Martín-Isla, C.; Campello, V.M.; Izquierdo, C.; Kushibar, K.; Sendra-Balcells, C.; Gkontra, P.; Sojoudi, A.; Fulton, M.J.; Weldebirhan Arega, T.; Punithakumar, K.; et al. Deep Learning Segmentation of the Right Ventricle in Cardiac MRI: The M&Ms Challenge. Biomed. Health Inform. 2023, 27, 3302–3313. [Google Scholar]
- Dang, H.; Li, M.; Tao, X.; Zhang, G.; Qi, X. LVSegNet: A novel deep learning-based framework for left ventricle automatic segmentation using magnetic resonance imaging. Comput. Commun. 2023, 208, 124–135. [Google Scholar] [CrossRef]
- Morris, E.D.; Ghanem, A.I.; Dong, M.; Pantelic, M.V.; Walker, E.M.; Glide-Hurst, C.K. Cardiac substructure segmentation with deep learning for improved cardiac sparing. Med. Phys. 2020, 47, 576–586. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Khened, M.; Kollerathu, V.A.; Krishnamurthi, G. Fully convolutional multi-scale residual DenseNets for cardiac segmentation and automated cardiac diagnosis using ensemble of classifiers. Med. Image Anal. 2019, 51, 21–45. [Google Scholar] [CrossRef] [PubMed]
- Zotti, C.; Luo, Z.; Lalande, A.; Jodoin, P.M. Convolutional Neural Network with Shape Prior Applied to Cardiac MRI Segmentation. IEEE J. Biomed. Health Inf. 2019, 23, 1119–1128. [Google Scholar] [CrossRef]
- Qin, C.; Bai, W.; Schlemper, J.; Petersen, S.E.; Piechnik, S.K.; Neubauer, S.; Rueckert, D. Joint learning of motion estimation and segmentation for cardiac MR image sequences. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2018, Proceedings of the 21st International Conference, Granada, Spain, 16-20 September 2018; Springer: Cham, Switzerland, 2018; pp. 472–480. [Google Scholar]
- Vigneault, D.M.; Xie, W.; Ho, C.Y.; Bluemke, D.A.; Noble, J.A. Ω-Net (Omega-Net): Fully automatic, multi-view cardiac MR detection, orientation, and segmentation with deep neural networks. Med. Image Anal. 2018, 48, 95–106. [Google Scholar] [CrossRef]
- Wang, C.; Smedby, Ö. Automatic whole heart segmentation using deep learning and shape context. In International Workshop on Statistical Atlases and Computational Models of the Heart; Springer: Cham, Switzerland, 2017; pp. 242–249. [Google Scholar]
- Yang, X.; Bian, C.; Yu, L.; Ni, D.; Heng, P.A. 3d convolutional networks for fully automatic fine-grained whole heart partition. In International Workshop on Statistical Atlases and Computational Models of the Heart; Springer: Cham, Switzerland, 2017; pp. 181–189. [Google Scholar]
- Clough, J.R.; Oksuz, I.; Byrne, N.; Schnabel, J.A.; King, A.P. Explicit topological priors for deep-learning based image segmentation using persistent homology. In Proceedings of the 26th International Conference, Information Processing in Medical Imaging, IPMI, Hong Kong, China, 2–7 June 2019; pp. 16–28. [Google Scholar]
- Oktay, O.; Ferrante, E.; Kamnitsas, K.; Heinrich, M.; Bai, W.; Caballero, J.; Cook, S.A.; de Marvao, A.; Dawes, T.; O’Regan, D.P.; et al. Anatomically Constrained Neural Networks (ACNNs): Application to Cardiac Image Enhancement and Segmentation. IEEE Trans. Med. Imaging 2018, 37, 384–395. [Google Scholar] [CrossRef]
- Chen, X.; Williams, B.M.; Vallabhaneni, S.R.; Czanner, G.; Williams, R.; Zheng, Y. Learning active contour models for medical image segmentation. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11632–11640. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Karimi, D.; Salcudean, S.E. Reducing the hausdorff distance in medical image segmentation with convolutional neural networks. IEEE Trans. Med. Imag. 2020, 39, 499–513. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 2012, 26, 297–302. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Ciçek, Ö.; Abdulkadir, A.; Lienkamp, S.S. 3D U-net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]

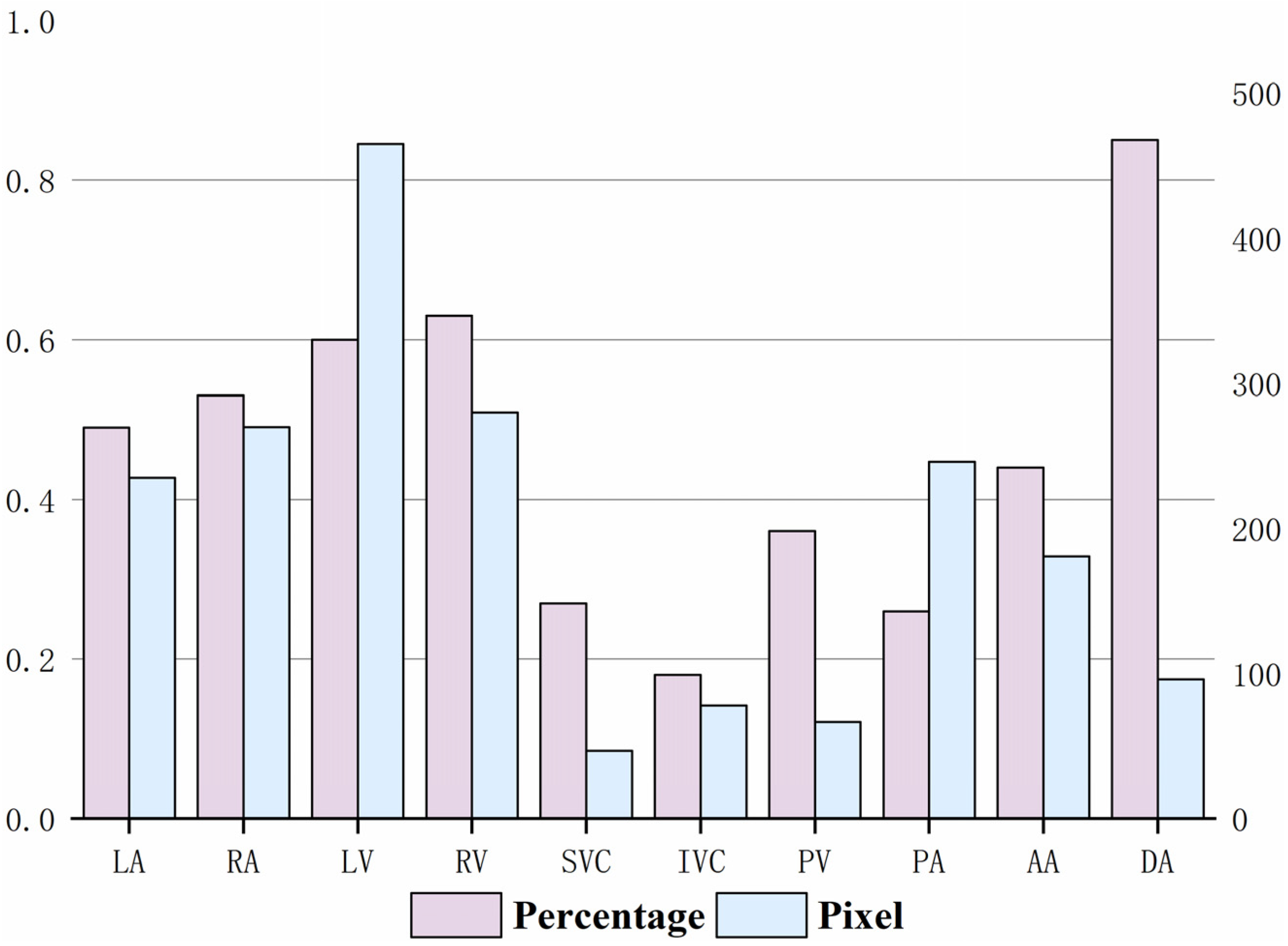
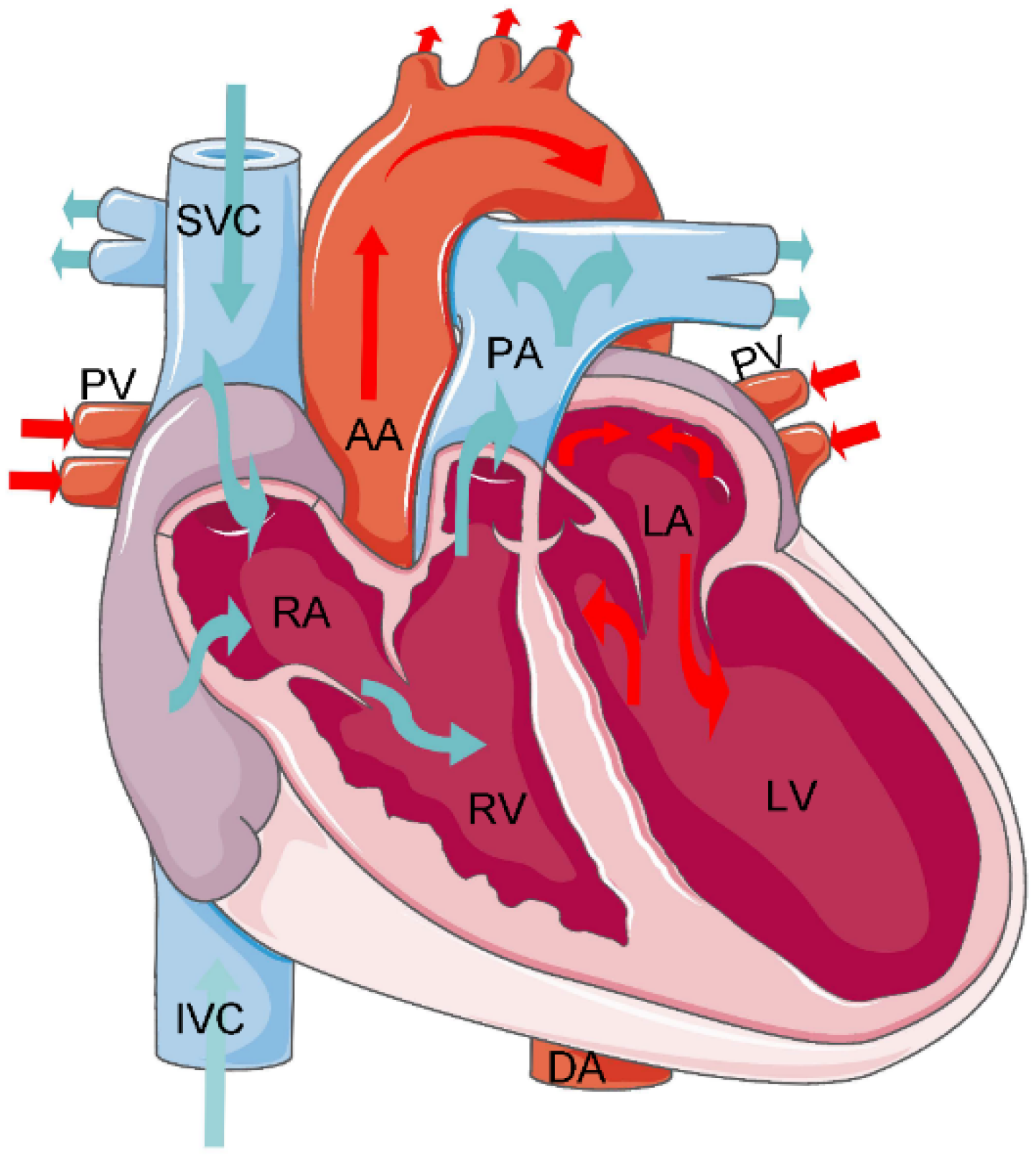

| Substructures | Acronym | Anatomical Position |
|---|---|---|
| Left Ventricle | LV | The left ventricle is located in the lower left part of the heart, below the left atrium, and in the left rear of the right ventricle, which is conical. In the four-chamber view of transverse CT, the left ventricle is located in the upper left. |
| Right Ventricle | RV | The right ventricle is located in the lower right part of the heart, in the anterior lower part of the right atrium. In the four-chamber view of transverse CT, the right ventricle is located in the upper right. |
| Left Atrium | LA | The left atrium is located in the upper left part of the heart and is the most posterior heart cavity. In the four-chamber view of transverse CT, the left atrium is located in the lower left. |
| Right Atrium | RA | The right atrium is located in the upper right part of the heart, on the right and anterior side of the left atrium. In the four-chamber view of transverse CT, the right atrium is located in the lower right. |
| Ascending Aorta | AA | The ascending aorta is connected to the left ventricle. In CT, the aorta is the largest cardiac blood vessel in the mediastinum and is presented in a circular structure in the transverse position. |
| Descending Aorta | DA | In CT, the descending aorta is located beside the spine and has a circular structure. |
| Pulmonary Artery | PA | The pulmonary artery starts from the bottom of the right ventricle. In the transverse CT, the left and right pulmonary arteries extend from the main pulmonary artery to both sides, presenting a tree structure. |
| Pulmonary Vein | PV | On the axial CT, the pulmonary veins extend to both sides, showing a ‘reptile‘ shape due to the small diameter. |
| Inferior Vena Cava | IVC | In the four-chamber view of transverse CT, the inferior vena cava is often located at the bottom of the heart and is closely related to the liver. |
| Superior Vena Cava | SVC | The superior vena cava is located on the right side of the ascending aorta in the transverse CT; its diameter is smaller than that of the ascending aorta. |
| Group | Coarse Segment Group | Fine Segment Group |
|---|---|---|
| 1 | LV RA AA DA SVC IVC | LA RV PV PA |
| 2 | LA LV RA RV | AA DA PA PV SVC IVC |
| 3 | LA LV PV AA DA | RA RV IVC SVC PA |
| Grouping | LA | RA | LV | RV | SVC | IVC | PA | PV | AA | DA |
|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | 0.884 | 0.846 | 0.806 | 0.851 | 0.0003 | 0.662 | 0.843 | 0.0003 | 0.892 | 0.875 |
| Group 2 | 0.853 | 0.851 | 0.879 | 0.868 | 0.641 | 0.520 | 0.808 | 0.362 | 0.856 | 0.862 |
| Group 3 | 0.823 | 0.837 | 0.818 | 0.832 | 0.0002 | 0.0005 | 0.788 | 0.275 | 0.871 | 0.870 |
| Substructures | DSC | Recall | Precision | HD/mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U-Net | Two -Staged | Proposed Method | U-Net | Two -Staged | Proposed Method | U-Net | Two -Staged | Proposed Method | U-Net | Two -Staged | Proposed Method | |
| LA | 0.809 | 0.853 | 0.853 | 0.779 | 0.840 | 0.840 | 0.847 | 0.850 | 0.850 | 0.355 | 0.301 | 0.301 |
| RA | 0.837 | 0.851 | 0.851 | 0.842 | 0.875 | 0.875 | 0.834 | 0.837 | 0.837 | 0.492 | 0.422 | 0.422 |
| LV | 0.878 | 0.879 | 0.879 | 0.870 | 0.871 | 0.871 | 0.887 | 0.889 | 0.889 | 0.352 | 0.367 | 0.367 |
| RV | 0.856 | 0.868 | 0.868 | 0.825 | 0.873 | 0.873 | 0.856 | 0.864 | 0.864 | 0.411 | 0.383 | 0.383 |
| SVC | 0.355 | 0.641 | 0.816 | 0.574 | 0.650 | 0.801 | 0.250 | 0.676 | 0.832 | 3.874 | 1.887 | 0.345 |
| IVC | 0.302 | 0.520 | 0.801 | 0.208 | 0.459 | 0.818 | 0.551 | 0.711 | 0.876 | 3.912 | 2.603 | 0.366 |
| PA | 0.804 | 0.808 | 0.902 | 0.764 | 0.767 | 0.909 | 0.854 | 0.864 | 0.895 | 0.548 | 0.554 | 0.284 |
| PV | 0.190 | 0.362 | 0.797 | 0.258 | 0.379 | 0.754 | 0.422 | 0.577 | 0.835 | 5.237 | 3.431 | 0.351 |
| AA | 0.850 | 0.856 | 0.928 | 0.823 | 0.817 | 0.903 | 0.884 | 0.930 | 0.954 | 0.479 | 0.392 | 0.213 |
| DA | 0.856 | 0.862 | 0.873 | 0.826 | 0.829 | 0.936 | 0.909 | 0.912 | 0.818 | 0.411 | 0.346 | 0.312 |
| Substructures | DSC | Recall | Precision | HD/mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D U-Net | nnU-Net | Proposed Method | 3D U-Net | nnU-Net | Proposed Method | 3D U-Net | nnU-Net | Proposed Method | 3D U-Net | nnU-Net | Proposed Method | |
| LA | 0.833 | 0.842 | 0.853 | 0.815 | 0.821 | 0.840 | 0.835 | 0.844 | 0.850 | 0.473 | 0.315 | 0.301 |
| RA | 0.820 | 0.817 | 0.851 | 0.821 | 0.832 | 0.875 | 0.817 | 0.827 | 0.837 | 0.513 | 0.521 | 0.422 |
| LV | 0.871 | 0.882 | 0.879 | 0.863 | 0.878 | 0.871 | 0.873 | 0.890 | 0.889 | 0.357 | 0.372 | 0.367 |
| RV | 0.792 | 0.831 | 0.868 | 0.791 | 0.829 | 0.873 | 0.784 | 0.829 | 0.864 | 0.589 | 0.551 | 0.383 |
| SVC | 0.712 | 0.780 | 0.816 | 0.722 | 0.750 | 0.970 | 0.723 | 0.776 | 0.832 | 0.602 | 0.574 | 0.345 |
| IVC | 0.568 | 0.782 | 0.801 | 0.584 | 0.774 | 0.801 | 0.591 | 0.791 | 0.876 | 2.801 | 0.574 | 0.366 |
| PA | 0.751 | 0.792 | 0.902 | 0.742 | 0.757 | 0.818 | 0.766 | 0.784 | 0.895 | 0.586 | 0.554 | 0.284 |
| PV | 0.527 | 0.546 | 0.797 | 0.526 | 0.535 | 0.909 | 0.521 | 0.577 | 0.835 | 3.152 | 3.431 | 0.351 |
| AA | 0.858 | 0.876 | 0.928 | 0.846 | 0.864 | 0.754 | 0.860 | 0.910 | 0.954 | 0.447 | 0.392 | 0.213 |
| DA | 0.802 | 0.839 | 0.873 | 0.809 | 0.821 | 0.903 | 0.813 | 0.827 | 0.818 | 0.351 | 0.346 | 0.312 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, X.; Du, R.; Zhong, Y.; Lu, Y.; Song, T. Anatomical Prior-Based Automatic Segmentation for Cardiac Substructures from Computed Tomography Images. Bioengineering 2023, 10, 1267. https://doi.org/10.3390/bioengineering10111267
Wang X, Li X, Du R, Zhong Y, Lu Y, Song T. Anatomical Prior-Based Automatic Segmentation for Cardiac Substructures from Computed Tomography Images. Bioengineering. 2023; 10(11):1267. https://doi.org/10.3390/bioengineering10111267
Chicago/Turabian StyleWang, Xuefang, Xinyi Li, Ruxu Du, Yong Zhong, Yao Lu, and Ting Song. 2023. "Anatomical Prior-Based Automatic Segmentation for Cardiac Substructures from Computed Tomography Images" Bioengineering 10, no. 11: 1267. https://doi.org/10.3390/bioengineering10111267
APA StyleWang, X., Li, X., Du, R., Zhong, Y., Lu, Y., & Song, T. (2023). Anatomical Prior-Based Automatic Segmentation for Cardiac Substructures from Computed Tomography Images. Bioengineering, 10(11), 1267. https://doi.org/10.3390/bioengineering10111267