Heart Murmur Classification Using a Capsule Neural Network
Abstract
:1. Introduction
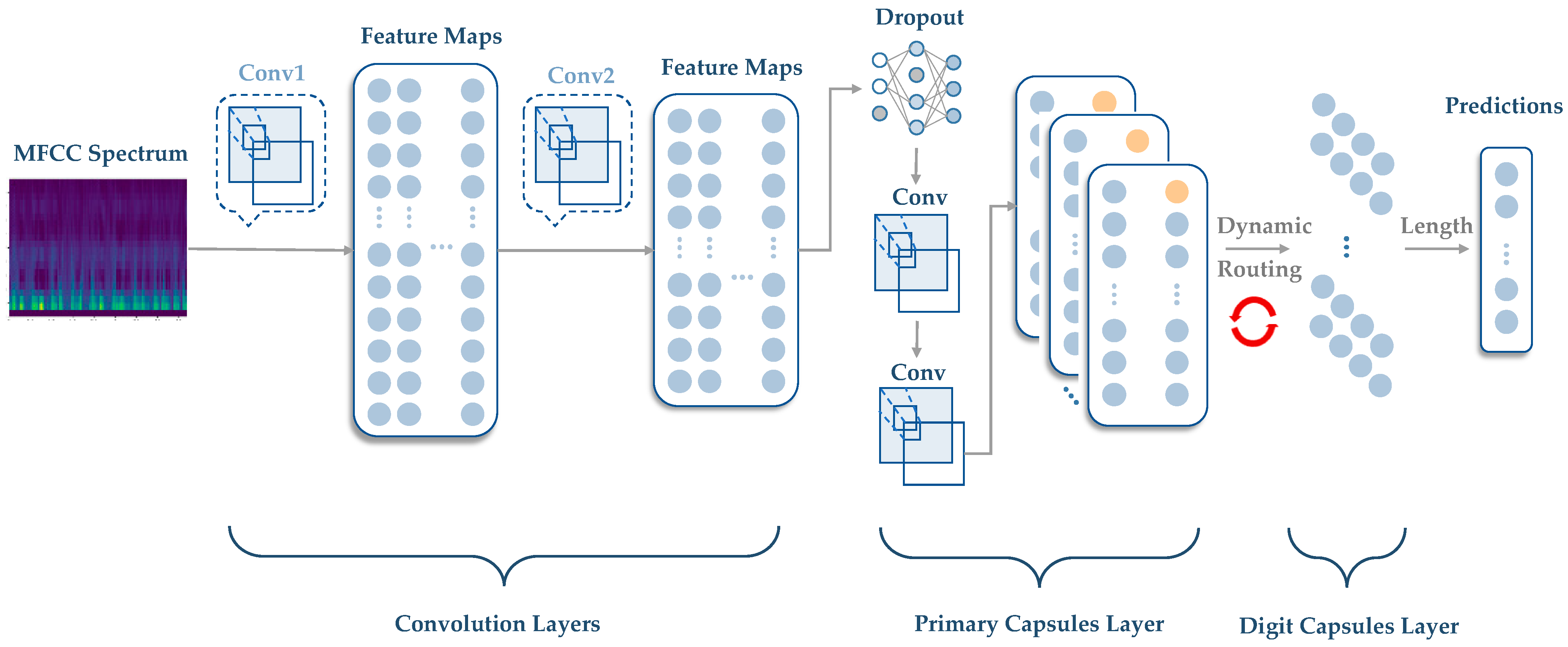
2. Methodological Description of CapsNet
2.1. Data Preprocessing
- (a)
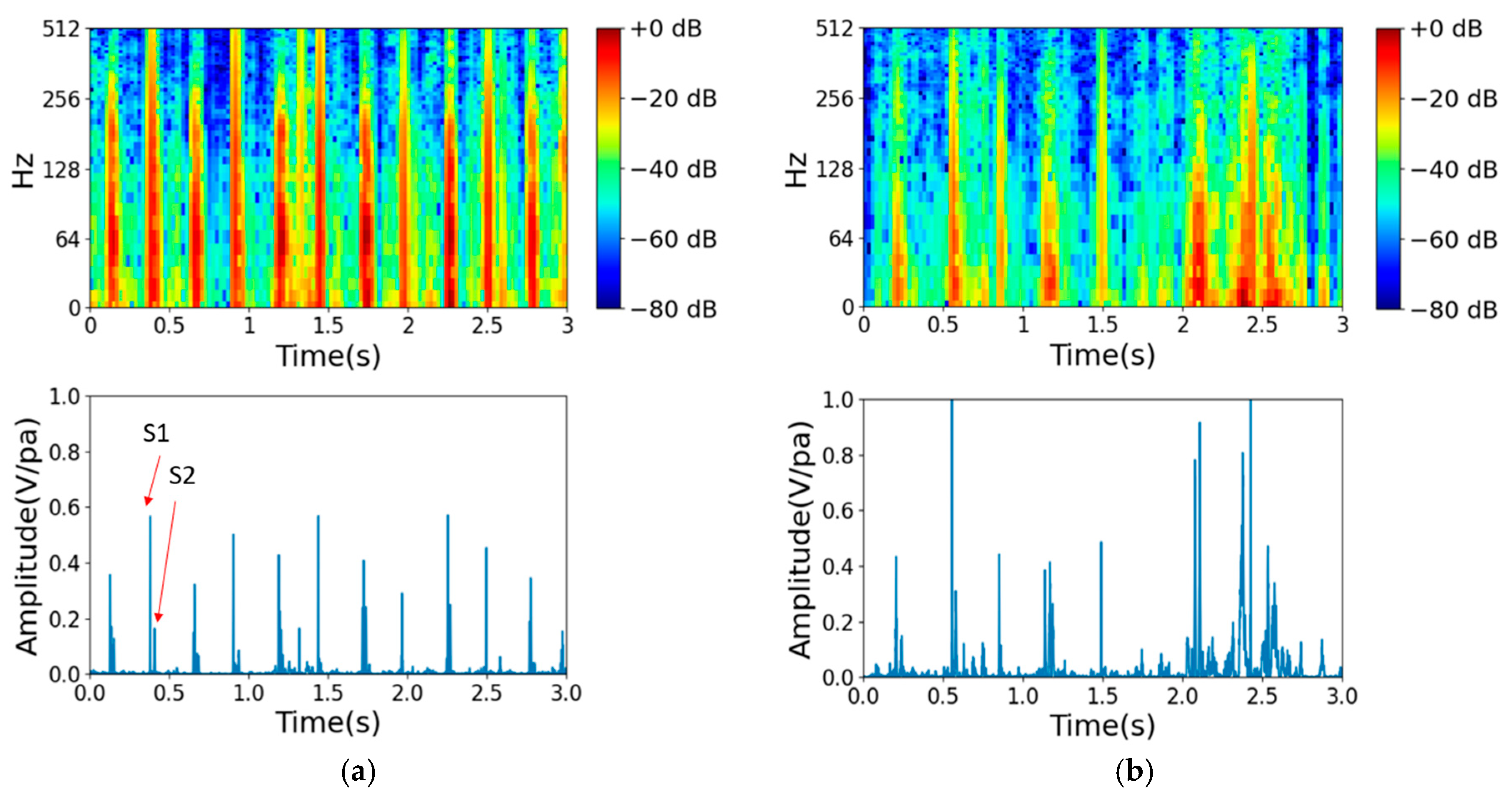
- Signal segmentation: Each segment typically corresponds to a fixed time duration in seconds. The default time duration of each segment is 5 s, which corresponds to 220.5 k samples at a sampling rate of 44.1 kHz.
- (b)
- Downsampling: Downsampling can be performed to decrease the computational load and storage requirements while preserving the essential information in the heart signal. Our downsampling rate was reduced from 44.1 kHz to 2 kHz, as in the 2016 PhysioNet heart sound database. With this downsampling rate, the integrity of heart sounds below 1 kHz is maintained.
- (c)
- Normalization: This step is the process of scaling the heart sound signal to a standard range between −1 and 1 to prevent clipping or distortion.
- (d)
- MFCC spectrum analysis: To extract features from the audio data, the mel-frequency cepstral coefficients (MFCCs) can be computed using a signal processing library such as librosa [30]. MFCCs capture important characteristics of audio signals, such as the spectral envelope and the spectral distribution of energy over time. The resulting MFCC spectrum can then be passed through the primary capsule layer of a CapsNet model to extract local features and encode them into capsule vectors. These capsule vectors can then be used to classify heart murmurs or other cardiac abnormalities. The CapsNet model offers the advantage of detecting multiple abnormalities simultaneously due to its ability to represent multiple features in a single capsule vector.
2.2. Methodology of CapsNet
- (a)
- Routing initialization: The output of the primary capsule layer is a set of capsule vectors , where is the number of capsules in the primary capsule layer.
- (b)
- Routing iteration: The routing algorithm iteratively updates the coupling coefficients based on the agreement between the capsule vectors and the output vectors of the higher layer capsules. The goal is to increase the coupling coefficients between capsules that are in agreement and decrease the coupling coefficients between capsules that are not in agreement.
3. Experiments and Results
3.1. 2016 PhysioNet Heart Sound Database
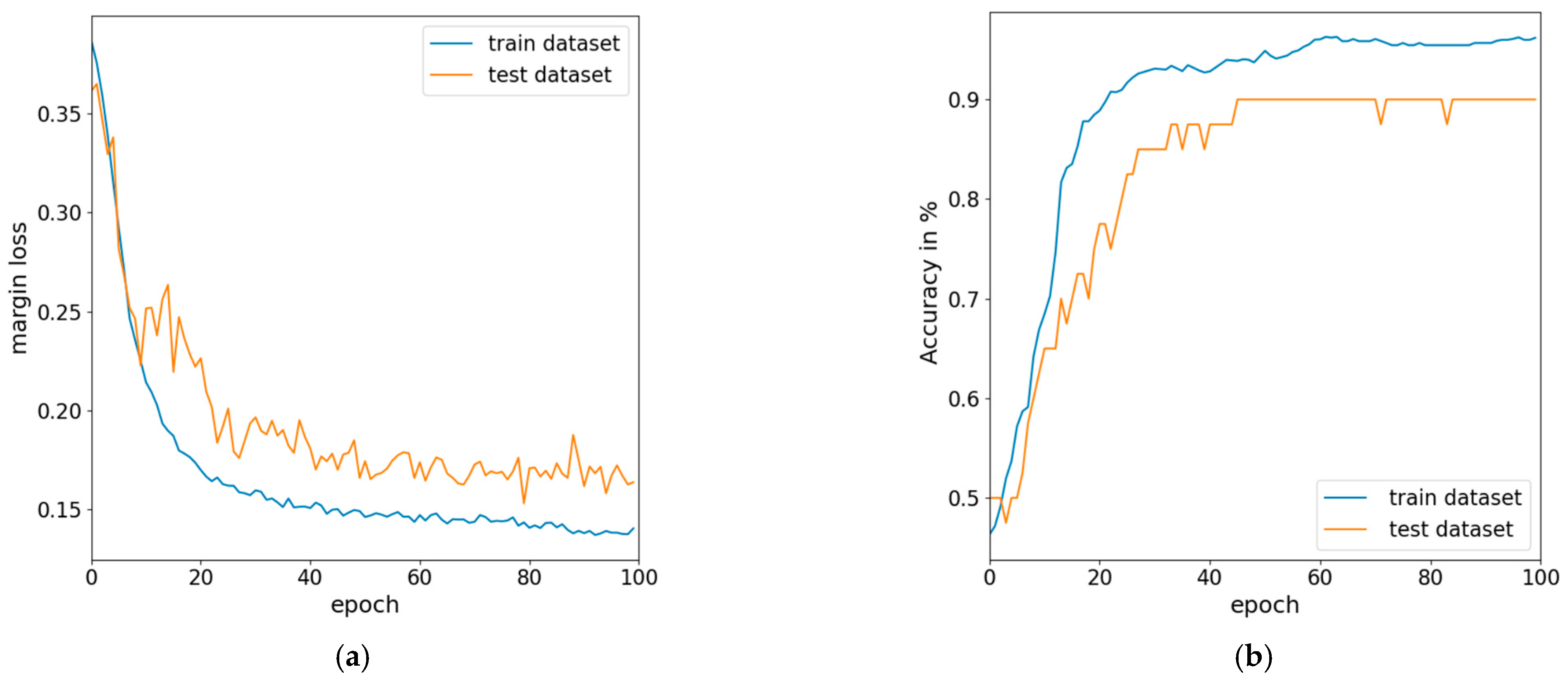
Training and Validation
3.2. Fine-Tuned Model and Testing with Further Data
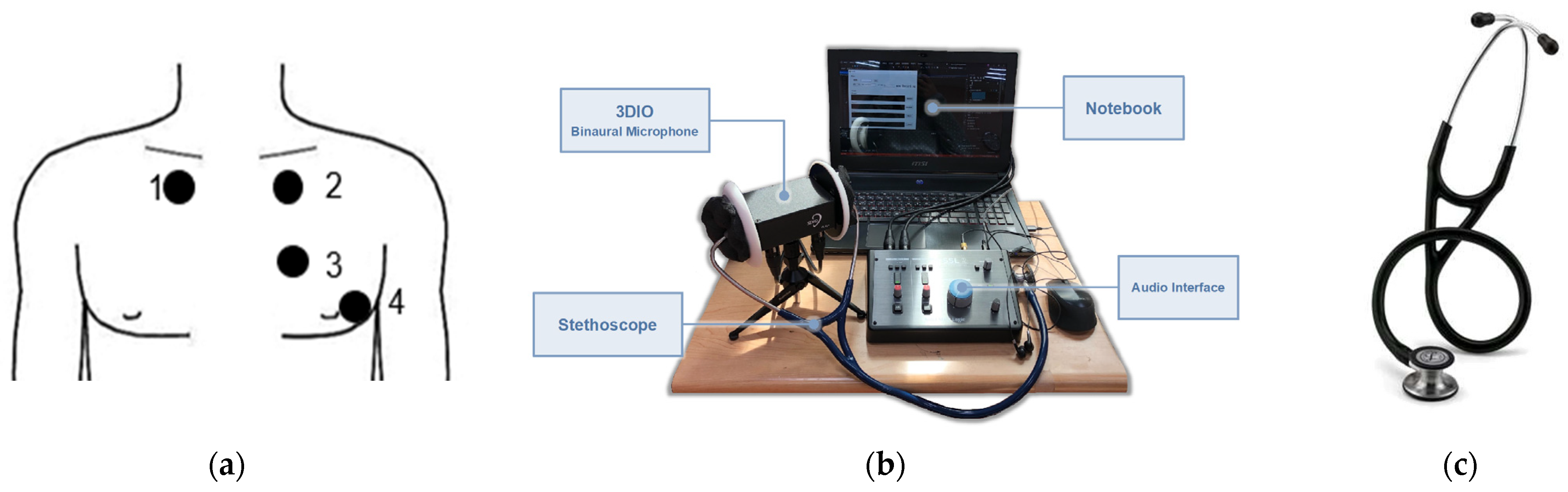
Hardware Setup and Signal Collection
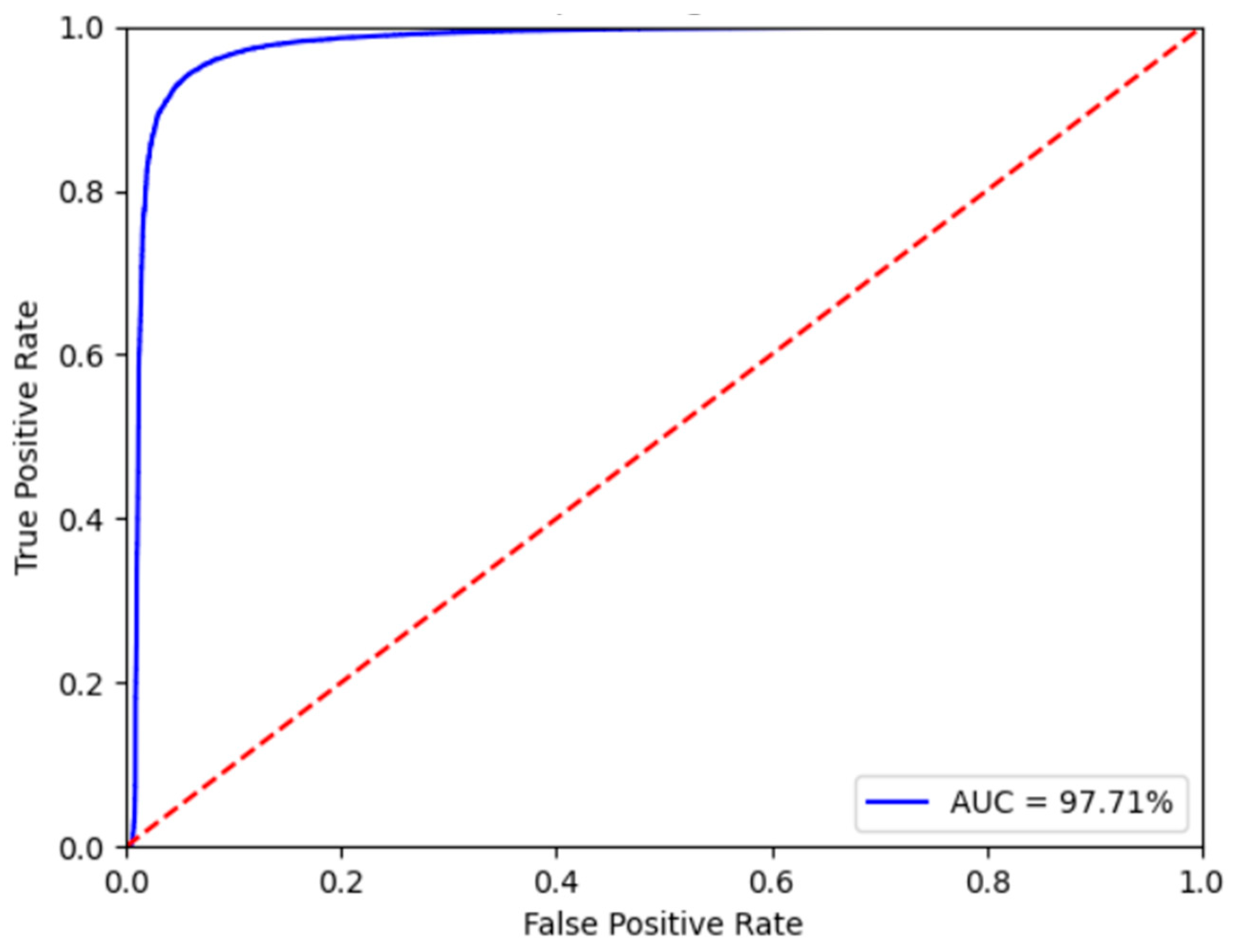
3.3. Fine-Tuned Model Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Latif, S.; Usman, M.; Rana, R.; Qadir, J. Phonocardiographic Sensing Using Deep Learning for Abnormal Heartbeat Detection. IEEE Sens. J. 2018, 18, 9393–9400. [Google Scholar] [CrossRef]
- Bhatikar, S.R.; DeGroff, C.; Mahajan, R.L. A classifier based on the artificial neural network approach for cardiologic auscultation in pediatrics. Artif. Intell. Med. 2005, 33, 251–260. [Google Scholar] [CrossRef]
- Liu, R.; Rong, Y.; Peng, Z. A review of medical artificial intelligence. Glob. Health J. 2020, 4, 42–45. [Google Scholar] [CrossRef]
- Benjamens, S.; Dhunnoo, P.; Mesko, B. The state of artificial intelligence-based FDA-approved medical devices and algorithms: An online database. NPJ Digit. Med. 2020, 3, 118. [Google Scholar] [CrossRef] [PubMed]
- Ramkumar, P.N.; Kunze, K.N.; Haeberle, H.S.; Karnuta, J.M.; Luu, B.C.; Nwachukwu, B.U.; Williams, R.J. Clinical and Research Medical Applications of Artificial Intelligence. Arthroscopy 2021, 37, 1694–1697. [Google Scholar] [CrossRef]
- Kumar, D.; Carvalho, P.; Antunes, M.; Paiva, R.P.; Henriques, J. Heart murmur classification with feature selection. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 4566–4569. [Google Scholar] [CrossRef]
- Vepa, J. Classification of heart murmurs using cepstral features and support vector machines. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 2539–2542. [Google Scholar] [CrossRef]
- Maglogiannis, I.; Loukis, E.; Zafiropoulos, E.; Stasis, A. Support Vectors Machine-based identification of heart valve diseases using heart sounds. Comput. Methods Programs Biomed. 2009, 95, 47–61. [Google Scholar] [CrossRef]
- Huang, P.K.; Yang, M.C.; Wang, Z.X.; Huang, Y.J.; Lin, W.C.; Pan, C.L.; Guo, M.H. Augmented detection of septal defects using advanced optical coherence tomography network-processed phonocardiogram. Front. Cardiovasc. Med. 2022, 9, 1041082. [Google Scholar] [CrossRef]
- Shekhar, R.; Vanama, G.; John, T.; Issac, J.; Arjoune, Y.; Doroshow, R.W. Automated identification of innocent Still’s murmur using a convolutional neural network. Front. Pediatr. 2022, 10, 923956. [Google Scholar] [CrossRef]
- Lu, P.; Guo, S.; Zhang, H.; Li, Q.; Wang, Y.; Wang, Y.; Qi, L. Research on Improved Depth Belief Network-Based Prediction of Cardiovascular Diseases. J. Healthc. Eng. 2018, 2018, 8954878. [Google Scholar] [CrossRef]
- Brunese, L.; Martinelli, F.; Mercaldo, F.; Santone, A. Deep learning for heart disease detection through cardiac sounds. Procedia Comput. Sci. 2020, 176, 2202–2211. [Google Scholar] [CrossRef]
- Centeno-Bautista, M.A.; Rangel-Rodriguez, A.H.; Perez-Sanchez, A.V.; Amezquita-Sanchez, J.P.; Granados-Lieberman, D.; Valtierra-Rodriguez, M. Electrocardiogram Analysis by Means of Empirical Mode Decomposition-Based Methods and Convolutional Neural Networks for Sudden Cardiac Death Detection. Appl. Sci. 2023, 13, 3569. [Google Scholar] [CrossRef]
- Rajpurkar, P.H.; Awni, Y.; Haghpanahi, M.; Bourn, C.; Ng, A.Y. Cardiologist-Level Arrhythmia Detection with Convolutional Neural Networks. arXiv 2017, arXiv:1707.01836. [Google Scholar] [CrossRef]
- Li, F.; Tang, H.; Shang, S.; Mathiak, K.; Cong, F. Classification of Heart Sounds Using Convolutional Neural Network. Appl. Sci. 2020, 10, 3956. [Google Scholar] [CrossRef]
- Choi, S.; Jiang, Z. Cardiac sound murmurs classification with autoregressive spectral analysis and multi-support vector machine technique. Comput. Biol. Med. 2010, 40, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ning, D.; Feng, S. A Novel Capsule Network Based on Wide Convolution and Multi-Scale Convolution for Fault Diagnosis. Appl. Sci. 2020, 10, 3659. [Google Scholar] [CrossRef]
- Yildirim, O. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Meintjes, A.; Lowe, A.; Legget, M. Fundamental Heart Sound Classification using the Continuous Wavelet Transform and Convolutional Neural Networks. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 409–412. [Google Scholar] [CrossRef]
- Liu, C.; Springer, D.; Li, Q.; Moody, B.; Juan, R.A.; Chorro, F.J.; Castells, F.; Roig, J.M.; Silva, I.; Johnson, A.E.W.; et al. An open access database for the evaluation of heart sound algorithms. Physiol. Meas. 2016, 37, 2181–2213. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef]
- Hinton, G.; Sabour, S.; Frosst, N. Matrix Capsules with Emrouting. In Proceedings of the ICLR2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Chen, T.Y.; Wang, Z.H.; Yang, X.; Jiang, K. A deep capsule neural network with stochastic delta rule for bearing fault diagnosis on raw vibration signals. Measurement 2019, 148, 106857. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, G.; Scherer, R.; Wei, W.; Woźniak, M. Overview of Capsule Neural Networks. J. Internet Technol. 2022, 23, 33–44. [Google Scholar]
- Zhang, W.; Tang, P.; Zhao, L. Remote sensing image scene classification using CNN-CapsNet. Remote Sens. 2019, 11, 494. [Google Scholar] [CrossRef]
- Lei, Y.; Wu, Z.; Li, Z.; Yang, Y.; Liang, Z. BP-CapsNet: An image-based Deep Learning method for medical diagnosis. Appl. Soft Comput. 2023, 146, 110683. [Google Scholar] [CrossRef]
- Butun, E.; Yildirim, O.; Talo, M.; Tan, R.S.; Rajendra Acharya, U. 1D-CADCapsNet: One dimensional deep capsule networks for coronary artery disease detection using ECG signals. Phys. Med. 2020, 70, 39–48. [Google Scholar] [CrossRef] [PubMed]
- El Boujnouni, I.; Harouchi, B.; Tali, A.; Rachafi, S.; Laaziz, Y. Automatic diagnosis of cardiovascular diseases using wavelet feature extraction and convolutional capsule network. Biomed. Signal Process. Control 2023, 81, 104497. [Google Scholar] [CrossRef]
- Freitas, N.R.; Vieira, P.M.; Cordeiro, A.; Tinoco, C.; Morais, N.; Torres, J.; Anacleto, S.; Laguna, M.P.; Lima, E.; Lima, C.S. Detection of bladder cancer with feature fusion, transfer learning and CapsNets. Artif. Intell. Med. 2022, 126, 102275. [Google Scholar] [CrossRef]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.W.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and music signal analysis in python. In Proceedings of the 14th Python in Science Conference, Austin, TX, USA, 6–12 July 2015; pp. 18–25. [Google Scholar]
- Heaton, J. Ian Goodfellow, Yoshua Bengio, Aaron Courville: Deep learning. Genet. Program. Evolvable Mach. 2017, 19, 305–307. [Google Scholar] [CrossRef]
- 3DIO Sound. 3DIO Free Space Binaural Microphone. Available online: https://3diosound.com/products/free-space-binaural-microphone (accessed on 1 October 2023).
- Keras. ReduceLROnPlateau Class. Available online: https://keras.io/api/callbacks/reduce_lr_on_plateau/ (accessed on 6 December 2022).


| Layer (Type) | Output Shape | Trainable Params |
|---|---|---|
| input_1 (InputLayer) | (None, 128, 16, 1) | 0 |
| conv1 (Conv2D) | (None, 60, 4, 256) | 20,992 |
| primarycap_conv2d (Conv2D) | (None, 57, 1, 256) | 1,048,832 |
| primarycap_reshape (Reshape) | (None, 912, 16) | 0 |
| primarycap_squash (Dynamic routing repeated five times) | (None, 912, 16) | 0 |
| digitcaps (CapsuleLayer) | (None, 2, 16) | 466,944 |
| Capsnet_Output (OutputLayer) | (None, 2) | 0 |
| mask (Mask) | (None, None) | 0 |
| capsnet (Length) | (None, 2) | 0 |
| decoder (Sequential) | (None, 128, 16, 1) | 6,329,344 |
| Total trainable params: | 7,866,112 | |
| Learning_Rate | Epochs | Routings |
|---|---|---|
| 0.0025 | 100 | 5 |
| Normal | Abnormal | ||
|---|---|---|---|
| Normal | 2507 (TP) | 41 (FP) | 98.39% Precision: TP/(TP + FP) |
| Abnormal | 447 (FN) | 2029 (TN) | 81.95% (TN/(TN + FN)) |
| 84.87% Recall: TP/(TP + FN) | 98.02% (TN/(TN + FP)) | 90.29% Accuracy: (TP + TN)/Total |
| Training Accuracy | Validation Accuracy | Training Time (h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | Accuracy | |
| CapsNet | 97.58% | 95.96% | 96.77% | 96.79% | 98.39% | 84.87% | 91.13% | 90.29% | 15.7 |
| AlexNet | 94.10% | 93.74% | 93.73% | 93.74% | 75.14% | 73.74% | 73.49% | 73.91% | 18.9 |
| VGG19 | 98.29% | 98.28% | 98.28% | 98.28% | 77.81% | 76.88% | 76.78% | 77.01% | 24.3 |
| GoogLeNet | 98.56% | 97.12% | 97.83% | 97.82% | 75.12% | 74.23% | 74.01% | 74.82% | 15.1 |
| ResNet50 | 98.95% | 98.92% | 98.95% | 98.95% | 83.91% | 76.31% | 74.91% | 76.31% | 84.3 |
| 3DIO Binaural Microphone Equipment Standard | |
|---|---|
| Frequency response range | 60 Hz–20 kHz |
| Sensitivity | −28 ± 3 dBV/Pa @ 1 kHz RI = 3.9 KHz Vcc = 5 V |
| Signal-to-noise ratio | 80 dB @ 1 kHz |
| Output impedance | 2.4 kΩ ± 30% @ 1 kHz |
| Operating voltage | 2.4 kΩ ± 30% @ 1 kHz |
| Mic diameter | 10 mm |
| Layer | Filter | Kernel Size | Strides | Batch Size | |
|---|---|---|---|---|---|
| 10 s | Conv1 | 256 | 9 | 2 | 8 |
| primarycap_conv2d | 16 | 4 | 2 | ||
| 5 s | Conv1 | 256 | 9 | 2 | 8 |
| primarycap_conv2d | 16 | 4 | 1 | ||
| 3 s | Conv1 | 128 | 7 | 1 | 16 |
| primarycap_conv2d | 8 | 4 | 1 | ||
| 1 s | Conv1 | 224 | 3 | 1 | 32 |
| primarycap_conv2d | 32 | 2 | 1 | ||
| Segmentation Length | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|
| 10 s | 100% | 72.72% | 84.21% | 81.25% |
| 5 s | 90.48% | 92.68% | 91.57% | 91.67% |
| 3 s | 75.98% | 82.88% | 79.28% | 79.26% |
| 1 s | 71.39% | 77.56% | 74.35% | 74.24% |
| Initial Value | Decay | Unimproved Times | Training Accuracy | Test Accuracy | |
|---|---|---|---|---|---|
| Reduce learning rate (ReduceLROnPlateau [33]) | 0.0025 | 0.15 | 3 | 93.93% | 91.67% |
| Learning rate decay | 0.005 | 0.1 | - | 92.14% | 87.50% |
| Fixed learning rate | 0.0025 | - | - | 92.20% | 79.17% |
| Training Accuracy | Test Accuracy | Training Time (h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | Accuracy | |
| CapsNet | 94.95% | 92.89% | 93.91% | 93.93% | 90.48% | 92.68% | 91.57% | 91.67% | 5.2 |
| AlexNet | 97.59% | 97.52% | 97.55% | 97.56% | 69.77% | 73.17% | 71.43% | 71.43% | 6.8 |
| VGG19 | 93.94% | 90.56% | 92.23% | 92.13% | 77.78% | 81.40% | 79.54% | 78.57% | 13.4 |
| GoogLeNet | 92.93% | 90.82% | 91.86% | 91.85% | 80.00% | 76.19% | 78.05% | 78.57% | 5.1 |
| ResNet50 | 90.54% | 89.36% | 89.28% | 89.36% | 7812% | 75.00% | 74.29% | 75.00% | 15.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, Y.-T.; Liu, Y.-H.; Zheng, Z.-W.; Chen, C.-C.; Lin, M.-C. Heart Murmur Classification Using a Capsule Neural Network. Bioengineering 2023, 10, 1237. https://doi.org/10.3390/bioengineering10111237
Tsai Y-T, Liu Y-H, Zheng Z-W, Chen C-C, Lin M-C. Heart Murmur Classification Using a Capsule Neural Network. Bioengineering. 2023; 10(11):1237. https://doi.org/10.3390/bioengineering10111237
Chicago/Turabian StyleTsai, Yu-Ting, Yu-Hsuan Liu, Zi-Wei Zheng, Chih-Cheng Chen, and Ming-Chih Lin. 2023. "Heart Murmur Classification Using a Capsule Neural Network" Bioengineering 10, no. 11: 1237. https://doi.org/10.3390/bioengineering10111237
APA StyleTsai, Y.-T., Liu, Y.-H., Zheng, Z.-W., Chen, C.-C., & Lin, M.-C. (2023). Heart Murmur Classification Using a Capsule Neural Network. Bioengineering, 10(11), 1237. https://doi.org/10.3390/bioengineering10111237








