Organoid Cultures In Silico: Tools or Toys?
Abstract
1. Introduction
2. COMs of Organoid Formation
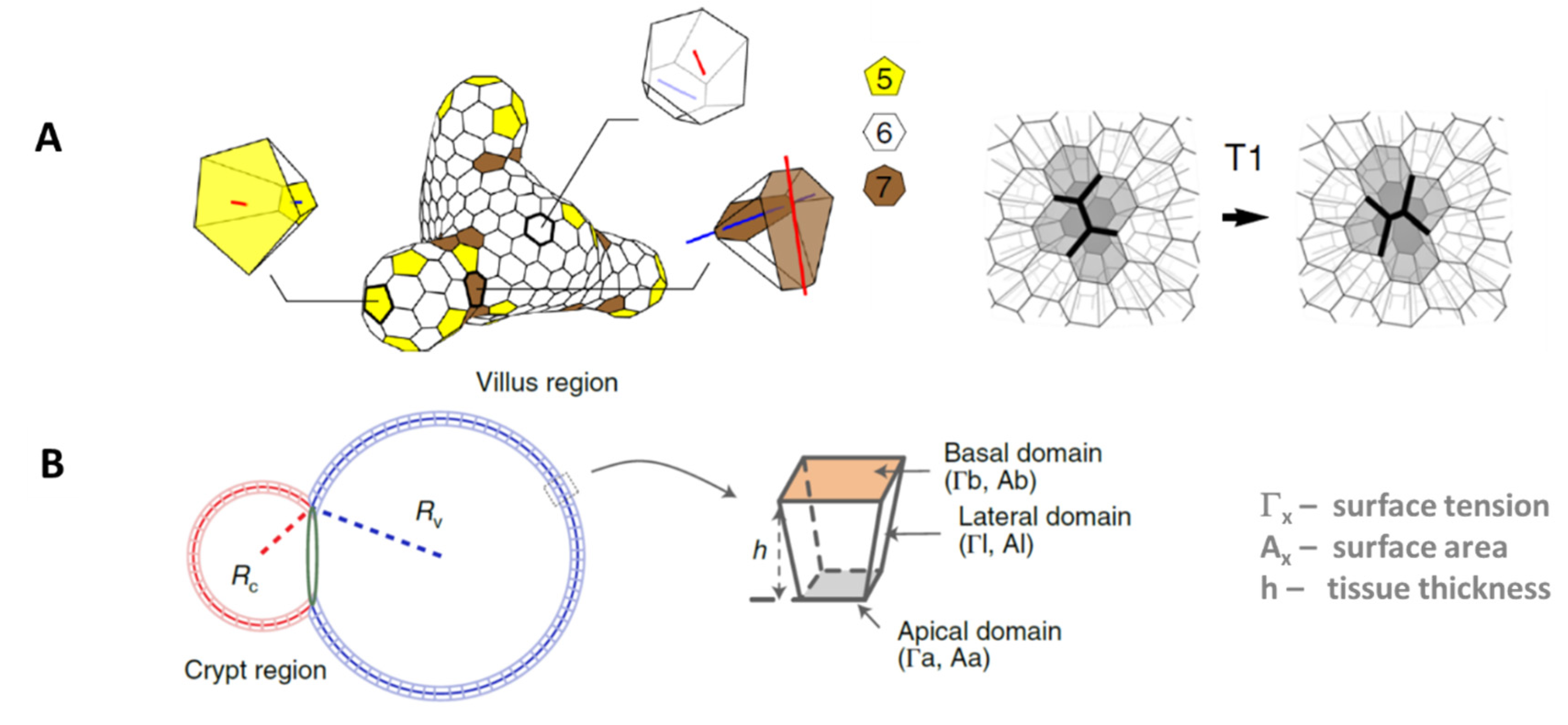
3. Optimizing Organoid Culture
4. Steps towards In Silico Disease and Therapy Modelling
5. Summary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Corrò, C.; Novellasdemunt, L.; Li, V.S.W. A brief history of organoids. Am. J. Physiol. Cell Physiol. 2020, 319, C151–C165. [Google Scholar] [CrossRef] [PubMed]
- Eiraku, M.; Watanabe, K.; Matsuo-Takasaki, M.; Kawada, M.; Yonemura, S.; Matsumura, M.; Wataya, T.; Nishiyama, A.; Muguruma, K.; Sasai, Y. Self-organized formation of polarized cortical tissues from ESCs and its active manipulation by extrinsic signals. Cell Stem Cell 2008, 3, 519–532. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Vries, R.G.; Snippert, H.J.; van de Wetering, M.; Barker, N.; Stange, D.E.; van Es, J.H.; Abo, A.; Kujala, P.; Peters, P.J.; et al. Single Lgr5 stem cells build crypt-villus structures in vitro without a mesenchymal niche. Nature 2009, 459, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Heydari, Z.; Moeinvaziri, F.; Agarwal, T.; Pooyan, P.; Shpichka, A.; Maiti, T.K.; Timashev, P.; Baharvand, H.; Vosough, M. Organoids: A novel modality in disease modeling. Biodes Manuf. 2021, 4, 689–716. [Google Scholar] [CrossRef] [PubMed]
- Bock, C.; Boutros, M.; Camp, J.G.; Clarke, L.; Clevers, H.; Knoblich, J.A.; Liberali, P.; Regev, A.; Rios, A.C.; Stegle, O.; et al. Human Cell Atlas ‘Biological Network’ Organoids. The Organoid Cell Atlas. Nat. Biotechnol. 2021, 39, 13–17. [Google Scholar] [CrossRef] [PubMed]
- van den Brink, S.C.; van Oudenaarden, A. 3D gastruloids: A novel frontier in stem cell-based in vitro modeling of mammalian gastrulation. Trends Cell Biol. 2021, 31, 747–759. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Kim, T.H. Recent Advances in Multicellular Tumor Spheroid Generation for Drug Screening. Biosensors 2021, 11, 445. [Google Scholar] [CrossRef]
- Montes-Olivas, S.; Marucci, L.; Homer, M. Mathematical Models of Organoid Cultures. Front. Genet. 2019, 10, 873. [Google Scholar] [CrossRef]
- Norfleet, D.; Park, E.; Kemp, M. Computational Modeling of Organoid Development. Curr. Opin. Biomed. Eng. 2020, 13, 113–118. [Google Scholar] [CrossRef]
- Yan, H.; Konstorum, A.; Lowengrub, J.S. Three-Dimensional Spatiotemporal Modeling of Colon Cancer Organoids Reveals that Multimodal Control of Stem Cell Self-Renewal is a Critical Determinant of Size and Shape in Early Stages of Tumor Growth. Bull. Math. Biol. 2018, 80, 1404–1433. [Google Scholar] [CrossRef]
- Thalheim, T.; Quaas, M.; Herberg, M.; Braumann, U.D.; Kerner, C.; Loeffler, M.; Aust, G.; Galle, J. Linking stem cell function and growth pattern of intestinal organoids. Dev. Biol. 2018, 433, 254–261. [Google Scholar] [CrossRef] [PubMed]
- Okuda, S.; Takata, N.; Hasegawa, Y.; Kawada, M.; Inoue, Y.; Adachi, T.; Sasai, Y.; Eiraku, M. Strain-triggered mechanical feedback in self-organizing optic-cup morphogenesis. Sci. Adv. 2018, 4, eaau1354. [Google Scholar] [CrossRef]
- Kang, W.; Ferruzzi, J.; Spatarelu, C.P.; Han, Y.L.; Sharma, Y.; Koehler, S.A.; Mitchel, J.A.; Khan, A.; Butler, J.P.; Roblyer, D.; et al. A novel jamming phase diagram links tumor invasion to non-equilibrium phase separation. iScience 2021, 24, 103252. [Google Scholar] [CrossRef]
- Štorgel, N.; Krajnc, M.; Mrak, P.; Štrus, J.; Ziherl, P. Quantitative Morphology of Epithelial Folds. Biophys. J. 2016, 110, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Langlands, A.J.; Almet, A.A.; Appleton, P.L.; Newton, I.P.; Osborne, J.M.; Näthke, I.S. Paneth Cell-Rich Regions Separated by a Cluster of Lgr5+ Cells Initiate Crypt Fission in the Intestinal Stem Cell Niche. PLoS Biol. 2016, 14, e1002491. [Google Scholar] [CrossRef] [PubMed]
- Pin, C.; Watson, A.J.; Carding, S.R. Modelling the spatio-temporal cell dynamics reveals novel insights on cell differentiation and proliferation in the small intestinal crypt. PLoS ONE 2012, 7, e37115. [Google Scholar] [CrossRef] [PubMed]
- Buske, P.; Galle, J.; Barker, N.; Aust, G.; Clevers, H.; Loeffler, M. A comprehensive model of the spatio-temporal stem cell and tissue organisation in the intestinal crypt. PLoS Comput. Biol. 2011, 7, e1001045. [Google Scholar] [CrossRef] [PubMed]
- McMurtrey, R.J. Analytic Models of Oxygen and Nutrient Diffusion, Metabolism Dynamics, and Architecture Optimization in Three-Dimensional Tissue Constructs with Applications and Insights in Cerebral Organoids. Tissue Eng. Part C Methods 2016, 22, 221–249. [Google Scholar] [CrossRef] [PubMed]
- Leedale, J.A.; Kyffin, J.A.; Harding, A.L.; Colley, H.E.; Murdoch, C.; Sharma, P.; Williams, D.P.; Webb, S.D.; Bearon, R.N. Multiscale modelling of drug transport and metabolism in liver spheroids. Interface Focus 2020, 10, 20190041. [Google Scholar] [CrossRef] [PubMed]
- Buske, P.; Przybilla, J.; Loeffler, M.; Sachs, N.; Sato, T.; Clevers, H.; Galle, J. On the biomechanics of stem cell niche formation in the gut--modelling growing organoids. FEBS J. 2012, 279, 3475–3487. [Google Scholar] [CrossRef]
- Pin, C.; Parker, A.; Gunning, A.P.; Ohta, Y.; Johnson, I.T.; Carding, S.R.; Sato, T. An individual based computational model of intestinal crypt fission and its application to predicting unrestrictive growth of the intestinal epithelium. Integr. Biol. 2015, 7, 213–228. [Google Scholar] [CrossRef] [PubMed]
- Almet, A.A.; Hughes, B.D.; Landman, K.A.; Näthke, I.S.; Osborne, J.M. A Multicellular Model of Intestinal Crypt Buckling and Fission. Bull. Math. Biol. 2018, 80, 335–359. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Vashishta, M.; Kong, L.; Wu, X.; Lu, J.J.; Guha, C.; Dwarakanath, B.S. The Role of Notch, Hedgehog, and Wnt Signaling Pathways in the Resistance of Tumors to Anticancer Therapies. Front. Cell Dev. Biol. 2021, 9, 650772. [Google Scholar] [CrossRef]
- Sachs, N.; Papaspyropoulos, A.; Zomer-van Ommen, D.D.; Heo, I.; Böttinger, L.; Klay, D.; Weeber, F.; Huelsz-Prince, G.; Iakobachvili, N.; Amatngalim, G.D.; et al. Long-term expanding human airway organoids for disease modeling. EMBO J. 2019, 38, e100300. [Google Scholar] [CrossRef] [PubMed]
- Hof, L.; Moreth, T.; Koch, M.; Liebisch, T.; Kurtz, M.; Tarnick, J.; Lissek, S.M.; Verstegen, M.M.A.; van der Laan, L.J.W.; Huch, M.; et al. Long-term live imaging and multiscale analysis identify heterogeneity and core principles of epithelial organoid morphogenesis. BMC Biol. 2021, 19, 37. [Google Scholar] [CrossRef]
- Okuda, S.; Inoue, Y.; Adachi, T. Three-dimensional vertex model for simulating multicellular morphogenesis. Biophys. Physicobiol. 2015, 12, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Rozman, J.; Krajnc, M.; Ziherl, P. Collective cell mechanics of epithelial shells with organoid-like morphologies. Nat. Commun. 2020, 11, 3805. [Google Scholar] [CrossRef] [PubMed]
- Mammoto, A.; Ingber, D.E. Cytoskeletal control of growth and cell fate switching. Curr. Opin. Cell Biol. 2009, 21, 864–870. [Google Scholar] [CrossRef]
- Pérez-González, C.; Ceada, G.; Greco, F.; Matejčić, M.; Gómez-González, M.; Castro, N.; Menendez, A.; Kale, S.; Krndija, D.; Clark, A.G.; et al. Mechanical compartmentalization of the intestinal organoid enables crypt folding and collective cell migration. Nat. Cell Biol. 2021, 23, 745–757. [Google Scholar] [CrossRef]
- Tallapragada, N.P.; Cambra, H.M.; Wald, T.; Keough Jalbert, S.; Abraham, D.M.; Klein, O.D.; Klein, A.M. Inflation-collapse dynamics drive patterning and morphogenesis in intestinal organoids. Cell Stem Cell 2021, 28, 1516–1532.e14. [Google Scholar] [CrossRef]
- Yang, Q.; Xue, S.L.; Chan, C.J.; Rempfler, M.; Vischi, D.; Maurer-Gutierrez, F.; Hiiragi, T.; Hannezo, E.; Liberali, P. Cell fate coordinates mechano-osmotic forces in intestinal crypt formation. Nat. Cell Biol. 2021, 23, 733–744. [Google Scholar] [CrossRef] [PubMed]
- Rosenbluth, J.M.; Schackmann, R.C.J.; Gray, G.K.; Selfors, L.M.; Li, C.M.; Boedicker, M.; Kuiken, H.J.; Richardson, A.; Brock, J.; Garber, J.; et al. Organoid cultures from normal and cancer-prone human breast tissues preserve complex epithelial lineages. Nat. Commun. 2020, 11, 1711. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.J.; Kim, D.; Tak, K.Y.; Hwang, S.; Kim, J.; Sim, N.S.; Cho, J.M.; Choi, D.; Ji, Y.; Hur, J.K.; et al. Salivary gland organoid culture maintains distinct glandular properties of murine and human major salivary glands. Nat. Commun. 2022, 13, 3291. [Google Scholar] [CrossRef]
- Drasdo, D.; Höhme, S. A single-cell-based model of tumor growth in vitro: Monolayers and spheroids. Phys. Biol. 2005, 2, 133–147. [Google Scholar] [CrossRef]
- O’Dea, R.D.; Byrne, H.M.; Waters, S.L. Continuum modelling of in vitro tissue engineering: A review. In Computational Modeling in Tissue Engineering; Geris, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 229–266. [Google Scholar]
- Ellis, M.A.; Dalwadi, M.P.; Ellis, M.J.; Byrne, H.M.; Waters, S.L. A Systematically Reduced Mathematical Model for Organoid Expansion. Front. Bioeng. Biotechnol. 2021, 9, 670186. [Google Scholar] [CrossRef] [PubMed]
- Berger, E.; Magliaro, C.; Paczia, N.; Monzel, A.S.; Antony, P.; Linster, C.L.; Bolognin, S.; Ahluwalia, A.; Schwamborn, J.C. Millifluidic culture improves human midbrain organoid vitality and differentiation. Lab Chip 2018, 18, 3172–3183. [Google Scholar] [CrossRef]
- Thalheim, T.; Siebert, S.; Quaas, M.; Herberg, M.; Schweiger, M.R.; Aust, G.; Galle, J. Epigenetic Drifts during Long-Term Intestinal Organoid Culture. Cells 2021, 10, 1718. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Farin, H.F.; van Es, J.H.; Clevers, H.; Langer, R.; Karp, J.M. Niche-independent high-purity cultures of Lgr5+ intestinal stem cells and their progeny. Nat. Methods 2014, 11, 106–112. [Google Scholar] [CrossRef]
- Shin, W.; Wu, A.; Min, S.; Shin, Y.C.; Fleming, R.Y.D.; Eckhardt, S.G.; Kim, H.J. Spatiotemporal Gradient and Instability of Wnt Induce Heterogeneous Growth and Differentiation of Human Intestinal Organoids. iScience 2020, 23, 101372. [Google Scholar] [CrossRef]
- Nikolaev, M.; Mitrofanova, O.; Broguiere, N.; Geraldo, S.; Dutta, D.; Tabata, Y.; Elci, B.; Brandenberg, N.; Kolotuev, I.; Gjorevski, N.; et al. Homeostatic mini-intestines through scaffold-guided organoid morphogenesis. Nature 2020, 585, 574–578. [Google Scholar] [CrossRef]
- Kozlowski, M.T.; Crook, C.J.; Ku, H.T. Towards organoid culture without Matrigel. Commun. Biol. 2021, 4, 1387. [Google Scholar] [CrossRef] [PubMed]
- Eichinger, J.F.; Grill, M.J.; Kermani, I.D.; Aydin, R.C.; Wall, W.A.; Humphrey, J.D.; Cyron, C.J. A computational framework for modeling cell-matrix interactions in soft biological tissues. Biomech. Model. Mechanobiol. 2021, 20, 1851–1870. [Google Scholar] [CrossRef]
- Xu, H.; Jiao, Y.; Qin, S.; Zhao, W.; Chu, Q.; Wu, K. Organoid technology in disease modelling, drug development, personalized treatment and regeneration medicine. Exp. Hematol. Oncol. 2018, 7, 30. [Google Scholar] [CrossRef] [PubMed]
- Drost, J.; Clevers, H. Organoids in cancer research. Nat. Rev. Cancer 2018, 18, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Zhu, J.; Jiang, M.; Sang, L.; Hao, K.; He, H. The Combination of Cell Cultured Technology and In Silico Model to Inform the Drug Development. Pharmaceutics 2021, 13, 704. [Google Scholar] [CrossRef] [PubMed]
- Gritti, N.; Lim, J.L.; Anlaş, K.; Pandya, M.; Aalderink, G.; Martínez-Ara, G.; Trivedi, V. MOrgAna: Accessible quantitative analysis of organoids with machine learning. Development 2021, 148, dev199611. [Google Scholar] [CrossRef] [PubMed]
- Mergenthaler, P.; Hariharan, S.; Pemberton, J.M.; Lourenco, C.; Penn, L.Z.; Andrews, D.W. Rapid 3D phenotypic analysis of neurons and organoids using data-driven cell segmentation-free machine learning. PLoS Comput. Biol. 2021, 17, e1008630. [Google Scholar] [CrossRef]
- Karolak, A.; Poonja, S.; Rejniak, K.A. Morphophenotypic classification of tumor organoids as an indicator of drug exposure and penetration potential. PLoS Comput. Biol. 2019, 15, e1007214. [Google Scholar] [CrossRef]
- Bues, J.; Biočanin, M.; Pezoldt, J.; Dainese, R.; Chrisnandy, A.; Rezakhani, S.; Saelens, W.; Gardeux, V.; Gupta, R.; Sarkis, R.; et al. Deterministic scRNA-seq captures variation in intestinal crypt and organoid composition. Nat. Methods 2022, 19, 323–330. [Google Scholar] [CrossRef]
- Herring, C.A.; Simmons, R.K.; Freytag, S.; Poppe, D.; Moffet, J.J.D.; Pflueger, J.; Buckberry, S.; Vargas-Landin, D.B.; Clément, O.; Echeverría, E.G.; et al. Human prefrontal cortex gene regulatory dynamics from gestation to adulthood at single-cell resolution. Cell 2022, 185, 4428–4447.e28. [Google Scholar] [CrossRef]
- Kueh, H.Y.; Champhekar, A.; Nutt, S.L.; Elowitz, M.B.; Rothenberg, E.V. Positive feedback between PU.1 and the cell cycle controls myeloid differentiation. Science 2013, 341, 670–673. [Google Scholar] [CrossRef] [PubMed]
- Thalheim, T.; Herberg, M.; Loeffler, M.; Galle, J. The Regulatory Capacity of Bivalent Genes-A Theoretical Approach. Int. J. Mol. Sci. 2017, 18, 1069. [Google Scholar] [CrossRef] [PubMed]
- Fleck, J.S.; Jansen, S.M.J.; Wollny, D.; Zenk, F.; Seimiya, M.; Jain, A.; Okamoto, R.; Santel, M.; He, Z.; Camp, J.G.; et al. Inferring and perturbing cell fate regulomes in human brain organoids. Nature 2022. [Google Scholar] [CrossRef] [PubMed]
- Del Sol, A.; Jung, S. The Importance of Computational Modeling in Stem Cell Research. Trends Biotechnol. 2021, 39, 126–136. [Google Scholar] [CrossRef]
- Flöttmann, M.; Scharp, T.; Klipp, E. A stochastic model of epigenetic dynamics in somatic cell reprogramming. Front. Physiol. 2012, 3, 216. [Google Scholar] [CrossRef]
- Yachie-Kinoshita, A.; Onishi, K.; Ostblom, J.; Langley, M.A.; Posfai, E.; Rossant, J.; Zandstra, P.W. Modeling signaling-dependent pluripotency with Boolean logic to predict cell fate transitions. Mol. Syst. Biol. 2018, 14, e7952. [Google Scholar] [CrossRef]
- Sen, D.; Voulgaropoulos, A.; Keung, A.J. Effects of early geometric confinement on the transcriptomic profile of human cerebral organoids. BMC Biotechnol. 2021, 21, 59. [Google Scholar] [CrossRef]
- Hushka, E.A.; Yavitt, F.M.; Brown, T.E.; Dempsey, P.J.; Anseth, K.S. Relaxation of Extracellular Matrix Forces Directs Crypt Formation and Architecture in Intestinal Organoids. Adv. Healthc. Mater. 2020, 9, e1901214. [Google Scholar] [CrossRef]
- Rodríguez-Colman, M.J.; Schewe, M.; Meerlo, M.; Stigter, E.; Gerrits, J.; Pras-Raves, M.; Sacchetti, A.; Hornsveld, M.; Oost, K.C.; Snippert, H.J.; et al. Interplay between metabolic identities in the intestinal crypt supports stem cell function. Nature 2017, 543, 424–427. [Google Scholar] [CrossRef]
- Li, S.; Lu, C.W.; Diem, E.C.; Li, W.; Guderian, M.; Lindenberg, M.; Kruse, F.; Buettner, M.; Floess, S.; Winny, M.R.; et al. Acetyl-CoA-Carboxylase 1-mediated de novo fatty acid synthesis sustains Lgr5+ intestinal stem cell function. Nat. Commun. 2022, 13, 3998. [Google Scholar] [CrossRef]
- Roy, M.; Finley, S.D. Metabolic reprogramming dynamics in tumor spheroids: Insights from a multicellular, multiscale model. PLoS Comput. Biol. 2019, 15, e1007053. [Google Scholar] [CrossRef] [PubMed]
- Mead, B.E.; Hattori, K.; Levy, L.; Imada, S.; Goto, N.; Vukovic, M.; Sze, D.; Kummerlowe, C.; Matute, J.D.; Duan, J.; et al. Screening for modulators of the cellular composition of gut epithelia via organoid models of intestinal stem cell differentiation. Nat. Biomed. Eng. 2022, 6, 476–494. [Google Scholar] [CrossRef] [PubMed]
- Park, J.C.; Jang, S.Y.; Lee, D.; Lee, J.; Kang, U.; Chang, H.; Kim, H.J.; Han, S.H.; Seo, J.; Choi, M.; et al. A logical network-based drug-screening platform for Alzheimer’s disease representing pathological features of human brain organoids. Nat. Commun. 2021, 12, 280. [Google Scholar] [CrossRef] [PubMed]
- Dalal, C.K.; Johnson, A.D. How transcription circuits explore alternative architectures while maintaining overall circuit output. Genes Dev. 2017, 31, 1397–1405. [Google Scholar] [CrossRef] [PubMed]
- Rauth, S.; Karmakar, S.; Batra, S.K.; Ponnusamy, M.P. Recent advances in organoid development and applications in disease modeling. Biochim. Biophys. Acta Rev. Cancer 2021, 1875, 188527. [Google Scholar] [CrossRef]
- Keysselt, K.; Kreutzmann, T.; Rother, K.; Kerner, C.; Krohn, K.; Przybilla, J.; Buske, P.; Löffler-Wirth, H.; Loeffler, M.; Galle, J.; et al. Different in vivo and in vitro transformation of intestinal stem cells in mismatch repair deficiency. Oncogene 2017, 36, 2750–2761. [Google Scholar] [CrossRef]
- Germann, P.; Marin-Riera, M.; Sharpe, J. ya||a: GPU-Powered Spheroid Models for Mesenchyme and Epithelium. Cell Syst. 2019, 8, 261–266.e3. [Google Scholar] [CrossRef]
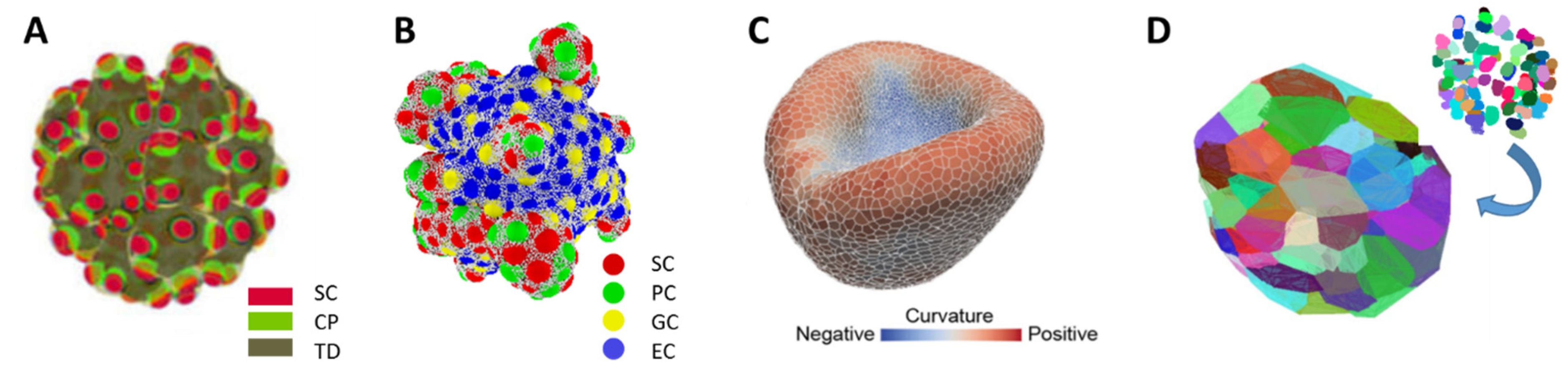
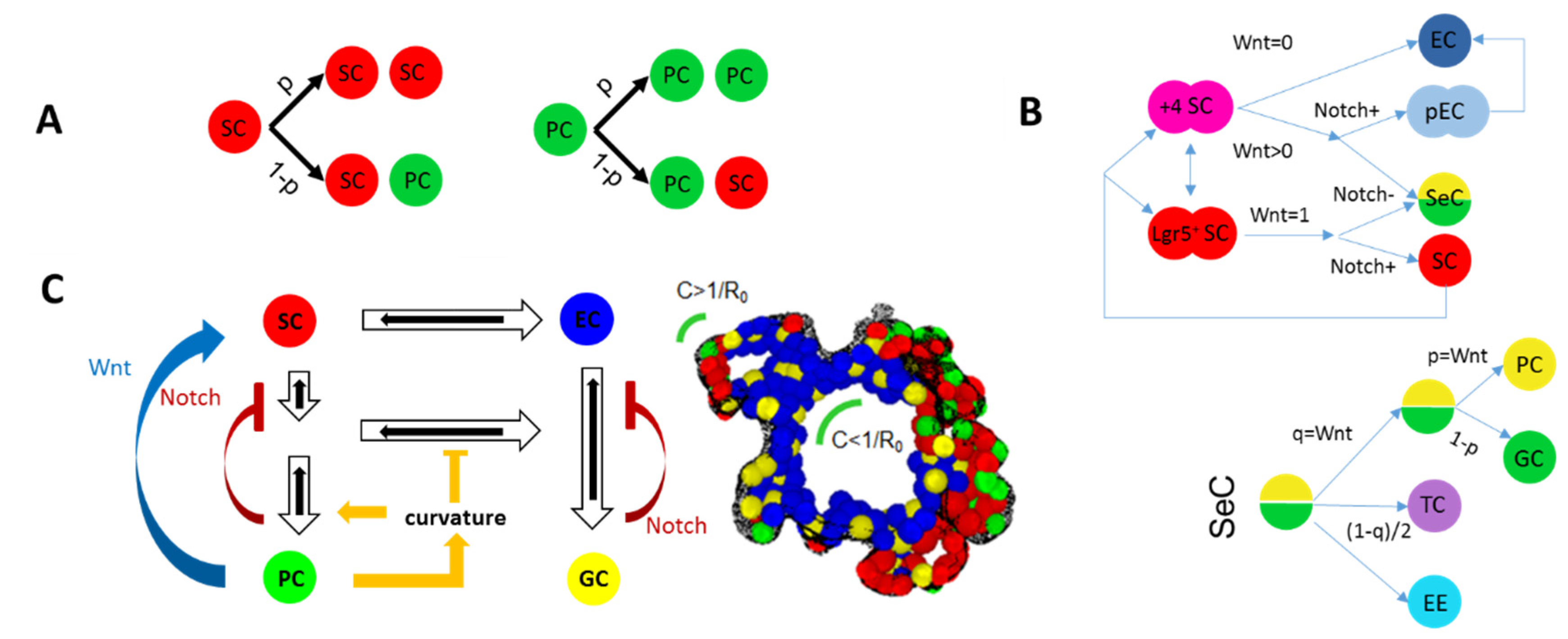

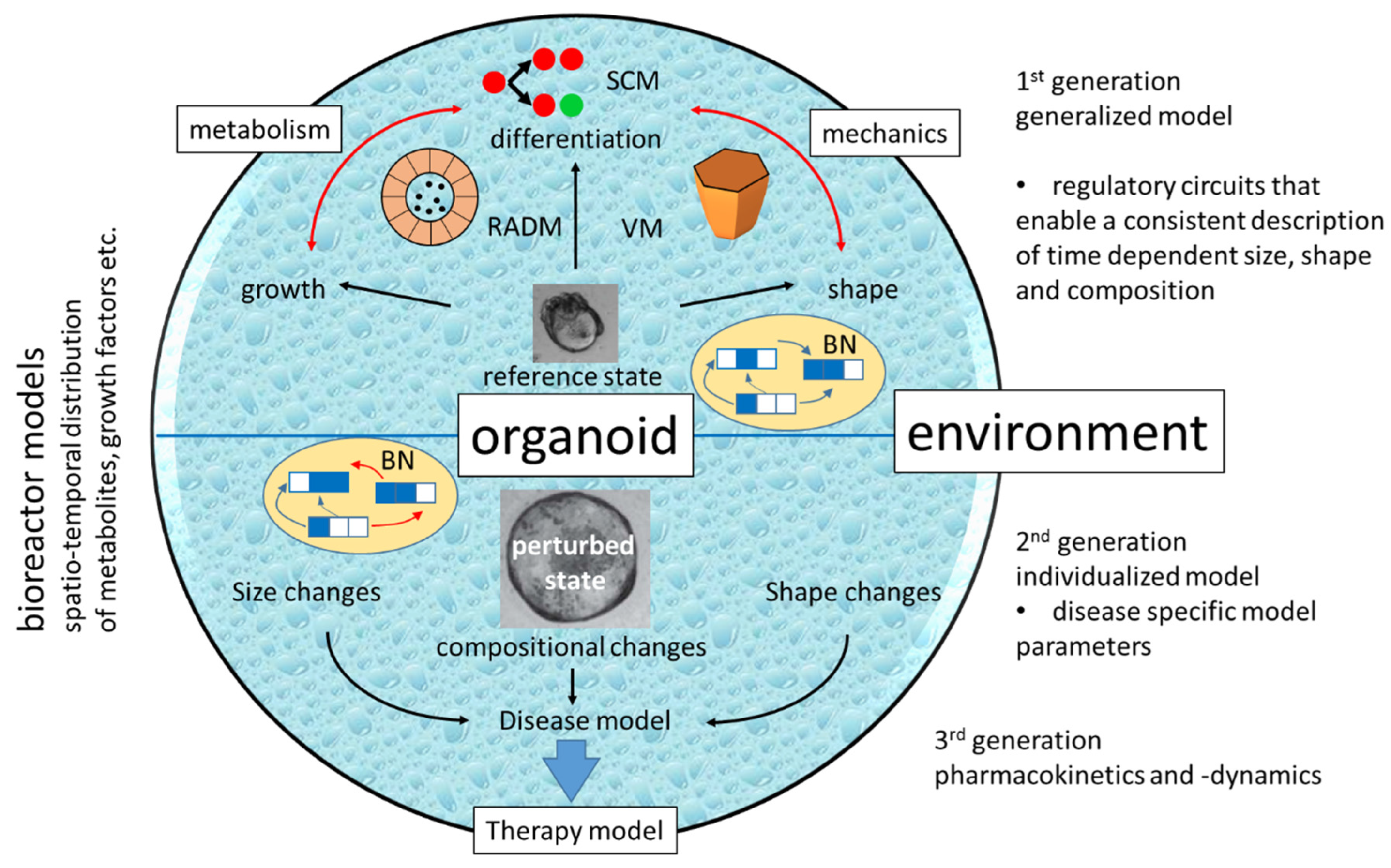
| Organoid Described by: | Example | Pros | Cons |
|---|---|---|---|
| Spatio-temporal distribution of cell densities | Figure 1A |
|
|
| Objects: spherical cells, polymer network | Figure 1B |
|
|
| Objects: prism-like cells | Figure 1C |
|
|
| Voronoi-polyhedrons generated from cell center distributions | Figure 1D |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thalheim, T.; Aust, G.; Galle, J. Organoid Cultures In Silico: Tools or Toys? Bioengineering 2023, 10, 50. https://doi.org/10.3390/bioengineering10010050
Thalheim T, Aust G, Galle J. Organoid Cultures In Silico: Tools or Toys? Bioengineering. 2023; 10(1):50. https://doi.org/10.3390/bioengineering10010050
Chicago/Turabian StyleThalheim, Torsten, Gabriela Aust, and Joerg Galle. 2023. "Organoid Cultures In Silico: Tools or Toys?" Bioengineering 10, no. 1: 50. https://doi.org/10.3390/bioengineering10010050
APA StyleThalheim, T., Aust, G., & Galle, J. (2023). Organoid Cultures In Silico: Tools or Toys? Bioengineering, 10(1), 50. https://doi.org/10.3390/bioengineering10010050






