Brain Tumor Detection and Classification Using Deep Learning and Sine-Cosine Fitness Grey Wolf Optimization
Abstract
1. Introduction
- Introduce an enhanced model to improve brain tumor diagnosis.
- It proposes a Brain Tumor Classification Model (BCM-CNN) based on an advanced 3D model using Enhanced Convolutional Neural Network (BCM-CNN).
- The proposed Brain Tumor Classification Model (BCM-CNN) is based on two submodules; (i) CNN hyperparameters optimization using an adaptive dynamic sine-cosine fitness grey wolf optimizer (ADSCFGWO) algorithm followed by trained Model, and (ii) segmentation model.
- The ADSCFGWO algorithm draws from both the sine cosine and grey wolf algorithms in an adaptable framework that uses both algorithms’ strengths.
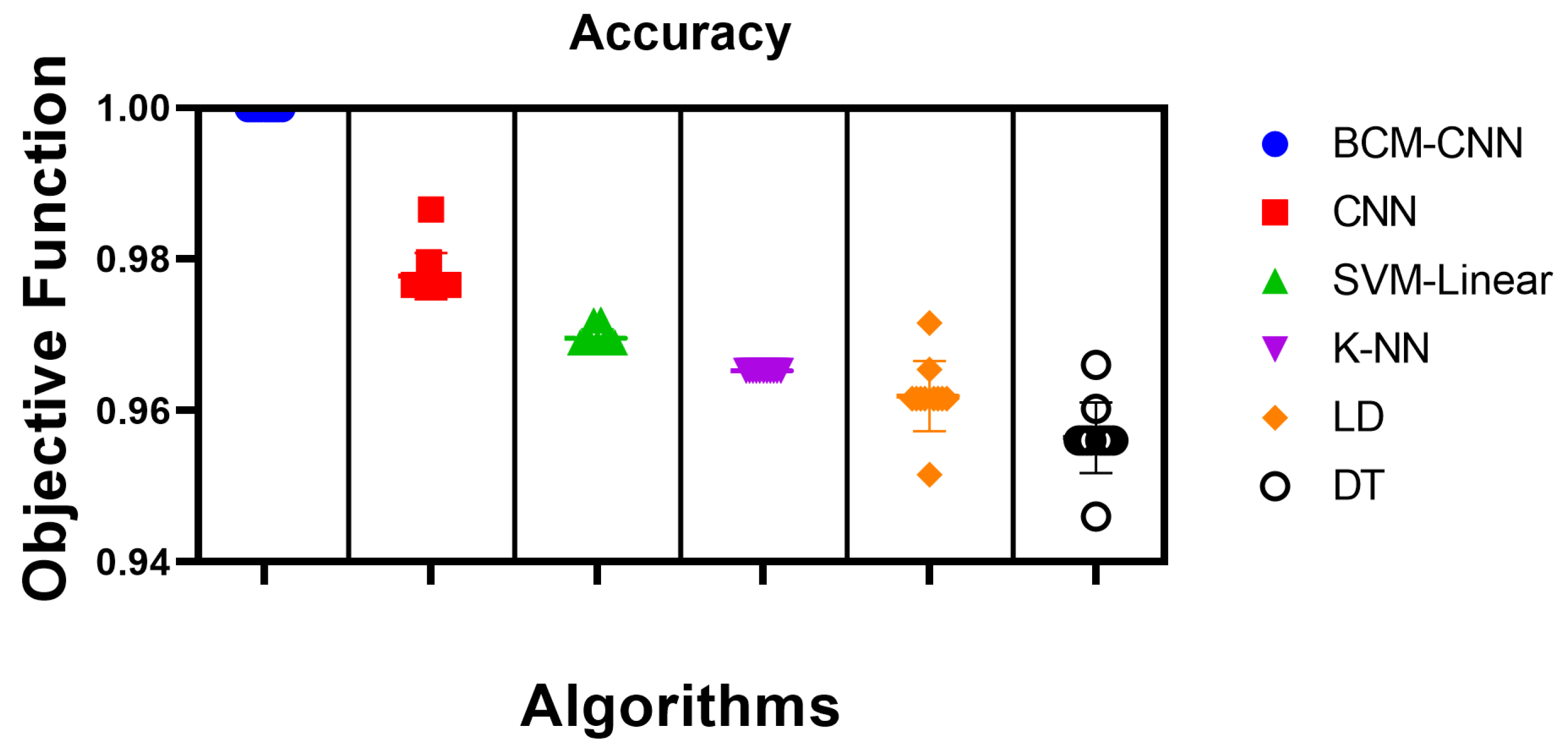
- The experimental results show that the BCM-CNN as a classifier achieved the best results due to the enhancement of the CNN’s performance by the CNN optimization’s hyperparameters.
2. Related Work
2.1. Deep Learning-Based Techniques
2.2. Machine Learning-Based Techniques
2.3. Hybrid-Based Techniques
| Reference | Used Technique | Dataset | Accuracy | Advantages | Disadvantages |
|---|---|---|---|---|---|
| [26] | 16-layer VGG-16 deep NN | Hospitals’ dataset from 2010–2015, China | 98% | Improve multi-class brain tumor classification accuracy. | Small dataset |
| [27] | CNN-based DL model | REMBRANDT | 100% for two-class classification | AI-based transfer learning surpasses machine learning for brain tumor classification. | — |
| [28] | CNN technique for a three-class classification | Figshare | 98% | Transfer learning techniques is a highly effective strategy when medical pictures are scarce. | Samples from the category meningioma were misclassified. overfitting with smaller training data. |
| [31] | RCNN-based model | Openly accessible datasets from Figshare and Kaggle | 98.21% | Low execution time that is optimal for real time processing. Operate on limited-resources systems | Limited to object detection and need to implement brain segmentation. |
| [36] | Hybrid CNN-SVM | BRATS 2015 | 98.49% | Provide effective classification technique for brain tumor | Need to consider the size and location of brain tumor. |
| [37] | SVM and k-NN classifiers | Figshare, 2017 | 97.25% | Extended ROI’s shallow and deep properties improve classifier performance | Accuracy need to be improved |
| [29] | Deep inception residual network | Publicly accessible brain tumor imaging dataset with 3064 pictures | 99.69% | Achieves high classification performance. | Large number of parameters. Maximum computational time. |
| [40] | CNN model for multi-classification | Publicly released clinical datasets | 99.33% | CNN models can help doctors and radiologists validate their first brain tumor assessment | — |
| [33] | Kernel-based SVM | Figshare | 97% | Can detect whether brain tumor is benign and malignant. | Small dataset. Classification accuracy need to be increased. |
| [30] | Transfer learning-based classification | Figshare | 99.02% | Accurately detect brain tumors. Transfer learning in healthcare can help doctors make quick, accurate decisions. | Classification accuracy need to be increased. |
| [34] | Multi-classification model | Three different publicly datasets | 90.27% | Low computational time. Help doctors in making better classification decisions for brain cancers. | Classification accuracy need to be increased. |
| [32] | ImageNet-based ViT | Figshare | 98.7% | Accurately detect brain tumors. Helps radiologists make the right patient-based decision | Needs to consider the size and location of brain tumor |
| [38] | Deep learning-based automatic multimodal classification | BraTs 2015, BraTs 2017, BraTs 2018 | 97.8% | Feature extraction improved classification accuracy and reduced processing time | Classification accuracy need to be increased |
| [39] | Hybrid deep learning-based | ISLES2015 and BRATS2015 | 96% | Perform multi-class classification for brain tumor | Classification accuracy need to be increased |
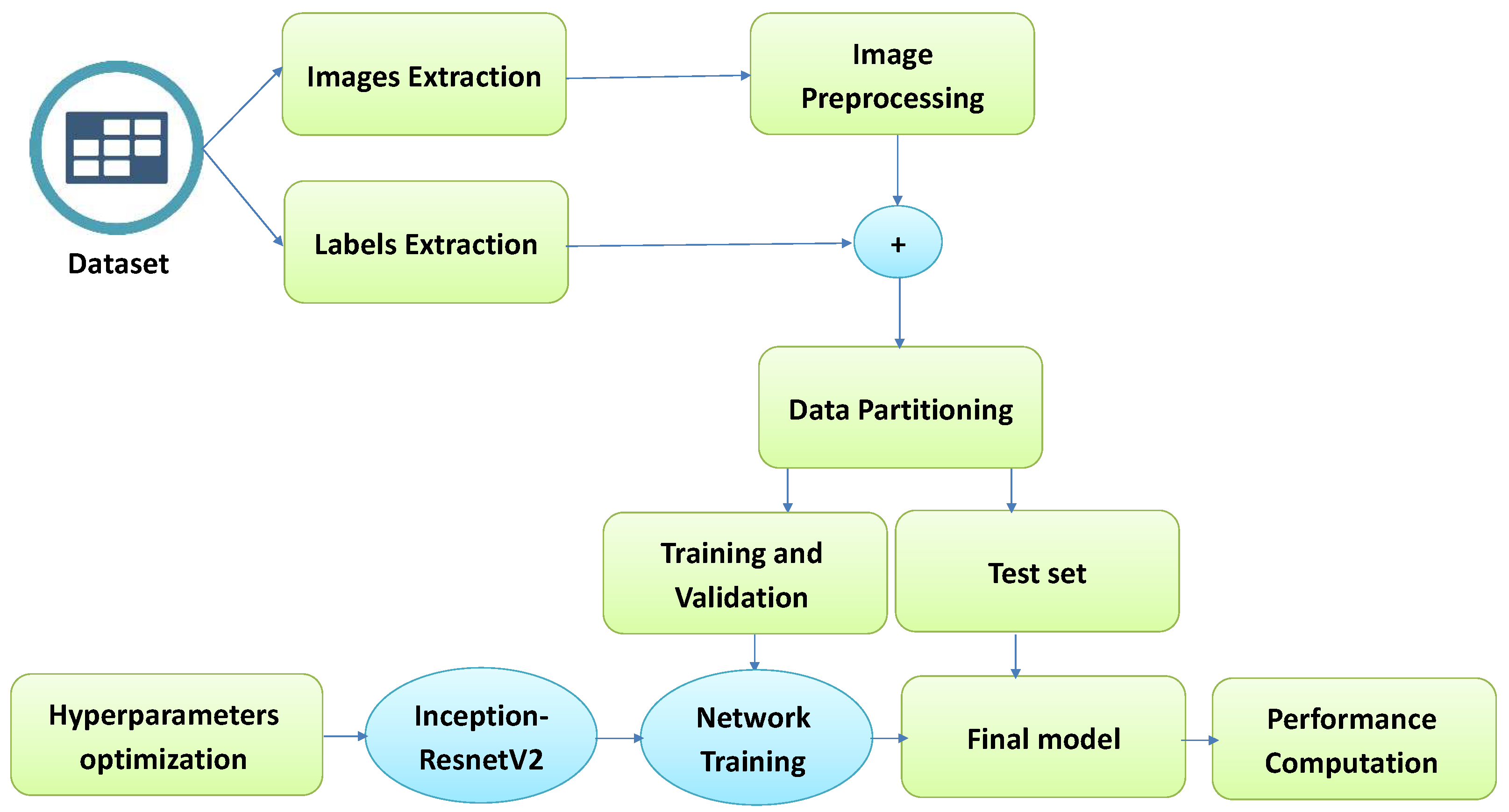
3. Brain Tumor Classification Model Based CNN (BCM-CNN)
3.1. CNN Hyperparameters Optimization
3.2. ADSCFGWO for CNN Hyperparameters
| Algorithm 1 ADSCFGWO algorithm |
|
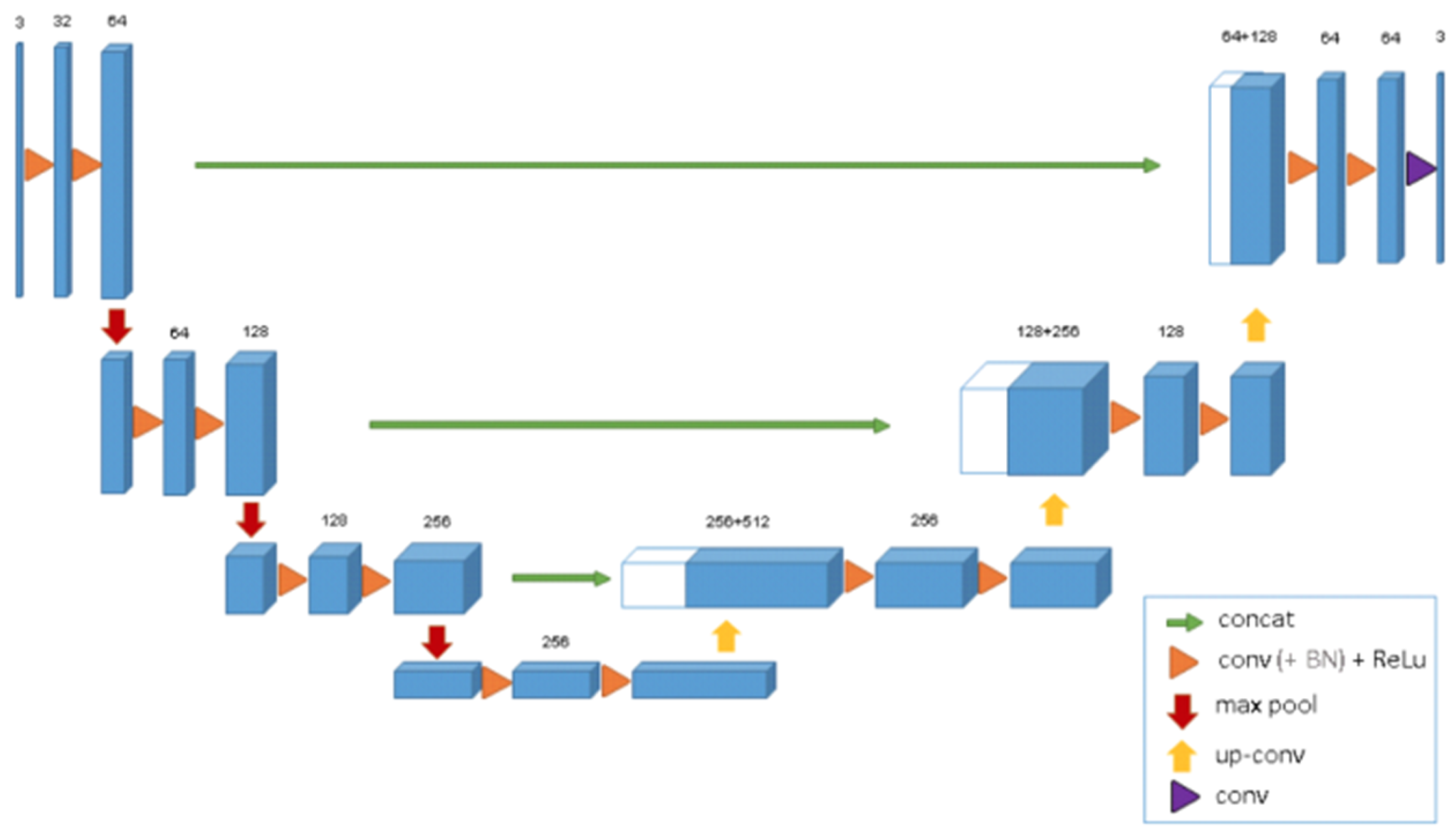
3.3. 3D U-Net Architecture Segmentation Model
4. Experimental Results
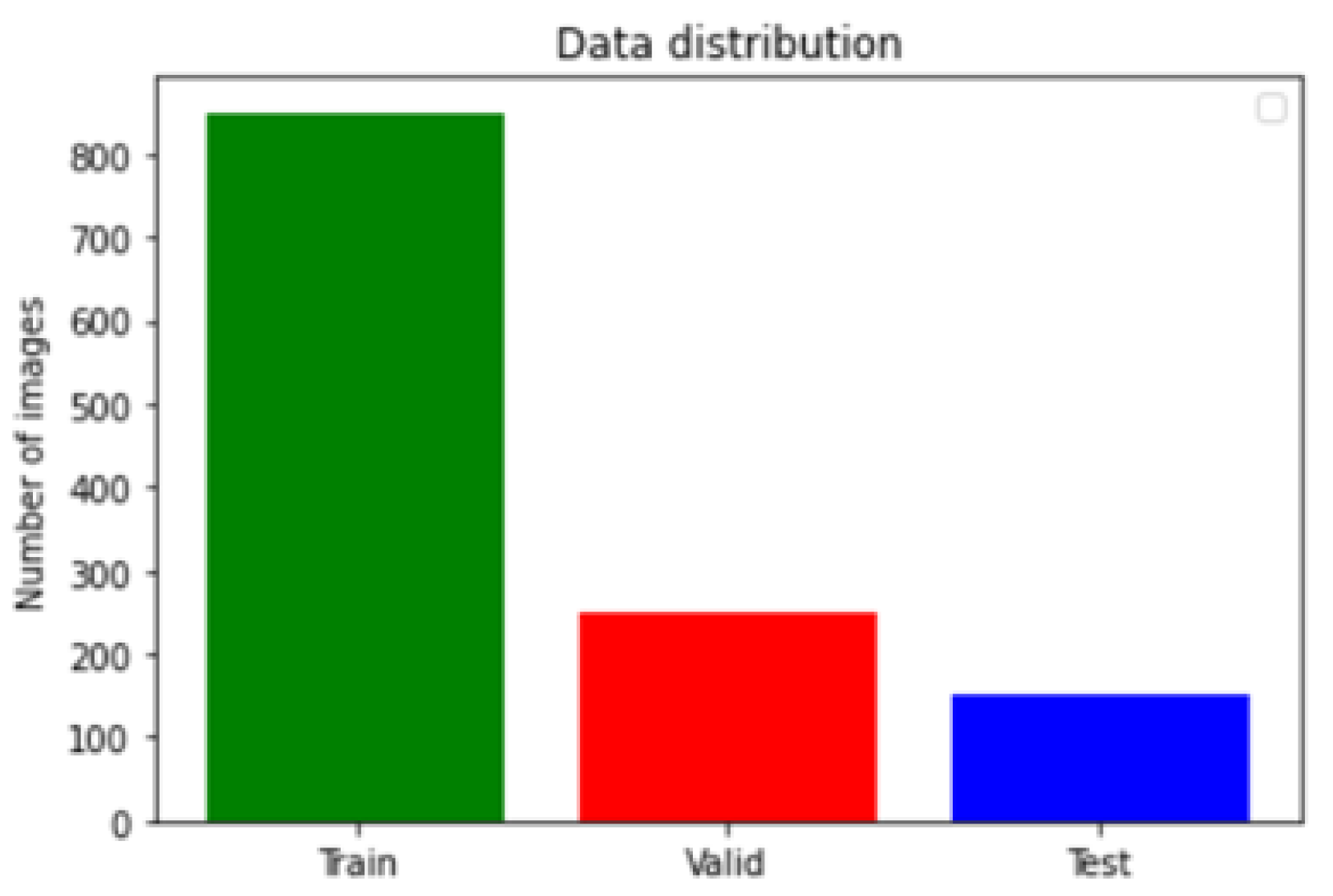
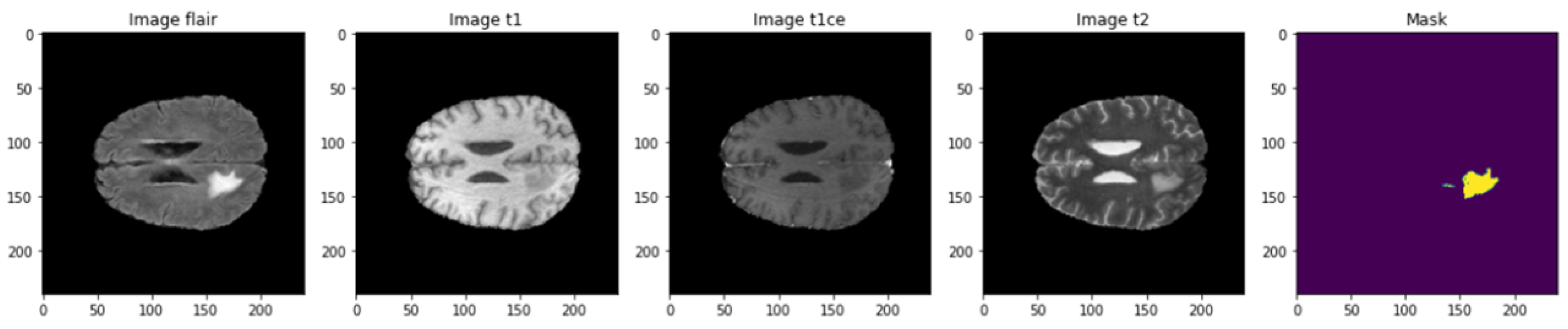
4.1. Dataset Description
4.2. Performance Metrics Used in CNN
4.3. The BCM-CNN Evaluation
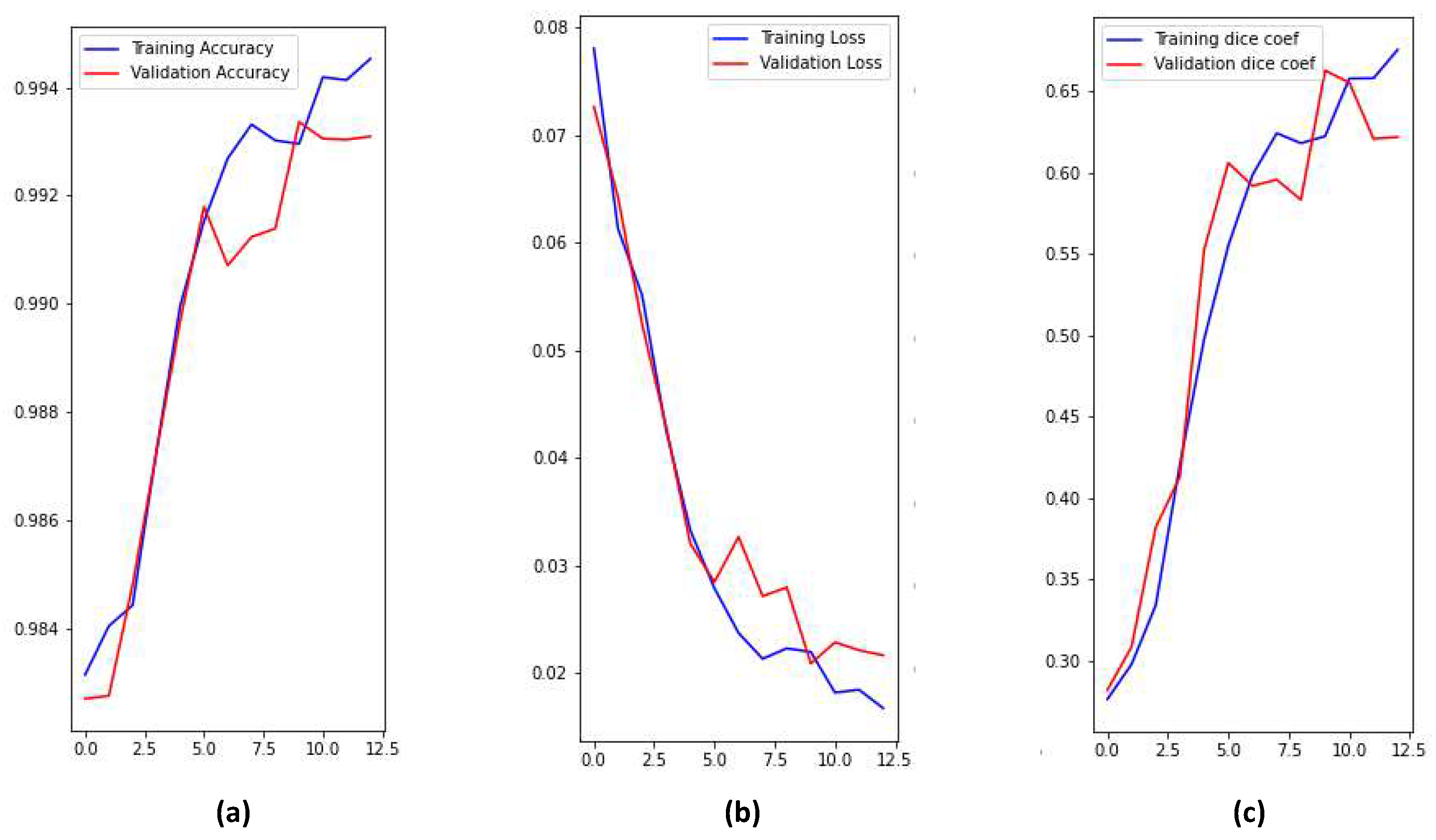
4.4. 3D U-Net Segmentation Model
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| DL | Deep Learning |
| CNN | Convolutional Neural Network |
| BCM-CNN | Brain Tumor Classification Model based on CNN |
| ADSCFGWO | Adaptive Dynamic Sine-Cosine Fitness Grey Wolf Optimizer |
| WHO | World Health Organization |
| MEG | Magneto Encephalon Graph |
| CT | Computed Tomography |
| EEG | Ultrasonography, Electro Encephalon Graph |
| SPECT | Single-Photon Emission Computed Tomography |
| PET | Positron Emission Tomography |
| MRI | Magnetic Resonance Imaging |
| CAD | Computer-Aided Diagnosis |
| NN | Neural Network |
| FC | Fully Connected |
| DT | Decision Tree |
| NB | Naive Bayes |
| LD | Linear Discrimination |
| SVM | Support Vector Machine |
| AUC | Area Under the Curve |
| LD | Linear Discriminant |
| Quantile-Quantile |
References
- Al-Galal, S.A.Y.; Alshaikhli, I.F.T.; Abdulrazzaq, M.M. MRI brain tumor medical images analysis using deep learning techniques: A systematic review. Health Technol. 2021, 11, 267–282. [Google Scholar] [CrossRef]
- Rahman, M.L.; Reza, A.W.; Shabuj, S.I. An internet of things-based automatic brain tumor detection system. Indones. J. Electr. Eng. Comput. Sci. 2022, 25, 214–222. [Google Scholar] [CrossRef]
- Key Statistics for Brain and Spinal Cord Tumors. Available online: https://www.cancer.org/cancer/brain-spinal-cord-tumors-adults/about/key-statistics.html (accessed on 20 September 2022).
- Ayadi, W.; Elhamzi, W.; Charfi, I.; Atri, M. Deep CNN for Brain Tumor Classification. Neural Process. Lett. 2021, 53, 671–700. [Google Scholar] [CrossRef]
- Liu, J.; Li, M.; Wang, J.; Wu, F.; Liu, T.; Pan, Y. A survey of MRI-based brain tumor segmentation methods. Tsinghua Sci. Technol. 2014, 19, 578–595. [Google Scholar] [CrossRef]
- Amin, J.; Sharif, M.; Haldorai, A.; Yasmin, M.; Nayak, R.S. Brain tumor detection and classification using machine learning: A comprehensive survey. Complex Intell. Syst. 2021, 8, 3161–3183. [Google Scholar] [CrossRef]
- Jayade, S.; Ingole, D.T.; Ingole, M.D. Review of Brain Tumor Detection Concept using MRI Images. In Proceedings of the 2019 International Conference on Innovative Trends and Advances in Engineering and Technology (ICITAET), Shegoaon, India, 27–28 December 2019. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, L.F.; Zhang, X.; Han, Y.; Nan, H.Y.; Hu, Y.C.; Hu, B.; Yan, S.L.; Zhang, J.; Cheng, D.L.; et al. Glioma Grading on Conventional MR Images: A Deep Learning Study With Transfer Learning. Front. Neurosci. 2018, 12, 804. [Google Scholar] [CrossRef]
- Nazir, M.; Shakil, S.; Khurshid, K. Role of deep learning in brain tumor detection and classification (2015 to 2020): A review. Comput. Med. Imaging Graph. 2021, 91, 101940. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Mirjalili, S.; Abdelhamid, A.A.; Ibrahim, A.; Khodadadi, N.; Eid, M.M. Meta-Heuristic Optimization and Keystroke Dynamics for Authentication of Smartphone Users. Mathematics 2022, 10, 2912. [Google Scholar] [CrossRef]
- El-kenawy, E.S.M.; Albalawi, F.; Ward, S.A.; Ghoneim, S.S.M.; Eid, M.M.; Abdelhamid, A.A.; Bailek, N.; Ibrahim, A. Feature Selection and Classification of Transformer Faults Based on Novel Meta-Heuristic Algorithm. Mathematics 2022, 10, 3144. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Mirjalili, S.; Alassery, F.; Zhang, Y.D.; Eid, M.M.; El-Mashad, S.Y.; Aloyaydi, B.A.; Ibrahim, A.; Abdelhamid, A.A. Novel Meta-Heuristic Algorithm for Feature Selection, Unconstrained Functions and Engineering Problems. IEEE Access 2022, 10, 40536–40555. [Google Scholar] [CrossRef]
- Ibrahim, A.; Mirjalili, S.; El-Said, M.; Ghoneim, S.S.M.; Al-Harthi, M.M.; Ibrahim, T.F.; El-Kenawy, E.S.M. Wind Speed Ensemble Forecasting Based on Deep Learning Using Adaptive Dynamic Optimization Algorithm. IEEE Access 2021, 9, 125787–125804. [Google Scholar] [CrossRef]
- El-kenawy, E.S.M.; Abutarboush, H.F.; Mohamed, A.W.; Ibrahim, A. Advance Artificial Intelligence Technique for Designing Double T-shaped Monopole Antenna. Comput. Mater. Contin. 2021, 69, 2983–2995. [Google Scholar] [CrossRef]
- Samee, N.A.; El-Kenawy, E.S.M.; Atteia, G.; Jamjoom, M.M.; Ibrahim, A.; Abdelhamid, A.A.; El-Attar, N.E.; Gaber, T.; Slowik, A.; Shams, M.Y. Metaheuristic Optimization Through Deep Learning Classification of COVID-19 in Chest X-Ray Images. Comput. Mater. Contin. 2022, 73, 4193–4210. [Google Scholar] [CrossRef]
- Lee, G.; Nho, K.; Kang, B.; Sohn, K.A.; Kim, D. Predicting Alzheimer’s disease progression using multi-modal deep learning approach. Sci. Rep. 2019, 9, 1952. [Google Scholar] [CrossRef] [PubMed]
- Sharma, K.; Kaur, A.; Gujral, S. Brain Tumor Detection based on Machine Learning Algorithms. Int. J. Comput. Appl. 2014, 103, 7–11. [Google Scholar] [CrossRef]
- Agrawal, M.; Jain, V. Prediction of Breast Cancer based on Various Medical Symptoms Using Machine Learning Algorithms. In Proceedings of the 2022 6th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 28–30 April 2022; pp. 1242–1245. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Mahedy Hasan, S.M.; Champa, A.I.; AsifZaman, M.; Hasan, M.K. Prediction of Liver Disorders using Machine Learning Algorithms: A Comparative Study. In Proceedings of the 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT), Dhaka, Bangladesh, 28–29 November 2020; pp. 111–116. [Google Scholar] [CrossRef]
- Swain, D.; Pani, S.K.; Swain, D. A Metaphoric Investigation on Prediction of Heart Disease using Machine Learning. In Proceedings of the 2018 International Conference on Advanced Computation and Telecommunication (ICACAT), Bhopal, India, 28–29 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, W.; Sun, L.; Huang, J.; Han, L.; Zhang, D. Dual Attention Multi-Instance Deep Learning for Alzheimer’s Disease Diagnosis With Structural MRI. IEEE Trans. Med Imaging 2021, 40, 2354–2366. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; El-Kenawy, E.S.M.; Alotaibi, B.; Amer, G.M.; Abdelkader, M.Y.; Ibrahim, A.; Eid, M.M. Robust Speech Emotion Recognition Using CNN+LSTM Based on Stochastic Fractal Search Optimization Algorithm. IEEE Access 2022, 10, 49265–49284. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Alhussan, A.A.; Khafaga, D.S.; El-Kenawy, E.S.M.; Ibrahim, A.; Eid, M.M.; Abdelhamid, A.A. Pothole and Plain Road Classification Using Adaptive Mutation Dipper Throated Optimization and Transfer Learning for Self Driving Cars. IEEE Access 2022, 10, 84188–84211. [Google Scholar] [CrossRef]
- Srikanth, B.; Suryanarayana, S.V. Multi-Class classification of brain tumor images using data augmentation with deep neural network. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Tandel, G.S.; Balestrieri, A.; Jujaray, T.; Khanna, N.N.; Saba, L.; Suri, J.S. Multiclass magnetic resonance imaging brain tumor classification using artificial intelligence paradigm. Comput. Biol. Med. 2020, 122, 103804. [Google Scholar] [CrossRef]
- Deepak, S.; Ameer, P. Brain tumor classification using deep CNN features via transfer learning. Comput. Biol. Med. 2019, 111, 103345. [Google Scholar] [CrossRef] [PubMed]
- Kokkalla, S.; Kakarla, J.; Venkateswarlu, I.B.; Singh, M. Three-class brain tumor classification using deep dense inception residual network. Soft Comput. 2021, 25, 8721–8729. [Google Scholar] [CrossRef] [PubMed]
- Özlem, P.; Güngen, C. Classification of brain tumors from MR images using deep transfer learning. J. Supercomput. 2021, 77, 7236–7252. [Google Scholar] [CrossRef]
- Kesav, N.; Jibukumar, M. Efficient and low complex architecture for detection and classification of Brain Tumor using RCNN with Two Channel CNN. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6229–6242. [Google Scholar] [CrossRef]
- Tummala, S.; Kadry, S.; Bukhari, S.A.C.; Rauf, H.T. Classification of Brain Tumor from Magnetic Resonance Imaging Using Vision Transformers Ensembling. Curr. Oncol. 2022, 29, 7498–7511. [Google Scholar] [CrossRef]
- Pareek, M.; Jha, C.K.; Mukherjee, S. Brain Tumor Classification from MRI Images and Calculation of Tumor Area. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2020; pp. 73–83. [Google Scholar] [CrossRef]
- Ayadi, W.; Charfi, I.; Elhamzi, W.; Atri, M. Brain tumor classification based on hybrid approach. Vis. Comput. 2020, 38, 107–117. [Google Scholar] [CrossRef]
- Konar, D.; Bhattacharyya, S.; Panigrahi, B.K.; Behrman, E.C. Qutrit-Inspired Fully Self-Supervised Shallow Quantum Learning Network for Brain Tumor Segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6331–6345. [Google Scholar] [CrossRef]
- Khairandish, M.; Sharma, M.; Jain, V.; Chatterjee, J.; Jhanjhi, N. A Hybrid CNN-SVM Threshold Segmentation Approach for Tumor Detection and Classification of MRI Brain Images. IRBM 2022, 43, 290–299. [Google Scholar] [CrossRef]
- Öksüz, C.; Urhan, O.; Güllü, M.K. Brain tumor classification using the fused features extracted from expanded tumor region. Biomed. Signal Process. Control 2022, 72, 103356. [Google Scholar] [CrossRef]
- Khan, M.A.; Ashraf, I.; Alhaisoni, M.; Damaševičius, R.; Scherer, R.; Rehman, A.; Bukhari, S.A.C. Multimodal Brain Tumor Classification Using Deep Learning and Robust Feature Selection: A Machine Learning Application for Radiologists. Diagnostics 2020, 10, 565. [Google Scholar] [CrossRef]
- Kadry, S.; Nam, Y.; Rauf, H.T.; Rajinikanth, V.; Lawal, I.A. Automated Detection of Brain Abnormality using Deep-Learning-Scheme: A Study. In Proceedings of the 2021 Seventh International conference on Bio Signals, Images, and Instrumentation (ICBSII), Chennai, India, 25–27 March 2021. [Google Scholar] [CrossRef]
- Irmak, E. Multi-Classification of Brain Tumor MRI Images Using Deep Convolutional Neural Network with Fully Optimized Framework. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 1015–1036. [Google Scholar] [CrossRef]
- Khafaga, D.S.; Alhussan, A.A.; El-Kenawy, E.S.M.; Ibrahim, A.; Eid, M.M.; Abdelhamid, A.A. Solving Optimization Problems of Metamaterial and Double T-Shape Antennas Using Advanced Meta-Heuristics Algorithms. IEEE Access 2022, 10, 74449–74471. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Lecture Notes in Computer Science; Springer International Publishing: Berlin, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Özgün, Ç.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016; Springer International Publishing: Berlin, Germany, 2016; pp. 424–432. [Google Scholar] [CrossRef]
- BRaTS 2021 Task 1 Dataset, RSNA-ASNR-MICCAI Brain Tumor Segmentation (BraTS) Challenge 2021. Available online: https://www.kaggle.com/datasets/dschettler8845/brats-2021-task1?select=BraTS2021_Training_Data.tar (accessed on 20 September 2022).
- Nour, M.; Cömert, Z.; Polat, K. A Novel Medical Diagnosis model for COVID-19 infection detection based on Deep Features and Bayesian Optimization. Appl. Soft Comput. 2020, 97, 106580. [Google Scholar] [CrossRef] [PubMed]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A.E. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef]
- Benmahamed, Y.; Teguar, M.; Boubakeur, A. Application of SVM and KNN to Duval Pentagon 1 for transformer oil diagnosis. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3443–3451. [Google Scholar] [CrossRef]
- Benmahamed, Y.; Kemari, Y.; Teguar, M.; Boubakeur, A. Diagnosis of Power Transformer Oil Using KNN and Nave Bayes Classifiers. In Proceedings of the 2018 IEEE 2nd International Conference on Dielectrics (ICD), Budapest, Hungary, 1–5 July 2018. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| CNN training options (Default) RateDropFactor Momentum Learn L2Regularization LearnRateDropPeriod GradientThreshold GradientThresholdMethod ValidationData VerboseFrequency ValidationPatience ValidationFrequency ResetInputNormalization CNN training options (Custom) InitialLearnRate ExecutionEnvironment MiniBatchSize MaxEpochs Verbose Shuffle LearnRateSchedule Optimizer | 0.1000 0.9000 1.0000 10 Inf l2norm imds 50 Inf 50 1 1.0000 gpu 8 20 0 every-epoch piecwise ADSCFGWO |
| No. | Operation | Complexity |
|---|---|---|
| 1 | Initialization | |
| 2 | Calculate objective function | |
| 3 | Finding best solutions | |
| 4 | Updating position of current grey wolf by fitness | |
| 5 | Updating position of current individual by Sine Cosine | |
| 6 | Updating objective function | |
| 7 | Finding best fitness | |
| 8 | Updating parameters | |
| 9 | Producing the best fitness |
| Parameter | Value |
|---|---|
| a | [0, 2] |
| ,,, | [0, 1] |
| # Runs (Repeat the whole algorithm) | 11 |
| # Iterations () | 80 |
| # Agents (Population size n) | 10 |
| No. | Metrics | Calculation |
|---|---|---|
| 1 | Accuracy | |
| 2 | Sensitivity | |
| 3 | Specificity | |
| 4 | Precision (PPV) | |
| 5 | Negative Predictive Value (NPV) | |
| 6 | F1-score |
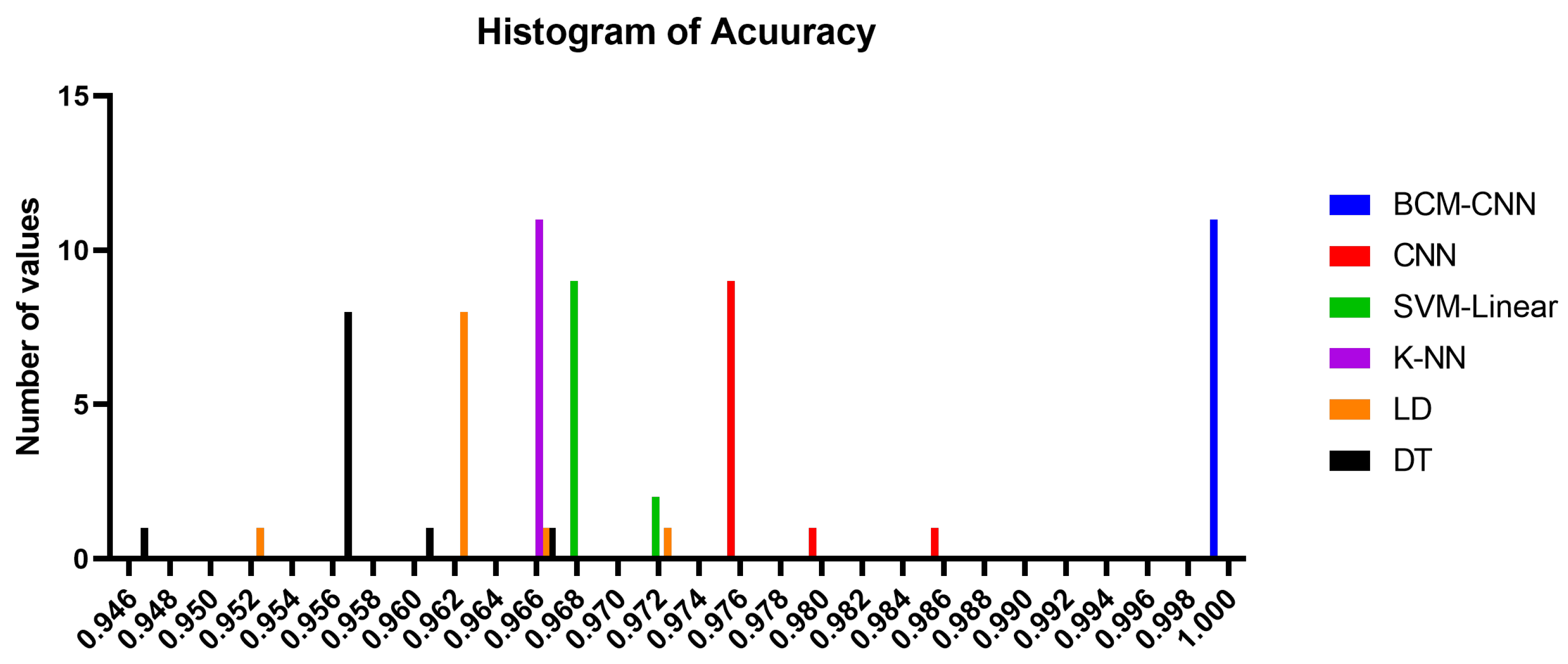
| Accuracy | Sensitivity (TRP) | Specificity (TNP) | p Value (PPV) | N Value (NPV) | F1-Score | |
|---|---|---|---|---|---|---|
| BCM-CNN | 0.99980004 | 0.99980004 | 0.99980004 | 0.99980004 | 0.99980004 | 0.9998 |
| CNN | 0.9765625 | 0.975609756 | 0.977198697 | 0.966183575 | 0.983606557 | 0.970874 |
| SVM-Linear | 0.968992248 | 0.956937799 | 0.977198697 | 0.966183575 | 0.970873786 | 0.961538 |
| K-NN | 0.965250965 | 0.956937799 | 0.970873786 | 0.956937799 | 0.970873786 | 0.956938 |
| LD | 0.961538462 | 0.947867299 | 0.970873786 | 0.956937799 | 0.964630225 | 0.952381 |
| DT | 0.956022945 | 0.947867299 | 0.961538462 | 0.943396226 | 0.964630225 | 0.945626 |
| BCM-CNN | CNN | SVM-Linear | K-NN | LD | DT | |
|---|---|---|---|---|---|---|
| Number of values | 11 | 11 | 11 | 11 | 11 | 11 |
| Minimum | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9515 | 0.946 |
| 25% Percentile | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
| Median | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
| 75% Percentile | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
| Maximum | 0.9998 | 0.9866 | 0.972 | 0.9653 | 0.9715 | 0.966 |
| Range | 0 | 0.01 | 0.003 | 0 | 0.02 | 0.02 |
| 10% Percentile | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9535 | 0.948 |
| 90% Percentile | 0.9998 | 0.9852 | 0.972 | 0.9653 | 0.9703 | 0.9649 |
| 95% CI of median | ||||||
| Actual confidence level | 98.83% | 98.83% | 98.83% | 98.83% | 98.83% | 98.83% |
| Lower confidence limit | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
| Upper confidence limit | 0.9998 | 0.9796 | 0.9719 | 0.9653 | 0.9654 | 0.9602 |
| Mean | 0.9998 | 0.9777 | 0.9695 | 0.9653 | 0.9619 | 0.9564 |
| Std. Deviation | 0 | 0.00306 | 0.001195 | 0 | 0.00462 | 0.004649 |
| Std. Error of Mean | 0 | 0.0009226 | 0.0003603 | 0 | 0.001393 | 0.001402 |
| Lower 95% CI of mean | 0.9998 | 0.9757 | 0.9687 | 0.9653 | 0.9588 | 0.9533 |
| Upper 95% CI of mean | 0.9998 | 0.9798 | 0.9703 | 0.9653 | 0.965 | 0.9595 |
| Coefficient of variation | 0.000% | 0.3130% | 0.1232% | 0.000% | 0.4803% | 0.4860% |
| Geometric mean | 0.9998 | 0.9777 | 0.9695 | 0.9653 | 0.9619 | 0.9564 |
| Geometric SD factor | 1 | 1.003 | 1.001 | 1 | 1.005 | 1.005 |
| Lower 95% CI of geo. mean | 0.9998 | 0.9757 | 0.9687 | 0.9653 | 0.9588 | 0.9533 |
| Upper 95% CI of geo. mean | 0.9998 | 0.9798 | 0.9703 | 0.9653 | 0.965 | 0.9595 |
| Harmonic mean | 0.9998 | 0.9777 | 0.9695 | 0.9653 | 0.9619 | 0.9564 |
| Lower 95% CI of harm. mean | 0.9998 | 0.9757 | 0.9687 | 0.9653 | 0.9588 | 0.9533 |
| Upper 95% CI of harm. mean | 0.9998 | 0.9798 | 0.9703 | 0.9653 | 0.965 | 0.9595 |
| Quadratic mean | 0.9998 | 0.9777 | 0.9695 | 0.9653 | 0.9619 | 0.9564 |
| Lower 95% CI of quad. mean | 0.9998 | 0.9757 | 0.9687 | 0.9653 | 0.9588 | 0.9533 |
| Upper 95% CI of quad. mean | 0.9998 | 0.9798 | 0.9703 | 0.9653 | 0.965 | 0.9595 |
| Skewness | 2.887 | 1.924 | −0.2076 | −0.2118 | ||
| Kurtosis | 8.536 | 2.047 | 4.001 | 3.839 | ||
| Sum | 11 | 10.76 | 10.66 | 10.62 | 10.58 | 10.52 |
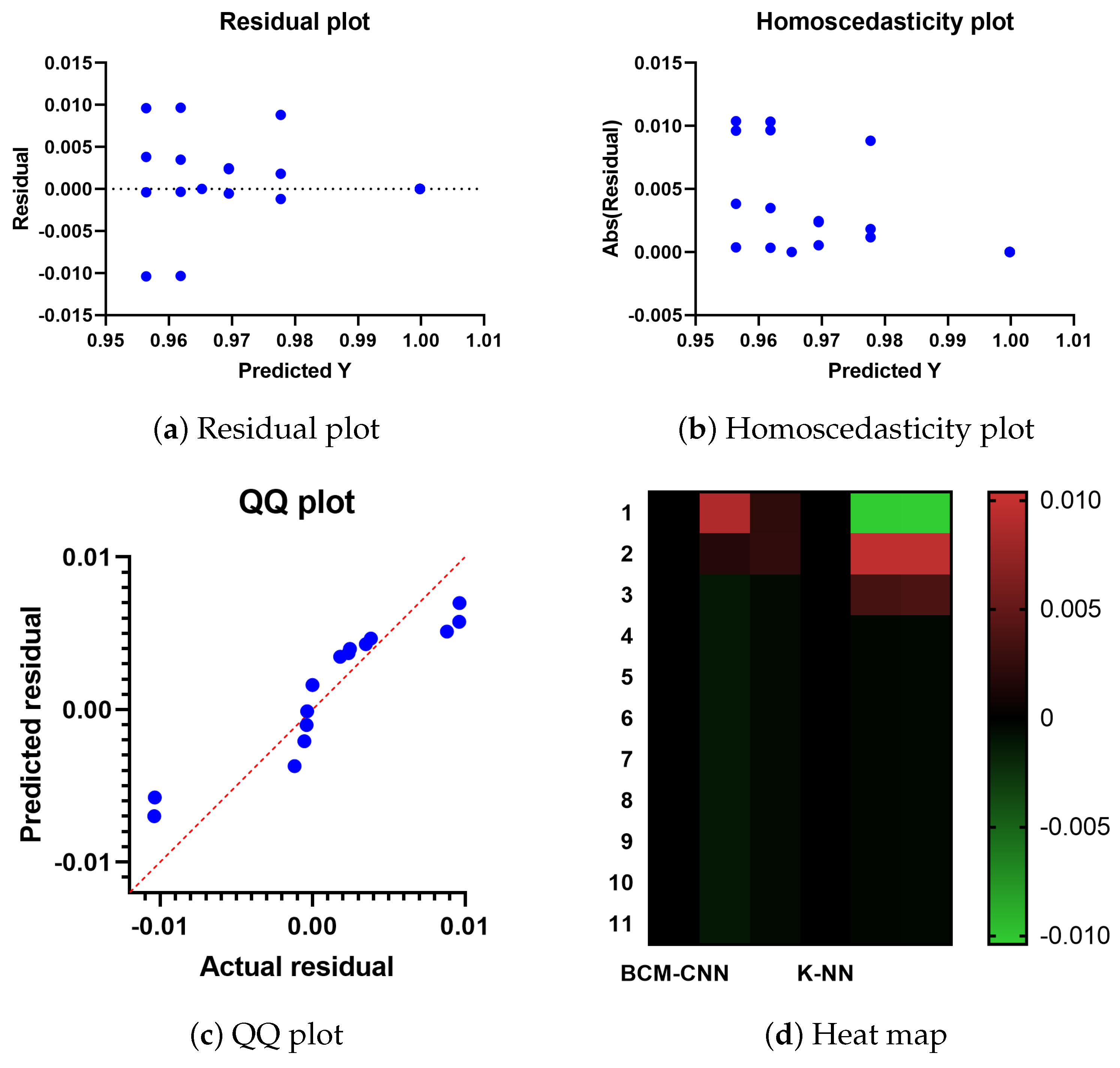
| SS | DF | MS | F (DFn, DFd) | p Value | |
|---|---|---|---|---|---|
| Treatment (between columns) | 0.01323 | 5 | 0.002646 | F (5, 60) = 295.4 | p < 0.0001 |
| Residual (within columns) | 0.0005374 | 60 | 0.000008957 | - | - |
| Total | 0.01377 | 65 | - | - | - |
| BCM-CNN | CNN | SVM-Linear | K-NN | LD | DT | |
|---|---|---|---|---|---|---|
| Theoretical median | 0 | 0 | 0 | 0 | 0 | 0 |
| Actual median | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
| Number of values | 11 | 11 | 11 | 11 | 11 | 11 |
| Wilcoxon Signed Rank Test | ||||||
| Sum of signed ranks (W) | 66 | 66 | 66 | 66 | 66 | 66 |
| Sum of positive ranks | 66 | 66 | 66 | 66 | 66 | 66 |
| Sum of negative ranks | 0 | 0 | 0 | 0 | 0 | 0 |
| P value (two tailed) | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| Exact or estimate? | Exact | Exact | Exact | Exact | Exact | Exact |
| Significant (alpha = 0.05)? | Yes | Yes | Yes | Yes | Yes | Yes |
| How big is the discrepancy? | ||||||
| Discrepancy | 0.9998 | 0.9766 | 0.969 | 0.9653 | 0.9615 | 0.956 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ZainEldin, H.; Gamel, S.A.; El-Kenawy, E.-S.M.; Alharbi, A.H.; Khafaga, D.S.; Ibrahim, A.; Talaat, F.M. Brain Tumor Detection and Classification Using Deep Learning and Sine-Cosine Fitness Grey Wolf Optimization. Bioengineering 2023, 10, 18. https://doi.org/10.3390/bioengineering10010018
ZainEldin H, Gamel SA, El-Kenawy E-SM, Alharbi AH, Khafaga DS, Ibrahim A, Talaat FM. Brain Tumor Detection and Classification Using Deep Learning and Sine-Cosine Fitness Grey Wolf Optimization. Bioengineering. 2023; 10(1):18. https://doi.org/10.3390/bioengineering10010018
Chicago/Turabian StyleZainEldin, Hanaa, Samah A. Gamel, El-Sayed M. El-Kenawy, Amal H. Alharbi, Doaa Sami Khafaga, Abdelhameed Ibrahim, and Fatma M. Talaat. 2023. "Brain Tumor Detection and Classification Using Deep Learning and Sine-Cosine Fitness Grey Wolf Optimization" Bioengineering 10, no. 1: 18. https://doi.org/10.3390/bioengineering10010018
APA StyleZainEldin, H., Gamel, S. A., El-Kenawy, E.-S. M., Alharbi, A. H., Khafaga, D. S., Ibrahim, A., & Talaat, F. M. (2023). Brain Tumor Detection and Classification Using Deep Learning and Sine-Cosine Fitness Grey Wolf Optimization. Bioengineering, 10(1), 18. https://doi.org/10.3390/bioengineering10010018










