Synoptic Time Scale Variability in Precipitation and Streamflows for River Basins over Northern South America
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region and Datasets
2.2. Precipitation
2.3. Streamflows
2.4. Data Selection and Processing
2.5. Wave Number-Frequency Power Spectra and Fourier Filters
2.6. Seasonal Synoptic Anomalies
2.7. Decomposition of Time Series
2.8. Synoptic Modes of Variability and Their Variances Explained
2.9. Seasonal Variance Explained by the Synoptic Modes of Variability
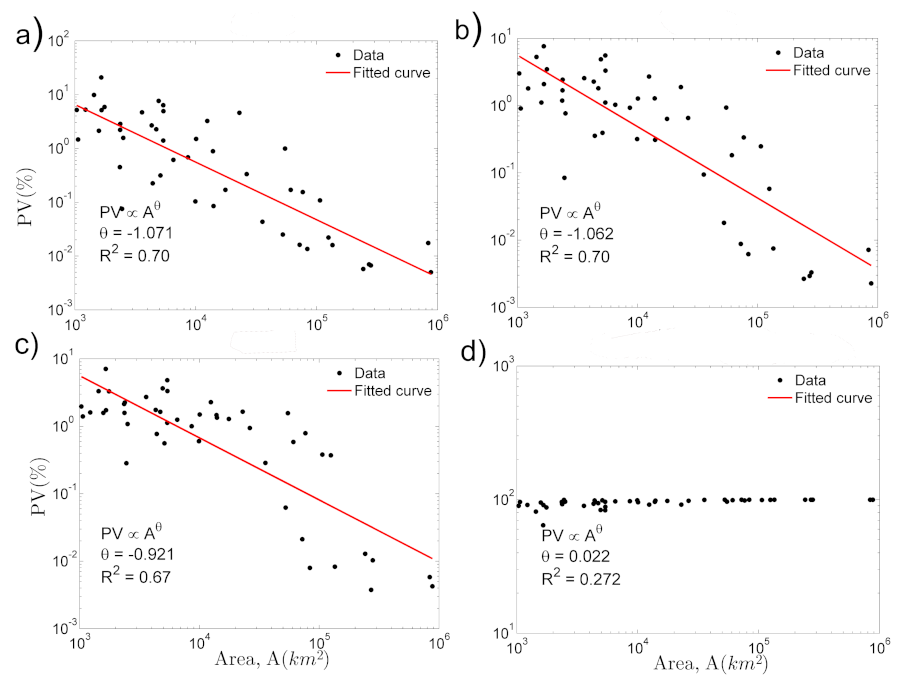
2.10. Relationships between the Variance Explained by the Synoptic Modes of Variability and the Area of Catchments
3. Results and Analysis
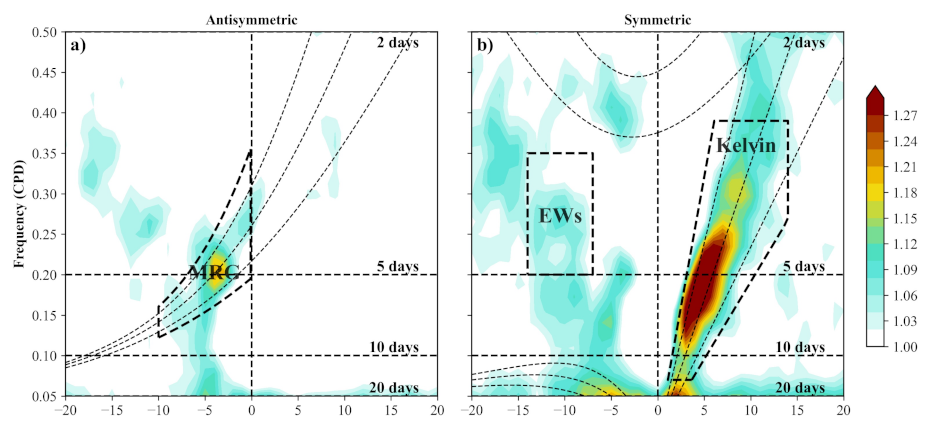
3.1. Wave Number-Frequency Power Spectra and Fourier Filters
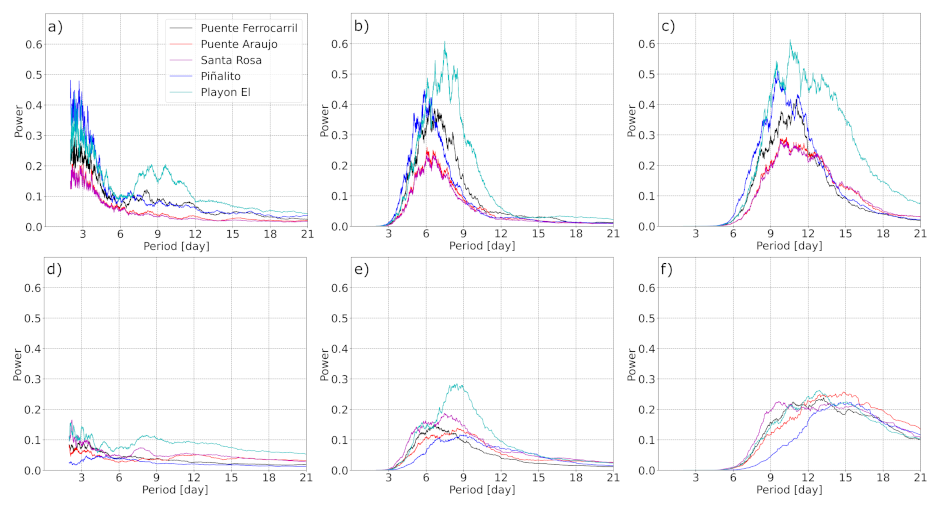
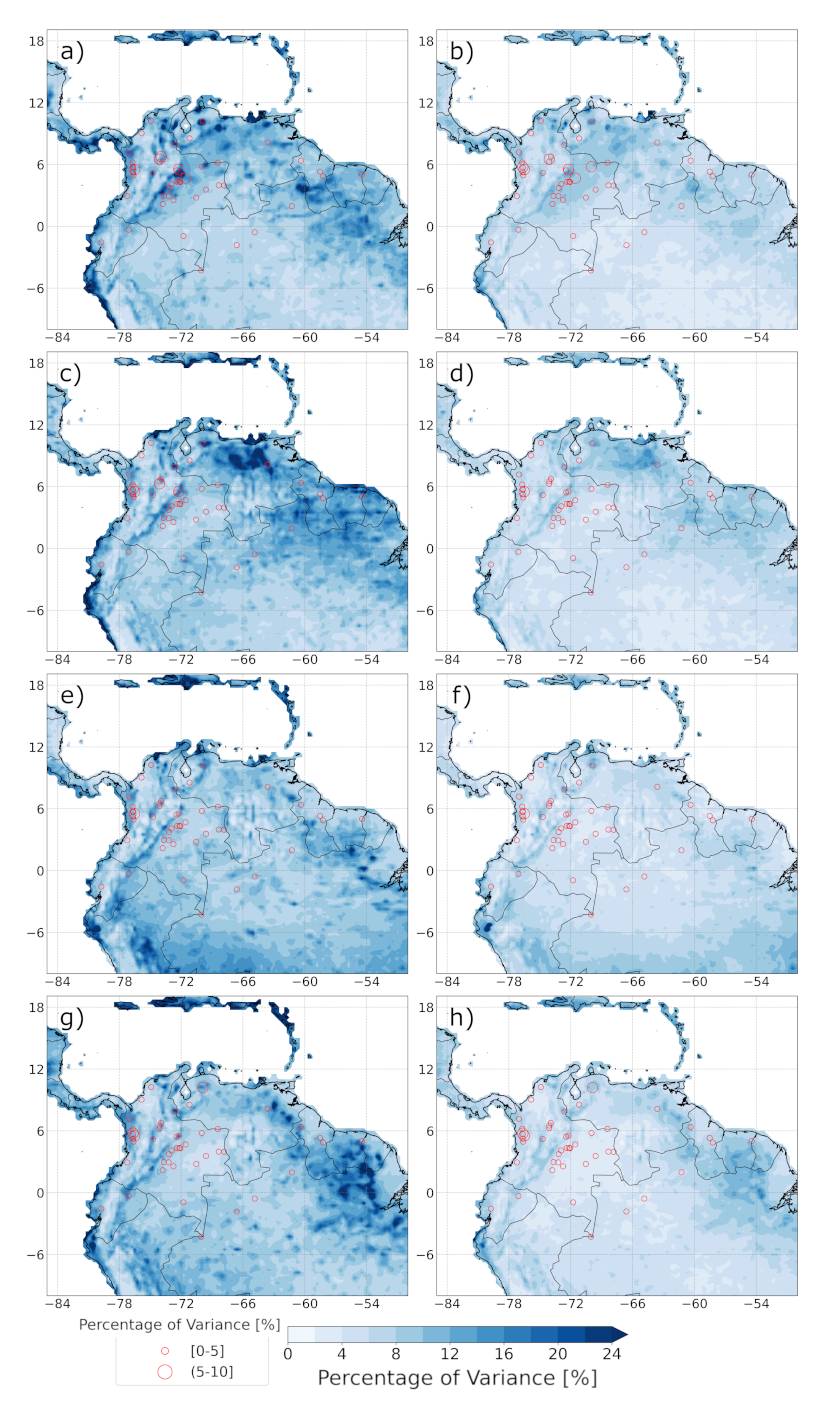
3.2. Synoptic Modes of Variability in Precipitation and Streamflows
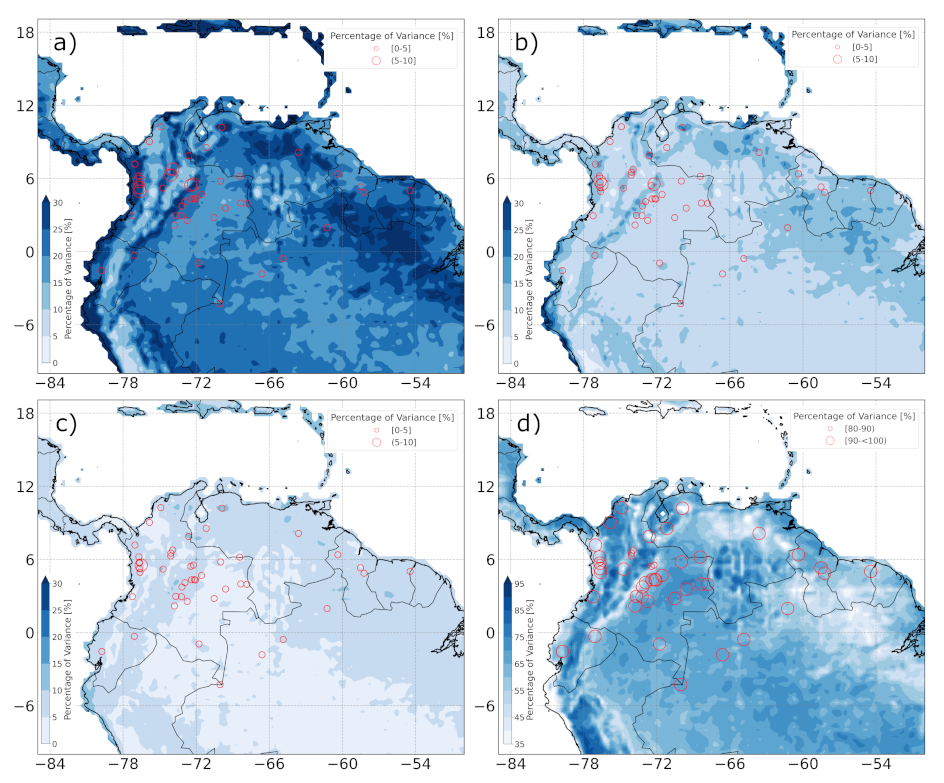
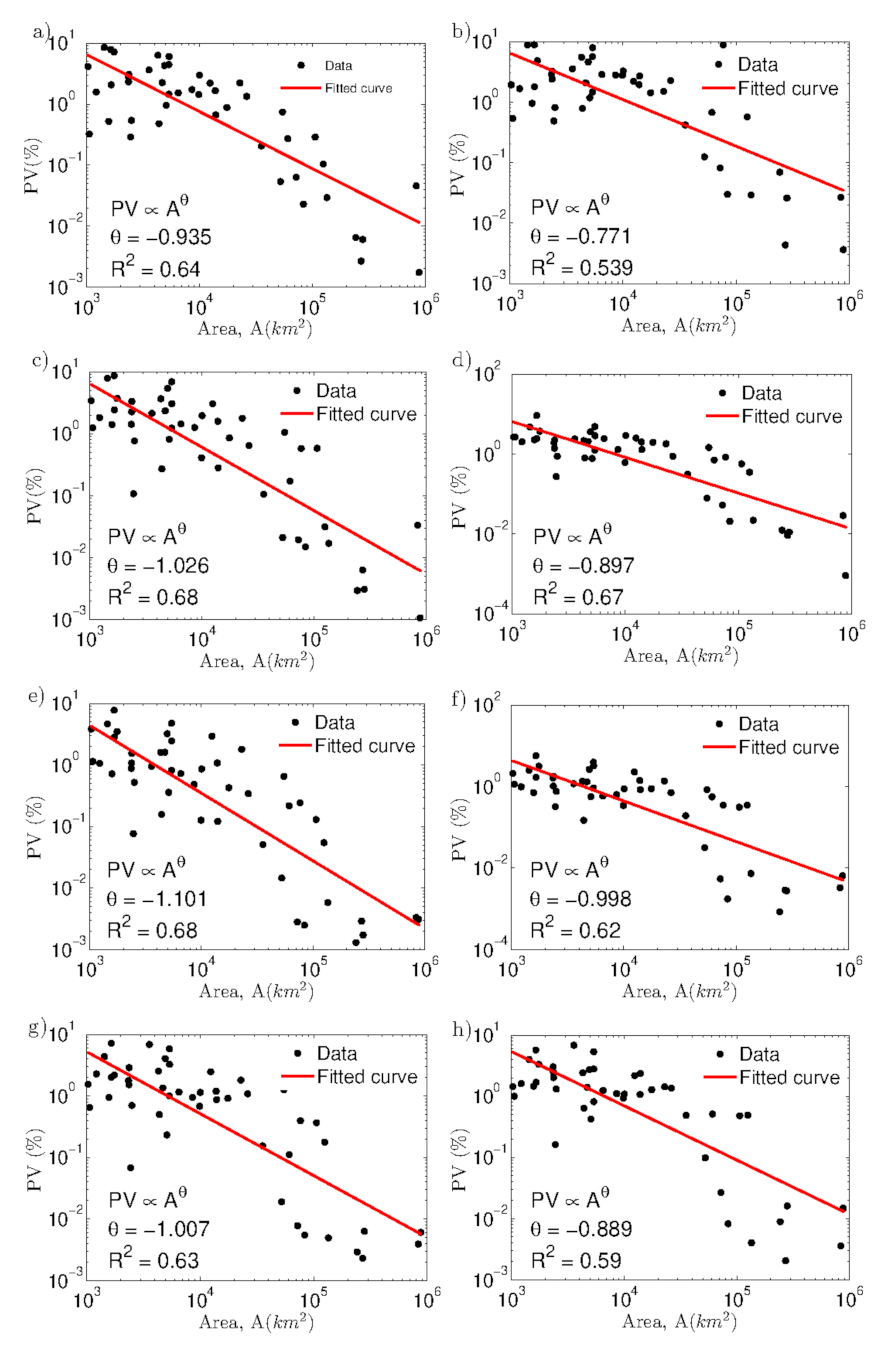
3.3. Variance Explained by the Synoptic Modes of Variability for Daily Streamflows and Its Relationship with the Area of Catchments
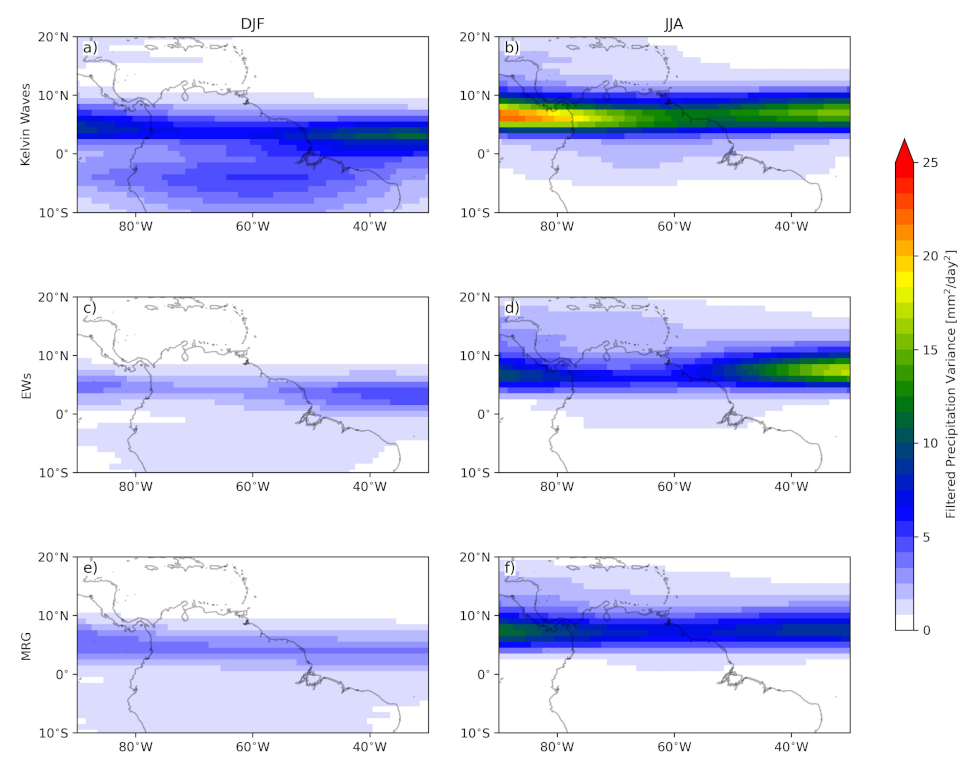
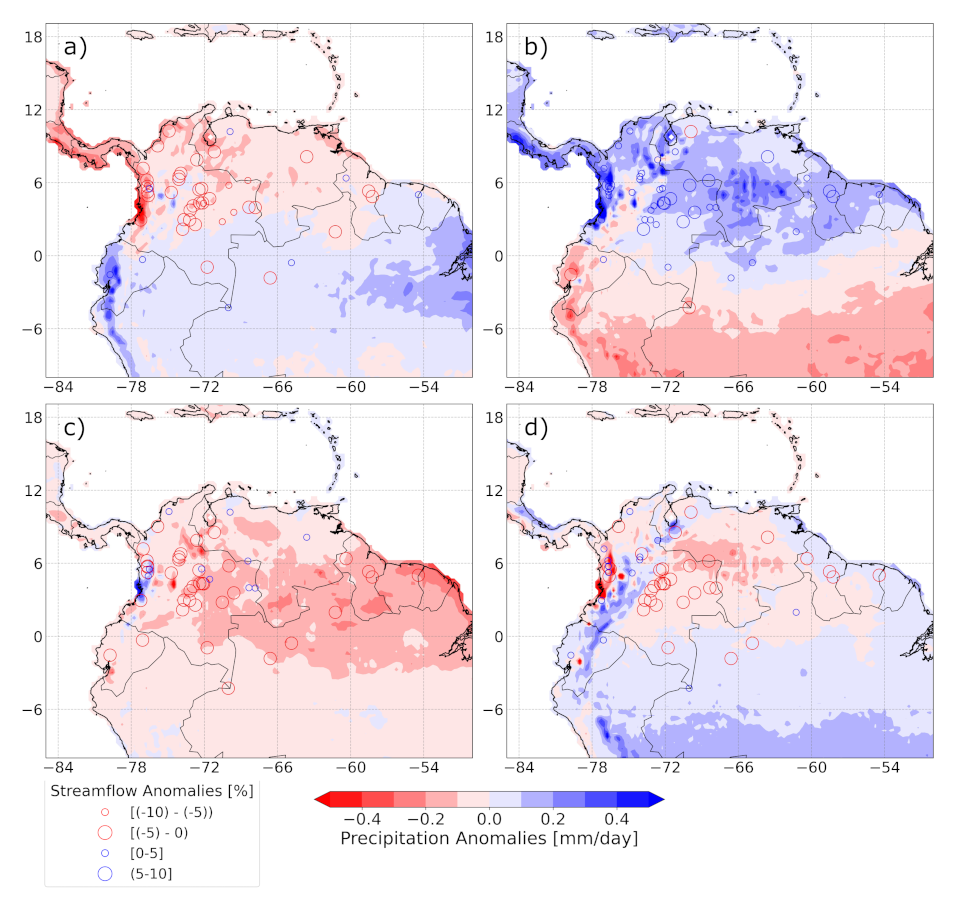
3.4. Seasonal Synoptic Anomalies
3.5. Seasonal Variance Explained by the Synoptic Modes of Variability
4. Conclusions
5. Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CHIRPS | climate hazards group infrared precipitation with station data |
| EEMD | ensemble empirical mode decomposition |
| EMD | empirical mode decomposition |
| EWs | easterly waves |
| GRDC | Global Runoff Data Centre |
| IDEAM | Instituto de Hidrología, Meteorología y Estudios Ambientales |
| IMF | intrinsic mode function |
| MCs | mesoscale convective systems |
| MRG | mixed Rossby-gravity waves |
| NSA | northern South America |
| SMV | synoptic mode of variability |
| SO-HYBAM | Sistema de Observación - HYdrogeoquímica de la Cuenca AMazónica |
| WIG | westward inertio-gravity waves |
References
- Garreaud, R.D.; Aceituno, P. Atmospheric Circulation and Climatic Variability. In The Physical Geography of South America; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Franzke, C.L.E.; Barbosa, S.; Blender, R.; Fredriksen, H.; Laepple, T.; Lambert, F.; Nilsen, T.; Rypdal, K.; Rypdal, M.; Scotto, M.G.; et al. The Structure of Climate Variability Across Scales. Rev. Geophys. 2020, 58, e2019RG000657. [Google Scholar] [CrossRef]
- Mekonnen, A.; Rossow, W.B. The Interaction Between Deep Convection and Easterly Waves over Tropical North Africa: A Weather State Perspective. J. Clim. 2011, 24, 4276–4294. [Google Scholar] [CrossRef]
- Cornforth, R.; Mumba, Z.; Parker, D.J.; Berry, G.; Chapelon, N.; Diakaria, K.; Diop-Kane, M.; Ermert, V.; Fink, A.H.; Knippertz, P.; et al. Synoptic Systems. In Meteorology of Tropical West Africa; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 40–89. [Google Scholar] [CrossRef]
- Li, W.; Liu, Z.; Luo, C. Characteristics of the synoptic time scale variability over the South China Sea based on Tropical Rainfall Measuring Mission. Meteorol. Atmos. Phys. 2012, 115, 163–171. [Google Scholar] [CrossRef]
- Wheeler, M.; Kiladis, G.N. Convectively Coupled Equatorial Waves: Analysis of Clouds and Temperature in the Wavenumber–Frequency Domain. J. Atmos. Sci. 1999, 56, 374–399. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Wheeler, M.C.; Haertel, P.T.; Straub, K.H.; Roundy, P.E. Convectively coupled equatorial waves. Rev. Geophys. 2009, 47, 1–42. [Google Scholar] [CrossRef]
- Dias, J.; Leroux, S.; Tulich, S.N.; Kiladis, G.N. How systematic is organized tropical convection within the MJO? Geophys. Res. Lett. 2013, 40, 1420–1425. [Google Scholar] [CrossRef]
- Agudelo, P.A.; Hoyos, C.D.; Curry, J.A.; Webster, P.J. Probabilistic discrimination between large-scale environments of intensifying and decaying African Easterly Waves. Clim. Dyn. 2011, 36, 1379–1401. [Google Scholar] [CrossRef]
- Dominguez, C.; Done, J.M.; Bruyère, C.L. Easterly wave contributions to seasonal rainfall over the tropical Americas in observations and a regional climate model. Clim. Dyn. 2020, 54, 191–209. [Google Scholar] [CrossRef]
- Jaramillo, L.; Poveda, G.; Mejía, J.F. Mesoscale convective systems and other precipitation features over the tropical Americas and surrounding seas as seen by TRMM. Int. J. Climatol. 2017, 37, 380–397. [Google Scholar] [CrossRef]
- Zuluaga, M.D.; Houze, R.A. Extreme Convection of the Near-Equatorial Americas, Africa, and Adjoining Oceans as seen by TRMM. Mon. Weather Rev. 2015, 143, 298–316. [Google Scholar] [CrossRef]
- Giraldo-Cardenas, S.; Arias, P.A.; Vieira, S.C.; Zuluaga, M.D. Easterly waves and precipitation over northern South America and the Caribbean. Int. J. Climatol. 2021. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Peixoto, J.P.; Oort, A.H.; Covey, C.; Taylor, K. Physics of Climate. Phys. Today 1992, 45, 67. [Google Scholar] [CrossRef]
- Siegert, C.M.; Leathers, D.J.; Levia, D.F. Synoptic typing: Interdisciplinary application methods with three practical hydroclimatological examples. Theor. Appl. Climatol. 2017, 128, 603–621. [Google Scholar] [CrossRef]
- Tarasova, L.; Merz, R.; Kiss, A.; Basso, S.; Blöschl, G.; Merz, B.; Viglione, A.; Plötner, S.; Guse, B.; Schumann, A.; et al. Causative classification of river flood events. WIREs Water 2019, 6, e1353. [Google Scholar] [CrossRef] [PubMed]
- Hunt, K.M.; Dimri, A. Synoptic-scale precursors of landslides in the western Himalaya and Karakoram. Sci. Total Environ. 2021, 776, 145895. [Google Scholar] [CrossRef]
- WMO. World Meteorological Organization. Meteorological Systems for Hydrological Purposes; Technical Report; WMO: Geneva, Switzerland, 2003. [Google Scholar]
- Duchon, C.E. Lanczos Filtering in One and Two Dimensions. J. Appl. Meteorol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Salas, H.D.; Carmona, A.; Poveda, G. Variabilidad interdiaria de la precipitación en Medellín (Colombia) asociada con las ondas tropicales del este y su comportamiento durante las fases del ENSO. In Proceedings of the XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA E HIDROLOGÍA, 2012; Available online: https://repositorio.unal.edu.co/handle/unal/10650 (accessed on 19 January 2022).
- Carmona, A.M.; Poveda, G. Detection of long-term trends in monthly hydro-climatic series of Colombia through Empirical Mode Decomposition. Clim. Chang. 2014, 123, 301–313. [Google Scholar] [CrossRef]
- Wang, W.c.; Chau, K.w.; Xu, D.m.; Chen, X.Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; hui Lei, X.; Wang, H.; hua Zhang, X.; jun You, J.; feng Tan, Q.; lian Liu, X. Teleconnection analysis of monthly streamflow using ensemble empirical mode decomposition. J. Hydrol. 2020, 582, 124411. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lu, W.; Xin, X.; Zhang, Y.; Cheng, W.; Yu, T. Monthly Rainfall Forecasting Using EEMD-SVR Based on Phase-Space Reconstruction. Water Resour. Manag. 2016, 30, 2311–2325. [Google Scholar] [CrossRef]
- Wu, Z.; Schneider, E.K.; Kirtman, B.P.; Sarachik, E.S.; Huang, N.E.; Tucker, C.J. The modulated annual cycle: An alternative reference frame for climate anomalies. Clim. Dyn. 2008, 31, 823–841. [Google Scholar] [CrossRef]
- Wu, M.L.C.; Reale, O.; Schubert, S.D. A Characterization of African Easterly Waves on 2.5–6-Day and 6–9-Day Time Scales. J. Clim. 2013, 26, 6750–6774. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Garreaud, R.; Poveda, G.; Arias, P.A.; Molina-Carpio, J.; Masiokas, M.; Viale, M.; Scaff, L. Hydroclimate of the Andes Part I: Main Climatic Features. Front. Earth Sci. 2020, 8, 64. [Google Scholar] [CrossRef]
- Arias, P.A.; Garreaud, R.; Poveda, G.; Espinoza, J.C.; Molina-Carpio, J.; Masiokas, M.; Viale, M.; Scaff, L.; van Oevelen, P.J. Hydroclimate of the Andes Part II: Hydroclimate Variability and Sub-Continental Patterns. Front. Earth Sci. 2021, 8. [Google Scholar] [CrossRef]
- Poveda, G.; Waylen, P.R.; Pulwarty, R.S. Annual and inter-annual variability of the present climate in northern South America and southern Mesoamerica. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 234, 3–27. [Google Scholar] [CrossRef]
- Ortega, G.; Arias, P.A.; Villegas, J.C.; Marquet, P.A.; Nobre, P. Present-day and future climate over central and South America according to CMIP5/CMIP6 models. Int. J. Climatol. 2021, 41, 6713–6735. [Google Scholar] [CrossRef]
- Braz, D.F.; Ambrizzi, T.; da Rocha, R.P.; Algarra, I.; Nieto, R.; Gimeno, L. Assessing the Moisture Transports Associated With Nocturnal Low-Level Jets in Continental South America. Front. Environ. Sci. 2021, 9, 657764. [Google Scholar] [CrossRef]
- Collins, J.M.; Chaves, R.R.; da Silva Marques, V. Temperature Variability over South America. J. Clim. 2009, 22, 5854–5869. [Google Scholar] [CrossRef][Green Version]
- Sörensson, A.A.; Ruscica, R.C. Intercomparison and Uncertainty Assessment of Nine Evapotranspiration Estimates Over South America. Water Resour. Res. 2018, 54, 2891–2908. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; et al. Global reanalysis: Goodbye ERA-Interim, hello ERA5. ECMWF Newsl. 2019, 159, 17–24. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Fekete, B.M.; Vörösmarty, C.J.; Grabs, W. High-resolution fields of global runoff combining observed river discharge and simulated water balances. Glob. Biogeochem. Cycles 2002, 16, 15. [Google Scholar] [CrossRef]
- Huaman, L.; Schumacher, C.; Kiladis, G.N. Eastward-Propagating Disturbances in the Tropical Pacific. Mon. Weather Rev. 2020, 148, 3713–3728. [Google Scholar] [CrossRef]
- Brueck, M.; Nuijens, L.; Stevens, B. On the Seasonal and Synoptic Time-Scale Variability of the North Atlantic Trade Wind Region and Its Low-Level Clouds. J. Atmos. Sci. 2015, 72, 1428–1446. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3. [Google Scholar] [CrossRef]
- Rato, R.; Ortigueira, M.; Batista, A. On the HHT, its problems, and some solutions. Mech. Syst. Signal Process. 2008, 22, 1374–1394. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Kammler, D.W. A First Course in Fourier Analysis; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Rose, C.; Smith, M.D. Mathematical Statistics with Mathematica; Springer: New York, NY, USA, 2002. [Google Scholar]
- Frasson, R.P.d.M.; Pavelsky, T.M.; Fonstad, M.A.; Durand, M.T.; Allen, G.H.; Schumann, G.; Lion, C.; Beighley, R.E.; Yang, X. Global Relationships Between River Width, Slope, Catchment Area, Meander Wavelength, Sinuosity, and Discharge. Geophys. Res. Lett. 2019, 46, 3252–3262. [Google Scholar] [CrossRef]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
- Galster, J.C. Natural and anthropogenic influences on the scaling of discharge with drainage area for multiple watersheds. Geosphere 2007, 3, 260. [Google Scholar] [CrossRef]
- Salazar, J.F.; Villegas, J.C.; Rendón, A.M.; Rodríguez, E.; Hoyos, I.; Mercado-Bettín, D.; Poveda, G. Scaling properties reveal regulation of river flows in the Amazon through a “forest reservoir”. Hydrol. Earth Syst. Sci. 2018, 22, 1735–1748. [Google Scholar] [CrossRef]
- Poveda, G.; Vélez, J.I.; Mesa, O.J.; Cuartas, A.; Barco, J.; Mantilla, R.I.; Mejía, J.F.; Hoyos, C.D.; Ramírez, J.M.; Ceballos, L.I.; et al. Linking Long-Term Water Balances and Statistical Scaling to Estimate River Flows along the Drainage Network of Colombia. J. Hydrol. Eng. 2007, 12, 4–13. [Google Scholar] [CrossRef]
- Wheeler, M.C.; Nguyen, H. Tropical Meteorology And Climate | Equatorial Waves. In Encyclopedia of Atmospheric Sciences, 2nd ed.; North, G.R., Pyle, J., Zhang, F., Eds.; Academic Press: Cambridge, MA, USA, 2015; pp. 102–112. [Google Scholar] [CrossRef]
- Matsuno, T. Quasi-Geostrophic Motions in the Equatorial Area. J. Meteorol. Soc. Japan. Ser. II 1966, 44, 25–43. [Google Scholar] [CrossRef]
- Straub, K.H.; Kiladis, G.N. Observations of a Convectively Coupled Kelvin Wave in the Eastern Pacific ITCZ. J. Atmos. Sci. 2002, 59, 30–53. [Google Scholar] [CrossRef]
- Wheeler, M.; Kiladis, G.N.; Webster, P.J. Large-Scale Dynamical Fields Associated with Convectively Coupled Equatorial Waves. J. Atmos. Sci. 2000, 57, 613–640. [Google Scholar] [CrossRef]
- Roundy, P.E.; Frank, W.M. A Climatology of Waves in the Equatorial Region. J. Atmos. Sci. 2004, 61, 2105–2132. [Google Scholar] [CrossRef]
- Serra, Y.L.; Rowe, A.; Adams, D.K.; Kiladis, G.N. Kelvin Waves during GOAmazon and Their Relationship to Deep Convection. J. Atmos. Sci. 2020, 77, 3533–3550. [Google Scholar] [CrossRef]
- Mayta, V.C.; Kiladis, G.N.; Dias, J.; Dias, P.L.S.; Gehne, M. Convectively Coupled Kelvin Waves Over Tropical South America. J. Clim. 2021, 34, 6531–6547. [Google Scholar] [CrossRef]
- Andrés-Doménech, I.; García-Bartual, R.; Montanari, A.; Marco, J.B. Climate and hydrological variability: The catchment filtering role. Hydrol. Earth Syst. Sci. 2015, 19, 379–387. [Google Scholar] [CrossRef]
- Molina, R.D.; Salazar, J.F.; Martínez, J.A.; Villegas, J.C.; Arias, P.A. Forest-Induced Exponential Growth of Precipitation Along Climatological Wind Streamlines Over the Amazon. J. Geophys. Res. Atmos. 2019, 124, 2589–2599. [Google Scholar] [CrossRef]
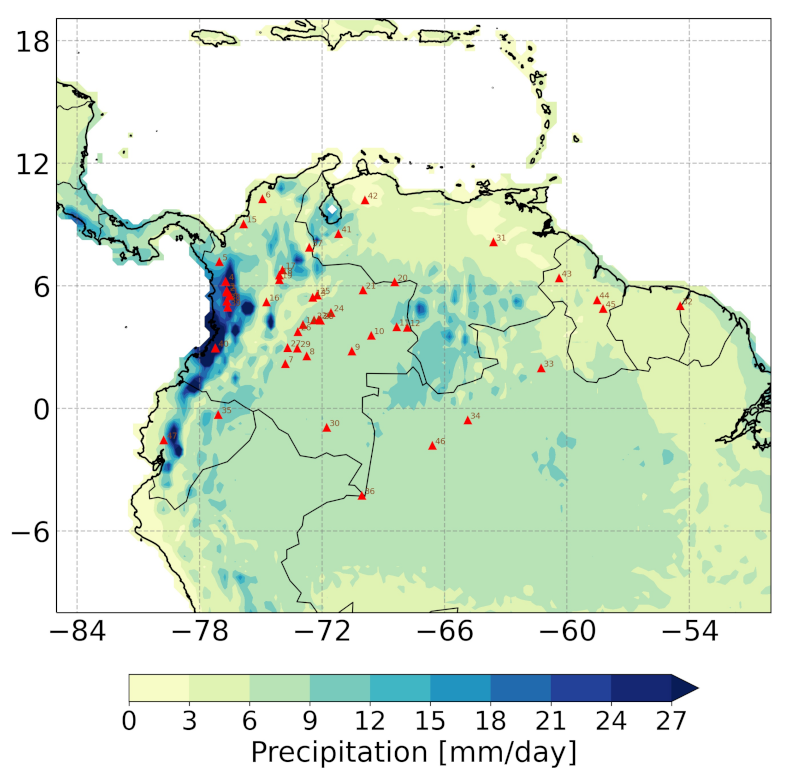
| Dataset | Number of Series | Period | Available |
|---|---|---|---|
| IDEAM | 30 | 2000–2010 | http://dhime.ideam.gov.co |
| SO–HYBAM | 6 | 2003–2013 | https://hybam.obs-mip.fr |
| GRDC | 11 | 1978–1988 | https://www.bafg.de/GRDC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas, H.D.; Valencia, J.; Builes-Jaramillo, A.; Jaramillo, A. Synoptic Time Scale Variability in Precipitation and Streamflows for River Basins over Northern South America. Hydrology 2022, 9, 59. https://doi.org/10.3390/hydrology9040059
Salas HD, Valencia J, Builes-Jaramillo A, Jaramillo A. Synoptic Time Scale Variability in Precipitation and Streamflows for River Basins over Northern South America. Hydrology. 2022; 9(4):59. https://doi.org/10.3390/hydrology9040059
Chicago/Turabian StyleSalas, Hernán D., Juliana Valencia, Alejandro Builes-Jaramillo, and Alejandro Jaramillo. 2022. "Synoptic Time Scale Variability in Precipitation and Streamflows for River Basins over Northern South America" Hydrology 9, no. 4: 59. https://doi.org/10.3390/hydrology9040059
APA StyleSalas, H. D., Valencia, J., Builes-Jaramillo, A., & Jaramillo, A. (2022). Synoptic Time Scale Variability in Precipitation and Streamflows for River Basins over Northern South America. Hydrology, 9(4), 59. https://doi.org/10.3390/hydrology9040059







