Abstract
Nowadays, the Mediterranean region is generally recognized as a climate change hot spot given its strong response to global warming, with relevant impacts on rainfall amount and distribution. Within this context, in this work the temporal variability of rainfall at annual, seasonal and monthly scale was analyzed in Italy using rainfall data extracted from the reanalysis dataset ERA5-Land during the period 1950–2020. In particular, rainfall trend magnitude and significance have been estimated by means of non-parametric tests applied to 3215 grid points falling within the Italian territory. The main results of this analysis evidenced only a few relevant trends at the annual scale, mostly involving northern Italy (positive trend) and the Sardinia region (negative trend). At seasonal scale, the results showed a marked negative trend in winter, characterizing almost all the Italian territory, while in the other seasons a positive trend was identified in the majority of grid points, especially in the Alps. Finally, at the monthly scale, September was identified as the month of the year with the highest percentage of grid points with positive trends mainly located in central, southern, and north-eastern Italy.
1. Introduction
The Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) provides the most up-to-date physical science understanding of climate change [1]. In this latest report, the anthropogenic influence on the existing state of the climate and how future climate may specifically affect different regions of the world are described. As a result, higher precipitation has been forecast worldwide, with the exception of few specific regions. These include the Mediterranean basin, which is considered as a prominent climate change hot spot [2]. In fact, in this area, an increase in hydrological, agricultural and ecological droughts has been observed as a consequence of the detected rainfall decrease. Moreover, considering a global warming of at least 2 °C, higher temperature extremes, an increase in droughts and aridity, a precipitation decrease, an increase in wildfires, a rise in mean and extreme sea levels, and a decrease in snow cover have been projected [1]. Due to the severe impacts of climate change in the Mediterranean basin, several studies on the temporal evolution of the main hydrological variables have been performed in this area, with particular attention been paid to rainfall. The results of these studies performed at different timescales, from monthly to annual, evidenced a general rainfall reduction in the western side of the Mediterranean basin [3,4]. In particular, several rainfall trend studies have focused on the Italian territory, although, due to the lack of a national database, these studies have essentially been conducted at a regional or slightly larger scale [5]. In fact, in Italy, data collection has been independently managed by the single regions since 1998; therefore, data significantly from differ one region to another with regard to time aggregation, quality and observation period. Anyway, the results of the regional studies performed in Italy mainly evidence a decrease in annual rainfall especially in the southern [6,7,8] and in the central regions of the country [9,10], while in its northern part, the decreasing tendencies in the annual values resulted rarely significant [11].
Recently, in order to overcome the lack of spatially distributed data, several global rainfall datasets have been created using different methodologies. Among these, the reanalysis is very popular because it produces a consistent time series of multiple climates by reprocessing meteorological data using the most recent models and the most up-to-date observation data [12]. Due to the advantages of global coverage and long time series, reanalysis is very suitable for application in many fields such as climate change [13,14], hydrological studies [15,16], water resource, and environmental management [17]. Obviously, both the differences between ground-based and satellite measurements, and between measurement and reanalysis datasets affect the magnitude and the variability of precipitation estimates [18]. In fact, past studies have evidenced these differences among reanalysis and the other types of datasets, such as the satellite or the rain gauge-based ones, showing large differences in the annual and seasonal estimates over the tropical oceans, in complex mountain areas, in northern Africa, and in some high-latitude regions [19]. Anyway, the ability of reanalysis products to reproduce the global precipitation tendency has been demonstrated in previous studies [20]. The climate global reanalysis produced by the European Center for Medium Weather Forecast (ECMWF), called European Reanalysis (ERA), is among the most well-known and used datasets. One of the first ECMWF projects was ERA-15 [21], launched in 1979, which produces a reanalysis for approximately 15 years using an optimal interpolation (OI) assimilation scheme. Reanalyses were available at 6-h intervals with a spatial resolution of 125 km. Another reanalysis product was the ERA-40 [22], which covered the period from 1957 to 2002 and benefited from the advances in computational resources and in observing systems, with the availability of assimilable data provided by a succession of satellite-borne instruments. This made it possible to implement a three-dimensional variational (3D-Var) assimilation scheme and to increase the vertical resolution of the model from the 31 levels used for ERA-15 to 60 levels of ERA-40. Resolution was added to the stratosphere and lower mesosphere and in the planetary boundary layer. Reanalysis was available at the same spacing (125 km) and time resolution (6 h) as for the ERA-15. Further improvement occurred with ERA-Interim [23], which made use of a 4D-Var assimilation scheme, and provided reanalysis data at 6-h time intervals with an improved spatial resolution (80 km). Progress in modelling and data assimilation resulted in systematically better forecast performance and a more accurate description of the hydrological cycle than ERA-40 [24]. Finally, the ERA5 dataset [25] is the fifth generation of reanalysis produced by ECMWF within the Copernicus Climate Change Service (C3S) of the European Commission. ERA5 assimilates a large number of atmospheric, satellite and ground-based observational data using a 4D-Var technique, and it can be considered a state-of-the-art global reanalysis. High-resolution hourly atmospheric data in ERA5 (reanalysis) are available with a spatial resolution of 31 km, from 1950 to almost real time.
The aim of this paper was to overcome the problem of data fragmentation in Italy to perform a trend analysis at the national scale. With this aim, data from the ERA5-Land reanalysis dataset from 1950 to 2020 were used to detect possible trends in annual, monthly and seasonal rainfall in Italy.
2. Materials and Methods
2.1. ERA5-Land
ERA5-Land is a replay of the land component of the ERA5 climate reanalysis at a finer horizontal resolution (9 km) and with a series of improvements making it more ac-curate for all types of land applications [26]. ERA5-Land does not assimilate additional observation data, but the evolution of the model is driven by the atmospheric fields obtained from the lowest ERA5 model level, which is 10 m above the surface, interpolated from the ERA5 resolution (31 km) to ERA5-Land resolution (9 km) via a linear interpolation method and with additional lapse-rate correction derived from ERA5 [27]. This operates an atmospheric forcing that indirectly takes into account the measurement data, and ensures better adherence to the reality of the obtained results. In this work, the total precipitation field of ERA5-Land was used, including both large-scale and convective precipitation [28]. This parameter represents the average, over the model grid box, of the total amount of water accumulated during a particular time period, calculated as accumulated liquid and frozen water, comprising rain and snow, falling to the Earth’s surface. The units of precipitation are depth in meters, representing the depth that water would have if it was spread evenly over the grid box. The accumulation fields in the ERA5-Land (with hourly steps from 1 to 24) are accumulated from the beginning of the forecast to the end of the forecast step. The maximum accumulation is over 24 h, and for the used convention, it corresponds to the accumulations ending at 00 UT. For the total precipitation field, it represents the daily total precipitation during the previous day. These daily data were downloaded from the Climate Data Store (CDS) for the entire time interval from 1950 to 2020, and subsequently aggregated to obtain the monthly accumulated precipitation. Figure 1 shows the 3215 grid points falling within the Italian territory.
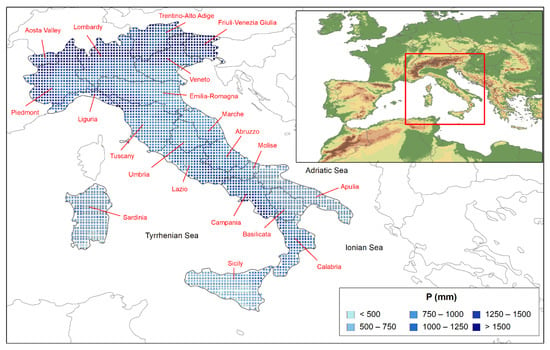
Figure 1.
Localization of the study area with an indication in red of the regions and spatial distribution of the average annual precipitation during the period 1950–2020.
2.2. Case Study
The Mediterranean basin can be considered one of the most socio-politically important areas in the world, connecting three continents (Europe and its southern peninsulas to the north, southwestern Asia to the east, and the Maghreb region of northern Africa to the south) and counting twenty-one countries making up its coastline [29]. Among these countries, Italy can be considered particularly important from a climatological point of view due to its long shape, spreading over more than ten degrees of latitude from north to south, to its position in the middle of the western Mediterranean and to the distribution of mountains in its territory [30]. In fact, Italian climate is affected by these features and presents dry, warm summers (on average over 22 °C) and moderate wet winters (Mediterranean climate). Specifically, following the Koppen–Geiger classification [31], it is characterized by two different climatic groups, a temperate/mesothermal climate affecting the peninsular regions and the islands, and a continental/microthermal climate in the northern and north-eastern areas of the country.
Figure 1 and Figure 2 show, respectively, the mean annual and seasonal rainfall evaluated during the observation period for the 3215 grid points falling within the Italian territory.
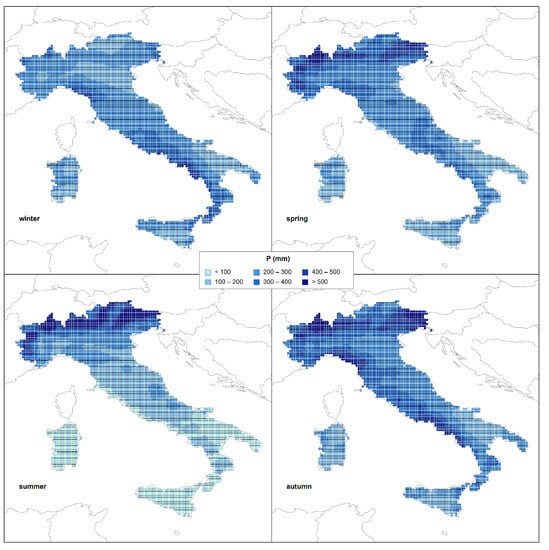
Figure 2.
Average seasonal precipitation during the period 1950–2020.
2.3. Trend Analysis
In order to evaluate the trend magnitude, the Theil–Sen estimator was applied [32]. The slope estimates of N pairs of monthly or seasonal or annual rainfall pairs were evaluated with the following equation:
in which Pj and Pi are the rainfall values at time tj and ti (j > i), respectively.
The N values of Qk must be ranked from smallest to largest and then the median of these N values is the Theil–Sen estimator of slope calculated as
The non-parametric Mann–Kendall test [33,34] was further applied to assess the statistical significance of the trends.
The test statistic S is evaluated with the following equation:
in which n is the number of data, P is the rainfall value at times i and j (j > i) and sgn is a function given as
The variance of S is evaluated as
in which ti is the number of ties of extent i and m is the number of tied rank groups.
For n larger than 10, the standard normal Z test statistic is evaluated as the Mann–Kendall test statistic as follows:
By applying a two-tailed test, for a specified significance level α, the significance of the trend can be evaluated.
3. Results
Table 1 summarizes the results of the trend analysis applied to the annual seasonal and monthly rainfall values, for a significance level equal to 90%. As regards the yearly values, the results, expressed as percentages of grid points, show that the majority of the grid points (approximately 86%) do not present significant trends. Only 9.5% of the grid points present positive tendencies, with a maximum rate higher than 40 mm/10 years, localized in the northern areas of Italy and in an area in the south of the country, between Apulia and Basilicata (Figure 3). On the contrary, significant negative trends (4.8%) are mainly present in the Sardinia region, in a small part of Sicily and in a few grid points in the Tyrrhenian side in both northern and southern Italy. In this latter area, the negative rates reach values lower than −20 mm/10 years (Figure 3).

Table 1.
Percentages of the grid points showing positive or negative trends.
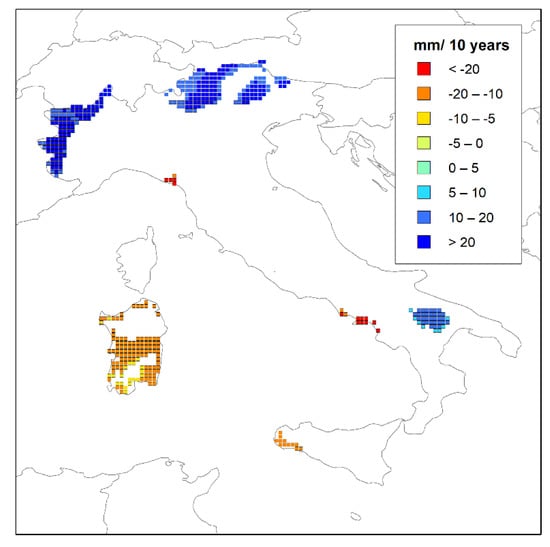
Figure 3.
Spatial distribution of the trend results at annual scale.
For the trend analysis performed at the seasonal scale, seasons were divided considering December, January and February as winter, March, April and May as spring, June, July and August as summer and September, October and November as autumn. The results evidence different trends among the seasons, as summarized in Table 1 and showed in Figure 4, Figure 5, Figure 6 and Figure 7.
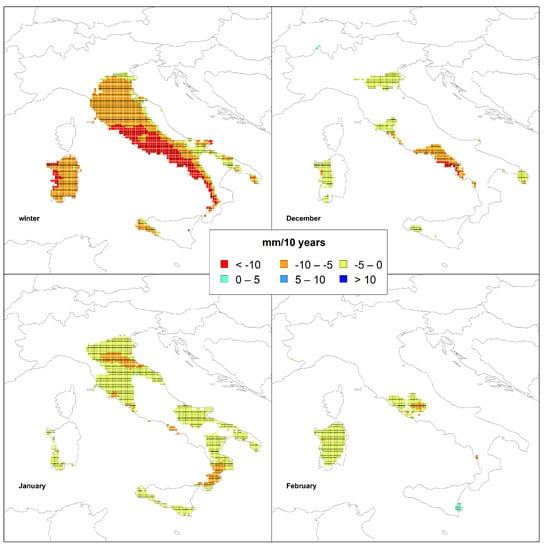
Figure 4.
Spatial distribution of the trend results in winter.
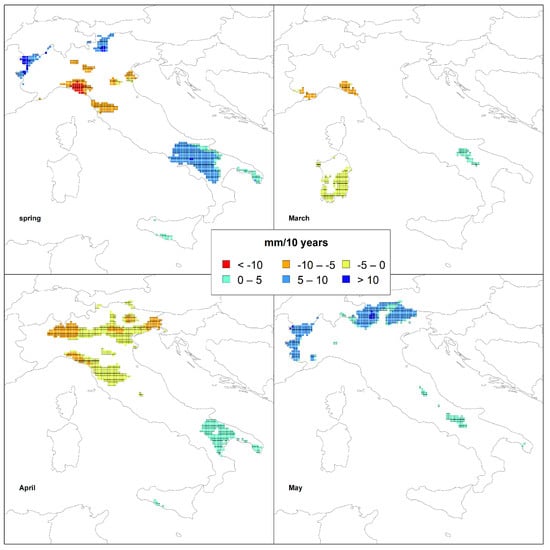
Figure 5.
Spatial distribution of the trend results in spring.
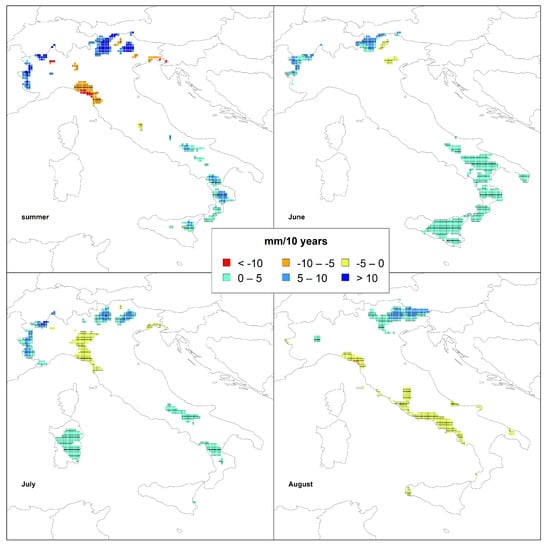
Figure 6.
Spatial distribution of the trend results in summer.
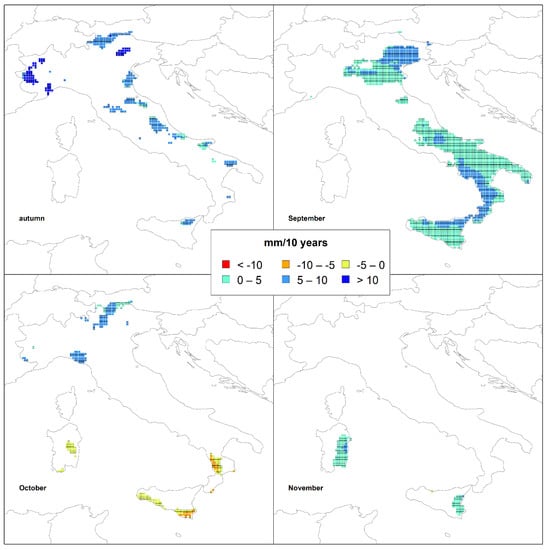
Figure 7.
Spatial distribution of the trend results in autumn.
In winter, a prevalent negative tendency was detected, with 44% of grid points presenting significant values and with only a grid point showing a positive trend (Table 1). Figure 4 displays the spatial results of these negative trends, mainly identified in central Italy, on the Tyrrhenian side of central and southern Italy, in Sardinia, in Sicily, in Apulia and in few areas of the Adriatic side of the country. In particular, in some areas of the Tyrrhenian side, the negative rates are lower than −20 mm/10 years. The only grid point with a positive trend was identified in Sicily with a rate of approximately +9 mm/10 years.
This trend behavior, detected at a seasonal scale in winter, was confirmed at the monthly scale. January (Table 1) is the month with the largest distribution of grid points presenting negative significant trends (approximately 34%). The lowest rates (approximately −8 mm/10 years) were mainly identified (Figure 4) in the central and southern side of the Calabria region, in some inner areas between northern and central Italian peninsula and in small areas on the Tyrrhenian side of the country. Other negative significant trends, but with rates of few millimeters in 10 years, were identified on the western side of Sardinia, in the southern part of Sicily and in some areas of southern and central Italy. In December, approximately 13% of grid points (Table 1) present significant negative trends while only two grid points, located on the Alps, show positive tendencies. The lowest magnitudes (lower than −10 mm/10 years) were detected in grid points located on the Tyrrhenian side of central Italy, between Campania and Lazio. Negative trends, but with small rates, have also been identified in Sardinia, in Sicily, in Apulia, and in some areas of central and northern Italy (Figure 4). February (Table 1) is the winter month with the lowest percentage of negative trends (only approximately 10%), mainly located in Sardinia and in central Italy (Figure 4). Conversely, there are nine grid points in the south-eastern side of Sicily showing increasing trends with a maximum rate of approximately 6 millimeters in 10 years.
Regarding spring, the results show opposite tendencies in the Italian territory (Table 1), with approximately 13% of grid points evidencing a positive trend and approximately 5% of the grid points presenting negative values. The increasing values are located in a large area of central-southern Italy (with rates also higher than +10 mm/10 years), on the Alps and in few grid points in Sicily (Figure 5).
Instead, the negative trends are located in small areas of central and northern Italy, with rates of approximately −10 mm/10 years. On a monthly scale, May is the spring month with the highest number of grid points (approximately 12%) presenting positive trends (Table 1), mainly located in northern Italy and especially across the Alps, with a maximum rate equal to +11.3 mm/10 years (Figure 5). Conversely, April is the month with the highest percentage (approximately 17%) of grid points showing negative tendencies (with rates of approximately −8 mm/10 years), mainly located in north-central Italy. Always in April, 5% of the grid points, all located in the southern part of the Italian peninsula, also showed negative trends. The lowest percentages of both positive (approximately 1%) and negative (approximately 5%) trends among the spring months were identified in March. The negative results were mainly identified in Sardinia and in Liguria, while the positive ones in small inner areas of southern Italy.
Summer comprises 10% of the grid points with positive trends (Table 1), mainly located in the Alps and in southernmost regions of Italy (Figure 6).
The highest rate is approximately +21 mm/10 years, detected in small areas of northern Italy (near the Alps). In this season, approximately 3% of grid points also showed negative trends, located only in small areas of northern Italy. Among the summer months, June is the one presenting the highest number of grid points with a positive tendency (17%), located in southern Italy and in the Alps, where the maximum rate of approximately +10 mm/10 years was evaluated (Table 1 and Figure 6). In July, 12.5% of the grid points (Table 1) across the Alps, in Sardinia and in central-southern Italy evidenced increasing rainfall values (Figure 6), while an opposite behavior was identified in 4% of the grid points located in a large area of northern Italy (with rates of approximately −5 mm/10 years). August is the only summer month in which the number of grid points with negative tendencies is higher than the one with positive trends: 7.1% vs. 5.3%, respectively (Table 1). Figure 6 shows the clear contrast between these different tendencies in August, with negative values in some areas of the Tyrrhenian and opposite trends in the north-eastern side of Italy.
Finally, autumn is the season with the highest percentage of grid points (Table 1) and no significant trends (approximately 90%). In fact, only slightly more than 300 grid points (approximately 10%) showed positive trends identified in several clusters distributed across the Italian peninsula (Figure 7), with the highest magnitude of approximately +16 mm/10 years. September is the month of the year in which the highest percentage (approximately 43%) of grid points with positive trends was identified (Table 1), although the maximum rate is approximately +8 mm/10 years (Figure 7). These points are mainly located in central, southern, and in an area of north-eastern Italy. In contrast with September, November is absolutely the month of the year with the lowest number of grid points with significant trends (approximately 4%). In fact, only 119 grid points in Sardinia and Sicily present positive trends, with a maximum rate of approximately +6 mm/10 years (Figure 7). In October, the percentage of grid points presenting negative or positive trends is quite similar (3.9% vs. 3.7%). The negative values are located in Calabria, Sicily, and Sardinia, with a maximum magnitude of approximately 7 mm/10 years in absolute value, while the positive trends are located in small areas of northern Italy with a maximum rate of approximately 10 mm/10 years.
4. Discussion
The results of this study represent an evaluation of the rainfall tendency on a large territory, such as the Italian peninsula. This analysis was made possible by means of the use of the ERA5-Land reanalysis dataset that allows one to also have data in areas without rain gauges or lacking several data. For these problems, having an alternative data source can be very useful considering the limitations present in these datasets. As an example, the reanalysis products can approximately reproduce the seasonal variations in nighttime and daytime rainfall, but not always the contrast between nighttime and daytime [35]. Additionally, the reanalysis outputs usually overestimate drizzle and light rainfall frequencies and, at the same time, underestimate the extreme rainfall frequency, failing to capture extreme precipitation [36]. Moreover, a large overestimation of the summer rainfall can also occur over land areas, mainly due to extreme convective precipitation [37]. Anyway, previous studies have demonstrated the ability of reanalysis products in reproducing the rainfall tendency [20]. In order to deal with the problem of reproducing the different variables, the ERA5 dataset provides an associated 10-member Ensemble of Data Assimilations (EDA) system [38], which has lower spatial (60 km) and temporal (3 h) resolution. This ensemble is required for the 4D-Var data assimilation procedure, but it can also be used for an estimate of the relative random uncertainty of the ERA5 high-resolution realization. The dispersion of the values obtained from the ensemble provides, in fact, an overall measure of the uncertainty of the model used, to be understood as an estimate of the relative accuracy of the ERA5 (or ERA5-Land [39]) system. It is important to emphasize that the uncertainty defined by the ensemble is not a classical measure of the error of the reanalysis products, and should not be used at face value but to have an estimate of the areas and periods in which the products are more or less reliable [40]. Unfortunately, uncertainty estimates are only available for authorized users of ECMWF.
The results obtained in this study highlight that on a yearly scale, no diffuse significant trends have been detected, while on a seasonal scale, especially in winter, some negative tendencies are clearer. These outputs seem to be in contrast with the results obtained in regional analysis, specifically for the Italian territory, by means of annual data measured by rainfall stations [8,9,10]. Anyway, within these comparisons, it is necessary to highlight that the observation period is often different: as such, severe drought periods present in some timespans of the observation period can largely influence the trend detection [30]. Nevertheless, the results obtained both in this and previous works show that a poor trend detection on a yearly scale often hides important seasonal tendencies e.g., [41]. In particular, the impact of global warming on the seasonal distribution of rainfall for the study area could determine the long dry spell in seasons usually considered recharge periods for superficial and deep water bodies. This impact could severely influence water availability for large areas.
5. Conclusions
In this paper, the temporal variability of rainfall at annual, seasonal and monthly scale was analyzed in Italy using rainfall data extracted from the reanalysis dataset ERA5-Land during the period 1950–2020. The use of the ERA5-Land dataset allowed us to perform a spatially distributed analysis at national scale, thus overcoming the major problem of the rain gauge networks providing only point measurements and presenting lacking data in the rainfall series. Results did not evidence marked significant trends on a yearly scale but, on the contrary, enabled us to identify some negative tendencies on a seasonal scale, especially in winter, in several areas of Italy and with high magnitude. This is an important output for the impact that these tendencies can have on water resource management, because the winter season in the Mediterranean climate is often a rainy period useful for the recharge of superficial and deep water bodies. This impact of global warming, if confirmed in the future, could determine severe droughts in large sections of the study area.
Author Contributions
Conceptualization, T.C.; methodology, F.C., T.C. and R.C.; software, F.C. and T.C.; formal analysis, F.C. and T.C.; validation: R.C. and T.C.; investigation, F.C. and T.C.; data curation, F.C. and T.C.; writing—original draft preparation, F.C., T.C. and R.C.; writing—review and editing, F.C., T.C and R.C.; visualization, T.C.; supervision, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Tuel, A.; Eltahir, E.A.B. Why Is the Mediterranean a Climate Change Hot Spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018, 32, 433–445. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Vicente-Serrano, S.M.; Domínguez-Castro, F.; Murphy, C.; Reig, F.; Tramblay, Y.; Trigo, R.M.; Luna, M.Y.; Turco, M.; Noguera, I.; et al. Long-term precipitation in Southwestern Europe reveals no clear trend attributable to anthropogenic forcing. Environ. Res. Lett. 2020, 15, 094070. [Google Scholar] [CrossRef]
- Caloiero, T.; Caroletti, G.N.; Coscarelli, R. IMERG-Based Meteorological Drought Analysis over Italy. Climate 2021, 9, 65. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Montaldo, N.; Sarigu, A. Potential links between the North Atlantic Oscillation and decreasing precipitation and runoff on a Mediterranean area. J. Hydrol. 2017, 553, 419–437. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Gaudio, R.; Leonardo, G.P. Precipitation trend and concentration in the Sardinia region. Theor. Appl. Climatol. 2019, 137, 297–307. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Leopardi, M. Precipitation and temperature trends over central Italy (Abruzzo Region): 1951–2012. Theor. Appl. Climatol. 2019, 135, 959–977. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Lee, H.S.; Zardi, D. Analysis of Rainfall Trends and Extreme Precipitation in the Middle Adriatic Side, Marche Region (Central Italy). Water 2019, 11, 1948. [Google Scholar] [CrossRef] [Green Version]
- Todeschini, S. Trends in long daily rainfall series of Lombardia (northern Italy) affecting urban stormwater control. Int. J. Climatol. 2012, 32, 900–919. [Google Scholar] [CrossRef]
- Caroletti, G.N.; Coscarelli, R.; Caloiero, T. Validation of Satellite, Reanalysis and RCM Data of Monthly Rainfall in Calabria (Southern Italy). Remote Sens. 2019, 11, 1625. [Google Scholar] [CrossRef] [Green Version]
- Chinita, M.J.; Richardson, M.; Teixeira, J.; Miranda, P.M.A. Global mean frequency increases of daily and sub-daily heavy precipitation in ERA5. Environ. Res. Lett. 2021, 16, 074035. [Google Scholar] [CrossRef]
- Kireeva, M.; Frolova, N.; Rets, E.; Samsonov, T.; Entin, A.; Kharlamov, M.; Telegina, E.; Povalishnikova, E. Evaluating climate and water regime transformation in the European part of Russia using observation and reanalysis data for the 1945–2015 period. Int. J. River Basin Manag. 2020, 18, 491–502. [Google Scholar] [CrossRef]
- Nkiaka, E.; Nawaz, N.R.; Lovett, J.C. Evaluating Global Reanalysis Datasets as Input for Hydrological Modelling in the Sudano-Sahel Region. Hydrology 2017, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Pelosi, A.; Terribile, F.; D’Urso, G.; Chirico, G.B. Comparison of ERA5-Land and UERRA MESCAN-SURFEX Reanalysis Data with Spatially Interpolated Weather Observations for the Regional Assessment of Reference Evapotranspiration. Water 2020, 12, 1669. [Google Scholar] [CrossRef]
- Hassler, B.; Lauer, A. Comparison of Reanalysis and Observational Precipitation Datasets Including ERA5 and WFDE5. Atmosphere 2021, 12, 1462. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Li, Y.; Qin, S.; Mao, Y.; Wang, K. Precipitation unevenness in gauge observations and eight reanalyses from 1979 to 2018 over China. J. Clim. 2021, 34, 9797–9810. [Google Scholar] [CrossRef]
- Gibson, J.K.; Kållberg, P.; Uppala, S.; Hernandez, A.; Nomura, A.; Serrano, E. ECMWF Re-Analysis Project Report Series 1. Available online: https://www.ecmwf.int/sites/default/files/elibrary/1997/9584-era-description.pdf (accessed on 21 December 2021).
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; Da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, d.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Simmons, A.; Uppala, S.; Dee, D.; Kobayashi, S. ERA-Interim: New ECMWF Reanalysis Products from 1989 Onwards. In ECMWF Newsletter, No. 110; ECMWF: Reading, UK, 2007; Volume 110, pp. 25–35. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Dutra, E.; Muñoz-Sabater, J.; Boussetta, S.; Komori, T.; Hirahara, S.; Balsamo, G. Environmental Lapse Rate for High-Resolution Land Surface Downscaling: An Application to ERA5. Earth Space Sci. 2020, 7, e2019EA000984. [Google Scholar] [CrossRef] [Green Version]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1950 to 1980, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2021. Available online: https://cds.climate.copernicus.eu/cdsapp#!/datashomet/reanalysis-era5-land?tab=overview (accessed on 21 December 2021).
- UNEP/MAP. State of the Mediterranean Marine and Coastal Environment; UNEP/MAP—Barcelona Convention: Athens, Greece, 2012; Available online: http://www.undp.org/content/dam/turkey/docs/Publications/EnvSust/akdenizrapor.pdf (accessed on 21 December 2021).
- Caloiero, T.; Caroletti, G.N.; Coscarelli, R. TRMM-based rainfall temporal analysis over Italy. SN Appl. Sci. 2020, 2, 1270. [Google Scholar] [CrossRef]
- Köppen, W. Das Geographische System der Klimate. Handbuch der Klimatologie; Köppen, W., Geiger, R., Eds.; Verlag von Gebrüder Borntraeger: Berlin, Germany, 1936; Volume 1, pp. 1–44. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin & Company Limited: London, UK, 1962. [Google Scholar]
- Zhou, C.; Wang, K. Contrasting Daytime and Nighttime Precipitation Variability between Observations and Eight Reanalysis Products from 1979 to 2014 in China. J. Clim. 2017, 30, 6443–6464. [Google Scholar] [CrossRef]
- He, S.; Yang, J.; Bao, Q.; Wang, L.; Wang, B. Fidelity of the Observational/Reanalysis Datasets and Global Climate Models in Representation of Extreme Precipitation in East China. J. Clim. 2019, 32, 195–212. [Google Scholar] [CrossRef]
- Serreze, M.C.; Hurst, C.M. Representation of Mean Arctic Precipitation from NCEP–NCAR and ERA Reanalyses. J. Clim. 2000, 13, 182–201. [Google Scholar] [CrossRef]
- Isaksen, L.; Bonavita, M.; Buizza, R.; Fisher, M.; Haseler, J.; Leutbecher, M.; Raynaud, L. Ensemble of Data Assimilations at ECMWF.; ECMWF: Reading, UK, 2010; Available online: https://www.ecmwf.int/en/elibrary/10125-ensemble-data-assimilations-ecmwf (accessed on 21 December 2021).
- Jedlička, K.; Valeš, J.; Hájek, P.; Kepka, M.; Pitoňák, M. Calculation of Agro-Climatic Factors from Global Climatic Data. Appl. Sci. 2021, 11, 1245. [Google Scholar] [CrossRef]
- Hennermann, K. ERA5 Uncertainty Estimation. 2020. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+uncertainty+estimation (accessed on 21 December 2021).
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).