Abstract
The Nilwala river basin is prone to frequent flooding during the southwest monsoon and second intermonsoon periods. Several studies have recommended coupling 1D and 2D models for flood modelling as they provide sufficient descriptive information of floodplains with greater computational efficiency. This study aims to couple a 1D hydrological model (HEC-HMS) with a 2D hydraulic model (iRIC) to simulate flooding in the Nilwala river basin. Hourly rainfall and streamflow data of three flood events were used for calibration and validation of HEC-HMS. The model performed exceptionally well considering the Nash–Sutcliffe coefficient, percent bias, and root mean square error. The flood event of May 2017 was simulated on iRIC using the streamflow hydrographs modelled by HEC-HMS. An overall accuracy of 81.5% was attained when the simulated extent was compared with the surveyed flood extent. The accuracy of the simulated flood depth was assessed using the observed water level at Tudawa gauging station, which yielded an NSE of 0.94, PBIAS of −4.28, RMSE of 0.18 and R2 of 0.95. Thus, the coupled model provided an accurate estimate of the flood extent and depth and can be further developed for hydrological flood forecasting on a regional scale.
1. Introduction
A significant consequence of climate change is the increased frequency and intensity of extreme weather events [1]. Germanwatch described Sri Lanka as being among the top ten most affected countries due to climate change in 2018, with a global climate risk index of 19.0 [2]. Regional studies conducted on rainfall trends in Sri Lanka have indicated both increasing and decreasing patterns [3,4,5]. It was found that there was a higher tendency for short-duration high-intensity rainfall events to occur within the island [4], which often resulted in water-related natural hazards. Floods are destructive and occur more frequently than other natural disasters [6], with Asia being one of the most affected regions [7]. The Fifth Assessment Report of the IPCC states with medium confidence that the magnitude and frequency of recent floods are comparable to or surpass historical floods [1].
Sri Lanka was recently devastated by floods and landslides due to heavy southwest monsoonal rainfall in May 2017. This natural disaster led to 219 deaths, affecting approximately 230,000 families [8]. The most adversely affected districts by this disaster were Kalutara, Galle, Matara, Hambantota, and Ratnapura. Flooding occurred in towns, villages, and agricultural land bordering the Kalu, Nilwala, and Gin rivers. Matara city is located in the floodplain of the Nilwala river basin, an area prone to flooding at the onset of the southwest monsoonal rains. Matara is the administrative capital of the Matara district and is considered a commercial hub. The risk of flooding is significantly greater in urban areas, such as Matara city where impervious surfaces prevent infiltration and cause runoff to generate quickly [9].
A past study identified precipitation within the basin increases from the south to the north with an increasing elevation [10]. Thus, a significant proportion of the rainfall that contributes to flooding in the lower coastal plains occurs in the basin’s upper region. There is a considerable period of time for extreme precipitation in upper Nilwala to accumulate into floods in the lower coastal floodplains. With the recent advances in information and communication technology, this study aims to assess the feasibility of applying a 1D–2D coupled model to simulate flooding in real-time that could provide sufficient lead time for evacuation and disaster preparation.
The Post Disaster Needs Assessment (PDNA) was conducted following the disaster in 2017 and identified several vital interventions: strengthening of the country’s early warning system, the conduction of hazard risks, and vulnerability assessments were points focused on. Moreover, studies have shown that mortalities caused by floods depend on the scale or severity of the flood, the possibility of an early warning mechanism, and evacuation [11]. Computational models can be used to understand the nature of the flood and simulate hydrological responses to various control measures [12]. They can also generate flood risk maps for planning and developing the resiliency of high-risk regions [13]. The existing early warning system of the Nilwala river basin consists of a network of water gauging stations with extreme water levels categorized as alert, minor flood, and major flood. Flood warnings are issued based on this water level and its trend. There remains room for improvement of the system through flood modeling.
Hydraulic models can be classified dimensionally as 1D, 2D, and 3D models. Three-dimensional models were developed relatively recently, requiring more descriptive parameters that remain unavailable for most basins [14]. The simplest representation of flow in a stream is as a one-dimensional flow in a longitudinal direction. Although these models are computationally efficient, they demonstrate certain limitations; namely the topological discretization of topography as cross-sections of the floodplain [15], the subjectivity of the location and orientation of cross-sections, and the incapability of simulating lateral diffusion of the flood wave [16]. A 2D model solves for water flow equations, both in longitudinal and lateral planes by using either finite element or finite volume analysis methods [17]. They can provide additional detailed information on the floodplain and allow the visualization of flood extent, but are computationally more demanding, requiring greater processing power and storage capacity.
In this study, we coupled a 1D hydrological model to a 2D hydraulic model. The upper portion of the basin is modelled one-dimensionally to carry the flood wave to the two-dimensionally modelled coastal floodplains, which is an urban area with a high risk of flooding. The coupled model will generate comprehensive information of the floodplain with greater computational efficiency [13]. The coupled model allows one to alter the roughness coefficient of the simulation extent, provide a more detailed description of the topography, simulate overland flow, and can be easily visualized as two-dimensional maps [12]. Teng et al., [18] describes several methods to couple a 1D model with a 2D model. These include; modelling a section of the stream in 1D and the rest in 2D, coupling a 1D drainage model with a 2D flood model [19], and coupling a 1D river model with a 2D floodplain model [14,20,21]. This study uses the second approach, where Hydrologic Engineering Center—Hydrologic Modelling System (HEC-HMS) is used to simulate drainage in upper Nilwala and is externally coupled with the 2D hydraulic model, the Nays2DFlood solver, in the International River Interface Cooperative (iRIC).
This approach has been successfully used for flood forecasting and urban flood management. A study conducted in the Brahmani and Baitarani river delta in India by coupling SWAT and SWMM with iRIC yielded satisfactory results and was able to identify the depth and extent of inundation [19]. A similar study using a coupled model conducted in China was similarly successful and capable of assessing the effects of water conservancy structures within the simulation extent [22].
HEC-HMS is a rainfall-runoff hydrological model developed by the United States Army Corps of Engineers used extensively to simulate the hydrological response of catchments [23,24,25]. This model is used to estimate the runoff generated upstream of the 2D flood modeling extent and to provide the boundary conditions required for flood simulation. HEC-HMS was selected in this study due to its versatility in modeling hydrological processes and ability to model storm events. Nays2DFlood solver in iRIC is a 2D hydraulic model used for flood inundation mapping [19,26,27,28,29]. The iRIC is a recent hydraulic model that can model large flood events [30]. Owing to the nature of its recency, it has not been applied widely, but was able to simulate flooding in ungauged catchments where data are scarce. It is a free open-source software developed by Yasuyuki Shimizu and Toshiki Iwasaki of Hokkaido University, Japan.
2. Materials and Methods
2.1. Study Area
Figure 1 depicts the Nilwala river basin located along the southern coast of Sri Lanka. The river is 72 km in length and originates at Panilkanda, north-east of Deniyaya, at 1050 m above mean sea level [10]. The total drainage area of the river basin is 1025 km2 [31]. Steep longitudinal slopes characterize the basin’s upper region, while the lower basin consists of gentle slopes [31,32]. It passes several small towns such as Deniyaya, Morawaka, and Akuressa and flows into the ocean Thotamuna close to Matara city. The catchment is located in the wet zone, with most of the upper catchment covered by rainforests. A significant portion of the basin is used for cultivating agricultural crops such as paddy, coconut, tea, rubber, cinnamon, and citronella [32,33].
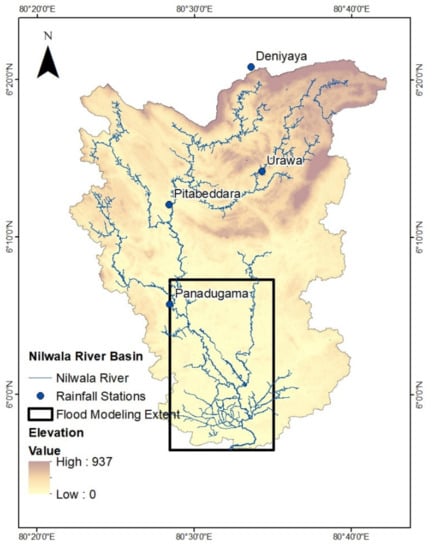
Figure 1.
Nilwala river basin.
2.2. Data
Hourly rainfall and streamflow data required for simulation were obtained from the Irrigation Department of Sri Lanka. The Nilwala river has three streamflow gauging stations; Urawa, Pitabeddara, and Panadugama, from which hourly streamflow data were collected. Continuous data of the 2017 flood event were not available for Urawa and Panadugama stations. Thus, calibration and validation of HEC-HMS was undertaken solely using data obtained from Pitabeddara. Hourly precipitation data from four stations in upper Nilwala; Deniyaya, Panadugama, Pitabeddara, and Urawa were additionally used. The data used in this study are summarized in Table 1.

Table 1.
Summary of data used in study.
2.3. Rainfall-Runoff Modelling Using HEC-HMS
The Hydrologic Engineering Center—Hydrologic Modelling System (HEC-HMS) model was designed by the US Army Corps of Engineers as a rainfall-runoff model to determine the hydrological response of watersheds [34]. It was developed for dendritic watersheds and has a wide array of applications, including urban drainage, flood-loss reduction, flood early warning system planning, reservoir spillway design, stream restoration, flow forecasting, surface erosion, sediment routing, and systems operation [35].
The Nilwala basin was delineated and divided into 20 subbasins using the HEC-GeoHMS extension in ArcGIS. Terrain preprocessing and basin processing tools were used to generate the basin model file containing the drainage network and delineated basin. Next, precipitation was estimated using the Thiessen polygon method [36], and suitable weights for each subbasin were defined to create a meteorological model. The basin and meteorological models were imported into HEC-HMS. Hourly precipitation data from the Deniyaya, Panadugama, Pitabeddara, and Urawa gauging stations, and observed discharge data for the selected events were imported into the HEC-HMS interface.
HEC-HMS allows for the separate modelling of hydrological processes; loss, transformation, baseflow, and routing with several models for each process. The selection of the model for each process should be based on the catchment characteristics, data availability, and whether the simulation is event-based or continuous [25].
The Snyder unit hydrograph method [37] was selected to simulate the transform in conjunction with the deficit and constant loss method, and the recession baseflow model [38]. The lag time, to be used in the Snyder unit hydrograph was defined as the time period between the centroid of excess rainfall and the peak discharge. It was calculated for each subbasin using the following relationship;
where = basin coefficient, = length of the mainstream from the outlet to the basin divide, = length along the mainstream from the outlet nearest the watershed centroid and = a conversion factor (0.75 for SI units).
The Muskingum–Cunge method [39] was used to model routing in all reaches with a Manning’s n coefficient of 0.040 [40,41]. Parameters such as reach length and slope were estimated using topographical maps. A deterministic optimization approach was followed with NSE set as the objective function. Optimization trials were carried out for the deficit and constant loss model, and the recession baseflow model to determine proper parameters. Table 2 lists the parameters optimized in HEC-HMS.

Table 2.
Parameters optimized in HEC-HMS model.
The model was initially applied to the basin’s upper region reaching up to Pitabeddara due to the lack of reliable streamflow data below this point. Once the model was calibrated and validated, it was then extended to the entire basin. For the simulation, three flood events were selected: May 2017, May 2018, and September 2019. The May 2018 and September 2019 events were used for calibration, while the May 2017 event was used to validate the model. The two selected events for calibration had both reported flooding, although not at the magnitude of the May 2017 flooding event.
2.4. Hydrodynamic Modelling Using Nays2DFlood Solver in iRIC
The International River Interface Cooperative (iRIC) is a free numerical simulation software consisting of various computational solvers to decipher hydrological problems. Nays2DFlood is one such solver in iRIC, which is used for flood simulation. The iRIC software platform was initiated by Professor Yasuyuki Shimizu (Hokkaido University) and Dr. Jonathan Nelson (USGS). Nays2DFlood relies on unsteady 2-dimensional plane flow simulations using boundary-fitted coordinates as the general curvilinear coordinates [42]. This solver can be applied to river basins with sparse data, especially in developing regions as it only requires the DEM without specific topographical dimensions of the river.
The equation of continuity (Equation (2)) and equations of motion (Equations (3) and (4)) of two-dimensional unsteady flows in a rectangular coordinate system are expressed as;
where,
where, = water depth, = time, = flow velocity in direction, = flow velocity in direction, = gravitational acceleration, = water surface elevation, and are riverbed shear stress in and directions, respectively, = riverbed friction coefficient, = eddy viscosity coefficient, = density of water, = inflow through a box culvert, a sluice pipe or a pump per unit area, and = rainfall [42]. These basic equations, which present in a rectangular coordinate system, are mapped to a generalized curvilinear coordinate system. The shape of the simulation mesh can be changed by accomplishing this depending on the boundary conditions [42].
The inputs required for iRIC are the DEM, satellite images, and streamflow hydrographs at the inlet points. The 30 m SRTM DEM from the United States Geological Survey (USGS) was used for the simulation, while the required background satellite images were obtained from Google Earth. Next, a calculation grid with 80 m grid size was created by defining a grid centerline representing the river’s flow. Values for nI, nJ, and W were defined, where nI = number of divisions in the longitudinal direction, nJ = number of divisions in the transverse division, and W = grid width in the transverse direction. Subsequently, calculation conditions were set, including boundary conditions, initial conditions, roughness conditions, and an appropriate time step for computation. The inflow streams identified earlier were then located on the grid. The discharge hydrographs obtained from the HEC-HMS model were then imported into iRIC manually and set as boundary conditions.
Impermeable objects such as roads, banks, embankments, and other flood control structures were located on the grid as obstacles. Matara city was outlined as an area of the grid occupied by buildings, and its areal fraction occupied by buildings was defined. Most calculation conditions of iRIC were left as default with a numerical upwind scheme used as the finite differential method. The northern, eastern and western boundaries were set as inflow boundaries while the southern boundary was modelled as having free outflow. The resulting inundation map’s accuracy was determined by comparison with a survey of the flood extent carried out by the Irrigation Department. The depth of flooding was validated using observed water level data at Tudawa gauging station.
2.5. Statistical Evaluation
Both models were statistically evaluated using Nash–Sutcliffe efficiency (NSE) [43], percent bias (PBIAS) [44], and root mean square error (RMSE).
The NSE indicates the goodness of fit of simulated data to observed data. It is calculated using the following equation, given by Nash and Sutcliffe (1970).
where = value of th observation, = value of th simulation, = mean of observations and = total observations. NSE values range from −∞ to 1, with an NSE of 1 indicating a perfect fit.
The PBIAS measures a simulated data’s tendency to be greater than or lesser than the observed values [44]. A negative value of PBIAS indicates a model overestimation bias, while a positive value indicates a model underestimation bias. A PBIAS value of 0 is optimal.
The RMSE was performed for quantifying the prediction error in terms of the units of the variable calculated by the model [45].
3. Results and Discussion
3.1. Calibration and Validation of HEC-HMS
The Irrigation Department has only recently begun collecting hourly streamflow and rainfall data from gauging stations at Panadugama, Pitabeddara, and Urawa. Thus, only three storm events were found with significant precipitation that resulted in downstream flooding. Of the three selected events, the May 2018 and September 2019 events were selected for model calibration. The flooding event of May 2017, considerably more intense among the events, was selected for validation and subsequently modelled using iRIC.
The Snyder unit hydrograph method for transformation produced excellent results during calibration and validation processes. A past study conducted within the Nilwala river basin confirmed that the Snyder transformation method provided the most accurate results [46]. Another study conducted in the Attanagalu Oya basin using HEC-HMS concluded that the Snyder unit hydrograph simulated flow with greater reliability than the Clark unit hydrograph and SCS Curve Number methods [23]. Moreover, the study recommends applying this model in conjunction with the deficit and constant loss model to simulate river flow in the country’s wet zone [23].
The recession baseflow model in HEC-HMS simulates a catchment behavior when flow recedes exponentially and was designed primarily for event simulations [34]. Recession baseflow and the Muskingum–Cunge routing method were successfully used to predict flow in the Nilwala river basin [46]. The downstream regions of the basin display a characteristic gentle slope, modelled more accurately using the Muskingum–Cunge method [47]. Detailed river cross-sectional data could not be obtained for the study, and thus the parameters for the routing model were estimated using the basin model generated by HEC-GeoHMS and satellite imagery. Moreover, obtaining 8-point cross-sectional data could significantly improve model performance. Alternatively, a trapezoidal shape design was specified for the routing channels.
During optimization, it was understood that the loss parameters influenced the peak of discharge, while the baseflow parameters affected the initial flow and recession curve. The transformation and routing processes influenced the time of the peak. After several optimization trials, the model was adequately calibrated for selected flood events.
Figure 2a depicts the observed and simulated hydrographs for the May 2018 event, while Figure 2b shows the September 2019 flood event. The May 2018 event provided the values of 0.93 NSE and 0.3 RMSE (Table 3), categorized as being excellent according to the criteria suggested by Moriasi et al., [48] for monthly hydrological simulations. The September 2019 event produced an NSE value of 0.746 after calibration and can be categorized as useful while having an RMSE value of 0.5. The PBIAS for both events was negative, −10.95% and −4.82%, respectively, indicating an overestimation bias.
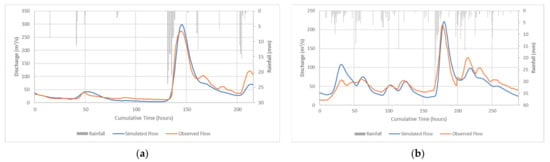
Figure 2.
HEC-HMS calibration at Pitabeddara station: (a) May 2018 storm event; (b) September 2019 storm event.

Table 3.
Statistical evaluation HEC-HMS calibration and validation steps.
The observed and simulated hydrograph at Pitabeddara gauging stations for the May 2017 event is shown in Figure 3. The calibrated parameters were averaged and validated using the May 2017 event. As mentioned earlier, this event is a comparatively more severe flood event, and rainfall frequency analysis has classified this event as having a return interval of 75–100 years [49]. Due to the severity, the gauge station at Pitabeddara was completely flooded during the event’s peak. The peak discharge of the flood was estimated by flood marks. Thus, there remains considerable uncertainty in the peak discharge of this event. However, the simulated flow using averaged parameters showed the goodness of fit with the observed flow with an NSE value of 0.927, a PBIAS of −8.33%, and an RMSE value of 0.3. As with calibration, the PBIAS indicates a model overestimation bias.
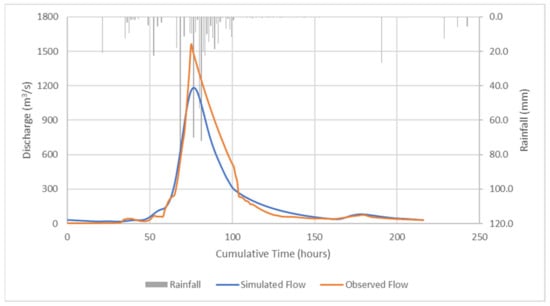
Figure 3.
HEC-HMS Validation using May 2017 flood event at Pitabeddara.
3.2. Hydraulic Model Simulation
Initial simulation runs identified that the model could not correctly identify the flow path of the mainstream in specific regions due to the coarser 30 m DEM used. As a result, the elevation file was modified to indicate the river’s correct flow path. A study conducted for flood simulation in Kabul using iRIC, Shokory et al., [28] modified the DEM similarly as the flood would not pass over the original DEM. Initially, the model was applied to a smaller region, including Matara and the region immediately north of the city. This overestimated the city’s flood as the model failed to account for flooding that occurred above this region. Thus, the simulation extent was extended further upstream up to Akuressa for more accurate simulation.
Six inlets were located within the simulation extent (Figure 4a). The hydrographs in Figure 4b, which were obtained using the HEC-HMS model were set as the boundary conditions for Nays2DFlood at each inlet. The highest contribution was seen from inlet 1, the main river, and included flow generated from a larger proportion of the upper catchment. Inlet 2, the second-largest contributor, represents a tributary of the Nilwala river, Kirama Oya.
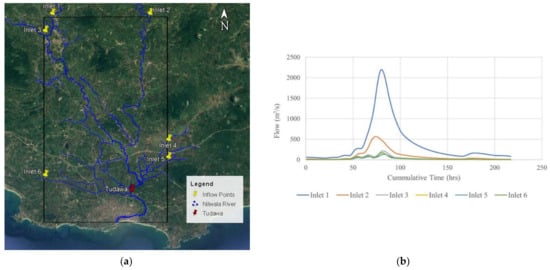
Figure 4.
(a) 2D flood modeling extent and inflow locations. (b) Input hydrographs for flood modeling.
Paddy cultivation represents the primary land use of the region surrounding Matara city. The 30 m DEM could not recognize the complicated network of interconnected minor canals that characterize this region. The roughness coefficient was taken as 0.15 for forested areas and 0.09 [46] for other areas based on land cover and by reviewing past studies and literature [41]. Moreover, a section of Matara city was incorrectly simulated as being flooded when in fact flooding did not occur. We attribute this to faults in the DEM, that was unable to detect flood control structures such as bunds on either side of the river due to topographical changes that might have occurred owing to its production and low resolution.
The extent of flooding was verified using a survey of the flood extent carried out by the Department of Irrigation for the 2017 May flood event (Figure 5). The survey was carried out by considering flood marks and accounts of the residents in the months shortly after the flood event. An accuracy assessment (Table 4) using 10,000 random points was carried out to compare the simulated flood extent with the surveyed extent, with a maximum simulated depth greater than 0.5 m being considered as a flood, based on the classification of Hamdan et al., [50]. The producer’s accuracy details the number of reference points (i.e., surveyed points) classified correctly to the total number of reference points for that particular class. The user’s accuracy represents the correctly simulated points to the total number of points simulated for its respective class. The results of the assessment indicated an overall accuracy of 81.5%. The relatively lower producer’s accuracy for inundated class (70.1%) when compared with the higher user’s accuracy (81.5%) indicates a higher error of observed inundated points being simulated as unaffected.
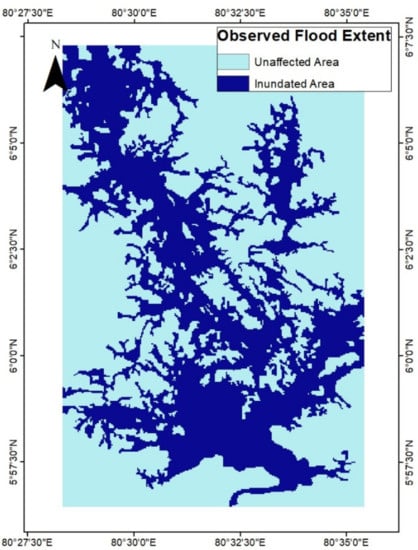
Figure 5.
The surveyed flood extent of May 2017 flood event (Source: Department of Irrigation, Sri Lanka).

Table 4.
Accuracy assessment of flood extent simulation using iRIC.
The simulated flood depth accuracy was verified using observed water levels at Tudawa station, located north of Matara city. This resulted in; NSE = 0.94, PBIAS = −4.28, RMSE = 0.18 and R2 = 0.95 (Figure 6).
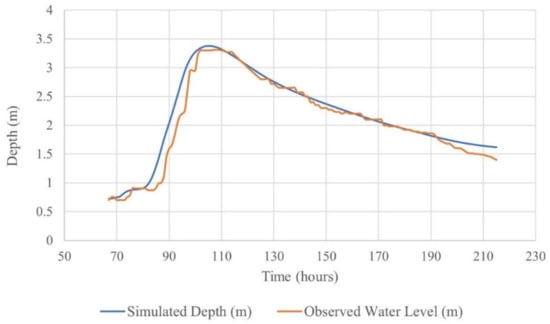
Figure 6.
Comparison of observed water level and simulated flood depth of May 2017 flood at Tudawa.
In Figure 7a, depths over 7 m were observed towards the northern aspect of the simulation extent close to the main river’s inflow points and its tributary Kirama Oya (i.e., inlets 1 and 2, from Figure 4). There remains uncertainty in flood depth in the upper regions as the model fails to consider any inundation that may have occurred upstream of the simulation extent which is modelled as purely one-dimensional. Furthermore, the conservation of momentum flow and the return flow of water at the linkage sites were neglected [18]. However, when considering the region closer to Matara, a maximum depth of 5 m was simulated. Comparing the velocity magnitude map (Figure 7b) with the background image affirms that the model could correctly identify the river’s flow path.
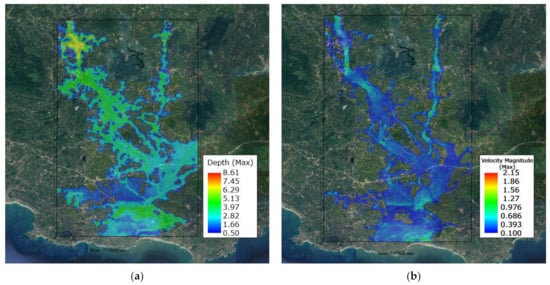
Figure 7.
iRIC simulation results of 2017 May flood event: (a) maximum flood depth and (b) maximum flood velocity at Nilwala river downstream area (Matara City and surrounding area).
Shokory et al., [28] studied the influence of rainfall and streamflow on flooding. The study found that rainfall did not significantly impact flooding in the Kabul case study, with the difference between the two resulting in the formation of “puddles”. The Nilwala basin showed similar characteristics as the flood occurs mainly due to heavy precipitation in the upper catchment [10]. This can be clearly understood when comparing the input hydrographs generated using HEC-HMS for the May 2017 event (Figure 4). In addition, a rainfall gauging station with the capability to measure hourly precipitation within the simulated extent was unavailable. Due to these reasons, the rainfall within the basin was omitted from the simulation.
As this study seeks to develop a tool that could be applied for real-time flood forecasting, the time required to simulate needs to be considered. The grid size of the generated mesh will affect the simulation time where a grid with higher resolution will produce more accurate results but will require a significantly longer time to complete the simulation. Thus, an 80 m grid size was selected to produce results faster with acceptable accuracy.
During the May 2017 flood event, it took approximately 36 h for the flood peak to reach Tudawa. The average time taken to run the hydraulic model was close to 5 h, but this could be further reduced by using a machine with greater computational power. However, the model did simulate within an acceptable period, with sufficient lead time for taking necessary precautions based on the generated flood risk maps.
A flood risk map (Figure 8) was generated based on the May 2017 flood event. Regions were classified as high, medium and low risk according to the flood depth [50]. Such maps generated for different return periods can aid in the design and planning of infrastructure, flood control structures, and provide guidance in community resiliency development projects. In addition, maps generated in real-time during a storm event can be used to issue flood warnings and provide specific instructions for evacuation where needed.
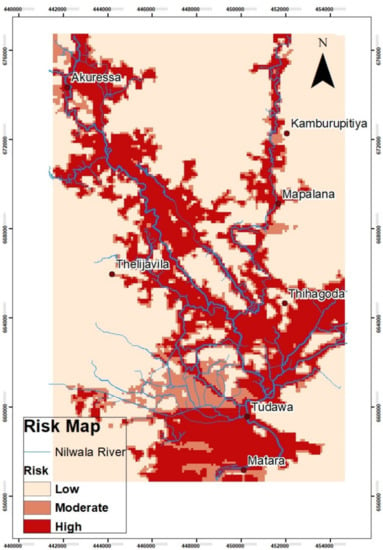
Figure 8.
Flood risk map of Nilwala River downstream (Matara City and surrounding area) for May 2017 flood event.
4. Conclusions
The Nilwala river basin’s upper region was modelled in HEC-HMS using the Snyder unit hydrograph method to simulate transformation, while the Muskingum–Cunge routing model, deficit and constant loss model, and recession baseflow model were used to model routing, loss and baseflow, respectively. The model was calibrated and validated using three flood events: May 2018 and September 2019 events for calibration and the May 2017 event for validation. The model performed well considering the Nash–Sutcliffe efficiency, percent bias, and root mean square error. Simulated stream hydrographs from HEC-HMS were externally coupled with iRIC to simulate inundation in Matara for the 2017 May flood event. The neglection of upstream flooding, momentum transfer and return flow at the linkage site presented major limitations of the model. The accuracy of the DEM used will greatly impact the performance of iRIC. However, the extent of flooding was estimated, with an overall accuracy of 81.50%. The accuracy of simulated flood depth was verified using water levels at the Tudawa gauging station which resulted in an NSE of 0.94, a PBIAS of −4.28, an RMSE of 0.18 and an R2 of 0.95. Based on these values, it can be concluded that the 1D–2D coupled model can accurately identify the extent of flooding in addition to the flood depth. Nevertheless, the model’s accuracy should be further improved by simulating more events with available observed flood data. Moreover, the model should be tested in the field using real-time flood events to evaluate its feasibility as a tool for flood forecasting and early warning systems. Accordingly, a flood risk map was developed for the May 2017 flood event. Further studies should be undertaken to develop such maps for storms with different return periods and for various climate change scenarios.
Author Contributions
Conceptualization, M.H.J.P.G. and K.S.; methodology, L.D. and M.R., M.K.N.K.; software, L.D. and M.R.; validation, M.H.J.P.G., M.K.N.K. and M.R.; data curation, T.J.M.; writing—original draft preparation, L.D.; writing—review and editing, M.H.J.P.G. and K.S.; supervision, M.H.J.P.G. and M.K.N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. Climate Change 2013—The Physical Science Basis. Contribution of Group I to the Fifth Assessment report of the Intergovernmental panel on Climate Change; Stocker, T., Plattner, G., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Eckstein, D.; Kunzel, V.; Schafer, L.; Winges, M. Global Climate Risk Index 2020; Germanwatch: Berlin, Germany, 2019. [Google Scholar]
- Karunathilaka, K.L.A.A.; Dabare, H.K.V.; Nandalal, K.D.W. Changes in Rainfall in Sri Lanka during 1966–2015. Eng. J. Inst. Eng. Sri Lanka 2017, 50, 39–48. [Google Scholar] [CrossRef]
- Naveendrakumar, G.; Vithanage, M.; Kwon, H.H.; Iqbal, M.C.M.; Pathmarajah, S.; Obeysekera, J. Five decadal trends in averages and extremes of rainfall and temperature in Sri Lanka. Adv. Meteorol. 2018, 2018, 4217917. [Google Scholar] [CrossRef]
- Gunarathna, M.H.J.P.; Kumari, M.K.N. Rainfall trends in Anuradhapura: Rainfall analysis for agricultural planning. Rajarata Univ. J. 2013, 1, 38–44. [Google Scholar]
- Smith, K.; Ward, R. Floods: Physical Processes and Human Impacts; Wiley: Hoboken, NJ, USA, 1998; ISBN 978-0-471-95248-0. [Google Scholar]
- Herath, S. Flood Characteristics and Mitigation Issues Flood Trends around the world. UNU—Japan-Keio Joint Training Workshop on “Water Governance”; United Nations University Centre: Tokyo, Japan, 2002. [Google Scholar]
- Ministry of Disaster Management; Ministry of National Policies and Economic Affairs. Sri Lanka Rapid Post Disaster Needs Assessment: Floods and Landslides; Ministry of Disaster Management: Colombo, Sri Lanka; Ministry of National Policies and Economic Affairs: Colombo, Sri Lanka, 2017.
- Dayaratne, S.T.; Perera, B.J.C. Regionalisation of impervious area parameters of urban drainage models. Urban Water J. 2008, 5, 231–246. [Google Scholar] [CrossRef]
- Weerasinghe, K.D.N.; Elkaduwa, W.K.B.; Panabokke, C.R. Agro-climatic risk and irrigation need of the Nilwala Basin of southern Sri Lanka. In Proceedings of the Irrigation Drainage in the New Millenium, Fort Collins, CO, USA, 20–24 June 2000; pp. 455–469. [Google Scholar]
- Jonkman, S.N.; Vrijling, J.K. Loss of life due to floods. J. Flood Risk Manag. 2008, 1, 43–56. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Tutulic, D. On the use of 1d and coupled 1d-2d modelling approaches for assessment of flood damage in urban areas. Urban Water J. 2009, 6, 183–199. [Google Scholar] [CrossRef]
- Timbadiya, P.V.; Patel, P.L.; Porey, P.D. A 1D–2D Coupled Hydrodynamic Model for River Flood Prediction in a Coastal Urban Floodplain. J. Hydrol. Eng. 2015, 20, 05014017. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Petaccia, G.; Brufau, P.; García-Navarro, P. Conservative 1D-2D coupled numerical strategies applied to river flooding: The Tiber (Rome). Appl. Math. Model. 2016, 40, 2087–2105. [Google Scholar] [CrossRef]
- Samuels, D. Cross-section locations in 1-D models. In Proceedings of the 2nd International Conference on River Flood Hydraulics, Wallingford, UK, 17–20 September 1990; White, W., Watts, J., Eds.; Wiley: Chichester, UK, 1990; pp. 339–350. [Google Scholar]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Anees, M.; Abdullah, K.; Nordin, M.N.; Rahman, N.N.N.; Syakir, M.; Kadir, O. One- and Two-Dimensional Hydrological Modelling and Their Uncertainties. In Flood Risk Management; Hromadka, T., Rao, P., Eds.; IntechOpen: London, UK, 2017; p. 324. [Google Scholar]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Rai, P.K.; Dhanya, C.T.; Chahar, B.R. Coupling of 1D models (SWAT and SWMM) with 2D model (iRIC) for mapping inundation in Brahmani and Baitarani river delta. Nat. Hazards 2018, 92, 1821–1840. [Google Scholar] [CrossRef]
- Lea, D.; Yeonsu, K.; Hyunuk, A. Case study of HEC-RAS 1D-2D coupling simulation: 2002 Baeksan flood event in Korea. Water 2019, 11, 2048. [Google Scholar] [CrossRef]
- Knebl, M.R.; Yang, Z.L.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS/RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, X.; Liu, Y.; Tang, W.; Xu, J.; Fu, Z. Assessment of flood inundation by coupled 1d/2d hydrodynamic modeling: A case study in mountainous watersheds along the coast of southeast China. Water 2020, 12, 822. [Google Scholar] [CrossRef]
- Halwatura, D.; Najim, M.M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rwasoka, D.T.; Nhapi, I.; Dube, T. Ungauged runoff simulation in Upper Manyame Catchment, Zimbabwe: Application of the HEC-HMS model. Phys. Chem. Earth 2016, 100, 371–382. [Google Scholar] [CrossRef]
- Tassew, B.; Belete, M.; Miegel, K. Application of HEC-HMS model for flow simulation in the Lake Tana Basin: The case of Gigel Abay Catchment, Upper Blue Nile Basin, Ethiopia. Hydrology 2019, 6, 21. [Google Scholar] [CrossRef]
- Wongsa, S. Simulation of Thailand Flood 2011. Int. J. Eng. Technol. 2014, 6, 452–458. [Google Scholar] [CrossRef]
- Jamrussri, S.; Toda, Y. Simulating past severe flood events to evaluate the effectiveness of nonstructural flood countermeasures in the upper Chao Phraya River Basin, Thailand. J. Hydrol. Reg. Stud. 2017, 10, 82–94. [Google Scholar] [CrossRef]
- Shokory, J.A.N.; Tsutsumi, J.I.G.; Sakai, K. Flood Modeling and Simulation using iRIC: A Case Study of Kabul City. E3S Web Conf. 2016, 7, 5–11. [Google Scholar] [CrossRef]
- Gopinatha, S.; Nagarajanb, N. Hydrodynamic simulation of urban stormwater drain (Delhi city, India) using iRIC model. J. Appl. Res. Technol. 2018, 16, 374–381. [Google Scholar]
- Nelson, J.M.; Shimizu, Y.; Abe, T.; Asahi, K.; Gamou, M.; Inoue, T.; Iwasaki, T.; Kakinuma, T.; Kawamura, S.; Kimura, I.; et al. The international river interface cooperative: Public domain flow and morphodynamics software for education and applications. Adv. Water Resour. 2016, 93, 62–74. [Google Scholar] [CrossRef]
- Atkins. Atkins CRP-DBIP Computational framework specific to Nilwala Ganga basin. In Climate Resilience Improvement Project (CRIP); Department of Irrigation: Colombo, Sri Lanka, 2017. [Google Scholar]
- Jayawardana, J.M.C.K.; Jayathunga, T.R.; Edirisinghe, E.A. Water quality of Nilwala River, Sri Lanka in relation to land use practices. Sri Lanka J. Aquat. Sci. 2016, 21, 77–94. [Google Scholar] [CrossRef][Green Version]
- De Silva, M.P.; Karunatileka, R.; Thiemann, W. Study of some physicochemical properties of Nilwala River waters in Southern Sri Lanka with special reference to effluents resulting from anthropogenic activities. J. Environ. Sci. Health Part A Environ. Sci. Eng. 1988, 23, 381–398. [Google Scholar] [CrossRef]
- Scharffenberg, B.; Bartles, M.; Brauer, T.; Fleming, M.; Karlovits, G. Hydrologic Modeling System HEC-HMS—User’s Manual; USACE: Washington, DC, USA, 2018. [Google Scholar]
- USACE. Hydrologic Modeling System, HEC-HMS Applications Guide; USACE: Washington, DC, USA, 2017. [Google Scholar]
- Thiessen, A. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Snyder, F.F. Synthetic unit-graphs. Eos Trans. Am. Geophys. Union 1938, 19, 447–454. [Google Scholar] [CrossRef]
- Te Chow, V.; Maidment, D.R.; Mays, L.W. Applied Hydrology, 2nd ed.; McGraw Hill Book Co.: Singapore, 1988. [Google Scholar]
- Cunge, J.A. On the subject of a flood propagation computation method (Muskingum method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains. Geol. Surv. Water-Supply Pap. 2339 1993, 42, 350–355. [Google Scholar]
- Shimizu, Y.; Inoue, T.; Suzuki, E.; Kawamura, S.; Iwasaki, T.; Hamaki, M.; Omura, K.; Kakegawa, E.; Yoshida, T. iRIC Software Nays2DFlood Solver Manual; The International River Interface Cooperative (iRIC): Hokkaido, Japan, 2015. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models, part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison With Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Ratnayake, U.; Sachindra, D.A.; Nandalal, K.D.W. Rainfall Forecasting for Flood Prediction in the Nilwala Basin. In Proceedings of the International Conference on Sustainable Built Environment (ICSBE-2010), Kandy, Sri Lanka, 13–14 December 2010. [Google Scholar]
- Feldman, A. Hydrologic Modeling System Technical Reference Manual; USACE: Washington, DC, USA, 2000. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Irrigation Department. Inundation Maps of the Nilwala River Flood in May 2017; Irrigation Department: Colombo, Sri Lanka, 2017.
- Hamdan, A.N.A.; Abbas, A.A.; Najm, A.T. Flood hazard analysis of proposed regulator on Shatt Al-Arab River. Hydrology 2019, 6, 80. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).