Abstract
The Precipitation-Runoff Modeling System (PRMS) was used to develop a simulation of watershed hydrology on the island of Puerto Rico for the period 1981–2017, concentrating on the Río Grande de Arecibo, a river with some of the highest streamflows on the island. This development is part of the U.S. Geological Survey’s (USGS) National Hydrologic Model (NHM) infrastructure which supports coordinated, comprehensive, and consistent hydrologic modeling at the watershed scale for the coterminous United States (CONUS). A goal of the NHM program is to expand the domain outside of CONUS, leading to a PRMS application in Puerto Rico. This model was used to simulate the effects of Hurricane Maria on daily streamflow and provide information at locations where streamgages were damaged by the hurricane. Comparisons with streamflow estimates made by indirect methods in the field, up to ten times higher than simulated values, lends insight into the uncertainties in both the indirect methods and model simulated values and helps to identify potential error in the daily streamflow estimates. The PRMS can be applied to look at the effects of changes in climate and land use, water management, industrial and public water usage, and many other factors that affect hydrology on the island of Puerto Rico. The model is also designed as a support tool for the USGS National Water Census which provides comprehensive reporting of national information on withdrawal, conveyance, consumptive use, and return flow by water-use category.
1. Introduction
Hurricanes, including Hugo in 1989 and Georges in 1998, have periodically affected Puerto Rico [1]. The hurricane season of 2017 was particularly active with the passing of Hurricane Irma 50 miles to the north of Puerto Rico on 6 September 2017 as a category-5 hurricane [2], followed by the direct landfall and passage over the island by Hurricane Maria on 20 September 2017 as a category-4 hurricane with sustained winds of 155 miles per hour [3,4]. A rainfall-runoff simulation of peak streamflows during the Hurricane Maria landfall can be used to gain insight into the streamflow estimates made at sites with hurricane-damaged gaging stations. Using model-simulated streamflows complements other methods of streamflow estimation.
Previous modeling of the surface hydrology of Puerto Rico concentrated on specific features and locations on the island (Figure 1). The hydraulic routing model HYDRAUX was applied to the Lago Loíza reservoir (Figure 2) near the city of San Juan to develop estimations of water volumes at the reservoir based on rainfall and streamflow data [5]. Discharge into the Lago Loíza reservoir was simulated using an artificial neural network (ANN) application [6]. The ANN was trained to simulate streamflow based on observed rainfall and evapotranspiration; the latter being based on observed daily air temperature. Van Beusekom et al. [7] developed Precipitation Runoff Modeling System (PRMS) models to compare simulations based on five static parameterizations of land cover with those based on dynamically varying parameters derived from four land cover scenes for the period 1953–2012. These four regions (Figure 1 and Figure 2) include (1) a moderate rainfall region north of the Cordillera Central, (2) a dry region south of the Cordillera Central, (3) a wet region east of the Cordillera Central surrounding Sierra de Luquillo, and (4) a moderate rainfall region west of the Cordillera Central. Isla de Culebra and Vieques are not included in this classification. The results of this modeling effort indicated that projected changes in land cover must be considered in water resource management planning. The input data for these PRMS simulations provide a starting point for creating a National Hydrologic Model (NHM)-compatible representation of the rainfall-runoff process in Puerto Rico, described herein. The Río Grande de Arecibo (Figure 2) has some of the highest observed flows in Puerto Rico, on the order of 10,000 ft3/s [3], so representing this river and the surrounding hydrology is the focus of the calibration process in this study. With a drainage area of 170 square miles on the northern slope of the Cordillera Central (Figure 1), Río Grande de Arecibo flows northerly from a headwater about 960 m in elevation to a coastal outlet near the town of Arecibo (Figure 2).

Figure 1.
Map showing the study area, Puerto Rico.
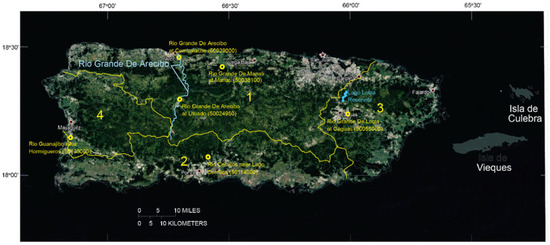
Figure 2.
Four hydrogeographic regions in Puerto Rico [7] and location of streamgaging sites. These four regions are (1) a moderate rainfall region north of the Cordillera Central (Figure 1), (2) a dry region south of the Cordillera Central, (3) a wet region east of the Cordillera Central surrounding Sierra de Luquillo (Figure 1), and (4) a moderate rainfall region west of the Cordillera Central.
The purpose of this report is to describe the development, calibration, and application of a rainfall-runoff model in the Río Grande de Arecibo area of Puerto Rico using PRMS and examine its application to estimate streamflows during Hurricane Maria. The simulation is referred to as the PRMS Arecibo model [8].
2. Study Area
The island and Commonwealth of Puerto Rico is approximately 8900 square kilometers (km2) and is located between the northeastern Caribbean Sea and Atlantic Ocean (Figure 1). Topographically, Puerto Rico is dominated by interior mountain ranges surrounded by flat-lying coastal plains to the north and south. With a maximum elevation of 1338 m at Cerro de Punta, the Cordillera Central dominates the landscape of the southern two-thirds of Puerto Rico [7]. The northeastern part of the island is dominated by the Sierra de Luquillo, which has a maximum elevation of 1075 m at El Toro peak [9]. The topography of the island is reflected in the geologic setting which can be generalized as carbonate terrain along the north coast, igneous terrain including volcanoclastic deposits and valley-fill deposits in upland and mountainous areas of the Cordillera Central and Sierra de Luquillo, and discontinuous alluvial fans and delta deposits along the south coast [10].
The Sierra de Luquillo is the wettest region of the island, with annual rainfall of nearly 4.5 m (177 inches) in the upper elevations [11]. Island wide, rainfall has large interannual variability due to broad-scale storm patterns and hurricanes. Typically, there is an early rainfall season from May through June and a late rainfall season from August to November, with an island-wide dry season from January to April [11]. Based on gridded climate data published by the Puerto Rico AGricultural WATER (PRAGWATER) management data repository [12], daily temperature in Puerto Rico for 2009–2017 ranged from 15.7 °C (4 December 2010) to 32.7 °C (9 September 2016), and annual rainfall ranged from 1.50 m (59.1 inches) in 2015 to 2.95 m (116.3 inches) in 2017. Large precipitation events can cause landslide threats to homes and infrastructure in the mountainous interior, and floods that affect people and infrastructure on the populated coastal plains [13,14]
Hurricane Irma and Maria both affected Puerto Rico in September of 2017. Rainfall totals in Puerto Rico from Hurricane Irma were between 0.25 and 0.38 m (10 and 15 inches) for the period 5–7 September 2017 in the higher elevations [2]. Rainfall totals for Hurricane Maria ranged from 0.13 to 0.64 m (5 to 25 inches) for the period 19–21 September 2017, with much of the central part of the island estimated to have totals of 0.38 m (15 inches) or greater [4]. One location in the southeast part of Puerto Rico had a storm-total rainfall of nearly 0.97 m (38 inches). Precipitation at U.S. Geological Survey (USGS) streamgages for 18–22 September 2017 was as high as 0.74 m (29 inches) at the Bo. Beatriz raingage near Caguas [3]. Streamflows were at record and near-record levels [4]. As a result of winds or flooding, 84 streamgages were damaged and did not record flow during the storm [15]. The north coast of Puerto Rico was struck most heavily by Hurricane Maria. Indirect streamflow measurements and step-backwater analyses, which utilize high-water marks in conjunction with estimated relations between stage and flow, were used to estimate peak flow and reconstruct rating curves at locations where gages were damaged [3]. Given the number of stations destroyed, alternate estimates of daily streamflow such as estimated by PRMS could be used to cross-check field estimates of streamflow and to study the contributions of various components of the water budget during such extreme events.
3. Materials and Methods
The USGS has developed the NHM infrastructure to support coordinated, comprehensive, and consistent hydrologic modeling at the watershed scale for the conterminous United States (CONUS) and allow models to be built for scales ranging from the entirety of the CONUS to single watersheds [16]. The NHM infrastructure supports rainfall-runoff modeling with the PRMS which is a physical-process watershed model that runs on a daily time step and is used to simulate and assess watershed response to hydrologic controls [17]. Watershed response includes daily streamflow using several user-defined solutions, and several other water budget metrics such as evapotranspiration. Units of streamflow in this report are cubic feet per second (ft3/s); otherwise, units are in the SI system.
3.1. PRMS Model
PRMS subdivides a watershed into the smallest homogeneous area, which is referred to as a hydrologic response unit (HRU). The locations, dimensions, and attributes of the HRUs in a watershed, and the surface-water routing network are compiled in the Geospatial Fabric for National Hydrologic Modeling [18]. Each stream segment receives runoff from the hillslopes of the associated HRU, and streamflow is routed downstream to the next stream segment. The PRMS model setup includes specifying modules that simulate key hydrologic processes such as evapotranspiration, runoff, and streamflow [17]. The streamflow module, for example, has three user-specified options: a simple module that represents streamflow as the sum of runoff, interflow, and groundwater discharge; the Muskingum module [17]; and a module which simply sets stream-segment outflows to be equal to inflows. Our study indicated that the Muskingum module did not show a clear advantage over the simpler module. Other modules allow similar flexibility in representation of processes. Reservoir releases are estimated and incorporated into the model as point inflows.
Many model input parameters were calibrated by Van Beusekom et al. [7] for the time period 1953–2012 using a variety of eight-year calibration periods; therefore, the model development in this study combines the 1981–2017 Daymet input data [19] with the parameters from the 1953–2012 study (i.e., topographic, vegetation, and soils characteristics) as the baseline calibration, followed by the calibration effort that focuses on the Arecibo basin. The calibration for the Arecibo basin was completed in two overarching steps. The first involved manual adjustments of parameters and examination of response of streamflow. Experimentation with input parameters before calibration is a good way to develop a better understanding of the sensitivity of the model and test alternate solution modules. The insight gained from the manual adjustment of parameters helped guide the setup of the second overarching step, the automated calibration using Luca (Let Us CAlibrate) software version 1 [20] (Reston, VA, USA) which was specifically designed for calibration of PRMS model applications. Whereas other calibration codes are not automated for multiple steps or easily interfaced with PRMS, Luca uses a multiple objective, stepwise, automated calibration strategy. An objective function is defined, usually targeted at minimizing errors between the simulated and observed values, and a shuffled complex evolution global search algorithm is used to perturb the model input to satisfy the objective function. Multiple steps can be defined in Luca, with different parameters, variables, and objective functions in each step. Solar radiation data from the PRAGWATER management data repository [12] are available for the 2009–2017 period; therefore, it was decided to make 2009–2017 the Luca calibration period and the 1981–2008 period was used for verification. A summary of the different model modifications through this development process is shown in Table 1.

Table 1.
Precipitation-Runoff Modeling System (PRMS) model development sequence; ET: Evapotranspiration; DAYMET [19]; PRAGWATER [12].
3.2. Baseline Model
The baseline model uses the spatial units and static parameters calibrated by Van Beusekom et al. [7] (Figure 3). Model region 1 defined by Van Beusekom et al. [7] (Figure 2) is dominated by the Río Grande de Arecibo and is used for this study. Atmospheric forcings data compiled for the 1980–2017 period include daily minimum and maximum air temperature and daily total rainfall derived from the Daymet version 3 data product [19]. The PRMS standard output commonly assumes the first year of the simulation as a ‘warmup period’, during which the model’s initial conditions dissipate; therefore, the simulation period is 1981–2017. The modules chosen for baseline calibration are listed in Table 2. Daily clear-sky shortwave radiation was computed by PRMS (soltab and ddsolrad modules) for comparison with total radiation from the PRAGWATER management data repository [12].
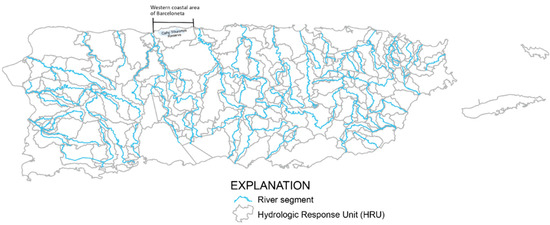
Figure 3.
Hydrologic Response Units (HRUs) and stream segments in Puerto Rico PRMS model.

Table 2.
Precipitation-Runoff Modeling System modules used for setup of the model.
3.3. Manual Adjustment of Parameters
The primary objective for manual adjustment of parameters of the PRMS Arecibo model was to match the timing and magnitude of observed and modeled streamflow at selected streamgages. Stations with over 20 years of data are distributed across the island (Figure 2) and the largest observed streamflows were in the Río Grande de Arecibo; thus, the manual adjustment of parameters concentrated on matching PRMS daily streamflow with observed daily streamflow at site number 50029000 (Rio Grande de Arecibo at Cambalache) and further upstream at site number 50024950 (Rio Grande de Arecibo at Utuado) (Figure 2 and Table 3) [21]. The sensitivity of simulation output to the manually perturbed input parameters can be used to identify and provide starting parameter values for the automated calibration. The manual effort lends insight into which input parameters are most important to the output values most needing adjustment, such as peak river flows. The manual calibration functions as a first step to identify and test the important variables for the simulation, leading to the Luca calibration.

Table 3.
Streamgaging stations on the Río Grande de Arecibo with discharge data suitable for model calibration and comparison [21]; NAD27, North American Datum of 1927.
3.3.1. Representation of Solar Radiation and Evapotranspiration
The PRMS Arecibo model uses the soltab module to compute daily shortwave radiation or daily potential solar radiation. The ddsolrad module converts potential solar radiation to actual solar radiation with the degree-day method [17,22]. The other option to compute actual solar radiation in PRMS is the Cloud-Cover Solar-Radiation distribution module, ccsolrad, which uses a relation between sky cover and daily range in air temperature and a relation between solar radiation and sky cover [17,22]. The ddsolrad module is most applicable to regions where predominantly clear skies prevail on days without precipitation whereas the ccsolrad module is for humid areas when cloud cover is prevalent even on days without precipitation. Even though Puerto Rico is a humid environment, clear skies tend to prevail on days without precipitation, as seen in the data [12]. The clear sky criterion is considered important so the ddsolrad module was chosen. The computed solar radiation was calibrated to measured data regardless of the module used.
The potential solar radiation Re, which is the maximum radiation at the top of the atmosphere, is calculated based on the latitude and solar declination [17] (p. 78), and net surface short-wave solar radiation Rn, which is the approximation of the net energy available, is calculated as:
where Sz is the land slope and rrat is the ratio of surface to extraterrestrial daily solar radiation from the degree-day curves, based on daily maximum air temperature [17,22]. For days with precipitation greater than a user-defined limit, Rn is adjusted by an empirical coefficient that varies seasonally. Although the degree-day curves are designed to estimate only the net short-wave solar radiation, the GOES-PRWEB database provides estimated net radiation data (including all short-wave and long-wave radiation components) (Jacobs and others, 2008) and is used as the target for model calibration [23].
Daily potential evapotranspiration (PET) is computed using the potet_pt module which solves the Priestly-Taylor equation:
where: α is the Priestly-Taylor coefficient, vp is the slope of the saturation vapor pressure versus air temperature curve in kilopascals per degrees Celsius, λ is the latent heat of vaporization in calories/gram, and the psychrometric constant γ is computed as:
where Z is the land elevation above sea level in feet. The parameter α was adjusted and can account for uncertainty or bias in solar-radiation approximations. G is the heat flux density to the ground in megajoules per square meter per day, and is computed as:
where Tn-1 and Tn are the average air temperatures on the previous day and current day in degrees Celsius. The heat capacity of the soil is considered constant in this formulation, although it actually varies with soil type and moisture.
The parametrization of the streamflow routing was examined by comparing the muskinghum module, which uses the Muskingum flow-routing method to compute streamflow, and the strmflow_in_out module, which sets the outflow of each stream segment to the inflow. The parameters of the muskinghum module were also adjusted and the results examined.
3.3.2. Incorporating the Effects of Reservoir Releases
Reservoirs and lakes were not explicitly represented in the 1953–2012 simulation-period model, and as such, PRMS simulates only unregulated or natural flows from runoff. The discharge from reservoir releases can be accounted for in PRMS as specified point inflows, using the variables npoigages and nobs, and the timeseries is input from the main data file [17]. The most common and largest reservoir releases occur during high rainfall events, concurrent with the peak instantaneous streamflow, so neglecting reservoirs could account for errors and uncertainty in simulating peak daily streamflows as seen in the following comparisons between streamflows and reservoir flows.
Two regulated reservoirs that substantially effect daily streamflows in Puerto Rico were identified. Lago Dos Bocas (Figure 4) has a surface area of approximately 1.3 square kilometers and is controlled by the Dos Bocas Dam. Built in 1942 by the Puerto Rico Electric Power Authority for a hydroelectric power plant [24], the reservoir discharges to the Río Grande de Arecibo. Lago Cerrillos has a surface area of approximately 1.5 square kilometers and discharges to Río Cerrillos through the Lago Cerrillos Dam (Figure 4). This dam was constructed in 1991 as part of the multipurpose Río Portugues and Bucana Project to provide flood protection, water supply, and recreation facilities for the municipality of Ponce (Figure 4) [25]. Continuous records of releases at these reservoirs were not available, but the volumes released can be determined from the observed rates at which reservoir water levels drop multiplied by the reservoir area. Increases in reservoir water level are not included in the determination of reservoir releases as they correspond to surface inflows or precipitation. ET fluxes from the reservoir surface are assumed to be small relative to the computed reservoir flows. The relationship between water stage and the reservoir water-surface area were supplied by sedimentation studies at Lago Dos Bocas [24] and Lago Cerrillos [25]. Given this information, a time series of estimated reservoir releases was constructed.

Figure 4.
Reservoirs with substantial effects on river flows.
The record of reservoir levels at Lago Dos Bocas begins 30 March 1999 and at Lago Cerrillos it begins 1 July 1992. Each of these datasets has some missing data. In order to estimate missing reservoir release data during the 1981–2017 period, a statistical best-fit relationship was developed between streamflows and reservoir releases for the measured values. Releases from Lago Dos Bocas affect flows at Río Grande de Arecibo at Cambalache (50029000). A least-squares regression equation was developed between observed flows at Cambalache and the estimated reservoir releases at Lago Dos Bocas (Figure 5). For the period of time before the reservoir-level record started at Lago Dos Bocas (30 March 1999), the best-fit equation shown in Figure 5 is used to provide reservoir flows based on total flows at Río Grande de Arecibo at Cambalache. With a Pearson’s R-value of 0.47, the relationship between Lago Dos Bocas reservoir flow and Río Grande de Arecibo at Cambalache flows is poor (Figure 5) but the best-fit equation is designed only to estimate the potential added flow, which is only about 10 percent of the total flow.
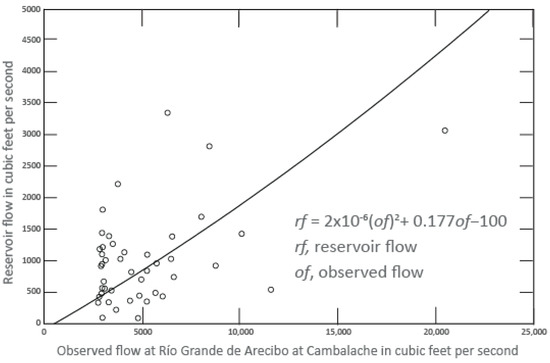
Figure 5.
Regression equations for flows from Lago Dos Bocas.
Estimated time series of releases from Lago Dos Bocas (Figure 6) are added to the Río Grande de Arecibo at the location of Lago Dos Bocas (Figure 4). The reservoir outlet flows are input to the model through the npoigages option which defined the location and flow into the river network. Average reservoir flows are 9.9 percent of the average Río Grande de Arecibo at Cambalache flows. Inspection of the data in Figure 6 indicates that reservoir flows are 15% of total flows during Hurricane Irma and as much as 53% of total flows for a rainfall event on 29 March 2012. For the period 15 October 1983–30 September 1996, neither the record of reservoir levels at Lago Dos Bocas nor the measurement of flows at Río Grande de Arecibo at Cambalache exist. Flows from the reservoir are not simulated for this period.
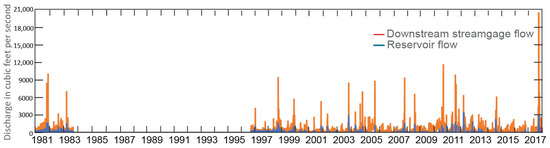
Figure 6.
Computed Lago Dos Bocas reservoir releases and observed flow (including reservoir flows) at Río Grande de Arecibo at Cambalache.
3.3.3. Representation of Depression Storage
Realistic depression-storage parameters are needed for a proper representation of peak streamflow. Depression storage is parameterized in PRMS by the average depression storage depth dprst_depth_avg, the depression storage area dprst_area, and the fraction of the depression storage area that can generate surface runoff as a function of storage volume dprst_frac_open. The parameterization of depression storage not only affects the surface storage effects in the simulation but also provides a more detailed representation of the volume and timing of runoff.
Viger et al. [26] used a depression storage representation for a PRMS application in the Upper Flint River Basin, Georgia. For this application, the largest water bodies, such a lakes and reservoirs, were not considered part of the depression storage, but smaller water bodies were included, and the hydraulic connectivity of these smaller bodies were estimated from the topography. However, most studies of depression storage concentrated on microtopography rather than small water bodies. Sneddon and Chapman [27] used a photogrammetric technique to determine the microtopography of areas along a hillslope and estimated depression storage based on the depth and volume of depressions and a computer search technique which identifies local minima in the topography. Hu et al. [28] developed depression storage and outflow curves from an experimental apparatus, with some numerical confirmation. Rossi and Ares [29] developed a set of plot-scale field experiments at the semi-arid Patagonian Monte in Argentina to estimate the effect of depression storage areas and infiltration rates on overland flows and a numerical model was fitted to the field data. Mwendera and Feyen [30] estimated depression storage from microtopographic data measured on microcatchments subjected to simulated rainfall. A relation was developed between depression storage and slope steepness. Elbasit et al. [31] investigated depression storage through laboratory application for small roughness height values. A relationship was also shown between depression storage Ds in mm, relative roughness RR in mm, and land slope SZ:
This equation is designed for microtopography, but if the roughness height is given a large value of 0.5 m to represent smaller water bodies and a land slope of 0.00005, the depression storage depth from equation 5 is 51 mm or about 2 inches. This is considered a very approximate but acceptable value for dprst_depth_avg in the manual parameter adjustment.
The relation between depression storage outflow and slope noted in Mwendera and Feyen [30] and Elbasit et al. [31] indicates that the percentage of depression storage area open to outflow should be higher in mountainous high slope regions and lower in coastal flat areas. The parameter dprst_frac_open in the NHM Puerto Rico model, which describes the fraction of depression storage area open to outflow, is varied according to the elevation. Given the difference in elevation between the coast and the upper reaches of the Río Grande de Arecibo, the empirical equation was developed:
where Z is the land elevation in feet above sea level. This allows for the fraction of depression storage area open to outflow to be very low in the coastal areas and approach the entire depression storage area in the mountainous upper reaches.
The primary objective of the depression storage parameter adjustment is to improve the representation of peak streamflows which tend to be underestimated. The effects of the depression storage parameters on peak flows are investigated in the manual calibration.
3.3.4. Automated Calibration with LUCA
Based on the results and finding of the initial manual adjustment of the parameters, the PRMS Arecibo model was calibrated using the Luca software version 1 [20] (Reston, VA, USA). The calibration sequence was based on a multi-step method described by Hay et al. [32] for a model of the Yampa River basin of Colorado. A number of the parameters and variables used in the Yampa River model, such as parameters dealing with snow melt, are not relevant to Puerto Rico. The stepwise method was modified to adjust the input parameters (Table 4) to provide the best fit with observed data in the PRMS Arecibo model.

Table 4.
Parameters of the Precipitation-Runoff Modeling System that were automatically calibrated using the Let-Us-Calibrate (Luca) program.
The Luca calibration of the NHM Puerto Rico model was accomplished in four steps (Table 5). The objective function for each step is to minimize the least-squares fit of the observed and simulated values listed in Table 5 in the column “calibration target”, without weighting. Following the examples of several previous applications [7,33], the first Luca step involves calibrating the simulated solar radiation to the data from the PRAGWATER GOES-PRWEB management data repository [12], adjusted to net short- and long-wave radiation using the methodology described by Jacobs et al. [23]. The calibration period is 2009–2017 to coincide with the period of availability of the GOES-PRWEB data.

Table 5.
Details of four-step Luca calibration application.
The calibration target for the second step is the potential evapotranspiration (PET) data. Solar radiation, tmin, tmax, vapor pressure, and wind speed data from the PRAGWATER GOES-PRWEB management data repository [12] is used to develop this PET target. The calibration adjusts a (model variable pt_alpha) in the Priestly–Taylor equation (Equation (2)) on a monthly basis as the entire model domain. In the manual calibration, α was already manually adjusted for fit as a temporally constant value, so the Luca calibration can test if monthly values produce better results.
The third step in the Luca calibration adjusts the parameters soil2gw_max and ssr2gw_exp, which control the transfer of water to the groundwater from the capillary reservoirs and the gravity reservoirs respectively, to match simulated and observed values for only the lower 90 percent of daily flows ranked by magnitude. The choice of using the lower 90th percentile of observed daily flows is based on examination of the magnitudes of the major peaks in observed data. The 90th percentile reasonably divides the base flow and smaller peaks from the isolated high peaks that represent major events (Figure 7); therefore, the third Luca step adjusts PET by each region based on non-peak flows. The Luca calibration concentrates on the flow at the Río Grande de Arecibo at Cambalache (Figure 2).

Figure 7.
Observed daily flows at field stations and lower 90th percentile of observed daily flows.
The fourth Luca calibration step (Table 5) adjusts two input parameters, applied to each hydrogeographic area separately, based on fitting simulated to observed values for the upper 10th percentile of observed daily flows, the peak flows. These two parameters: carea_max and pref_flow_den, are described in Table 4 and affect the contributing areas and the routing of preferential flow, which are factors relevant to the timing and magnitude of peak flows [7,33]. They are parameters that affect more rapidly varying flows and work for the calibration of peak flows.
3.3.5. Applications to the Hydrology of Hurricane Maria
The PRMS Arecibo model, calibrated with Luca, can provide information for a variety of applications within the limits of the model design. All model input and output files are available from Swain [8]. Two such applications are examined in this publication. The first application takes advantage of the fact that the model simulation period includes the landfall of Hurricane Maria on 20 September 2017, allowing comparison between observed and simulated storm-induced peak daily streamflows to get insight into both. A total of 84 stations were damaged by the hurricane; therefore, streamflow at these stations were estimates based on indirect measurements or models of streamflow during this period. The streamflows simulated by the PRMS Arecibo model can be used to estimate missing station streamflow but are limited by the accuracy and biases of the model. By using both ‘estimated’ and ‘simulated’ values, an improved estimate of the actual peak flows may be possible. The second application provides information that can be used to examine the effects of Hurricane Maria on freshwater outflows for the coastal HRU corresponding to the western coastal area of the municipality of Barceloneta (Figure 3). The HRU is connected to a nonresistance channel segment to represent the runoff to the coast. This allows the net runoff from this HRU to exit without the resistance of a river channel, equivalent to coastal outflow. This HRU area contains the Caño Tiburones Reserve (Figure 3), established in 1998, the largest wetland area in the Commonwealth (approximately 7000 acres). Prior to establishment as a Reserve, this area has undergone various manmade changes including drainage for agricultural uses in the 1940s [34]. Computing hurricane-induced coastal outflow in this area could support determining the effects on wetland viability and offshore mixing and salinity.
4. Results
The previous efforts by Van Beusekom et al. [7] to develop and calibrate a PRMS model for the whole of Puerto Rico for the 1953–2012 period were combined with the updated time-series data for the 1981–2017 simulation period to create the baseline model. The calibration efforts include a manual adjustment of parameters followed by an automated calibration with the Luca software version 1 (Reston, VA, USA).
4.1. Manual Calibrated Model Fit
Several modules and input parameters were experimentally perturbed to determine sensitivity and relevance to the calibration objective of accurately simulating peak flow magnitude and timing. Peak daily-mean streamflows and cumulative daily flows at the streamflow stations were consistently underestimated by the baseline model and after manual adjustment of parameters. Increasing model complexity by implementation of Muskingum streamflow routing (rather than the simpler strmflow_in_out module) did not improve estimates of peak streamflow, cumulative flow or other model performance criteria, and the strmflow_in_out module was used for all calibration.
The degree-day solar radiation configuration was examined by adjusting the intercept in the degree-day equation dday_intcp. A time-invariant dday_intcp value of −14.95 dday was found to produce a simulated average net solar radiation over the 2009–2017 calibration period of 315.6 Langleys compared to the PRAGWATER net short- and longwave data value of 332.4 Langleys, a 5.05 percent difference. Although the degree-day curves are designed to only estimate the net short-wave solar radiation, this calibration allows simulated values to match the field-estimated net short- and longwave radiation and better reflect the actual net radiation affecting ET. The monthly variation of the coefficients in the degree-day equation is not considered in the manual calibration, as this level of complexity is more appropriate for the subsequent Luca automated calibration.
The Priestly-Taylor coefficient α was adjusted to calibrate evapotranspiration rates based on cumulative streamflow. A constant value of α = 1.27 (model parameter pt_alpha) produced an average PET of 0.146 in/day for the calibration period 2009–2017 and an average PET of 0.148 in/day for the verification period 1981–2008. The values derived from PRAGWATER data have an average PET of 0.151 in/day for the calibration period 2009–2017 and 0.143 in/day for the verification period 1981–2008. The simulated to measured difference is 3.31 percent for the calibration period and 3.50 percent for the verification period. The monthly variation of α is not considered in the manual adjustment.
With the manually calibrated solar radiation and PET, cumulative flows at Río Grande de Arecibo at Cambalache are substantially improved over the pre-calibration model simulation (Figure 8). This is a strong indicator that the proper representation of the ET process is essential to the representation of cumulative flows in the PRMS Arecibo model. The flows upstream at Utuado, which was not calibrated, matches well until November 2003, when the manual calibration underestimates cumulative flow until approximately September 2009 (Figure 8).
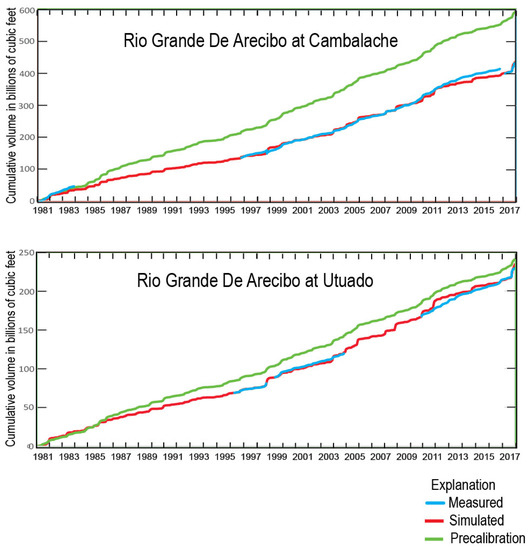
Figure 8.
Cumulative flows at observation stations with manual adjustment of solar-radiation, evapotranspiration, and depression-storage parameters.
The depression storage parameters were varied in the manual calibration process with the effects on peak flows as the primary calibration criteria. Some experimentation with values of dprst_depth_avg and dprst_frac_open indicated the chosen value of dprst_depth_avg equal to 2 in. and dprst_frac_open from Equation (6) produced the highest simulated peak flow values. The baseline model consistently underpredicted peak flows but calibrating depression storage allowed peak daily streamflows closer to measured values (Figure 9). The storage of precipitation in depressions increases the effect that antecedent conditions have on runoff and streamflows and discharge from the open storage areas increases the peak flows.
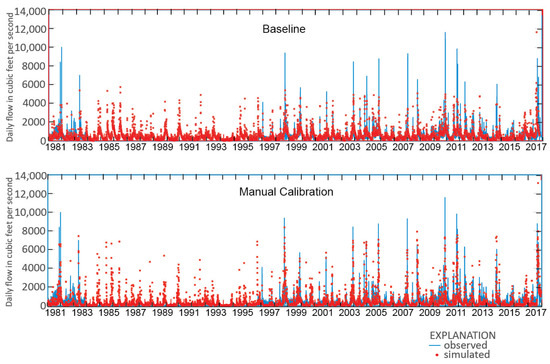
Figure 9.
Daily flows at Río Grande de Arecibo simulated in baseline and manual adjustment models with observed values.
4.2. Automated Calibration with Luca
While manual calibration can provide subjective insights into parameters that can improve the PRMS model application for Puerto Rico, automatic calibration follows objective steps that have demonstrated success [7,20,33]. The application of Luca as described in the ‘Methods’ section required several separate calibration sessions, as only one flow-calibration site (streamgage data) is used per calibration step. The four steps of the Luca calibration as outlined in Table 5 were performed with the calibration concentrating on streamflow fit at station 50029000 Río Grande de Arecibo at Cambalache (Table 3), with post-calibration checks at other stations.
The Luca calibration is accomplished in four steps (Table 5). The first step in the Luca calibration, matching solar radiation, provides a monthly temporal variation in the parameters for the degree-day equation dday_slope and dday_intcp (Table 4 and Table 5). In the manual calibration a single value of these parameters was selected for all months, but the Luca calibration allows separate monthly values, which appear to follow a seasonal trend. The assumed relationship between air temperature and the ratio of surface to extraterrestrial solar radiation accounts for a number of atmospheric factors, primarily cloud cover. The empirical adjustment of the dday_slope and dday_intcp value represents this relationship. The values of dday_slope have the most distinct seasonal trend, with the highest values in spring and lowest values in fall (Figure 10). The values of dday_intcp tend to be highest in the summer but have more variability between months. Temporal variations in these Luca calibrated parameters could be due to monthly variations in average cloud cover not accounted for in the assumed relationship between temperature and cloud cover. While calibrated values varied by month, they were not calibrated to vary spatially.
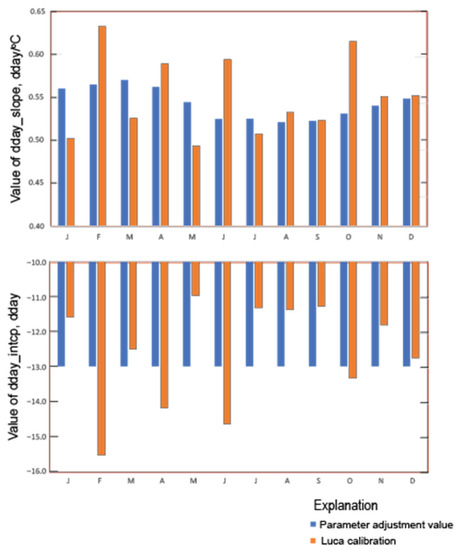
Figure 10.
Degree-day solar radiation parameters dday_slope and dday_intcp before and after Luca calibration step 1.
The solar radiation generated in the Luca calibration fits the GOES-PRWEB data somewhat better than the solar radiation from the manual calibration. For the calibration period 2009–2017, the daily mean manual calibration radiation is 315.6 Langleys, the daily mean Luca calibration radiation is 330.8 Langleys, and the daily mean measured GOES-PRWEB radiation is 332.4 Langleys. The manual calibration yielded an error of 5.05 percent and the Luca calibration an error of 0.48 percent. The Luca calibration substantially improved the mean daily radiation fit, and the improvement in the highest monthly mean radiation values is visually apparent (Figure 11).

Figure 11.
Monthly average solar radiation in manual calibration, Luca calibration, and measured data.
The second step in the Luca calibration is calibrating the Priestly-Taylor evapotranspiration coefficient α (pt_alpha) using potential evapotranspiration (PET) data derived from the PRAGWATER database. The Priestley-Taylor coefficient represents a variety of surface factors that affect ET, including surface cover and soil moisture, and requires calibration for a specific environment. Somewhat of a seasonal trend is visible (Figure 12), with the lowest values occurring in the spring, corresponding to the dry season. The higher values of α are near the upper limit of the Luca calibration range of 1.35. These high values indicate that other parameters in equations Equation (1) or Equation (2) may be inducing underestimation of solar radiation or ET, or the calibration target for ET may be somewhat high for some months. The average of the Luca-calibrated α values is 1.257, very close to the standard 1.26 value. Temporal differences in the Luca calibrated Priestley-Taylor coefficient could be due to monthly changes in surface cover, soil moisture, and other factors. The seasonal variation of α has been associated with atmospheric humidity [35], and the rainy season in Puerto Rico begins around April, when the Luca calibration indicates some of the lowest α values (Figure 12).
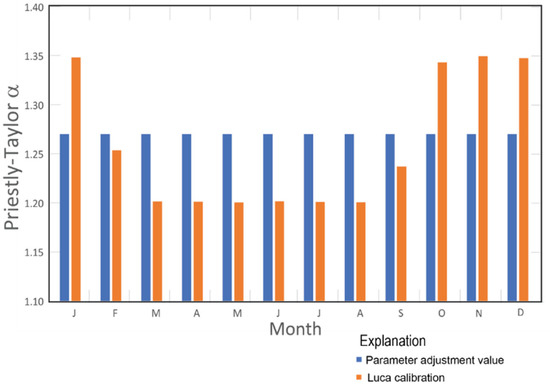
Figure 12.
Evapotranspiration parameter α (pt_alpha) before and after Luca calibration step 2.
As outlined in Table 5, the third Luca calibration step adjusts the soil2gw_max and ssr2gw_exp parameters by matching observed and simulated daily streamflow for the lowest 90% exceedance of monthly flows (low flows) at each individual zone’s flow station. The fourth step calibrates the carea_max and pref_flow_den parameters (Table 5) based on all flows, including the peak flows that were not used for calibration in step 3. These steps are primarily designed to calibrate the distribution and timing of simulated flows, with the potential to improve peak flow representation compared to the manual calibration. The adjustment of soil parameters in step 3 and river parameters in step 4 represents the uncertain infiltration and runoff variables such as maximum infiltration rate, groundwater storage, overland flow resistance, and riverbank storage.
Comparisons of streamflow at the Río Grande de Arecibo at Cambalache from the Luca-calibrated simulation to the manually calibrated simulation indicated improvement in all statistics for the Luca calibration (Table 6). A Root Mean Square Error (RMSE) is computed as the square-root of the average measured-to-computed flow-difference squared residual [36]. The improvement in the Luca-calibrated simulation flow RMSE is similar for both the calibration and verification periods (Table 6). The Nash-Sutcliffe (N-S) coefficient or efficiency index [37], which quantifies how well a model simulation can predict the outcome variable, is applied to seasonal streamflow at Río Grande de Arecibo at Cambalache separately for the calibration and verification periods. The improvement in the N-S coefficient in the Luca-calibrated flows compared to the manual-calibrated flows is marginal, 1.8 percent for the calibration period and 1.3 percent for the verification period (Table 6). The N-S coefficient is biased towards high values, so it is suitable to indicate peak-flow errors. At the Río Grande de Arecibo at Utuado station, upstream of Río Grande de Arecibo at Cambalache, most statistics indicate a poorer fit than at Cambalache for the calibration period. The RMSE values are distinctly better at Utuado than at Cambalache for the verification period, but the RMSE is not an absolute comparison of accuracy between different flow stations, because locations with higher magnitude streamflows inherently have larger RMSE values. As calibration was only implemented at Cambalache, the calibration fit at Utuado is expected to be somewhat less close, but both sites should have related flow patterns.

Table 6.
Statistics of streamflow for the manual calibration and completed four-step Luca calibration; N-S: Nash–Sutcliffe; RMSE: root mean square error.
A comparison of the cumulative observed and simulated flows between the manual adjustment (Figure 8) and the Luca calibration (Figure 13) gives some insight into the statistical results in Table 6. The improvement in fit between measured and computed values for the Luca calibration is visually apparent, albeit subtle. The fluctuations in the computed cumulative plots are higher than those in the measured data, indicating multiday periods of higher and lower flows.
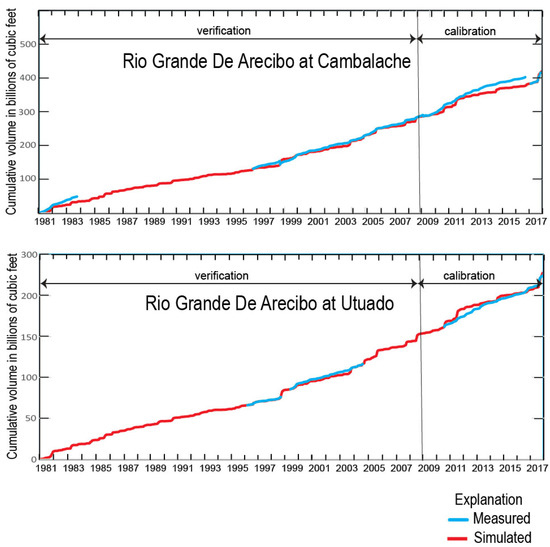
Figure 13.
Cumulative daily flows at observation stations with Luca calibration of parameters. Horizontal lines show years used for validation and for calibration.
Although the statistics for the Luca calibration are marginally better, a substantial improvement cannot be shown. This indicates two possible but not mutually exclusive explanations. Firstly, the manual calibration approximated the chosen parameters closely enough that Luca could not appreciably improve them. Secondly, the variables that might be adjusted to create a substantially improved simulation were either not part of the calibrations or not represented in PRMS. These possible explanations indicate that future model improvements would depend on additional parameterization for calibration or applying a model algorithm that better represents the physics of the flow system.
The observed daily streamflow data displayed in Figure 14 indicates the fit of the Luca calibrated simulations at Río Grande de Arecibo at Cambalache and Río Grande de Arecibo at Utuado. The multiday periods of higher-than-measured and lower-than-measured flows noted on Figure 13 can be seen in the daily flows of Figure 14. At the driest times, the model tends to underestimate flows. There is a considerable number of times at Cambalache when flows are in the range of 1000 to 2000 ft3/s and the model overestimates flows. In addition, although the calibration has substantially improved matching of the highest peak flows, some are still underestimated. One interpretation is that the “flashiness” of the model, the tendency to drain rapidly, which allows for better representation of high peak flows, is causing medium-magnitude flow drainage to happen too quickly, and subsequent low flows are deficient. The baseline model was less flashy but did not represent peak flows as well as the Luca calibrated model (Figure 9).
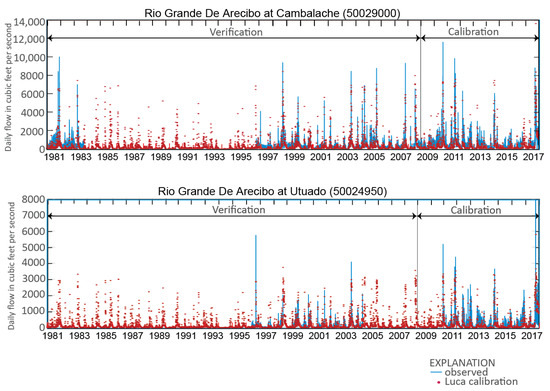
Figure 14.
Modeled daily streamflows at observation stations, with Luca calibration. Horizontal bars indicate years used for validation and calibration.
The overall water budget for the entire simulation period indicates that about 63 percent of the rainfall is lost to evapotranspiration, about 37 percent is runoff to the ocean, and a much smaller amount to change in storage (Table 7). The PRMS control volume includes the watersheds, rivers, and groundwater storage. Flows in and out of this control volume are designated external and flows within the control volume designated internal (Table 7). The mass conservation error in the model is 0.00 percent. The surface runoff to rivers is slightly under two-thirds of the recharge to groundwater, and the sum of these two quantities equals the coastal outflows minus the change in storage of the entire system (Table 7). The simulated yearly ET values of 38.1 inches per year correspond to an average of 0.104 inches per day. Values of ET in the Luquillo experimental forest of Puerto Rico were estimated at 0.121 ± 0.053 inches per day [38], so the simulated values are somewhat lower than this forested value. The inclusion of higher elevation, less vegetated areas may explain lower values.

Table 7.
External and internal water budget for entire simulation period; positive values indicate flux into the model watersheds.
5. PRMS Arecibo Model Application: Delineating Hydrology of Hurricane Maria
On 20 September 2017, Hurricane Maria made landfall over Puerto Rico. The streamflow data was lost at the northern streamgages along the Río Grande de Arecibo at Utuado and Cambalache (Table 3 and Figure 2). The loss of streamflow data during a hurricane is common but very detrimental to any attempts to study the hydrologic effects of the hurricane, and alternate methods to estimate the streamflow are important.
5.1. Comparing Simulated Hurricane Streamflows to Field Estimates
Examining concurrent measured and PRMS Arecibo model simulated peak daily streamflow events over 6000 ft3/s on the Río Grande de Arecibo during the study period indicate that, in most of the events, the simulated values underestimate the measured values by less than 37 percent, and in two cases somewhat overestimate the flows (Table 8). The simulated peak daily streamflow for Hurricane Maria is the highest simulated peak in the study period. The PRMS Arecibo model simulation of daily values indicates a Hurricane Maria peak average daily streamflow of 7598 ft3/s at Cambalache (Table 8) and 2722 ft3/s at Utuado.

Table 8.
Peak measured streamflows over 6000 cfs during period of simulation.
At streamgages where data are missing, a standard field procedure is to implement an indirect method which estimates peak flows based on high-water marks recorded after a major hydrologic event. Such an indirect method was attempted at Río Grande de Arecibo at Cambalache after Hurricane Maria. To translate high-water mark elevations to streamflow, the two-dimensional finite volume hydrodynamic model SToRM [39] was used. Multiple SToRM runs are performed to reconstruct the 20 September 2017, flood using a mixture of original surveyed high-water mark data and lidar elevation data [21]. The instantaneous peak streamflow is the highest flow at any time during a period, whereas the peak daily mean streamflow is the highest value of the average daily flow during a period. It is difficult to estimate the ratio of instantaneous to daily mean peak flows, as the ratio depends on the entire time series of flows over the day. Estimates of instantaneous peak streamflow at Cambalache from this indirect method are very high, 185,000–188,000 ft3/s, and the estimation is considered poor, because high water marks are very limited and vary by about 0.7 m from left to right bank at the downstream boundary. Due to these factors, there is no approved daily peak flow value in the National Water Information system database (USGS, 2022) at the time of publication for Río Grande de Arecibo at Cambalache for 21–22 September 2017 and for Río Grande de Arecibo below Utuado for 21 September 2017. Given the very high estimates of instantaneous flows from the indirect method, an investigation of other measured peak flow events during the simulation period could provide insight.
The PRMS Arecibo model simulation, although it is limited by a one-day timestep, can be a partial alternative to indirect methods, lending insight into storm flows that are essential in determining urban flooding and storm damage potential. The model-simulated streamflow is based on mass conservation rather than computations using water levels, so it provides a time series that indirect methods cannot. The simulation results have uncertainties and bias, as determined during the calibration process, that must be considered when using model results for prediction.
It is interesting to note the substantial lower variability in simulated peaks than the measured peaks; the measured peaks have a standard deviation of 1576 ft3/s and the simulated peaks a standard deviation of only 524 ft3/s. A simulation variability lower than measured variability can indicate additional physical processes or details not accounted for in the simulation. Of the major storm events shown in Table 8, the highest ratio of measured to simulated peak daily streamflow is 1.587 for Hurricane Otto in 6–8 October 2010. If this is used as a maximum ratio of measured to simulated values, the simulated value of 7598 ft3/s indicates that the daily peak streamflow at Río Grande de Arecibo at Cambalache likely did not exceed 12,060 ft3/s. This would indicate that the indirect estimate of instantaneous peak over an order of magnitude higher than the simulated daily peak is unlikely and would not be an accurate guide in making an indirect estimate of the daily peak streamflow.
One further comparison also supports the PRMS Arecibo model simulation of peak daily streamflows. Hurricane Georges had a maximum measured total rainfall of 28.36 inches in Puerto Rico [40] and a measured peak daily streamflow of 9390 ft3/s at Cambalache (Table 8). Hurricane Maria had a maximum measured total rainfall of 37.9 inches [1], 9.5 inches more than the maximum for Georges. It would be expected from this rainfall information that peak daily streamflows for Hurricane Maria would be somewhat proportionally higher than peak daily streamflows from Hurricane Georges, as the simulation certainly indicates. Conservation of mass is an important part of the simulation (Table 7) and provides a constraint that is often not available in indirect methods. It is possible that the flooding from Hurricane Maria could have expanded the flow section of the Río Grande de Arecibo and more flow occurs than PRMS simulates, but this would still be constrained by the total water available.
Model results always depend on the completeness of the input data and missing and estimated rainfall record during Hurricane Maria can be a factor in the accuracy of the simulation. The Daymet dataset used to specify rainfall input to the PRMS Arecibo model utilizes 61 stations to interpolate rainfall for Puerto Rico, but only 23 of these gages functioned throughout all of Hurricane Maria. The interpolation scheme is then limited with fewer data points and less spatial coverage, but interpolated values are still applied to all locations and may still be reasonable approximations of actual rainfall magnitudes.
5.2. Examining Coastal Hurricane Flows
Coastal runoff from the western area of Barceloneta (Figure 3) is simulated with the Luca calibrated model by allocating the excess water from this HRU to a simulated channel of no resistance. The simulated flow time series includes the 20 September 2017 landfall of Hurricane Maria. The total simulated flows along the western coastal area of Barceloneta have periodic daily peaks similar to channelized streamflows, with most peaks below 3000 ft3/s (Figure 15). The simulated daily peak flow associated with Hurricane Maria is 4488 ft3/s, not as high as sites on the Río Grande de Arecibo but it is the highest streamflow in the Barceloneta time series. Coastal flows in Barceloneta tend to be somewhat less than one-half of the flows at Río Grande de Arecibo at Cambalache (Figure 14 and Figure 15).
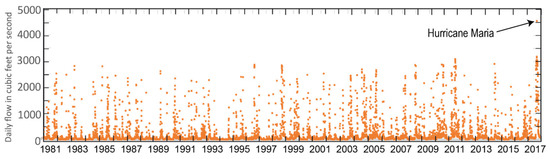
Figure 15.
Simulated coastal flow in the western coastal area of the municipality of Barceloneta.
Because this HRU contains several different hydrologic areas, including the Caño Tiburones Reserve, it could be desirable to split it into smaller HRUs for greater spatial resolution. This would also allow differentiation between the runoff from the Reserve and other nearby areas for water-quality concerns. Substantial observed data are needed to validate the simulation of the Caño Tiburones Reserve and define smaller-scale variations in coastal flow. The runoff time series simulated in Figure 15, as well as the equivalent in any other coastal area, can be used to define freshwater outflows for offshore salinity analyses and other research.
6. Discussion
The PRMS Arecibo model represents the hydrology of a watershed in western Puerto Rico through simulation of the rainfall-runoff process. Observed streamflow in the model domain is characterized by low-frequency high-amplitude flows, driven by rainfall events. Streamflow at Río Grande de Arecibo at Cambalache has additional low frequency, high-amplitude flows driven by periodic releases of water from the Lago Dos Bocas reservoir. Calibration of the PRMS model focused largely on improving simulation of these characteristic peak flows and delineating the processes controlling them. Improvements over the baseline and manually adjusted models in matching simulated seasonal and cumulative flows to observed values were seen at the site on the Río Grande de Arecibo at Cambalache for the Luca calibration. Although the Luca calibration provided the closest match, it was preceded by a manual calibration that was very useful in parameter development. The manual calibration aided in examining the effects of depression storage and release, which were shown to be important in matching peak flows.
The PRMS Arecibo model simulation of Hurricane Maria was applied to estimating daily streamflow at locations on the Río Grande de Arecibo where streamgage data were lost during the storm. Comparison of model results and streamflow estimates at Río Grande de Arecibo during Hurricane Maria’s peak streamflow event indicates that field estimates from indirect methods can overestimate flow. This conclusion is supported by comparing measured and computed peak flows from other high flow events in the study time series.
The application of the PRMS Arecibo model to coastal outflows from the western coastal area of Barceloneta during Hurricane Maria indicates considerable outflows, approximately one-half of those at Río Grande de Arecibo at Cambalache (Figure 14 and Figure 15), so monitoring streamflows alone does not provide sufficient information on total freshwater outflow at the coast. This has implications to studies of offshore salinity and ecology where the effects of freshwater releases are of interest as well as landslides affected by overland flow. Observations of direct coastal outflows is lacking and would be required to validate this effort.
The current model is useful in representing multi-daily flows and coastal outflows and can be used to look at the effects of alternate hydrologic scenarios and major storms. As is the case with most model development, the simulations are most useful when looking at differences in scenarios with specific changes in controlling variables. In this capacity, the PRMS Arecibo model can be used to look at effects of changes in climate and land use, water management, industrial and public water usage, and many other factors that affect hydrology on the island of Puerto Rico.
7. Model Limitations
In order to use any model simulation properly, the capabilities and limitations of the simulation must be considered. When utilizing model results for the PRMS Arecibo model, this can be divided into the limitations of (1) the PRMS model code and (2) the simulation design and input data.
The limitations of the PRMS model code include:
- The PRMS model code simulates surface infiltration as Hortonian and/or Dunnian surface runoff [17] with a daily timestep. Surficial runoff is computed as the remainder after reaching the infiltration capacity. On a particular day in the simulation, the daily average rainfall might not exceed the daily infiltration capacity, but actual instantaneous rainfall may exceed infiltration and create runoff. The daily timestep limits all the processes simulated in the model to daily averages;
- Flows in streams are represented by a downstream-routing scheme without consideration of momentum or backwater effects. In mountainous areas it is often assumed that the streamflow slopes are high enough that downstream effects are minimal. However, at coastal outlets with tidal effects and in other low-slope flow regimes, the flow rate may be substantially affected by water levels. Additionally, overbank conditions that can dramatically affect flow area and volume are not represented in PRMS. Backwater effects could be most severe in extreme events, such as Hurricane Maria, where coastal storm surge pushes river water back from the shore;
- Groundwater interactions are approximated, and groundwater flow is not represented. Accounting for groundwater could be particularly important in the karst terrain along the north coast (Figure 1). Groundwater storage is computed based on user defined capacities. The PRMS model has been integrated with the MODFLOW groundwater model to form GSFLOW [41] to which the PRMS Arecibo model could be adapted and expanded to the full area of Puerto Rico to account for groundwater flow;
- One possible factor which may account for difficulties in representing peak flows is the daily simulation timestep. The PRMS model currently does not support shorter timesteps than a day. Accounting for phenomena with substantially shorter timescales than a day may be necessary to simulate runoff and streamflow in this hydrologic setting. Other model code features that could improve simulation of peak flow include a more sophisticated formula for river flow, such as a Mannings formulation that computes flow based on river channel and overbank properties, and more detailed representation of overland flow and infiltration.The limitations of the simulation design and input data include:
- Timeseries inputs of rainfall, solar radiation, and minimum and maximum temperatures are spatially interpolated from station data and averaged to daily values. This produces both spatial and temporal smoothing of the model forcing functions and therefore can cause peaks and troughs in simulated flows to be missed or inaccurately predicted. Rainfall in Puerto Rico largely develops in small convective systems, and weather stations could miss events or interpolate small events to larger areas. An applicable Nexrad [42] dataset would be useful in better defining the spatial variations in rainfall. These data are available for Puerto Rico and would help define the spatial uncertainty in rainfall that may affect the simulation. Another source of data, the Weather Research and Forecasting model, was used to downscale select general-circulation models to a 2-km horizontal resolution for Puerto Rico and the U.S. Virgin Islands [43];
- The discretization of the model domain into HRUs aggregates land use, elevation, and other spatial features into a single value. The runoff from a single HRU is considered a single daily value reaching a defined stream segment. The boundaries of HRUs are assumed to be accurate dividing lines for the surface-water flow direction. Finer resolution HRUs can be created with sufficient field data to account for heterogeneous regions of the study area;
- Calibration to the Río Grande de Arecibo and streamgage Río Grande de Arecibo at Cambalache emphasizes one of the largest streamflows in Puerto Rico, but it cannot be assumed the parameters relevant to the Río Grande de Arecibo watershed apply to the rest of the island. Further calibration of other river basins using additional station data would be needed for a complete simulation of Puerto Rico;
- Changes in land use, water use, and other spatial features over the 1981–2017 simulation period are not accounted for and remain static in the model over this time period. Previous modeling studies indicate that neglecting multi-decadal land-cover change can make substantial simulation differences [7], and it would be reasonable to consider it is a factor in this simulation’s 37-year period.
- The calibration of infiltration and groundwater parameter does not include PRMS parameters soil_moist_max and soil_rechr_max which are the maximum available water-holding capacity of the soil profile and the maximum available water-holding capacity, respectively. These parameters can have substantial effects on the simulation, and possibly peak flows
8. Summary
The PRMS modeling code was used to develop a hydrologic simulation on the Arecibo River watershed on the island of Puerto Rico, referred to as the PRMS Arecibo model. The simulation is based on a previous simulation [7] which used the Geospatial Fabric for National Hydrologic Modeling [18] to provide HRU geometries, locations, dimensions, and features along with the surface-water routing network. Time-series data for rainfall, solar radiation, and minimum and maximum temperatures were derived from the Daymet version 3 data product [19] to develop a simulation of the period 1981–2017.
Initial calibration efforts involved adjustments to evapotranspiration, channel routing, depression storage, and flow connectivity parameters and observation of the simulation responses at streamflow stations along the Río Grande de Arecibo. It was found that quantifying reservoir releases helped account for some of the simulation’s underestimation of streamflows. The depression-storage parameters were found to have a substantial effect on peak streamflows and were adjusted to better match the previously underestimated peak flows. A four-step Luca calibration was implemented which calibrated solar radiation, evapotranspiration, low daily streamflows, and all daily streamflows. This effort produced better measured-to-simulated fits for both the calibration period of 2009–2017 and the verification period of 1981–2008.
The PRMS Arecibo model simulated the effects of Hurricane Maria on daily streamflow, and comparisons at locations on the Río Grande de Arecibo with missing streamflow data lend insight into the uncertainties in the estimated observed peak flows and model simulated values. Missing streamflow estimates made with indirect methods on the Río Grande de Arecibo were compared with simulation results, indicating that the model can be used to check field estimates and supply streamflow values when measurements are not available. The use of simulation results must consider the inherent uncertainty and biases in the model, but simulations can lend important insight into the hydrologic response during major storms.
Coastal flows are examined during Hurricane Maria in the western area of the municipality of Barceloneta. These results indicate that coastal flows are a substantial part of offshore freshwater discharge during major storm events and monitoring streamflows alone does not provide sufficient information on total freshwater flow at the coast. This method can be applied to any of the coastal HRUs to estimate freshwater contribution to the offshore areas. The other regions included in the model domain that were not examined can be calibrated in the same fashion as the Arecibo region. Thus, the PRMS Arecibo model could be expanded to all of Puerto Rico and applied to look at the effects of changes in climate and land use, water management, industrial and public water usage, and many other factors that affect hydrology on the island of Puerto Rico.
Author Contributions
Conceptualization, E.D.S. and J.C.B.; Methodology, E.D.S. and J.C.B.; Software, E.D.S. and J.C.B.; Validation, E.D.S.; Formal Analysis, E.D.S.; Investigation, E.D.S.; Resources, E.D.S. and J.C.B.; Data Curation, E.D.S. and J.C.B.; Writing—Original Draft Preparation, E.D.S. and J.C.B.; Writing—Review and Editing, E.D.S.; Visualization, E.D.S. and J.C.B.; Supervision, E.D.S.; Project Administration, E.D.S.; Funding Acquisition, E.D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding. The work was performed as part of the authors’ duties as employees of the U.S. Government.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and simulation model presented in this paper is available in the USGS model archive located at https://doi.org/10.5066/P9IMU17O (accessed on 3 November 2022).
Acknowledgments
The authors would like to thank John Stamm, Steve Markstrom, Jacob LaFontaine, and the USGS NHM team for their advice and support through the entire model development and calibration effort.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FEMA. Hurricanes Irma and Maria in Puerto Rico. FEMA P-2020/October 2018. p. 296. Available online: https://www.fema.gov/sites/default/files/2020-07/mat-report_hurricane-irma-maria-puerto-rico_2.pdf (accessed on 3 November 2022).
- Cangialosi, J.P.; Latto, A.S.; Berg, R. Hurricane Irma 30 August–12 September 2017. National Hurricane Center Tropical Cyclone Report. 30 June 2018. Available online: https://www.nhc.noaa.gov/data/tcr/AL112017_Irma.pdf (accessed on 19 December 2018).
- Byrne, M.J. Sr. Monitoring storm tide, flooding, and precipitation from Hurricane Maria in Puerto Rico and the U.S. Virgin Islands, September 2017. U.S. Geological Survey Open-File Report 2019–1065. 2019, p. 16. [CrossRef]
- Pasch, R.J.; Penny, A.B.; Berg, R. Hurricane Maria 16–30 September 2017. National Hurricane Center Tropical Cyclone Report. 10 April 2018. Available online: https://www.nhc.noaa.gov/data/tcr/AL152017_Maria.pdf (accessed on 19 December 2018).
- Sepúlveda, N.; Pérez-Blair, F.; DeLong, L.L.; Lopez-Trujillo, D. Real-Time Rainfall-Runoff Model of the Carraízo-Reservoir Basin in Puerto Rico; U.S. Geological Survey Water-Resources Investigations Report 95–4235; U.S. Geological Survey: Reston, VA, USA, 1996. [Google Scholar]
- Swain, E.D.; Gómez-Fragoso, J.; Torres-Gonzalez, S. Projecting Impacts of Climate Change on Water Availability Using Artificial Neural Network Techniques: J. Water Resour. Plan. Manag. 2017, 143, 12. [Google Scholar] [CrossRef]
- Van Beusekom, A.E.; Hay, L.E.; Viger, R.J.; Gould, W.A.; Collazo, J.A.; Khalyani, A.H. The effects of changing land cover on streamflow simulation in Puerto Rico. J. Am. Water Resour. Assoc. 2014, 50, 1575–1593. [Google Scholar] [CrossRef]
- Swain, E.D. PRMS Simulator Used to Assess Rainfall, Runoff, and River Flow for the National Hydrologic Model (NHM) Puerto Rico; U.S. Geological Survey: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Murphy, S.F.; Stallard, R.F.; Larsen, M.C.; Gould, W.A. Physiography, geology, and land cover of four watersheds in eastern Puerto Rico. In Water Quality and Landscape Processes of Four Watersheds in Eastern Puerto Rico; Professional Paper 1789–A; Murphy, S.F., Stallard, R.F., Eds.; U.S. Geological Survey: Reston, VA, USA, 2012; p. 22. Available online: https://pubs.er.usgs.gov/publication/pp1789A (accessed on 3 November 2022).
- Renken, R.A.; Ward, W.C.; Gill, I.P.; Gómez-Gómez, F.; Rodríguez-Martínez, J. Geology and Hydrogeology of the Caribbean Islands Aquifer System of the Commonwealth of Puerto Rico and the U.S. Virgin Islands; Professional Paper 14192002; U.S. Geological Survey: Reston, VA, USA, 2002; p. 139. Available online: https://pubs.usgs.gov/pp/pp1419/pdf/BOOK.PDF (accessed on 3 November 2022).
- Calvesbert, R.J. Climate of Puerto Rico and the US Virgin Islands: Climatography of the US; US Department of Commerce, Environmental Services Administration, Silver Springs: Rockville, MD, USA, 1970; pp. 52–60.
- Puerto Rico Agricultural Water Management. Monthly Estimated Soil Moisture Saturation. 2020. Available online: https://pragwater.com/monthly-estimated-soil-moisture-saturation/ (accessed on 22 September 2020).
- Larsen, M.C.; Simon, S. A Rainfall Intensity-Duration Threshold for Landslides in a Humid-Tropical Environment, Puerto Rico, Geografiska Annaler. Ser. A Phys. Geogr. 1993, 75, 13–23. [Google Scholar] [CrossRef]
- West, J.; Davis, L.; Bendezú, R.L.; Gandía, Y.D.A.; Hughes, K.S.; Godt, J.; Peek, L. Principles for Collaborative Risk Communication: Reducing Landslide Losses in Puerto Rico. J. Emerg. Manag. 2021, 19, 41–61. [Google Scholar] [CrossRef] [PubMed]
- U.S. Geological Survey. Equipment repair and replacement—Surface water gages in Texas, Florida, Puerto Rico, and U.S. Virgin Islands. 2021. Available online: https://www.usgs.gov/natural-hazards/usgs-supplemental-disaster-recovery-activities/equipment-repair-and-replacement?qt-science_support_page_related_con=0#qt-science_support_page_related_con (accessed on 3 November 2022).
- Regan, R.S.; Juracek, K.E.; Hay, L.E.; Markstrom, S.L.; Viger, R.J.; Driscoll, J.M.; LaFontaine, J.H.; Norton, P.A. The U.S. Geological Survey National Hydrologic Model infrastructure: Rationale, description, and application of a watershed-scale model for the conterminous United States. Environ. Model. Softw. 2019, 111, 192–203. [Google Scholar] [CrossRef]
- Markstrom, S.L.; Regan, R.S.; Hay, L.E.; Viger, R.J.; Webb, R.M.T.; Payn, R.A.; LaFontaine, J.H. PRMS-IV, the Precipitation-Runoff Modeling System, Version 4; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2015; Book 6, Chapter B7. [Google Scholar] [CrossRef]
- Viger, R.J.; Bock, A. The Geospatial Fabric Feature Set for National Hydrologic Modeling; U.S. Geological Survey Data Set: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; ORNL DAAC: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]
- Hay, L.E.; Umemoto, M. Multiple—Objective Stepwise Calibration Using Luca, 2007, USGS Open-File Report 2006-1323; 25p. Available online: https://pubs.usgs.gov/of/2006/1323/ (accessed on 3 November 2022).
- U.S. Geological Survey. USGS water data for the Nation: U.S. Geological Survey National Water Information System database. 2022. Available online: https://waterdata.usgs.gov/nwis (accessed on 3 November 2022).
- Leavesley, G.H.; Lichty, R.W.; Troutman, B.M.; Saindon, L.G. Precipitation-Runoff Modeling System—User’s Manual: U.S. Geological Survey Water-Resources Investigations Report 83–4238; U.S. Geological Survey: Reston, VA, USA, 1983; p. 207. [Google Scholar]
- Jacobs, J.; Mecikalski, J.; Paech, S. Satellite-Based Solar Radiation, Net Radiation, and Potential and Reference Evapo-Transpiration Estimates over Florida; A Technical Report; the State of Florida Water Management Districts: West Palm Beach, FL, USA, 2008. [Google Scholar]
- Soler-López, L.R. Sedimentation survey of Lago Dos Bocas, Utuado, Puerto Rico, January 2010. 2012, U.S. Geological Survey Scientific Investi-gations Map 3217, 1 sheet. Available online: https://pubs.usgs.gov/sim/3217/ (accessed on 3 November 2022).
- Soler-López, L.R. Sedimentation Survey of Lago Cerrillos, Ponce, Puerto Rico, April-May 2008; U.S. Geological Survey Scientific Investigations Report 2011-5057; U.S. Geological Survey: Reston, VA, USA, 2011. [Google Scholar]
- Viger, R.J.; Hay, L.E.; Jones, J.W.; Buell, G.R. Effects of including surface depressions in the application of the Precipitation-Runoff Modeling System in the Upper Flint River Basin, Georgia. In U.S. Geological Survey Scientific Investigations Report 2010–5062; U.S. Geological Survey: Reston, VA, USA, 2010; p. 36. [Google Scholar]
- Sneddon, J.; Chapman, T.G. Measurement and Analysis of Depression on a Hillslope. Hydrol. Process. 1989, 3, 1–13. [Google Scholar] [CrossRef]
- Hu, L.; Bao, W.; Shi, P.; Wang, J.; Lu, M. Simulation of overland flow considering the influence of topographic depressions. Sci. Rep. 2020, 10, 6128. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.J.; Ares, J.O. Depression storage and infiltration effects on overland flow depth-velocity-friction at desert conditions: Field plot results and model, Hydrol. Earth Syst. Sci. 2012, 16, 3293–3307. [Google Scholar] [CrossRef]
- Mwendera, E.J.; Feyen, J. Estimation of depression storage and Manning’s resistance coefficient from random roughness measurements. Geoderma 1992, 52, 235–250. [Google Scholar] [CrossRef]
- Elbasit, M.A.M.A.; Abu-Zreig, O.; Majed, M.; Chandra, S.P.; Yasuda, H.; Gang, L. Estimation of surface depression storage capacity from random roughness and slope. Water SA 2020, 46, 404–409. [Google Scholar] [CrossRef]
- Hay, L.; Leavesley, G.; Clark, M.; Markstrom, S.; Viger, R.; Umemoto, M. Step Wise, Multiple Objective Calibration of a Hydrologic Model for a Snowmelt Dominated Basin. J. Am. Water Resour. Assoc. 2006, 42, 877–890. [Google Scholar] [CrossRef]
- LaFontaine, J.H.; Jones, L.E.; Painter, J.A. Simulations of Hydrologic Response in the Apalachicola-Chattahoochee-Flint River Basin, Southeastern United States; U.S. Geological Survey Scientific Investigations Report 2017–5133; U.S. Geological Survey: Reston, VA, USA, 2017; p. 112. [Google Scholar] [CrossRef]
- Caño Tiburones Nature Reserve. In Puerto Rico Department of Natural and Environmental Resources; 2007. Available online: https://www.drna.pr.gov/wp-content/uploads/2015/04/Reserva-Natural-Ca%C3%B1o-Tiburones.pdf (accessed on 3 November 2022).
- Tongwane, M.I.; Savage, M.J.; Tsubo, M.; Moeletsi, M.E. Seasonal variation of reference evapotranspiration and Priestley-Taylor coefficient in the eastern Free State, South Africa. Agric. Water Manag. 2017, 187, 122–130. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M.; Ryberg, K.R.; Archfield, S.A.; Gilroy, E.J. Statistical Methods in Water Resources; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2020; Book 4, Chapter A3; p. p. 458. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part 1: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Wu, W.; Hall, C.A.S.; Scatena, F.N.; Quackenbush, L.J. Spatial modelling of evapotranspiration in the Luquillo experimental forest of Puerto Rico using remotely-sensed data. J. Hydrol. 2006, 328, 733–752. [Google Scholar] [CrossRef]
- Simões, F.J.M. SToRM: A Model for 2D environmental hydraulics. In Proceedings of the the 3rd Joint Federal Interagency Conference on Sedimentation and Hydrologic Modeling, Reno, NV, USA, 19–23 April 2015; 2017; pp. 350–362. [Google Scholar]
- Guiney, J.L. Preliminary Report, Hurricane Georges 15 September–01 October 1998. National Hurricane Center. 1999. Available online: https://www.nhc.noaa.gov/data/tcr/AL071998_Georges.pdf (accessed on 3 November 2022).
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW-Coupled Ground-water and Surface-water FLOW Model Based on the inTEGRATION of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005); U.S. Geological Survey Techniques and Methods 6-D1, U.S. Geological Survey: Reston, VA, USA, 2008; p. 240. [Google Scholar]
- Kitzmiller, D.; Miller, D.; Fulton, R.; Ding, F. Radar and multisensory precipitation estimation techniques in National Weather Service hydrologic operations. J. Hydrol. Eng. 2013, 18, 133–142. [Google Scholar] [CrossRef]
- Bowden, J.; Wootten, A.; Terando, A.; Boyles, R. Weather Research and Forecasting (WRF): Puerto Rico and US Virgin Islands Dynamical Downscaled Climate Change Projections; U.S. Geological Survey: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).