Structuralization of Complicated Lotic Habitats Using Sentinel-2 Imagery and Weighted Focal Statistic Convolution
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Data Sets
3. Methods
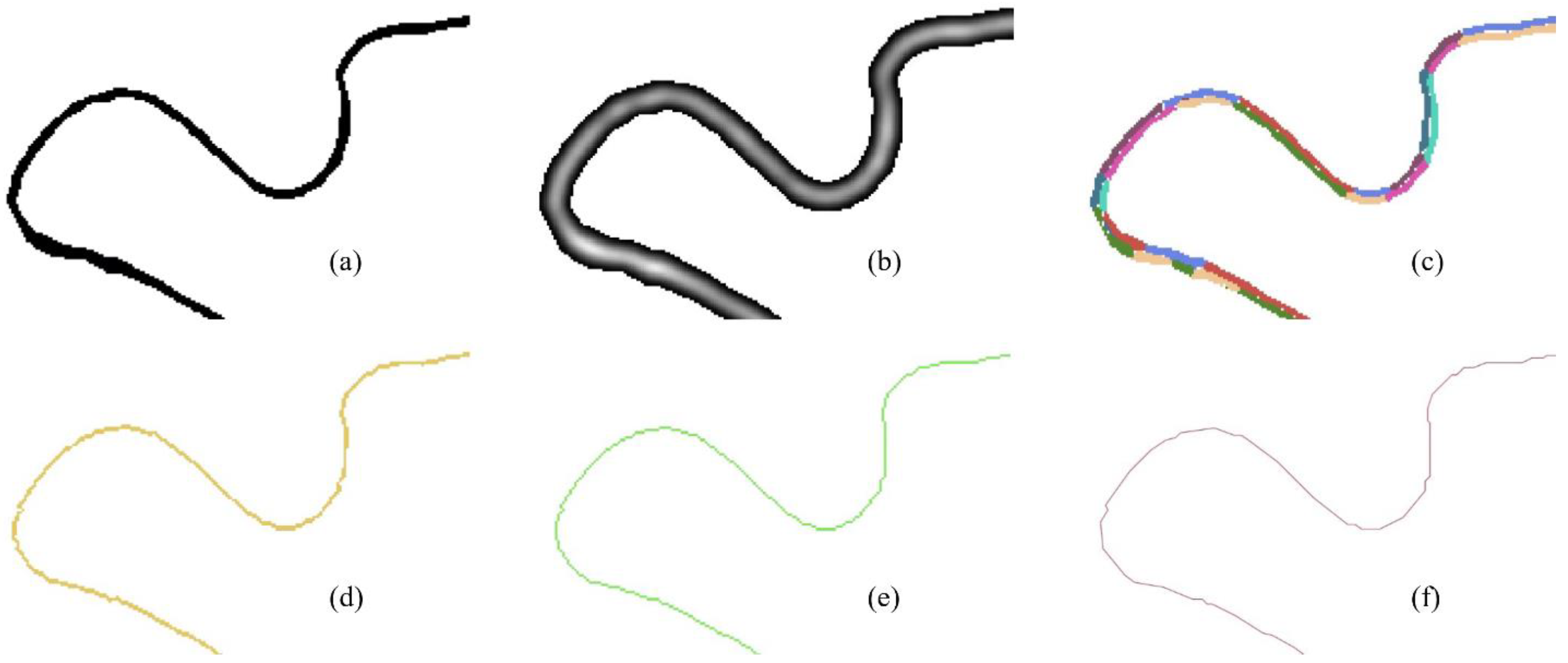
3.1. Lotic Habitat Delineation
3.2. Lotic Habitat Centerline Delineation
3.3. Accuracy Assessment
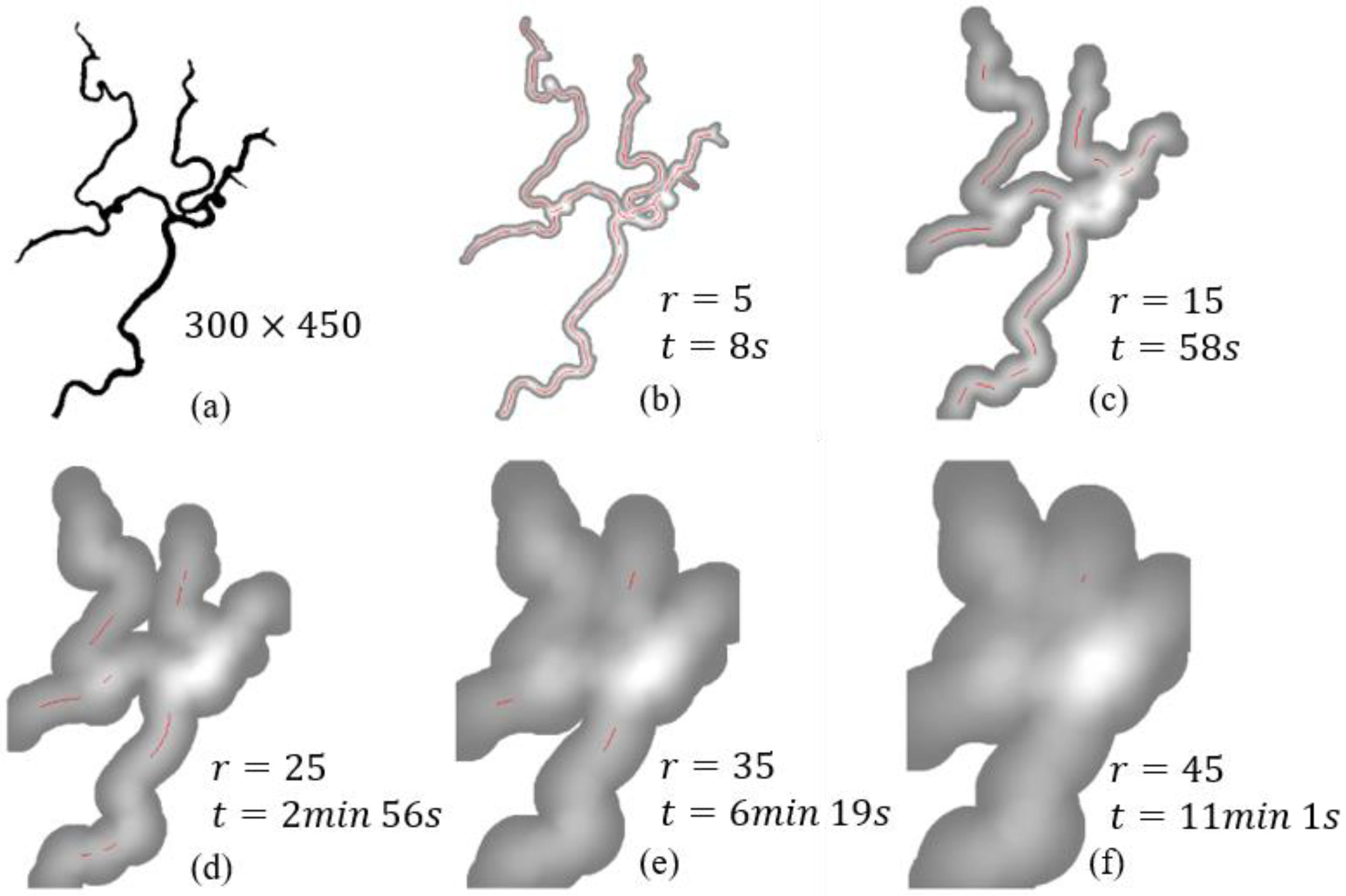
3.4. Multi-Level Structuralization of Complicated River Network
4. Results and Discussions
4.1. Centerline Extraction and Accuracy Assessment
4.2. Parameter Sensitivity and Multi-Level Structuralization
4.3. Planar Geometric Attributes Derivation and the Width–Abundance Pattern
5. Conclusions
Author Contributions
Data Availability Statement
Conflicts of Interest
Code Availability Statement
Abbreviations and Notations
References
- Fisher, W.L.; Bozek, M.A.; Vokoun, J.C.; Jacobson, R.B. Freshwater aquatic habitat measurements. In Fisheries Techniques, 3rd ed.; American Fisheries Society: Bethesda, MD, USA, 2012; pp. 101–161. [Google Scholar]
- Bain, M.B.; Stevenson, N.J. Aquatic Habitat Assessment; Asian Fisheries Society: Bethesda, MD, USA, 1999. [Google Scholar]
- Jones, A.E.; Hodges, B.R.; McClelland, J.W.; Hardison, A.K.; Moffett, K.B. Residence-time-based classification of surface water systems. Water Resour. Res. 2017, 53, 5567–5584. [Google Scholar] [CrossRef]
- Mulder, T.; Syvitski, J.P.; Skene, K.I. Modeling of erosion and deposition by turbidity currents generated at river mouths. J. Sediment. Res. 1998, 68, 124–137. [Google Scholar] [CrossRef]
- Hizzett, J.L.; Hughes Clarke, J.E.; Sumner, E.J.; Cartigny, M.; Talling, P.; Clare, M. Which triggers produce the most erosive, frequent, and longest runout turbidity currents on deltas? Geophys. Res. Lett. 2018, 45, 855–863. [Google Scholar] [CrossRef]
- Lane, S.N.; Westaway, R.M.; Murray Hicks, D. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Montgomery, D.R. Valley formation by fluvial and glacial erosion. Geology 2002, 30, 1047–1050. [Google Scholar] [CrossRef]
- Constantine, J.A.; Dunne, T. Meander cutoff and the controls on the production of oxbow lakes. Geology 2008, 36, 23–26. [Google Scholar] [CrossRef]
- Seybold, H.; Andrade, J.S.; Herrmann, H.J. Modeling river delta formation. Proc. Natl. Acad. Sci. USA 2007, 104, 16804–16809. [Google Scholar] [CrossRef]
- Strokal, M.; Ma, L.; Bai, Z.; Luan, S.; Kroeze, C.; Oenema, O.; Velthof, G.; Zhang, F. Alarming nutrient pollution of Chinese rivers as a result of agricultural transitions. Environ. Res. Lett. 2016, 11, 024014. [Google Scholar] [CrossRef]
- He, R.; Yang, X.; Gassman, P.W.; Wang, G.; Yu, C. Spatiotemporal characterization of nutrient pollution source compositions in the Xiaohong River Basin, China. Ecol. Indic. 2019, 107, 105676. [Google Scholar] [CrossRef]
- Kiedrzyńska, E.; Kiedrzyński, M.; Urbaniak, M.; Magnuszewski, A.; Skłodowski, M.; Wyrwicka, A.; Zalewski, M. Point sources of nutrient pollution in the lowland river catchment in the context of the Baltic Sea eutrophication. Ecol. Eng. 2014, 70, 337–348. [Google Scholar] [CrossRef]
- Dalu, T.; Wasserman, R.J.; Magoro, M.L.; Froneman, P.W.; Weyl, O.L. River nutrient water and sediment measurements inform on nutrient retention, with implications for eutrophication. Sci. Total Environ. 2019, 684, 296–302. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.N.; Kroeze, C.; Strokal, M. Human waste: An underestimated source of nutrient pollution in coastal seas of Bangladesh, India and Pakistan. Mar. Pollut. Bull. 2017, 118, 131–140. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Wang, L.; Xu, M.; Cohen, S.; Liu, K. Derivation of spatially detailed lentic habitat map and inventory at a basin scale by integrating multispectral Sentinel-2 satellite imagery and USGS Digital Elevation Models. J. Hydrol. 2021, 603, 126876. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 data for land cover/use mapping: A review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Farhadi, H. Reliability assessment of water quality index based on guidelines of national sanitation foundation in natural streams: Integration of remote sensing and data-driven models. Artif. Intell. Rev. 2021, 54, 4619–4651. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Liu, Y.; Liu, H.; Beck, R.; Reif, M.; Emery, E.; Young, J.; Wu, Q. Mapping freshwater chlorophyll-a concentrations at a regional scale integrating multi-sensor satellite observations with Google earth engine. Remote Sens. 2020, 12, 3278. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain analysis using digital elevation models in hydrology. In Proceedings of the 23rd ESRI International Users Conference, San Diego, CA, USA, 7–11 July 2003. [Google Scholar]
- Moore, I.D.; Grayson, R.; Ladson, A. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Metz, M. A new GRASS GIS toolkit for Hortonian analysis of drainage networks. Comput. Geosci. 2011, 37, 1162–1173. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models (TauDEM); Utah State University: Logan, UT, USA, 2005; Volume 3012, p. 2018. [Google Scholar]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Shreve, R.L. Statistical law of stream numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- Ngoc, D.D.; Loisel, H.; Jamet, C.; Vantrepotte, V.; Duforêt-Gaurier, L.; Minh, C.D.; Mangin, A. Coastal and inland water pixels extraction algorithm (WiPE) from spectral shape analysis and HSV transformation applied to Landsat 8 OLI and Sentinel-2 MSI. Remote Sens. Environ. 2019, 223, 208–228. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bibiloni, P.; González-Hidalgo, M.; Massanet, S. General-purpose curvilinear object detection with fuzzy mathematical morphology. Appl. Soft Comput. 2017, 60, 655–669. [Google Scholar] [CrossRef]
- Soille, P.; Pesaresi, M. Advances in mathematical morphology applied to geoscience and remote sensing. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2042–2055. [Google Scholar] [CrossRef]
- Clode, S.P.; Zelniker, E.E.; Kootsookos, P.J.; Clarkson, I.V.L. A phase coded disk approach to thick curvilinear line detection. In Proceedings of the 2004 12th European Signal Processing Conference, Vienna, Austria, 6–10 September 2004; pp. 1147–1150. [Google Scholar]
- Clode, S.; Rottensteiner, F.; Kootsookos, P.; Zelniker, E. Detection and vectorization of roads from lidar data. Photogramm. Eng. Remote Sens. 2007, 73, 517–535. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Shan, J.; Zhang, J.; Zhang, Y. Road centerline extraction in complex urban scenes from LiDAR data based on multiple features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7448–7456. [Google Scholar]
- Clode, S.; Kootsookos, P.J.; Rottensteiner, F. The Automatic Extraction of Roads from LIDAR Data; ISPRS: Istanbul, Turkey, 2004. [Google Scholar]
- Liu, Y. Automatically Structuralize the Curvilinear Glacier Using Phase-coded Convolution. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Beshr, A.M.; Mohamed, A.K.; ElGalladi, A.; Gaber, A.; El-Baz, F. Structural characteristics of the Qena Bend of the Egyptian Nile River, using remote-sensing and geophysics. Egypt. J. Remote Sens. Space Sci. 2021, 24, 999–1011. [Google Scholar] [CrossRef]
- Nones, M. Remote sensing and GIS techniques to monitor morphological changes along the middle-lower Vistula river, Poland. Int. J. River Basin Manag. 2021, 19, 345–357. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Nones, M.; Guerrero, M. Deriving planform morphology and vegetation coverage from remote sensing to support river management applications. Front. Environ. Sci. 2021, 9, 657354. [Google Scholar] [CrossRef]
- McPherson, A.K.; Moreland, R.S.; Atkins, J.B. Occurrence and Distribution of Nutrients, Suspended Sediment, and Pesticides in the Mobile River Basin, Alabama, Georgia, Mississippi, and Tennessee, 1999–2001; US Department of the Interior: Washington, DC, USA; US Geological Survey: Montgomery, AL, USA, 2003.
- Atkins, J.B.; Zappia, H.; Robinson, J.L.; McPherson, A.K.; Moreland, R.S.; Harned, D.A.; Johnston, B.F.; Harvill, J.S. Water Quality in the Mobile River Basin, Alabama, Georgia, and Mississippi, and Tennessee, 1999–2001; US Geological Survey: Montgomery, AL, USA, 2004.
- Liu, A.; Ming, J.; Ankumah, R.O. Nitrate contamination in private wells in rural Alabama, United States. Sci. Total Environ. 2005, 346, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, W.W.; Dinnel, S.P.; Wiseman, W.J. Salinity stratification in a river-dominated estuary. Estuaries 1990, 13, 145–154. [Google Scholar] [CrossRef]
- Liu, Y.; Kwan, M.-P.; Wu, Z. Visualizing and quantifying the spatiotemporal expansion of the Blue Lentic Belt in Alabama and Mississippi. Water Res. 2022, 217, 118444. [Google Scholar] [CrossRef] [PubMed]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Dubes, R.; Jain, A.K. Clustering techniques: The user’s dilemma. Pattern Recognit. 1976, 8, 247–260. [Google Scholar] [CrossRef]
- Tou, J.T.; Gonzalez, R.C. Pattern Recognition Principles; Addison-Wesley Publishing: Boston, MA, USA, 1974. [Google Scholar]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis, and Machine Vision; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bachelot, B.; Uriarte, M.; Zimmerman, J.K.; Thompson, J.; Leff, J.W.; Asiaii, A.; Koshner, J.; McGuire, K. Long-lasting effects of land use history on soil fungal communities in second-growth tropical rain forests. Ecol. Appl. 2016, 26, 1881–1895. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Stuckens, J.; Coppin, P.; Bauer, M. Integrating contextual information with per-pixel classification for improved land cover classification. Remote Sens. Environ. 2000, 71, 282–296. [Google Scholar] [CrossRef]
- Zhan, C. A hybrid line thinning approach. In Proceedings of the Autocarto-Conference, Minneapolis, MN, USA, 30 October–1 November 1993; p. 396. [Google Scholar]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Maragos, P.; Schafer, R. Morphological skeleton representation and coding of binary images. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1228–1244. [Google Scholar] [CrossRef]
- Su, Y.; Zhong, Y.; Zhu, Q.; Zhao, J. Urban scene understanding based on semantic and socioeconomic features: From high-resolution remote sensing imagery to multi-source geographic datasets. ISPRS J. Photogramm. Remote Sens. 2021, 179, 50–65. [Google Scholar] [CrossRef]
- Planet. Planet Application Program Interface: In Space for Life on Earth; Planet: San Francisco, CA, USA, 2017; Volume 2017, p. 40. [Google Scholar]
- Saalfeld, A. Topologically consistent line simplification with the Douglas-Peucker algorithm. Cartogr. Geogr. Inf. Sci. 1999, 26, 7–18. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Ghosh, S.; Mistri, B. Hydrogeomorphic significance of sinuosity index in relation to river instability: A case study of Damodar River, West Bengal, India. Int. J. Adv. Earth Sci. 2012, 1, 49–57. [Google Scholar]
- Mueller, J.E. An introduction to the hydraulic and topographic sinuosity indexes. Ann. Assoc. Am. Geogr. 1968, 58, 371–385. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, X.; Yang, Q.; Huang, Z. Numerical and experimental study the effects of river width changes on flow characteristics in a flume. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Guangzhou, China, 8–10 March 2019; p. 042004. [Google Scholar]
- Juez, C.; Hassan, M.A.; Franca, M.J. The origin of fine sediment determines the observations of suspended sediment fluxes under unsteady flow conditions. Water Resour. Res. 2018, 54, 5654–5669. [Google Scholar] [CrossRef]
- Downing, J.A.; Prairie, Y.; Cole, J.; Duarte, C.; Tranvik, L.; Striegl, R.G.; McDowell, W.; Kortelainen, P.; Caraco, N.; Melack, J. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Seekell, D.A.; Pace, M.L.; Tranvik, L.J.; Verpoorter, C. A fractal-based approach to lake size-distributions. Geophys. Res. Lett. 2013, 40, 517–521. [Google Scholar] [CrossRef]




| Task | Data Source | Spatial Resolution | Spectral Configuration | Capture Date | Coverage |
|---|---|---|---|---|---|
| Meandering river channel delineation | Sentinel-2, ESA | 10 m | R, G, B, and NIR | 4/26/2019 | 300 km2 centered on 86°56′W, 33°44′N |
| Braided river network delineation | Sentinel-2, ESA | 10 m | R, G, B, and NIR | 3/19/2019 | The Mobile–Tensaw River Delta |
| Meandering river channel ground truth | PlanetScope | 3 m | R, G, B, and NIR | 4/26/2019 | 300 km2 centered on 86°56′W, 33°44′N |
| Hydrologic reference | NED, USGS | 10 m | - | - | The MRB |
| Northwest Aspect: 292.5°~337.5° Code: 8 | North Aspect: 337.5°~360°, 0°~22.5° Code: 1 | Northeast Aspect: 22.5°~67.5° Code: 2 |
| West Aspect: 247.5°~292.5° Code: 7 | No Data | East Aspect: 67.5°~112.5° Code: 3 |
| Southwest Aspect: 202.5°~247.5° Code: 6 | South Aspect: 157.5°~202.5° Code: 5 | Southeast Aspect: 112.5°~157.5° Code: 4 |
| Centerline Length (km) | Length Accuracy (%) | Centerline Average Displacement (m) | Topological Consistency (Number of Links) | |
|---|---|---|---|---|
| Ground truth | 47.54 | - | - | 1 |
| Hydrologic method | 47.98 | 99.09 | 15.64 | 1 |
| Morphological method | 48.10 | 98.83 | 9.87 | 3 |
| PCD + MCMC | 36.31 | 76.38 | 7.60 | 31 |
| WFSC + Aspects | 48.01 | 99.01 | 9.58 | 1 |
| Level k | Kernel Radius rk | Gap Tolerance gk | Length Threshold * lk | Buffer Zone Width bk |
|---|---|---|---|---|
| 1 | 7 | 10 | 50 | 14 |
| 2 | 10 | 20 | 100 | 20 |
| 3 | 20 | 30 | 150 | 40 |
| 4 | 35 | 100 | 150 | 70 |
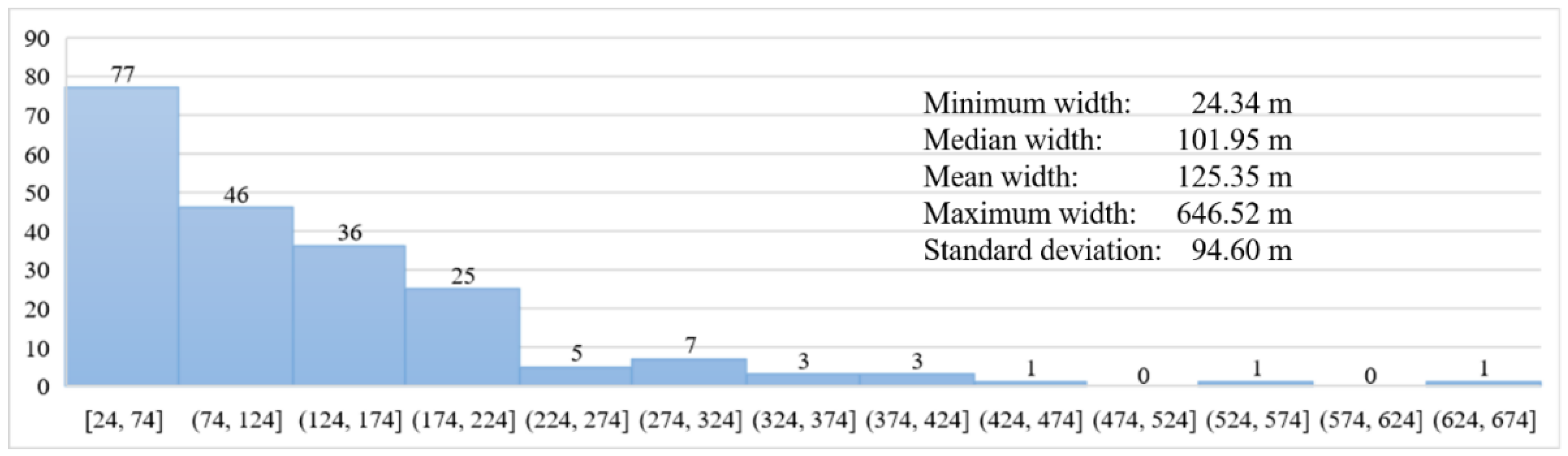
| Surface Area (ha, 104 m2) | Meander Length (km) | Straight Length (km) | Width (m) | Sinuosity Index | |
|---|---|---|---|---|---|
| Min | 1.990 | 0.532 | 0.375 | 24.338 | 1.000 |
| Median | 13.800 | 1.318 | 1.140 | 101.953 | 1.121 |
| Mean | 34.596 | 2.186 | 1.684 | 125.353 | 1.274 |
| Max | 994.910 | 18.827 | 17.374 | 646.516 | 4.622 |
| Std. | 83.568 | 2.442 | 1.815 | 94.599 | 0.444 |
| Function | Equation | Estimated Link Abundance with W = 24.34 m * | |
|---|---|---|---|
| Linear | 0.742 | 158 | |
| Power | 0.860 | 482 | |
| Logarithmic | 0.977 | 225 | |
| Ground truth | - | - | 205 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Kwan, M.-P. Structuralization of Complicated Lotic Habitats Using Sentinel-2 Imagery and Weighted Focal Statistic Convolution. Hydrology 2022, 9, 195. https://doi.org/10.3390/hydrology9110195
Liu Y, Kwan M-P. Structuralization of Complicated Lotic Habitats Using Sentinel-2 Imagery and Weighted Focal Statistic Convolution. Hydrology. 2022; 9(11):195. https://doi.org/10.3390/hydrology9110195
Chicago/Turabian StyleLiu, Yang, and Mei-Po Kwan. 2022. "Structuralization of Complicated Lotic Habitats Using Sentinel-2 Imagery and Weighted Focal Statistic Convolution" Hydrology 9, no. 11: 195. https://doi.org/10.3390/hydrology9110195
APA StyleLiu, Y., & Kwan, M.-P. (2022). Structuralization of Complicated Lotic Habitats Using Sentinel-2 Imagery and Weighted Focal Statistic Convolution. Hydrology, 9(11), 195. https://doi.org/10.3390/hydrology9110195








