Intra-Storm Pattern Recognition through Fuzzy Clustering
Abstract
1. Introduction
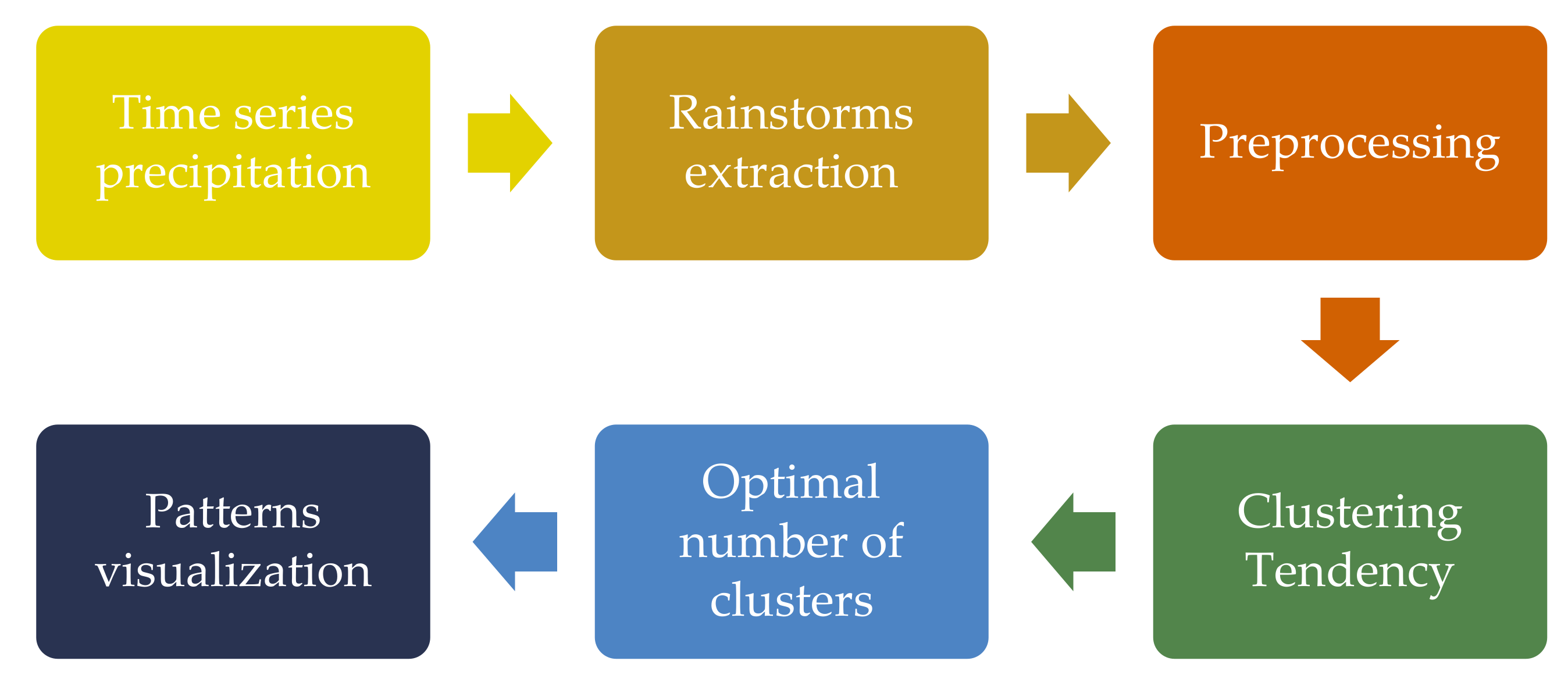
2. Materials and Methods
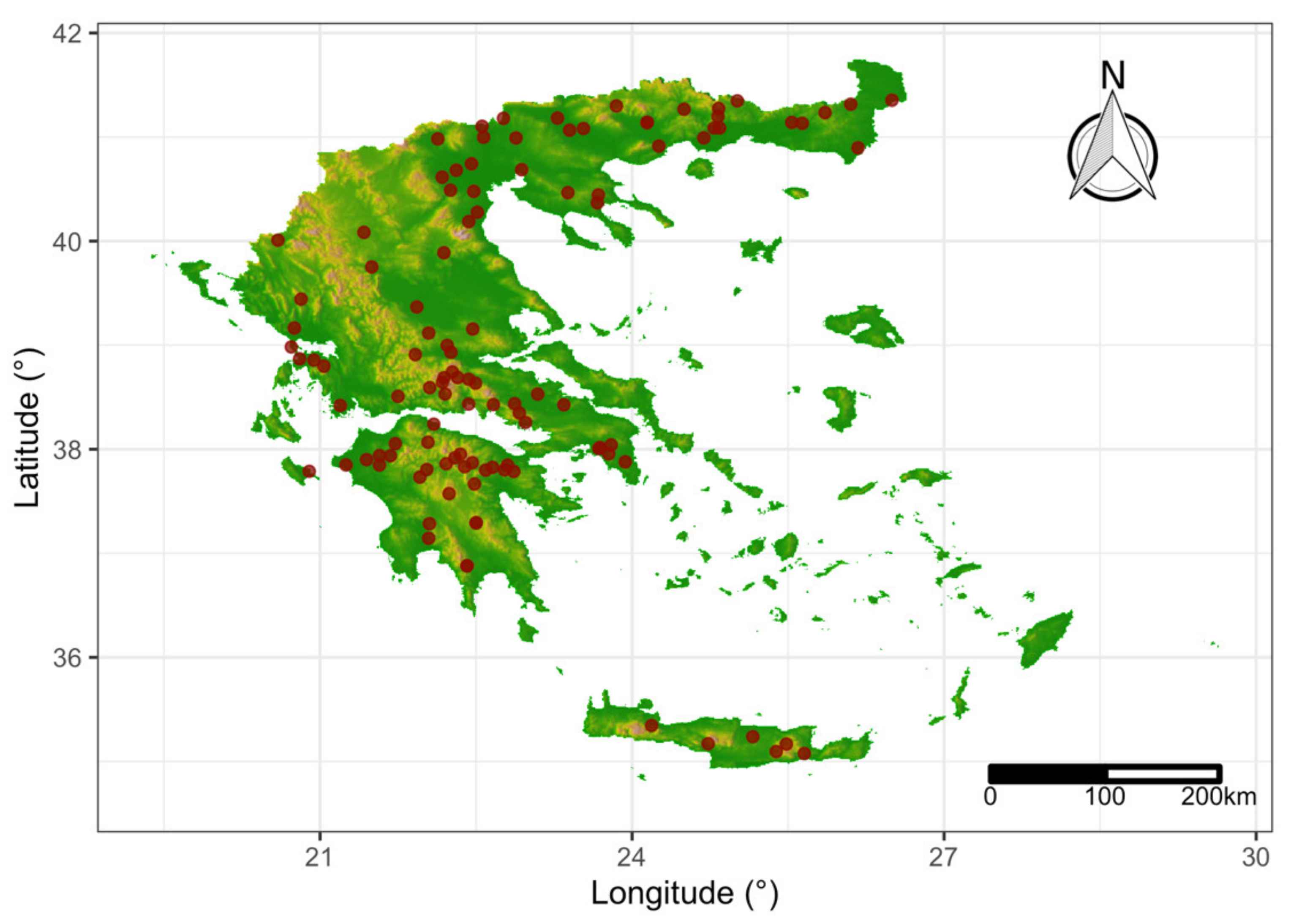
2.1. Data Acquisition and Processing
2.2. Extraction of Rainstorms
- The time intervals of rainstorms that come from the same month are distributed exponentially.
- The rainstorms are separated by a minimum critical time duration of no precipitation (CD) or inter-event time [19].
- There is a seasonal pattern for CD that is assumed to have constant monthly values.
- The probability density function is:where ω is the average storm arrival rate andwhere is the storm interarrival time, is the storm duration, and is the dry time between storms.
| Algorithm 1: Temporal model of CD |
 |
2.3. Preprocessing
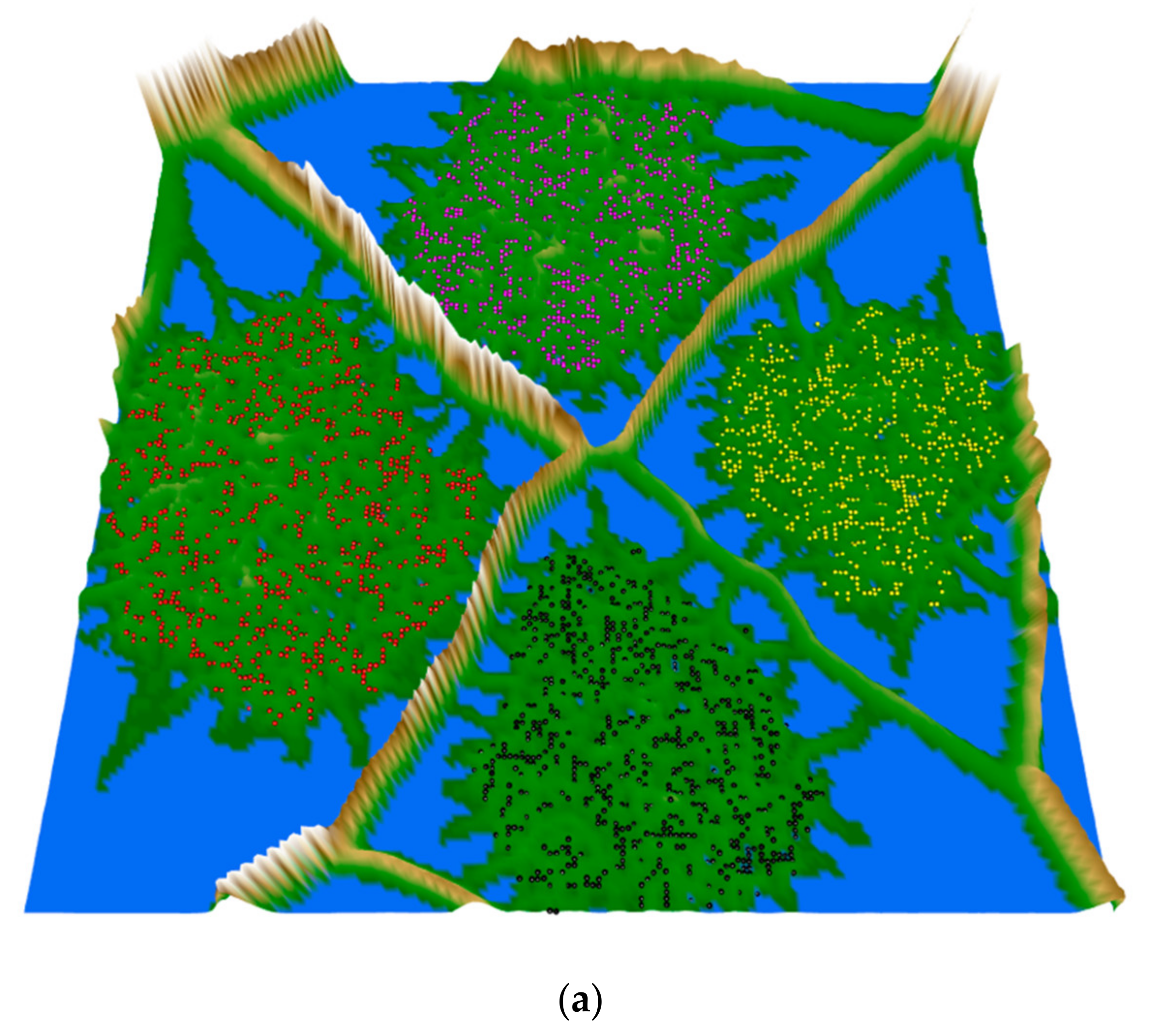
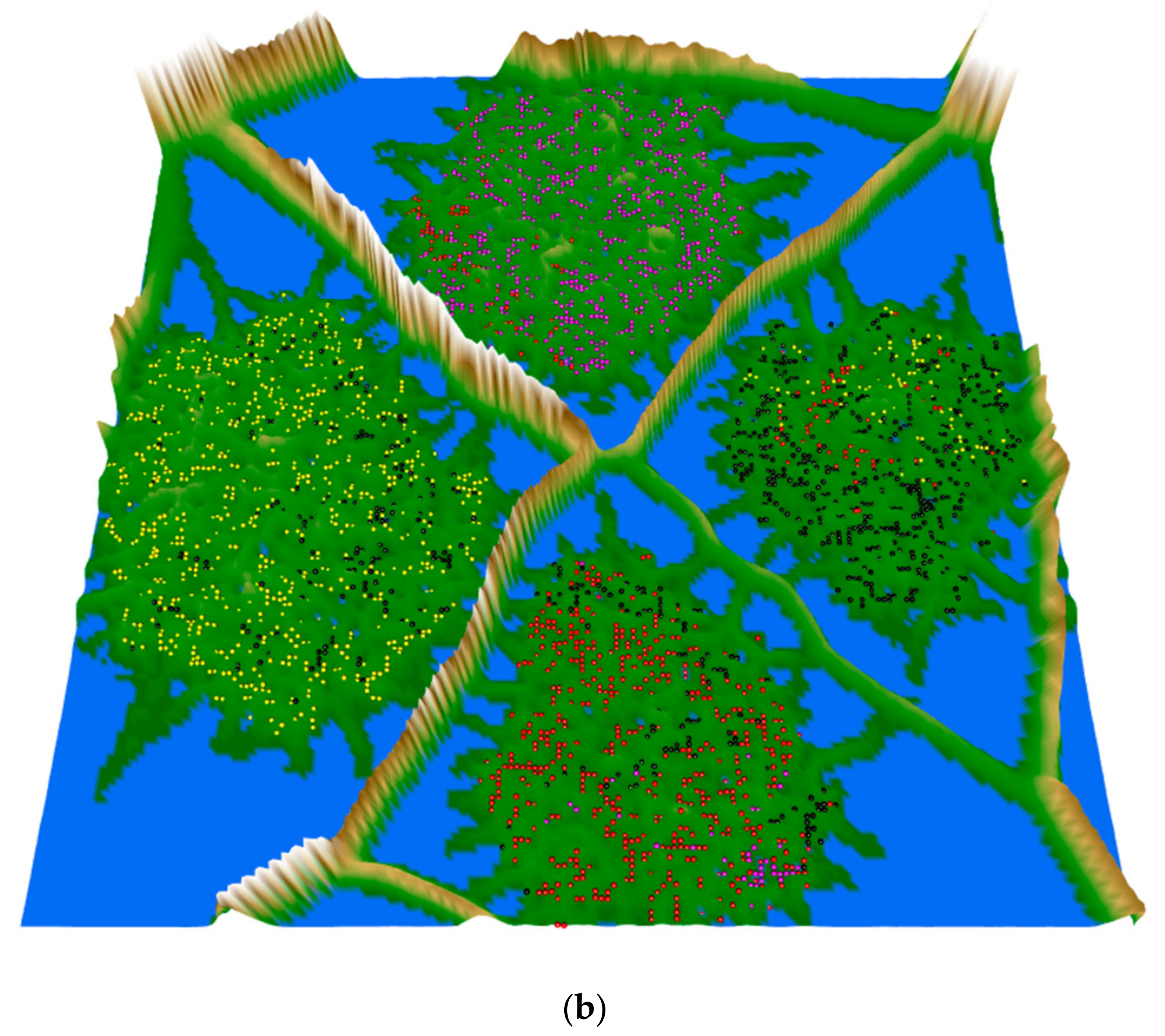
2.4. Clustering Tendency
2.5. Fuzzy Clustering
2.6. Optimal Number of Clusters
| Algorithm 2: Optimal number of clusters using FCM |
 |
2.7. Projecting Data Using Non-Linear Mapping
3. Results and Discussion
3.1. Rainstorms Extraction
3.2. Clustering Tedency
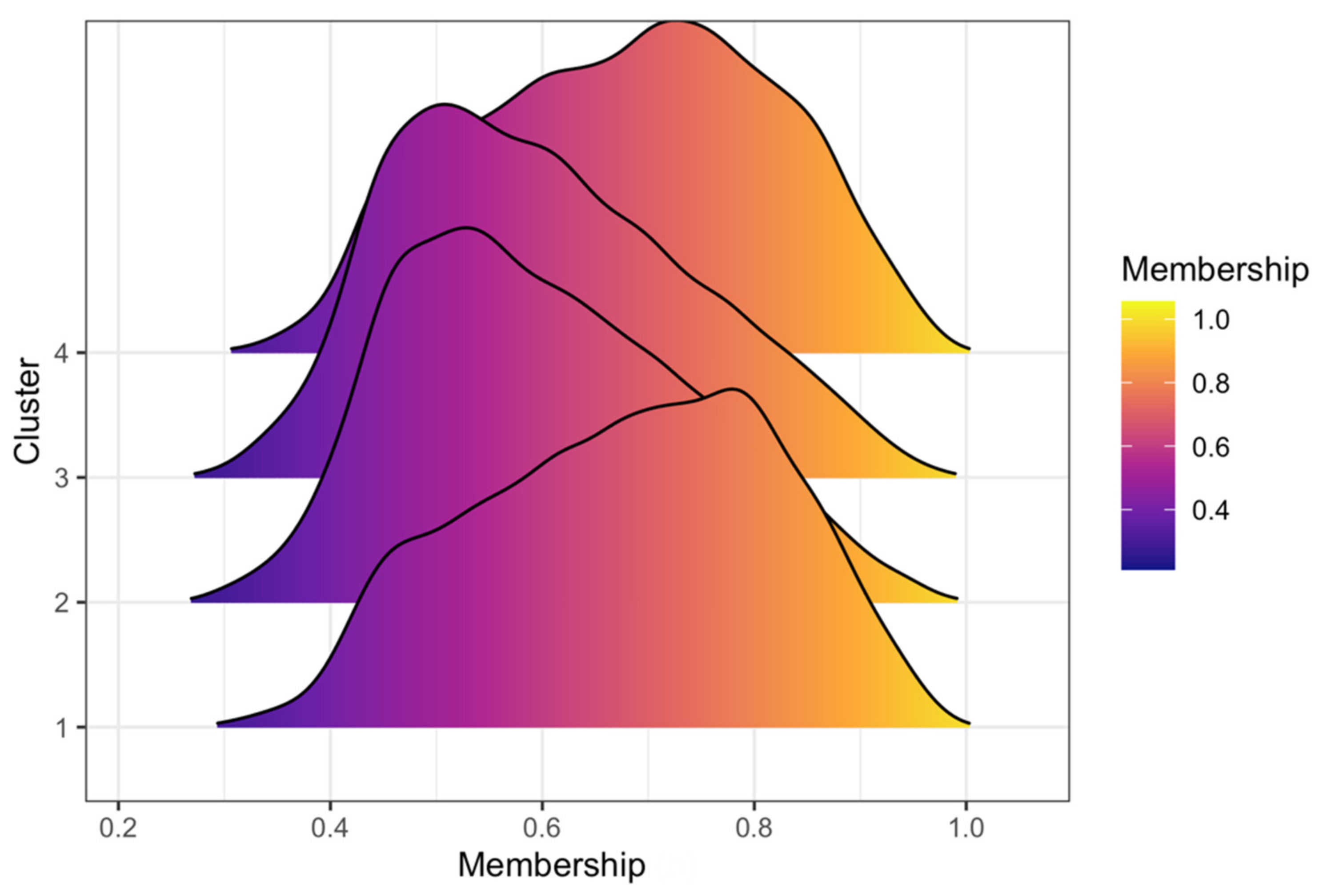
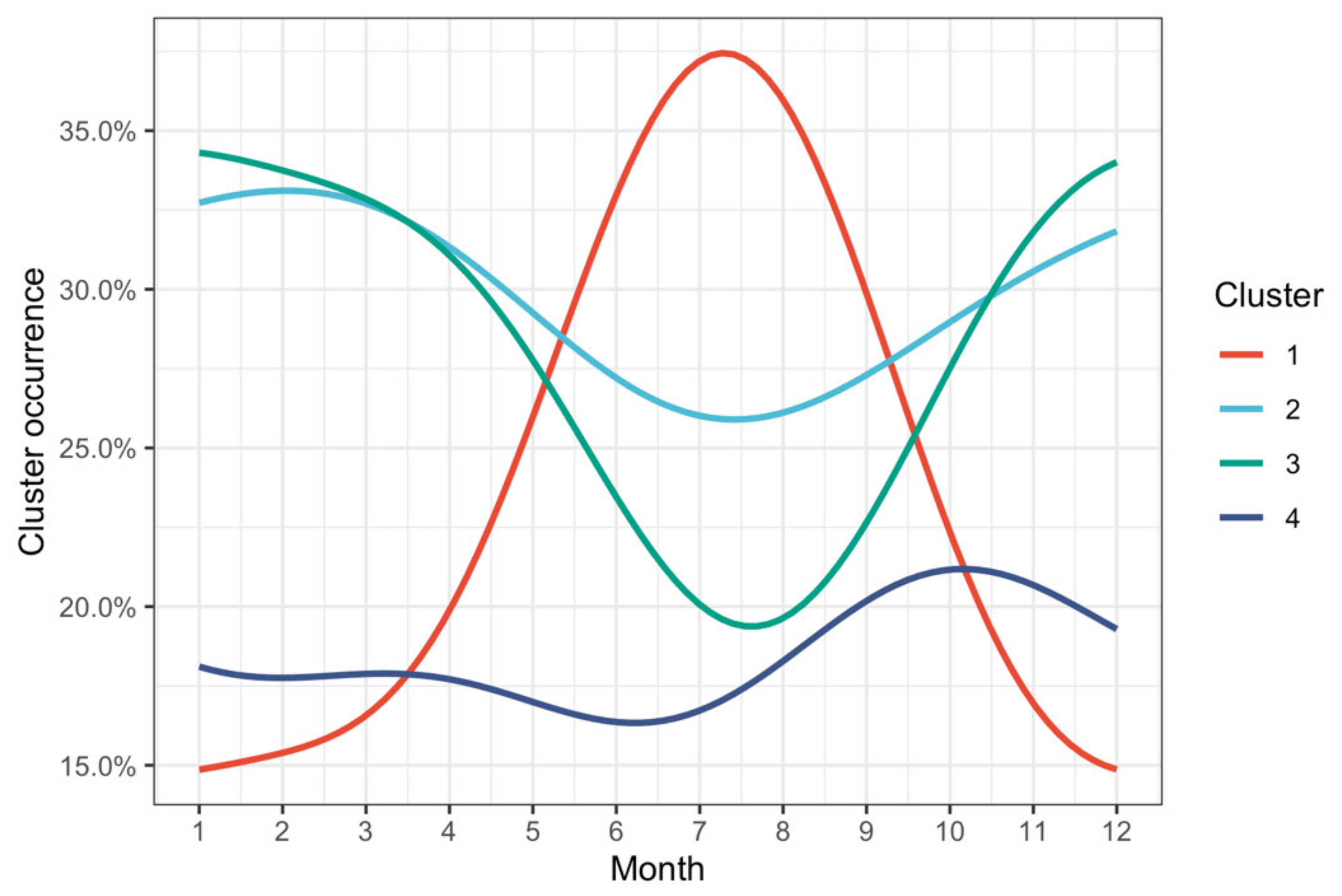
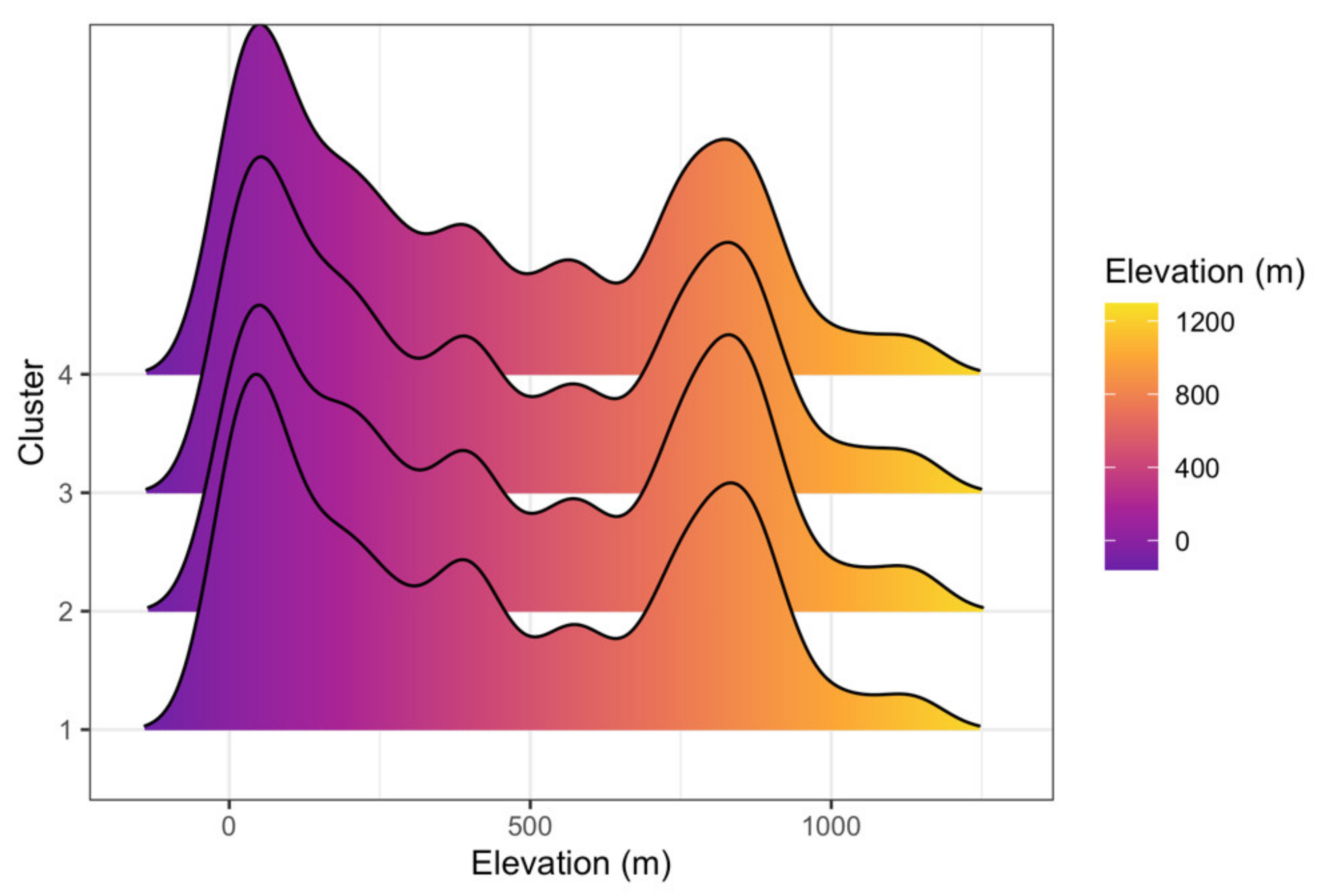
3.3. Clustering Results and Visualization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haan, C.T.; Allen, D.M.; Street, J.O. A Markov Chain Model of Daily Rainfall. Water Resour. Res. 1976, 12, 443–449. [Google Scholar] [CrossRef]
- Gao, C.; Xu, Y.-P.; Zhu, Q.; Bai, Z.; Liu, L. Stochastic Generation of Daily Rainfall Events: A Single-Site Rainfall Model with Copula-Based Joint Simulation of Rainfall Characteristics and Classification and Simulation of Rainfall Patterns. J. Hydrol. 2018, 564, 41–58. [Google Scholar] [CrossRef]
- Urdiales, D.; Meza, F.; Gironás, J.; Gilabert, H. Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile. Water 2018, 10, 145. [Google Scholar] [CrossRef]
- Onof, C.; Wang, L.-P. Modelling Rainfall with a Bartlett–Lewis Process: New Developments. Hydrol. Earth Syst. Sci. 2020, 24, 2791–2815. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; De Power, B.F.; Valdes, J.B. Rectangular Pulses Point Process Models for Rainfall: Analysis of Empirical Data. J. Geophys. Res. Atmos. 1987, 92, 9645–9656. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.J.; Blenkinsop, S.; Kilsby, C.G. Downscaling Transient Climate Change Using a Neyman–Scott Rectangular Pulses Stochastic Rainfall Model. J. Hydrol. 2010, 381, 18–32. [Google Scholar] [CrossRef]
- Onof, C.; Chandler, R.E.; Kakou, A.; Northrop, P.; Wheater, H.S.; Isham, V. Rainfall Modelling Using Poisson-Cluster Processes: A Review of Developments. Stoch. Environ. Res. Risk Assess. 2000, 14, 384–411. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. Some Models for Rainfall Based on Stochastic Point Processes. Proc. R. Soc. Lond. Math. Phys. Sci. 1987, 410, 269–288. [Google Scholar]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. A Point Process Model for Rainfall: Further Developments. Proc. R. Soc. Lond. Math. Phys. Sci. 1988, 417, 283–298. [Google Scholar]
- Brigandì, G.; Aronica, G.T. Generation of Sub-Hourly Rainfall Events through a Point Stochastic Rainfall Model. Geosciences 2019, 9, 226. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Buyse, E.; De Baets, B. A Stochastic Design Rainfall Generator Based on Copulas and Mass Curves. Hydrol. Earth Syst. Sci. 2010, 14, 2429–2442. [Google Scholar] [CrossRef]
- Huff, F.A. Time Distribution of Rainfall in Heavy Storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Bonta, J. Development and Utility of Huff Curves for Disaggregating Precipitation Amounts. Appl. Eng. Agric. 2004, 20, 641. [Google Scholar] [CrossRef]
- Yin, S.; Xie, Y.; Nearing, M.A.; Guo, W.; Zhu, Z. Intra-Storm Temporal Patterns of Rainfall in China Using Huff Curves. Trans. ASABE 2016, 59, 1619–1632. [Google Scholar]
- Loukas, A.; Quick, M.C. Spatial and Temporal Distribution of Storm Precipitation in Southwestern British Columbia. J. Hydrol. 1996, 174, 37–56. [Google Scholar] [CrossRef]
- Dunkerley, D. Identifying Individual Rain Events from Pluviograph Records: A Review with Analysis of Data from an Australian Dryland Site. Hydrol. Process. Int. J. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
- Yu, R.; Xu, Y.; Zhou, T.; Li, J. Relation between Rainfall Duration and Diurnal Variation in the Warm Season Precipitation over Central Eastern China. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- USDA-ARS. Science Documentation: Revised Universal Soil Loss Equation, Version 2 (RUSLE 2); USDA-Agricultural Research Service: Washington, DC, USA, 2013.
- Restrepo-Posada, P.J.; Eagleson, P.S. Identification of Independent Rainstorms. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Wang, W.; Yin, S.; Xie, Y.; Nearing, M.A.; Wang, W.; Yin, S.; Xie, Y.; Nearing, M.A. Minimum Inter-Event Times for Rainfall in the Eastern Monsoon Region of China. Trans. ASABE 2019, 62, 9–18. [Google Scholar] [CrossRef]
- Vantas, K.; Sidiropoulos, E.; Loukas, A. Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece. Water 2019, 11, 1050. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Sheikholeslami, G.; Chatterjee, S.; Zhang, A. Wavecluster: A Multi-Resolution Clustering Approach for Very Large Spatial Databases. In Proceedings of the 24th International Conference on Very Large Databases (VLDB), New York, NY, USA, 24–27 August 1998; Volume 98, pp. 428–439. [Google Scholar]
- Nayak, J.; Naik, B.; Behera, H. Fuzzy C-Means (FCM) Clustering Algorithm: A Decade Review from 2000 to 2014. Comput. Intell. Data Min. Vol. 2015, 2, 133–149. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Academic Press: Burlington, MA, USA, 2009; ISBN 978-1-59749-272-0. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An Examination of Procedures for Determining the Number of Clusters in a Data Set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Dikbas, F.; Firat, M.; Koc, A.C.; Gungor, M. Classification of Precipitation Series Using Fuzzy Cluster Method. Int. J. Climatol. 2012, 32, 1596–1603. [Google Scholar] [CrossRef]
- Zeybekoğlu, U.; Keskin, A.Ü. Defining Rainfall Intensity Clusters in Turkey by Using the Fuzzy C-Means Algorithm. Geofizika 2020, 37, 181–195. [Google Scholar] [CrossRef]
- Hsu, K.-C.; Li, S.-T. Clustering Spatial–Temporal Precipitation Data Using Wavelet Transform and Self-Organizing Map Neural Network. Adv. Water Resour. 2010, 33, 190–200. [Google Scholar] [CrossRef]
- Lana, X.; Rodríguez-Solà, R.; Martínez, M.; Casas-Castillo, M.; Serra, C.; Burgueño, A. Characterization of Standardized Heavy Rainfall Profiles for Barcelona City: Clustering, Rain Amounts and Intensity Peaks. Theor. Appl. Climatol. 2020, 142, 255–268. [Google Scholar] [CrossRef]
- Nojumuddin, N.S.; Yusof, F.; Yusop, Z. Identification of Rainfall Patterns in Johor. Appl. Math. Sci. 2015, 9, 1869–1888. [Google Scholar] [CrossRef]
- Bonta, J.V. Stochastic Simulation of Storm Occurence, Depth, Duration and within-Storm Intensities. Trans. ASAE 2004, 47, 1573–1584. [Google Scholar] [CrossRef]
- Wu, S.-J.; Yang, J.-C.; Tung, Y.-K. Identification and Stochastic Generation of Representative Rainfall Temporal Patterns in Hong Kong Territory. Stoch. Environ. Res. Risk Assess. 2006, 20, 171–183. [Google Scholar] [CrossRef]
- Williams-Sether, T. Empirical, Dimensionless, Cumulative-Rainfall Hyetographs Developed from 1959–1986 Storm Data for Selected Small Watersheds in Texas; US Geological Survey: Reston, VA, USA, 2004.
- Azli, M.; Rao, A.R. Development of Huff Curves for Peninsular Malaysia. J. Hydrol. 2010, 388, 77–84. [Google Scholar] [CrossRef]
- Amponsah, A.O.; Daraio, J.A.; Khan, A.A. Implications of Climatic Variations in Temporal Precipitation Patterns for the Development of Design Storms in Newfoundland and Labrador. Can. J. Civ. Eng. 2019, 46, 1128–1141. [Google Scholar] [CrossRef]
- Zeimetz, F.; Schaefli, B.; Artigue, G.; Hernández, J.G.; Schleiss, A.J. Swiss Rainfall Mass Curves and Their Influence on Extreme Flood Simulation. Water Resour. Manag. 2018, 32, 2625–2638. [Google Scholar] [CrossRef]
- Bezak, N.; Šraj, M.; Rusjan, S.; Mikoš, M. Impact of the Rainfall Duration and Temporal Rainfall Distribution Defined Using the Huff Curves on the Hydraulic Flood Modelling Results. Geosciences 2018, 8, 69. [Google Scholar] [CrossRef]
- Jiang, P.; Yu, Z.; Gautam, M.R.; Yuan, F.; Acharya, K. Changes of Storm Properties in the United States: Observations and Multimodel Ensemble Projections. Glob. Planet. Chang. 2016, 142, 41–52. [Google Scholar] [CrossRef]
- Vantas, K.; Sidiropoulos, E.; Vafeiadis, M. Optimal Temporal Distribution Curves for the Classification of Heavy Precipitation Using Hierarchical Clustering on Principal Components. Glob. NEST J. 2019, 21, 530–538. [Google Scholar]
- Vantas, K.; Sidiropoulos, E.; Vafeiadis, M. A Data Driven Approach for the Temporal Classification of Heavy Rainfall Using Self-Organizing Maps. In Proceedings of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019; Volume 21, p. 1. [Google Scholar]
- Vantas, K. Hydroscoper: R Interface to the Greek National Data Bank for Hydrological and Meteorological Information. J. Open Source Softw. 2018, 3, 625. [Google Scholar] [CrossRef]
- Babu, G.J.; Rao, C.R. Goodness-of-Fit Tests When Parameters Are Estimated. Sankhyā Indian J. Stat. 2004, 66, 63–74. [Google Scholar]
- Vantas, K.; Sidiropoulos, E.; Vafeiadis, M. Rainfall Temporal Distribution in Thrace by Means of an Unsupervised Machine Learning Method. In Proceedings of the Protection and Restoration of the Environment XIV, Thessaloniki, Greece, 3–6 July 2018; Volume 1, pp. 555–564. [Google Scholar]
- Bezdek, J.C.; Hathaway, R.J. VAT: A Tool for Visual Assessment of (Cluster) Tendency. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN’02 (Cat. No.02CH37290). Honolulu, HI, USA, 12–17 May 2002; pp. 2225–2230. [Google Scholar]
- Hopkins, B.; Skellam, J.G. A New Method for Determining the Type of Distribution of Plant Individuals. Ann. Bot. 1954, 18, 213–227. [Google Scholar] [CrossRef]
- Husson, F.; Lê, S.; Pagès, J. Exploratory Multivariate Analysis by Example Using R, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2017; ISBN 978-0-429-22543-7. [Google Scholar]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: Boston, MA, USA, 1981; ISBN 978-1-4757-0452-5. [Google Scholar]
- Huang, M.; Xia, Z.; Wang, H.; Zeng, Q.; Wang, Q. The Range of the Value for the Fuzzifier of the Fuzzy C-Means Algorithm. Pattern Recognit. Lett. 2012, 33, 2280–2284. [Google Scholar] [CrossRef]
- Oppel, H.; Fischer, S. A New Unsupervised Learning Method to Assess Clusters of Temporal Distribution of Rainfall and Their Coherence with Flood Types. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Lin, G.-F.; Wu, M.-C. A SOM-Based Approach to Estimating Design Hyetographs of Ungauged Sites. J. Hydrol. 2007, 339, 216–226. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In KDD’96; AAAI Press: Palo Alto, CA, USA, 1996. [Google Scholar]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Bonta, J.V.; Rao, A.R. Regionalization of Storm Hyetographs. JAWRA J. Am. Water Resour. Assoc. 1989, 25, 211–217. [Google Scholar] [CrossRef]
- Bonta, J.V.; Shahalam, A. Cumulative Storm Rainfall Distributions: Comparison of Huff Curves. J. Hydrol. 2003, 42, 65–74. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Ultsch, A. U*-Matrix: A Tool to Visualize Clusters in High Dimensional Data; Technical Report, Nr. 36; University of Marburg, Department of Computer Science: Marburg, Germany, 2003. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Ultsch, A.; Mörchen, F. ESOM-Maps: Tools for Clustering, Visualization, and Classification with Emergent SOM; Technical Report, Nr. 46; University of Marburg, Department of Computer Science: Marburg, Germany, 2003. [Google Scholar]
- Dasgupta, S.; Gupta, A. An Elementary Proof of a Theorem of Johnson and Lindenstrauss. Random Struct. Algorithms 2003, 22, 60–65. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A. Uncovering High-Dimensional Structures of Projections from Dimensionality Reduction Methods. MethodsX 2020, 7, 101093. [Google Scholar] [CrossRef]
- Thrun, M.C.; Lerch, F. Visualization and 3D Printing of Multivariate Data of Biomarkers. In Proceedings of the 24th Conference on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 6 March 2016. [Google Scholar]
- Vantas, K.; Sidiropoulos, E.; Evangelides, C. Rainfall erosivity and its estimation: Conventional and machine learning methods. In Soil Erosion-Rainfall Erosivity and Risk Assessment; IntechOpen: London, UK, 2019. [Google Scholar]
- Koutsoyiannis, D. A Stochastic Disaggregation Method for Design Storm and Flood Synthesis. J. Hydrol. 1994, 156, 193–225. [Google Scholar] [CrossRef]
- Hensel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Book 4, Hydrologic Analysis and Interpretation; U.S. Geological Survey: Reston, VA, USA, 2002.
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2021. [Google Scholar]
- Vantas, K. Hyetor: R Package to Analyze Fixed Interval Precipitation Time Series. Available online: https://github.com/kvantas/hyetor (accessed on 20 March 2021).
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. E1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071). TU Wien. Available online: https://cran.r-project.org/web/packages/e1071 (accessed on 20 March 2021).
- Thrun, M.C.; Stier, Q. Fundamental Clustering Algorithms Suite. SoftwareX 2021, 13, 100642. [Google Scholar] [CrossRef]
- Kassambara, A.; Mundt, F. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses. Available online: https://cran.r-project.org/web/packages/factoextra/ (accessed on 20 March 2021).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]




| CD (h) | Min | Mean | Median | Max | SD | Skew | Kurtosis | CV |
|---|---|---|---|---|---|---|---|---|
| January | 2 | 5.4 | 5 | 13 | 1.6 | 1.40 | 4.77 | 0.19 |
| February | 2 | 5.0 | 5 | 10 | 1.4 | 0.90 | 1.39 | 0.16 |
| March | 2 | 5.9 | 5 | 12 | 1.8 | 0.95 | 0.82 | 0.20 |
| April | 4 | 6.3 | 6 | 10 | 1.4 | 0.62 | −0.20 | 0.16 |
| May | 4 | 6.8 | 6 | 12 | 1.9 | 0.91 | 0.49 | 0.24 |
| June | 4 | 8.2 | 8 | 13 | 2.1 | 0.15 | −0.50 | 0.34 |
| July | 5 | 9.3 | 9 | 13 | 2.0 | −0.17 | −0.01 | 0.58 |
| August | 5 | 7.8 | 8 | 11 | 2.1 | 0.12 | −1.73 | 0.70 |
| September | 6 | 9.1 | 9.5 | 11 | 1.6 | −0.52 | −1.03 | 0.45 |
| October | 2 | 7.4 | 7 | 13 | 1.9 | 0.36 | 0.78 | 0.25 |
| November | 2 | 6.7 | 6 | 11 | 1.6 | 0.25 | 0.17 | 0.19 |
| December | 2 | 5.2 | 5 | 11 | 1.4 | 0.85 | 2.00 | 0.16 |
| Cluster | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Cluster Ratio (%) | 19.5 | 30.86 | 30.84 | 18.79 |
| Duration (h) | 12.5 | 16 | 16.5 | 14.5 |
| Precipitation depth (mm) | 20.7 | 23.2 | 23.7 | 21.9 |
| Intensity (mm/h) | 1.82 | 1.66 | 1.66 | 1.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vantas, K.; Sidiropoulos, E. Intra-Storm Pattern Recognition through Fuzzy Clustering. Hydrology 2021, 8, 57. https://doi.org/10.3390/hydrology8020057
Vantas K, Sidiropoulos E. Intra-Storm Pattern Recognition through Fuzzy Clustering. Hydrology. 2021; 8(2):57. https://doi.org/10.3390/hydrology8020057
Chicago/Turabian StyleVantas, Konstantinos, and Epaminondas Sidiropoulos. 2021. "Intra-Storm Pattern Recognition through Fuzzy Clustering" Hydrology 8, no. 2: 57. https://doi.org/10.3390/hydrology8020057
APA StyleVantas, K., & Sidiropoulos, E. (2021). Intra-Storm Pattern Recognition through Fuzzy Clustering. Hydrology, 8(2), 57. https://doi.org/10.3390/hydrology8020057






