Abstract
Historically, snowpack trends have been assessed using one fixed date to represent peak snow accumulation prior to the onset of melt. Subsequent trend analyses have considered the peak snow water equivalent (SWE), but the date of peak SWE can vary by several months due to inter-annual variability in snow accumulation and melt patterns. A 2018 assessment evaluated monthly SWE trends. However, since the month is a societal construct, this current work examines daily trends in SWE, cumulative precipitation, and temperature. The method was applied to 13 snow telemetry stations in Northern Colorado, USA for the period from 1981 to 2018. Temperature trends were consistent among all the stations; warming trends occurred 63% of the time from 1 October through 24 May, with the trends oscillating from warming to cooling over about a 10-day period. From 25 May to 30 September, a similar oscillation was observed, but warming trends occurred 86% of the time. SWE and precipitation trends illustrate temporal patterns that are scaled based on location. Specifically, lower elevations stations are tending to record more snowfall while higher elevation stations are recording less. The largest SWE, cumulative precipitation, and temperature trends were +30 to −70 mm/decade, +30 to −30 mm/decade, and +4 to −2.8 °C/decade, respectively. Trends were statistically significance an average of 25.8, 4.5, and 29.4% of the days for SWE, cumulative precipitation, and temperature, respectively. The trend in precipitation as snow ranged from +/−2%/decade, but was not significant at any station.
1. Introduction
Seasonal snow, i.e., snow that accumulates and persists all winter [1], covers about 42% of the land surface of the Northern Hemisphere [2]. This snow is an important water resource [3] and the presence of snow cover alters the local energy balance [4] due to the increase in albedo [5,6]. However, the snowpack has been changing in regions where a seasonal snow cover is present [2,7]. For such regions that have extended periods of snow cover, one common date is used to represent peak snow water equivalent (SWE). In the Western United States, April 1st is often used as SWE data have been collected on or about this date at over 2000 locations since as early as 1936 [8]. Trend analyses have shown a decrease in April 1st SWE across much of this domain [9,10,11,12,13,14]. However, this surrogate date under-represents peak SWE [15] and when snow course data are used, measurements are often taken 3–4 days prior to the first of the month [16,17]. Further, non-stationarity [18] may result in a change in the timing of peak SWE [19].
Combined investigations of SWE, precipitation, and temperature data illustrate that snowpack changes are complex [6,11,12,14,17,20,21]. For example, in Northern Colorado there was little net change in winter precipitation with some warming in the winter, yet there were monthly variations: November and March were warmer and drier, December and January were warmer and wetter, while February and May were cooler and wetter [17]. While the monthly analysis is at a finer temporal resolution, a month is still an arbitrary human-defined time step. To determine snowpack climatology, Fassnacht and Derry [22] showed that using daily data was more appropriate [19,20,21,23].
Most of the snowpack analyses have used a single date in time to identify change [9,10,11,12,13,14], and even monthly analyses [17] may be too coarse of a temporal resolution to fully identify the patterns of snowpack change, thus, this work evaluates trends in SWE at a daily time-step. We also examine trends in the precipitation and temperature data related to SWE trends [6,11,12,14,17,20,21], but on a daily time step. We investigate the correlation of trends in these three niveo-meteorological variables. Since many studies have examined trends over large regions [2,7,9,10,11,12,13,14,24] or group stations [20] or trends [19] together, we investigate what the patterns of daily trends for individual stations [6,17]. We pose the following research questions: (1) what are the daily trends in SWE, cumulative precipitation and temperature? (2) what are the fluctuations in daily trends, and are there patterns over the year? (3) if temporal trend patterns exist, are there correlations between the three variables?
2. Study Domain and Data
We used 13 longer-term snow measurement stations (Figure 1a) located across the Northern Front Range of Colorado (NFRCo), as per Fassnacht et al. [17] (Figure 1b). This regional domain is located in the state of Colorado within the Western United Stated (Figure 1c). These SNOTEL stations [8,25] were divided into those on the west side of Rocky Mountain National Park (RMNP), denoted as orange stations, and those on the east side of RMNP, denoted as purple (Figure 1a), as per Clow [20]. The SNOTEL stations range in elevation from 2612 to 3265 m.a.sl. (Copeland Lake and Willow Park, respectively) (Figure 1a). The area around each of the stations is moderately sloped and nine of the stations are somewhat south-facing, i.e., the northness (sine slope x cosine aspect) [26] is negative (Table 1). From the 30-m resolution U.S. Geological Survey National Land Cover Database, all stations are in evergreen forest except Phantom Valley that is in considered to be in developed, open space (Table 1). Their characteristics are also described in Fassnacht et al. [17].
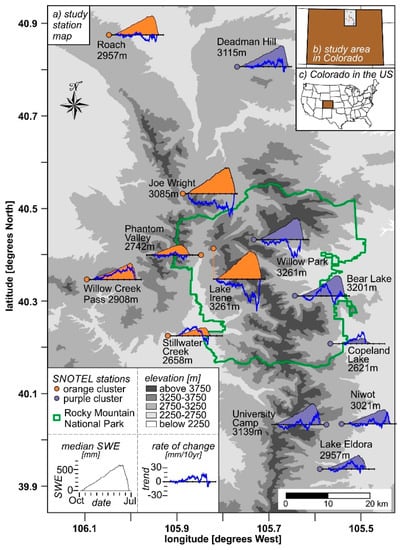
Figure 1.
Location of (a) the 13 SNOTEL data collection stations (b) within the Northern Front Range of the state of Colorado (c) in the Western United States. The median niveograph and the daily SWE trend of each station over the period of record is presented in (a), scaled according to the legend. The SNOTEL orange and purple stations refer to those on the western and eastern side of Rocky Mountain National Park, as used by Clow [20] and Fassnacht et al. [17].

Table 1.
The characteristic of the 13 SNOTEL stations (see Figure 1a) including station number (#), and location: latitude (lat), longitude (long), and elevation (elev). The slope and northness (sine slope x cosine aspect) are derived from the U.S. Geological Survey National Elevation Dataset. The canopy density is from the U.S. Geological Survey National Land Cover Database (NLCD). The NLCD land cover is evergreen forest for all stations, except * Phantom Valley that is denoted as developed, open space. The mean peak snow water equivalent (SWE), mean annual temperature (temp), and mean annual precipitation (precip) are from the SNOTEL station data.
The SNOTEL data were retrieved from the Natural Resources Conservation Service (NRCS) National Water and Climate Center at <https://www.wcc.nrcs.usda.gov/> [8,25]. Most of these stations have been monitoring snow and precipitation since the late 1970s. We used the water year (WY; 1 October to 30 September) for the period from 1981 to 2018 for all stations except Stillwater Creek that began recording in WY 1986 (1 October 1985). The Copeland Lake station was missing data for WY 1983. The quality-controlled data [27] from Fassnacht et al. [17] were used in the current study, with the addition of the WY 2016 to 2018 data.
The mean peak SWE varied from 147 mm at Copeland Lake, the lowest elevation station with the warmest annual temperature of 5.26 °C, to 700 mm at Lake Irene, the second highest station with the coldest mean temperature at 0.48 °C (Table 1). Mean annual precipitation varied from 482 mm at Stillwater Creek to 1132 mm at Joe Wright (Table 1). Example of SWE, temperature and precipitation conditions are presented for the Lake Irene station (Figure 2). Since this paper focuses on snow, the entire SWE time series is shown in Figure 2a; averages are shown for the other variables.
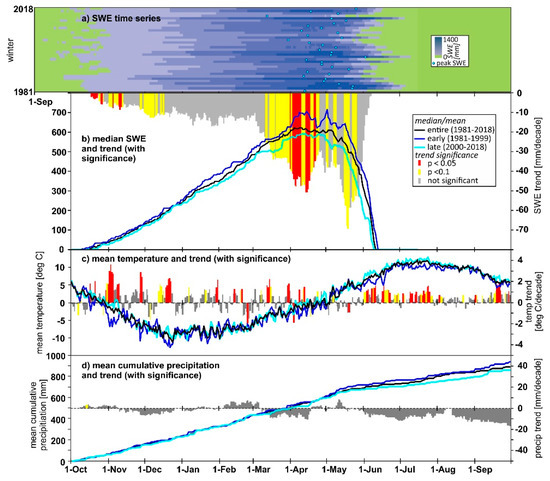
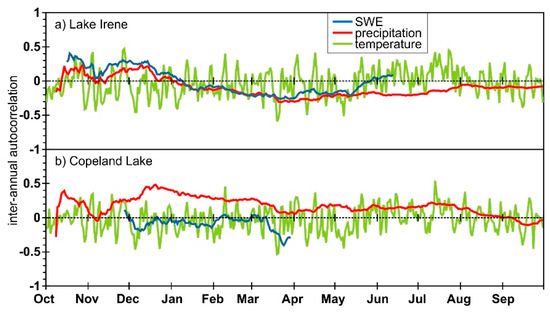
Figure 2.
Lake Irene SNOTEL station (a) SWE time series for each year from 1981 to 2018 and the inter-annual autocorrelation (red line), (b) median SWE, (c) mean temperature, and (d) mean cumulative precipitation, all for entire period of record plus first and last half of the period of record. The SWE time series (a) starts in September to illustrate that snow does fall and occasionally accumulates prior to the start of the water year, October 1.
3. Methodology
SWE is a memory of snowpack processes that is initially dominated by accumulation which is driven by precipitation, but also a function of temperature conditions. The SWE time period for each station differed (Figure 1); the start date began once at least 17 of the total years of record had snow accumulation (ranging from 11 October at Joe Wright to 27 November at Copeland Lake), and ended once fewer than 18 years had complete melt (ranging from 29 March at Copeland Lake to 20 June at University Camp). We use cumulative precipitation rather than daily precipitation data due to inter-annual inconsistency in daily precipitation [28] and the numerical instability of analyzing a daily time series with many zeros. The cumulative precipitation trend analysis began on 8 October through 30 September; the first week was ignored to remove statistical problems due to an abundance of zero data. The temperature time series is shorter (starting in the late 1980s) and, due to changes in location and the sensor itself, there is a problem with discontinuity [29,30,31]. A co-located adjustment was presented in Oyler et al. [30] and used by Ma et al. [31]. The data from Ma et al. [31] were used in this analysis.
We evaluated the annual fraction of the precipitation that fell as snow. Since no specific observations of snow versus rain were available, we used the probability of snow versus air temperature linear function developed for Colorado [32]. This has been applied to other areas where no snow observations were available [33].
There is autocorrelation in the time series of daily values, but for the trend analysis the inter-annual autocorrelation could influence analysis results. We examined the autocorrelation for each day over the 38 years of record. Statistically, the autocorrelation is only relevant for a particular day when the trends are significant, as per the Mann-Kendall test [34,35,36]. The autocorrelation coefficient was computed at a lag of one timestep (lag-1), i.e., one year [37].
The significance of each daily trend was computed using the non-parametric Mann-Kendall test [34,35,36]. Two levels of significance levels were computed for each day, per variables and station: confidence levels of p < 0.05 (called significant) and p < 0.10 (called moderately significant). While we computed all trends regardless of significance level, we focused on the Lake Irene station to illustrate the significance of the trends in the three niveo-meteorological variables (plotted in Figure 2b–d).
Each time series trend was computed using the Theil-Sen median slope of the all pairs of linear trends [36,38,39]. This is a non-parametric approach that determines a monotonic trend across all time steps, regardless of missing years [36]. While the length of record influences the trend [40], outliers have a limited impact on the computation of the Theil-Sen slope [41].
To reduce visual clutter, the time series of daily trends for the west/orange stations were plotted separately from the east/purple stations, and there are individual plots for SWE and cumulative precipitation yielding four figures. Due to the nature of the temperature trends, all station trends are presented in one plot; the period with the greatest warming and cooling trends were highlighted. To reduce the “noise” that was apparent in the daily trends, a seven-day running average applied to the SWE and cumulative precipitation daily trends for seven of the stations that represented the extent of the variability in trends. The plots were visually evaluated to identify temporal trend periods, i.e., periods of increasing, no change or decreasing trends.
Finally, the daily temperature trends and daily SWE trends were plotted against the daily cumulative precipitation trends; the daily temperature trends were also plotted against the daily SWE trends for a subset of four stations. Each of the three plots was visually examined to evaluate any potential correlation between the variable trends per station. Where a potential correlation existed, the daily points were divided into the temporal trend periods identified above.
4. Results
On average, accumulation begins in October at most stations (e.g., Figure 2a,b), and November at the lower elevation stations (e.g., Copeland Lake) (Figure 1a). Complete melt-out of the snowpack occurs between late April and early July, depending on the characteristics of the station, including elevation and land cover type (Table 1, [42]), temperature patterns (e.g., Figure 2c), and the amount of snowfall in the year (e.g., Figure 2d). Similarly, there is inter-annual variability in the date and quantity of peak SWE (e.g., Figure 2a). At some stations, such as the highest elevation Lake Irene station, the first decade of the period of record had a 12.5% lower peak SWE than the last decade (Figure 2b). The decadal differences in temperature and precipitation were less obvious (Figure 2c and Figure 2d, respectively). These specific temporal differences were an impetus to evaluate trends on a daily basis.
On average, 70% of the annual precipitation fell as snow, ranging from 58% at Copeland Lake to 78% at Lake Irene and Deadman Hill. There is a strong correlation between amount of precipitation as snow and elevation (Figure 3a). However, there is mix of trends from the largest decrease of 1.9% per decade at Copeland Lake to an increase of 1.5% and 1.7% per decade at Willow Park and Willow Creek Pass, respectively (Figure 3b).
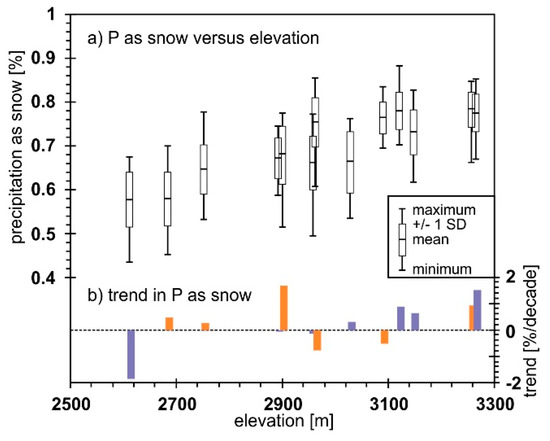
Figure 3.
(a) Variation of precipitation as snow as a function of elevation, and (b) trend in the annual total precipitation as snow. Note that none of the trends are statistically significant.
For the Lake Irene station, the inter-annual autocorrelation (AC) of SWE is largest early in the accumulation period, i.e., in mid-October (~0.40), and once there is consistent snow on the ground from mid-November through mid-December (~0.21 to 0.31) (Figure 4a). There is a negative AC from mid-January through mid-May (maximum of −0.26) and then a small AC at the end of the melt season in early June. For Copeland Lake, SWE AC was smaller and mostly negative (Figure 4b). The AC for cumulative precipitation is similar to SWE at Lake Irene, except it begins negative and then remains negative (and small) into the summer (Figure 4a). At Copeland Lake, the precipitation AC is mostly positive with a 20-day period (12 to 31 December) with AC > 0.4 (Figure 4b). The temperature inter-annual AC fluctuates with a period of about 5.5 days (66 cycles in a year) for both stations (Figure 4a,b). The temperature AC is more than 0.4 on 9 (and 2) days at Lake Irene (Copeland Lake), respectively, and less than −0.4 on 13 (and 8) days (Figure 4a,b). The same patterns of low AC values were observed for all the other stations.
On average, SWE, cumulative precipitation, and temperature trends were statistically significant at a value p-value < 0.1 for 25.8, 4.5, and 29.4% of the total days, respectively (Figure 5). SWE trends were statistically significant at all stations except the two most northerly stations, Roach and Deadman Hill (Figure 1a); only Bear Lake illustrated both increasing and decreasing trends that were significant (Figure 5a). When significant SWE trends were observed, they often occurred at or about peak SWE. For some stations, such as Lake Irene (Figure 2b) or Copeland Lake (Figure 5a), significant SWE trends occurred throughout the year. Cumulative precipitation trends were only significant at a p-value < 0.05 for 0.9% of the station days (Figure 5b). Using the same significance level, 17.1 (0.9)% of the station days had positive (negative) trends (Figure 5c).
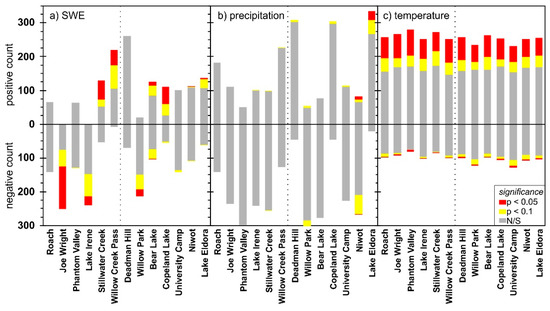
Figure 5.
Significance of the daily trends for (a) SWE, (b) cumulative precipitation, and (c) temperature, differentiated by positive and negative trends illustrating the confidence levels of p < 0.05, p < 0.10, and not significant (N/S).
There are large fluctuations in the temperature trends over the water year, with an average periodicity of about 10 days (35 local maxima per year in the trends of Figure 6a). These include some pronounced periods, such as the greatest warming from 29 October to 11 November, with a maximum of 3.4 to 4 °C/decade (Phantom Valley and Copeland Lake, respectively) occurring on 1 or 2 November (Figure 6b). There is also a mid-December warming for 13 days with a maximum of 2.3 to 3.4 °C/decade occurring on 19 December (Lake Irene and Niwot, respectively). The longest sustained cooling period was 20 to 26 February with the coolest trend of 1.6 to 2.7 °C/decade (Willow Creek Park and University Camp, respectively) on 24 February (Figure 6c). Starting on 25 May, the magnitude of the fluctuations is less (56%) than the previous period, and most of the daily trends are warming (Figure 6a). For the earlier, winter period (1 October to 24 May), warming occurs 63% of the time with a mean warming of 0.37 °C/decade, while warming occurs 82% of the time for the spring-summer period (25 May to 30 September) with a mean warming of 0.63 °C/decade.
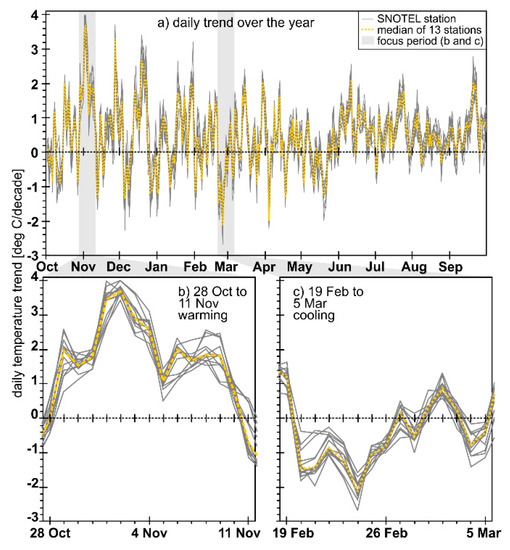
Figure 6.
Daily temperature trends for the 13 SNOTEL stations plus the median of the trends for (a) the entire year, (b) the greatest warming period (28 October to 11 November), and (c) the greatest cooling period (19 February to 5 March).
There are also fluctuations in the daily SWE and cumulative precipitation trends (Figure 7a and Figure 7b, respectively). However, while there is daily noise, there are more distinct longer period patterns present, especially for the purple east-side stations (Figure 7(aii,bii)). The temporal trend patterns for the orange west-side stations are mostly consistent across all the stations for both SWE and cumulative precipitation (Figure 7(ai,bi)). The SWE trends outliers are Willow Creek Pass (Figure 7(ai)) on the west side that is always positive and Willow Park on the east side that is almost always negative (Figure 7(aii)).
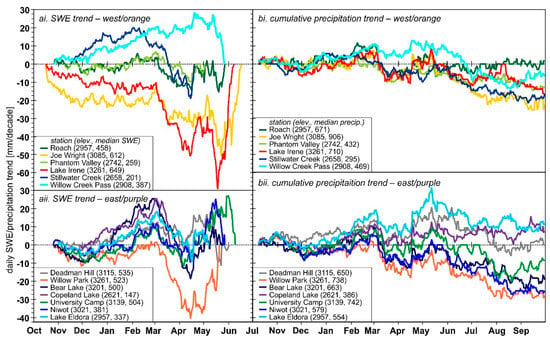
Figure 7.
(a) SWE and (b) cumulative precipitation daily trends for i. orange and ii. purple stations, as per Clow (2010) shown in Figure 1. For each station, the median peak SWE and median cumulative precipitation from October 1st through the complete disappearance of the snowpack are summarized in the legends.
The seven-day running average for SWE and cumulative precipitation (sumP) trends for seven representative stations (Figure 8), subset from Figure 7, show the beginning of the accumulation season through early December sees either no change or a slight decrease (yellow background). From December through the end of February, SWE and sumP is either not changing or increasing (green background). Next, there is about 1.5 months (through mid-April) of decreasing SWE trends, except at Willow Creek Pass that has a slight increase. Cumulative precipitation only decreases for about two weeks in early March, followed by no change for about a month. The 10-day increase in SWE and sumP in mid to late April is followed by a little change through early May. For SWE, mid-May through early June and for sumP through the end of July, there is a decrease. The exception is the end of the snow period at Lake Irene where there is an increase (Figure 8a). August and September sumP trends are a mix of increasing and decreasing (Figure 8c).
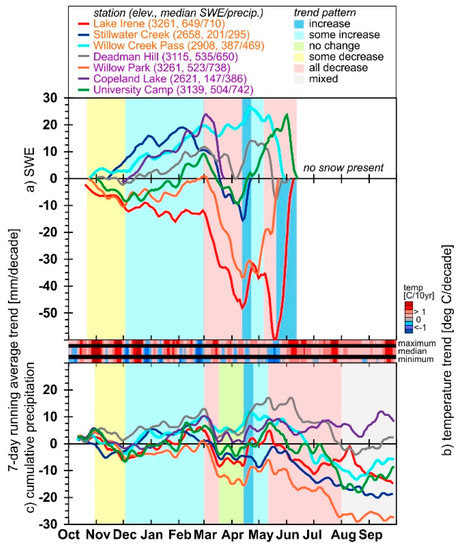
Figure 8.
Seven-day running average trends (a) SWE, (b) temperature, and (c) cumulative precipitation for 7 of the 13 SNOTEL stations shown in Figure 3. The first three SNOTEL stations are on the west-side and presented as orange in the legend and the last four are on the east-side and presented as purple. The same color scheme is used from Figure 4. Time periods of increasing, somewhat increasing, no change, somewhat decreasing, all decreasing, and mixed (both increasing and decreasing) trends are presented as colored bands.
From the four of 13 stations shown in Figure 9, the remaining stations show the same patterns, there is no correlation between sumP and temperature trends (Figure 9a). However, increasing (decreasing) sumP trends do correspond with increasing (decreasing) SWE trends (Figure 9b). There is no correlation between SWE and temperature trends (Figure 9c).
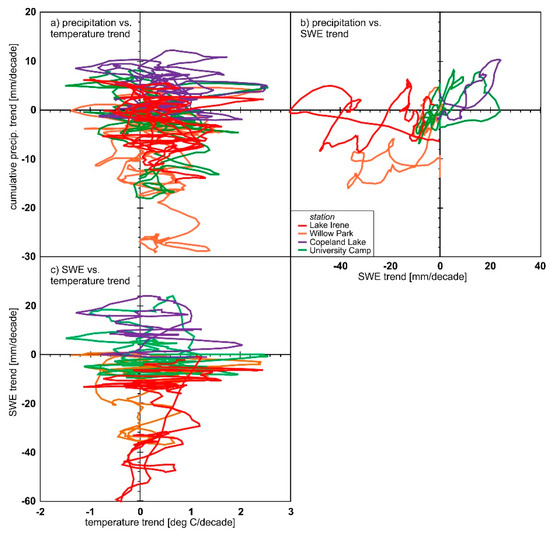
Figure 9.
Comparison of the 7-day running average (a) cumulative precipitation trend versus temperature trend, (b) cumulative precipitation trend versus SWE trend, and (c) SWE trend versus temperature trend for three sample stations.
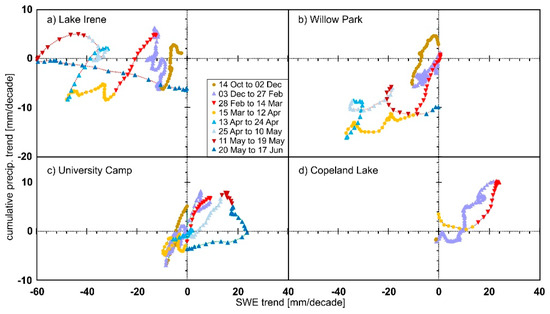
Using the temporal trend periods identified in Figure 8a,c, the correlation between sumP and SWE is similar (Figure 10). Most of the time periods illustrate a similar slope, i.e., correlation in the trend of cumulative precipitation with SWE trend changed at a similar rate, for the four stations (Figure 10a–d). This includes the first five periods from 14 October through 24 April. Most noticeable are the declines from 28 February to 14 March. The increasing SWE trend versus a decreasing precipitation trend at the end of the winter (20 May to 17 June) at Lake Irene presents itself as perpendicular to the firs, third and fifth time periods (Figure 10a). Since snow accumulates later and melts earlier at Copeland Lake (Figure 10d), only four of the eight time periods are available.
5. Discussion
While the daily time step trends in SWE and cumulative precipitation are complicated (Figure 8), there are distinct time periods with temporal patterns (Figure 9), such as the winter season beginning with less SWE at most stations then increasing through the end of February. By 1 March, there is a mean increase in SWE at 11 of 13 stations, but by 1 April, SWE is decreasing at all but two stations (Figure 7(ai,aii)). The 1 April decreases match previously research in many areas across the Western U.S. [9,10,11,12,13,14], with SWE decreasing at all stations from 1 March to 1 April [17]. This decrease in SWE continues through mid-April (Figure 8a), and corresponds to a decrease in precipitation at all stations (Figure 10) for the first two weeks of March, and at most stations through mid-April (Figure 8c). Later in April, all stations with snow (thus not Copeland Lake) saw an increase in SWE. This late season increase is not captured when using 1 April as the date of peak SWE [15]. This current analysis (Figure 6 and Figure 7) illustrates that even a monthly assessment of SWE trends [17], while more informative than a 1 April evaluation, does not fully establish the actual patterns (Figure 8). Further, the temporal trend periods do not align with monthly periods [22]. Unfortunately, daily (automated) snow data are available at fewer locations than monthly (usually manual) snow data [17], and the manual measurements extend over a longer time period of record that is twice as long across the Western U.S. [40]. Thus, where daily data are available, it is recommended that snowpack and meteorological trends be examined on a daily (Figure 6 and Figure 7), or at least weekly (Figure 8) time step [22].
The day to day noise is more pronounced for temperature than SWE or precipitation (Figure 6 versus Figure 7). Warming and cooling trends have short periodicities that do not match the typically used longer time periods, such as months [17], seasons [43], or the annual trends [44]. Overall temperatures are warming at all stations [30,31] with a weak inverse correlation between mean temperature trends and elevation. Specifically, higher elevation stations are tending to warm less than lower elevation stations with Willow Park, University Camp, and Lake Irene warming the least in the winter and summer. Bear Lake, located only 15 km southeast and 370 m lower than Willow Park, is warming the most over the entire year, especially in the summer. The Bear Lake area is a very popular destination for tourists [45], and Willow Park is much less accessible in the summer and is not accessible in the winter [46]. While differences in temperature trends among stations are possibly due to sensor issues [29,30,31], the trends are consistent among the stations (Figure 6 and Figure 8b) [31].
The warmest period of temperature increases, 13 days from 29 October to 10 November (Figure 5b), had a mean warming of 2.1 °C/decade with a maximum daily warming from 3.4 to 4 °C/decade on 2 November. With the exception of Roach, Phantom Valley, and Willow Creek Pass (Figure 7(ai)), this period is seeing a decrease in SWE (Figure 7(ai,aii)). The highest elevations (Joe Wright, Lake Irene, Willow Park) accumulate snow the earliest, and see the largest decrease in SWE. This is illustrated at Lake Irene (Figure 2b) where there is about twice as much SWE for the first decade compared to the last decade. During this warming period, there may be a lower net albedo due to decreasing precipitation (Figure 8c) meaning less fresh snow and thus fewer increases in albedo. Further, less snow could mean that there is more of an influence on albedo from the underlying vegetation or even vegetation protruding from the snowpack due to a lower snow depth. Dormant vegetation has a higher albedo than actively growing vegetation [47]. With a reduced net albedo, and thus more absorbed solar radiation [48], this could yield a more positive energy balance [5] that could influence or warm the near surface air temperature. Snow begins to accumulate during this time at the lowest elevation stations (Stillwater Creek and Copeland Lake), so it is possible that, combined with summer warming (Figure 6), a longer growing period for vegetation may occur in these locations. A longer growing season may result in more transpiration and loss of water that may otherwise become soil moisture recharge, groundwater, or streamflow [49,50].
The changing of the timing of precipitation (Figure 7b) alters snow accumulation patterns (Figure 7a, Figure 8a, Figure 9 and Figure 10). Combined with warmer temperatures (Figure 6), this may cause earlier snowmelt [20,21], which can cause earlier runoff [51,52,53]. This has been observed at most locations across Colorado [54]. Warming may also cause a change in the phase of the precipitation, specifically less snowfall [6,55]. In this study, precipitation phase is correlated with elevation (Figure 3a) due to the computation method [33] and the correlation of temperature with elevation at the SNOTEL scale in this area [56]. However, the change in the fraction of precipitation that falls as snow is not a function of elevation (Figure 3b) due to the combined changed in timing of precipitation (Figure 7b) and periodicity of the temperature trends (Figure 6a). These fractions of precipitation as snow (Figure 3a) and their trends could be different if observations of fresh snow were available [6,57], or a different method was used, such as the dewpoint temperature to distinguish snow from rain [58].
This paper analyzes daily trends in SWE and illustrates a correlation to cumulative precipitation (Figure 10) that is more difficult to illustrate using manual snow course data that only have a monthly time step [17,40] but do not have measured precipitation. This could be addressed using interpolation of station data [24] or modeling [59,60]. The SNOTEL stations used in this current analysis represent a point in space and over-represent the surrounding area [61], which could make interpolation of the station data [30] or trend results [24] difficult. Modeling [59,60] can ameliorate the point to area dilemma [62], but modeling is often at a resolution too coarse to adequately represent snowpack spatial variability in complex terrain [26,63]. An opportunity may be the combination of remote sensing, in situ data, and modeling [64,65].
6. Conclusions
Changes in temperature, precipitation, and SWE are variable in both time and space. Typically, the evaluation of trends in SWE use 1 April data, but these do not capture the nuance of a changing snowpack shown by evaluating trends in the daily data. These show temporal patterns that vary from 10 days to three months, and do not align with first of the month data. Noise was found in the daily trends, but a seven-day moving average removed much of this noise for SWE and precipitation. There were larger fluctuations from positive to negative in the temperature trends, with a five to 10-day period. After late May, temperatures were almost exclusively warming. Temperature trends were very similar among all stations, different that precipitation and SWE trends that varied less from week to week and more from location to location. The trends in SWE were partially correlated to cumulative precipitation over eight temporal periods. There was no correlation between temperature and precipitation or SWE. The limitations of using daily (automated) time-step data are their shorter records compared to monthly or annual (manual) data. Understanding temperature and SWE trends on a fine temporal scale is important for climatological, ecological, and hydrological studies, water resources management, as well as for recreation and tourism.
Author Contributions
Conceptualization, S.R.F., G.G.P. and N.B.H.V.; methodology, S.R.F. and G.G.P.; data retrieval and curation, S.R.F.; formal analysis, S.R.F.; writing—original draft preparation, S.R.F.; writing—review and editing, S.R.F., M.L.C., A.K.D.P., N.B.H.V., J.E.S. and M.E.T.; visualization, S.R.F.; project administration, S.R.F.; funding acquisition, G.G.P. and S.R.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Park Service Continental Divide Science and Learning Center of the Rocky Mountain National Park agreement number P12AC10943, and through the National Park Service Water Resources Division (NPS-WRD) Task agreement number P16AC00826.
Acknowledgments
We thank Daniel McGrath of Colorado State University who acquired the NPS-WRD funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richer, E.E.; Kampf, S.K.; Fassnacht, S.R.; Moore, C.C. Spatiotemporal index for analyzing controls on snow climatology: Application in the Colorado Front Range. Phys. Geogr. 2013, 34, 85–107. [Google Scholar] [CrossRef]
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. Global snow zone maps and trends in snow persistence 2001–2016. Int. J. Climatol. 2018, 38, 4369–4383. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Barry, R.; Gan, T.Y. The Global Cryosphere, Past, Present and Future; Cambridge University Press: Cambridge, UK, 2011; p. 472. [Google Scholar]
- Qu, X.; Hall, A. Assessing snow albedo feedback in simulated climate change. J. Clim. 2006, 19, 2617–2630. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Cherry, M.L.; Venable, N.B.H.; Saavedra, F. Snow and albedo climate change impacts across the United States Northern Great Plains. Cryosphere 2016, 10, 329–339. [Google Scholar] [CrossRef]
- Brown, R.D.; Robinson, D.A. Northern Hemisphere spring snow cover variability and change over 1922-2010 including an assessment of uncertainty. Cryosphere 2011, 5, 219–229. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture. Snow survey and water supply forecasting. In National Engineering Handbook; National Water and Climate Center (USDA): Portland, OR, USA, 2011. [Google Scholar]
- Cayan, D.R. Interannual climate variability and snowpack in the western United States. J. Clim. 1996, 9, 928–948. [Google Scholar] [CrossRef]
- Mote, P.W. Trends in snow water equivalent in the Pacific Northwest and their climatic causes. Geophys. Res. Lett. 2003, 30, 1601–1604. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Mote, P.W.; Clark, M.P.; Lettenmaier, D.P. Effects of temperature and precipitation variability on snowpack trends in the western United States. J. Clim. 2005, 18, 4545–4561. [Google Scholar] [CrossRef]
- Regonda, S.K.; Rajagopalan, B.; Clark, M.; Pitlick, J. Seasonal cycle shifts in hydroclimatology over the western United States. J. Clim. 2005, 18, 372–384. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Hidalgo, H.G.; Das, T.; Bonfils, C.; Santer, B.D.; Bala, G.; Dettinger, M.D.; Cayan, D.R.; Mirin, A.; et al. Attribution of Declining Western, U.S. Snowpack to Human Effects. J. Clim. 2008, 21, 6425–6444. [Google Scholar] [CrossRef]
- McCabe, G.J.; Wolock, D.M. Recent declines in western U.S. snowpack in the context of twentieth-century climate variability. Earth Interact. 2009, 13, 1–15. [Google Scholar] [CrossRef]
- Bohr, G.S.; Aguado, E. Use of April 1st SWE measurements as estimates of peak seasonal snowpack and total cold-season precipitation. Water Resour. Res. 2001, 37, 51–60. [Google Scholar] [CrossRef]
- Pagano, T.C. Quantification of the influence of snow course measurement date on climatic trends. Clim. Chang. 2012, 114, 549. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.; McGrath, D.; Patterson, G.G. Sub-seasonal snowpack trends in the rocky mountain national park area, Colorado, USA. Water 2018, 10, 562. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.R.; Stouffer, J.; Dettinger, M.D.; Krysanova, V. On critiques of “stationarity is dead: Whither water management?”. Water Resour. Res. 2015, 51, 7785–7789. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; López-Moreno, J.I. Patterns of trends in niveograph characteristics across the Western United States from snow telemetry data. Front. Earth Sci. 2020, 14. [Google Scholar] [CrossRef]
- Clow, D.W. Changes in the timing of snowmelt and streamflow in Colorado: A response to recent warming. J. Clim. 2010, 23, 2293–2306. [Google Scholar] [CrossRef]
- Harpold, A.; Brooks, P.; Rajagopal, S.; Heidbuchel, I.; Jardine, A.; Stielstra, C. Changes in snowpack accumulation and ablation in the intermountain west. Water Resour. Res. 2012, 48, W11501–W11511. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Derry, J.E. Defining similar regions of snow in the Colorado River Basin using self-organizing maps. Water Resour. Res. 2010, 46, W04507. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Deitemeyer, D.C.; Venable, N.B.H. Capitalizing on the daily time step of snow telemetry data to model the snowmelt components of the hydrograph for small watersheds. Hydrol. Process. 2014, 28, 4654–4668. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, H.; Zhang, X.; VanLooy, J. Changes in regional snowfall in Central North America (1961–2017): Mountain versus plains. Geosciences 2020, 10, 157. [Google Scholar] [CrossRef]
- National Water and Climate Center (USDA). Snow Survey and Water Supply Forecasting Program. Available online: https://www.wcc.nrcs.usda.gov/snotel/program_brochure.pdf (accessed on 18 February 2020).
- Sexstone, G.A.; Fassnacht, S.R. What drives basin scale spatial variability of snowpack properties in the Front Range of Northern Colorado? Cryosphere 2014, 8, 329–344. [Google Scholar] [CrossRef]
- Serreze, M.C.; Clark, M.P.; Armstrong, R.L.; McGinnis, D.A.; Pulwarty, R.S. Characteristics of the Western United States snowpack from snowpack telemetry (SNOTEL) data. Water Resour. Res. 1999, 35, 2145–2160. [Google Scholar] [CrossRef]
- Tumenjargal, S.; Fassnacht, S.R.; Venable, N.B.H.; Kingston, A.P.; Fernández-Giménez, M.E.; Batbuyan, B.; Laituri, M.J.; Kappas, M.; Adyabadam, G. Variability and change of climate extremes from indigenous herder knowledge and at meteorological stations across Central Mongolia. Front. Earth Sci. 2020, 14. [Google Scholar] [CrossRef]
- Julander, R.P.; Curtis, J.; Beard, A. The SNOTEL temperature dataset. Mt. Views Newslett. 2007, 1, 4–7. Available online: http://www.fs.fed.us/psw/cirmount/ (accessed on 18 February 2020).
- Oyler, J.W.; Dobrowski, S.Z.; Ballantyne, A.P.; Klene, A.E.; Running, S.W. Artificial amplification of warming trends across the mountains of the western United States. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Ma, C.; Fassnacht, S.R.; Kampf, S.K. How temperature sensor change affects warming trends and modeling–An evaluation across the State of Colorado. Water Resour. Res. 2019, 55, 9748–9764. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.H.; Khishigbayar, J.; Cherry, M.L. The probability of precipitation as snow derived from daily air temperature for high elevation Areas of Colorado, United States. In Cold and Mountain Region Hydrological Systems Under Climate Change: Towards Improved Projections, Proceedings of the Symposium H02, IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; IAHS: Wallingford, UK, 2013; Volume 360, pp. 65–70. [Google Scholar]
- Fassnacht, S.R.; Allegretti, A.M.; Venable, N.B.H.; Fernández-Giménez, M.E.; Tumenjargal, S.; Kappas, M.; Laituri, M.J.; Batbuyan, B.; Pfohl, A.K.D. Merging indigenous knowledge systems and station observations to estimate uncertainty of precipitation change in Central Mongolia. Hydrology 2018, 5, 46. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 163–171. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975; p. 272. ISBN 978-0195208375. [Google Scholar]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Wiley: New York, NY, USA, 1987; p. 320. ISBN 978-0471288787. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, 1, 2, and 3. Proc. K. Ned. Akad. Wetenschap. A 1950, 53, 386–392, 521–525, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Hultstrand, M. Snowpack variability and trends at long-term stations in Northern Colorado, USA. Proc. Int. Assoc. Hydrol. Sci. 2015, 371, 131–136. [Google Scholar] [CrossRef]
- Venable, N.B.H.; Fassnacht, S.R.; Adyabadam, G.; Tumenjargal, S.; Fernández-Giménez, M.; Batbuyan, B. Does the length of station record influence the warming trend that is perceived by mongolian herders near the Khangai Mountains? Pirineos 2012, 167, 71–88. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; López-Moreno, J.I.; Ma, C.; Weber, A.N.; Pfohl, A.K.D.; Kampf, S.K.; Kappas, M. Spatio-temporal Snowmelt Variability across the Headwaters of the Southern Rocky Mountains. Front. Earth Sci. 2017, 11, 505–514. [Google Scholar] [CrossRef]
- Van Pelt, W.J.J.; Kohler, J.; Liston, G.E.; Hagen, J.O.; Luks, B.; Reijmer, C.H.; Pohjola, V.A. Multidecadal climate and seasonal snow conditions in Svalbard. J. Geophys. Res. Earth Surf. 2016, 121, 2100–2117. [Google Scholar] [CrossRef]
- IPCC. Global Warming of 1.5 °C; An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018.
- National Park Service. NPS Stats National Park Service Visitor Use Statistics. Available online: https://irma.nps.gov/STATS/Reports/Park (accessed on 23 February 2020).
- National Park Service. Rocky Mountain National Park. 2019. Available online: https://www.nps.gov/romo/index.htm (accessed on 23 February 2020).
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Burston, R.M.; Kilmister, I.F.; Dee, M.; Campbell, P.A. Out of the sun. In Sacrifice; CMC International Records: Raleigh, NC, USA, 1995. [Google Scholar]
- Tung, C.-P.; Haith, D.A. Global-Warming effects on New York streamflows. J. Water Resour. Plan. Manag. 1995, 121, 216–225. [Google Scholar] [CrossRef]
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in snowmelt runoff timing in western North America under a “business as usual” climate change scenario. Clim. Chang. 2004, 62, 217–232. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes toward earlier streamflow timing across western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Fritze, H.; Stewart, I.T.; Pebesma, E. Shifts in western North American snowmelt runoff regimes for the recent warm decades. J. Hydrometeorol. 2011, 12, 989–1006. [Google Scholar] [CrossRef]
- Pfohl, A.K.D.; Fassnacht, S.R. Evaluating methods of streamflow timing to approximate snowmelt contribution in high-elevation mountain watersheds. Geophys. Res. Lett. 2020. in review, submission 2019GL083419. [Google Scholar]
- McCabe, G.J.; Wolock, D.M.; Valentin, M. Warming is driving decreases in snow fractions while runoff efficiency remains mostly unchanged in snow-covered areas of the Western United States. J. Hydrometeor. 2018, 19, 803–814. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Fassnacht, S.R.; Pulido-Velazquez, D.; Pfohl, A.K.D.; Morán-Tejeda, E.; Venable, N.B.H.; Pardo-Igúzquiza, E.; Puntenney-Desmond, K. Intra-day variability of temperature and its lapse rates over mountainous terrain: Comparing MODIS Land Surface Temperature data with coarse and fine scale surface measurements. Int. J. Climatol. 2020, in press. [Google Scholar]
- Huntington, T.G.; Hodgkins, G.A.; Keim, B.D.; Dudley, R.W. Changes in the proportion of precipitation occurring as snow in New England (1949–2000). J. Clim. 2004, 17, 2626–2636. [Google Scholar] [CrossRef]
- Marks, D.; Kimball, J.; Tingey, D.; Link, T.E. The sensitivity of snowmelt processes to climate conditions and forest cover during rain-on-snow: A study of the 1996 Pacific Northwest Flood. Hydrol. Process. 1998, 12, 1569–1587. [Google Scholar] [CrossRef]
- Kapnick, S.B.; Delworth, T.L. Controls of global snow under a changed climate. J. Clim. 2013, 26, 5537–5562. [Google Scholar] [CrossRef]
- Mote, P.W.; Li, S.; Lettenmaier, D.P.; Xiao, M.; Engel, R. Dramatic declines in snowpack in the western US. npj Clim. Atmos. Sci. 2018, 1, 2. [Google Scholar] [CrossRef]
- Meromy, L.; Molotch, N.P.; Link, T.E.; Fassnacht, S.R.; Rice, R. Subgrid variability of snow water equivalent at operational snow stations in the western United States. Hydrol. Process. 2013, 27, 2383–2400. [Google Scholar] [CrossRef]
- Blöschl, G. Scaling issues in snow hydrology. Hydrol. Process. 1999, 13, 2149–2175. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Heath, J.T.; Musselman, K.; Revuelto, J.; Latron, J.; Morán-Tejedaa, E.; Jonas, T. Spatial variability of snow density over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D. Spatiotemporal estimation of snow depth using point data from snow stakes, digital terrain models, and satellite data. Hydrol. Process. 2017, 31, 1966–1982. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Soubeyroux, J.M.; Gascoin, S.; Alonso-Gonzalez, E.; Durán-Gómez, N.; Lafaysse, M.; Vernay, M.; Carmagnola, C.; Morin, S. Long-term trends (1958–2017) in snow cover duration and depth in the Pyrenees. Int. J. Clim. 2020, 1–15. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).