Evaluation of General Circulation Models over the Upper Ouémé River Basin in the Republic of Benin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Observational Data
2.3. Models
2.4. Model Performance
- The use of U-test will help to assess whether the numerical general circulation models (GCMs) are sufficiently reliable.
- The correlation is used to quantify the linear relationship between observed rainfall and those simulated by the models. The calculation of the Pearson correlation coefficient is based on the calculation of the covariance between the two variables. The correlation coefficient is actually the standardization of the covariance.
- The difference between the standard deviations of observed rainfall and those simulated by the models provides information on the simulation of interannual variability by the models.
- MBE makes it possible to quantify the average systematic error (mean bias) of each model. The better the accuracy of the estimation model, the lower the mean bias. A positive bias indicates a tendency to overestimate the model, conversely a negative bias indicates that the estimated values are underestimated compared to those actually observed. The average bias (MBE) is calculated from the following formula:where X is the value of the parameter considered for each year (period from April to October) for the period of 55 years (1951–2005); Obs corresponds to observations and Sim to simulations. N is the number of years (i.e., 55 years) and M is the number of stations considered for each model on our study site.
- MAE allows to quantify the amplitude of the average errors regardless of the positive or negative biases (magnitude of the differences between the simulated and observed values). The mean absolute error (MAE) is defined as follows:
- RMSE allows to include evidence of not only the errors in the mean value but also those in the interannual variability of the simulated versus observed data. If the RMSE is almost identical to the mean absolute error (and not zero), a systematic error affects the mean value of the simulated values and the error on the variability is therefore low or zero. On the other hand, if the RMSE is greater than the MAE (and not zero), the simulated values are affected both by an error in the mean value of the data but also by an error in the interannual variability. RMSE is often used to describe the dispersion of observations and simulations (the lower the RMSE is, the more that the prediction models are related the observations). The RMSE is calculated according to the following formula:Statistical analyses were performed using the statistical software R 3.5.1 (R Development Core Team, http://www.R-project.org) with packages stats and forecast.
3. Results
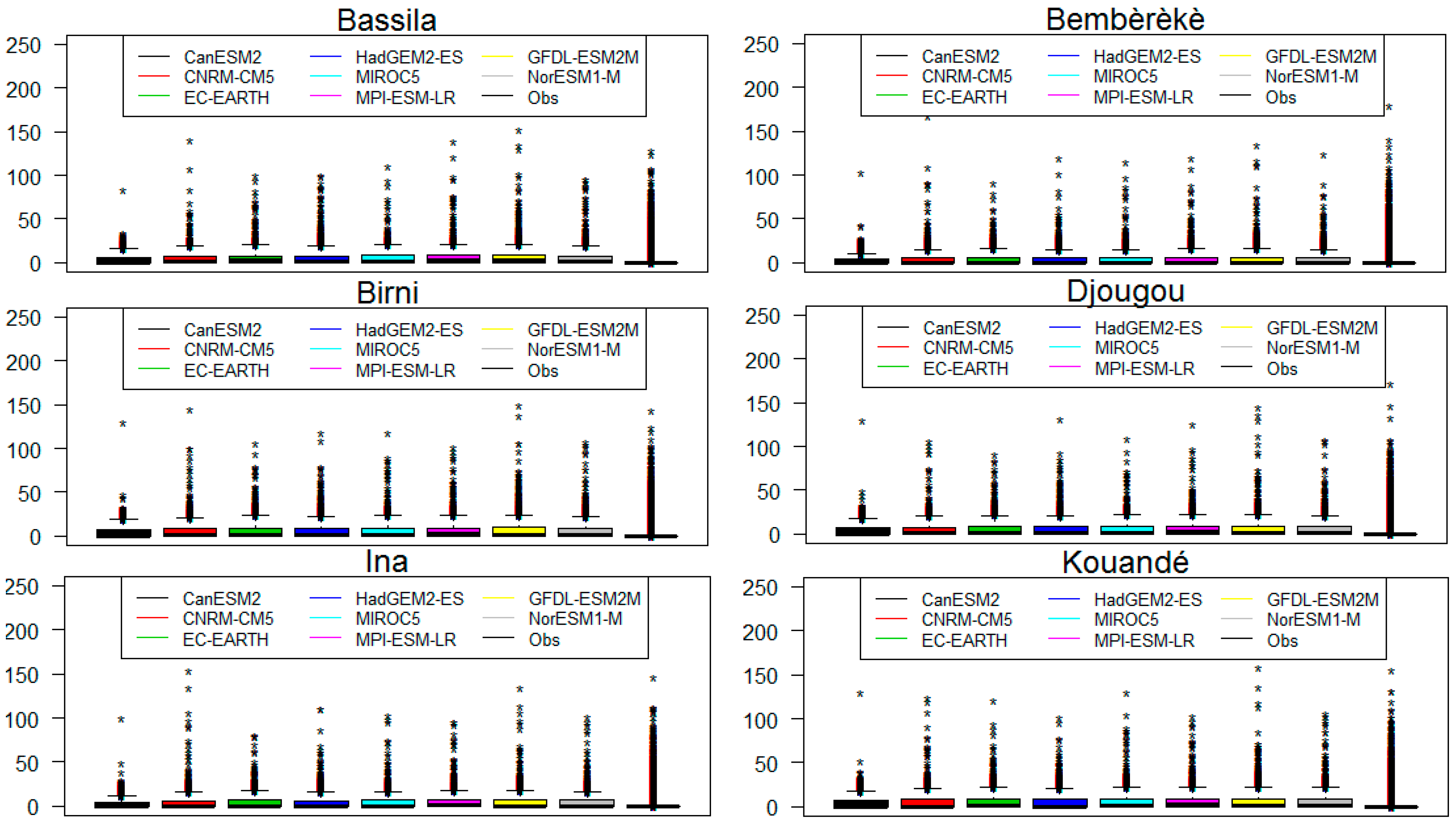
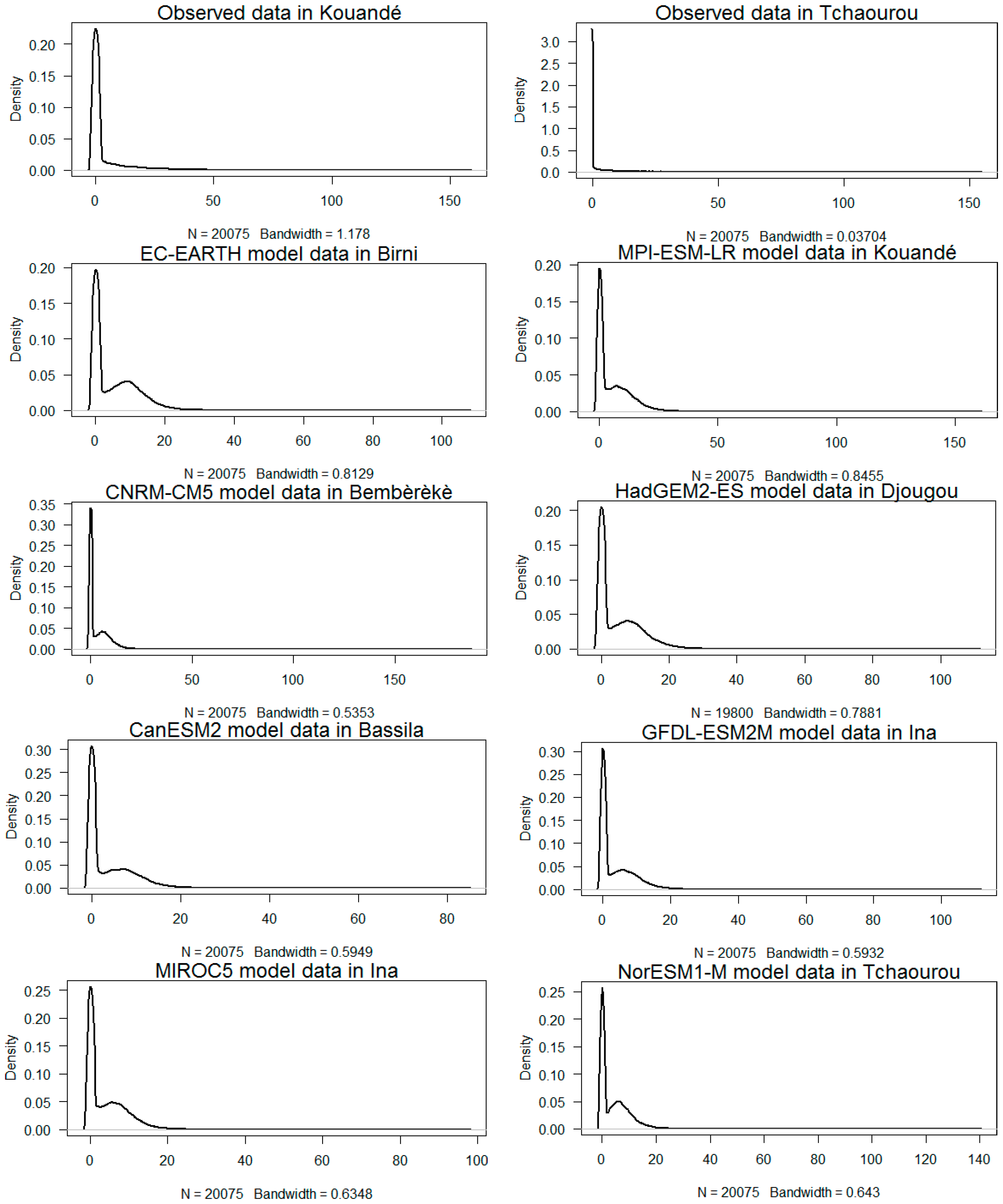
3.1. U-Test Results
3.2. Correlation Test Results
3.3. Interannual Variability
3.4. Statistic Criteria Results
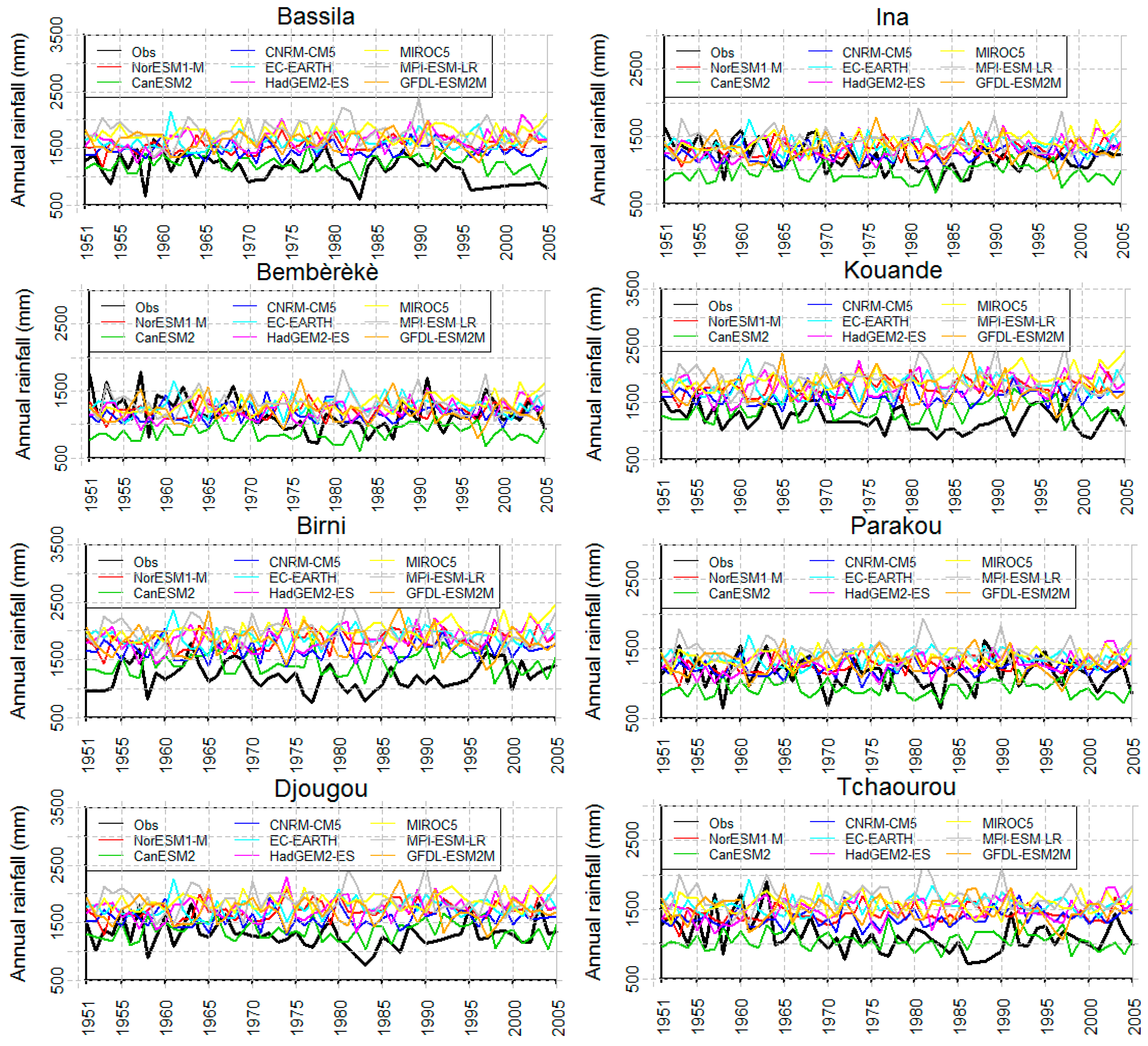
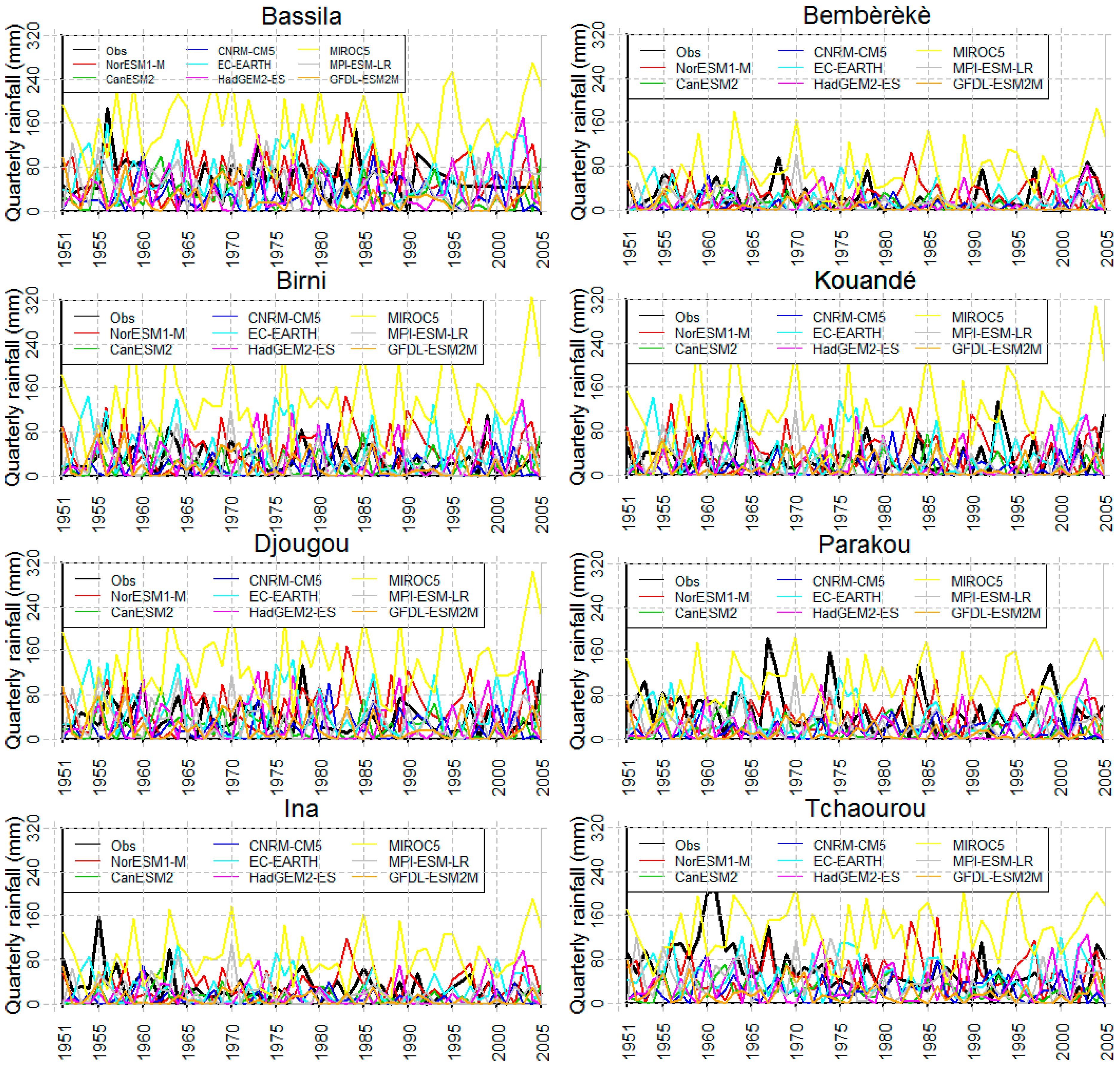
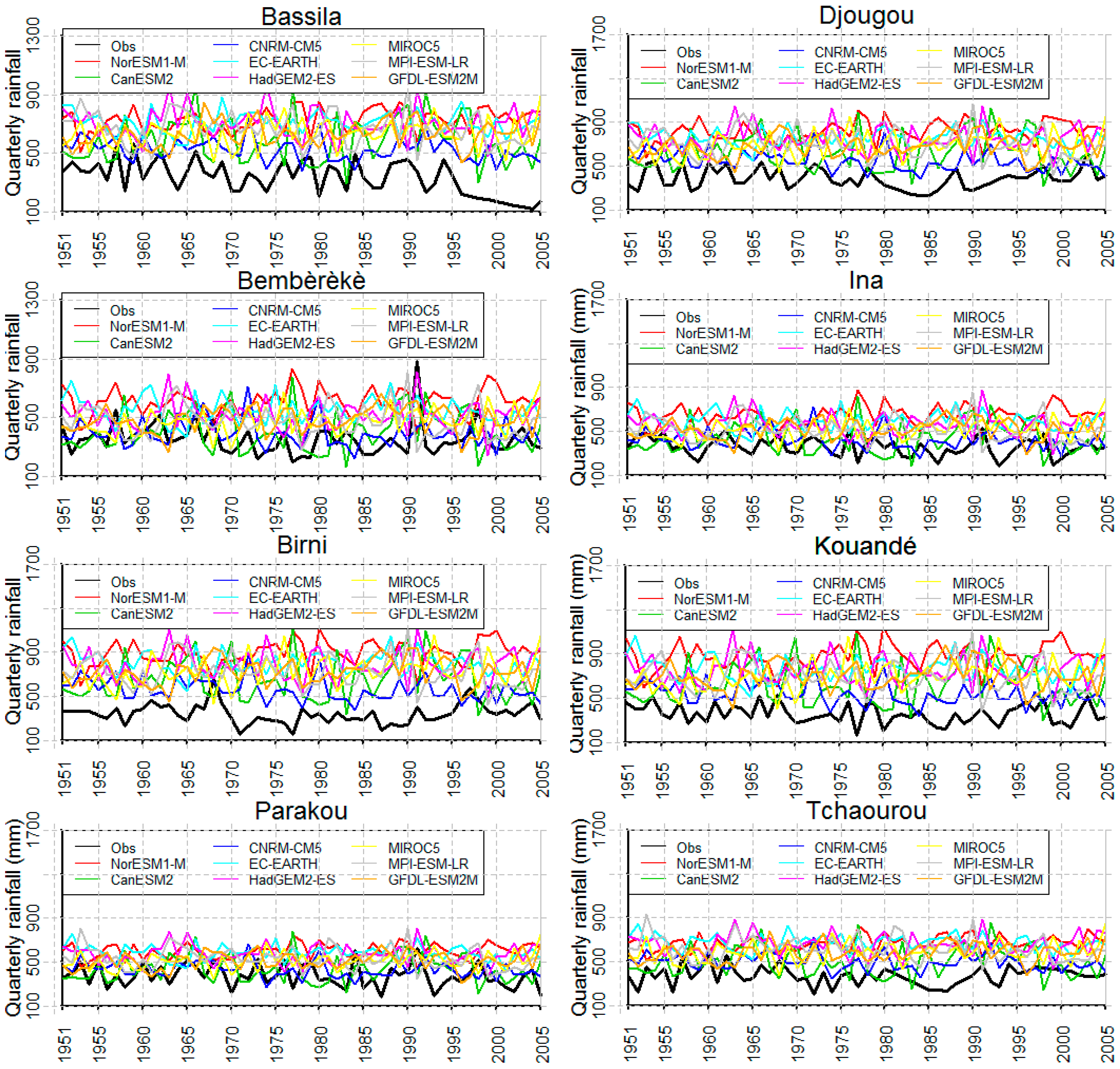
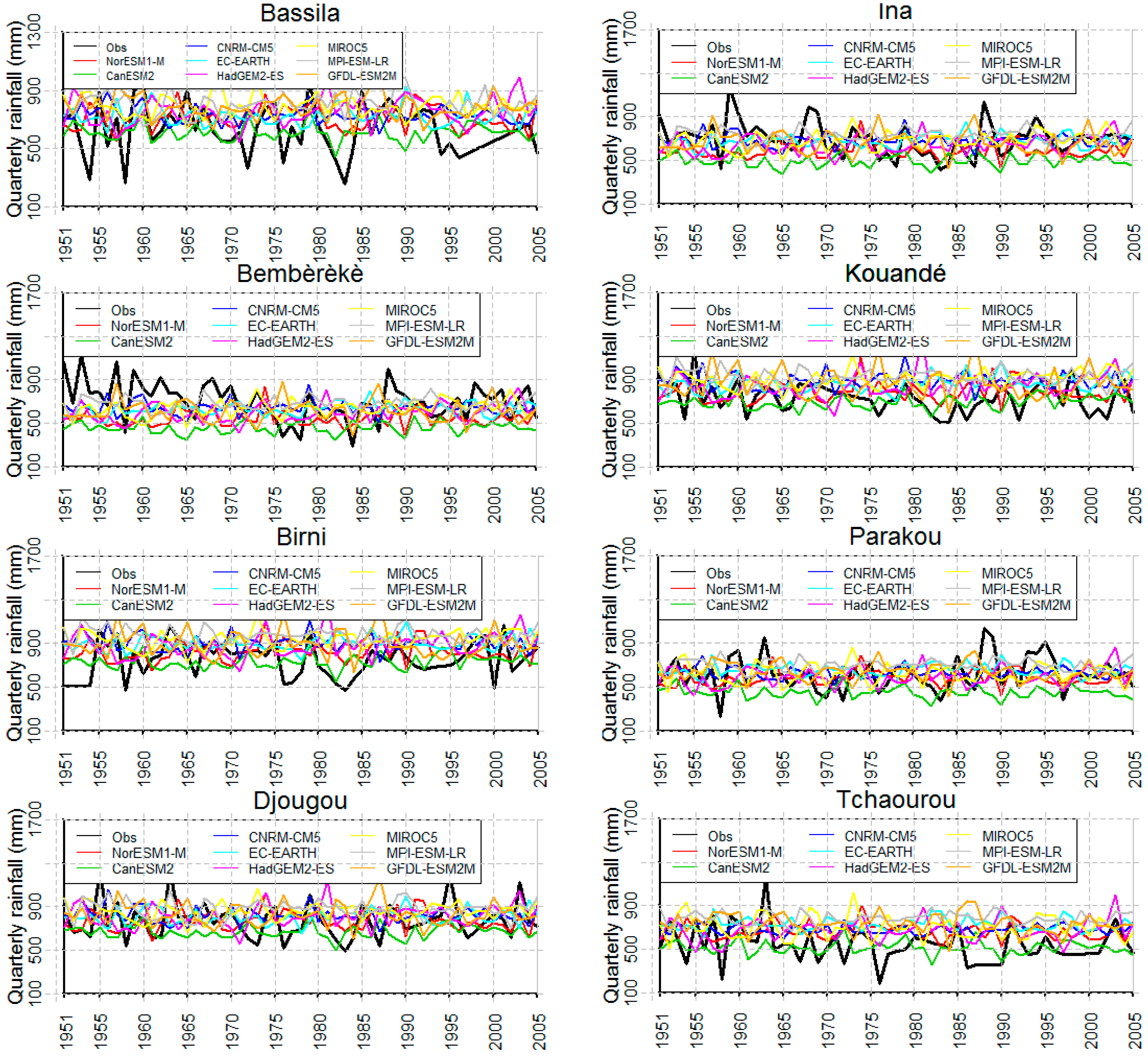
3.5. Rainfall Cumulation Evolution
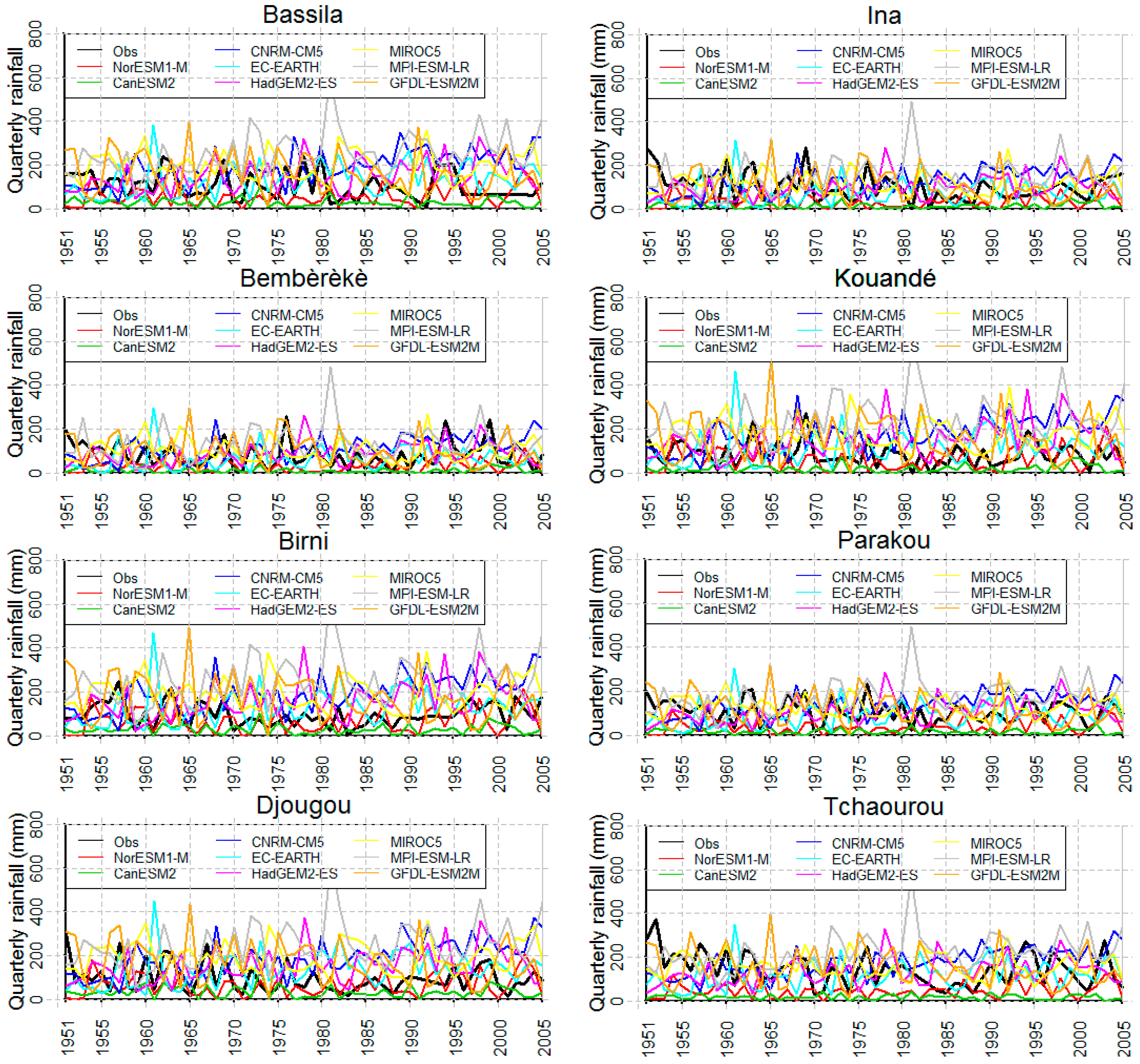
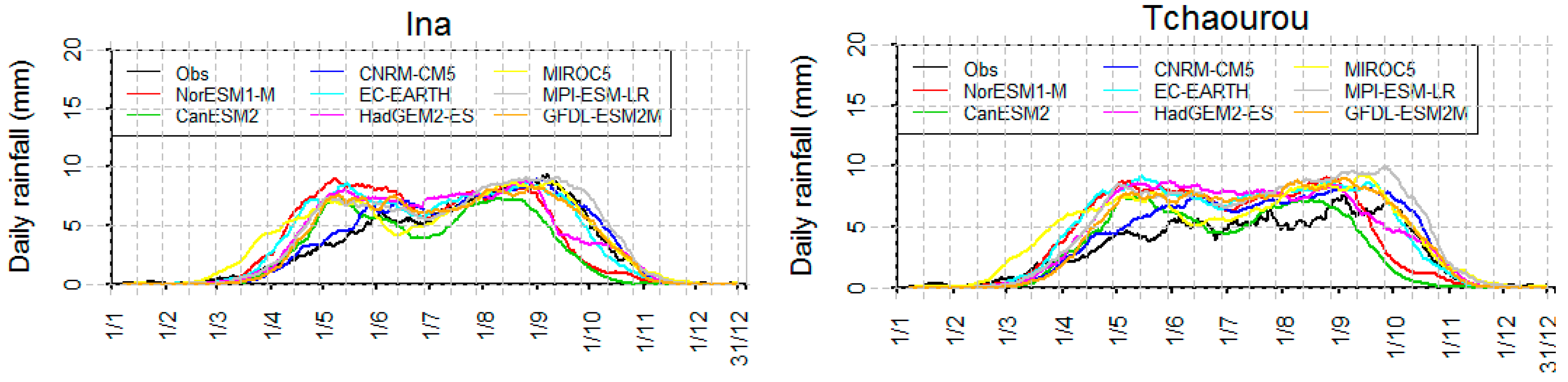
3.6. Seasonal Cycles Evolution
3.7. Observed and Simulated Precipitation Indices Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gnitou, G.T.; Ma, T.; Tan, G.; Ayugi, B.; Nooni, I.K. Evaluation of the Rossby Centre Regional Climate Model Rainfall Simulations over West Africa Using Large-Scale Spatial and Temporal Statistical Metrics. Atmosphere 2019, 10, 802. [Google Scholar] [CrossRef]
- Kamworapan, S. Evaluation of CMIP5 Global Climate Models for Simulating Climatological Temperature and Precipitation for Southeast Asia. Adv. Meteorol. 2019, 2019, 1067365. [Google Scholar] [CrossRef]
- Tolika, K.; Maheras, P.; Vafiadis, M.; Anagnostopoulou, C. Comparaison de deux scenarios (statistique et dynamique) concernant les precipitations hivernales. Climatologie 2007, 4, 73–90. [Google Scholar] [CrossRef]
- Dutrieux, P. Évaluation de simulations du modèle régional canadien du climat (MRCC5) au-dessus de l’atlantique nord. In Mémoire de la Maîtrise en Sciences de L’atmosphère; Université du Québec à Montréal: Montréal, QC, Canada, 2016; p. 125. [Google Scholar]
- Bader, D.C.; Covey, C.; Gutowski, W.J., Jr.; Held, I.M.; Kunkel, K.E.; Miller, R.L.; Tokrnakian, R.T.; Zhang, M.H. A Report by the U.S. Climate Change Science Program and the Subcommittee on Global Change Research. In Climate Models: An Assessment of Strengths and Limitations; Department of Energy, Office of Biological and Environmental Research: Washington, DC, USA, 2008; p. 124. [Google Scholar]
- Laprise, R.; de Elía, R.; Caya, D.; Biner, S.; Lucas-Picher, P.; Diaconescu, E.; Leduc, M.; Alexandru, A.; Separovic, L. Challenging some tenets of Regional Climate Modelling. Meteorol. Atmos. Phys. 2008, 100, 3–22. [Google Scholar] [CrossRef]
- Leung, L.R.; Mearns, L.O.; Giorgi, F.; Wilby, R.L. Regional climate research. Bull. Am. Meteorol. Soc. 2003, 84, 89–95. [Google Scholar]
- Khan, N.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N.; Son, M. Model in Simulating Daily Precipitation and. Water 2018, 10, 1793. [Google Scholar] [CrossRef]
- Le Treut, H. Évolution Climatique: Les Modèles et Leurs Limites. Available online: http://www.cnrs.fr/publications/imagesdelaphysique/couv-PDF/IdP2005/05Letreut.pdf (accessed on 12 July 2016).
- Giannini, A.; Biasutti, M.; Held, I.M.; Sobel, A.H. A global perspective on African climate. Clim. Chang. 2008, 90, 359–383. [Google Scholar] [CrossRef]
- Biasutti, M.; Giannini, A. Robust Sahel drying in response to late 20th century forcings. Geophys. Res. Lett. 2006, 33, 10–13. [Google Scholar] [CrossRef]
- Hoerling, M.P.; Hurrell, J.W.; Xu, T. Tropical origins for recent North Atlantic climate change. Science 2001, 292, 90–92. [Google Scholar] [CrossRef] [PubMed]
- GIEC. Bilan 2007 des Changements Climatiques. Contribution des Groupes de Travail I, II et III au Quatrième Rapport D’évaluation du Groupe D’experts Intergouvernemental sur L’évolution du Climat [Équipe de Rédaction Principale, Pachauri, R.K. et Reisinger, A. (Publié Sous la Direction de~)]. GIEC: Genève, Suisse, 2007. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ar4_syr_fr.pdf (accessed on 12 July 2018).
- Kamga Foamouhoue, A.; Buscarlet, E. Simulation du climat de l’Afrique de l’Ouest à l’aide d’un modèle climatique régional: Validation sur la période 1961–1990. La Météorologie 2006, 8, 28. [Google Scholar] [CrossRef]
- COI. Synthèse des Travaux du Projet Acclimate de la Commission de L’océan Indien Alexandre Magnan, Virginie, Duvat. 2012. Available online: http://www.commissionoceanindien.org/archives/society.ioconline.org/fileadmin/Acclimate/SYNTHESE Accli681 mate_01.pdf1 (accessed on 5 January 2015).
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing Climate Information Needs at the Regional Level: The CORDEX Framework. Bulletin 2009, 58, 3. [Google Scholar]
- Mahé, G.I.L.; Triboulet, J.P. Analysis of a Sahelian annual rainfall index from 1896 to 2000; the drought continues. Hydrol. Sci. J. 2002, 47, 563–572. [Google Scholar]
- Olivry, J.-C. De l’évolution de la puissance des crues des grands cours d’eau intertropicaux d’Afrique depuis deux décennies. Rev. Geogr. Alp. 1994, 12, 101–108. [Google Scholar]
- Gachon, L.G.; Bokoye, A.I.; Parishkura, D.; Cotnoir, A.; Tramblay, Y.; Vigeant, G. Groupe de travail II Variabilité, extrêmes et changements climatiques au Sahel: De l’observation à la modélisation. In dans Rapport des Contributions Canadiennes au Projet ACDI—CILSS (#A030978-002); Appui Aux Capacités D’adaptation Aux Changements Climatiques; Environnement Canada: Montréal, QC, Canada, 2007. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K.; Robeson, S.M. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Environ. 2009, 43, 749–752. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? -Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Ansari, A.R.; Bradley, R.A. Rank-sum tests for dispersions. Ann. Math. Stat. 1960, 31, 1174–1189. [Google Scholar] [CrossRef]
- Kostopoulou, E.; Giannakopoulos, C.; Anagnostopulou, C.H.R.; Tolika, K.; Maheras, P.; Vafiadis, M. Simulating Maximum and Minimum temperatures over Greece: A comparison of three modeling techniques. Theor. Appl. Climatol. 2006, 90, 65–82. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Demirel, M.C.; Chung, E. Selection of multi-model ensemble of general circulation models for the simulation of precipitation and maximum and minimum temperature based on spatial assessment metrics. Hydrol. Earth Syst. Sci. 2019, 23, 4803–4824. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2053–2075. [Google Scholar] [CrossRef] [PubMed]
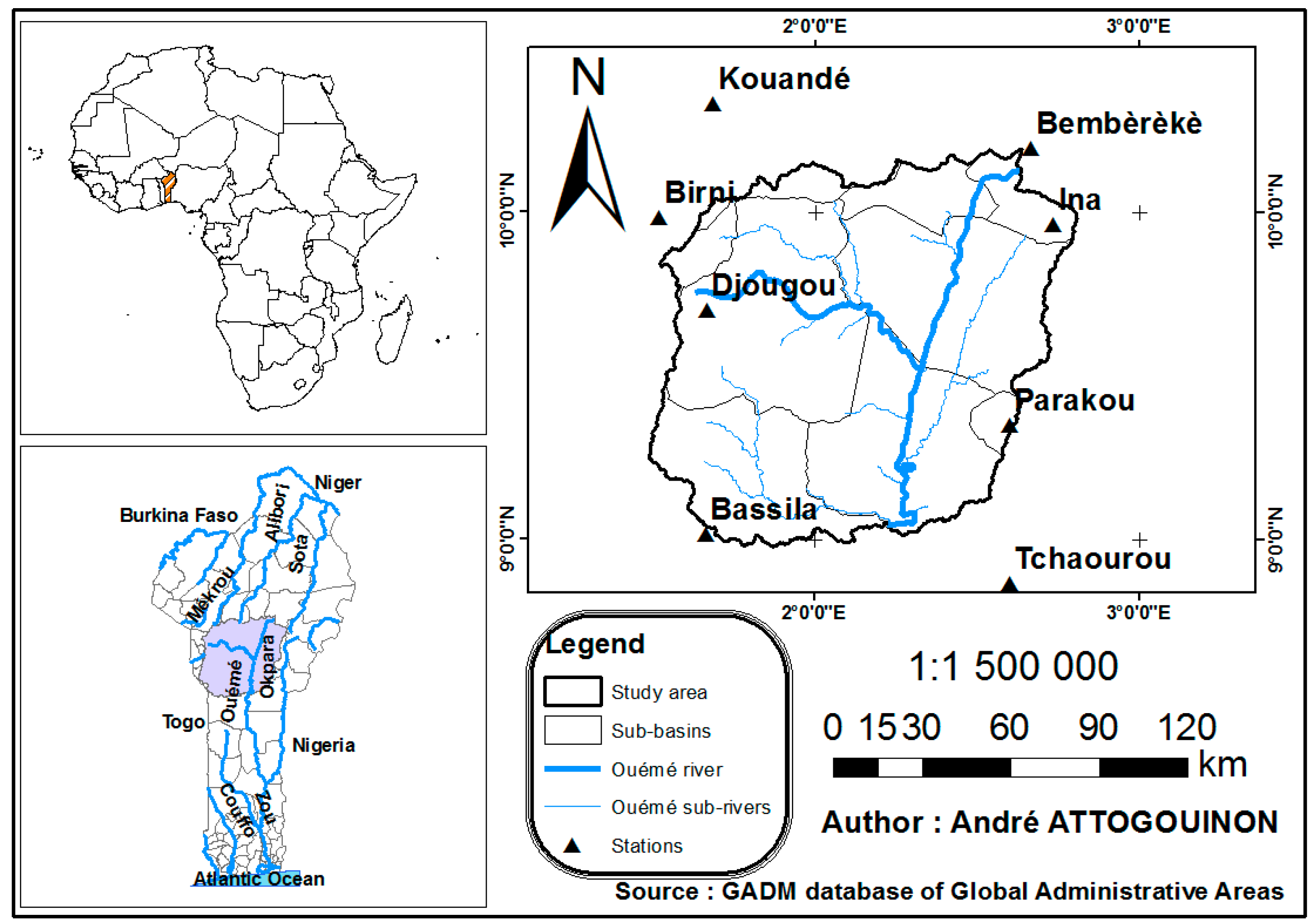



| Stations | Benin Meteo Agency Code | Long. (Degrees) | Lat. (Degrees) | Elevation (m) |
|---|---|---|---|---|
| Bassila | D037 | 1.667 | 9.017 | 384 |
| Bembèrèkè | D024 | 2.662 | 10.223 | 491 |
| Birni | D026 | 1.517 | 9.983 | 430 |
| Djougou | D030 | 1.662 | 9.692 | 439 |
| Ina | D027 | 2.727 | 9.969 | 358 |
| Kouandé | D019 | 1.683 | 10.333 | 442 |
| Parakou | D034 | 2.612 | 9.357 | 392 |
| Tchaourou | D038 | 2.600 | 325 | 325 |
| Research Centers | Acronym(s) for Centers | Model Name | Resolution (Long. × Lat.; Degrees) |
|---|---|---|---|
| Canadian Centre for Climate Modelling and Analysis Canada | CCCma | CanESM2 | 2.81 × 2.79 |
| Centre National de Recherches Météorologiques, Centre Européen de Recherche et de Formation Avancée en Calcul Scientifique France | CNRM-CERFACS | CNRM-CM5 | 1.41 × 1.4 |
| EC-EARTH consortium published at Irish Centre for High-End Computing Netherlands/Ireland | ICHEC | EC-EARTH | 1.13 ×1.12 |
| Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology Japan | MIROC | MIROC5 | 1.41 × 1.39 |
| Met Office Hadley Centre England | MOHC | HadGEM2-ES | 1.875 × 1.25 |
| Max Planck Institute for Meteorology Germany | MPI-M | MPI-ESM-LR | 1.875 × 1.85 |
| Bjerknes Centre for Climate Research, Norwegian Meteorological Institute Norway | NCC, NMI | NorESM1-M | 1.875 × 1.85 |
| Geophysical Fluid Dynamics Laboratory USA | NOAA-GFDL | GFDL-ESM2M | 2.5 × 2.0 |
| Indices | Name | Indices Calculation | Definition | Unit |
|---|---|---|---|---|
| Frequency Indices (adapted from WMO 2009) | ||||
| R10mm | Number of heavy rainfall days | RRij 10 mm | Annual count of days when days rainfall 10 mm | Days |
| R20mm | Number of very heavy rainfall days | RRij 20 mm | Annual count of days when days rainfall 20 mm | Days |
| R25mm | Number of extremely heavy rainfall days | Annual count of days when days rainfall 25 mm | Days | |
| CDD | Consecutive dry days | Maximum number of consecutive days with RR < 1 mm | Days | |
| CWD | Consecutive wet days | Maximum number of consecutive days with RR 1 mm | Days | |
| Intensity Indices (adapted from WMO 2009) | ||||
| SDII | Simple daily intensity index | Annual mean rainfall when PRCP > 1 mm | mm/day | |
| RX1day | Maximum daily rainfall | Maximum 1-day Rainfall | mm | |
| RX3day | Maximum 3-day rainfall | Rx3dayj = max(RRij) | Maximum 3-day rainfall | mm |
| RX5day | Maximum 5-day rainfall | Rx5dayj = max(RRij) | Maximum 5-day rainfall | mm |
| R95p | Very wet day | Annual total rainfall when RR > 95 percentile | mm | |
| R99p | Extremely wet day | Annual total rainfall when RR > 99 percentile | mm | |
| CanESM2 | CNRM-CM5 | EC-EARTH | HadGEM2-ES | MIROC5 | MPI-ESM-LR | NorESM1-M | GFDL-ESM2M | |
|---|---|---|---|---|---|---|---|---|
| Bassila | 0.184 | 0.191 | 0.176 | −0.041 | 0.164 | 0.161 | 0.169 | 0.181 |
| Bembèrèkè | 0.169 | 0.179 | 0.180 | −0.042 | 0.168 | 0.169 | 0.173 | 0.183 |
| Birni | 0.198 | 0.223 | 0.207 | −0.066 | 0.190 | 0.196 | 0.196 | 0.200 |
| Djougou | 0.206 | 0.213 | 0.189 | −0.050 | 0.169 | 0.195 | 0.198 | 0.203 |
| Ina | 0.178 | 0.208 | 0.195 | −0.049 | 0.191 | 0.194 | 0.169 | 0.190 |
| Kouandé | 0.192 | 0.211 | 0.203 | −0.058 | 0.195 | 0.204 | 0.179 | 0.199 |
| Parakou | 0.155 | 0.182 | 0.165 | −0.042 | 0.146 | 0.164 | 0.159 | 0.159 |
| Tchaourou | 0.154 | 0.175 | 0.171 | −0.044 | 0.140 | 0.174 | 0.149 | 0.172 |
| CanESM2 | CNRM-CM5 | EC-EARTH | HadGEM2-ES | MIROC5 | MPI-ESM-LR | NorESM1-M | GFDL-ESM2M | |
|---|---|---|---|---|---|---|---|---|
| Bassila | −4.038 | −3.467 | −3.299 | −3.124 | −3.014 | −2.47 | −3.168 | −2,825 |
| Bembèrèkè | −5.562 | −4.511 | −4.711 | −4.583 | −4.581 | −4.07 | −4.572 | −4,615 |
| Birni | −3.853 | −3.247 | −2.991 | −2.864 | −2.959 | −2.32 | −2.833 | −2.808 |
| Djougou | −4.508 | −3.996 | −3.805 | −3.589 | −3.685 | −3.01 | −3.633 | −3.513 |
| Ina | −4.966 | −4.041 | −4.087 | −4.022 | −4.033 | −3.47 | −3.981 | −3.998 |
| Kouandé | −3.833 | −3.032 | −2.983 | −2.819 | −2.892 | −2.29 | −2.729 | −2.832 |
| Parakou | −5.574 | −4.839 | −4.645 | −4.631 | −4.630 | −3.97 | −4.579 | −4.541 |
| Tchaourou | −4.369 | −3.731 | −3.307 | −3.245 | −3.184 | −2.69 | −3.267 | −3.052 |
| mean | −4.588 | −3.858 | −3.729 | −3.609 | −3.622 | −3.04 | −3.595 | −3.523 |
| CanESM2 | CNRM-CM5 | EC-EARTH | HadGEM2-ES | MIROC5 | MPI-ESM-LR | NorESM1-M | GFDL-ESM2M | |
|---|---|---|---|---|---|---|---|---|
| MBE | 0.349 | 0.948 | 1.389 | 1.395 | 1.773 | 1.774 | 1.173 | 1.326 |
| MAE | 4.645 | 4.966 | 5.309 | 6.441 | 5.630 | 5.579 | 5.210 | 5.228 |
| RMSE | 9.249 | 9.467 | 9.661 | 10.834 | 9.905 | 10.171 | 9.720 | 9.834 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | −28.84 | 276.02 | 340.22 |
| CNRM-CM5 | 233.82 | 313.81 | 370.75 |
| EC-EARTH | 393.69 | 438.35 | 499.13 |
| HadGEM2-ES | 359.82 | 423.53 | 483.06 |
| MIROC5 | 465.35 | 499.47 | 552.99 |
| MPI-ESM-LR | 484.26 | 518.63 | 588.60 |
| NorESM1-M | 324.20 | 391.89 | 451.12 |
| GFDL-ESM2M | 330.62 | 400.24 | 476.57 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | 2.62 | 266.37 | 330.19 |
| CNRM-CM5 | 257.92 | 320.84 | 376.33 |
| EC-EARTH | 392.78 | 431.29 | 489.14 |
| HadGEM2-ES | 371.49 | 426.76 | 483.15 |
| MIROC5 | 375.24 | 422.41 | 478.15 |
| MPI-ESM-LR | 484.71 | 512.75 | 578.13 |
| NorESM1-M | 325.92 | 381.52 | 441.24 |
| GFDL-ESM2M | 357.47 | 411.49 | 486.63 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | −22.35 | 34.57 | 44.99 |
| CNRM-CM5 | 23.13 | 33.20 | 44.74 |
| EC-EARTH | 1.44 | 38.09 | 49.80 |
| HadGEM2-ES | 14.78 | 37.53 | 49.82 |
| MIROC5 | 73.78 | 80.61 | 96.35 |
| MPI-ESM-LR | −11.79 | 36.22 | 46.40 |
| NorESM1-M | 5.59 | 38.78 | 49.16 |
| GFDL-ESM2M | −25.02 | 34.71 | 46.49 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | 175.86 | 221.80 | 274.20 |
| CNRM-CM5 | 130.02 | 156.93 | 185.79 |
| EC-EARTH | 317.09 | 319.75 | 344.76 |
| HadGEM2-ES | 302.55 | 308.02 | 340.29 |
| MIROC5 | 246.64 | 260.30 | 293.04 |
| MPI-ESM-LR | 257.90 | 268.62 | 305.08 |
| NorESM1-M | 369.46 | 373.58 | 401.31 |
| GFDL-ESM2M | 242.52 | 252.48 | 286.50 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | −100.75 | 172.99 | 209.05 |
| CNRM-CM5 | 66.37 | 159.27 | 196.17 |
| EC-EARTH | 70.35 | 168.39 | 206.76 |
| HadGEM2-ES | 44.49 | 170.21 | 210.89 |
| MIROC5 | 88.36 | 178.54 | 218.08 |
| MPI-ESM-LR | 131.96 | 190.90 | 229.99 |
| NorESM1-M | 369.46 | 373.58 | 201.33 |
| GFDL-ESM2M | 73.15 | 179.87 | 228.97 |
| MBE | MAE | RMSE | |
|---|---|---|---|
| CanESM2 | −81.61 | 85.41 | 104.73 |
| CNRM-CM5 | 60.57 | 102.69 | 120.39 |
| EC-EARTH | 4.82 | 82.89 | 105.89 |
| HadGEM2-ES | 27.56 | 79.68 | 100.46 |
| MIROC5 | 56.03 | 87.87 | 109.27 |
| MPI-ESM-LR | 106.17 | 125.90 | 157.62 |
| NorESM1-M | 54.37 | 75.70 | 95.54 |
| GFDL-ESM2M | 39.98 | 94.17 | 119.69 |
| CanESM2 Model | CNRM-CM5 Model | EC-EARTH Model | |||||||
| MBE | MAE | RMSE | MBE | MAE | RMSE | MBE | MAE | RMSE | |
| CWD | 32.99 | 32.99 | 33.82 | 43.18 | 43.18 | 43.84 | 47.41 | 47.41 | 47.99 |
| SDII | −7.82 | 7.82 | 8.38 | −7.26 | 7.27 | 7.82 | −6.92 | 6.93 | 7.52 |
| CDD | −3.27 | 6.32 | 8.47 | −2.29 | 6.33 | 8.07 | −6.59 | 7.87 | 9.68 |
| RX1day | −50.81 | 51.64 | 56.79 | −39.20 | 45.87 | 52.73 | −39.36 | 40.05 | 49.81 |
| R3day | −44.75 | 46.25 | 53.86 | −32.48 | 43.99 | 53.00 | −31.04 | 38.64 | 47.26 |
| RX5day | −43.20 | 46.23 | 56.27 | −32.58 | 43.48 | 53.99 | −28.20 | 40.37 | 51.19 |
| R10mm | 1.37 | 14.26 | 17.28 | 12.00 | 15.55 | 17.81 | 19.54 | 21.54 | 24.22 |
| R20mm | −16.76 | 16.83 | 17.89 | −15.52 | 15.53 | 16.63 | −14.61 | 14.65 | 15.97 |
| R25mm | −13.33 | 13.33 | 14.17 | −12.64 | 12.64 | 13.55 | −12.23 | 12.22 | 13.20 |
| R95P | −100.79 | 103.84 | 121.96 | −57.82 | 80.10 | 99.00 | −43.70 | 71.49 | 88.88 |
| R99P | −32.86 | 35.24 | 43.26 | −16.86 | 35.13 | 45.62 | −19.52 | 31.35 | 40.53 |
| HadGEM2-ES Model | MIROC5 Model | MPI-ESM-LR Model | |||||||
| MBE | MAE | RMSE | MBE | MAE | RMSE | MBE | MAE | RMSE | |
| CWD | 45.79 | 45.79 | 46.42 | 48.08 | 48.08 | 48.62 | 47.54 | 47.54 | 48.19 |
| SDII | −6.59 | 6.91 | 7.52 | −7.11 | 7.11 | 7.69 | −6.44 | −6.47 | 7.10 |
| CDD | −6.59 | 7.65 | 9.47 | −7.57 | 7.87 | 9.92 | −6.01 | 7.51 | 9.33 |
| RX1day | −39.76 | 44.19 | 50.81 | −34.93 | 39.73 | 46.33 | −31.43 | 39.75 | 47.09 |
| R3day | −31.09 | 38.64 | 47.22 | −25.89 | 36.07 | 43.84 | −21.66 | 37.99 | 48.15 |
| RX5day | −28.92 | 38.19 | 48.72 | −24.49 | 37.33 | 47.29 | −19.91 | 37.62 | 49.22 |
| R10mm | 20.00 | 22.27 | 24.99 | 17.12 | 20.34 | 22.77 | 26.27 | 27.37 | 30.34 |
| R20mm | −14.09 | 14.21 | 15.45 | −14.48 | 14.54 | 15.80 | −11.77 | 12.11 | 13.55 |
| R25mm | −12.26 | 12.26 | 13.23 | −12.22 | 12.22 | 13.11 | −11.16 | 11.18 | 12.23 |
| R95P | −44.48 | 70.05 | 88.43 | −36.09 | 66.21 | 84.60 | −13.28 | 68.18 | 88.06 |
| R99P | −16.56 | 33.04 | 42.16 | −10.66 | 30.75 | 39.49 | −2.70 | 32.90 | 45.21 |
| NorESM1-M Model | GFDL-ESM2M Model | |||||
|---|---|---|---|---|---|---|
| MBE | MAE | RMSE | MBE | MAE | RMSE | |
| CWD | 43.32 | 43.32 | 43.98 | 44.73 | 44.73 | 45.57 |
| SDII | −6.87 | 6.87 | 7.47 | −6.86 | 6.87 | 7.48 |
| CDD | −5.11 | 7.59 | 9.57 | −4.32 | 6.97 | 8.95 |
| RX1day | −36.27 | 40.92 | 48.04 | −34.95 | 38.91 | 46.24 |
| R3day | −28.02 | 37.13 | 45.19 | −25.89 | 35.08 | 44.26 |
| RX5day | −23.76 | 37.45 | 46.96 | −22.10 | 37.99 | 47.75 |
| R10mm | 16.38 | 19.30 | 21.80 | 17.89 | 20.92 | 24.43 |
| R20mm | −13.95 | 14.03 | 15.33 | −13.39 | 13.80 | 15.05 |
| R25mm | −12.02 | 12.02 | 12.96 | −11.62 | 11.65 | 12.67 |
| R95P | −43.05 | 69.39 | 87.67 | −34.84 | 68.56 | 85.09 |
| R99P | −11.69 | 30.74 | 40.38 | −9.27 | 29.95 | 38.88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attogouinon, A.; Lawin, A.E.; Deliège, J.-F. Evaluation of General Circulation Models over the Upper Ouémé River Basin in the Republic of Benin. Hydrology 2020, 7, 11. https://doi.org/10.3390/hydrology7010011
Attogouinon A, Lawin AE, Deliège J-F. Evaluation of General Circulation Models over the Upper Ouémé River Basin in the Republic of Benin. Hydrology. 2020; 7(1):11. https://doi.org/10.3390/hydrology7010011
Chicago/Turabian StyleAttogouinon, André, Agnidé E. Lawin, and Jean-François Deliège. 2020. "Evaluation of General Circulation Models over the Upper Ouémé River Basin in the Republic of Benin" Hydrology 7, no. 1: 11. https://doi.org/10.3390/hydrology7010011
APA StyleAttogouinon, A., Lawin, A. E., & Deliège, J.-F. (2020). Evaluation of General Circulation Models over the Upper Ouémé River Basin in the Republic of Benin. Hydrology, 7(1), 11. https://doi.org/10.3390/hydrology7010011





