Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows
Abstract
1. Introduction
- Sensitivity analysis for assessing the necessity of bias correcting various climate variables when using climate scenario data as input for hydrological models.
- Projecting future changes in high flow parameters in six medium-scale catchments in the Northwestern part of Germany.
- Evaluating the performance of BC methods of different complexity.
2. Data and Study Area
2.1. Climatological Data
2.1.1. Observational Data
2.1.2. Coordinated Downscaling Experiment for Europe (CORDEX) Data
2.2. Study Area
3. Methods
3.1. General Procedure
3.2. Hydrological Model PANTA RHEI
Calibration and Validation
3.3. Sensitivity Analysis for Climate Variables
3.4. Bias Correction for Hydrological Modeling
3.4.1. Linear Scaling
3.4.2. Local Intensity Scaling (LOCI)
3.4.3. Power Transformation
3.4.4. Distribution Mapping
3.4.5. Inter-Sectoral Impact-Model Intercomparison Project (ISI-MIP) Approach
3.4.6. Delta Change
3.5. Evaluation of Bias-Correction Methods
4. Results
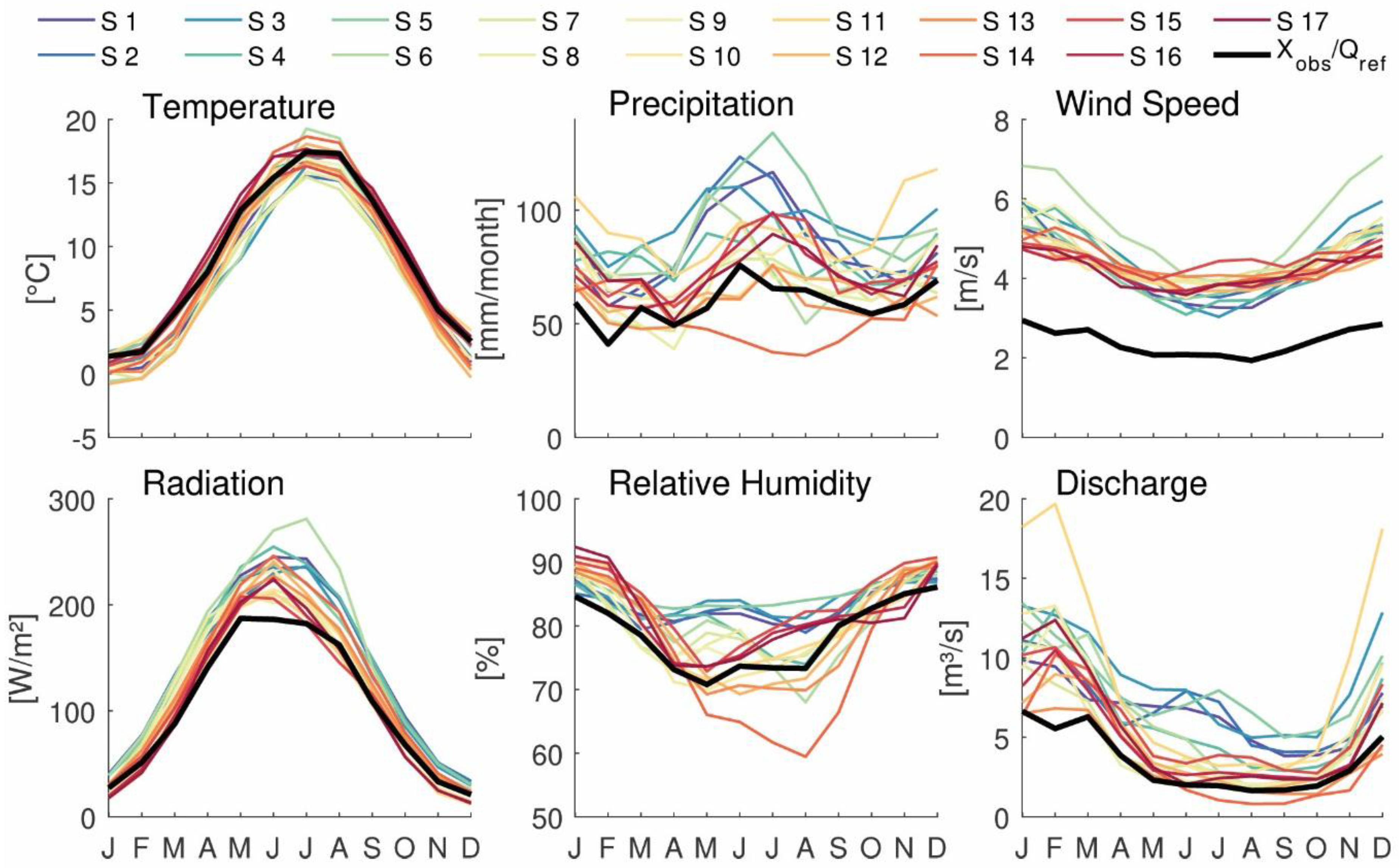
4.1. Climatological and Hydrological Bias in the Historical Period
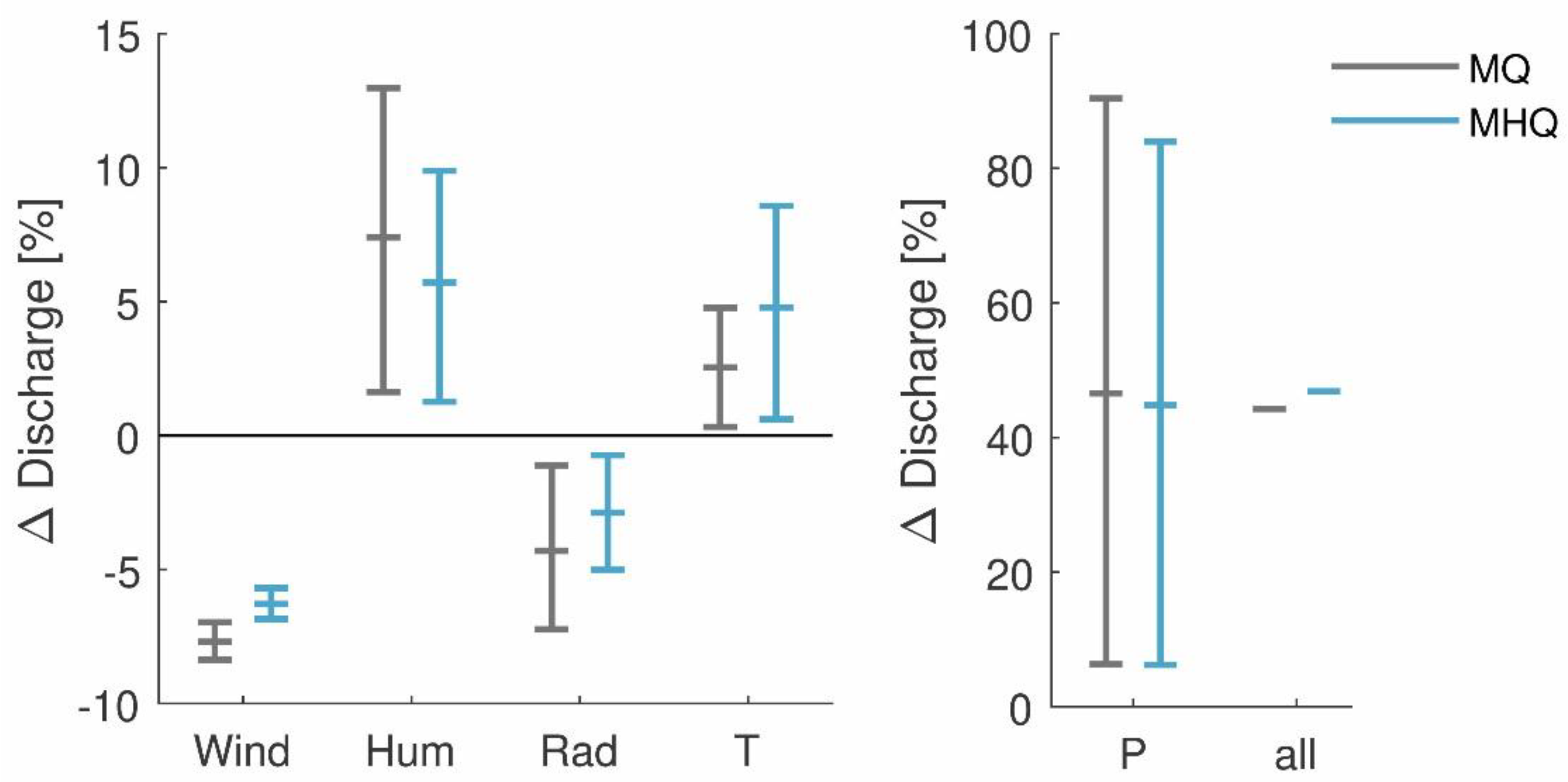
4.2. Sensitivity of Simulated Discharge against Biases in CORDEX Data
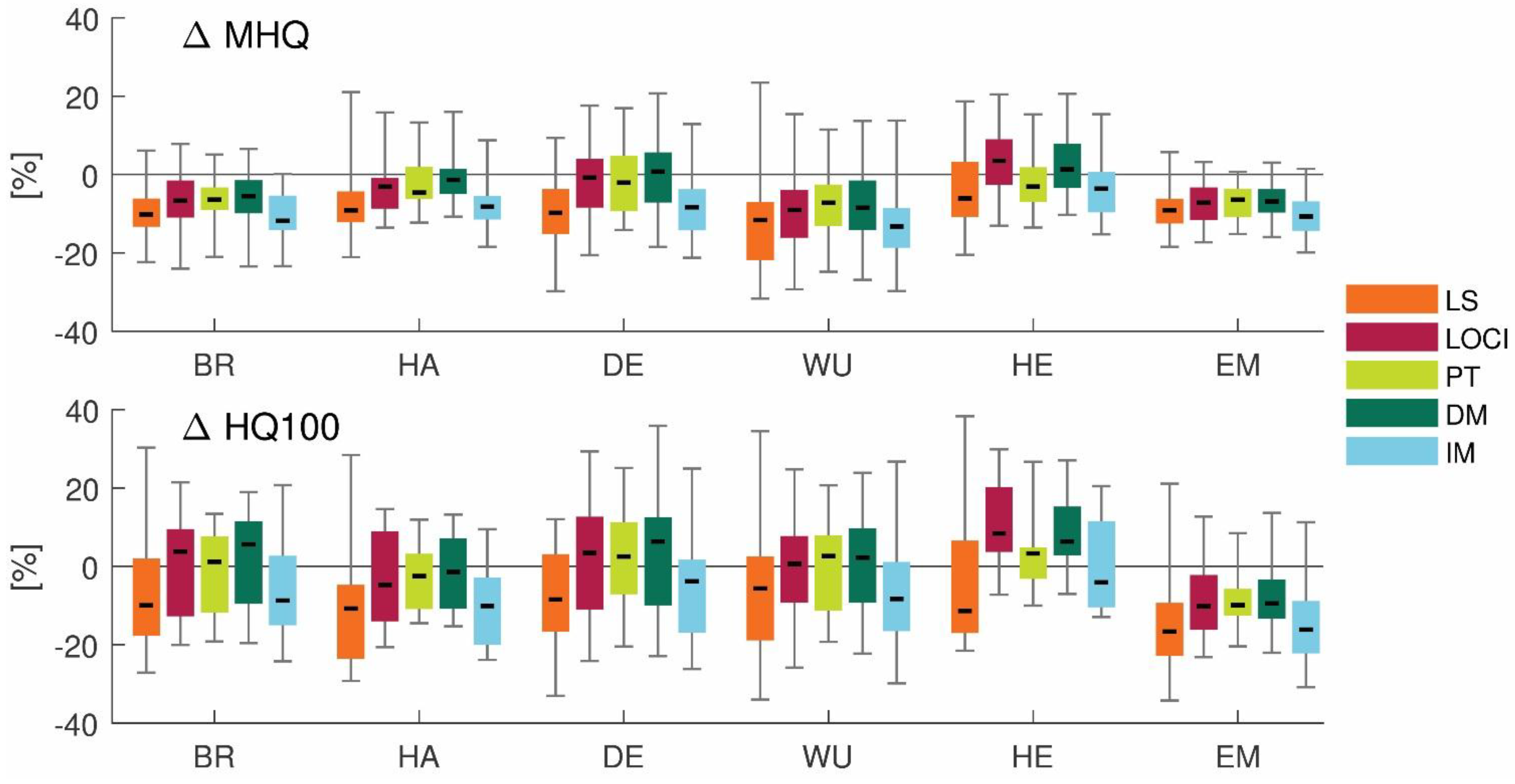
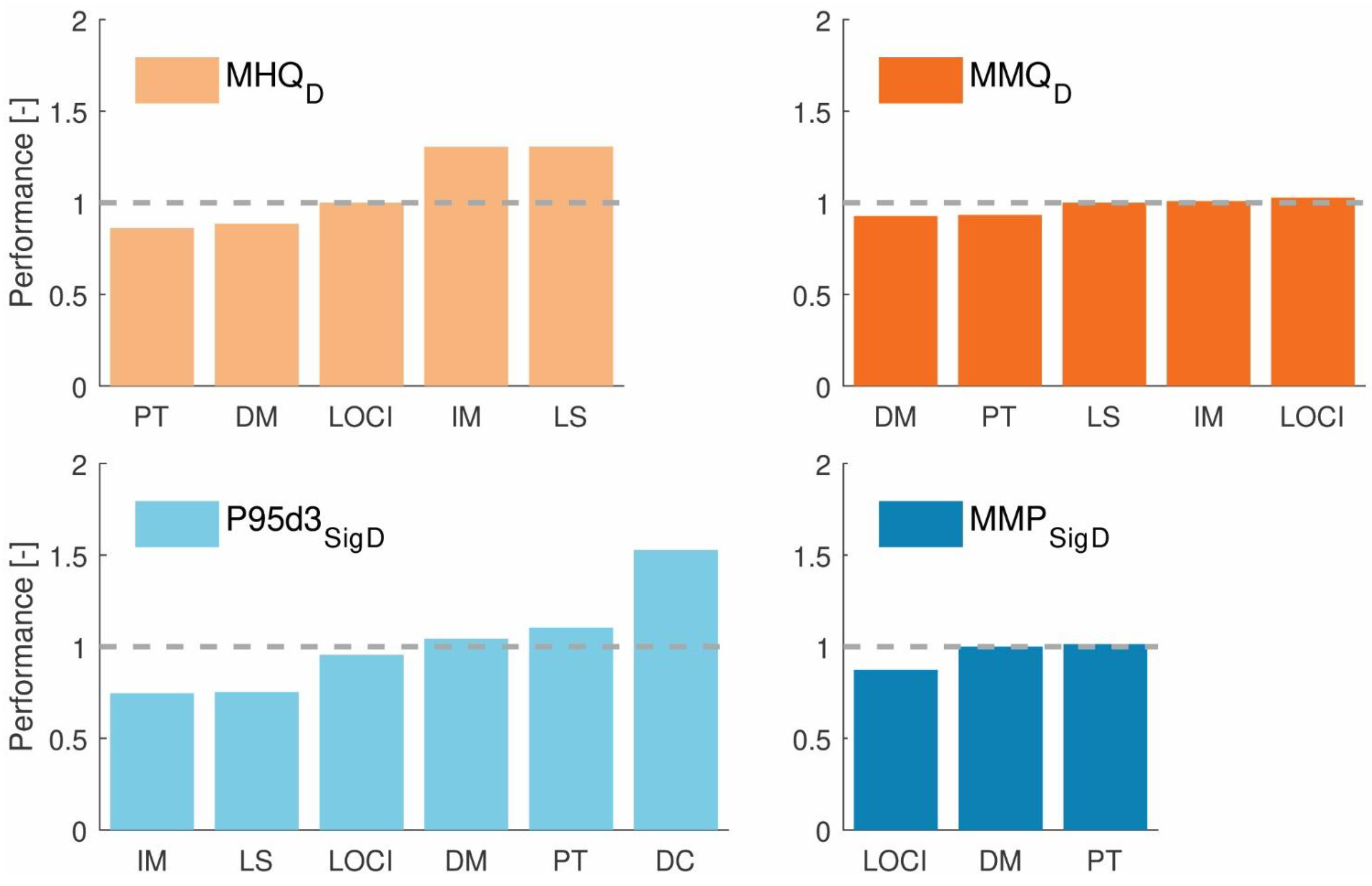
4.3. Effects of Bias Correction on High Flow Simulation during the Historical Period
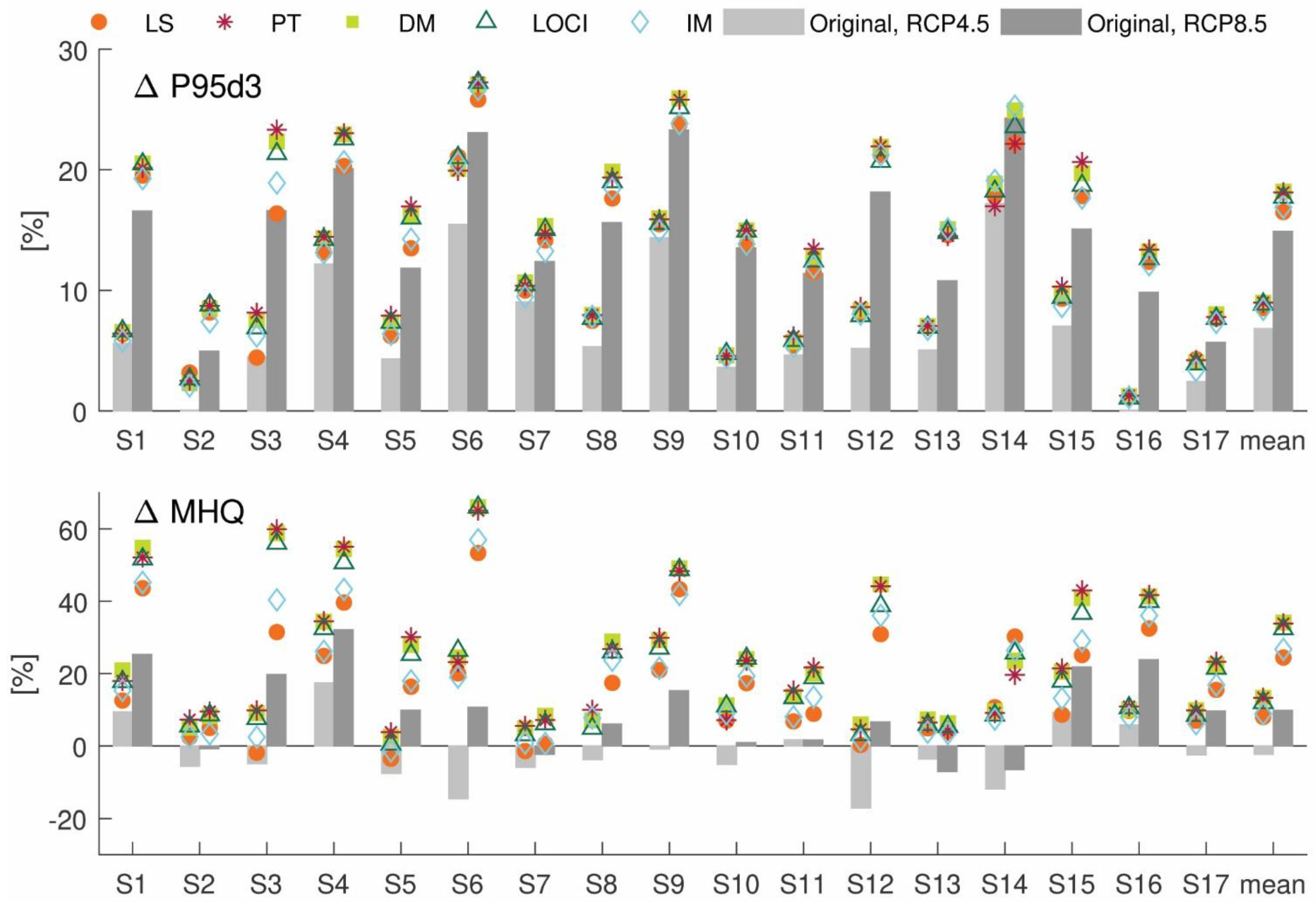
4.4. Impact of Bias Correction on the Future Projections of Precipitation and Discharge
4.5. Evaluation of Climate Scenarios
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachaur, R.K., Meyer, L.A., Eds.; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014; ISBN 978-92-9169-143-2. [Google Scholar]
- Pendergrass, A.G.; Hartmann, D.L. Changes in the Distribution of Rain Frequency and Intensity in Response to Global Warming. J. Clim. 2014, 27, 8372–8383. [Google Scholar] [CrossRef]
- Dai, A.; Rasmussen, R.M.; Liu, C.; Ikeda, K.; Prein, A.F. A new mechanism for warm-season precipitation response to global warming based on convection-permitting simulations. Clim. Dyn. 2017, 321, 1481. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.M.; Ikeda, K.; Liu, C.; Clark, M.P.; Holland, G.J. The future intensification of hourly precipitation extremes. Nat. Clim. Change 2017, 7, 48–52. [Google Scholar] [CrossRef]
- Alfieri, L.; Dottori, F.; Betts, R.; Salamon, P.; Feyen, L. Multi-Model Projections of River Flood Risk in Europe under Global Warming. Climate 2018, 6, 6. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Kundzewicz, Z.W.; Huang, S.; Vetter, T.; Gerstengarbe, F.-W.; Werner, P. Climatological drivers of changes in flood hazard in Germany. Acta Geophys. 2013, 61, 463–477. [Google Scholar] [CrossRef]
- NLWKN. Globaler Klimawandel—Wasserwirtschaftliche Folgen für das Binnenland. Gesamtbericht des Projektes KliBiW Themenbereich Hochwasser; NLWKN: Norden, Germany, 2017. [Google Scholar]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should we apply bias correction to global and regional climate model data?”. Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
- Rauscher, S.A.; Coppola, E.; Piani, C.; Giorgi, F. Resolution effects on regional climate model simulations of seasonal precipitation over Europe. Clim. Dyn. 2010, 35, 685–711. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- NLWKN. Globaler Klimawandel—Wasserwirtschaftliche Folgen für das Binnenland. Niedrigwasser; NLWKN: Norden, Germany, 2014. [Google Scholar]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Hattermann, F.F. Does bias correction increase reliability of flood projections under climate change? A case study of large rivers in Germany. Int. J. Climatol. 2014, 34, 3780–3800. [Google Scholar] [CrossRef]
- Teng, J.; Potter, N.J.; Chiew, F.H.S.; Zhang, L.; Wang, B.; Vaze, J.; Evans, J.P. How does bias correction of regional climate model precipitation affect modelled runoff? Hydrol. Earth Syst. Sci. 2015, 19, 711–728. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Bolton, D. The Computation of Equivalent Potential Temperature. Mon. Wea. Rev. 1980, 108, 1046–1053. [Google Scholar] [CrossRef]
- Smiatek, G.; Kunstmann, H.; Senatore, A. EURO-CORDEX regional climate model analysis for the Greater Alpine Region: Performance and expected future change. J. Geophys. Res. Atmos. 2016, 121, 7710–7728. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Riedel, G.; Lichtenberg, T. Panta Rhei User Manual; Department of Hydrology, Water Management and Water Protection of TU Braunschweig: Braunschweig, Germany; Institut für Wassermanagement IfW: Braunschweig, Germany, 2017. [Google Scholar]
- Kreye, P. Mesoskalige Bodenwasserhaushaltsllierung mit Nutzung von Grundwassermessungen und satellitenbasierten Bodenfeuchtedaten. Ph.D. Thesis, University of Braunschweig, Braunschweig, Germany, 2015. [Google Scholar]
- Meon, G.; Pätsch, M.; van Phuoc, N.; Hong Quan, N. EWATEC-COAST: Technologies for Environmental and Water Protection of Coastal Regions in Vietnam. Contribution to 4th International Conference for Environment and Natural Resources – ICENR, Ho-Chi-Minh City, Vietnam, 17–18 June 2014; Cuvillier: Göttingen, Germany, 2014. [Google Scholar]
- Riedel, G.; Anhalt, M.; Meyer, S.; Weigl, E.; Meon, G. Erfahrung mit Radarprodukten bei der operationellen Hochwasservorhersage in Niedersachsen. KW - Korrespondenz Wasserwirtschaft 2017, 11, 664–671. [Google Scholar]
- Gelleszun, M.; Kreye, P.; Meon, G. Representative parameter estimation for hydrological models using a lexicographic calibration strategy. J. Hydrol. 2017, 553, 722–734. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A. Resampling of regional climate model output for the simulation of extreme river flows. J. Hydrol. 2007, 332, 487–496. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction—The ISI-MIP approach. Earth Syst. Dynam. 2013, 4, 219–236. [Google Scholar] [CrossRef]
- Räty, O.; Räisänen, J.; Ylhäisi, J.S. Evaluation of delta change and bias correction methods for future daily precipitation: Intermodel cross-validation using ENSEMBLES simulations. Clim. Dyn. 2014, 42, 2287–2303. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- O’Gorman, P.A.; Muller, C.J. How closely do changes in surface and column water vapor follow Clausius–Clapeyron scaling in climate change simulations? Environ. Res. Lett. 2010, 5, 25207. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]

| Institution → | SMHI | IPSL-INERIS | KNMI | DMI | CLMcom | MPI-CSC |
|---|---|---|---|---|---|---|
| GCM ↓ RCM → | RCA4 | WRF331F | RACMO22E | HIRHAM5 | CCLM | REMO2009 |
| CNRM_CM5 | S1 | S12 | ||||
| EC-Earth | S2 | S7, S8 | S10 | S13 | ||
| IPSL-CM5A-MR | S3 | S6 | ||||
| HadGEM2-ES | S4 | S9 | S14 | |||
| MPI-ESM-LR | S5 | S15 | S16, S17 | |||
| NorESM1-M | S11 |
| Scenario | ∆T [°C] | ∆P [%] | ∆P95 [%] | ∆P95d3 [%] | ∆WD1 [%] | ∆Wind [%] | ∆Rad [%] | ∆Hum [%] | ∆MQ [%] | ∆MHQ [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | −1.3 | 38.1 | 3.2 | 8.1 | 33.0 | 94.1 | 31.3 | 6.8 | 67.4 | 39.9 |
| S2 | −1.6 | 40.6 | 4.2 | 10.7 | 34.5 | 105.8 | 29.3 | 6.1 | 74.4 | 52.5 |
| S3 | −1.4 | 54.7 | −1.4 | 5.2 | 52.1 | 112.2 | 22.5 | 7.3 | 122.9 | 72.5 |
| S4 | −0.3 | 29.9 | 0.6 | 5.8 | 25.7 | 100.8 | 30.7 | 4.8 | 60.0 | 40.4 |
| S5 | −0.2 | 56.7 | 7.6 | 13.3 | 42.9 | 103.2 | 24.5 | 8.7 | 110.2 | 65.6 |
| S6 | −1.1 | 30.5 | −0.3 | 1.4 | 28.1 | 143.2 | 36.4 | 0.8 | 52.4 | 67.1 |
| S7 | −2.1 | 10.3 | −14.2 | −9.8 | 20.1 | 122.0 | 12.5 | 2.8 | 24.8 | 33.0 |
| S8 | −1.6 | 10.0 | −15.5 | −10.5 | 20.0 | 123.6 | 14.2 | 2.0 | 26.6 | 26.3 |
| S9 | −1.0 | 12.0 | −10.0 | −7.4 | 18.0 | 122.5 | 15.1 | 2.3 | 36.9 | 44.9 |
| S10 | −1.1 | 22.3 | 1.3 | 4.4 | 18.8 | 101.7 | 3.5 | 1.6 | 56.3 | 63.8 |
| S11 | 0.0 | 48.5 | 6.4 | 11.2 | 38.1 | 106.4 | −2.5 | 3.7 | 121.4 | 105.1 |
| S12 | −1.4 | 3.6 | −9.0 | −10.4 | 10.7 | 95.7 | 13.7 | 2.7 | 11.5 | 16.1 |
| S13 | −1.4 | −3.9 | −7.9 | −9.3 | 3.4 | 107.0 | 14.5 | 1.0 | −4.6 | 3.7 |
| S14 | −0.3 | −14.6 | −12.6 | −13.7 | −6.2 | 105.3 | 19.2 | −2.8 | −3.0 | 18.9 |
| S15 | −0.6 | 22.6 | −5.6 | −5.1 | 24.5 | 112.3 | 4.1 | 6.8 | 52.6 | 18.4 |
| S16 | 0.3 | 20.3 | −5.4 | −2.0 | 22.6 | 93.4 | 0.9 | 4.4 | 34.5 | 28.4 |
| S17 | 0.6 | 22.3 | −6.9 | −1.6 | 25.2 | 94.9 | 0.8 | 4.2 | 44.3 | 38.5 |
| Mean | −0.8 | 23.8 | −3.9 | −0.6 | 24.2 | 108.5 | 15.9 | 3.7 | 52.3 | 43.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wörner, V.; Kreye, P.; Meon, G. Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows. Hydrology 2019, 6, 46. https://doi.org/10.3390/hydrology6020046
Wörner V, Kreye P, Meon G. Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows. Hydrology. 2019; 6(2):46. https://doi.org/10.3390/hydrology6020046
Chicago/Turabian StyleWörner, Vanessa, Phillip Kreye, and Günter Meon. 2019. "Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows" Hydrology 6, no. 2: 46. https://doi.org/10.3390/hydrology6020046
APA StyleWörner, V., Kreye, P., & Meon, G. (2019). Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows. Hydrology, 6(2), 46. https://doi.org/10.3390/hydrology6020046




