3.1. Model Performance Evaluation: Mathematical Test Functions
The CSS algorithm has previously been tested with some mathematical tests and structural optimization problems in the original reference [
41]. However, water resources management problems are more complex than structural problems and require a higher level of robustness in utilized approaches. In order to assess the performance of the proposed algorithm in complex and nonlinear problems in the field of water resources management, it is first applied to benchmark constrained and unconstrained mathematical optimization functions. For evaluation of robustness of the standard CSS algorithm and also assess the impact of utilizing the new method of updating on performance of the algorithm (called Enhanced CSS or ECSS in this section) [
45], the functions are optimized with both standard CSS and ECSS.
Although value of 0.5 for both tunable coefficients in Equation (7) (i.e., α and β) have been recommended in the reference paper of the CSS algorithm [
41], different values may result in better solutions. A sensitivity analysis for mathematical test functions shows that the value of 0.8 for these coefficients results in better solutions and increases the convergence rate of the algorithm. The best, worst, mean and standard deviation of the results are reported for 10 different runs of the algorithm for each of the mathematical test functions.
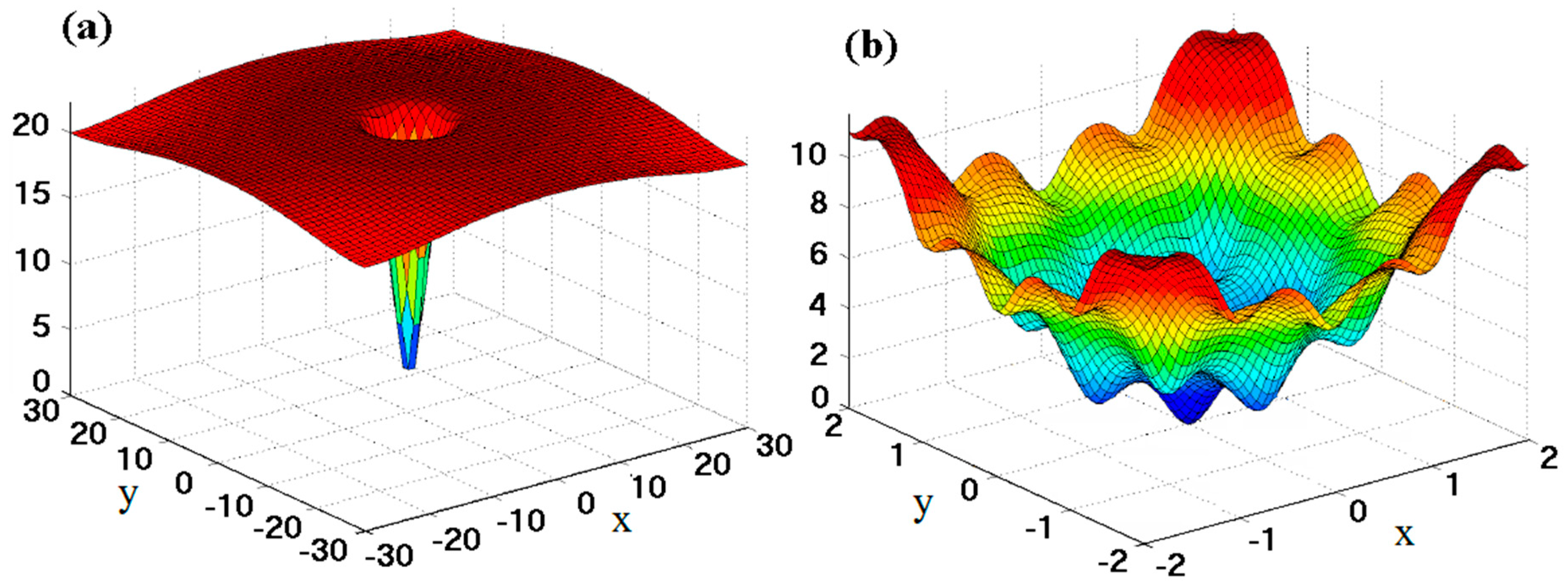
The first optimization problem is the Ackley’s function [
47], a continuous and multi-modal function defined by modulating an exponential function with a cosine wave of moderate amplitude. Ackley’s function is defined as:
where
c1 = 20,
c2 = 0.2,
c3 = 2
π and
n is taken equal to 2 here. The functions surface is a nearly flat outer region with moderate fluctuations converging to a hole in the middle. Multiple hills and valleys on the surface cause moderate complexity for optimization methods, as the search algorithms performing based on hill-climbing techniques are most likely to be trapped in local optima (
Figure 1). An algorithm with a large scanning span that searches a wider neighborhood would be able to avoid the valleys and located better optima. Therefore, Ackley’s function provides one of the reasonable test cases for the CSS algorithm. The results obtained by the CSS and ECSS algorithms as well as those obtained by Genetic Algorithm (GA) [
48], Honey-Bees Mating Optimization algorithm (HBMO) [
49] and Particle Swarm Optimization algorithm (PSO) [
50] are presented in
Table 1. The results for CSS and ECSS shown in
Table 1 are best out of ten runs of the algorithms. The ECSS algorithm with 10 CPs, reaches the fitness value of 2 × 10
6 after 440 function evaluations (44 iterations with 10 CPs) and the best fitness value of 0 (global optimum) after 930 function evaluations in the best run of the algorithm. Results show that all ten executions of the algorithms reach quite close to the global optimum value of the objective function, where the standard deviation of the objective function value over ten runs is 1.6 × 10
−15 for the CSS and 1.4 × 10
−15 for the ECSS.
Table 1 demonstrates the impact of using the new method of updating in the structure of the algorithm on the convergence rate of the algorithm, as ECSS shows higher convergence speed compared to the standard CSS. The table denotes that the CSS algorithm obtains more accurate values in smaller number function evaluations in comparison with the other metaheuristic rivals, in terms of accuracy and convergence speed.
The second numerical example is an unconstrained sine function defined as [
48]:
As seen in
Figure 2a, the search space for this function is a highly non-linear and multi-modal surface. The ECSS algorithm with 30 CPs reached the best fitness value of 38.85029 after 1590 function evaluations (53 iterations with 30 CPs). The results obtained by the CSS and ECSS algorithms as well as those obtained by GA [
48], HBMO [
49] and PSO [
50] are presented in
Table 2. The results for CSS and ECSS shown in
Table 2 are best out of ten runs of the algorithms. Results show that the standard deviation of objective function value is approximately zero, indicating that all 10 runs have converged to approximately one single solution. As seen from the
Table 2, the CSS algorithm performs considerably faster comparing to the other rival approaches, where the CSS and ECSS algorithms locate the optima with 1950 and 1590 times function evaluations, respectively.
To assess the performance of the CSS algorithm in handling constrained problems, a two-variable, two-constraint constrained exponential function is considered [
49], defined as (
Figure 2b):
Subject to:
The unconstrained objective function f (x1, x2) has a minimum solution at (3, 2) with a function value equal to zero. However, due to multiple constraints imposed to the function, this solution is not feasible and the constrained optimal solution is x = (2.2461, 2.3815) with a function value equal to f = 13.61227. The feasible region is only approximately 0.7% of the total search space, which is a narrow crescent-shaped region, and the optimum solution is lying on the second constraint.
Employing the ECSS algorithm with 20 CPs, the best obtained fitness value is 13.59087 at x = (2.23809,2.24677) after 600 function evaluations (30 iterations with 20 CPs). Results obtained by the CSS and ECSS algorithms as well as those obtained by GA [
48], HBMO [
49] and PSO [
50] are presented in
Table 3. The results for CSS and ECSS shown in
Table 3 are the best out of ten runs of the algorithms. All ten runs show a very small discrepancy with the global result as indicated by a very small value of the standard deviation. However, the ECSS reaches the global optima with less function evaluations. As seen in
Table 3, the ECSS algorithm finds the optima with considerably less function evaluations comparing the other metaheuristic approaches.
The last test function used for investigation of performance of the CSS algorithm facing highly non-linear multi-variable problems is the well-known multimodal and continuous Fletcher–Powell function [
47], which is a non-separable, non-linear, and irregular function, described as:
where
xj is the decision variable,
αj is a random coefficient within the range of –π and π,
aij and
bij are random coefficients within the range of −100 and 100, and
n is the dimension of the function (
Figure 3). The optimum point of the function is at
xj =
αj where the objection function value will be equal to zero. A 30-variable Fletcher–Powell function is chosen here to be optimized utilizing the CSS algorithm. The ECSS algorithm with 20 CPs, reaches the fitness value of 1246.37 after 2E5 function evaluations and the best fitness value of 440.29 after 2E6 function evaluations in the best run of the algorithm. The results obtained by ECSS algorithm as well as those obtained by the GA [
48], HBMO [
49], PSO [
50] and Nonlinear Programing (NLP) using LINGO 8.0 software [
49] are presented in
Table 4. The ECSS algorithm obtains more optimum values in smaller number function evaluations in comparison with the other metaheuristic rivals. However, due to complexity of the Fletcher–Powell function, the algorithm does not converge to optimal values at every attempt, as shown by a fairly large standard deviation value of 8805.65, for 10 runs of the algorithm. Multiple runs of the algorithm are needed to obtain the best optima achievable by the approach, as also seen in other algorithms [
49].
Results demonstrate that the standard CSS algorithm without any improvements is a robust and fast convergent approach which outperformed its other metaheuristic rivals in optimization of complex and multimodal mathematical functions and seems to be capable of handling the highly nonlinear and non-convex problem of large-scale reservoir operation. Results also indicate that utilizing the new method of updating in the structure of algorithm, referred here as enhanced CSS or ECSS, improves its convergence speed. The remainder of this paper presents application of the new approach in water supply and hydropower reservoir operation problems. In all reservoir operation problems presented in the next sections, the enhanced CSS algorithm is utilized and will simply be called the CSS algorithm.
3.2. Reservoir Operation Case Study
To evaluate the performance of the CSS algorithm in solution of large-scale water resources management problems, water-supply and hydropower operation of “Dez” reservoir in southern Iran has been considered. Total storage capacity of “Dez” reservoir in pre-defined normal water level is 2510 MCM and the average inflow of the reservoir over 40 years period from 1970–2010 is 5900 MCM. The initial storage of the reservoir is taken equal to 1430 MCM. The maximum and minimum allowable storage volumes are set equal to 3340 and 830 MCM, respectively. The maximum and minimum monthly water release set equal to 1000 MCM and zero, respectively. The coefficients of the volume-elevation curve defined by Equation (19) are used as: a = 249.83364, b = 0.58720, c = −1.37 × 10−5 and d = 1.526 × 10−9. The total installed capacity of hydroelectric power plant of the Dez reservoir is 650 MW, being operated with plant factor of 0.417 and 90% efficiency. The tail water level in downstream is assumed constant at 172 m above sea level.
These problems are solved here using the CSS algorithm for optimal monthly operation over 5, 20 and 40-year time spans, which are 60, 240 and 480 monthly periods, respectively. The water-supply operation and hydropower operation problems are solved using the CSS algorithm, separately, and results are shown for each operation type. The parameters of acceleration (ka) and velocity (kv) coefficients in Equation (7) are taken as 0.3, 0.3 and 0.5 for the 60, 240 and 480-month operational period problems, respectively, obtained via a tuning procedure. Tests show that for best results in reservoir operation optimization utilizing the CSS algorithm, the charged sphere radius (a) in the Equation (2) should be set close to zero (1E9). All the results presented here are obtained using 40, 100 and 1000 CPs for the 60, 240 and 480-month problems, respectively. The number of objective function evaluations is limited to 400,000 for all executions of the algorithm.
The water-supply and hydropower operation of “Dez” reservoir is first solved disregarding the effect of evaporation from the reservoir utilizing the CSS. The results of 5 executions of the algorithm are presented in
Table 5. Disregarding evaporation, the NLP solver (LINGO 9.0) produces the objective function values of 20.6 and 45.4 for the hydropower operation over 240, and 480 periods [
37]. Disregarding evaporation, the value of 45.8 for 480 months hydropower operation of “Dez” reservoir, using the LINGO 9.0, was also reported by earlier studies [
34]. The CSS approach results in optimal solution of 21.4936 and 50.3394 for 240 and 480 period hydropower problems, respectively.
The water-supply and hydropower operation of “Dez” reservoir is then solved considering the evaporation losses from the surface on the storage volume of the reservoir (
Table 6). The inclusion of evaporation further increases the non-linearity of the model, in particular for the hydropower operation model for which the well-known LINGO NLP solver has failed to find a feasible solution for 240 and 480 operational periods, as previously reported [
46]. The LINGO NLP solver (LINGO 9.0) has yielded optimum solutions of 0.732, 4.77, and 10.50 for the water-supply problem for 60, 240, and 480 months [
46]. The LINGO NLP solver was able to locate a near-optimal solution of 7.37 for the hydropower operation over the shortest operation period of 60 months, but failed to yield any feasible solution for the longer operation periods of 240 and 480 months, which may be due to the non-convexity of the hydropower operation, which is even higher for the 240 and 480-month problem [
46]. Failure in finding a feasible solution for 480-period hydropower operation of “Dez” reservoir considering the evaporation from the reservoir, using the NLP method, was reported by other studies as well [
34].
Gradient-based nonlinear programming (NLP) methods solve problems that do not involve high level of nonlinearity in objective function and constraints. However, in models with large number of decision variables and/or highly nonlinearity, these approaches tend to fail in locating feasible solutions, or converge to local optima [
51]. In long-period reservoir operations, or in models with evaporation losses consideration, the non-linearity and non-convexity of the model rises and gradient-based NLP solvers may not be a suitable choice since they may either produce local suboptimal solutions and/or may even fail to locate any feasible solutions.
It can be seen from
Table 6 that in all short and long operation period of 60, 240 and 480 months, the CSS algorithm can yield the near-optimal solutions in both water-supply and hydropower operation models. In longer operation periods of 240 and 480 months for the water-supply operation model, the CSS algorithm results in objective function values of 2.7302 and 9.4263 respectively. Comparing the results of the CSS algorithm with those obtained by LINGO 9.0 NLP solver demonstrates that the CSS approach outperforms the NLP method with the solutions of 4.77 and 10.5 for 240 and 480-month operation periods, respectively. In 240 and 480-month hydropower operation, the CSS results in near optimal solutions with objective function values of 22.9670 and 54.3472, respectively. The NLP method fails in producing any feasible solution for these problems, as noted earlier. These results indicate robustness of the CSS algorithm to solve both convex and non-convex, small-scale and large-scale, reservoir-operation problems.
Table 7 presents the results obtained by genetic algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO) and Big Bang-Big Crunch (BB-BC) algorithm for the current Dez reservoir operation problem [
37,
46,
52]. Comparing the results of
Table 6 and
Table 7 shows that in all operation problems, these algorithm yield solutions inferior to those obtained by the CSS approach, with the difference being more significant for the longer operation periods. For the 480-month operations, the solutions yielded by the GA and PSO algorithms are significantly far from the optimal solution.
All 10 runs of the CSS algorithm for simple and hydropower operations have resulted in feasible solutions; while some of the other metaheuristic approaches failed in locating feasible solutions for all executions. These results can be compared with those obtained by the conventional Ant Colony Optimization Algorithm (ACO) [
52]. The results show that ACO was capable of producing 10 feasible solutions for the simplest case of water-supply operation over 60 monthly periods and 8 feasible solutions for the hydropower operation over 60 monthly periods. In longer operation periods, i.e., 240 and 480 monthly periods, the number of runs with a feasible solution decrease. For 240 monthly periods, only 8 and 7 feasible solutions were created for water-supply and hydropower operations, respectively while for 480 monthly periods, ACO was only capable of producing one feasible solution for both water-supply and hydropower operation.
Table 7 shows that while GA was unable to find a feasible solution for the longest operation period, the PSO algorithm could produce feasible solution only for the shortest operation period [
37,
52].
Results from improved metaheuristics such as a version of Big Bang-Big Crunch (BB-BC) algorithm improved for reservoir operation problems called Constrained Big Bang-Big Crunch (CBB-BC) algorithm [
37] as well as Fully Constrained Ant Colony Optimization Algorithm (FCACOA) [
52] also show the ability to locate feasible solutions in all 10 runs of the algorithms, with inferior results compared to the CSS algorithm. It should be noted that the number of objective function evaluations was limited to 400,000 for the CBB-BC algorithm as well [
37].
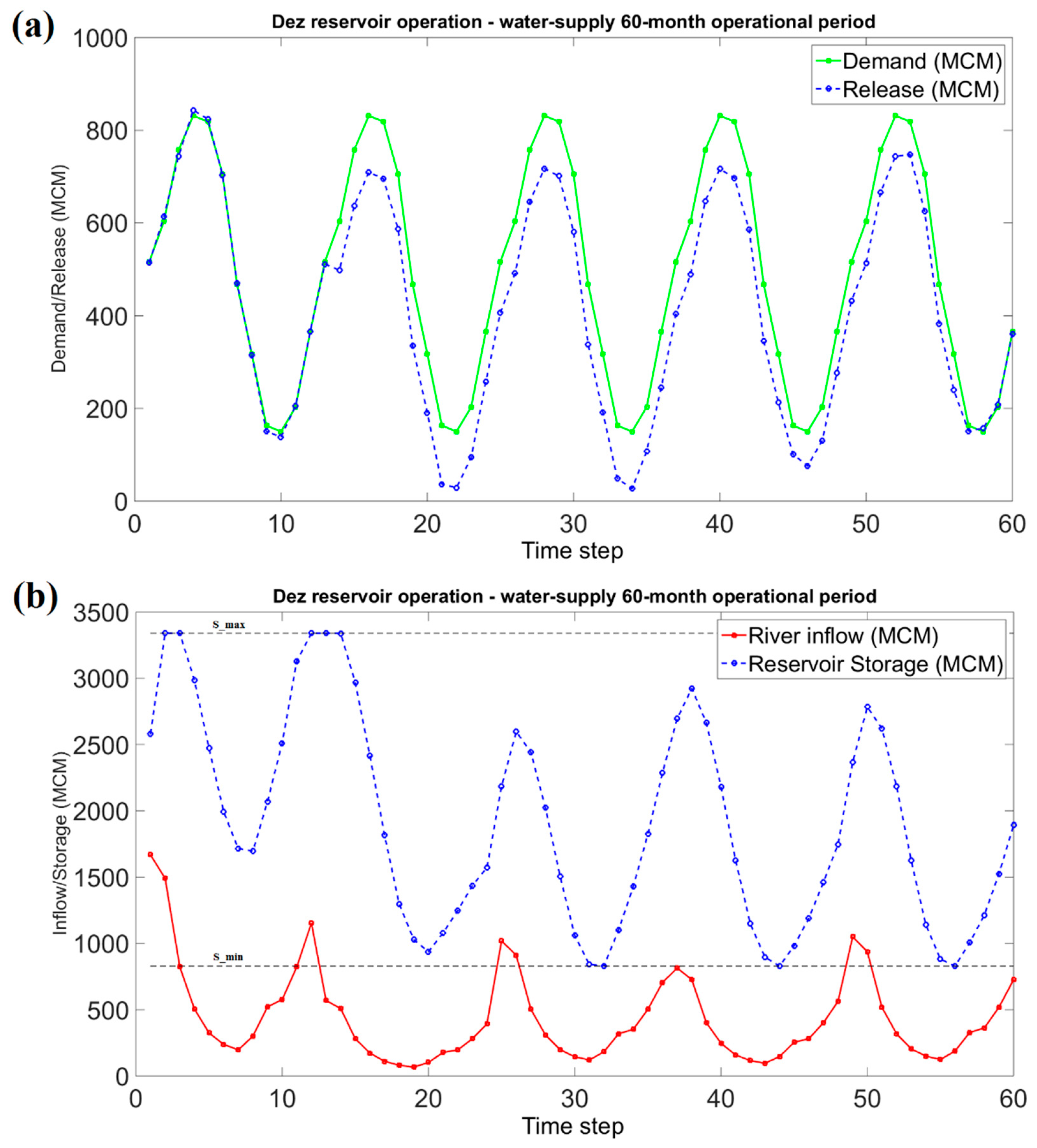
Figure 4a shows the best solution obtained by the CSS algorithm (monthly releases) for 60-month water-supply operation, considering evaporation losses, versus the monthly water demand defined by the problem.
Figure 4b illustrates the storage volume of the reservoir at each time step, calculated based on the releases ruled by the CSS algorithm and given river inflow. The
Figure 4 shows the storage volume at each time step is confined between maximum (S_max) and minimum (S_min) allowable storage, defined by the problem.
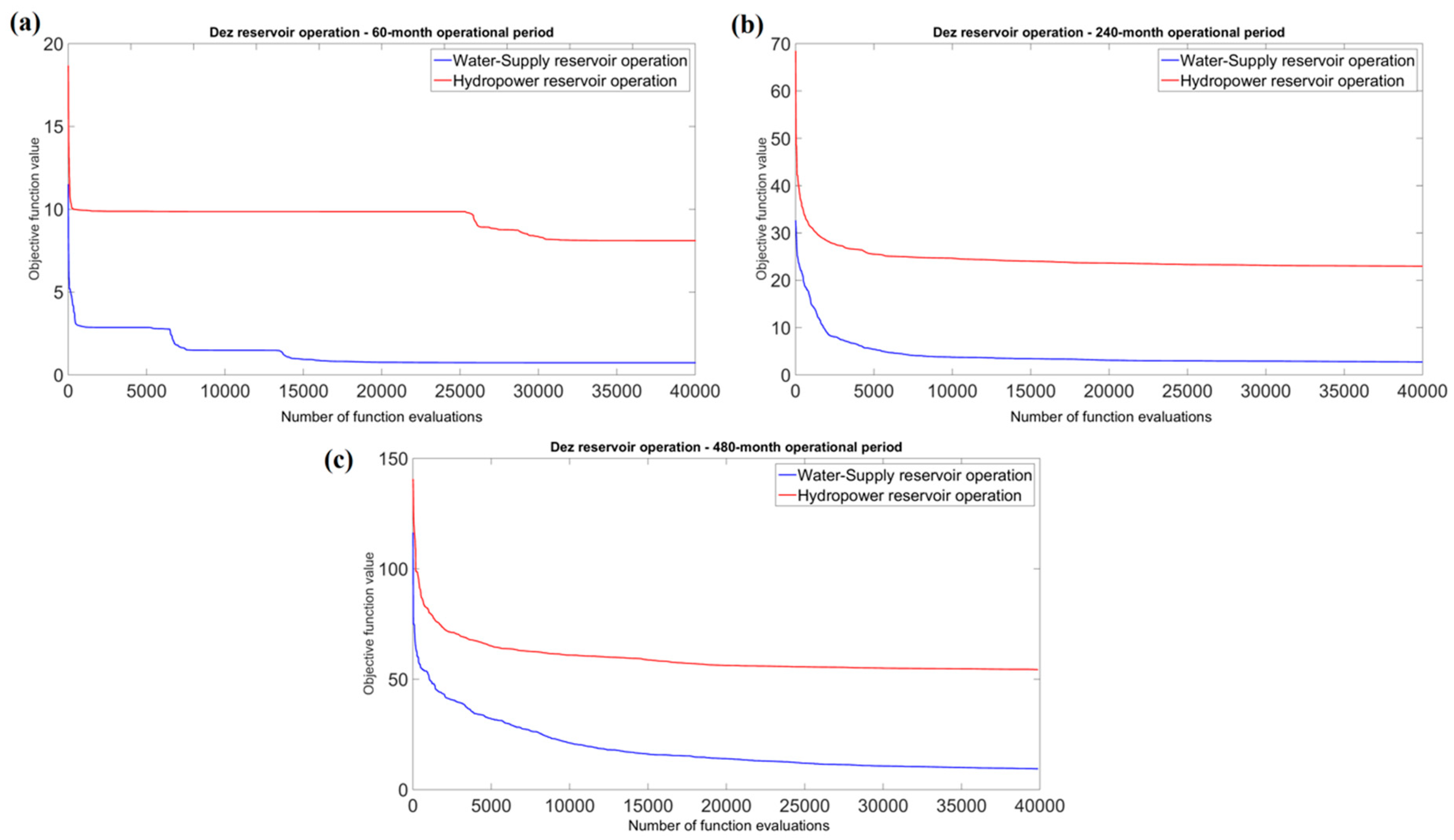
Figure 5 presents variation of the objective function value versus the number of function evaluations for the best solution obtained by the CSS algorithm for “Dez” reservoir water-supply and hydropower operation, over each operational period.