Evaluating Remote Sensing Model Specification Methods for Estimating Water Quality in Optically Diverse Lakes throughout the Growing Season
Abstract
1. Introduction
1.1. Background
1.2. Goals and Objectives
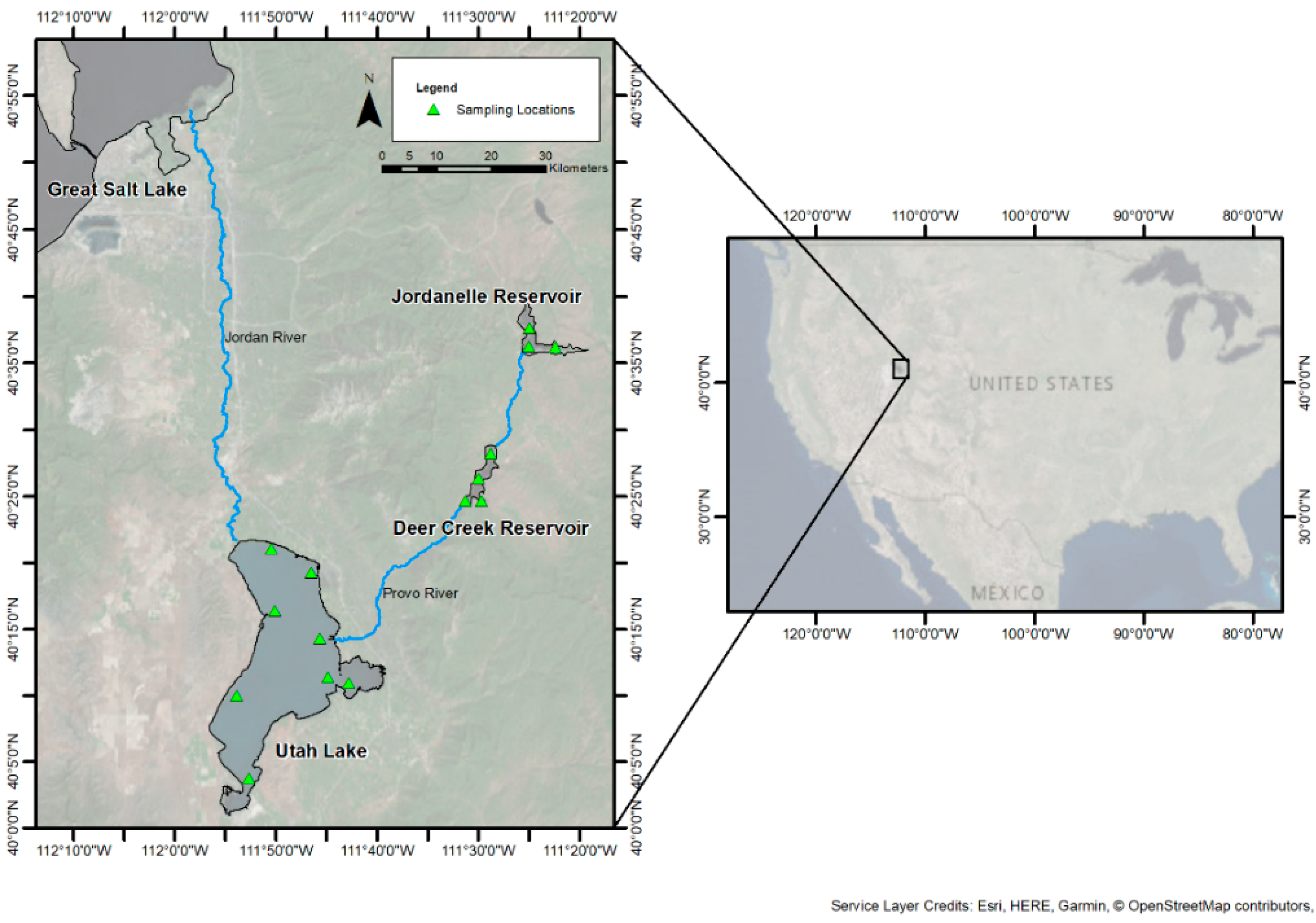
2. Study Area
2.1. Case Study Locations
2.2. Deer Creek Reservoir
2.3. Jordanelle Reservoir
2.4. Utah Lake
3. Methodology and Data
3.1. Data
3.2. Data Preparation
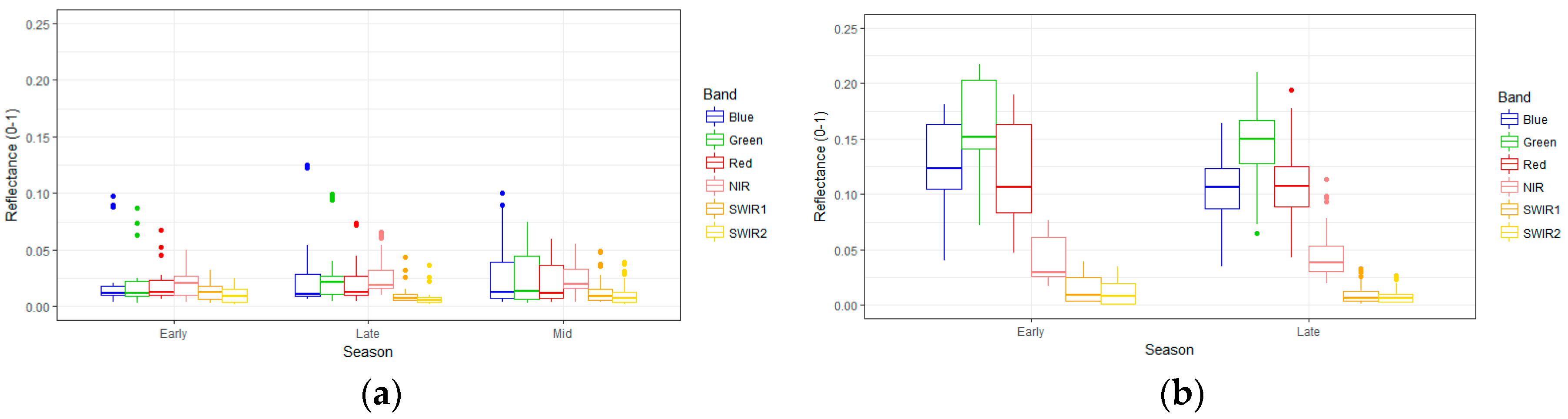
3.2.1. Field Data
3.2.2. Landsat Data
3.2.3. Field and Satellite Data Pairs
3.3. Multiple Linear Regression on Standard Forms
3.3.1. Overview of MLR and Coefficient Estimation
3.3.2. Select Algorithms for Evaluation
3.4. Statistical Learning–Multiple Linear Stepwise Regression
Overview of MLSR
4. Results
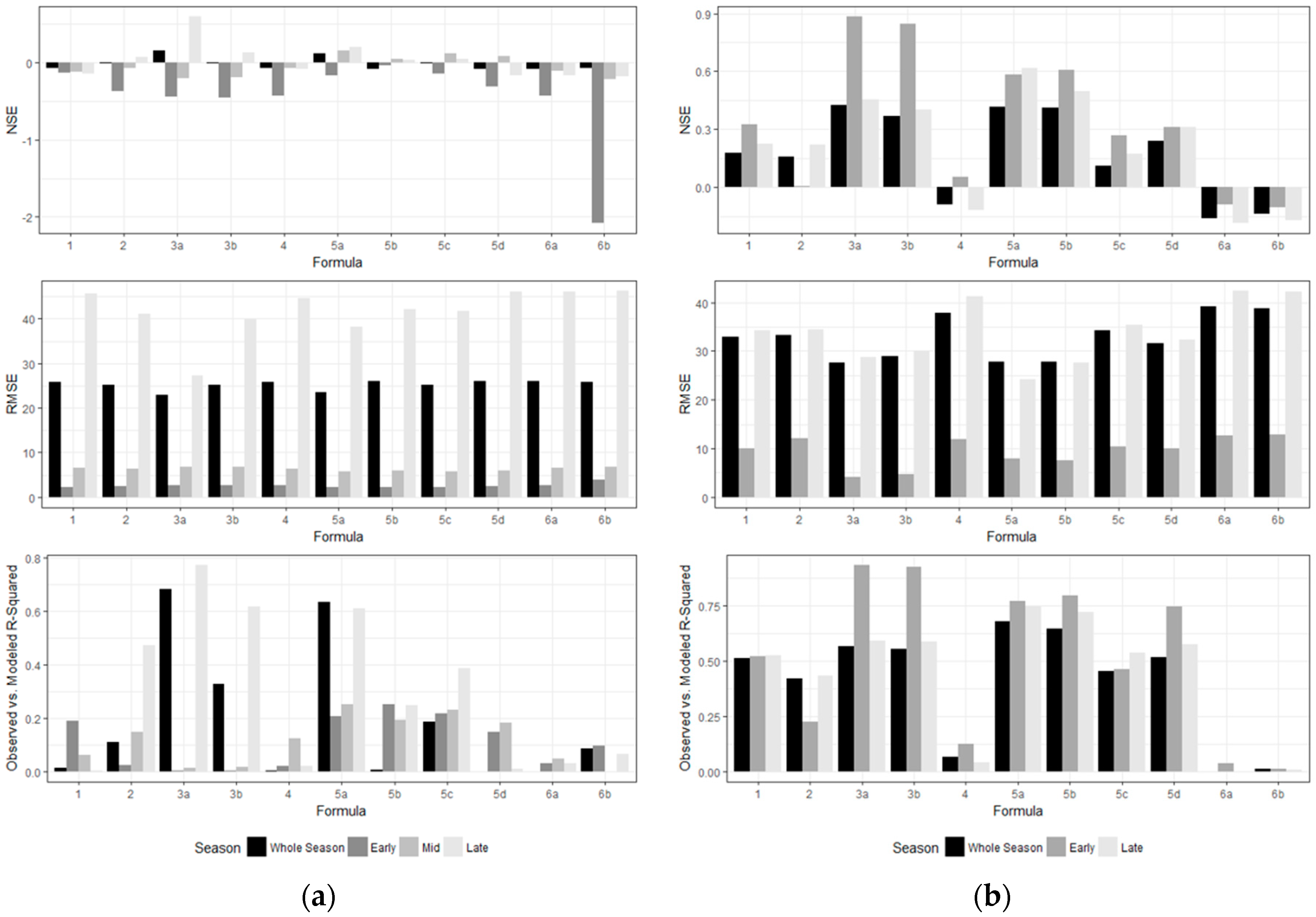
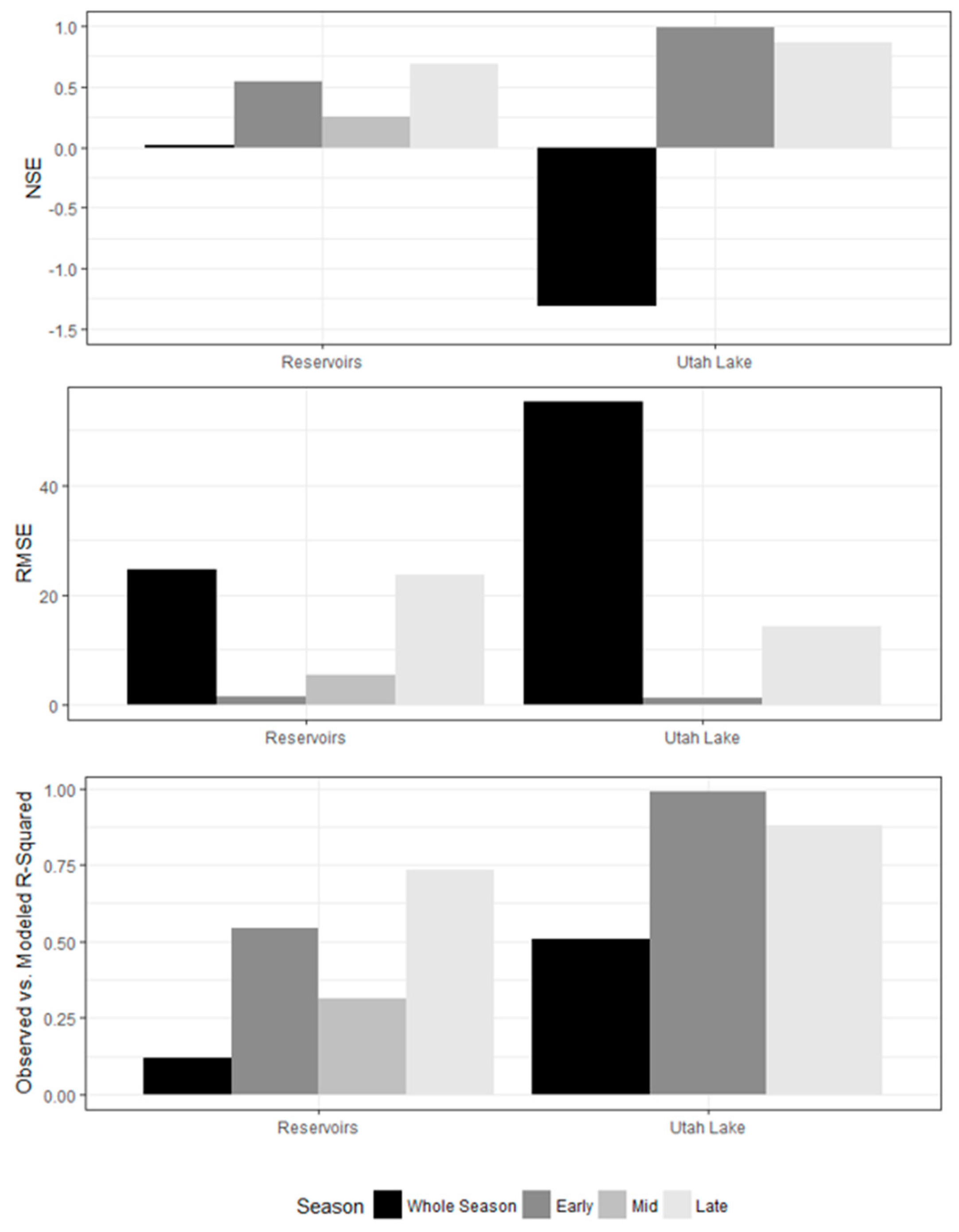
4.1. Single and Sub-Seasonal MLR Model Performance
4.2. Sub-Seasonal MLSR Models and Model Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Region | Season | Model |
|---|---|---|
| Reservoirs | Whole Season | |
| Early | (10) | |
| Mid | ||
| Late | ||
| Utah Lake | Whole Season | |
| Early | ||
| Late |
References
- Hambrook Berkman, J.A.; Canova, M.G. Algal biomass indicators. In U.S.G.S. Techniques of Water-Resources Investigations, Volume 9; United States Geological Survey: Reston, VA, USA, 2007; Section 7.4. [Google Scholar]
- Stadelmann, T.H.; Brezonik, P.L.; Kloiber, S. Seasonal patterns of chlorophyll a and Secchi disk transparency in lakes of east-central Minnesota: Implications for design of ground-and satellite-based monitoring programs. Lake Reserv. Manag. 2001, 17, 299–314. [Google Scholar] [CrossRef]
- Hansen, C.; Swain, N.; Munson, K.; Adjei, Z.; Williams, G.P.; Miller, W. Development of sub-seasonal remote sensing chlorophyll-a detection models. Am. J. Plant Sci. 2013, 4, 21. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P.; Adjei, Z. Long-term application of remote sensing chlorophyll detection models: Jordanelle reservoir case study. Nat. Resour. 2015, 6, 123. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P.; Adjei, Z.; Barlow, A.; Nelson, E.J.; Miller, A.W. Reservoir water quality monitoring using remote sensing with seasonal models: Case study of five central-Utah reservoirs. Lake Reserv. Manag. 2015, 31, 225–240. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.E.; Dekker, A.G.; Strömbeck, N.; Candiani, G. Assessment of water quality in lake garda (Italy) using Hyperion. Remote Sens. Environ. 2007, 109, 183–195. [Google Scholar] [CrossRef]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- Yacobi, Y.Z.; Gitelson, A.; Mayo, M. Remote sensing of chlorophyll in lake Kinneret using Highspectral-resolution radiometer and Landsat TM: Spectral features of reflectance and algorithm development. J. Plankton Res. 1995, 17, 2155–2173. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 Ali sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, X.; Kong, F.; Zhang, S.; Kong, W.; Hao, J.; Shang, L. Two-decade reconstruction of algal blooms in china’s lake Taihu. Environ. Sci. Technol. 2009, 43, 3522–3528. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.C.; Stumpf, R.P.; Bridgeman, T.B.; Michalak, A.M. Using Landsat to extend the historical record of lacustrine phytoplankton blooms: A Lake Erie case study. Remote Sens. Environ. 2017, 191, 273–285. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Hansen, C.H.; Burian, S.J.; Dennison, P.E.; Williams, G.P. Spatiotemporal variability of lake water quality in the context of remote sensing models. Remote Sens. 2017, 9, 409. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
- Nelson, S.A.; Soranno, P.A.; Cheruvelil, K.S.; Batzli, S.A.; Skole, D.L. Regional assessment of lake water clarity using satellite remote sensing. J. Limnol. 2003, 62, 27–32. [Google Scholar] [CrossRef]
- Lesht, B.M.; Barbiero, R.P.; Warren, G.J. A band-ratio algorithm for retrieving open-lake chlorophyll values from satellite observations of the great lakes. J. Great Lakes Res. 2013, 39, 138–152. [Google Scholar] [CrossRef]
- Woźniak, M.; Bradtke, K.M.; Darecki, M.; Krężel, A. Empirical model for phycocyanin concentration estimation as an indicator of cyanobacterial bloom in the optically complex coastal waters of the Baltic sea. Remote Sens. 2016, 8, 212. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Springer Science & Business Media: New York, NY, USA, 2012; Volume 4. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color 1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for Seawifs. J. Geophys. Res. Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.; Reid, R.P. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Toole, D.A.; Siegel, D.A.; Menzies, D.W.; Neumann, M.J.; Smith, R.C. Remote-sensing reflectance determinations in the coastal ocean environment: Impact of instrumental characteristics and environmental variability. Appl. Opt. 2000, 39, 456–469. [Google Scholar] [CrossRef] [PubMed]
- Han, L. Spectral reflectance with varying suspended sediment concentrations in clear and algae-laden waters. Photogram. Eng. Remote Sens. 1997, 63, 701–705. [Google Scholar]
- Mittenzwey, K.H.; Ullrich, S.; Gitelson, A.; Kondratiev, K. Determination of chlorophyll a of inland waters on the basis of spectral reflectance. Limnol. Oceanogr. 1992, 37, 147–149. [Google Scholar] [CrossRef]
- Tan, J.; Cherkauer, K.A.; Chaubey, I.; Troy, C.D.; Essig, R. Water quality estimation of river plumes in southern lake Michigan using Hyperion. J. Great Lakes Res. 2016, 42, 524–535. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Airborne hyperspectral remote sensing to assess spatial distribution of water quality characteristics in large rivers: The Mississippi river and its tributaries in Minnesota. Remote Sens. Environ. 2013, 130, 254–265. [Google Scholar] [CrossRef]
- Tan, J.; Cherkauer, K.A.; Chaubey, I. Using hyperspectral data to quantify water-quality parameters in the Wabash river and its tributaries, Indiana. Int. J. Remote Sens. 2015, 36, 5466–5484. [Google Scholar] [CrossRef]
- Bartholomew, P.J. Mapping and Modeling Chlorophyll-a Concentrations in the Lake Manassas Reservoir Using Landsat Thematic Mapper Satellite Imagery. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 2003. [Google Scholar]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton bloom status: Chlorophyll a biomass as an indicator of water quality condition in the southern Estuaries of Florida, USA. Ecol. Indic. 2009, 9, S56–S67. [Google Scholar] [CrossRef]
- Östlund, C.; Flink, P.; Strömbeck, N.; Pierson, D.; Lindell, T. Mapping of the water quality of lake Erken, Sweden, from imaging spectrometry and Landsat thematic mapper. Sci. Total Environ. 2001, 268, 139–154. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Fuller, L.M.; Aichele, S.S.; Minnerick, R.J. Predicting Water Quality by Relating Secchi-Disk Transparency and Chlorophyll a Measurements to Satellite Imagery for Michigan Inland Lakes, August 2002; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2004.
- Lin, S.; Novitski, L.N.; Qi, J.; Stevenson, R.J. Landsat TM/ETM+ and machine-learning algorithms for limnological studies and algal bloom management of inland lakes. J. Appl. Remote Sens. 2018, 12, 026003. [Google Scholar] [CrossRef]
- Brooks, B.W.; Lazorchak, J.M.; Howard, M.D.; Johnson, M.V.V.; Morton, S.L.; Perkins, D.A.; Reavie, E.D.; Scott, G.I.; Smith, S.A.; Steevens, J.A. In some places, in some cases, and at some times, harmful algal blooms are the greatest threat to inland water quality. Environ. Toxicol. Chem. 2017, 36, 1125–1127. [Google Scholar] [CrossRef] [PubMed]
- Utah Department of Environmental Quality (UDEQ). Jordanelle Reservoir Lake Report; UDEQ: Salt Lake City, UT, USA, 2004.
- Utah Department of Environmental Quality (UDEQ). Deer Creek Reservoir Lake Report; UDEQ: Salt Lake City, UT, USA, 2004.
- Utah Department of Environmental Quality (UDEQ). Utah Lake Report; UDEQ: Salt Lake City, UT, USA, 2006.
- Oberndorfer, R. (Central Utah Water Conservancy District, Salt Lake City, UT, USA); Hansen, C.H. (University of Utah, Salt Lake City, UT, USA). Reservoir condition discussion and suggested seasons. Personal communication, 2014. [Google Scholar]
- Whiting, M.C.; Brotherson, J.D.; Rushforth, S.R. Environmental interaction in summer algal communities of Utah Lake. Great Basin Nat. 1978, 38, 31–41. [Google Scholar]
- Rushforth, S.R.; Squires, L.E. New records and comprehensive list of the algal taxa of Utah lake, Utah, USA. Great Basin Nat. 1985, 45, 237–254. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. Geosci. Remote Sens. Lett. IEEE 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Johnson, R.; Strutton, P.G.; Wright, S.W.; McMinn, A.; Meiners, K.M. Three improved satellite chlorophyll algorithms for the Southern Ocean. J. Geophys. Res. Oceans 2013, 118, 3694–3703. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: New York, NY, USA, 2014; Volume 326. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Sass, G.Z.; Creed, I.F.; Bayley, S.E.; Devito, K.J. Understanding variation in trophic status of lakes on the boreal plain: A 20 years retrospective using Landsat tm imagery. Remote Sens. Environ. 2007, 109, 127–141. [Google Scholar] [CrossRef]
- Lathrop, R.G., Jr. Landsat thematic mapper monitoring of turbid inland water quality. Photogram. Eng. Remote Sens. 1992, 465–470. [Google Scholar]
- Duan, H.; Zhang, Y.; Zhang, B.; Song, K.; Wang, Z. Assessment of chlorophyll-a concentration and trophic state for lake Chagan using Landsat tm and field spectral data. Environ. Monit. Assess. 2007, 129, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.; Garbuzov, G.; Szilagyi, F.; Mittenzwey, K.H.; Karnieli, A.; Kaiser, A. Quantitative remote sensing methods for real-time monitoring of inland waters quality. Int. J. Remote Sens. 1993, 14, 1269–1295. [Google Scholar] [CrossRef]
- Mayo, M.; Gitelson, A.; Yacobi, Y.; Ben-Avraham, Z. Chlorophyll distribution in lake Kinneret determined from Landsat thematic mapper data. Remote Sens. 1995, 16, 175–182. [Google Scholar] [CrossRef]
- Brivio, P.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in lake garda using an image-based radiative transfer code for Landsat tm images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Tyler, A.; Svab, E.; Preston, T.; Présing, M.; Kovács, W. Remote sensing of the water quality of shallow lakes: A mixture modelling approach to quantifying phytoplankton in water characterized by high-suspended sediment. Int. J. Remote Sens. 2006, 27, 1521–1537. [Google Scholar] [CrossRef]
- Sudheer, K.; Chaubey, I.; Garg, V. Lake water quality assessment from Landsat thematic mapper data using neural network: An approach to optimal band combination selection1. J. Am. Water Resour. Assoc. 2006, 42, 1683–1695. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Kung, H.T.; Van Arsdale, R.B. Applications of Landsat-5 TM imagery in assessing and mapping water quality in Reelfoot lake, Tennessee. Int. J. Remote Sens. 2006, 27, 5269–5283. [Google Scholar] [CrossRef]
- Lathrop, R.G.; Lillesand, T.M. Use of thematic mapper data to assess water quality in green bay and central lake Michigan. Photogram. Eng. Remote Sens. 1986, 52, 671–680. [Google Scholar]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for Modis ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Removal of atmospheric effects from satellite imagery of the oceans. Appl. Opt. 1978, 17, 1631. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Casterlin, M.E.; Reynolds, W.W. Seasonal algal succession and cultural eutrophication in a north temperate lake. Hydrobiologia 1977, 54, 99–108. [Google Scholar] [CrossRef]
- Kutser, T. Quantitative detection of chlorophyll in cyanobacterial blooms by satellite remote sensing. Limnol. Oceanogr. 2004, 49, 2179–2189. [Google Scholar] [CrossRef]
| Lake | Season | Time-Window | Number of Pairs | Range and Average Field-Sampled Chl-a (µg/L) during Historical Sampling Period | Range and Average Field-Sampled Chl-a (µg/L) from Paired Samples |
|---|---|---|---|---|---|
| Utah Lake | Early | ±24 h | 10 | 0.8–45; 7.6 | 1.2–45; 9.4 |
| Late | ±24 h | 46 | 0.2–324.9; 38.3 | 0.2–185.5; 27.1 | |
| Deer Creek and Jordanelle Reservoirs | Early | Same day | 18 | 0.2–35.4; 6.9 | 0.2–6.3; 3.2 |
| Mid | ±24 h | 42 | 0.2–21.3; 4.3 | 0.2–21.3; 6.3 | |
| Late | Same day | 25 | 0.1–196; 7.2 | 0.2–196; 23.2 |
| # | Landsat Bands | References and Lake(s) Used for Calibration | Notes |
|---|---|---|---|
| 1 | B3/B1 | Recommended for use in high (>20 µg/L) chl-a conditions [13] and highly turbid lakes [49] | |
| 2 | B3/B4 | Recommended for use in high (>20 µg/L) chl-a conditions [13] | |
| 3 |
| Recommended for use in low (<20 µg/L) chl-a-a conditions [13] | |
| 4 | (B1−B3)/B2 | Accounts for the increased effect of inorganic suspended solids that occurs with decreased chl-a concentrations [13] | |
| 5 |
| Specifically used for shallow waters dominated by high levels of suspended sediments | |
| 6 |
|
| Performs well under high chl-a conditions [58] Based on similar to approaches in ocean color sensing for turbid waters [59,60] |
| Season | Selected Bands | NSE | RMSE | R2 | |
|---|---|---|---|---|---|
| Reservoirs | Whole Season | 0.02 | 24.7 | 0.12 | |
| Early | 0.54 | 1.5 | 0.54 | ||
| Mid | 0.25 | 5.4 | 0.32 | ||
| Late | 0.69 | 23.7 | 0.73 | ||
| Utah Lake | Whole Season | −1.3 | 55.2 | 0.5 | |
| Early | 0.99 | 1.2 | 0.99 | ||
| Late | 0.86 | 14.4 | 0.88 |
| Model Application | R2 | R2 with Season-Specific Model |
|---|---|---|
| Reservoir Late-model to Early-data | 0.4 | 0.48 |
| Reservoir Late-model to Mid-data | 0.08 | 0.32 |
| Lake Late-model to Early-data | 0.95 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hansen, C.H.; Williams, G.P. Evaluating Remote Sensing Model Specification Methods for Estimating Water Quality in Optically Diverse Lakes throughout the Growing Season. Hydrology 2018, 5, 62. https://doi.org/10.3390/hydrology5040062
Hansen CH, Williams GP. Evaluating Remote Sensing Model Specification Methods for Estimating Water Quality in Optically Diverse Lakes throughout the Growing Season. Hydrology. 2018; 5(4):62. https://doi.org/10.3390/hydrology5040062
Chicago/Turabian StyleHansen, Carly Hyatt, and Gustavious Paul Williams. 2018. "Evaluating Remote Sensing Model Specification Methods for Estimating Water Quality in Optically Diverse Lakes throughout the Growing Season" Hydrology 5, no. 4: 62. https://doi.org/10.3390/hydrology5040062
APA StyleHansen, C. H., & Williams, G. P. (2018). Evaluating Remote Sensing Model Specification Methods for Estimating Water Quality in Optically Diverse Lakes throughout the Growing Season. Hydrology, 5(4), 62. https://doi.org/10.3390/hydrology5040062






