Reconstruction of Water Infiltration Rate Reducibility in Response to Suspended Solid Characteristics Using Singular Spectrum Analysis: An Application to the Caspian Sea Coast of Nur, Iran
Abstract
:1. Introduction
2. Materials and Methods
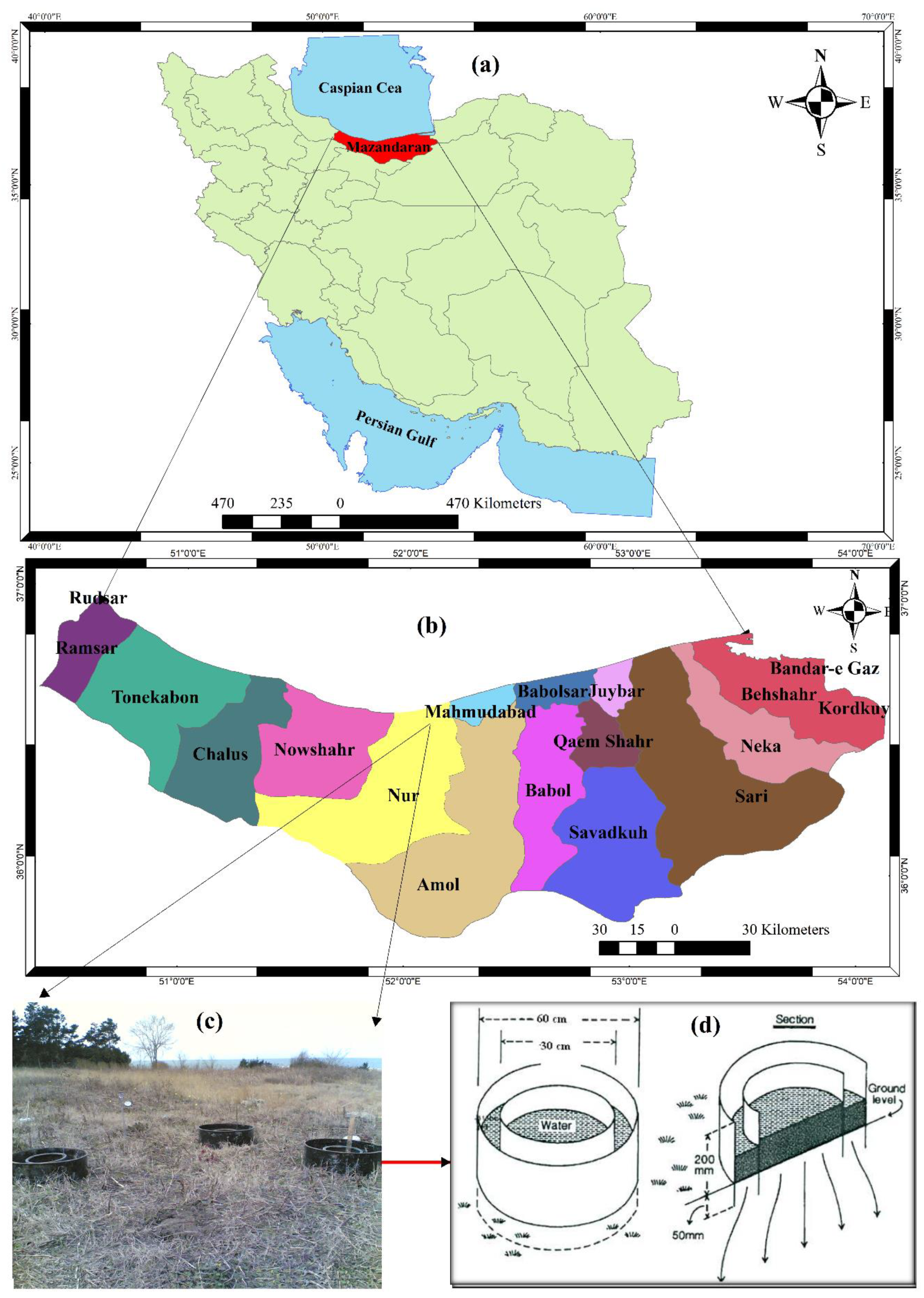
2.1. Application Area
2.2. Infiltration Rate Measurement
2.3. Set Up the Experiments
2.4. Statistical Analysis and Cohen’s d Effect Size Measure
2.5. SSA Structure
2.5.1. Embedding
2.5.2. Singular Value Decomposition
2.5.3. Eigentriple Grouping
2.5.4. Diagonal Averaging
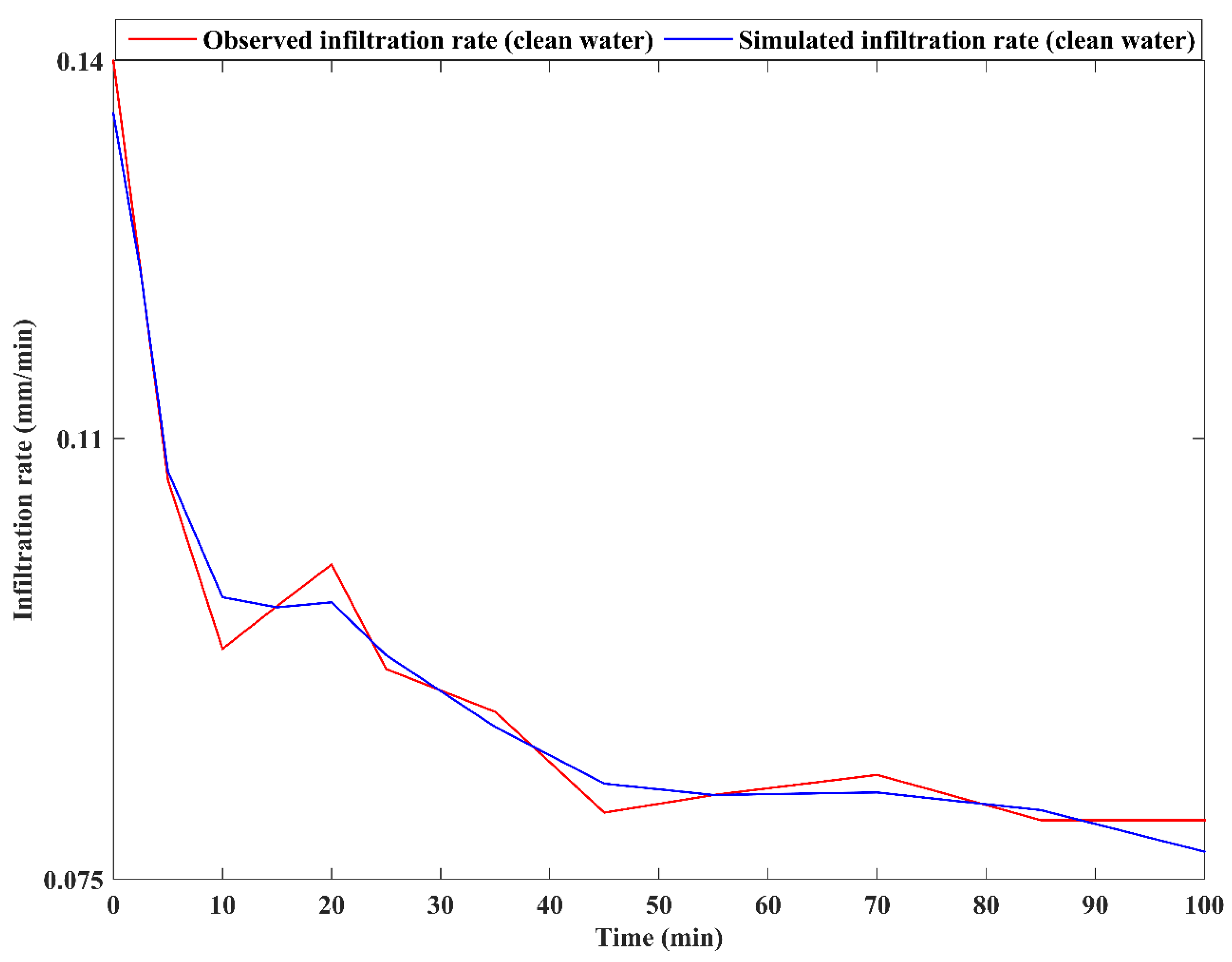
2.6. Assessment the Performance of the Reconstructed Infiltration Rates
3. Results
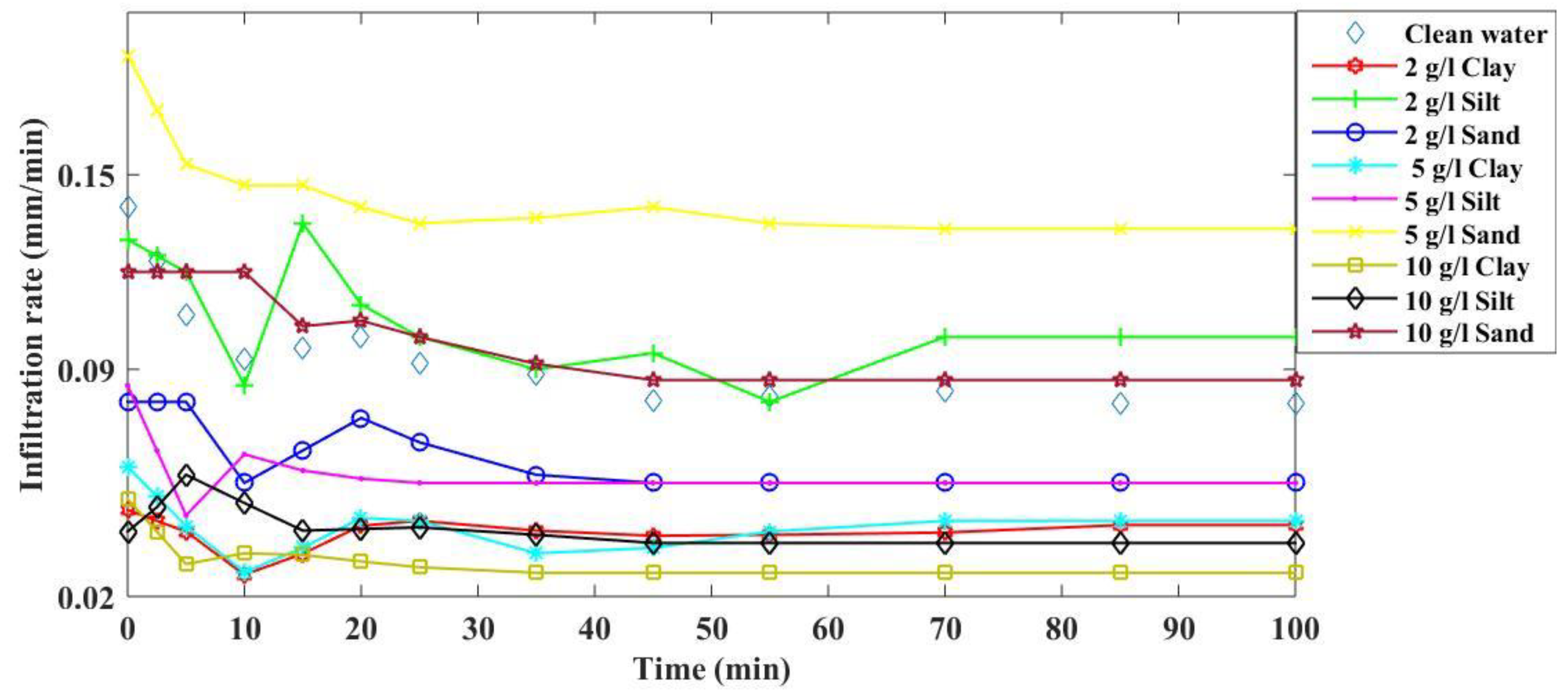
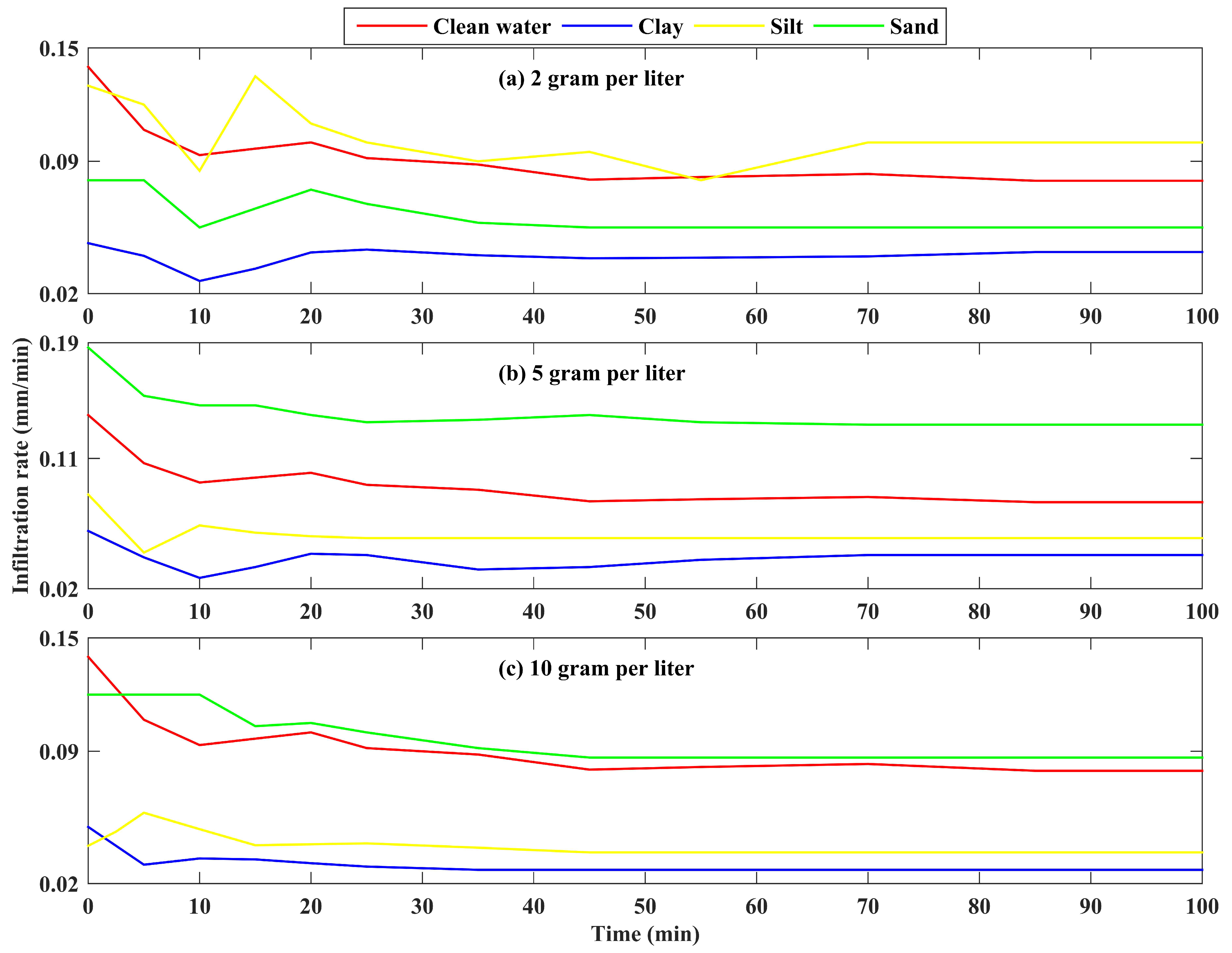
3.1. Infiltration Rate for Clay-Silt- and Sand-Sized Suspended Solids
3.2. Statistical Comparisons amongst the Defined Infiltration Rate Treatments
3.3. Reconstruction of Water Infiltration Rate using SSA
3.3.1. SSA Objects
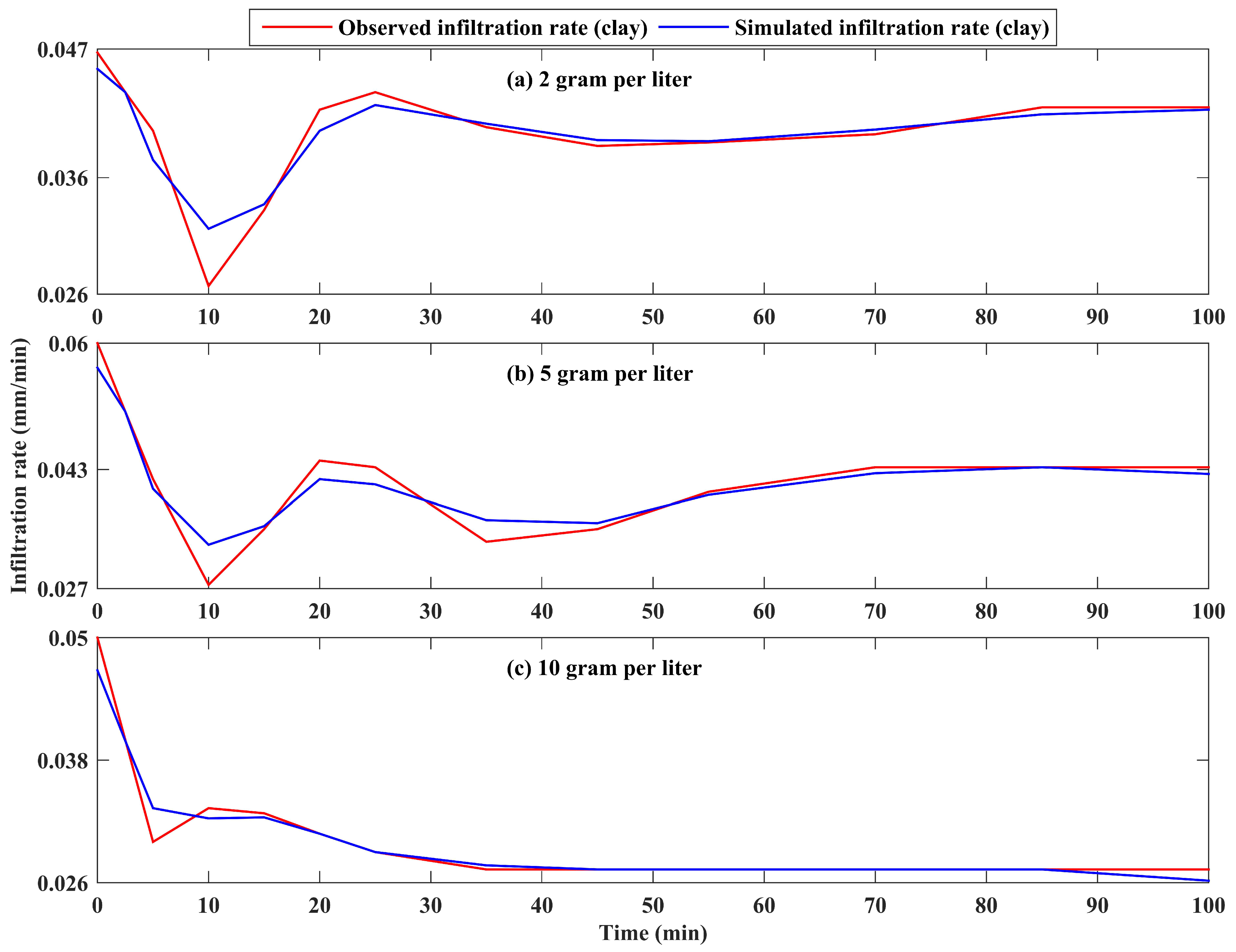
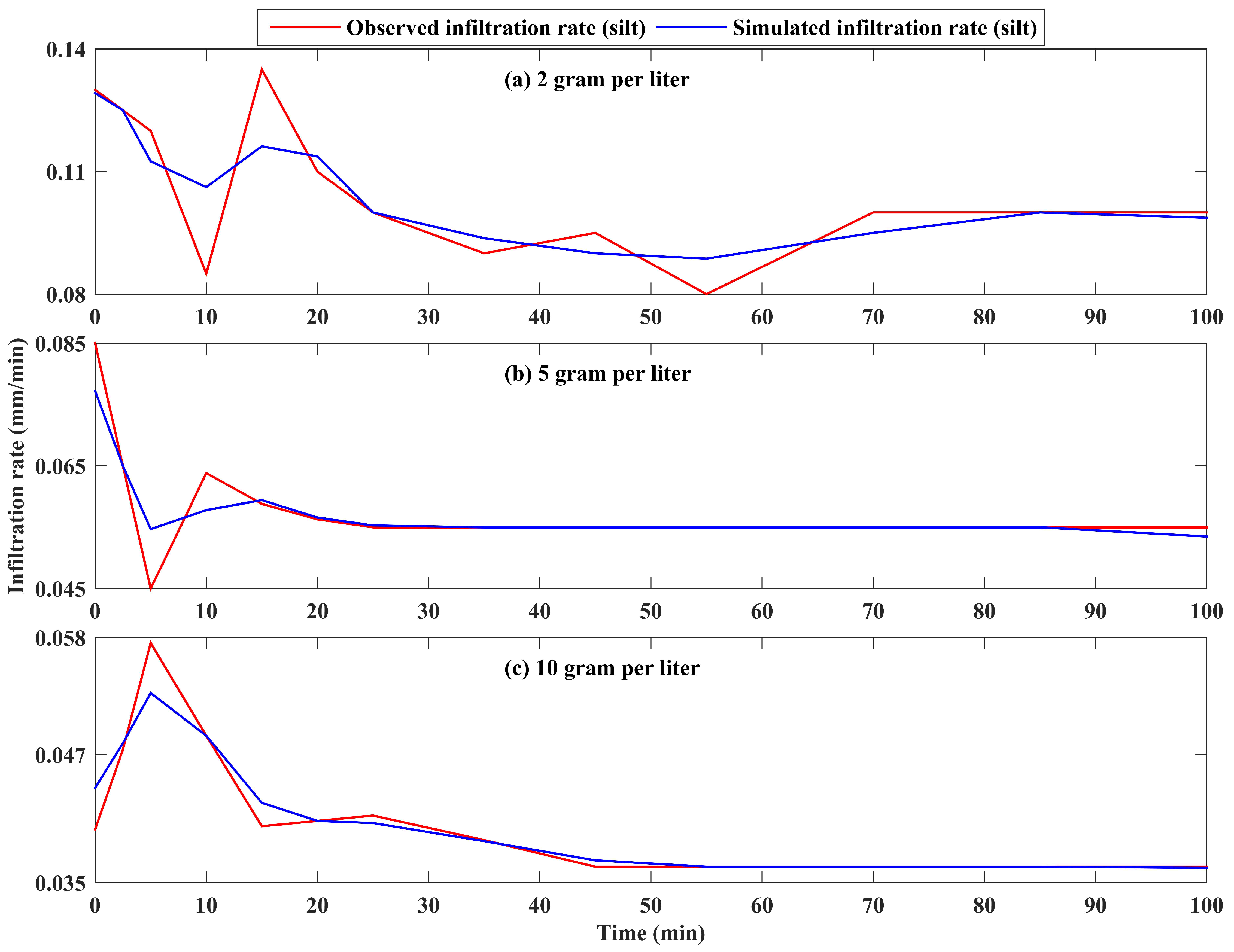
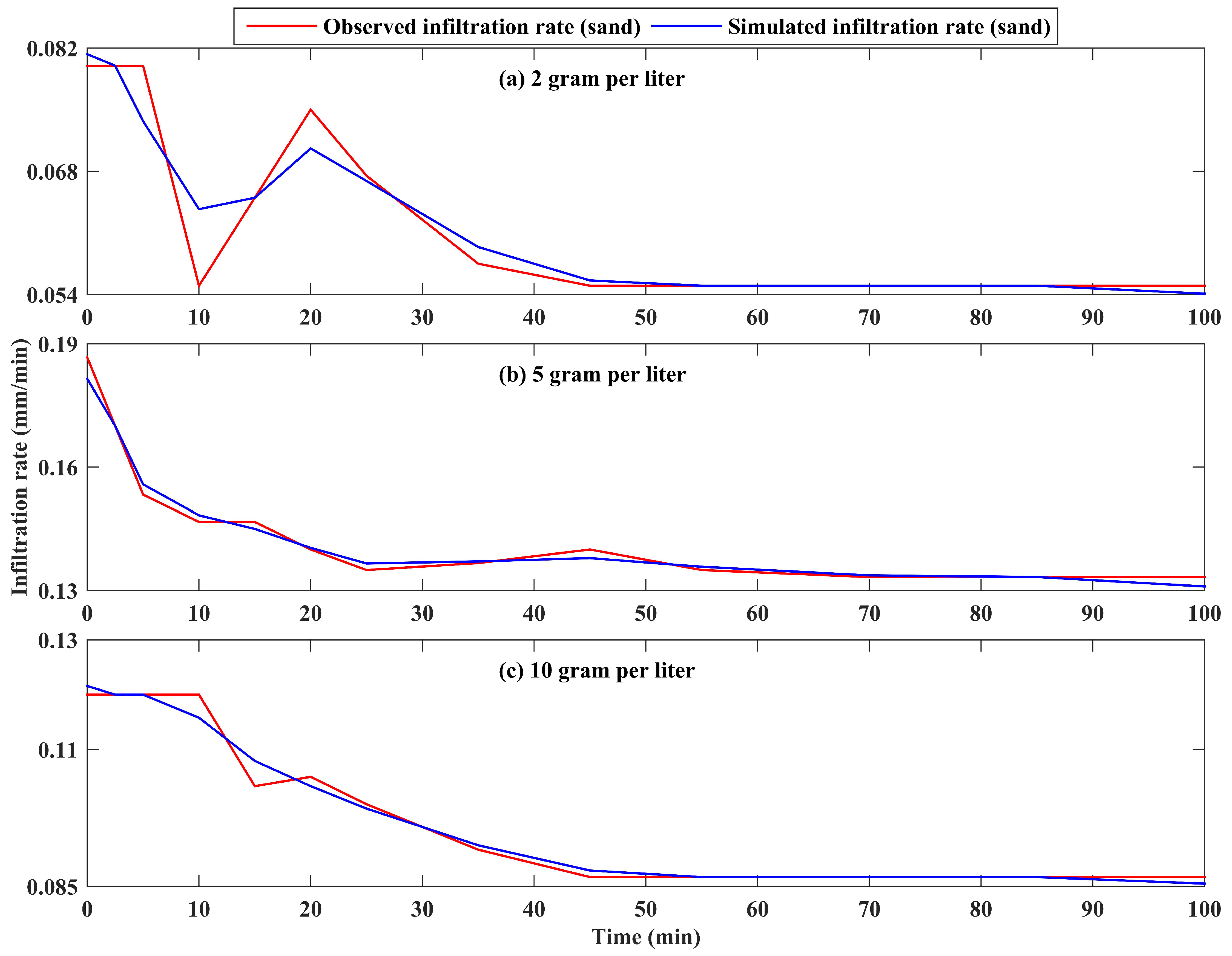
3.3.2. Comparison of Measured and Reconstructed Infiltration Rate
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jury, W.A.; Vaux, H.J. The emerging global water crisis: managing scarcity and conflict between water users. In Advances in Agronomy; Academic Press: Cambridge, MA, USA, 2007; Volume 95, pp. 1–76. [Google Scholar]
- Dillon, P. Future management of aquifer recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Martin, R. Clogging Issues Associated with Managed Aquifer Recharge Methods; IAH Commission on Managing Aquifer Recharge: Perth, Australia, 2013. [Google Scholar]
- Casanova, J.; Devau, N.; Pettenati, M. Managed aquifer recharge: an overview of issues and options. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J.-D., Ross, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 413–434. [Google Scholar]
- Schuh, W.M. Seasonal variation of clogging of an artificial recharge basin in a northern climate. J. Hydrol. 1990, 121, 193–215. [Google Scholar] [CrossRef]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Maddock, I. Groundwater in the environment: An introduction, by Paul L. Younger, 2007. Blackwell: London, 390 pages. ISBN 1-4051-2143-2. River Res. Appl. 2008, 24, 1377. [Google Scholar] [CrossRef]
- Baveye, P.; Vandevivere, P.; Hoyle, B.L.; DeLeo, P.C.; de Lozada, D.S. Environmental impact and mechanisms of the biological clogging of saturated soils and aquifer materials. Crit. Rev. Environ. Sci. Technol. 1998, 28, 123–191. [Google Scholar] [CrossRef]
- Vetter, A.; Mangelsdorf, K.; Wolfgramm, M.; Rauppach, K.; Schettler, G.; Vieth-Hillebrand, A. Variations in fluid chemistry and membrane phospholipid fatty acid composition of the bacterial community in a cold storage groundwater system during clogging events. Appl. Geochem. 2012, 27, 1278–1290. [Google Scholar] [CrossRef] [Green Version]
- Goss, D.W.; Smith, S.J.; Stewart, B.A.; Jones, O.R. Fate of suspended sediment during basin recharge. Water Resour. Res. 1973, 9, 668–675. [Google Scholar] [CrossRef]
- Goss, D.W.; Jones, O.R. Movement and accumulation of suspended sediment during basin recharge. AAPG Bull. 1973, 57, 468–480. [Google Scholar]
- Katznelson, R. Clogging of groundwater recharge basins by cyanobacterial mats. FEMS Microbiol. Lett. 1989, 62, 231–242. [Google Scholar] [CrossRef]
- Dillon, P.; Vanderzalm, J.; Page, D.; Barry, K.; Gonzalez, D.; Muthukaruppan, M.; Hudson, M. Analysis of ASR clogging investigations at three Australian ASR sites in a Bayesian context. Water 2016, 8, 442. [Google Scholar] [CrossRef]
- Page, D.; Miotliński, K.; Dillon, P.; Taylor, R.; Wakelin, S.; Levett, K.; Barry, K.; Pavelic, P. Water quality requirements for sustaining aquifer storage and recovery operations in a low permeability fractured rock aquifer. J. Environ. Manag. 2011, 92, 2410–2418. [Google Scholar] [CrossRef] [PubMed]
- Page, D.; Vanderzalm, J.; Miotliński, K.; Barry, K.; Dillon, P.; Lawrie, K.; Brodie, R.S. Determining treatment requirements for turbid river water to avoid clogging of aquifer storage and recovery wells in siliceous alluvium. Water Res. 2014, 66, 99–110. [Google Scholar] [CrossRef] [PubMed]
- Mahesha, A.; Lakshmikant, P. Saltwater Intrusion in Coastal Aquifers Subjected to Freshwater Pumping. J. Hydrol. Eng. 2014, 19, 448–456. [Google Scholar] [CrossRef]
- Melloul, A.J.; Goldenberg, L.C. Monitoring of seawater intrusion in coastal aquifers: basics and local concerns. J. Environ. Manag. 1997, 51, 73–86. [Google Scholar] [CrossRef]
- Sebben, M.L.; Werner, A.D.; Graf, T. Seawater intrusion in fractured coastal aquifers: A preliminary numerical investigation using a fractured Henry problem. Adv. Water Resour. 2015, 85, 93–108. [Google Scholar] [CrossRef]
- Masciopinto, C. Management of aquifer recharge in Lebanon by removing seawater intrusion from coastal aquifers. J. Environ. Manag. 2013, 130, 306–312. [Google Scholar] [CrossRef] [PubMed]
- Siriwardene, N.R.; Deletic, A.; Fletcher, T.D. Clogging of stormwater gravel infiltration systems and filters: Insights from a laboratory study. Water Res. 2007, 41, 1433–1440. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Ye, X.; Zhang, X. Clogging of saturated porous media by silt-sized suspended solids under varying physical conditions during managed aquifer recharge. Hydrol. Process. 2018, 32, 2254–2262. [Google Scholar] [CrossRef]
- Loève, M. Probability Theory, 4th ed.; Springer-Verlag: New York, NY, USA, 1977. [Google Scholar]
- Golyandina, N.; Nekrutkin, V.V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001; p. xii. 305p. [Google Scholar]
- Rodrigues, P.C.; de Carvalho, M. Spectral modeling of time series with missing data. Appl. Math. Model. 2013, 37, 4676–4684. [Google Scholar] [CrossRef]
- Golyandina, N.; Korobeynikov, A. Basic Singular Spectrum Analysis and forecasting with R. Comput. Stat. Data Anal. 2014, 71, 934–954. [Google Scholar] [CrossRef] [Green Version]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time-series. Phys. D 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Schoellhamer, D.H. Singular spectrum analysis for time series with missing data. Geophys. Res. Lett. 2001, 28, 3187–3190. [Google Scholar] [CrossRef] [Green Version]
- Golyandina, N.; Zhigljavsky, A.A. Singular Spectrum Analysis for Time Series; Springer: Heidelberg, Germany, 2013; p. vii. 119p. [Google Scholar]
- Shen, Y.; Peng, F.; Li, B. Improved singular spectrum analysis for time series with missing data. Nonlinear Process. Geophys. 2015, 22, 371–376. [Google Scholar] [CrossRef]
- Agac, K.; Baydaroglu, Ö.; Kocak, K. Reconstruction of gaps in flow series using singular spectrum analysis (SSA) and multi-channel SSA (M-SSA). In Proceedings of the 27th Conference on Weather Analysis and Forecasting/23rd Conference on Numerical Weather Prediction, Chicago, IL, USA, 28 June–3 July 2015. [Google Scholar]
- Kondrashov, D.; Feliks, Y.; Ghil, M. Oscillatory modes of extended Nile River records (AD 622-1922). Geophys. Res. Lett. 2005, 32, L10702. [Google Scholar] [CrossRef]
- Hansen, B.; Noguchi, K. Improved short-term point and interval forecasts of the daily maximum tropospheric ozone levels via singular spectrum analysis. Environmetrics 2017, 28, e2479. [Google Scholar] [CrossRef]
- Moreno, S.R.; dos Santos Coelho, L. Wind speed forecasting approach based on singular spectrum analysis and adaptive neuro fuzzy inference system. Renew. Energy 2018, 126, 736–754. [Google Scholar] [CrossRef]
- Golshan, M.; Colombani, N.; Mastrocicco, M. Assessing aquifer salinization with multiple techniques along the southern caspian sea shore (Iran). Water 2018, 10, 348. [Google Scholar] [CrossRef]
- Diamond, J.; Shanley, T. Infiltration rate assessment of some major soils. Irish Geogr. 2003, 36, 32–46. [Google Scholar] [CrossRef] [Green Version]
- Sidiras, N.; Roth, C.H. Infiltration measurements with double-ring infiltrometers and a rainfall simulator under different surface conditions on an Oxisol. Soil Tillage Res. 1987, 9, 161–168. [Google Scholar] [CrossRef]
- Bean, E.; Dukes, M. Evaluation of infiltration basin performance on coarse soils. J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Sieve Analysis of Fine and Coarse Aggregates; ASTM: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Sadeghi, S.H.; Kiani-Harchegani, M.; Younesi, H. Suspended sediment concentration and particle size distribution, and their relationship with heavy metal content. J. Earth Syst. Sci. 2012, 121, 63–71. [Google Scholar] [CrossRef]
- Sullivan, G.M.; Feinn, R. Using effect size—Or why the p value is not enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef] [PubMed]
- Carver, R.P. The case against statistical significance testing, revisited. J. Exp. Educ. 1993, 61, 287–292. [Google Scholar] [CrossRef]
- Hojat, M.; Xu, G. A visitor’s guide to effect sizes—Statistical significance versus practical (clinical) importance of research findings. Adv. Health Sci. Educ. Theory Pract. 2004, 9, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Amrhein, V.; Korner-Nievergelt, F.; Roth, T. The earth is flat (p > 0.05): Significance thresholds and the crisis of unreplicable research. PeerJ 2017, 5, e3544. [Google Scholar] [CrossRef] [PubMed]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 863. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Chapter 3—The significance of a product moment rs. In Statistical Power Analysis for the Behavioral Sciences; Cohen, J., Ed.; Academic Press: Cambridge, MA, USA, 1977; pp. 75–107. [Google Scholar]
- Sawilowsky, S. New Effect Size Rules of Thumb. J. Mod. Appl. Stat. Methods 2009, 8, 597–599. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.R.; Poskitt, D.S. A note on window length selection in singular spectrum analysis. Aust. N. Z. J. Stat. 2013, 55, 87–108. [Google Scholar] [CrossRef]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.-W.; Faizollahzadeh Ardabili, S.; Piran, M.J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinformatics 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Chau, K.-W. Use of meta-heuristic techniques in rainfall-runoff modelling. Water 2017, 9, 186. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.-T.; Wu, X.-Y.; Chau, K.W. Multiple criteria rainfall–runoff model calibration using a parallel genetic algorithm in a cluster of computers/Calage multi-critères en modélisation pluie–débit par un algorithme génétique parallèle mis en œuvre par une grappe d’ordinateurs. Hydrol. Sci. J. 2005, 50, 1087. [Google Scholar] [CrossRef]
- Holloway, D.M.; Harrison, L.G.; Kosman, D.; Vanario-Alonso, C.E.; Spirov, A.V. Analysis of pattern precision shows that Drosophila segmentation develops substantial independence from gradients of maternal gene products. Dev. Dyn. 2006, 235, 2949–2960. [Google Scholar] [CrossRef] [PubMed]
- Spellman, P.T.; Sherlock, G.; Zhang, M.Q.; Iyer, V.R.; Anders, K.; Eisen, M.B.; Brown, P.O.; Botstein, D.; Futcher, B. Comprehensive identification of cell cycle–regulated genes of the yeast saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell 1998, 9, 3273–3297. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Heravi, S.; Zhigljavsky, A. Forecasting European industrial production with singular spectrum analysis. Int. J. Forecast. 2009, 25, 103–118. [Google Scholar] [CrossRef]
- Golyandina, N. On the choice of parameters in Singular Spectrum Analysis and related subspace-based methods. Stat. Its Interface 2010, 3, 259–279. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef] [Green Version]
- Gerke, H.H. Preferential flow descriptions for structured soils. J. Plant Nutr. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Wang, Z.; Du, X.; Yang, Y.; Ye, X. Surface clogging process modeling of suspended solids during urban stormwater aquifer recharge. J. Environ. Sci. (China) 2012, 24, 1418–1424. [Google Scholar] [CrossRef]

| Slope (Percent) | Dominant Soil Texture Class | Volumetric Soil Water Content (Percent) | Gravimetric Soil Water Content (Percent) | Porosity (Percent) | Average of Matric Potential (Centibar) | Bulk Density (g/cm3) |
|---|---|---|---|---|---|---|
| 5 | Sandy loamy | 32.04 | 28.46 | 21.9 | 3.51 | 1.12 |
| Size of Suspended Solids | Clay | Silt | Sand |
|---|---|---|---|
| Clay fraction (percent) | 52 | 8 | 0 |
| Silt fraction(percent) | 12 | 54 | 0 |
| Sand fraction (percent) | 36 | 38 | 100 |
| Effect Size Description | Cohen’s d |
|---|---|
| Very small | 0.01 |
| Small | 0.20 |
| Medium | 0.50 |
| Large | 0.80 |
| Very large | 1.20 |
| Huge | ≥2.00 |
| Concentration | 2 g/L | 5 g/L | 10 g/L | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Treatment | Clay vs. CW | Silt vs. CW | Sand vs. CW | Clay vs. CW | Silt vs. CW | Sand vs. CW | Clay vs. CW | Silt vs. CW | Sand vs. CW |
| Cohen’s d | −3.24 | 0.72 | −3.05 | −3.81 | −2.80 | 9.58 | −5.23 | −3.31 | 0.51 |
| Description | Huge | Medium | Huge | Huge | Huge | Huge | Huge | Huge | Medium |
| Concentration and Treatment | 2 g/L Clay vs. 2 g/L Silt | 2 g/L Clay vs. 5 g/L Silt | 5 g/L Clay vs. 10 g/L Silt | 10 g/L Clay vs. 10 g/L Silt |
|---|---|---|---|---|
| Cohen’s d | −3.94 | −1.91 | 1.59 | −1.23 |
| Description | Huge | Very large | Very large | Very large |
| Suspended Solid Size | Concentration (g/L) | R2 | NS |
|---|---|---|---|
| Clean water/NA | 0 | 0.99 | 0.98 |
| Clay | 2 | 0.96 | 0.87 |
| 5 | 0.97 | 0.91 | |
| 10 | 0.98 | 0.95 | |
| Silty | 2 | 0.85 | 0.71 |
| 5 | 0.93 | 0.81 | |
| 10 | 0.95 | 0.91 | |
| Sand | 2 | 0.95 | 0.90 |
| 5 | 0.99 | 0.98 | |
| 10 | 0.99 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taie Semiromi, M.; Ghasemian, D. Reconstruction of Water Infiltration Rate Reducibility in Response to Suspended Solid Characteristics Using Singular Spectrum Analysis: An Application to the Caspian Sea Coast of Nur, Iran. Hydrology 2018, 5, 59. https://doi.org/10.3390/hydrology5040059
Taie Semiromi M, Ghasemian D. Reconstruction of Water Infiltration Rate Reducibility in Response to Suspended Solid Characteristics Using Singular Spectrum Analysis: An Application to the Caspian Sea Coast of Nur, Iran. Hydrology. 2018; 5(4):59. https://doi.org/10.3390/hydrology5040059
Chicago/Turabian StyleTaie Semiromi, Majid, and Davood Ghasemian. 2018. "Reconstruction of Water Infiltration Rate Reducibility in Response to Suspended Solid Characteristics Using Singular Spectrum Analysis: An Application to the Caspian Sea Coast of Nur, Iran" Hydrology 5, no. 4: 59. https://doi.org/10.3390/hydrology5040059
APA StyleTaie Semiromi, M., & Ghasemian, D. (2018). Reconstruction of Water Infiltration Rate Reducibility in Response to Suspended Solid Characteristics Using Singular Spectrum Analysis: An Application to the Caspian Sea Coast of Nur, Iran. Hydrology, 5(4), 59. https://doi.org/10.3390/hydrology5040059





