Influence of Precipitation Forcing Uncertainty on Hydrological Simulations with the NASA South Asia Land Data Assimilation System
Abstract
1. Introduction
2. Methods
2.1. Datasets
2.2. Model
3. Results & Discussion
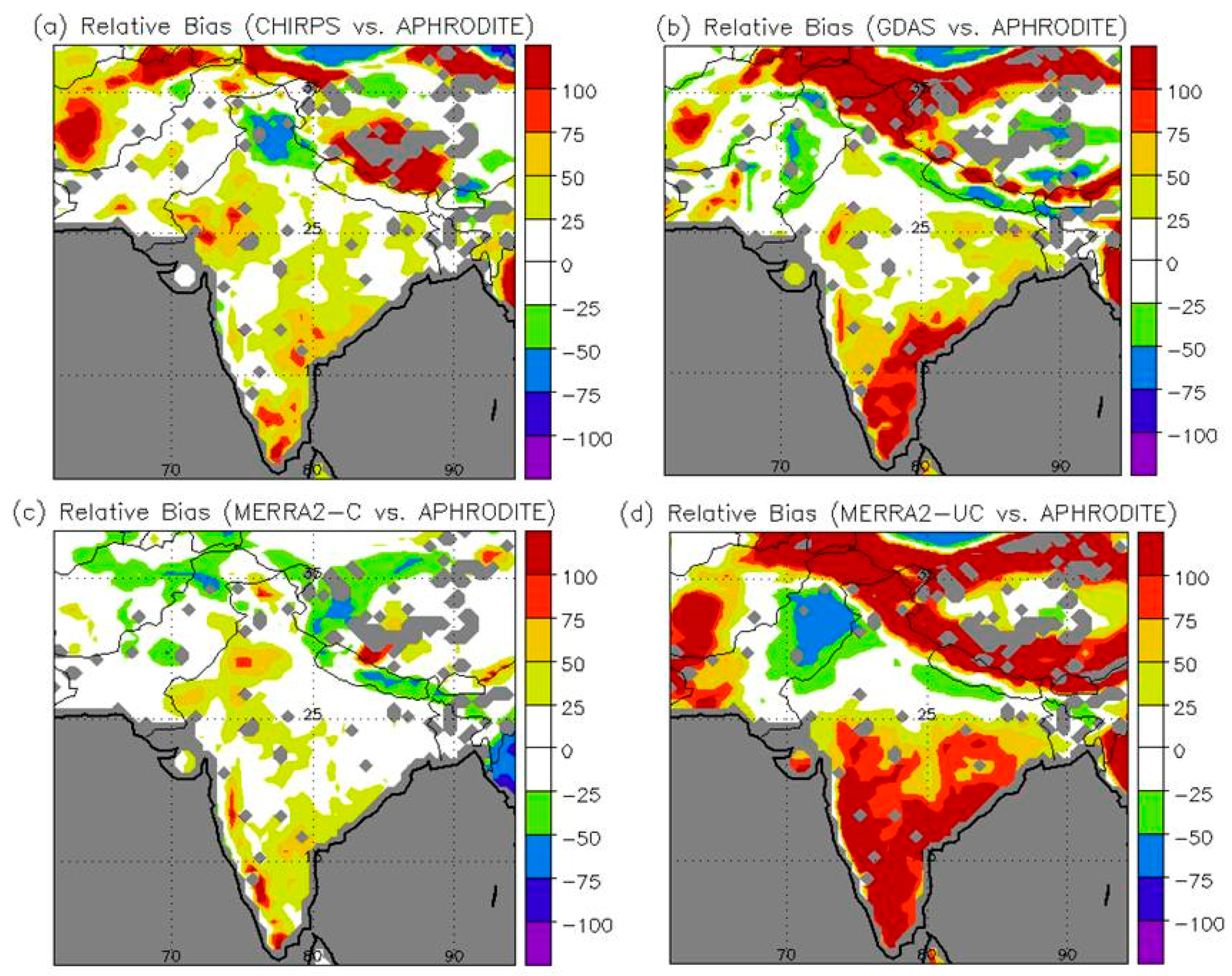
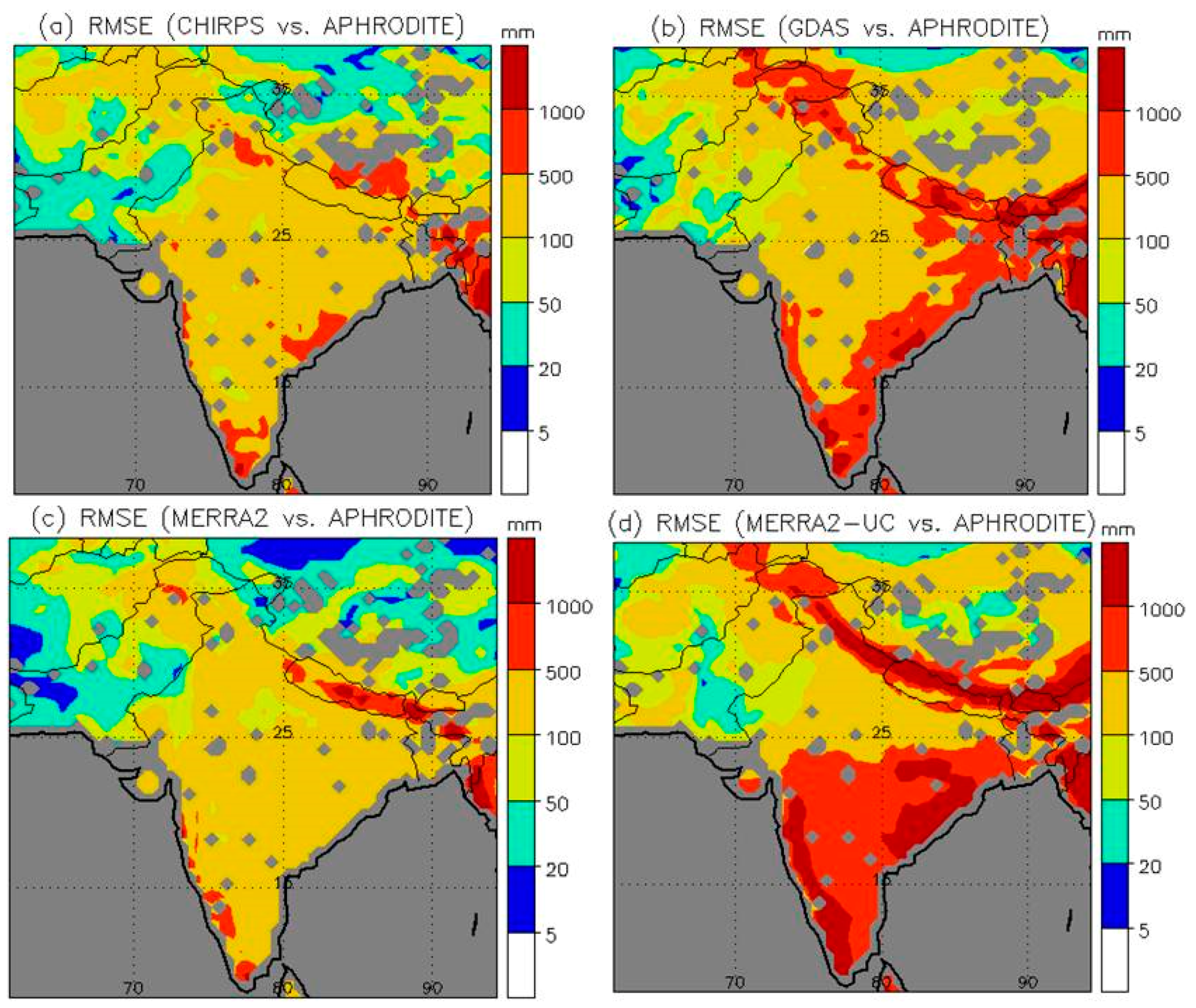
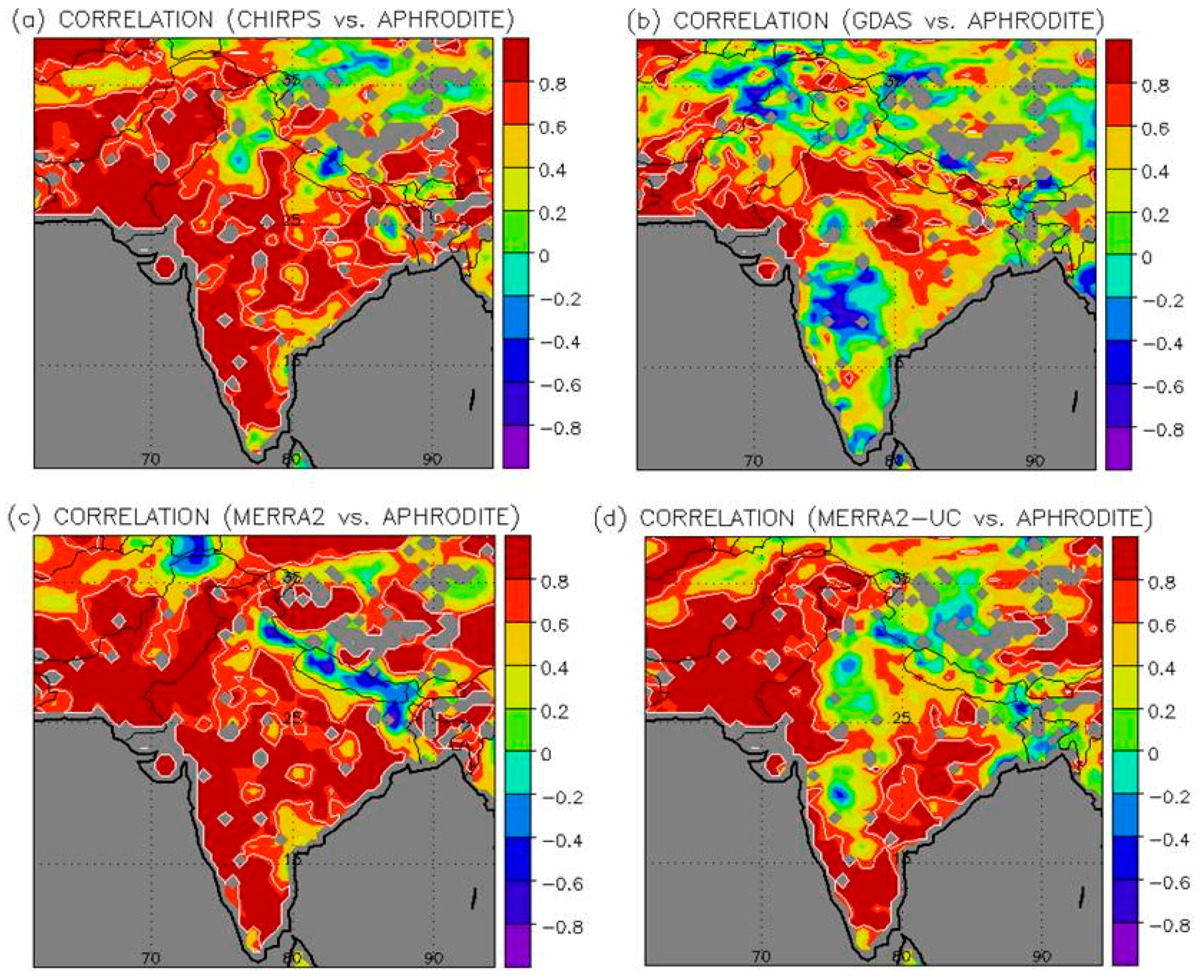
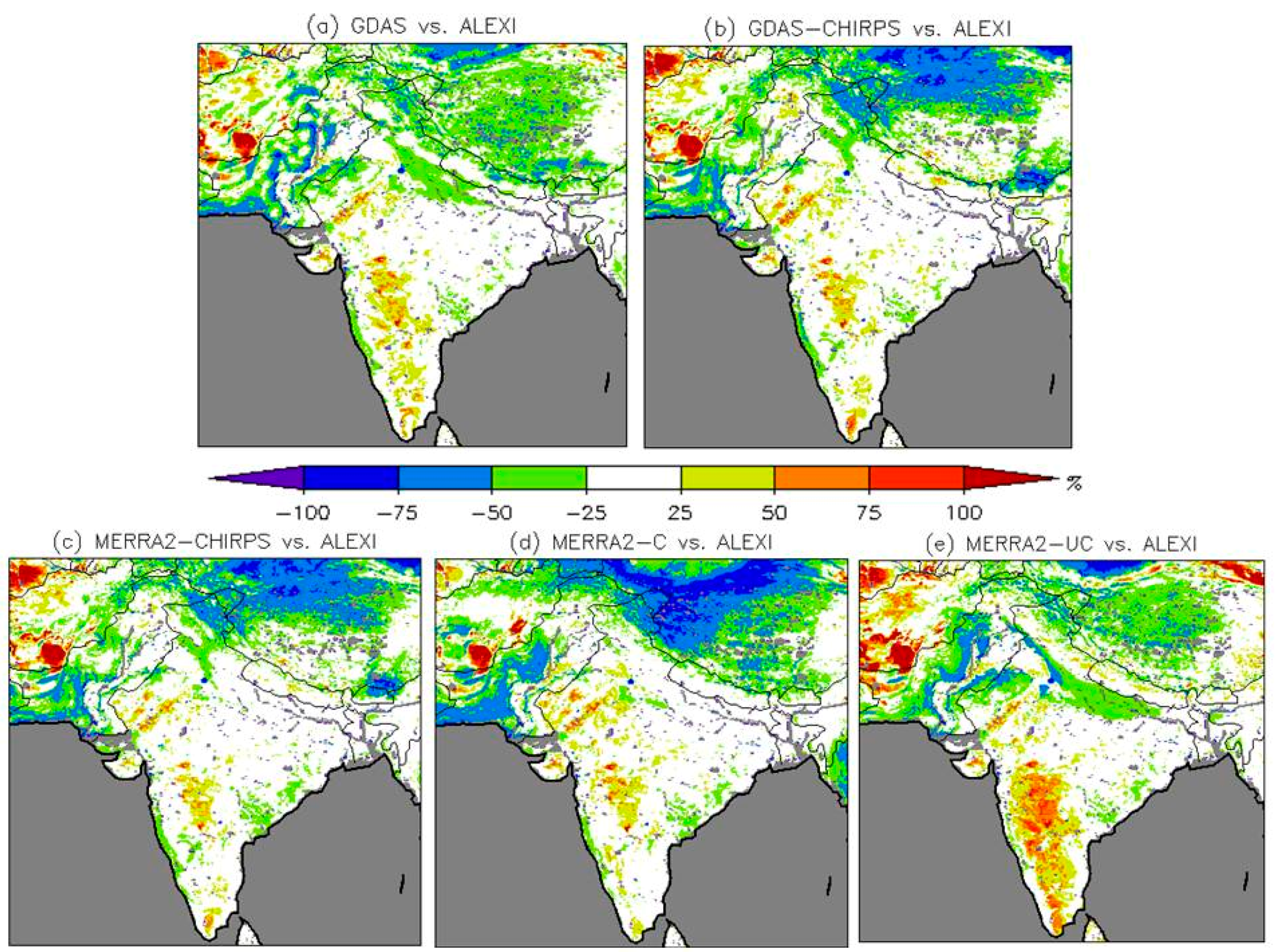
3.1. Meteorological Forcing
3.2. Evapotranspiration
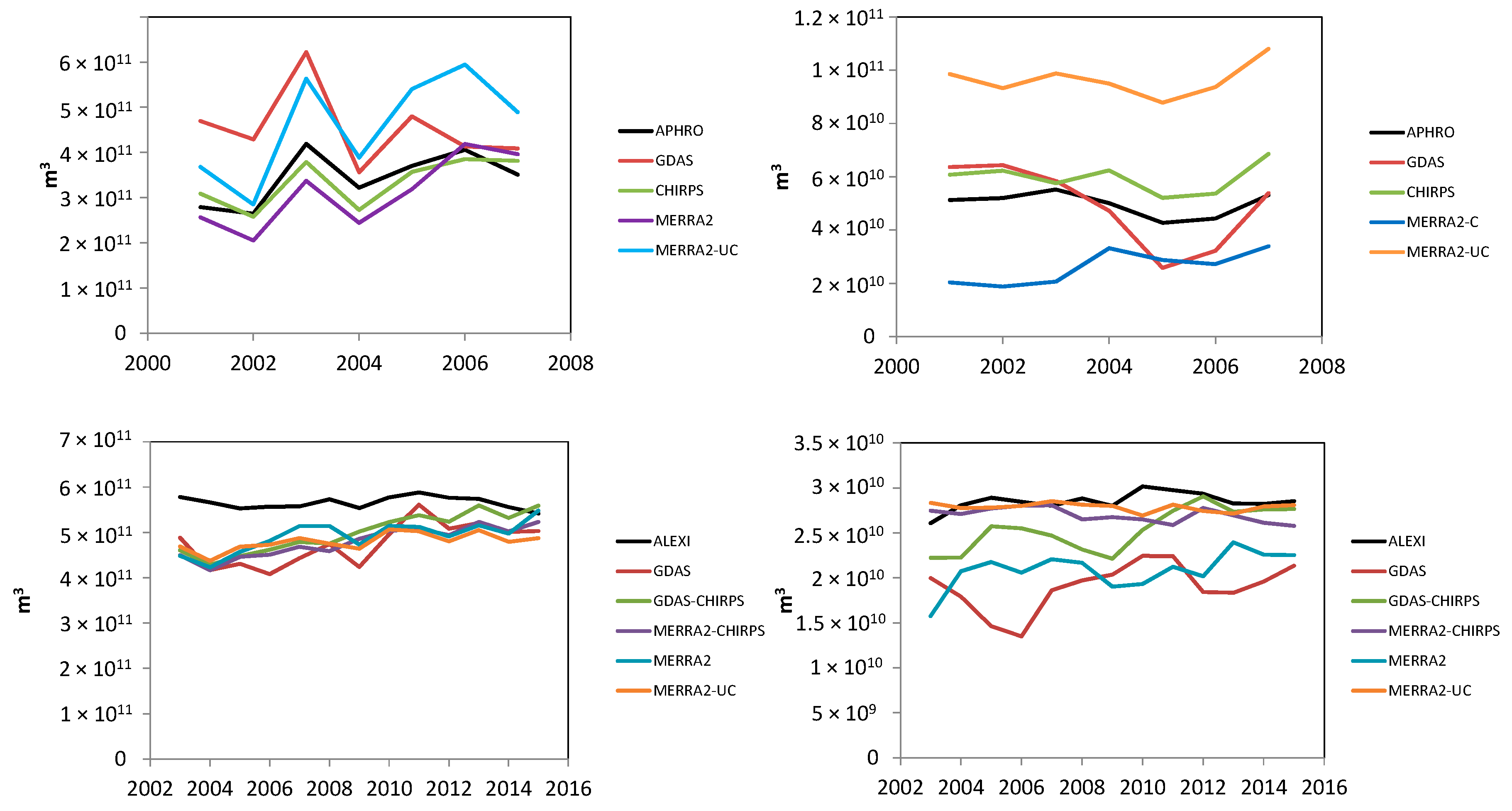
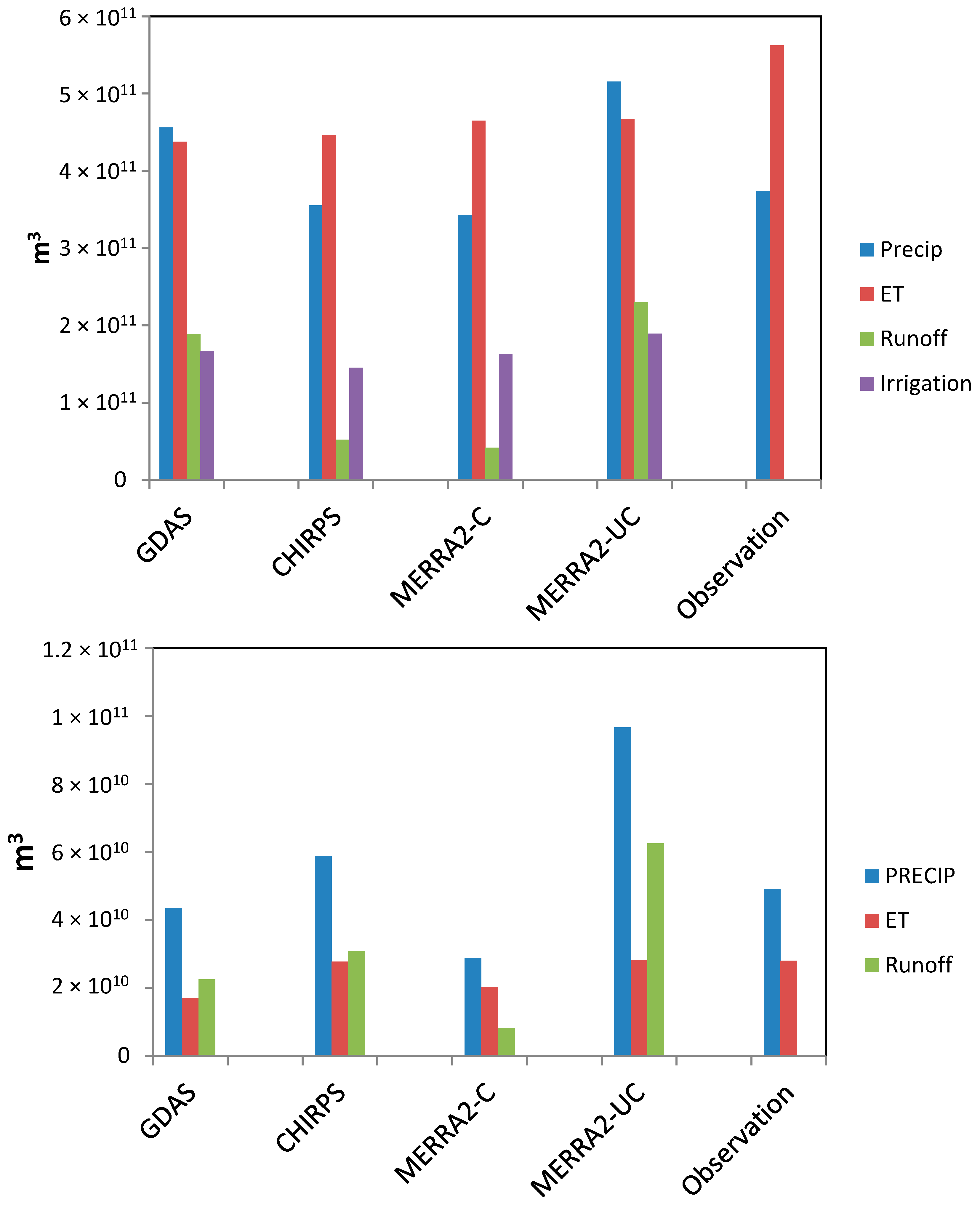
3.3. Basin Scale Analysis
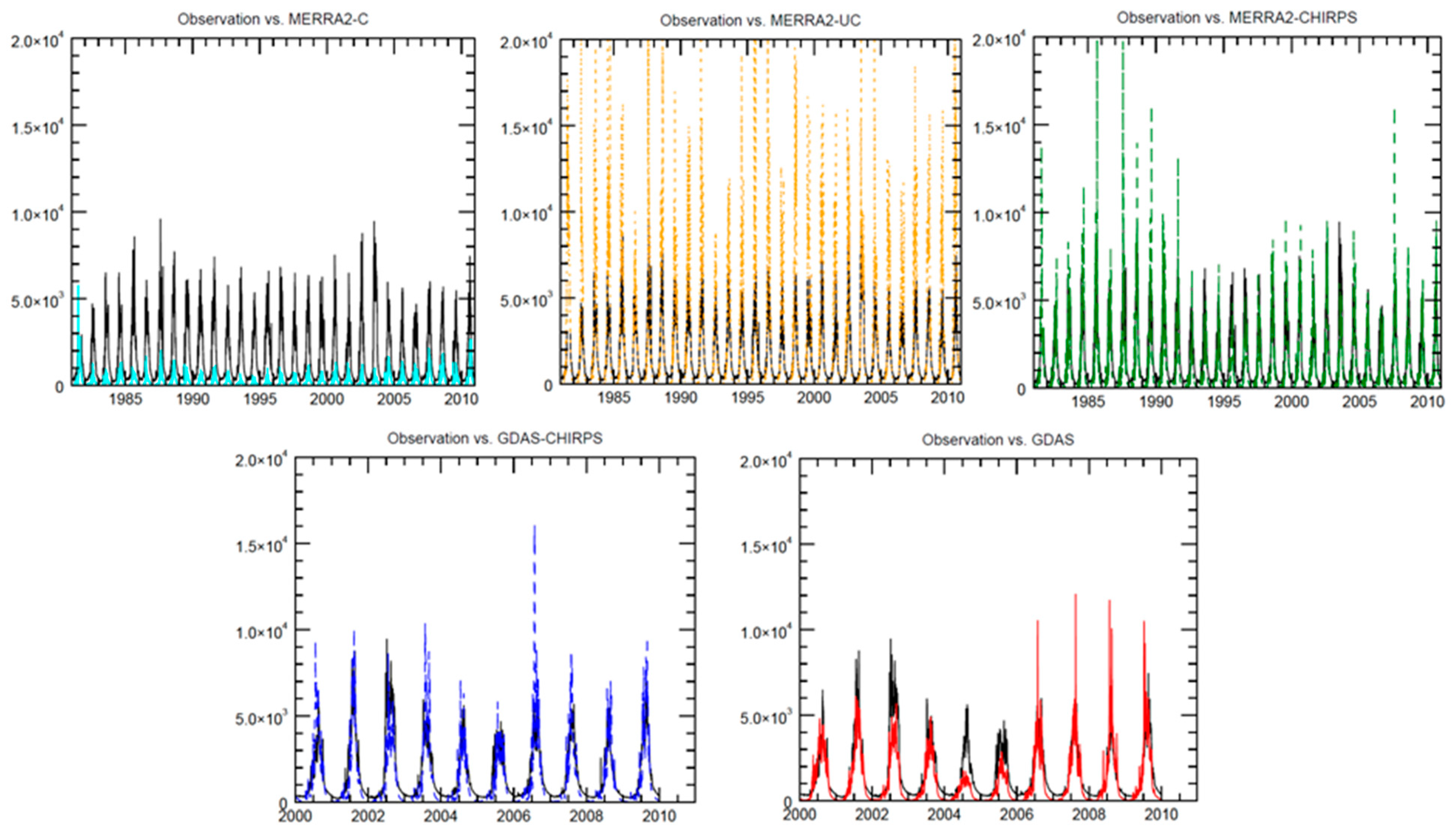
3.3.1. Precipitation and ET
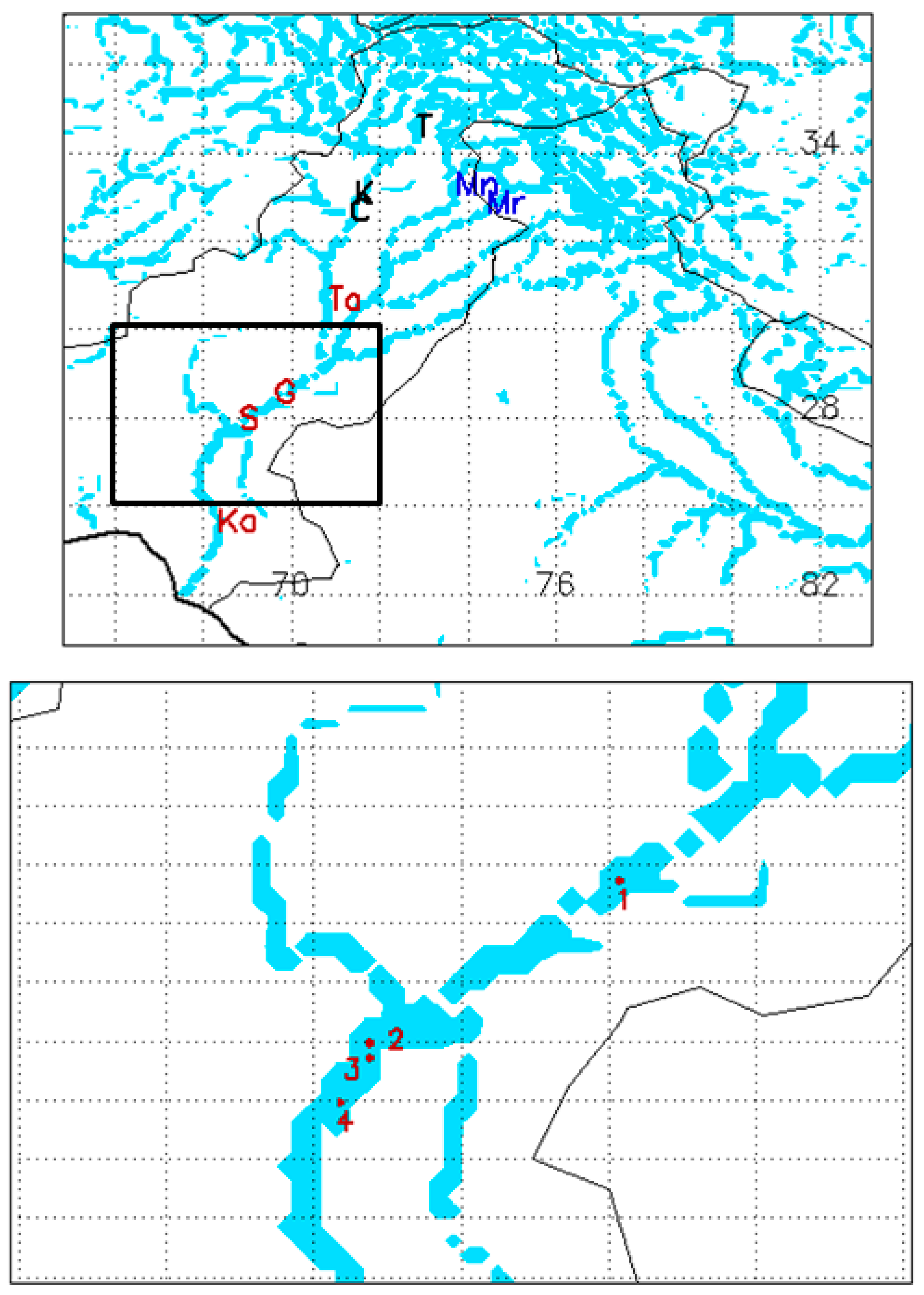
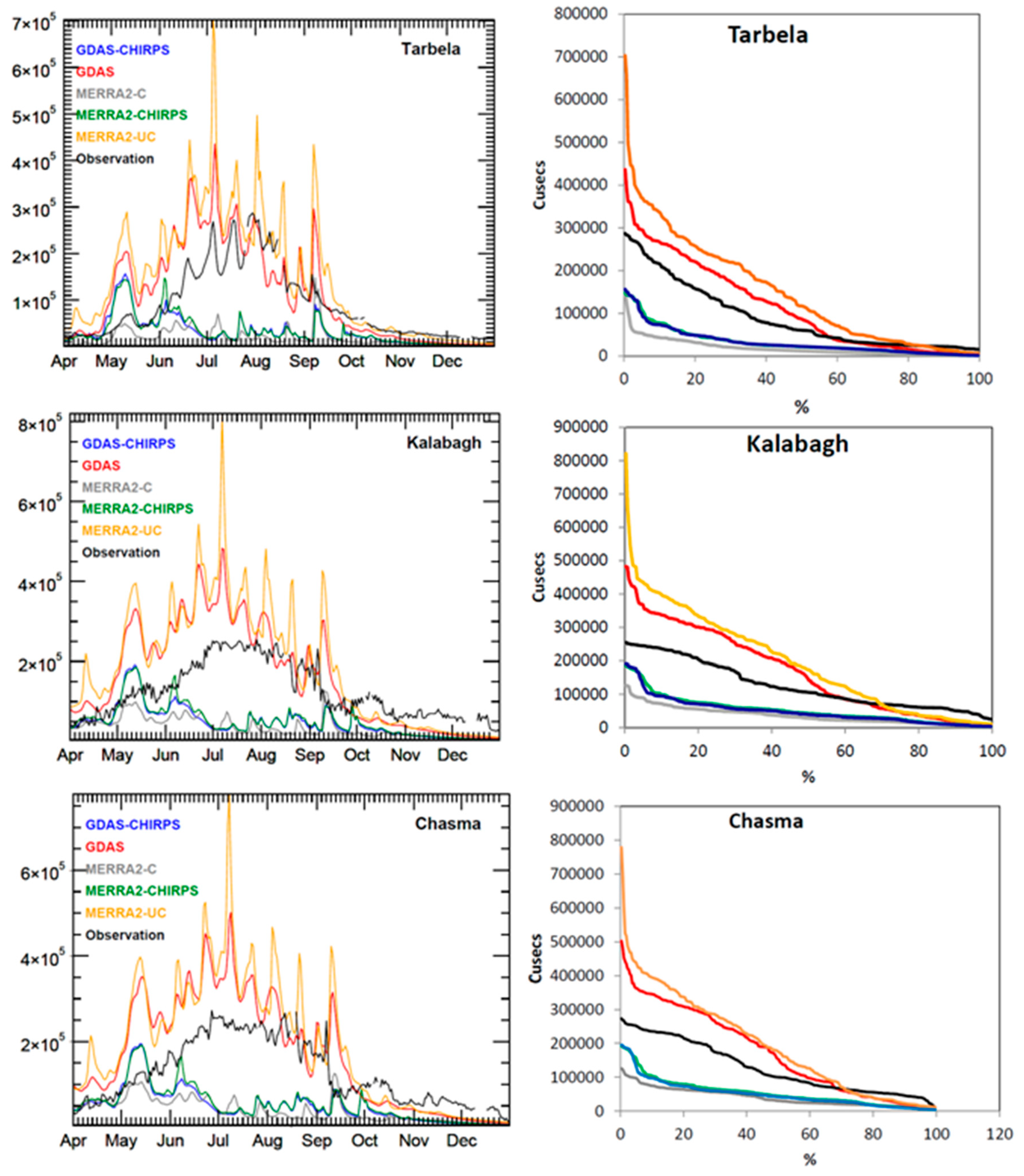
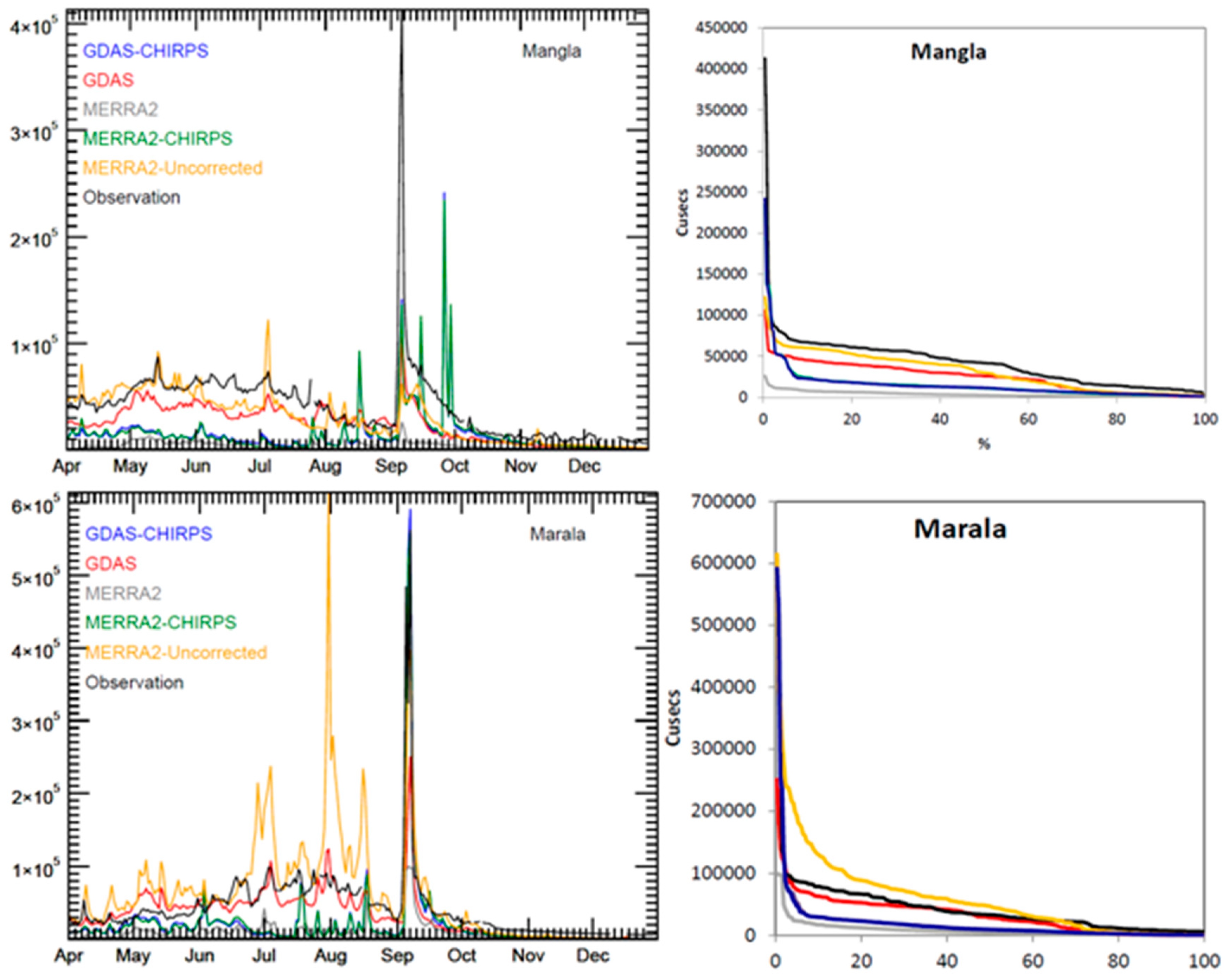
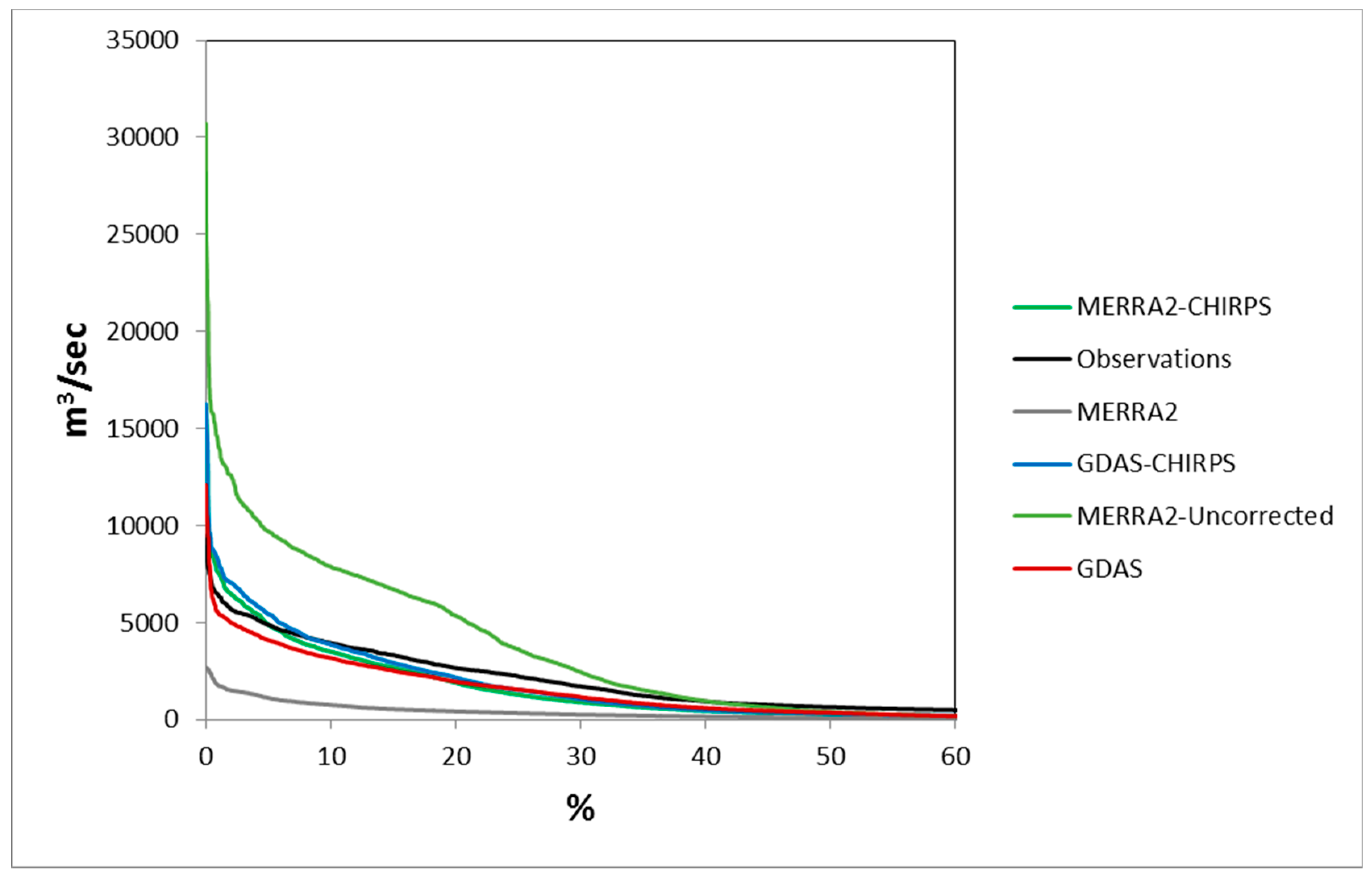
3.3.2. Streamflow
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hewitt, K. The Karakoram anomaly? Glacier expansion and the “elevation effect,” Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar] [CrossRef]
- Hewitt, K. Tributary glacier surges: An exceptional concentration at Panmah Glacier, Karakoram Himalaya. J. Glaciol. 2007, 53, 181–188. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Pellicciotti, F.; Bierkens, M.F.P. Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Mishra, V. Climatic uncertainty in Himalayan Water Towers. J. Geophys. Res. Atmos. 2015, 120, 2689–2705. [Google Scholar] [CrossRef]
- Ragettli, S.; Pellicciotti, F. Calibration of a physically based, spatially distributed hydrological model in a glacierized basin: On the use of knowledge from glaciometeorological processes to constrain model parameters. Water Resour. Res. 2012, 48, 1–20. [Google Scholar] [CrossRef]
- Winiger, M.; Gumpert, M.; Yamout, H. Karakorum-Hindukush-western Himalaya: Assessing high-altitude water resources. Hydrol. Process. 2005, 19, 2329–2338. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.; Kraaijenbrink, P.; Shrestha, A.B.; Bierkens, M.F. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Yamanokuchi, T.; Tadono, T.; Tomiyama, N. Detection of glacier lake using ALOS PALSAR data at Bhutan. In Proceedings of the American Geophysical Union, Fall Meeting 2010, San Francisco, CA, USA, 13–17 December 2010. [Google Scholar]
- Bajracharya, S.R.; Maharjan, S.; Shrestha, F.; Shrestha, B.; Wanqin, G.; Shiyin, L.; Xiaojun, Y.; Khattak, G.A. The Status of Glaciers in the Hindu Kush-Himalayas from satellite data. In Proceedings of the American Geophysical Union, Fall Meeting 2011, San Francisco, CA, USA, 5–9 December 2011. [Google Scholar]
- Bajracharya, S.R.; Maharjan, S.B.; Shrestha, F. The status and decadal change of glaciers in Bhutan from the 1980s to 2010 based on satellite data. Ann. Glaciol. 2014, 55, 159–166. [Google Scholar] [CrossRef]
- Bajracharya, S.R.; Maharjan, S.B.; Shrestha, F.; Bajracharya, O.R.; Baidya, S. Glacier Status in Nepal and Decadal Change from 1980 to 2010 Based on Landsat Data; International Centre for Integrated Mountain Development (ICIMOD): Kathmandu, Nepal, 2014. [Google Scholar]
- Bajracharya, S.R.; Maharjan, S.B.; Shrestha, F.; Guo, W.; Liu, S.; Immerzeel, W.; Shrestha, B. The glaciers of the Hindu Kush Himalayas: Current status and observed changes from the 1980s to 2010. Int. J. Water Resour. Dev. 2015, 31, 161–173. [Google Scholar] [CrossRef]
- Shrestha, M.N. Spatially distributed hydrological modelling considering land-use changes using remote sensing and GIS. In Proceedings of the Map Asia 2003, Kuala Lumpur, Malaysia, 17–19 July 2003. [Google Scholar]
- Shrestha, S.; Bastola, S.; Babel, M.S.; Dulal, K.N.; Magome, J.; Hapuarachchi, H.A.P.; Kazama, F.; Ishidaira, H.; Takeuchi, K. The assessment of spatial and temporal transferability of a physically based distributed hydrological model parameters in different physiographic regions of Nepal. J. Hydrol. 2007, 347, 153–172. [Google Scholar] [CrossRef]
- Nepal, S.; Krause, P.; Flügel, W.-A.; Fink, M.; Fischer, C. Understanding the hydrological system dynamics of a glaciated alpine catchment in the Himalayan region using the J2000 hydrological model. Hydrol. Process. 2013, 28, 1329–1344. [Google Scholar] [CrossRef]
- Dhar, S.; Mazumdar, A. Hydrological modelling of the Kangsabati river under changed climate scenario: Case study in India. Hydrol. Process. 2009, 23, 2394–2406. [Google Scholar] [CrossRef]
- Hengade, N.; Eldho, T.I. Assessment of LULC and climate change on the hydrology of Ashti Catchment, India using VIC model. J. Earth Syst. Sci. 2016, 125, 1623–1634. [Google Scholar] [CrossRef]
- Shah, R.D.; Mishra, V. Development of an experimental near real-time drought monitor for India. J. Hydrometeorol. 2015, 16, 327–345. [Google Scholar] [CrossRef]
- Mishra, V.; Shah, R.; Azhar, S.; Shah, H.; Modi, P.; Kumar, R. Reconstruction of droughts in India using multiple land surface models (1951–2015). Hydrol. Earth Syst. Sci. Discuss. 2017. [Google Scholar] [CrossRef]
- Hossain, F. Satellites as the panacea to transboundary limitations to longer range flood forecasting? Water Int. 2007, 32, 376–379. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and uncertainties in hydrological modeling of remote Hindu Kush-KarakoramHimalayan (HKH) basins: Suggestions for calibration strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Hossain, F.; Maswood, M.; Siddique-E-Akbor, A.H.; Yigzaw, W.; Mazumdar, L.C.; Ahmed, T.; Hossain, M.; Shah-Newaz, S.M.; Limaye, A.; Lee, H.; et al. A promising radar altimetry satellite system for operational flood forecasting in flood-prone Bangladesh. IEEE Geosci. Remote Sens. Mag. 2014, 2, 27–36. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Gaur, A.; Zwart, S.J. Integrating remote sensing and a process-based hydrological model to evaluate water use and productivity in a South Indian catchment. Agric. Water Manage. 2008, 95, 11–24. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land information system—An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Kato, H.; Rodell, M.; Beyrich, F.; Cleugh, H.; van Gorsel, E.; Liu, H.; Meyers, T.P. Sensitivity of land surface simulations to model physics, land characteristics, and forcings, at four CEOP Sites. J. Meteorol. Soc. Jpn. 2007, 87A, 187–204. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Olivera, F. Evaluation of the Global Land Data Assimilation System using global river discharge data and a Source-to-Sink routing scheme. Water Resour. Res. 2010, 46, W06507. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-term Daily Gridded Precipitation Dataset for Asia based on a Dense Network of Rain Gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Andermann, C.; Bonnet, S.; Gloaguen, R. Evaluation of precipitation data sets along the Himalayan front. Geochem. Geophys. Geosyst. 2011, 12, Q07023. [Google Scholar] [CrossRef]
- Kapnick, S.B.; Delworth, T.L.; Ashfaq, M.; Malyshev, S.; Milly, P.C.D. Snowfall less sensitive to warming in Karakoram than in Himalayas due to a unique seasonal cycle. Nat. Geosci. 2014, 7, 834–840. [Google Scholar] [CrossRef]
- Kanamitsu, M. Description of the NMC global data assimilation and forecast system. Weather Forecast. 1989, 4, 334–342. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suáreza, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randlesa, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2). J. Clim. 2017. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Kishtawal, C.M.; Pal, P.K. Skill of regional and global model forecast over Indian region. Theor. Appl. Climatol. 2016, 123, 629–636. [Google Scholar] [CrossRef]
- Shah, H.; Mishra, V. Uncertainty and Bias in Satellite Precipitation Estimates over the Indian Sub-continental River basins: Implications for streamflow simulation and Flood Prediction. J. Hydrometeorol. 2015, 17, 615–636. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA—NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011. [Google Scholar] [CrossRef]
- Ghatak, D.; Zaitchik, B.; Hain, C.; Anderson, M. The role of local heating in the 2015 Indian Heat Wave. Sci. Rep. 2017, 7, 7707. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M. Upscaling tower and aircraf fuxes from local to continental scales using thermal remote sensing. Agron. J. 2007, 99, 240–254. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration andmoisture stress across the continental United States: 1. Model formulation. J. Geophys. Res. 2007, 112, D11112. [Google Scholar] [CrossRef]
- Hain, C.R.; Crow, W.T.; Anderson, M.C.; Yilmaz, M.T. Diagnosing Neglected Soil Moisture Source–Sink Processes via a Termal Infrared–Based Two-Source Energy Balance Model. J. Hydrometeorol. 2015, 16, 1070–1086. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, J. New global hydrograph derived from spaceborne elevation data. Eos 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarplay, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Evans, J.P.; Zaitchik, B.F. Modeling the large scale water balance impact of different irrigation systems. Water Resour. Res. 2008, 44, W08448. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Anderson, M.C.; Zaitchik, B.F.; Hain, C.R.; Crow, W.T.; Ozdogan, M.; Chun, J.A.; Evans, J.P. Comparison of prognostic and diagnostic surface flux modeling approaches over the Nile River basin. Water Resour. Res. 2014, 50, 386–408. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Zaitchik, B.F.; Rodell, M. Impact of irrigation methods on land surface model spinup and initialization of WRF forecasts. J. Hydrometeorol. 2015. [Google Scholar] [CrossRef]
- Sanchez, P.A.; Ahamed, S.; Carré, F.; Hartemink, A.E.; Hempel, J.; Huising, J.; Lagacherie, P.; McBratney, A.B.; McKenzie, N.J.; Mendonça-Santos, M.L.; et al. Digital soil map of the world. Science 2009, 325, 680–681. [Google Scholar] [CrossRef] [PubMed]
- Getirana, A.C.V.; Boone, A.; Yamazaki, D.; Decharme, B.; Papa, F.; Mognard, N. The hydrological modeling and analysis platform (HyMAP): Evaluation in the Amazon basin. J. Hydrometeorol. 2012. [Google Scholar] [CrossRef]
- Scherrer, S.; Naef, F.; Faeh, A.O.; Cordery, I. Formation of runoff at the hillslope scale during intense precipitation. Hydrol. Earth Syst. Sci. 2007, 11, 907–922. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high altitude precipitation in the upper Indus Basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4755–4784. [Google Scholar] [CrossRef]
| Simulation | Resolution | Period | Land Surface Mode | Base Meteorological Forcing | Supplementary Precipitation |
|---|---|---|---|---|---|
| MERRA2 with corrected Precipitation | 10 km | 1980–2016 | Noah3.3 | MERRA2 | MERRA2 Corrected Precipitation |
| MERRA2 with uncorrected Precipitation | 10 km | 1980–2016 | Noah3.3 | MERRA2 | MERRA2 Uncorrected Precipitation |
| MERRA2-CHIRPS | 10 km | 1981–2016 | Noah3.3 | MERRA2 | CHIRPS |
| GDAS | 10 km | 2001–2016 | Noah3.3 | GDAS | GDAS |
| GDAS-CHIRPS | 10 km | 2001–2016 | Noah3.3 | GDAS | CHIRPS |
| Indus Basin (Pakistan) | GDAS | MERRA2-UC | MERRA2-C | MERRA2-CHIRPS | GDAS-CHIRPS | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | NSE | RMSE | NSE | RMSE | NSE | RMSE | NSE | RMSE | NSE | |
| Tarbela | 65,551.9 | 0.23 | 100,258 | −0.81 | 99,109.7 | −0.76 | 95,770.1 | −0.65 | 96,550.9 | −0.67 |
| Mangla | 31,559.0 | 0.26 | 32,221.8 | 0.23 | 51,251.6 | −0.95 | 42,559.9 | −0.34 | 42,141.3 | −0.32 |
| Marala | 36,022.6 | 0.53 | 56,568.2 | −0.15 | 54,894.9 | −0.08 | 39,416.3 | 0.44 | 40,112.9 | 0.42 |
| Kalabagh | 91,768.7 | −0.81 | 126,489 | −2.45 | 110,799 | −1.65 | 102,005 | −1.24 | 104,433 | −1.35 |
| Chasma | 91,374.9 | −0.52 | 121,648 | −1.69 | 112,319 | −1.30 | 103,420 | −0.95 | 106,488 | −1.07 |
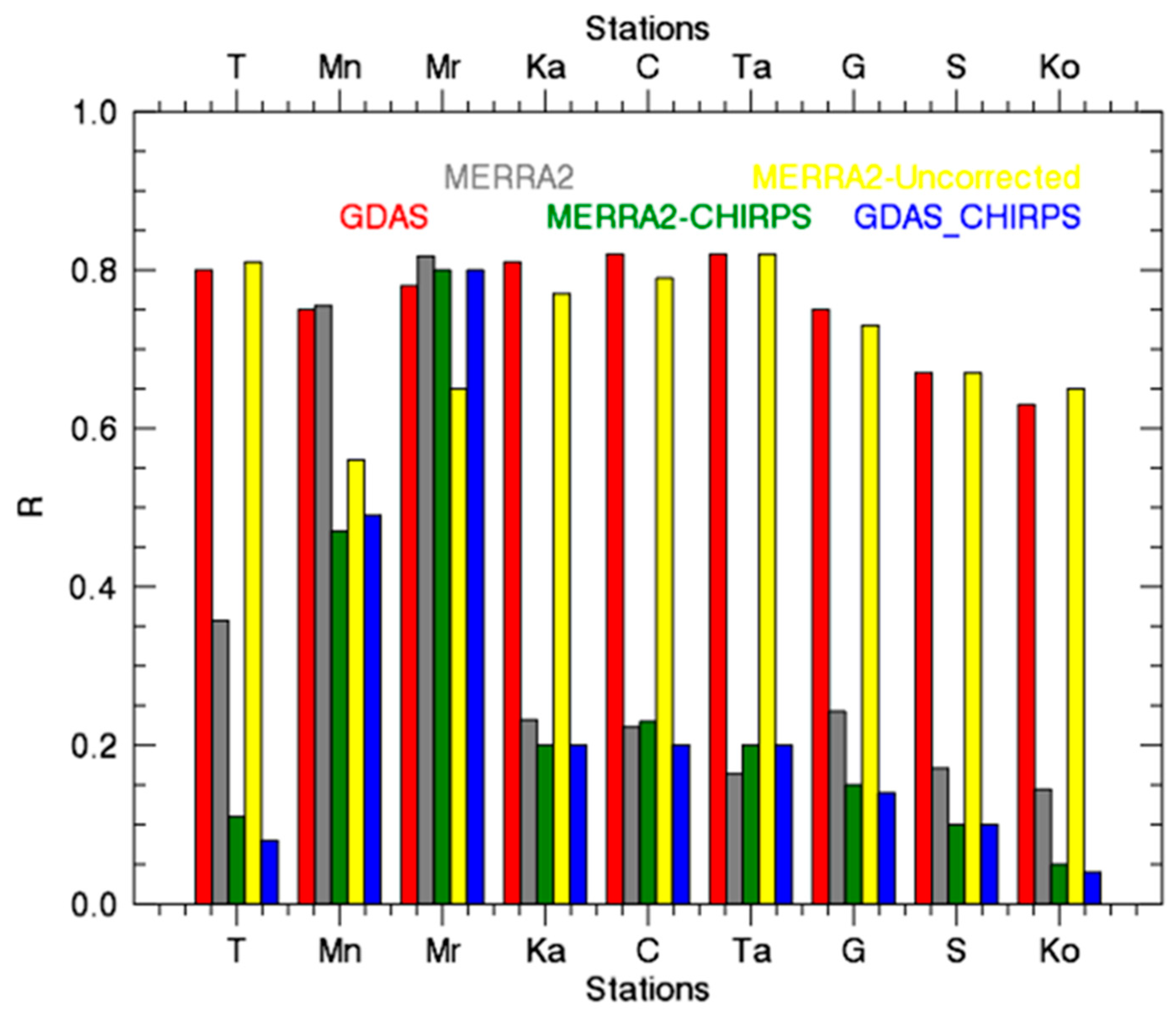
| R | GDAS | GDAS-CHIRPS | MERRA2-C | MERRA2-UC | MERRA2-CHIRPS |
|---|---|---|---|---|---|
| Site 1 | 0.84 | 0.54 | 0.65 | 0.85 | 0.53 |
| Site 2 | 0.75 | 0.49 | 0.60 | 0.80 | 0.47 |
| Site 3 | 0.71 | 0.5 | 0.57 | 0.78 | 0.49 |
| Site 4 | 0.79 | 0.6 | 0.61 | 0.8 | 0.55 |
| CHATTARA (Nepal) | GDAS (2001–2010) | GDAS-CHIRPS (2001–2010) | MERRA2-C (2001–2010) | MERRA2-UC (2001–2010) | MERRA2-CHIRPS (2001–2010) |
|---|---|---|---|---|---|
| R | 0.84 | 0.83 | 0.71 | 0.88 | 0.8 |
| RMSE | 970.003 | 1083.23 | 1864.18 | 2587.80 | 1149.37 |
| CHATTARA (Nepal) | GDAS (2001–2010) | GDAS-CHIRPS (2001–2010) | MERRA2-C (2001–2010) | MERRA2-UC (2001–2010) | MERRA2-CHIRPS (2001–2010) |
|---|---|---|---|---|---|
| R (Monsoonal Average) | 0.38 | 0.23 | −0.15 | 0.25 | 0.25 |
| RMSE (monsoon season only) | 1065.20 | 767.806 | 2750.17 | 3284.07 | 910.870 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghatak, D.; Zaitchik, B.; Kumar, S.; Matin, M.A.; Bajracharya, B.; Hain, C.; Anderson, M. Influence of Precipitation Forcing Uncertainty on Hydrological Simulations with the NASA South Asia Land Data Assimilation System. Hydrology 2018, 5, 57. https://doi.org/10.3390/hydrology5040057
Ghatak D, Zaitchik B, Kumar S, Matin MA, Bajracharya B, Hain C, Anderson M. Influence of Precipitation Forcing Uncertainty on Hydrological Simulations with the NASA South Asia Land Data Assimilation System. Hydrology. 2018; 5(4):57. https://doi.org/10.3390/hydrology5040057
Chicago/Turabian StyleGhatak, Debjani, Benjamin Zaitchik, Sujay Kumar, Mir A. Matin, Birendra Bajracharya, Christopher Hain, and Martha Anderson. 2018. "Influence of Precipitation Forcing Uncertainty on Hydrological Simulations with the NASA South Asia Land Data Assimilation System" Hydrology 5, no. 4: 57. https://doi.org/10.3390/hydrology5040057
APA StyleGhatak, D., Zaitchik, B., Kumar, S., Matin, M. A., Bajracharya, B., Hain, C., & Anderson, M. (2018). Influence of Precipitation Forcing Uncertainty on Hydrological Simulations with the NASA South Asia Land Data Assimilation System. Hydrology, 5(4), 57. https://doi.org/10.3390/hydrology5040057






