Abstract
Variability and covariability of land properties (soil, vegetation and subsurface geology) and remotely sensed soil moisture over the southeast and south-central U.S. are assessed. The goal is to determine whether satellite soil moisture memory contains information regarding land properties, especially the distribution karst formations below the active soil column that have a bearing on land-atmosphere feedbacks. Local (within a few tens of km) statistics of land states and soil moisture are considered to minimize the impact of climatic variations, and the local statistics are then correlated across the domain to illuminate significant relationships. There is a clear correspondence between soil moisture memory and many land properties including karst distribution. This has implications for distributed land surface modeling, which has not considered preferential water flows through geologic formations. All correspondences are found to be strongest during spring and fall, and weak during summer, when atmospheric moisture demand appears to dominate soil moisture variability. While there are significant relationships between remotely-sensed soil moisture variability and land properties, it will be a challenge to use satellite data for terrestrial parameter estimation as there is often a great deal of correlation among soil, vegetation and karst property distributions.
1. Introduction
Exchanges of heat, moisture, momentum, carbon, nutrients and other chemical species between land–atmosphere are important for weather, climate, hydrology, ecology, and a range of other natural and social sciences. In the aid of scientific understanding and prediction, numerical models have been developed to simulate and predict these exchanges and their effects. In weather and climate applications, land surface models (LSMs) have evolved from simple water and energy balance closure schemes into sophisticated modular codes incorporating the simulation of physical processes bridging many scientific disciplines [1,2,3,4,5].
The performance of LSMs depends on the availability of accurate data about the properties of land and their spatial distribution [6,7,8]. Different land properties are observed, and observable, with varying degrees of fidelity. For example, vegetation is fairly well monitored from satellite [9] and on the ground, especially where related to agriculture, forestry, and other economic resources [10,11,12]. Many satellite-based products such as vegetation or plant functional types [13] and physiological parameters like greenness, canopy density and height [14,15] are used as input to the ecological modules of LSMs. Identification of specific species using remote sensing remains very challenging [16]. Passive radiative measurements (shortwave reflection and longwave emission) are readily available from space when not obstructed by clouds or aerosols [17,18], but there are no direct remote-sensing measurements of canopy fluxes of water or carbon. Fluxes can be inferred from transport inversion models (carbon [19]), ecosystem models (e.g., primary productivity [20]), or other radiative retrievals (solar induced fluorescence for photosynthesis, carbon uptake and transpiration [21]).
Soils are unevenly surveyed around the globe, with measurements skewed toward agricultural areas and more developed countries [22]. Of particular importance for LSMs are characterizations of soil texture that affect the movement of water through the soil matrix, as well as chemical properties that affect the movement and uptake of nutrients by plants. There has been some progress in extraction of surface soil properties from satellite [23,24] usually only where bare soil is visible and with limited transferability of methods. However, the vertical structure of the soil throughout at least the rooting depth of vegetation (from the surface to several meters below the surface) is necessary for modeling the interaction of soil moisture with the atmosphere. Vertical structure information (soil horizons) typically requires field samples and laboratory testing, but spatial heterogeneity can be huge, making quality large-scale surveys very challenging. Satellite gravity measurements can be used to infer subsurface water storage, but at low spatial resolutions [25]. Nevertheless, there exist high-quality national, international and global-scale soils data sets applicable to land surface modeling [26,27,28].
Subsurface or vadose zone data, between the water table and the shallow realm of soil surveys, have historically been important for purposes of hydrologic modeling, constituting the least well observed portion of the “critical zone” [29]. However, application in LSMs has been fairly limited; LSMs typically assume a bedrock layer at a fixed depth, often not varying spatially, such that “baseflow” out of the bottom of the soil column is only a function of terrain slope and soil moisture in the lowest soil layer [30,31,32,33,34]. Much potentially useful geological data has been gathered as a result of fossil fuel exploration, but most of that data are proprietary and generally focused deeper than is typically hydrologically relevant for potential land-atmosphere interactions. Preferential flows and lateral water movement, above the water table as well as within, greatly affect local/regional hydrology [35,36]. Lumped hydrologic models are statistically calibrated to account for the cumulative effects of vadose zone characteristics on scales determined by catchment size (upstream of gauges and wells) [37,38]. Recent trends are toward distributed models of surface and subsurface water flow that are physically and structurally based [33,39,40,41], which require much more information at higher spatial granularity. For LSMs, inclusion of the spatial variations in preferential flow would provide a process currently missing, with impacts on soil drydown and land-atmosphere interactions [42,43].
The main motivation in this paper is to determine whether remotely-sensed soil moisture reflects the variations in land properties, especially the distribution subsurface karst formations, that could influence land-atmosphere feedbacks via the water cycle [44]. We demonstrate that satellite soil moisture sampled on near-daily intervals contains significant information about vegetation, soils and vadose zone properties. Variability in the vadose zone has not historically been considered important for land surface modeling and land-atmosphere interactions. Vegetation has long been understood to be an important modulator of near-surface soil moisture via transpiration, and woody species vertically redistribute water in the soil via their root systems to maintain moisture in their rhizosphere [45,46]. Soil properties, especially soil texture, control infiltration and drainage rates that affect drydown and the persistence of soil moisture anomalies [47]. However, subsurface geology, especially discrepancies between drainage characteristics of karst versus consolidated bedrock when near the surface, can also express in near-surface and surface soil moisture [36,42,43]. We focus on the southeastern and south-central (SE-SC) United States in this study, where a long warm (thawed) season and a great deal of heterogeneity in vegetation, soils and karst distributions exist, providing a good testbed for detection of signals from remote sensing. Additionally, good quality high-resolution surveys of properties and distributions of all three categories of characteristics optimize the likelihood of attribution of soil moisture changes to surface and subsurface variability of these characteristics.
2. Data Sets and Methods
2.1. SMAP
The Soil Moisture Active Passive (SMAP) satellite mission [48], despite failure of the active radar power supply, is producing a high-resolution global soil moisture product with higher information content that previous satellite soil moisture products [49]. The 9 km (nominally ≈5.6 arc min) resolution enhanced level 3 product based only on the passive sounder [50] is used for this study, representing soil moisture content in the top few centimeters of soil. As with all satellite soil moisture products, this is not a direct measurement of soil water content, but an estimate based on measurement of upwelling radiation (in this case polarized microwave radiation at specific wavelengths) that has been found to correlate strongly with the presence of water at the Earth’s surface. Maps of urbanization, lakes and open water bodies are used to screen out regions of likely signal contamination and systematic error [50]. Where vegetation is not sparse, plant water content attenuates the signal to some degree; we do not screen out data from any vegetated areas as the temporal variability from these areas is still informative as described below. SMAP has an 8-day orbital repeat period, but due to the scanning pattern there may be, at mid-latitudes, anywhere from 0 to 3 days between measurements at any location. For this analysis, data spanning 29°–40° N, 104°–83° W are considered (the domain shown in Figure 1) spanning April 2015 through October 2017.
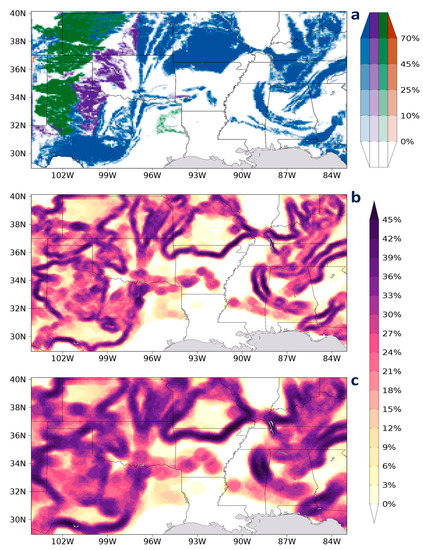
Figure 1.
Domain of study showing: (a) distribution of shallow karst coverage in each 9 km grid cell; carbonates (blue), evaporates (green), unconsolidated pseudokarst (purple), volcanic (orange); spatial standard deviation of total karst coverage percentage within radii of (b) 0.3°; (c) 0.5°.
The soil moisture variable considered in this analysis is soil moisture memory (SMM), which is the time in days at which the lagged autocorrelation of soil moisture S: drops to 1/e, where t is time and is lag, both in days. This calculation is performed independently for boreal spring, summer and fall for (season registered to the earlier of the two dates compared for each lag) and separately for data from AM and PM overpasses. With data missing at any location from about 50–70% of days depending on overpass patterns, autocorrelations for each lag are calculated from all lagged data pairs where neither datum is missing. This maximizes the data available for the SMM estimates. A linear regression is then applied to the log of the correlation at each lag , which behaves like a first-order Markov process [51], and the intersection of the regression with gives the memory time scale . For any particular day and overpass (AM or PM), swaths of all available data over the study area are used. Viewed at any arbitrary 9 km grid cell, what results are two time series, one for AM overpasses and one for PM, with data present for a fraction of the days. For each lag, at least 25 data pairs must be available in the season for to be calculated; enough days have data so that 75–80% of grid cells have at least 8 of the 20 possible lags contributing to the estimate of .
Three approaches to calculating the linear regressions were tested: a simple unweighted approach, one where at each lag is weighted by the sample size, and one where weights based on sample size and . The last approach, which presumes that estimation of becomes less confident as autocorrelations become small, is found to produce generally better correspondences with land surface and subsurface characteristics, and is used throughout this study. The value of SMM in days for any season is the geometric mean of from AM and PM overpasses. All land surface data sets described below are interpolated or projected to the same 9 km equidistant cylindrical grid as the SMAP data, and are listed in Table 1.

Table 1.
List of land properties examined in this study.
2.2. Karst
The United States Geologic Survey (USGS) recently produced the most complete and accurate karst database to date over the U.S. [52]. Spatial data was compiled from lithologic map units on state geologic survey maps at scales ranging from 12–250 m, cave and karst field researchers, as well as the research and experience of the authors. GIS polygon data delineate the type of karst and two depth categories: shallow and deep, which are divided at a depth of 15.2 m. Only the shallow karsts are considered here, as they are much more likely to affect surface soil moisture. Most karst in SE-SC U.S. develops from carbonate rock, but the data set also indicates evaporate, unconsolidated calcareous, and volcanic karsts. Data are projected onto the 9 km SMAP grid as the percentage of karst polygon area in each grid cell.
2.3. Soils
Two soils data sets are examined. First, the top layer of a multi-layer gridded version of the State Soil Geographic Database (STATSGO) data set is used, which provides a small set of soil texture classes from which soil properties are assigned [53]. The gridded data are at 30 arc s resolution over the conterminous United States (CONUS) on a latitude–longitude grid, and four parameters are assigned to each class: porosity, saturated hydraulic conductivity, surface suction head, and the “b” parameter of Clapp and Hornberger [54]. The STATSGO data set has a long history of use for land surface modeling, but the limited number of classes (12 are used here) means characterizations are not very precise.
A more detailed characterization of soils over CONUS is provided by the Soil Survey Geographic Database (SSURGO) [28]. The gridded version of the data, gSSURGO [55], is available at 90 m resolution over CONUS. These data have been subsampled to 180 m on the original Albers Equal Area projection and then regridded based on area-weighted map unit coverage to the same 30 arc s grid as the STATSGO data above using GRASS-7.2.2 [56]. Twelve parameters are retained: average percentages of sand, silt, clay and organic matter content, available water capacity, saturated hydraulic conductivity (both depth-weighted arithmetic means and harmonic means are provided), bulk density, porosity, horizon thickness, volumetric content of soil water retained at 33 kPa, and plant available volumetric water in the top 25 cm of soil.
For use in the following comparisons, both STATSGO and gSSURGO data are aggregated from the 30 arc s grid to the SMAP 9 km grid by bilinear interpolation, which, given the disparity in grid resolutions, amounts to an area averaging.
2.4. Vegetation
The central and eastern portions of the SE-SC domain have nearly complete vegetation cover. Vegetation affects, and is affected by, soil moisture largely through water flux to the atmosphere via transpiration, which is closely related to the rate of photosynthesis [57]. Solar-induced fluorescence (SIF) can be measured by satellite, and corresponds to the amount of chlorophyll present in plants. A proportionality exists between SIF, photosynthesis and transpiration [58] that is useful for this investigation. The Global Ozone Monitoring Experiment-2 (GOME-2) SIF version 27, level 3 data set [21] merges retrievals from the GOME-2 instruments on the MetOp-A and -B satellites, covering the period 2007–2017 at monthly time resolution, but a spatial resolution of only 0.5°—much coarser than the other data used in this study. Nevertheless, it represents a way to correlate vegetation with both soil moisture and the other surface and subsurface properties described above. Monthly means and intra-monthly sampling variances are provided for three derivations of SIF: a direct estimate, an estimate based on a clear-sky proxy of surface photosynthetically active radiation (PAR), and a PAR-normalized (by solar zenith angle) fluorescence at 737 nm, as well as for normalized difference vegetation index (NDVI). These fields are projected to the SMAP 9 km grid by bilinear interpolation.
2.5. Analysis Methods
There are many factors that affect SMM and contribute to its variability, and it is a challenge to differentiate them. Past studies have used statistical techniques like Granger causality to isolate the soil moisture signal from other factors in climate variability [59,60,61]. There are several outstanding issues in this study that warrant a careful approach to signal extraction. One problem is that weather is a confounding factor independent of land properties, particularly for a short data set like SMAP; weather variability can lead to significant precipitation heterogeneity on scales of 10 to 100 km, contributing to similar heterogeneity in soil moisture. In order to minimize the impact of weather variability, comparisons need to be as localized as possible, better isolating the structural heterogeneity of the land. The common 9 km grid allows for a fairly high-resolution assessment relative to synoptic and even mesoscale weather systems. Furthermore, the regridding of the various data sets to the SMAP 9 km grid, along with possible geo-registration errors and other sources of error, can degrade signal and add noise, negatively impacting the direct spatial correlations upon which linear regression techniques are based. A strongly aggregating approach insensitive to such data set disparities is needed to wring out any signal that is present.
Our solution is to concentrate on isolating and attributing local variability in SMM to local variability in land properties. This approach can also be applied among land properties, but is born out of initial tests to detect the signal of karst variability on SMM. As shown in Figure 1, karst distribution over SE-SC U.S. tends to be in coherent bands and areas separated by broad areas with no karst. Considered on the granularity of the SMAP data, for each grid cell we pick all neighboring cells within a selected radius and calculate the spatial correlation between SMM and each of the gridded land properties, as well as among the properties. We have tested radii of 0.3° and 0.5° for all properties except vegetation, where 0.5° and 1° radii have been tested.
We expect, with so many variables potentially affecting SMM and noise in observed data, that strong localized spatial correlations are most likely to be detected for a land property that also has a high degree of variation within the radius, and insignificant where that property is fairly homogeneous. Figure 1b,c displays this variability for karst calculated at each radius, showing variability is strongest around the edges of formations. Other land properties have various patterns (not shown). We also investigate relationships among different land properties which might also be illuminating.
To test whether variability in any particular land property A may be related to variability in another variable B (which may be SMM or some other land property) over the SE-SC domain, the standard deviations of all terms within each radius centered on each land grid cell are calculated: , where each is a 2-dimensional field with values for each cell on the 9 km grid where neither A nor B has missing data. We additionally calculate the within-radius correlations between A and B at each grid cell: . Three domain-wide spatial correlations across all cells are then calculated: reveals the degree to which large and small local variability between A and B are spatially synchronized across SE-SC US; indicates whether there is emergence of strong covariability of land properties A and B where local variance in A is large; similarly links explained variance between A and B with local variance in A. and produce one-tailed distributions as we expect meaningful domain-wide correlation to be positive, but could be either positive or negative depending on the processes linking A and B, so this metric is judged as a two-tailed probability distribution.
Note that the degrees of freedom in these domain-wide spatial correlations necessarily decrease as the radius increases, giving another advantage to the choice of small radii for significance testing. Areas of missing data also reduce degrees of freedom. We find that the values of R estimated with the smaller radius are usually about the same or slightly higher than with the larger radius, even for SIF, verifying the advantage of using the smaller radius. We have also employed a non-parametric Monte Carlo approach for significance testing when variable B is SMM, creating 1000 samples of SMM by spatially shifting the grid quasi-randomly with cyclic lateral boundaries in both latitude and longitude and recalculating. This was found to be necessary after preliminary analysis with the karst data—the striping structure of the within-radius standard deviations surrounded by regions of zero variance shown in Figure 1b,c leads to a range of values of that do not cluster normally around 0 in a Monte Carlo test, although they do for the other two metrics. We make no assumptions about distributions for any land properties and use non-parametric significance testing for all comparisons with SMM.
As an additional test, we examine whether there is non-randomness in the within-radius correlations between paired variables across the entire SE-SC domain by calculating the inverse of the coefficient of variation of within-radius correlations (CV−1) of across all grid cells. Values near zero indicate there is no strong systematic positive or negative correlation (the sign of the covariance reflects the predominant sign of the within-radius correlations). A large amplitude suggests a robust, high-signal/low-noise relationship between the two variables across the domain.
3. Results
3.1. Relationships Among Land Surface Parameters
Before relating SMM to land properties, we look at the relationships among the properties. We expect to find a great deal of interdependence among some variables, especially within the same data set. However, it is the relationships across independent data sets that may be most informative.
Figure 2 is a “chicklet chart” showing values of and CV−1 calculated between each pair of land properties for the time-invariant soil and karst fields. Karst coverage terms are not intercompared because there is very little overlap between the different karst types. values (cells above the diagonal) show expectedly strong relationships among STATSGO parameters, which are constrained by coming from a relatively small lookup table. Among gSSURGO parameters, porosity is directly calculated from bulk density using a linear formula, so their local variances are perfectly correlated across the domain. Local variabilities among most gSSURGO parameters are generally highly correlated, with two exceptions: Organic matter content and thickness of sampled soil column. Variability in organic matter is highly correlated with variability in bulk density and porosity as the presence of organic matter in the soil strongly decreases density. Between STATSGO and gSSURGO, there is generally agreement similar to what is seen among gSSURGO parameters. However, it is interesting to note that porosity, which is one of only two parameters common between STATSGO and gSSURGO, shows a rather weak value of of only 0.25. Many LSMs still use STATSGO porosity values, which seem not to agree with the more laboratory-constrained gSSURGO values.
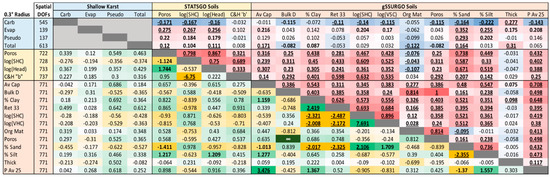
Figure 2.
Above the diagonal with a blue-to-red color scale: , the degree to which the magnitudes of local variability are spatially synchronized across the domain between the pair of parameters; below the diagonal with a yellow-to-green scale: the inverse of the coefficient of variation of within-radius correlations (CV−1) across the domain. For , values significant at the 95% confidence level based on indicated spatial degrees of freedom are bold, 99% confidence are underlined. For CV−1, values ≥1 are bold, ≥2 are underlined.
Variability in carbonate karst, which predominates in all but the western part of the SE-SC domain, is seen to be anticorrelated with variability in most soil properties, usually significantly so. Looking at CV−1 (cells below the diagonal in Figure 2), absolute values above 1.0 have a larger magnitude of mean within-radius correlations between the pair of parameters than the spatial standard deviation of those correlations across the domain. Those occur frequently for parameters within the same soils data set, but also between STATSGO and gSSURGO data wherein STATSGO porosity corresponds well to gSSURGO sand and silt percentages (but not porosity), and STATSGO suction head corresponds to gSSURGO silt percentage. Although none of the soils parameters correspond strongly to karst parameters (|CV−1| < 0.7), there is a clear tendency for the correspondences to be higher with gSSURGO than with STATSGO, again suggesting gSSURGO is more representative at these scales. Clay generally tends to be more prevalent over karst and sand less prevalent, so the preferential drainage typical of karst is often countered by the low conductivity of more clay soils above.
Correspondence between SIF parameters and those shown in Figure 2 are displayed in Figure 3. SIF varies in time, so seasonal mean parameters are shown in three sets of columns. SIF parameters show much higher values of when compared with gSSURGO properties than with STATSGO properties in all seasons, despite similar degrees of freedom. SIF also shows significant when compared to total karst, and often with carbonate karst, which dominates the total karst variability. Values are greatest during SON, when soil moistures are generally lowest and vegetation is the most stressed. The correspondence suggests a relationship between vegetation variability and karst variability that appears to be stronger than the correspondence between soils and karst variability (Figure 2). Not surprisingly, the correspondence between soils and vegetation variability is often as strong or stronger than between vegetation and karst, as the soils are in direct contact with the roots of the vegetation.
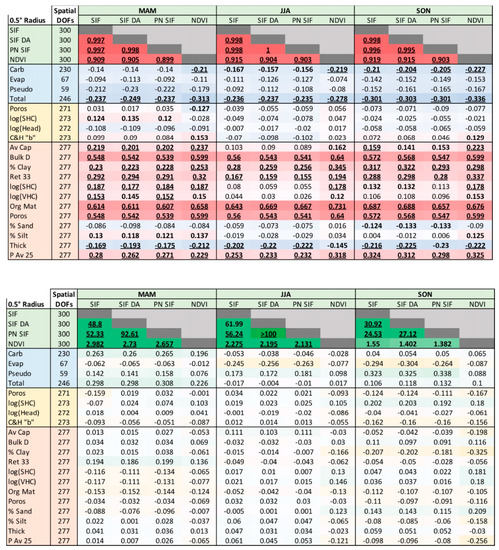
Figure 3.
As in Figure 2 including seasonal (spring = March–April–May “MAM”; summer = June–July–August “JJA”; fall = September–October–November “SON”) SIF parameters.
Meanwhile, CV−1 in Figure 3 is quite low for all but the pairings between SIF parameters. Between karst and SIF there is an interesting seasonal evolution in CV−1; Carbonate karst tends to covary with SIF and NDVI more prominently during MAM, but not other seasons, while over evaporative karst and unconsolidated pseudokarst, CV−1 grows in magnitude from spring to fall as soil moisture stress grows. Furthermore, plant vitality is anticorrelated with coverage of evaporative karst, which predominates in the far western part of the domain, but is positively correlated to pseudokarst.
3.2. Soil Moisture Memory and Land Surface Parameters
Figure 4 shows the non-parametric spatial correlation significances across the area of the local (within-radius) statistics described in Section 2.5 between SMM and the listed land properties as a function of season. Note that only a subset of the gSSURGO parameters are chosen. For and only high percentile rankings, corresponding to positive correlations, are representative of potential land property influence on SMM, so a one-tailed test is used. For either positive or negative values of can have a viable physical meaning relative to large , so a two-tailed test is appropriate.
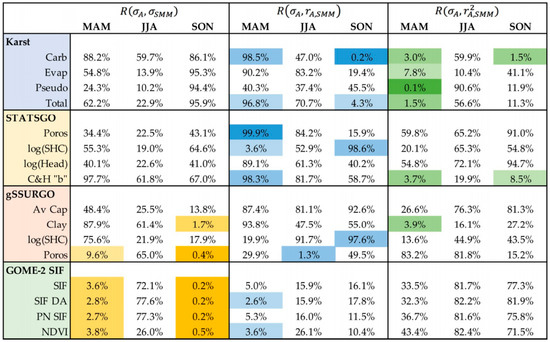
Figure 4.
Nonparametric rankings as a function of season for the domain wide spatial correlations R between within-radius standard deviation of the properties A listed at the left and the indicated terms: standard deviation of SMM on the left (yellow highlights); correlation between A and SMM (center, blue highlights); explained variance between A and SMM (right, green highlights). Highlight shades progress from lighter to darker for significance thresholds of 10%, 5% and 1% as described in the text.
Several features are evident in Figure 4. First, JJA has the weakest signal, suggesting that SMM is not greatly controlled by land properties in this season. JJA is a time of peak potential evapotranspiration, and the strong atmospheric demand for evaporated water becomes the dominant factor affecting soil moisture. Land properties are much more important determinants of spatial patterns of SMM during spring and fall. Second, local variations in vegetation properties are very strongly associated with local variability of SMM. During spring and fall, domain-wide correlations between within-radius standard deviations of GOME-SIF parameters and SMM are significant at confidence levels ranging from 96.2–99.8% (100% minus the ranking percentage shown). is an indicator of local correlations emerging clearly when there is more small-scale land properties variability . This is significant for the vegetation properties only during spring. Because SMAP retrievals preferentially detect water in and on vegetation when NDVI is large, SMM could actually be vegetation moisture memory in much of the eastern US, although the two memories are undoubtedly connected.
A third feature is that soil properties also show strong correspondence with SMM during spring and fall. Interestingly, while both STATSGO and gSSURGO data show emergent correspondence with SMM where there is large local variability in soil properties , gSSURGO shows more signal in direct correlation between the standard deviations , especially in fall. Karst also shows strong emergent correspondence. For pseudokarst, strong correspondence exists for local explained variance but not local correlation . This is an indicator that both positive and negative local correlations exist in different parts of the pseudokarst area in Oklahoma and Texas. This divergent feature can be understood in light of the final characteristic revealed in Figure 4, reversal of sign of the correlation in between spring and fall for SMM correspondence to karst and to saturated hydraulic conductivity (SHC).
Figure 5 illustrates our interpretation of the fact that the fraction of karst coverage is anticorrelated with SMM in spring but positively correlated in fall, while soil saturated hydraulic conductivity is positively correlated with SMM during spring and negatively correlated in fall. The crucial factor is that during spring soil moisture is generally at its maximum value in the climatological seasonal cycle, while in the fall it reaches its minimum. Particularly, in spring there is usually abundant moisture available below the surface while in fall there typically is not. Over most of the region, the seasonal cycle of precipitation is relatively weak, but there is a strong cycle of evaporation. Thus, their difference () switches from positive to negative in spring, and back to positive in fall. Soils with high conductivity are more effective at conducting subsurface soil moisture towards the surface as it dries in spring, ameliorating the variation of surface soil moisture seen by SMAP. This reddens the time spectrum of surface soil moisture and enhances lagged autocorrelations of soil moisture relative to soils with low hydraulic conductivity, which can dry down more quickly [62]. However, in fall the deeper soil is dry, and large hydraulic conductivity compounds gravitational drainage, removing any rainwater from shallow soils more quickly than for soils where conductivity is low, producing a whiter spectrum and reduced memory. This results in an opposite relationship to SMM as shown in Figure 5.
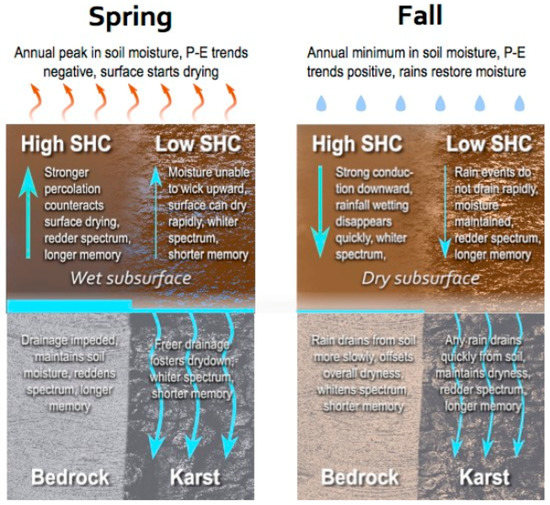
Figure 5.
Effects of soil saturated hydraulic conductivity (SHC), karst and solid bedrock on the vertical movement of water, and thus surface soil moisture memory, during different times of year with contrasting spatial correlations between land properties and soil moisture memory.
Karst, whose preferential drainage acts as an aid to baseflow at the bottom of the soil column, helps moist springtime soils dry more quickly, whitening the temporal spectrum of soil moisture that is reflected even at the surface. The result is an anticorrelation of karst coverage with SMM in spring. Where the bedrock is relatively impermeable, water stays in the soil column and memory is enhanced. During fall, water from rain showers drains more quickly through already dry soils over karst, preserving dry states and reducing variance in soil moisture, promoting SMM. Solid bedrock allows water to stay in the soil, which is countervalent to the climatologically dry states, enhancing variability, producing a whiter spectrum of soil moisture and reducing memory. Thus in fall, karst correlates positively to soil moisture memory.
These explanations are applicable over most of the SE-SC region, but certainly are not universally appropriate. Where there are pronounced wet and dry seasons, the way they phase with the annual cycle of net radiation, and thus potential evaporation, would lead to different relationships between SMM, soil properties and underlying geology.
4. Discussion and Conclusions
We have placed data sets of soil properties, subsurface karst distribution and vegetation characteristics on the same spatial grid as the SMAP level 3 product [50] and compared them over the SE-SC U.S. We examine whether local variability among land properties and SMM correlate across the SE-SC domain, and whether local spatial correlations are strong where local variability in land properties are large.
A novel result of this research is that there is a clear correspondence between SMM and the distribution of karst. This has been suggested by limited comparisons with in situ soil moisture measurements [61], but this study shows a widespread correlation across a large fraction of North America where karst is prevalent. This result has implications for LSM development. The geology below the soil column has not been considered in LSMs except as it affects the depth of the water table. Drainage of water through the vadose zone below the top few meters of soil has historically been treated as only a function of the slope of the terrain and wetness of the lowest soil layer [3,63]. These results suggest that baseflow parameterizations in LSMs should incorporate the effects of karst; recent research has suggested approaches to such parameterizations [64,65].
A major finding is that SMM is associated with a number of soil, vegetation and karst distributions during spring and fall, but not during summer. This is likely an indication that during summer, atmospheric conditions, particularly atmospheric evaporative demand, determine soil moisture variability much more directly than land properties. In the other seasons, land properties have much more influence on soil moisture persistence.
Another question that arises with this work is whether soil moisture data from remote sensing can be useful for the estimation of land properties in areas where soils or karst data are poor or unavailable. There are a number of techniques for a priori land parameter estimation [7], and this work shows that information about land properties are clearly reflected in SMAP soil moisture data. However, disentangling the nature of that information would be difficult as there is a high degree of cross-correlation among many different land parameters. Additional information, either from other independent properties of soil moisture or from other observable fields like surface temperature, would be needed to better constrain land parameter estimation among multiple properties.
Author Contributions
Conceptualization, P.A.D. and H.E.N.; Methodology, P.A.D. and H.E.N.; Formal Analysis, P.A.D.; Investigation, P.A.D. and H.E.N.; Data Curation, P.A.D.; Writing-Original Draft Preparation, P.A.D. and H.E.N.; Writing-Review & Editing, P.A.D. and H.E.N.; Visualization, P.A.D.; Project Administration, P.A.D.; Funding Acquisition, P.A.D.
Funding
This research was funded by National Aeronautics and Space Administration grant NNX13AQ21G.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the Exchanges of Energy, Water, and Carbon Between Continents and the Atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Pitman, A.J. The evolution of, and revolution in, land surface schemes designed for climate models. Int. J. Climatol. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.-L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3. [Google Scholar] [CrossRef]
- Best, M.J.; Pryor, M.; Clark, D.B.; Rooney, G.G.; Essery, R.L.H.; Ménard, C.B.; Edwards, J.M.; Hendry, M.A.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model. Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.; Rooney, G.G.; Essery, R.L.H.; Blyth, E.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model. Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef]
- Dirmeyer, P.A. The Value of Land Surface Data Consolidation. In Vegetation, Water, Humans and the Climate: A New Perspective on an Interactive System; Global Change—the IGBP Series; Springer: Berlin, Germany, 2004; pp. 245–296. ISBN 978-3-642-18948-7. [Google Scholar]
- Duan, Q.; Schaake, J.; Andréassian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L.; et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Lo, M.-H.; Famiglietti, J.S.; Yeh, P.J.-F.; Syed, T.H. Improving parameter estimation and water table depth simulation in a land surface model using GRACE water storage and estimated base flow data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant. Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Ramankutty, N.; Evan, A.T.; Monfreda, C.; Foley, J.A. Farming the planet: 1. Geographic distribution of global agricultural lands in the year 2000. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Ellis, E.C.; Goldewijk, K.K.; Siebert, S.; Lightman, D.; Ramankutty, N. Anthropogenic transformation of the biomes, 1700 to 2000. Glob. Ecol. Biogeogr. 2010, 19, 589–606. [Google Scholar] [CrossRef]
- Congalton, R.G.; Gu, J.; Yadav, K.; Thenkabail, P.; Ozdogan, M. Global Land Cover Mapping: A Review and Uncertainty Analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- Lawrence, P.J.; Chase, T.N. Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0). J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Sheeren, D.; Fauvel, M.; Josipović, V.; Lopes, M.; Planque, C.; Willm, J.; Dejoux, J.-F. Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series. Remote Sens. 2016, 8, 734. [Google Scholar] [CrossRef]
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J. The albedo of Earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; He, T.; Shi, Q. Estimating clear-sky all-wave net radiation from combined visible and shortwave infrared (VSWIR) and thermal infrared (TIR) remote sensing data. Remote Sens. Environ. 2015, 167, 31–39. [Google Scholar] [CrossRef]
- Rödenbeck, C.; Houweling, S.; Gloor, M.; Heimann, M. CO2 flux history 1982–2001 inferred from atmospheric data using a global inversion of atmospheric transport. Atmos. Chem. Phys. 2003, 3, 1919–1964. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. BioScience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: Methodology, simulations, and application to GOME-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef]
- Grunwald, S.; Thompson, J.A.; Boettinger, J.L. Digital Soil Mapping and Modeling at Continental Scales: Finding Solutions for Global Issues. Soil Sci. Soc. Am. J. 2011, 75, 1201–1213. [Google Scholar] [CrossRef]
- Ben-Dor, E. Quantitative Remote Sensing of Soil Properties. Adv. Agron. 2002, 75, 173–243. [Google Scholar] [CrossRef]
- Barnes, E.M.; Sudduth, K.A.; Hummel, J.W.; Lesch, S.M.; Corwin, D.L.; Yang, C.; Daughtry, C.S.T.; Bausch, W.C. Remote- and Ground-Based Sensor Techniques to Map Soil Properties. Available online: http://www.ingentaconnect.com/content/asprs/pers/2003/00000069/00000006/art00002 (accessed on 9 June 2018).
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Food and Agriculture Organization. The Digital Soil Map of the World, version 3.5; UNESCO: Rome, Italy, 1995. [Google Scholar]
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European policy support and public data requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service. Soil Survey Geographic (SSURGO) Database; United States Department of Agriculture: Washington, DC, USA, 2014.
- Anderson, S.P.; Bales, R.C.; Duffy, C.J. Critical Zone Observatories: Building a network to advance interdisciplinary study of Earth surface processes. Miner. Mag. 2008, 72, 7–10. [Google Scholar] [CrossRef]
- Yeh, P.J.-F.; Eltahir, E.A.B. Representation of Water Table Dynamics in a Land Surface Scheme. Part I: Model Development. J. Clim. 2005, 18, 1861–1880. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Lundquist, J.K.; Mirocha, J.D.; Smith, S.G.; Woodward, C.S.; Tompson, A.F.B. Development of a Coupled Groundwater-Atmosphere Model. Mon. Weather Rev. 2010, 139, 96–116. [Google Scholar] [CrossRef]
- Tian, W.; Li, X.; Cheng, G.-D.; Wang, X.-S.; Hu, B.X. Coupling a groundwater model with a land surface model to improve water and energy cycle simulation. Hydrol. Earth Syst. Sci. 2012, 16, 4707–4723. [Google Scholar] [CrossRef]
- Vergnes, J.-P.; Decharme, B.; Habets, F. Introduction of groundwater capillary rises using subgrid spatial variability of topography into the ISBA land surface model. J. Geophys. Res. 2014, 119, 11065–11086. [Google Scholar] [CrossRef]
- Koirala, S.; Yeh, P.J.-F.; Hirabayashi, Y.; Kanae, S.; Oki, T. Global-scale land surface hydrologic modeling with the representation of water table dynamics. J. Geophys. Res. 2014, 119, 75–89. [Google Scholar] [CrossRef]
- Schaller, M.F.; Fan, Y. River basins as groundwater exporters and importers: Implications for water cycle and climate modeling. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Good, S.P.; Noone, D.; Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 2015, 349, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Schaake, J.C.; Hamill, T.M.; Buizza, R.; Clark, M. HEPEX: The Hydrological Ensemble Prediction Experiment. Bull. Am. Meteorol. Soc. 2007, 88, 1541–1548. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K. Global-scale modeling of groundwater recharge. Hydrol. Earth Syst. Sci. 2008, 12, 863–885. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Condon, L.E.; Kollet, S.J. A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3. Geosci. Model. Dev. 2015, 8, 923–937. [Google Scholar] [CrossRef]
- De Graaf, I.E.M.; van Beek, R.L.P.H.; Gleeson, T.; Moosdorf, N.; Schmitz, O.; Sutanudjaja, E.H.; Bierkens, M.F.P. A global-scale two-layer transient groundwater model: Development and application to groundwater depletion. Adv. Water Res. 2017, 102, 53–67. [Google Scholar] [CrossRef]
- Gochis, D.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; Pan, L.; RafieeiNasab, A.; et al. WRF-Hydro Model. Source Code Version 5; NCAR Technical Note; UCAR/NCAR: Boulder, CO, USA, 2018; p. 107. [Google Scholar]
- Leeper, R.; Mahmood, R.; Quintanar, A.I. Influence of Karst Landscape on Planetary Boundary Layer Atmosphere: A Weather Research and Forecasting (WRF) Model–Based Investigation. J. Hydrometeorol. 2011, 12, 1512–1529. [Google Scholar] [CrossRef]
- Johnson, C.M.; Fan, X.; Mahmood, R.; Groves, C.; Polk, J.S.; Yan, J. Evaluating Weather Research and Forecasting Model Sensitivity to Land and Soil Conditions Representative of Karst Landscapes. Bound.-Layer Meteorol. 2018, 166, 503–530. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamies. Water Resour. Res. 2000, 36, 3–9. [Google Scholar] [CrossRef]
- Dawson, T.E. Hydraulic lift and water use by plants: Implications for water balance, performance and plant-plant interactions. Oecologia 1993, 95, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.B.; Sperry, J.S.; Dawson, T.E. Root water uptake and transport: Using physiological processes in global predictions. Trends Plant. Sci. 2000, 5, 482–488. [Google Scholar] [CrossRef]
- Salvucci, G.D. Limiting relations between soil moisture and soil texture with implications for measured, modeled and remotely sensed estimates. Geophys. Res. Lett. 1998, 25, 1757–1760. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kumar, S.V.; Dirmeyer, P.A.; Peters-Lidard, C.D.; Bindlish, R.; Bolten, J. Information theoretic evaluation of satellite soil moisture retrievals. Remote Sens. Environ. 2018, 204, 392–400. [Google Scholar] [CrossRef]
- Chan, S. Enhanced Level 3 Passive Soil Moisture Product Specification Document; Soil Moisture Active Passive (SMAP) Mission; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2016; p. 51.
- Schlosser, C.A.; Milly, P.C.D. A Model-Based Investigation of Soil Moisture Predictability and Associated Climate Predictability. J. Hydrometeorol. 2002, 3, 483–501. [Google Scholar] [CrossRef]
- Weary, D.J.; Doctor, D.H. Karst in the United States: A Digital Map Compilation and Database; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2014; p. 26.
- Miller, D.A.; White, R.A. A Conterminous United States Multilayer Soil Characteristics Dataset for Regional Climate and Hydrology Modeling. Earth Interact. 1998, 2, 1–26. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service. Gridded Soil Survey Geographic (gSSURGO) Database User Guide; United States Department of Agriculture: Washington, DC, USA, 2016; p. 64.
- GRASS Development Team. Geographic Resources Analysis Support. System (GRASS) Software; Open Source Geospatial Foundation. Available online: http://grass.osgeo.org (accessed on 7 February 2018).
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
- Green, J.K.; Konings, A.G.; Alemohammad, S.H.; Berry, J.; Entekhabi, D.; Kolassa, J.; Lee, J.-E.; Gentine, P. Regionally strong feedbacks between the atmosphere and terrestrial biosphere. Nat. Geosci. 2017, 10, 410–414. [Google Scholar] [CrossRef]
- Salvucci, G.D.; Saleem, J.A.; Kaufmann, R. Investigating soil moisture feedbacks on precipitation with tests of Granger causality. Adv. Water Resour. 2002, 25, 1305–1312. [Google Scholar] [CrossRef]
- Tuttle, S.; Salvucci, G. Empirical evidence of contrasting soil moisture-precipitation feedbacks across the United States. Science 2016, 352, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Norton, H.E.; Dirmeyer, P.A. Soil moisture memory in karst and non-karst terrains. Geophys. Res. Lett. 2018. in review. [Google Scholar]
- Shellito, P.J.; Small, E.E.; Livneh, B. Controls on surface soil drying rates observed by SMAP and simulated by the Noah land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 1649–1663. [Google Scholar] [CrossRef]
- Sellers, P.J.; Mintz, Y.; Sud, Y.C.; Dalcher, A. A Simple Biosphere Model (SIB) for Use within General Circulation Models. J. Atmos. Sci. 1986, 43, 505–531. [Google Scholar] [CrossRef]
- Vrettas, M.D.; Fung, I.Y. Toward a new parameterization of hydraulic conductivity in climate models: Simulation of rapid groundwater fluctuations in Northern California. J. Adv. Model. Earth Syst. 2015, 7, 2105–2135. [Google Scholar] [CrossRef]
- Vrettas, M.D.; Fung, I.Y. Sensitivity of transpiration to subsurface properties: Exploration with a 1-D model. J. Adv. Model. Earth Syst. 2017, 9, 1030–1045. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).