Effect of Observation Errors on the Timing of the Most Informative Isotope Samples for Event-Based Model Calibration

Abstract

Many studies have shown that isotope data are valuable for hydrological model calibration. Recent developments have made isotope analyses more accessible but event sampling still involves significant time and financial costs. Therefore, it is worth to study how many isotope samples are needed for hydrological model calibration and what the most informative sampling times are. In this study, we used synthetic data to investigate how systematic errors in the precipitation, streamflow and the isotopic composition of precipitation affect the information content of stream isotope samples for model calibration. The results show that model performance improves significantly when two or three isotope samples are used for calibration and that the most informative samples are taken on the falling limb. However, when there are errors in the rainfall isotopic composition, rising limb samples are more informative. Data errors caused the most informative samples to be more clustered and to occur earlier in the event compared to error free data. These results provide guidance on when to sample events for model calibration and thus help to reduce the cost and effort in obtaining useful data for model calibration.

1. Introduction

Changes in the chemistry and isotopic composition of stream water during rainfall events are frequently used to study runoff generation processes [1]. These water quality data can also be used to test and improve hydrological and hydrochemical models [2,3,4]. Isotope data can be particularly useful to improve model consistency and parameter identifiability [5,6,7,8,9].

Since planning fieldwork, collecting water samples, and analysing these samples is time consuming and expensive, and taking samples during the rising limb or at peak flow is logistically challenging in small catchments (<10 km²) with short response times, it is useful to evaluate the optimal number of samples and the best times to take samples for use in model calibration. A survey (see Supplementary Material 1) among 78 hydrologists on the optimal number of event samples for model calibration showed that almost two thirds of the respondents would take up to five samples per event and a bit more than a quarter of the respondents would take six to twenty samples per event. The respondents that identified themselves as field hydrologists would collect more samples for model calibration than those who identified themselves as modellers (e.g., 35% of the field hydrologists vs. 22% of the modellers would take 6 to 20 samples). Seven percent of the respondents would take many more samples and highlighted the need for continuous sampling (hourly or sub-hourly). While continuous isotope measurements are now possible [10], these data are still not widely available and most studies rely on data from a few samples.

When only one sample could be taken, most (57%) respondents would take a sample at peak flow. When two samples could be taken, the most frequently chosen combination was either one pre-event sample (sample taken before the rainfall event) and one sample at peak flow (29%) or one sample at peak flow and one sample on the falling limb (29%). When five samples could be taken, the most frequently chosen combination included a pre-event sample, a sample on the rising limb, a sample at peak flow and two samples on the falling limb (47%) (Figure S1). Field hydrologists find it most important to capture the rising limb (42% of the respondents) and peak flow (48%) and to ensure that samples are well spread over the event (44%). Thus, even though taking samples at peak flow and during the rising limb is challenging, most field hydrologists consider these samples to be most informative. Fewer modellers considered the rising limb samples to be the most informative for model calibration (12% of the modellers compared to 42% of the field hydrologists). Instead samples taken near peak flow were seen as most informative for model calibration (63%), followed by samples taken on the falling limb (29%) and pre-event samples (22%).

In a previous study, we investigated when isotope samples should be taken during an event to be most informative for event-based model calibration [11]. The results using synthetic data showed that in the absence of any data errors or model structural errors, two stream water samples, in addition to streamflow observations are sufficient to calibrate the Birkenes model. The two samples helped to constrain the parameters that describe the threshold storages for flow to occur from the two reservoirs, which could not be constrained based on the streamflow data alone [11]. The results, furthermore, showed that when only one sample is available, a sample taken on the falling limb is more informative for model calibration than a sample taken on the rising limb. However, the exact timing of the sample doesn’t matter much if two or more samples are available. These results fit the preference of the surveyed modellers for samples taken at peak flow and on the falling limb, and suggest that samples taken on the rising limb are less useful for model calibration and that field hydrologists can thus focus less on taking rising limb samples.

The use of synthetic streamflow and rainfall data without any errors allowed us to obtain a perfect model fit and to find the correct values for the parameters that describe the rate of flow from the two reservoirs [11]. However, in reality, there are errors in the data for the streamflow, rainfall and its isotopic composition because measurements contain errors [12,13] and because the rainfall is often not measured and sampled at a representative location for the catchment [14]. The relative errors can exceed 40% for rainfall [15], streamflow [12] and water quality [16]. Typical errors for rainfall are 33–45% at the 1 km² scale, while errors in streamflow are 50–100% for low flows, 10–20% for mid-high flows and 40% for high flows [13]. Errors in the data can adversely affect model calibration and actually be rather dis-informative than informative [17,18,19] because incorrect data will result in calibrated parameter values that are not suitable to describe functioning of the catchment. Therefore, it is important to consider how data errors impact the usefulness of isotope samples for model calibration, the number of samples needed for model calibration, and the timing of the most informative samples.

McIntyre and Wheater [20] evaluated different sampling strategies by comparing the performance of a phosphorus model for three conditions: (1) no data or structural errors, (2) data errors but no model structural errors, and (3) data errors and structure errors. They showed that a limited number of stream water samples could significantly improve the calibration of the model. Under conditions 1 and 2, four event samples were better than nine weekly samples for calibration and validation, while under condition 3 four event samples were as effective as 62 daily samples [20]. They also showed that data errors and model structural errors lead to a comparable calibration performance but much worse validation performance and larger values and ranges for standard error and bias.

In this study, we, therefore, extended our previous work and studied how data errors influence the efficient sampling strategy. We hypothesized that when rainfall and streamflow data are affected by measurement errors, more isotope samples are needed for model calibration, that stream isotope samples can help to partly compensate the errors in the streamflow or rainfall data, and that stream isotope samples can help to constrain more model parameters (i.e., for the case of the Birkenes model, the isotope data not only help to constrain the parameters that describe the threshold storage for flow to occur but also other parameters). Therefore, in this manuscript, we focussed on how systematic errors in rainfall and streamflow data affect the usefulness of stream water isotope samples for event-based model calibration, as well as how these data errors affect the timing of the most informative samples. Specifically, we addressed the following research questions:

• How do data errors, particularly systematic errors in precipitation, errors in the isotopic composition of precipitation and errors in streamflow, affect the information content of stream isotope samples for event-based model calibration?
• Does information on the isotopic composition of stream water help to constrain model parameters that are well constrained in the absence of any data errors?
• How do different data error types affect the timing of the most informative stream water samples for model calibration?

2. Methods

For this study, 102 synthetic time series, representing different catchment behaviours, rainfall events and errors were used to test the effect of data errors and the effectiveness of different sampling strategies for model calibration.

Firstly, error-free synthetic data series were generated using the Birkenes hydrochemical model [21]. Two different parameterizations (PI and PII) of the model represented two different hypothetical (or virtual) catchments. PI corresponds to published values for the Birkenes catchment in Norway and PII was chosen to represent a catchment with a faster response and faster and larger changes in the isotopic composition of stream water. For both virtual catchments, runoff and its isotopic composition were simulated for three rainfall events with the same rainfall intensity but different durations. This resulted in six error-free synthetic streamflow and tracer responses.

Secondly, four error types, including errors in the rainfall intensity, isotopic composition of the rainfall and two different types of errors in the streamflow, of four different magnitudes were introduced. The combination of two model parameterizations, three rainfall events, and the systematic errors (error free or four types of errors with four different magnitudes), resulted in 102 synthetic time series for streamflow and its isotopic composition (

Table 1. Overview of the 102 cases (synthetic time series) used in this study.

Subject	Parameterization	Event	Error
Description	PI PII	Small event Medium event Large event	Error free Four error types with four magnitudes
No. of variations	2	3	1 + 4 × 4 = 17

).

Thirdly, for each time series (i.e., case), the model was calibrated with all streamflow measurements and different subsets of stream isotope data (depending on sampling strategy), resulting in one representative parameter set for each subset of stream isotope data and each case. The model was then validated using all error free streamflow and stream isotope data. The sampling strategies tested in this study include a random selection (subsets of stream isotope samples were selected randomly), two intelligent selections (most informative stream isotope samples), a lower benchmark (no stream isotope data used for calibration) and an upper benchmark (all stream isotope data used for calibration). Both the intelligent sampling strategies and the alternatives are described in more detail later.

2.1. Birkenes Model

The Birkenes model is a lumped bucket-type coupled flow and tracer model (hydrochemical model). It was developed for a small (0.41 km²) headwater catchment in Norway [21,22] and has been applied worldwide [23,24,25,26,27,28]. The Birkenes model consists of two linear reservoirs (A and B) that represent a quick response (Q_A) and a slow response (Q_B) (Figure S3). Parameters AMIN and BMIN describe the threshold water level in the reservoirs before flow occurs, while parameters AK and BK describe the rate of outflow from the reservoirs (Q_A and Q_B, respectively). The fraction of flow from reservoir A that flows into reservoir B is determined by parameter AKSMX and the water level in reservoir B. When the water level in reservoir B is below the threshold water level (BMIN), all flow from reservoir A (Q_A) will go into reservoir B; the fraction decreases linearly with the water level above BMIN. Overflow (Q_OVER) occurs when the capacity of reservoir B (BMIN + BSIZE) is filled. The constant baseflow (Q_BASE) is represented by parameter QBASE, which is usually set to the minimum observed streamflow [6]. Evapotranspiration from reservoir A (ET_A) was set to 0.03 mm h⁻¹; it was assumed that there was no evaporation from reservoir B.

The stable isotope ¹⁸O was chosen in this study as an example of a conservative tracer, although ²H could have been used as well because they are both part of the water molecule and added naturally to the catchment during precipitation events. Fractionation due to soil and open water evaporation were assumed to be negligible (which is reasonable for forested boreal catchments without any lakes), so that the isotopic composition of the water stored in the catchment and the streamflow are only affected by mixing. The model assumes complete mixing within each of the two reservoirs. Consequently, the isotopic compositions of Q_A, Q_AB, and ET_A are the same as the isotopic composition of the water stored in reservoir A and the isotopic compositions of Q_OVER, Q_B and Q_BASE are the same as the isotopic composition of the water in reservoir B. The isotopic composition of total flow Q is the volume-weighted mean of the flow components (Figure S3).

While one has to be aware of the limitations of a such a simple model, particularly the assumption of complete mixing, the Birkenes model is suitable for event-based multi-criteria model calibration because it has a small number of parameters (7) and low data requirements (i.e., it only needs information on the isotopic composition of precipitation and stream water). Furthermore, it is functionally similar to some of the more recent coupled flow and tracer models (e.g., [3,29,30]). In particular, the model can be applied to predict short-term changes [6], therefore we ran the model with an hourly time step to simulate changes in streamflow and its isotopic composition at the event time scale.

2.2. Two Model Parameterizations and Three Events

We tested the effects of observation errors on model calibration for two parameter sets (PI and PII) and three different rainfall events. Parameter set PI was taken from Christophersen and Wright [21] and is based on model calibration to field data from the Birkenes catchment (AMIN = 13 mm, BMIN = 40 mm, BSIZE = 40 mm, AK = 3.33 × 10⁻² h⁻¹, BK = 1.90 × 10⁻³ h⁻¹, AKSMX = 0.75 and QBASE = 0.03 mm·h⁻¹, Figure S3). For parameter set PII, there is less water flowing from reservoir A to B (parameter AKSMX is 0.25 instead of 0.75), which results in a larger contribution from reservoir A to total streamflow (Q), less frequent overflow (Q_OVER), and larger changes in the isotopic composition of stream water (C_Q). The three rainfall events have a constant rainfall intensity of 4 mm h⁻¹ but differ in size: 12 mm (small event), 24 mm (medium event) and 48 mm (large event). The resulting six streamflow and tracer responses (Figure S4) represent the three different types of streamflow responses analysed by Wang et al. [11]: slow response (small events for PI and PII), fast response without overflow (medium event for PI and medium and large event for PII) and fast response with overflow (large event for PI).

2.3. Types of Observation Errors

We selected four different types of observation errors to determine how data errors affect the information content of stream isotope samples for model calibration. We focus on systematic errors in precipitation intensity (P), the isotopic composition of precipitation (C_P), and streamflow (Q). We focus on systematic errors, rather than random errors, because they have a clearer effect on model calibration than random errors. For each type of error, we considered four different magnitudes of error: large underestimation (− −), underestimation (−), overestimation (+), and large overestimation (+ +) (

Table 2. Overview of the four observation errors and their magnitudes.

Error Case	Error 1: P	Error 2: CP	Error 3: Q	Error 4: QRC
Large overestimation (+ +)	+20%	+2‰	+20%	+20%
Overestimation (+)	+10%	+1‰	+10%	+10%
Underestimation (−)	−10%	−1‰	−10%	−10%
Large underestimation (− −)	−20%	−2‰	−20%	−20%

). All model results were compared to the error-free (0) situation as a reference.

2.3.1. Error 1 (P): Systematic Error in the Precipitation Intensity

Errors in catchment average rainfall amount and intensity occur because of the errors in the point measurement (e.g., systematic errors caused by evaporation loss, under catch due to wind [31]), and because of errors in determining the catchment average rainfall (e.g., due to interpolation between different rain gauges or as a result of using data from rain gauges at non-representative locations in the catchment). The observation error (standard error) of mean rainfall is dependent on the scale of the catchment and can vary from 4 to 14% at the 0.01 km² scale, 33–45% at the 1 km² scale, and up to 65% at the 100 km² scale (including both systematic and random errors, see review by McMillan et al. [13]). Here, we analyse the effects of a 10% and 20% systematic error in rainfall amount on model calibration (Figure 1).

2.3.2. Error 2 (C_P): Systematic Error in the Isotopic Composition (δ¹⁸O) of Precipitation

Errors in the isotopic composition of rainfall can occur because the rainfall sampler does not represent the average precipitation in the catchment (e.g., due to the elevation effect on rainfall amount and rainfall isotopic composition), evaporation and fractionation from the rain gauge, and because of laboratory errors (i.e., precision of the isotope analyser). Fischer et al. [14] showed that the event average isotopic composition (δ¹⁸O) of rainfall across the 4.3 km² Alptal catchment could vary by 0.4 to 12.0‰. The isotopic composition of rainfall (δ¹⁸O) across the 62.4 km² HJ Andrews catchment varied between 2.6 and 7.4‰ [32]. Here, we analyse the effects of a 1‰ and 2‰ systematic error in the isotopic composition of the rainfall (Figure 1).

2.3.3. Errors 3 and 4 (Q and Q_RC): Systematic Errors in Streamflow

Errors in streamflow are dependent on the measurement method. Individual streamflow observations may have an error in the range of 2–19% [33,34]. However, the error in streamflow time series usually originates mainly due to the uncertainty in the rating curve. The error in streamflow data can therefore be ±50–100% for low flows, ±10–20% for medium or high (in-bank) flows, and ±40% for out of bank flows [13]. The errors in the rating curve affect both the dynamics of the streamflow (e.g., the difference between the minimum and maximum streamflow) and the mean streamflow (i.e., the water balance). To consider both situations, two types of streamflow errors were evaluated: a systematic increase or decrease in each streamflow observation (Error 3; Q) resulting in a changed mean streamflow and an error in the rating curve that affects the variability of the streamflow but not the mean streamflow (Error 4; Q_RC) (Figure 1). Technically the latter error was implemented by multiplying the difference of the actual and the mean streamflow by 110% or 120% for the small (+) and large (+ +) overestimation respectively, and similarly by 80% and 90% for the large (− −) and small (−) underestimation, respectively and then applying this modified difference to compute a changed streamflow value (Figure 1).

2.4. Model Setup, Calibration and Validation

The model calibration and validation process followed the methodology described in Wang et al. [11]. In short, the model was run for 100 weeks (warm up period) with the same rainfall event at the start of each week. The isotopic composition (δ¹⁸O) of precipitation (C_P) was set at −10‰ for the first 95 weeks, and to −15‰, −10‰, −5‰, −10‰, and −5‰ for the following five weeks to obtain a different initial isotopic composition in reservoirs A and B. The isotopic composition (δ¹⁸O) of the precipitation (C_P) during the event of interest (week 101) was set to −15‰, except for Error 2 for which it was changed to −17‰ (+ +), −16‰ (+), −14‰ (−), or −13‰ (− −).

The model was calibrated using the 100 streamflow observations (Q_obs; four observations before the event and 96 observations during the event), which contain errors when considering the effects of Errors 3 and 4, and a subset of the stream isotope data (C_Qobs) which were assumed to not have any errors. The subsets of the stream isotope data (i.e., stream isotope samples available for model calibration) were selected based on the stream water sampling strategies (see below). The model was validated using the error free streamflow data and all stream isotope data. The combined objective function (F) for the calibration and validation weighted the relative error in streamflow (F_Q) and the isotopic composition of stream water ($F_C$) equally:

$$F=\sqrt{\frac{F_Q{}^2+F_C{}^2}{2}}$$

(1)

where $F_Q$ and $F_C$ are calculated as:

$$F_Q=\frac{1}{m}{\displaystyle \sum }\frac{\left|Q_{obs}\left(i\right)-Q_{sim}\left(i\right)\right|}{Max\left(Q_{obs}\left(i\right)\right)-Min\left(Q_{obs}\left(i\right)\right)}$$

(2)

$$F_C=\frac{1}{n}{\displaystyle \sum }\frac{\left|C_{Qobs }\left(i\right)-C_{Qsim}\left(i\right)\right|}{Max\left(C_{Qobs}\left(i\right)\right)-Min\left(C_{Qobs}\left(i\right)\right)}$$

(3)

where Q_obs(i) is the observed streamflow (contains errors for the calibration for Errors 3 and 4 and error-free streamflow for the validation) at time i, Q_sim(i) is the simulated streamflow at time i, C_Qobs(i) is the error-free observed isotopic composition of stream water at time i, C_Qsim(i) is the simulated isotopic composition of stream water at time i, m is the number of streamflow observations, which was 100 for the model calibration or 96 for validation, n is the number of stream water samples and depended on the sampling strategy for calibration (see below) and was 96 for validation. We included the pre-event streamflow observations and their corresponding isotope data for model calibration because the survey results suggested that pre-event data are considered to be valuable for model calibration, but did not include them in the validation because we wanted to focus on the simulation of the changes in streamflow and its isotopic composition during the rainfall event, rather than how well the model simulated the pre-event conditions.

We used the SCE-UA method [35,36] for automatic calibration, which is considered to be a reliable and efficient algorithm for model calibration [37,38]. The initial ranges for the parameter values were set to 0.2 and 5 times the actual parameter value for the optimization, except for AKSMX for which a range of 0 to 1 was used. The SCE-UA method generates one optimal parameter set for each initial selection of parameter values (seed). In order to account for the influence of the initial selection of the parameter values, 25 different seeds were used for each model calibration (i.e., for each case and each subset of stream water samples). The 25 optimized calibration parameter sets from the 25 seeds were ranked based on the value of the combined objective function (F) for calibration and the five parameter sets with the best calibration performance were selected for validation. The parameter set with the median value of F for validation was chosen as the representative parameter set for that case and subset of stream water samples.

2.5. Stream Water Sampling Strategies

Based on our previous study, the information content of a stream isotope sample for model calibration depends on when it is taken during an event [11]. Therefore, we used two different sampling strategies (random selection and intelligent selection) with one, two or three stream water samples (n = 1, 2 or 3) and compared their model performance with a lower benchmark (n = 0) and an upper benchmark (n = 100). The lower benchmark (L) represents a situation where no isotope data are available for model calibration, while the upper benchmark (U) represents a situation where continuous isotope data are available. The random sample selection (R) represents sampling designs that focus on taking a certain number of samples during an event but do not consider the timing during the event. For intelligent selection (I), the stream isotope samples are taken at the time with the highest information content for model calibration (for the summary of sampling strategies, see

Table 3. Comparison of the different sampling strategies.

Sampling Strategy	Lower Benchmark (L)	Random Selection (Rn)	Intelligent Selection: Error Free Data (I0_n)	Intelligent Selection: Data with Errors (Ie_n)	Upper Benchmark (U)
No. of samples (n)	0	1–3	1–3	1–3	100
Planning	no	low	medium	medium	high
Field work	no	low	low	low	high
Lab work	no	low	low	low	high
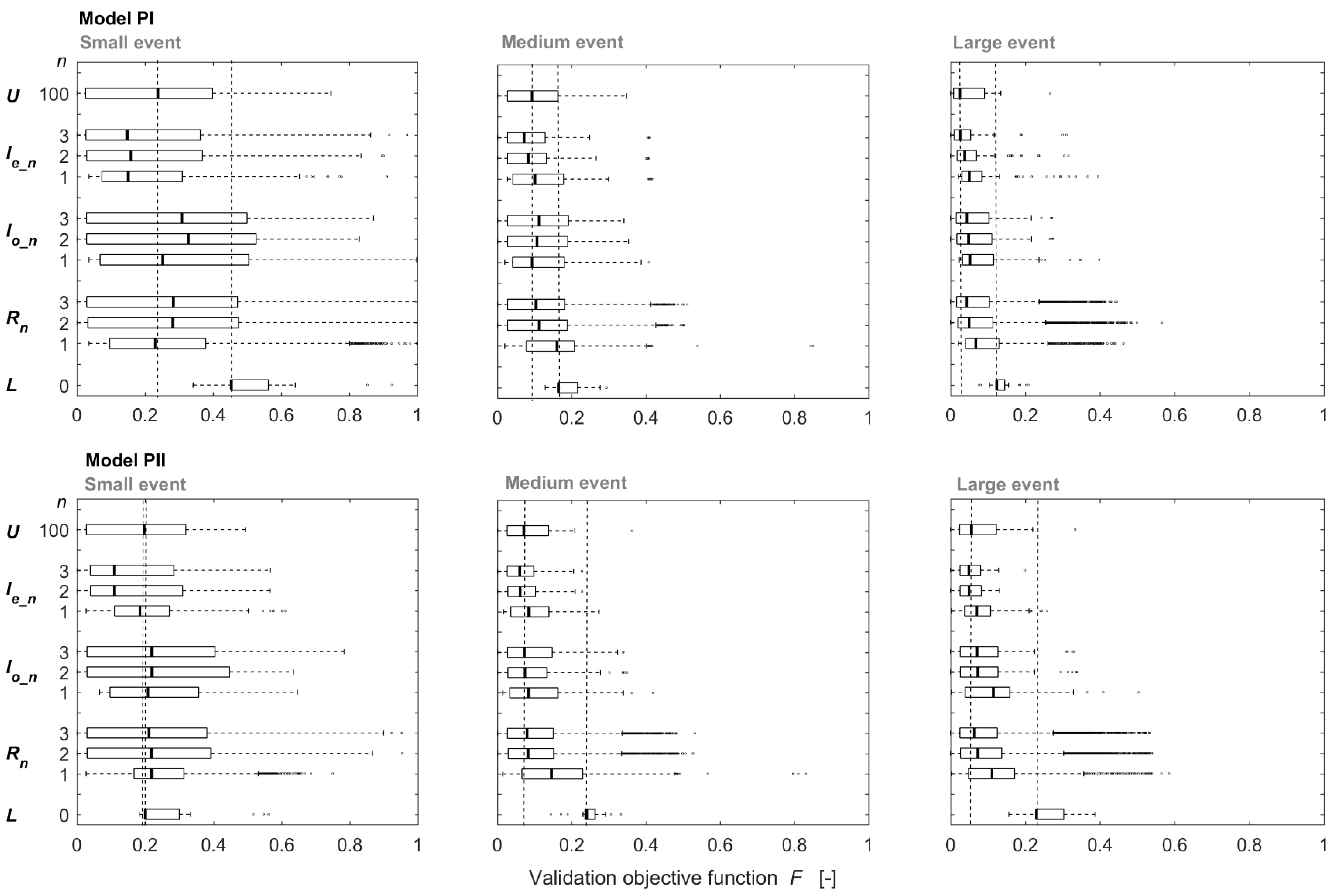
Summary	no	low-budget	economic	economic	luxury

). The sampling strategies were evaluated for each of the 102 cases by comparing their validation performance.

2.5.1. Lower and Upper Benchmarks (L and U)

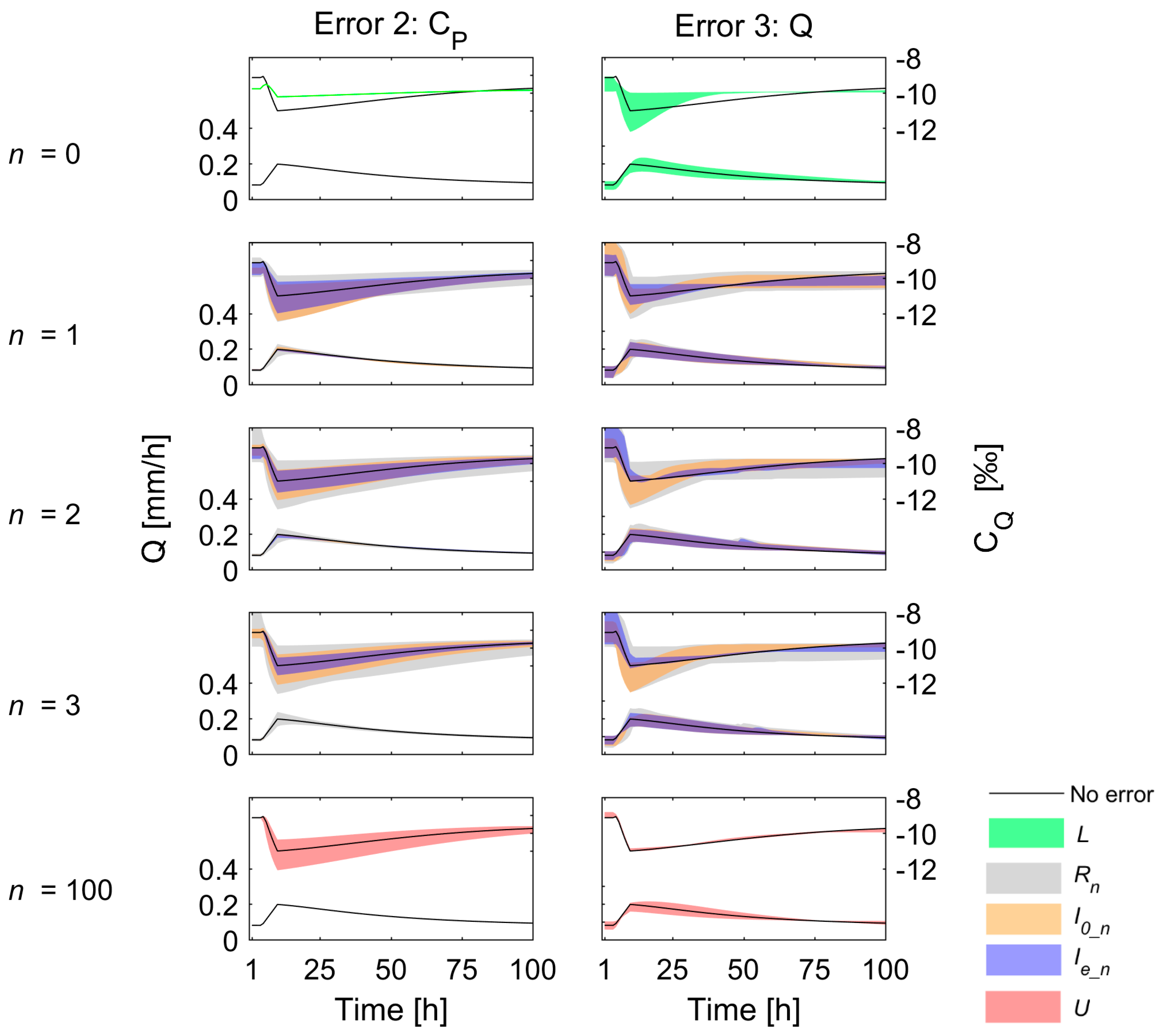
For the lower benchmark (L), the model was calibrated using only streamflow data, i.e., no information on the isotopic composition of stream water (n = 0). With the calibration and validation process described above, we obtained a representative parameter set and validation performance (F) for each case. For the upper benchmark (U), the model was calibrated using all information on the isotopic composition of stream water (n = 100) for each case, which also resulted in a representative parameter set and validation performance for each case.

2.5.2. Random Selection (R_n)

In addition to the lower and upper benchmarks (n = 0 and n = 100), we also investigated the value of one, two and three randomly selected isotope samples for model calibration (n = 1, 2, 3). For the situation with only one sample (n = 1), the model was calibrated with the isotopic data from one of the 100 possible sampling times alternately. For each potential sampling time, we obtained one representative parameter set and value of the validation objective function (F). We used the median value of F for these 100 potential sampling times and parameter sets to represent the median validation performance for the calibration with one random sample (R₁). This was done for each of the 102 cases. For the calibrations with two or three samples (n = 2 or 3), we calibrated the model with 1000 randomly selected pairs or triplets of samples that were at least five hours apart. The median value of F for these 1000 random pairs or triplets represents the median validation performance for the calibration with two or three random stream water samples (R₂ or R₃). The same random selected 1000 sampling pairs or triples were used for calibration for all 102 cases to allow comparison between the cases.

2.5.3. Intelligent Selection (I_{0_n} and I_{e_n})

Two different best sampling times were evaluated: (A) the best sampling times based on model performance from the case without any data errors (I_{0_n}) and (B) the times selected by comparing the median model performance for the five error-magnitudes (I_{e_n}) for each error type. The different error magnitudes were analysed together (i.e., the median performance for the five error magnitudes (− −, −, 0, +, + +) was used) because the magnitude of data errors is generally not known (and could otherwise be corrected for). Afterwards, we compared these two intelligent selections to study how observation errors affect the best sampling times.

(A) Best Sampling Times in the Case of No Errors (I_{0_n})

To find the sampling times that are most informative for model calibration when only one sample can be taken (n = 1), the model was calibrated using the isotope data for each potential sampling time alternately. The five sampling times with the lowest value of F for the validation were selected as the five best sampling times in the case of no errors (I_{0_1}) (see black crosses in Figure 2A, n = 1).

To search for the two most informative sampling times (n = 2), the model was calibrated for each of the five selected most informative first sampling times (I_{0_1}) and the isotope data from the remaining 99 potential sampling times. The values of F for the validation for each of the 495 pairs were ranked again and the sampling times with the five lowest values of F were selected as the best sampling pairs (I_{0_2}; see black and red crosses in Figure 2A, n = 2). This procedure to find the best sampling pairs assumes that the most informative sampling pairs include at least one sample from the five most informative first samples (which is elaborated on in the discussion).

To obtain the most informative sampling triplets (n = 3), the model was similarly calibrated for each of the five most informative sampling pairs and the isotope data from the remaining 98 potential sampling times. The five sampling triplets with the lowest value of F were selected as the best sampling times (I_{0_3}; see black, red and green crosses in Figure 2A, n = 3).

(B) Best sampling times in the case of errors (I_{e_n})

To determine the best sampling time in the case of data errors (I_{e_1}), the model was calibrated using the isotope data for each potential sampling time and the value of the objective function for the validation (F) was determined for each sampling time. This was done for all five error magnitudes (large underestimation (− −), underestimation (−), error free (0), overestimation (+) and large overestimation (+ +); Figure 2B). Then the median value of the objective function for the validation for the five different error magnitudes was calculated for each of the 100 potential sampling time steps. These 100 median values were ranked and the five sampling times with the lowest median value of $F$ were selected as the five best sampling times in the case of errors (I_{e_1}; see black plusses in Figure 2B, n = 1). The procedure to find the best sampling pairs or triplets in the case of observation errors is similar to the intelligent selection in the case of no errors (A), the only difference is that the median value of F of the five error magnitudes was ranked and the five sampling times with lowest median values were selected (I_{e_2} and I_{e_3}; Figure 2B).

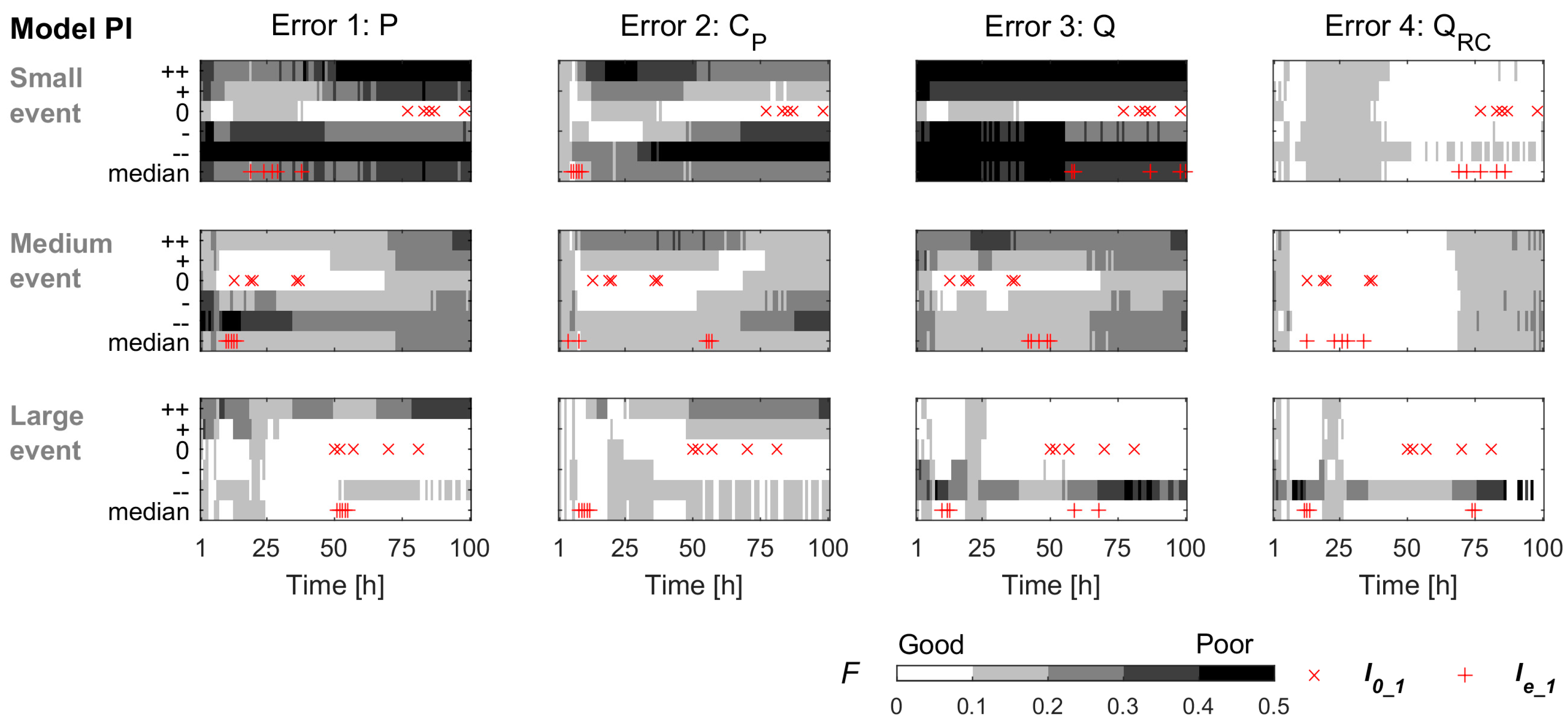
Since each error type influences the model performance differently, the procedure was repeated for each of the four error types, and the best sampling times (I_{e_n}) for each error type were selected separately. Thus, for each virtual catchment (PI or PII) and each of the three events (small event, medium event and large event), there were five most informative sampling times if there are no data errors (I_{0_n}) and 20 most informative samples when there are data errors (I_{e_n}, five for each error type). These most informative sampling times were further classified into four categories to see when sampling during an event is most informative for model calibration: pre-event sample (i.e., taken before the rainfall event), rising limb sample, near-peak sample (here defined as the period when flow is higher than 95% of the total increase in streamflow during the event), and falling limb sample.

3. Results

3.1. Effects of the Different Data Errors on Model Validation Performance

The four observation errors influenced the model validation performance differently. Error 1 (P; error in the precipitation intensity) and Error 2 (C_P; error in the isotopic composition (δ¹⁸O) of precipitation) had a large influence on the simulation of the isotopic composition of stream water, while Error 3 (Q; errors in streamflow) and Error 4 (Q_RC; errors in in the rating curve) mainly influenced the streamflow simulation (Figure 3 and Figure S5). The effect of the observation errors on model validation performance was larger for the small event than for the medium and large event (Figure 4), which suggests that model calibration for events with a slow response is more sensitive to data errors than the calibration for large events with larger changes in the amount of streamflow and the isotopic composition of streamflow during the event. As expected, the model validation performance decreased as the errors increased (Figure 4).

For most of the 102 cases, there was a significant improvement in model validation performance compared to the lower benchmark when one stream isotope sample was used, a smaller improvement when a second stream isotope sample was added, and little improvement by adding the third sample (Figure 4). For extreme cases with very large errors (e.g., large underestimation for Error 1 with model PI and the small event), there was little improvement in model performance or the performance was even worse than the lower benchmark when more isotope data were used for calibration (see blue triangles for Error 1 with the model PI and small event in Figure 4).

3.2. Effect of Stream Water Isotope Samples on Hydrograph Simulation and Parameter Identifiability

When no isotope data were available (n = 0, L), the model could simulate the streamflow reasonably well but the simulated response of the isotopic composition of the stream water was wrong and highly variable for the different parameter sets (Figure 3 and Figure S5). When using data from one or two stream isotope samples in model calibration, the simulations for the streamflow did not change significantly but the simulations for the isotopic composition of the streamflow improved significantly (Figure 3 and Figure S5). This result is expected because the parameters related to mixing (AMIN and BMIN; the threshold storage for flow to occur from reservoirs A and B) cannot be identified from streamflow data alone [29,39,40]. However, the variability in the simulated isotopic composition of the stream water was large, particularly for the randomly selected samples (grey uncertainty band in Figure 3 and Figure S5). The simulations for the model calibrated with two or three intelligently selected samples (I_{e_2} and I_{e_3}) were sometimes even better than for the upper benchmark (e.g., simulations of Error 2 in Figure 3 and Figure S5).

Because of the observation errors, the calibrated model parameter values differed from the real parameter values. Similar to the previous study when there were no data errors [11], the isotope samples helped to constrain the two mixing related parameters (AMIN and BMIN) that could not be determined based on the streamflow data alone (Figure 5 and Figure S6). For the systematic error in the streamflow data (Error 3, Q), stream isotope data also improved the identifiability of the parameters that determine the rate of flow from the reservoirs (AK and BK; Figure 6 and Figure S7). This indicates that the information contained in the isotope data can help to correct errors in the streamflow data. For the other three error types, parameters AK and BK could be identified without any isotope data (Figure S7).

3.3. Timing of the Most Informative Stream Isotope Samples for Model Calibration

3.3.1. Most Informative Stream Isotope Samples for Model Calibration (n = 1)

The majority of the most informative samples were falling limb samples. Of the 30 I_{0_1} samples (5 best samples × 3 events × 2 parameterizations), there was one sample near peak flow and the 29 other samples were all falling limb samples. Among the 120 I_{e_1} samples, there were three pre-event samples, 28 rising limb samples, 10 near-peak samples, and 79 falling limb samples. Errors in the model input (Error 1 (P) and Error 2 (C_P)) affected the timing of the most informative samples for model calibration more than the errors in streamflow data (Errors 3 (Q) and 4 (Q_RC)). For Error 1 (P), 30% of the I_{e_1} samples were near peak flow and 63% were falling limb samples. For Error 2 (C_P), 60% of the I_{e_1} samples were located on the rising limb and 33% on the falling limb; for Errors 3 and 4, 87% and 80% of the best samples were falling limb samples respectively (Figure 7 and Figure S8).

The effect of the timing of the stream isotope sample on model validation performance was larger when there are data errors than when there are no data errors (compare range of validation performance (i.e., grey scale of F) in Figure 7 and Figure S8). The timing of the most informative samples for model calibration when there are data errors (I_{e_1}) was more clustered than the timing of the best samples where they are no data errors (I_{0_1}), which indicates that the sampling time has a larger effect on model calibration when there are data errors (Figure 7 and Figure S8). Approximately two-thirds (68%) of the most informative first sampling times were earlier when data errors were included (I_{e_1}) than for the error free case (I_{0_1}). However, the effect of errors on the most informative sampling time depended on the streamflow response type. For the slow responses (small events for PI and PII) and fast response with overflow (large event for PI), 90% of I_{e_1} samples were earlier than I_{0_1} samples. For the fast response without overflow (medium event for PI and PII and large event for PII), only 45% of the I_{e_1} samples were earlier than I_{0_1} samples (Figure 7 and Figure S8).

3.3.2. Most Informative Sampling Pairs for Model Calibration (n = 2)

The two most common combinations of the most informative sample pairs when there are no data errors (I_{0_2}) were two falling limb samples (22 pairs) and one near-peak flow sample and one falling limb sample (6 pairs). However, the 120 I_{e_2} samples were more spread during the event and were affected differently by error types. The most common combinations were two falling limb samples (44 pairs), one near-peak flow sample and one falling limb sample (20 pairs), or one rising limb sample and one falling limb sample (19 pairs) (Figure 8 and Figure S9).

Similar to the most informative first samples (n =1), for each error type, the I_{e_2} samples were more clustered and earlier compared to I_{0_2} samples. Errors in the precipitation data (Error 1 (P) and Error 2 (C_P)) affected the timing of the most informative samples for model calibration most, so that rising limb samples were more often included in the most informative sampling pairs when there were errors. Error 3 (Q) only slightly affected the timing of the most informative sampling pairs, and the I_{e_2} samples not very different from the I_{0_2} samples. For Error 4 (Q_RC), the timing of the most informative sampling pairs was not significantly affected by the errors and the most informative sampling times were mainly falling limb samples, similar to the I_{0_2} samples (

Table 4. Difference in the timing of the most informative sampling pairs when there are data errors (I_{e_2}) and when there are no data errors (I_{0_2}).

Parameterization	PI			PII			Summary
Event Size	Small	Medium	Large	Small	Medium	Large
Same timing	QRC			QRC	QRC	Q	QRC
Small difference	Q	Q		Q	Q, P	QRC	Q
Large difference	P, CP 1	P, CP 1, QRC	P 2, CP, Q 1, QRC 3	P, CP	CP	P 2, CP	P, CP

¹ timing of one of the five most informative sampling pairs differed only slightly compared to the error free case; ² timing of one of the five most informative sampling pairs was the same as the error free case; ³ timing of two of the five most informative sampling pairs differed only slightly compared to the error free case.

, Figure 8 and Figure S9). This indicates that observation errors in the input data influence the timing of the most informative samples for model calibration more than errors in the streamflow data.

3.4. Effect of the Different Sampling Strategies on Model Performance

A central question was which sampling strategy was most effective for model calibration for each model parameterization (PI and PII) and event size (small, medium and large). To address this question, the validation performances (i.e., value of F) of all 17 error cases (one error-free case and 16 error cases (i.e., the four error types and their four magnitudes)), Table 1 were grouped together (see boxplots in Figure 9). The median value of F represented the median effectiveness of each sampling strategy. In general, stream water samples improved the model calibration compared to the lower benchmark. Small events were more affected by errors with worse validation performance than medium and large events. ANOVA test results show that the model performance when using two or three samples taken at the best sampling times when there are no errors (I_{0_2} or I_{0_3}) was not significantly different from the random selection of two or three samples (R₂ or R₃). However, intelligent selection considering errors (I_{e_n}) performed better than both (I_{0_n} and R_n) when there are data errors. With two or three intelligent samples (I_{e_n}), the median performance was better than the upper benchmark (only the large event for PI needed three samples, Figure 9). This means that a few carefully selected stream water samples can be valuable for improving model calibration.

4. Discussion

4.1. Value of Stream Isotope Data for Model Calibration

The use of information on the isotopic composition of stream water in model calibration improved the overall model validation performance and resulted in a lower value of the combined objective function and more constrained parameter sets compared to the lower benchmark. This is similar to the results of Wang et al. [11] for the case without data errors and the results of other studies that have also shown that the inclusion of isotope data can reduce parameter uncertainty and improve model performance (e.g., [3,6,41]). The use of data from two or three stream water samples resulted in model fits that were as good as or even outperformed the model calibrated with 100 samples (i.e., the upper benchmark), which would by definition not be possible for the error-free case. While accurate high-frequency isotope data would be beneficial for model testing, these results indicate that a few stream water samples can already be informative and effective for event-based model calibration. However, large observation errors had a negative effect on the model validation performance and resulted in a smaller improvement in overall model performance when using information on stream water isotopic composition (i.e., there was a smaller difference between the lower benchmark and upper benchmark for the large errors, see examples of Error 2 with overestimation in Figure 4). This suggests that the use of stream isotope data is less useful for improving model fits when very large observation errors are present, which confirms earlier discussions on the use of non-informative observations in model calibration [19,42].

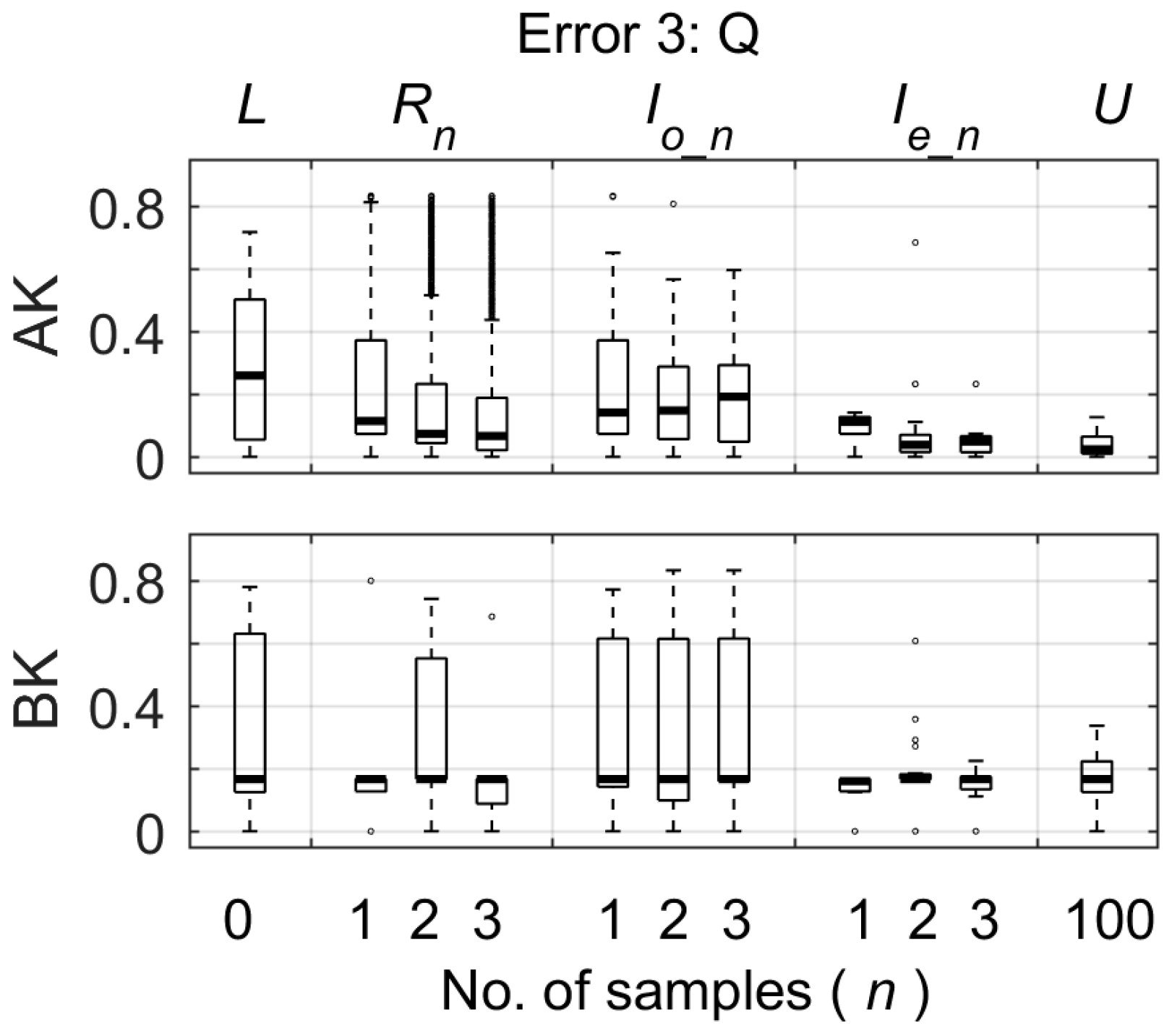
When there were systematic errors in the streamflow data, the stream water isotope data also helped to constrain the parameters that were well constrained in the absence of any data errors. In this study, parameters AK and BK that determine the rate of flow from the two reservoirs, were constrained by stream water isotope data when the systematic error in the streamflow data was large and caused a bias in the calibration of these parameters based on streamflow data alone (Figure 6).

4.2. Best Times to Sample Stream Water for Model Calibration

In our previous study [11], we showed that two samples are sufficient for model calibration when there are no errors in the data and model structure. We, furthermore, showed that when data from only one isotope sample was available, a sample taken on the falling limb was most informative for model calibration, but the timing of the sample did not influence model calibration significantly when two or more samples were available because the model was well calibrated, with a close to perfect model fit. In this study, we show that the most informative sampling times were affected by observational errors. Errors in the data result in more clustered and earlier best sampling times compared to the error free situation, which suggests that the sampling time has a larger effect on model calibration when errors are present and a perfect model fit is not possible. Under error-free conditions, it was sufficient to calibrate the flow related parameters with streamflow data, and only the parameters representative of the mixing processes (AMIN and BMIN) needed further identification. Therefore, the very late samples that contain most information on the mixing were most informative for model calibration. However, when there are errors in the streamflow data, the flow related parameters could no longer be calibrated perfectly with streamflow data. Therefore, earlier samples, which contain information on both the event dynamics and mixing process (i.e., early on the falling limb), were more informative. Since the analytical error for δ¹⁸O is very small (maximum 0.1‰ [7]) and the relative error related to the stream δ¹⁸O change during the event (except for the very small event) is also small compared to other observation errors, it is useful to use stream water samples to obtain a better calibration of the flow related parameters (such as AK and BK) and correct for errors in the streamflow (Q) data.

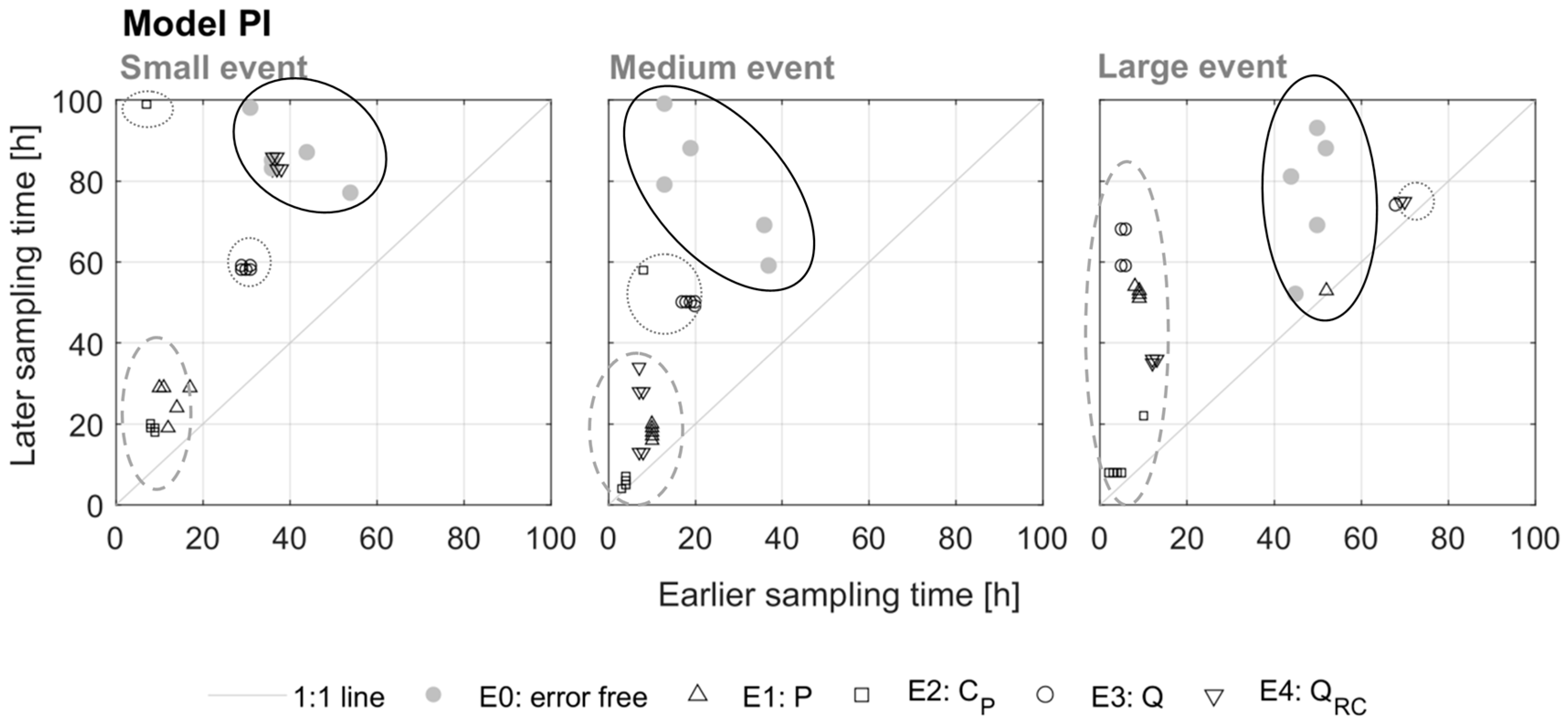
Except for Error 2, the majority (77%) of the most informative first samples were located on the falling limb. For over one third of the most informative sampling pairs, both samples were located on the falling limb and 72% of the most informative pairs included at least one falling limb sample. This suggests that, except when there are significant errors in the isotopic composition of precipitation, pre-event samples, samples taken on the rising limb and samples taken at peak flow are often not more informative for model calibration than samples from the falling limb. This is an important result as the rising limb and peak flow are the hardest to sample because of the short lead-times and logistical challenges. Interestingly, this model result reflects the results from our survey, which suggests that modellers consider rising limb samples to be less important for model calibration than field hydrologists.

The results on the most informative sampling times for the errors in the isotopic composition of precipitation (Error 2) were different, with 60% of the most informative first samples occurring on the rising limb. In the case of systematic errors in the isotopic composition of rainfall (e.g., due to sampling near the catchment outlet), stream isotope samples on the rising limb are particularly informative for model calibration as they describe the rapid change in the isotopic composition of the streamflow. With errors in catchment average precipitation intensity, the model performance also dropped and led to 30% of the most informative samples occurring near peak flow. These results suggest that for model calibration purposes, it is most beneficial to focus field efforts in the early part of the event on improving precipitation measurements and sampling the rainfall isotopic composition at representative locations.

4.3. Limitations and Transferability of This Virtual Study

In this study, two model parameterizations (PI and PII) and three rainfall events were used to reconstruct six different streamflow and tracer responses. In the real world, rainfall events are more diverse with changing antecedent conditions, different rainfall intensities and changes in the isotopic composition of the rainfall during the event. A poor temporal resolution of the rainfall isotopic composition also affects the model calibration results [3] but was not considered here. Even though our study is not representative of all streamflow and tracer responses, observation error characteristics, and potential sampling strategies, it provides a useful and flexible methodology to study event-based model calibration to analyse different sampling strategies and give guidance to limit the costs of sampling for event-based model calibration. The study demonstrates that synthetic data are useful to study the value of data by using modelling as a tool, which was also highlighted by Christophersen et al. [43]. Under well-controlled conditions, all types of events, catchments, data types and errors, sampling strategies can be tested and compared, which is not possible for field data. The synthetic data are more general from the perspective that they are not site-specific. The results of the value of data can help to decide when to sample events in the field to make sampling more cost and time efficient.

In order to compare the effect of different types of data errors more directly, only independent systematic errors were considered. In the real world, the data are influenced by multiple types of errors, the error characteristics are more complex and variable throughout the event, and the data are also influenced by random errors. Random errors were not tested in this study for two reasons. Firstly, the errors introduced may offset each other. Secondly, the sampling time with smaller errors would be chosen as the best sampling time regardless of random error types and magnitudes. As a result, the effect of random errors on model calibration cannot be quantified and compared as easily as the effect of systematic errors. Therefore, further studies on event-based model calibration with real data and a comparison of the effect of observation errors to this study are needed. The potentially compensating effects of random errors would also be interesting to test. We expect it would decrease the information content of each sample, although in a smaller less significant way than the systematic errors. Compared to our previous study, this observation error study illustrated the different effects of the different error types and how they changed the most informative sampling times. The same procedure can be used to test the effect of other systematic errors in the data on model calibration.

Model related errors (e.g., mixing assumption and model structural errors) were not included in this study. Potentially, the same method can be used to test the information content of different isotope samples for calibration with respect to model related errors, as was done in other studies to test different model structures [44,45] and multiple mixing assumptions [46].

When determining the most informative sampling pairs, we assumed that the most informative sampling pairs will include format least one of the five most informative first samples, and therefore the pairs that did not include one of the most informative first samples were neglected (i.e., two less informative single samples may form a more informative sampling pair). However, considering the large number of cases, testing all possible pairs would be computationally (too) challenging, even with the help from the ScienceCloud infrastructure at the University of Zurich that supports large scale computational research.

It is unavoidable that our interpretations are conditional on the choices we made for the events, virtual catchments and the applied model. The outcome, thus, might differ for other situations, but the general approach demonstrated in this paper would still be applicable and allow users to evaluate the value of different observations in their specific setting.

5. Conclusions

In this study we show the value of a few stream isotope samples, in addition to streamflow, precipitation and precipitation isotope data, for model calibration with explicitly considered the effect of different data error types. The findings of the study can be used to provide guidance on when to sample stream water during events to obtain the most informative data for model calibration.

The improvement in model performance was largest for the first sample, relatively small for the second sample and negligible for the third sample. The validation performance of the model calibrated with two or three intelligent samples was as good as (and sometimes even better than) the upper benchmark with 100 samples. However, when there were very large errors in the rainfall or streamflow data, the improvement in model performance by including stream isotope data was limited.

Data errors affected the calibration of small events more than the calibration of large events, probably because the δ¹⁸O change during the small event was smaller than for larger events. Input data errors (errors in the precipitation and isotopic composition of precipitation) affected the model performance more compared to errors in streamflow. When there were errors in the streamflow data, stream isotope samples helped to reduce the parameter uncertainty of the flow related parameters and improved the simulation of streamflow.

Data errors modified the most informative sampling times: these times were more clustered and earlier compared to the situation when there are no data errors but the majority of the most informative sampling times were still located on the falling limb. In other words, the rising limb and peak flow samples were less informative for model calibration than the falling limb samples. However, when there are significant errors in the isotopic composition of precipitation, rising limb samples were most informative for model calibration.

These findings can be used to guide field sampling for model calibration and contradict the widely held view of field hydrologists that it is important to take samples on the rising limb and at peak flow and makes it easier to sample events to improve model calibration. Our results highlighted the value of a limited number of stream water samples and indicate that even if only a few stream isotope samples are available (and even if these do not cover an entire event), these can still be useful for hydrological model calibration. Compared to the error-free cases in our previous study [11], more stream water samples were needed to achieve the same model performance and samples taken earlier during an event were more informative. These differences indicate that it is valuable to consider possible observation errors when determining the optimal sampling strategy as these errors can influence how many samples to take, and when during an event.