Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design
Abstract
1. Introduction
2. Study Area and Data
2.1. Selected Basins and Observed Streamflow
2.2. Rainfall Data Sets
3. Methodology
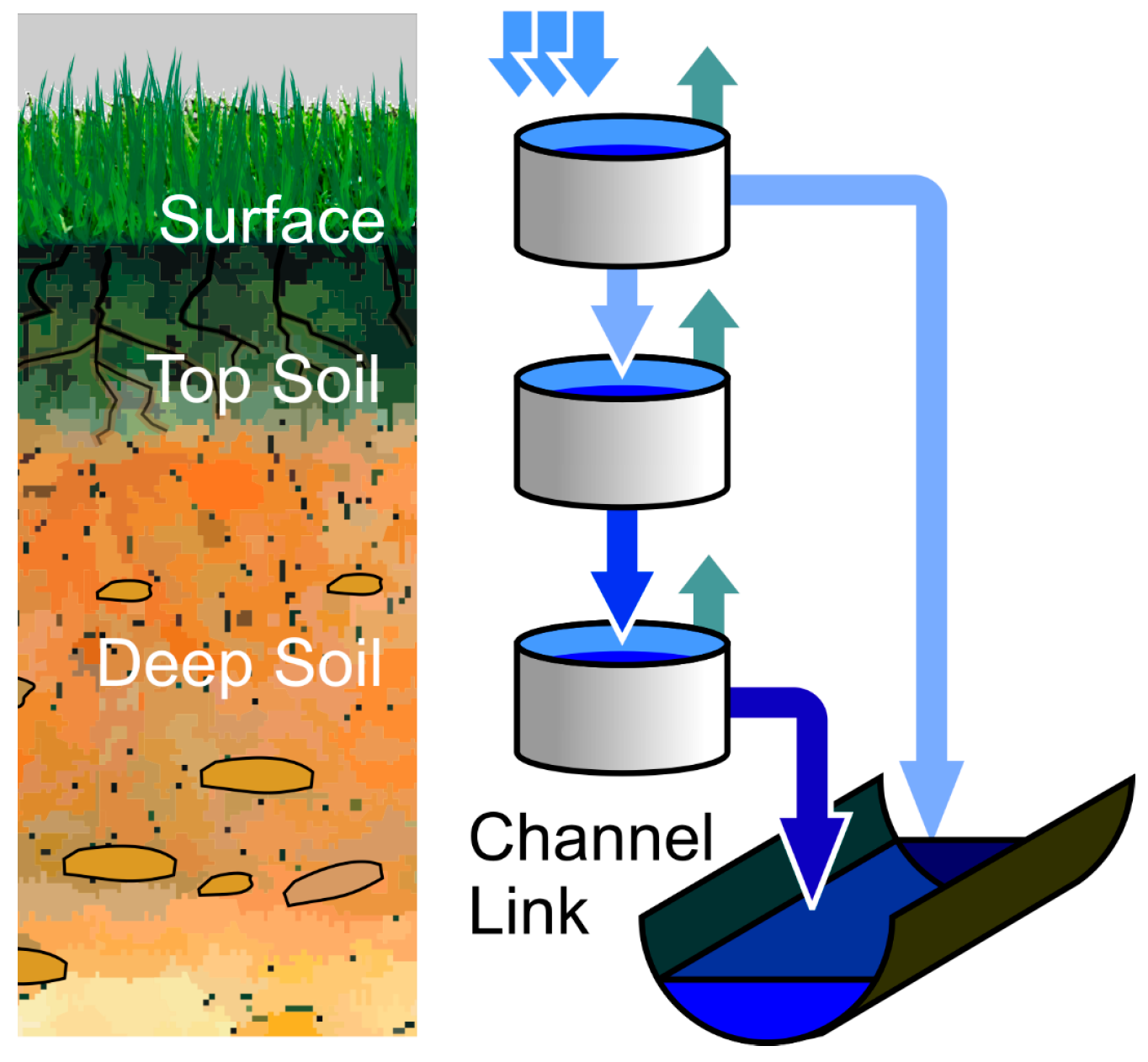
3.1. Distributed Hydrological Model
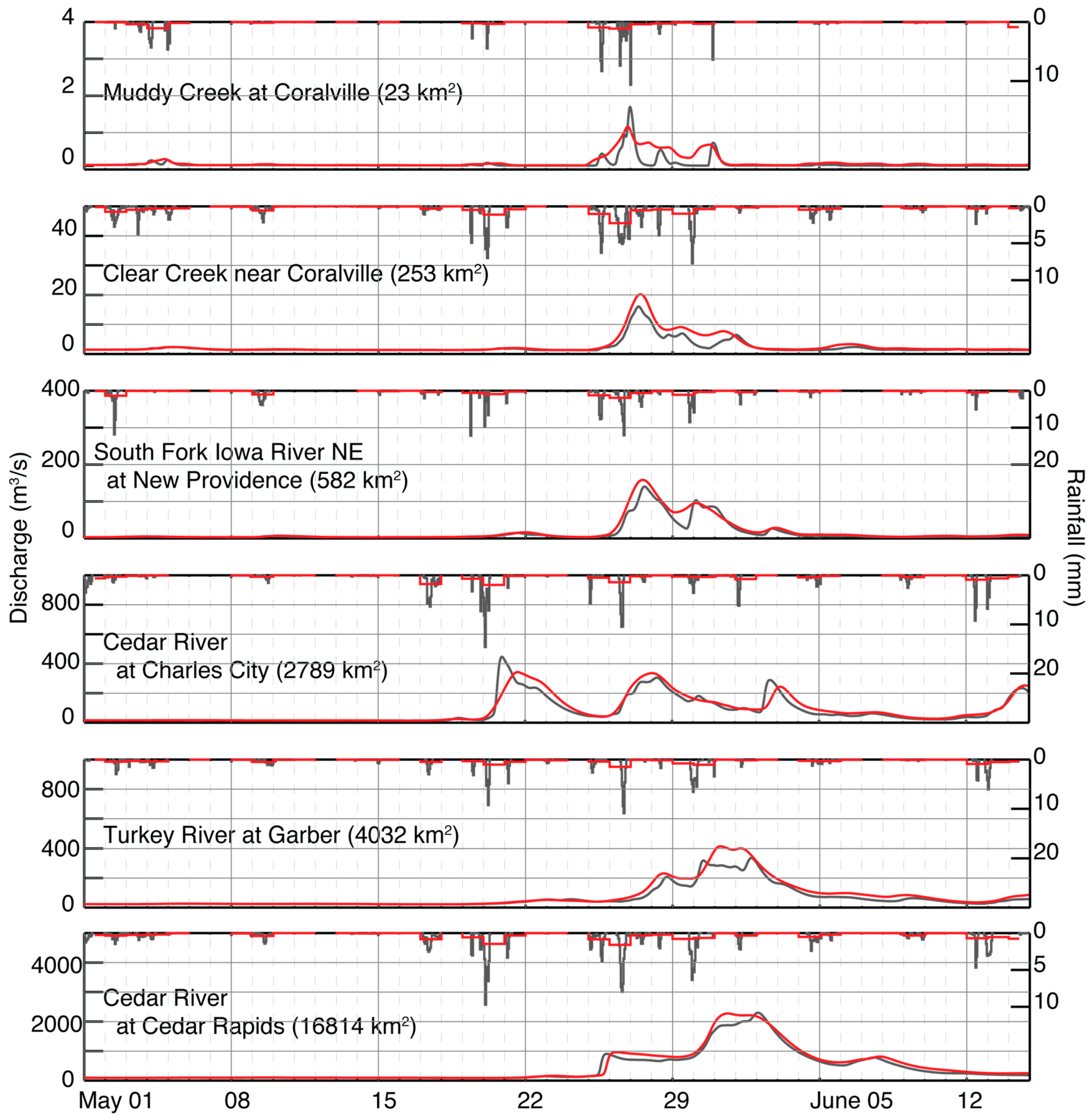
3.2. Model Sensitivity to Spatial and Temporal Resolution of Rainfall Datasets
3.3. Flood Projections Estimates
3.4. Flood Frequency Analysis
3.5. Sensitivity of Flood Frequency Analysis to Selected Period of Analysis and Record Length
4. Results
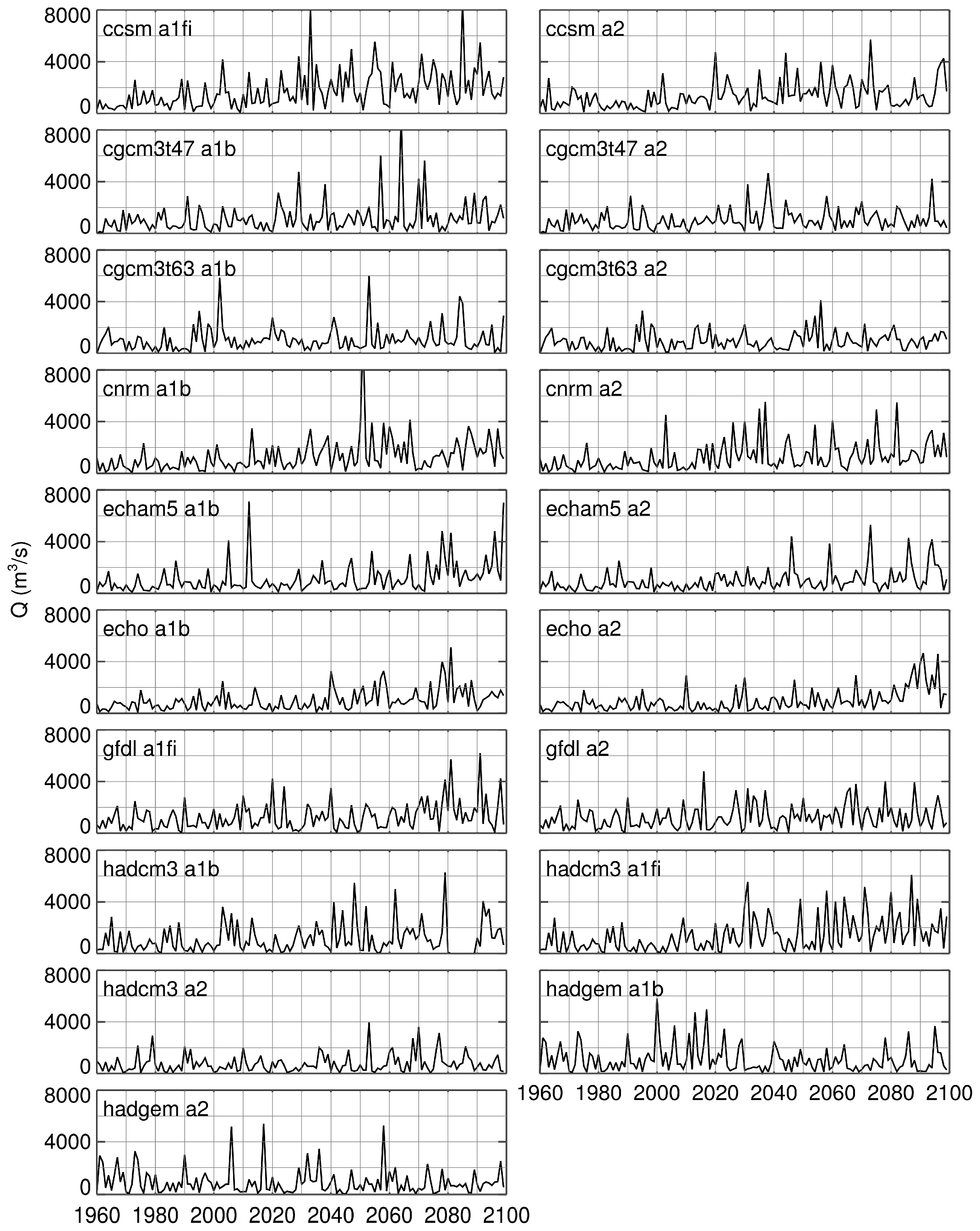
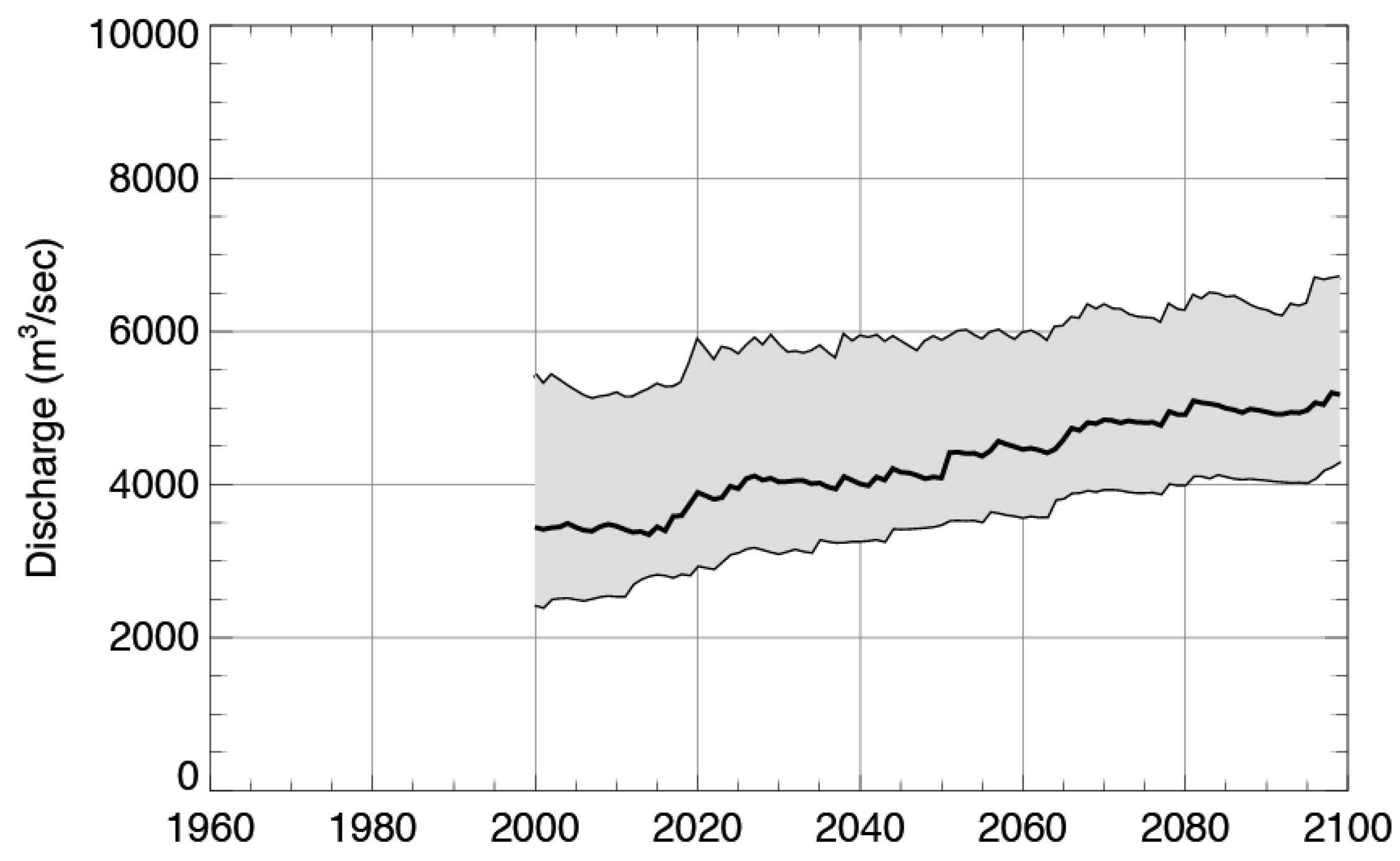
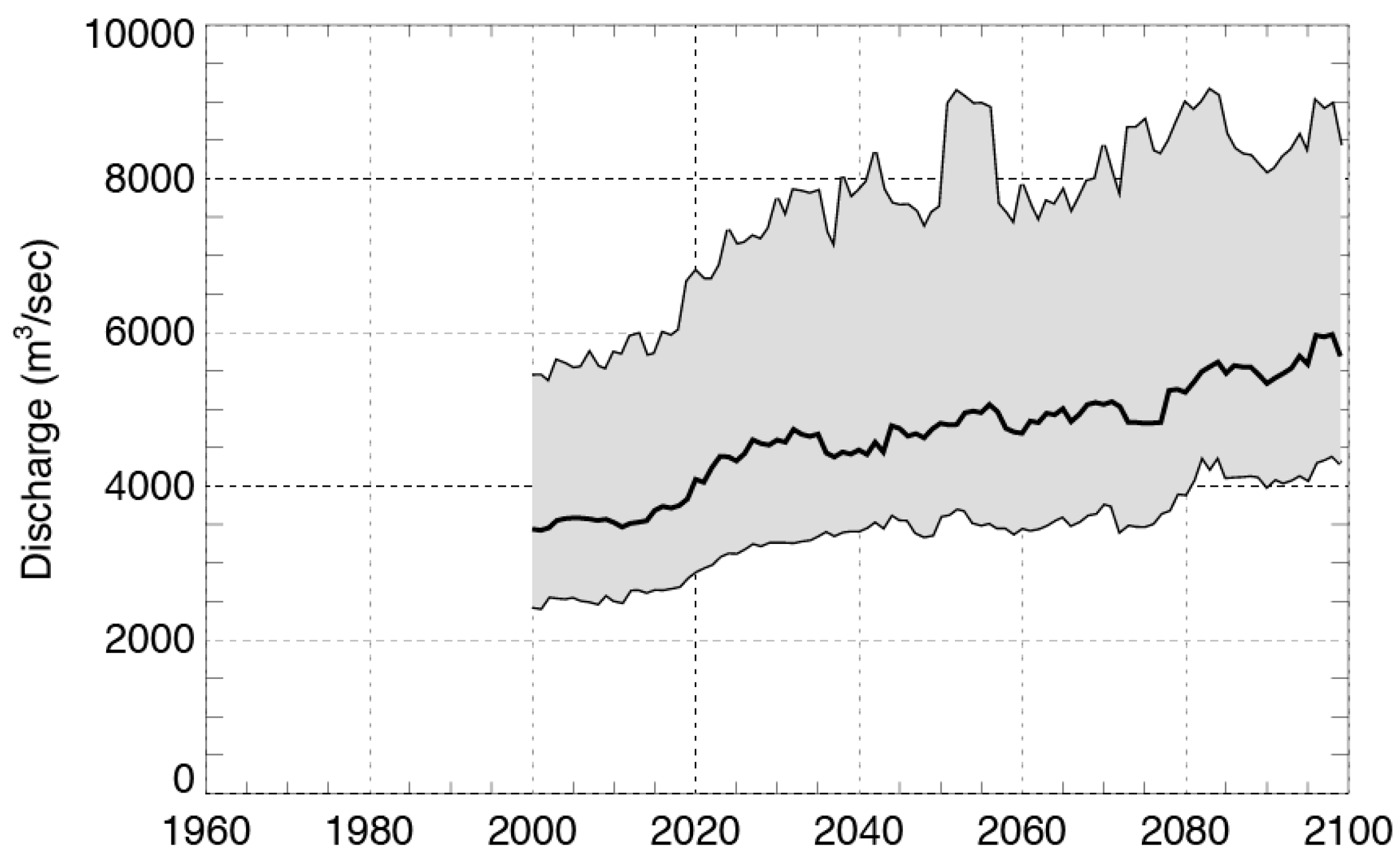
4.1. Projected Annual Peak Flows and Trends
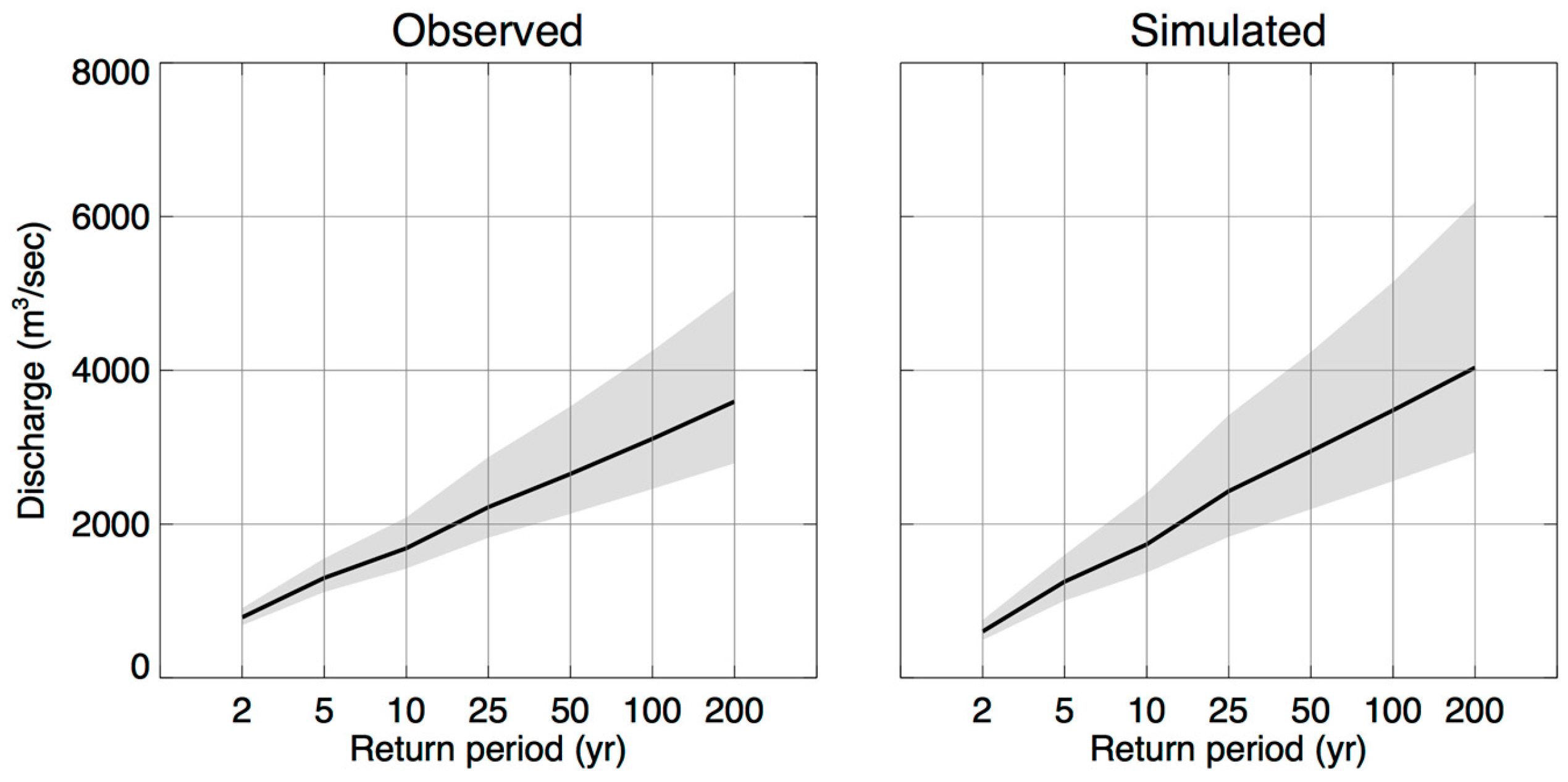
4.2. Projected Floods for Different Return Periods
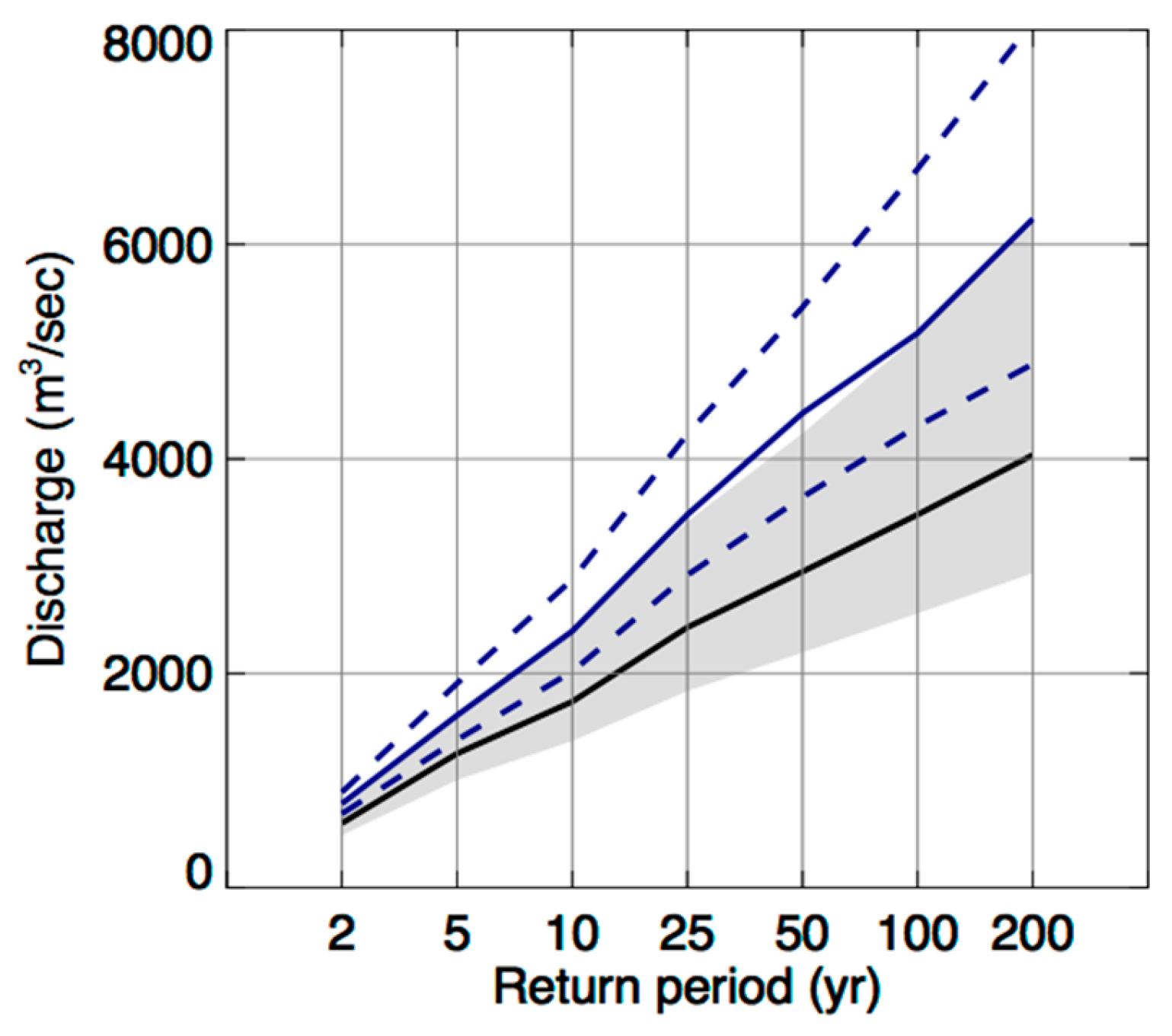
4.3. Changes in the 100-yr Flood Estimates and Their Sensitivity to Availability of Information
5. Discussion
6. Conclusions
- Historical measurements should be used to identify minimum spatio-temporal scales needed to reproduce with acceptable accuracy the historical rainfall distributions and streamflow data.
- The use of multiple climate models and future scenarios is recommended even though it may increase substantially the computational expense and require capacity building to enable data delivery and processing. Future work include exploring the results of applying the methodologies presented in this study over CMIP5 and CMIP6 datasets.
- Engineers should develop standards for non-stationarity that clarify the importance of abruptness and permanence as well as whether these are relevant for all moments of distributions.
- The use of confidence intervals is recommended as a means to compare scales of uncertainty at least until standard procedure for uncertainty integration is developed.
- Including all the available information of projected discharges into flood frequency analysis procedures is recommended, instead of using a limited amount of projected data.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC Climate The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Doocy, S.; Daniels, A.; Murray, S.; Kirsch, T.D. The Human Impact: a Historical Review of Events and Systematic Literature Review. PLoS Curr. Disasters 2013, 1, 1–32. [Google Scholar] [CrossRef]
- Marx, P.; Baer, M. The Potential Impacts of Climate Change on Transportation; National Research Council: Washington, DC, USA, 2002. [Google Scholar]
- Karl, T.R.; Melillo, J.M.; Peterson, T.C. Global climate change impacts in the United States; Cambridge University Press: Cambridge, UK, 2009; Volume 54, ISBN 0521144078. [Google Scholar]
- Wuebbles, D.; Meehl, G.; Hayhoe, K.; Karl, T.R.; Kunkel, K.; Santer, B.; Wehner, M.; Colle, B.; Fischer, E.M.; Fu, R.; et al. CMIP5 climate model analyses: Climate extremes in the United States. Bull. Am. Meteorol. Soc. 2014, 95, 571–583. [Google Scholar] [CrossRef]
- Nemry, F.; Demirel, H. Impacts of Climate Change on Transport: A Focus on Road and Rail Transport Infrastructures. JRC72217; Publications Office: Luxembourg, 2012; ISBN 978-92-79-27037-6. [Google Scholar]
- Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global warming increases the frequency of river floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Watkiss, P. Climate change and river floods in the European Union: Socio-economic consequences and the costs and benefits of adaptation. Glob. Environ. Chang. 2013, 23, 1737–1751. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. The changing nature of flooding across the central United States. Nat. Clim. Chang. 2015, 5, 250–254. [Google Scholar] [CrossRef]
- Milly, P.; Wetherald, R.T.; Dunne, K.A.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Villarini, G.; Smith, J.A.; Baeck, M.L.; Krajewski, W.F. Examining Flood Frequency Distributions in the Midwest U.S. J. Am. Water Resour. Assoc. 2011, 47, 447–463. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Huang, S.; Tecklenburg, J.; Hoffmann, P.; Koch, H.; Fournet, S.; Krysanova, V.; Müller, E.N.; et al. Comparing impacts of climate change on streamflow in four large African river basins. Hydrol. Earth Syst. Sci. 2014, 18, 1305–1321. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G.; Ahmed, K.F. Hydrological changes in the U.S. Northeast using the Connecticut River Basin as a case study: Part 2. Projections of the future. Glob. Planet. Chang. 2015, 133, 167–175. [Google Scholar] [CrossRef]
- Raje, D.; Priya, P.; Krishnan, R. Macroscale hydrological modelling approach for study of large scale hydrologic impacts under climate change in Indian river basins. Hydrol. Process. 2014, 28, 1874–1889. [Google Scholar] [CrossRef]
- Wu, C.; Huang, G.; Yu, H.; Chen, Z.; Ma, J. Impact of Climate Change on Reservoir Flood Control in the Upstream Area of the Beijiang River Basin, South China. J. Hydrometeorol. 2014, 15, 2203–2218. [Google Scholar] [CrossRef]
- Lespinas, F.; Ludwig, W.; Heussner, S. Hydrological and climatic uncertainties associated with modeling the impact of climate change on water resources of small Mediterranean coastal rivers. J. Hydrol. 2014, 511, 403–422. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Zabalza, J.; Vicente-Serrano, S.M.; Revuelto, J.; Gilaberte, M.; Azorin-Molina, C.; Morán-Tejeda, E.; García-Ruiz, J.M.; Tague, C. Impact of climate and land use change on water availability and reservoir management: Scenarios in the Upper Aragón River, Spanish Pyrenees. Sci. Total Environ. 2014, 493, 1222–1231. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, L.V.; Shafroth, P.B.; LeRoy Poff, N. Modeled intermittency risk for small streams in the Upper Colorado River Basin under climate change. J. Hydrol. 2015, 523, 768–780. [Google Scholar] [CrossRef]
- Tofiq, F.A.; Guven, A. Prediction of design flood discharge by statistical downscaling and General Circulation Models. J. Hydrol. 2014, 517, 1145–1153. [Google Scholar] [CrossRef]
- Kingston, D.G.; Taylor, R.G. Sources of uncertainty in climate change impacts on river discharge and groundwater in a headwater catchment of the Upper Nile Basin, Uganda. Hydrol. Earth Syst. Sci. 2010, 14, 1297–1308. [Google Scholar] [CrossRef]
- Kingston, D.G.; Thompson, J.R.; Kite, G. Uncertainty in climate change projections of discharge for the Mekong River Basin. Hydrol. Earth Syst. Sci. 2011, 15, 1459–1471. [Google Scholar] [CrossRef]
- Cameron, D.; Beven, K.; Naden, P. Flood frequency estimation by continuous simulation under climate change (with uncertainty). Hydrol. Earth Syst. Sci. 2000, 4, 393–405. [Google Scholar] [CrossRef]
- Quintero, F.; Sempere-Torres, D.; Berenguer, M.; Baltas, E. A scenario-incorporating analysis of the propagation of uncertainty to flash flood simulations. J. Hydrol. 2012, 460–461, 90–102. [Google Scholar] [CrossRef]
- Stoner, A.M.K.; Hayhoe, K.; Yang, X.; Wuebbles, D.J. An asynchronous regional regression model for statistical downscaling of daily climate variables. Int. J. Climatol. 2013, 33, 2473–2494. [Google Scholar] [CrossRef]
- Hayhoe, K. Development and dissemination of a high-resolution national climate change dataset. Final Rep. United States Geol. Surv. USGS G10AC00248. Available online: https//nccwsc. usgs. gov/displayproject/5050cc22e4b0be20bb30eacc/4f833ee9e4b0e84f608680df (accessed on 8 October 2014).
- Dixon, K.W.; Lanzante, J.R.; Nath, M.J.; Hayhoe, K.; Stoner, A.; Radhakrishnan, A.; Balaji, V.; Gaitán, C.F. Evaluating the stationarity assumption in statistically downscaled climate projections: Is past performance an indicator of future results? Clim. Chang. 2016, 135, 395–408. [Google Scholar] [CrossRef]
- Veilleux, A.G.; Cohn, T.A.; Flynn, K.M.; Mason, R.R., Jr.; Hummel, P.R. Estimating Magnitude and Frequency of Floods Using the PeakFQ Program; U.S. Geological Survey: Reston, VA, USA, 2006.
- U.S. Water Resources Council. Guidelines for Determining Flood Flow Frequency; Bull. 17B Reston of the Hydrology Subcommittee; U.S. Geological Survey, Office of Water Data Coordination: Reston, Virginia, 1982; p. 182. [Google Scholar]
- Meehl, G.A.; Covey, C.; Delworth, T.; Latif, M.; McAvaney, B.; Mitchell, J.F.B.; Stouffer, R.J.; Taylor, K.E. The WCRP CMIP3 multimodel dataset: A new era in climatic change research. Bull. Am. Meteorol. Soc. 2007, 88, 1383–1394. [Google Scholar] [CrossRef]
- Lin, Y.; Mitchell, K.E. The NCEP Stage II/IV hourly precipitation analyses: Development and applications. In Proceedings of the 19th Conference Hydrology, San Diego, CA, USA, 9–13 January 2005; pp. 2–5. [Google Scholar]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; Goska, R.; Kruger, A.; Langel, C.; Mantilllla, R.; Niemeier, J.; Quintero, F.; Seo, B.C.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Quintero, F.; Krajewski, W.F.; Mantilla, R.; Small, S.; Seo, B.-C. A Spatial–Dynamical Framework for Evaluation of Satellite Rainfall Products for Flood Prediction. J. Hydrometeorol. 2016, 17, 2137–2154. [Google Scholar] [CrossRef]
- Mantilla, R.; Gupta, V.K. A GIS numerical framework to study the process basis of scaling statistics in river networks. IEEE Geosci. Remote Sens. Lett. 2005, 2, 404–408. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F. Effect of River Network Geometry on Flood Frequency: A Tale of Two Watersheds in Iowa. J. Hydrol. Eng. 2017, 22, 6017004. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Analyzing the effects of excess rainfall properties on the scaling structure of peak discharges: Insights from a mesoscale river basin. Water Resour. Res. 2015, 51, 3900–3921. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Exploring the Effect of Reservoir Storage on Peak Discharge Frequency. J. Hydrol. Eng. 2013, 18, 1697–1708. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Connecting the power-law scaling structure of peak-discharges to spatially variable rainfall and catchment physical properties. Adv. Water Resour. 2014, 71, 32–43. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Insights into Expected Changes in Regulated Flood Frequencies due to the Spatial Configuration of Flood Retention Ponds. J. Hydrol. Eng. 2015, 20, 4015010. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R.; Small, S.J. Exploring the effects of hillslope-channel link dynamics and excess rainfall properties on the scaling structure of peak-discharge. Adv. Water Resour. 2014, 64, 9–20. [Google Scholar] [CrossRef]
- ElSaadani, M.; Krajewski, W.F. A Time-Based Framework for Evaluating Hydrologic Routing Methodologies Using Wavelet Transform. J. Water Resour. Prot. 2017, 9, 723–744. [Google Scholar] [CrossRef]
- Gupta, V.K.; Ayalew, T.B.; Mantilla, R.; Krajewski, W.F. Classical and generalized horton laws for peak flows in rainfall-runoff events. Chaos 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Seo, B.-C.C.; Cunha, L.K.; Krajewski, W.F. Uncertainty in radar-rainfall composite and its impact on hydrologic prediction for the eastern Iowa flood of 2008. Water Resour. Res. 2013, 49, 2747–2764. [Google Scholar] [CrossRef]
- Eash, D.A.; Barnes, K.K.; Veilleux, A.G. Methods for Estimating Annual Exceedance-Probability Discharges for Streams in Iowa, Based on Data through Water Year 2010; Scientific Investigations Report 2013–5086; USGS: Iowa City, IA, USA, 2013.
- Kendall, M. Rank Correlation Methods; Hodder Arnold: London, UK, 1995; Volume 3, ISBN 9780852641996. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- McLeod, A.A.I. Package “Kendall”. R Packag. 2011. Available online: https://cran.r-project.org/web/packages/Kendall/index.html (accessed on 2 Feburary 2018).
- Koutsoyiannis, D.; Montanari, A. Meurtre par imprudence de concepts scientifiques: Le cas de la stationnarité. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Camici, S.; Brocca, L. Impact of Climate Change on Flood Frequency Using Different Climate Models and Downscaling Approaches. J. Hydrol. 2013, 19, 1–15. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Gilroy, K.L.; McCuen, R.H. A nonstationary flood frequency analysis method to adjust for future climate change and urbanization. J. Hydrol. 2012, 414–415, 40–48. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
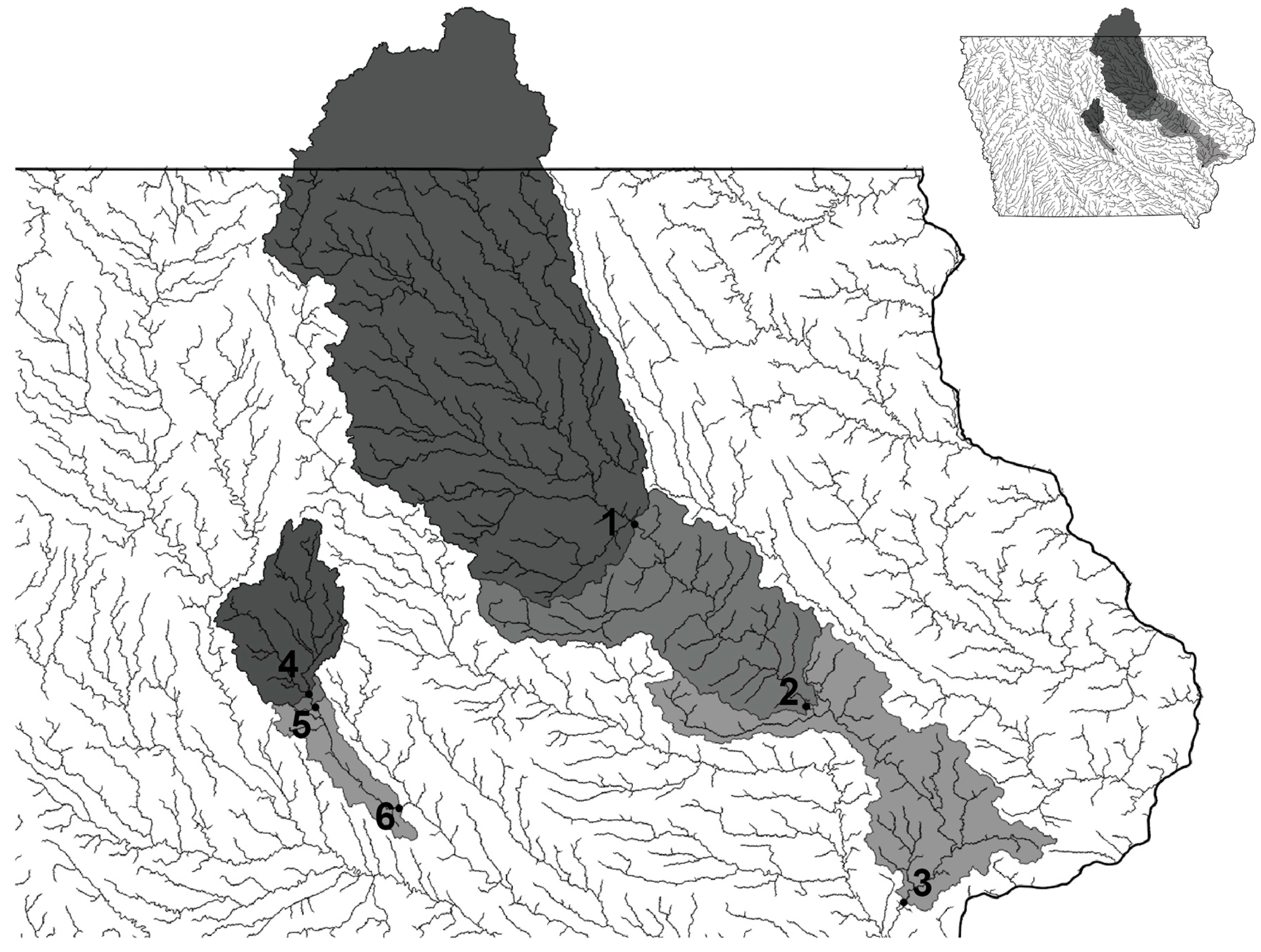
| Map (No.) * | Bridge Location | USGS Gauge (No.) | Drainage Area of Gauge (km2) |
|---|---|---|---|
| 1 | Cedar River: US 20 in Waterloo | 05464000 | 13,294 |
| 2 | Cedar River: US 151 in Cedar Rapids | 05464500 | 16,814 |
| 3 | Cedar River: I-80 near West Branch | 05465000 | 20,080 |
| 4 | Skunk River: US 30 in Ames | 05471000 | 1458 |
| 5 | Skunk River: I-35 south of Ames | 05471000 | 1458 |
| 6 | Skunk River: I-80 in Colfax | 05471050 | 2105 |
| Origin | CMIP3 Model | Scenarios |
|---|---|---|
| National Center for Atmospheric Research | CCSM3 | A1FI, A2 |
| Canadian Centre for Climate Modelling and Analysis | CGCM3.1-T47 * CGCM3.1-T63 * | A2, A1B A2, A1B |
| Centre National de Recerches Meteorologiques | CNRM-CM3 | A2, A1B |
| Max Planck Institute for Meteorology | ECHAM5 | A2, A1B |
| National Institute for Meteorological Research/Korea Meteorological Administration | ECHO-G | A2, A1B |
| NOAA Geophysical Fluid Dynamics Laboratory | GFDL–CM2.1 | A2, A1FI |
| UK Meteorological Office Hadley Centre | HADCM3 HADGEM1 | A1FI, A2, A1B A2, A1B |
| Model and Scenario | Mann-Kendall’s Tau | p-Value | p-Value < 0.05 |
|---|---|---|---|
| CCSM A1FI | 0.278 | 1.07 × 10−6 | true |
| CCSM A2 | 0.273 | 1.79 × 10−6 | true |
| CGCM3T47 A1B | 0.129 | 0.024 | true |
| CGCM3T47 A2 | 0.183 | 0.0013 | true |
| CGCM3T63 A1B | 0.031 | 0.58 | false |
| CGCM3T63 A2 | 0.095 | 0.095 | true |
| CNRM A1B | 0.300 | 1.19 × 10−7 | true |
| CNRM A2 | 0.242 | 2.37 × 10−5 | true |
| ECHAM5 A1B | 0.131 | 0.021 | true |
| ECHAM5 A2 | 0.205 | 0.00033 | true |
| ECHO A1B | 0.124 | 0.029 | true |
| ECHO A2 | 0.059 | 0.30 | false |
| GFDL A1FI | 0.053 | 0.35 | false |
| GFDL A2 | 0.120 | 0.035 | true |
| HADCM3 A1B | 0.091 | 0.11 | false |
| HADCM3 A1FI | 0.224 | 9.18 × 10−5 | true |
| HADCM3 A2 | −0.003 | 0.96 | false |
| HADGEM A1B | −0.017 | 0.77 | false |
| HADGEM A2 | −0.017 | 0.77 | false |
| 100 yr-Flood (5%, Median, 95%) | |||
|---|---|---|---|
| Basin | 1960–2009 | 1960–2099 | Difference (%) |
| Cedar River: US 20 in Waterloo (05464000) | 2378, 3219, 4884 | 4004, 4915, 6266 | 68, 52, 28 |
| Cedar River: US 151 in Cedar Rapids (05464500) | 2558, 3480, 5150 | 4306, 5173, 6705 | 68, 48, 30 |
| Cedar River: I-80 near West Branch (05465000) | 2607, 3514, 5218 | 4332, 5196, 6773 | 66, 47, 29 |
| Skunk River: US 30 in Ames (05471000) | 444, 635, 1019 | 652, 820, 1075 | 46, 29, 5 |
| Skunk River: I-35 south of Ames (05471000) | 466, 665, 1070 | 676, 836, 1105 | 44, 25, 3 |
| Skunk River: I-80 in Colfax (05471050) | 532, 738, 1168 | 793, 995, 1310 | 49, 34, 12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintero, F.; Mantilla, R.; Anderson, C.; Claman, D.; Krajewski, W. Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design. Hydrology 2018, 5, 19. https://doi.org/10.3390/hydrology5010019
Quintero F, Mantilla R, Anderson C, Claman D, Krajewski W. Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design. Hydrology. 2018; 5(1):19. https://doi.org/10.3390/hydrology5010019
Chicago/Turabian StyleQuintero, Felipe, Ricardo Mantilla, Christopher Anderson, David Claman, and Witold Krajewski. 2018. "Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design" Hydrology 5, no. 1: 19. https://doi.org/10.3390/hydrology5010019
APA StyleQuintero, F., Mantilla, R., Anderson, C., Claman, D., & Krajewski, W. (2018). Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design. Hydrology, 5(1), 19. https://doi.org/10.3390/hydrology5010019





