EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting
Abstract
1. Introduction
2. Methodology
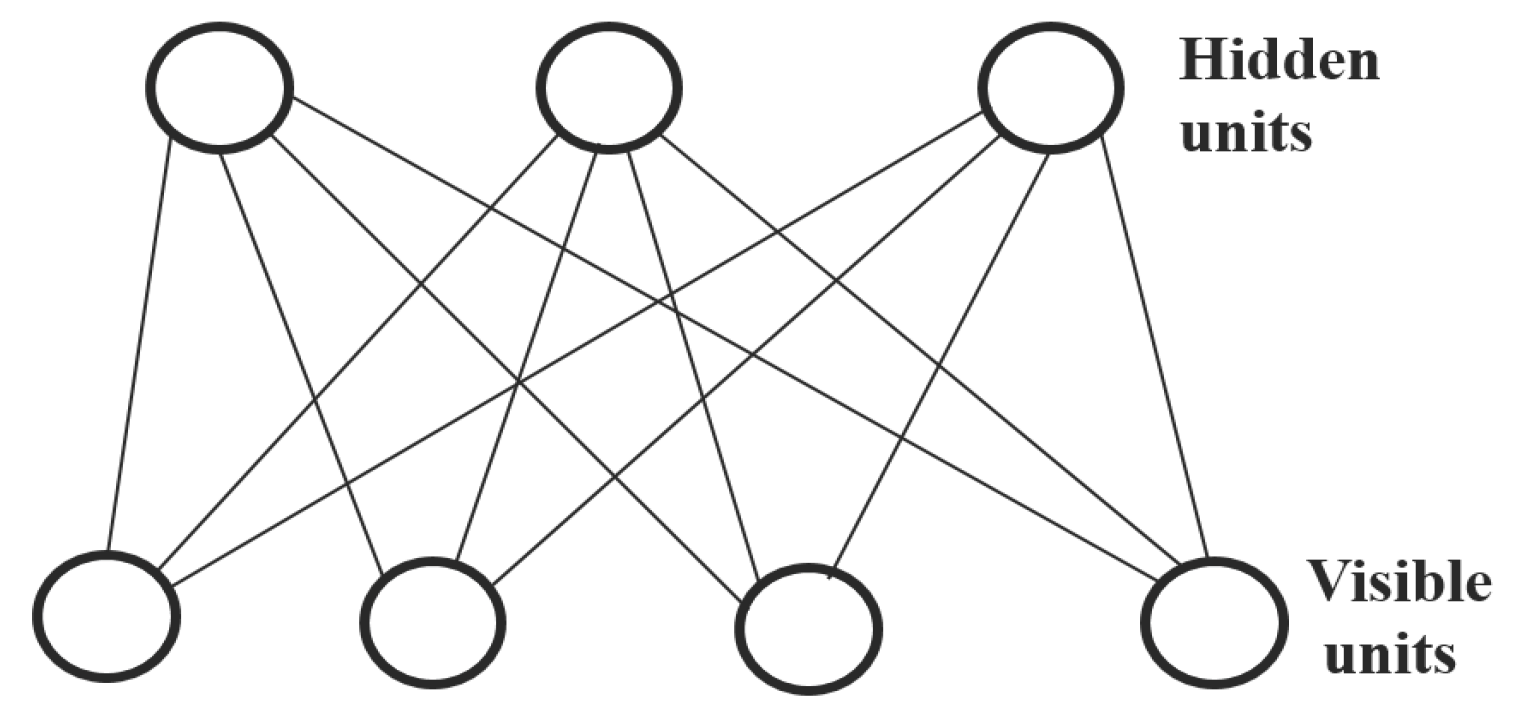
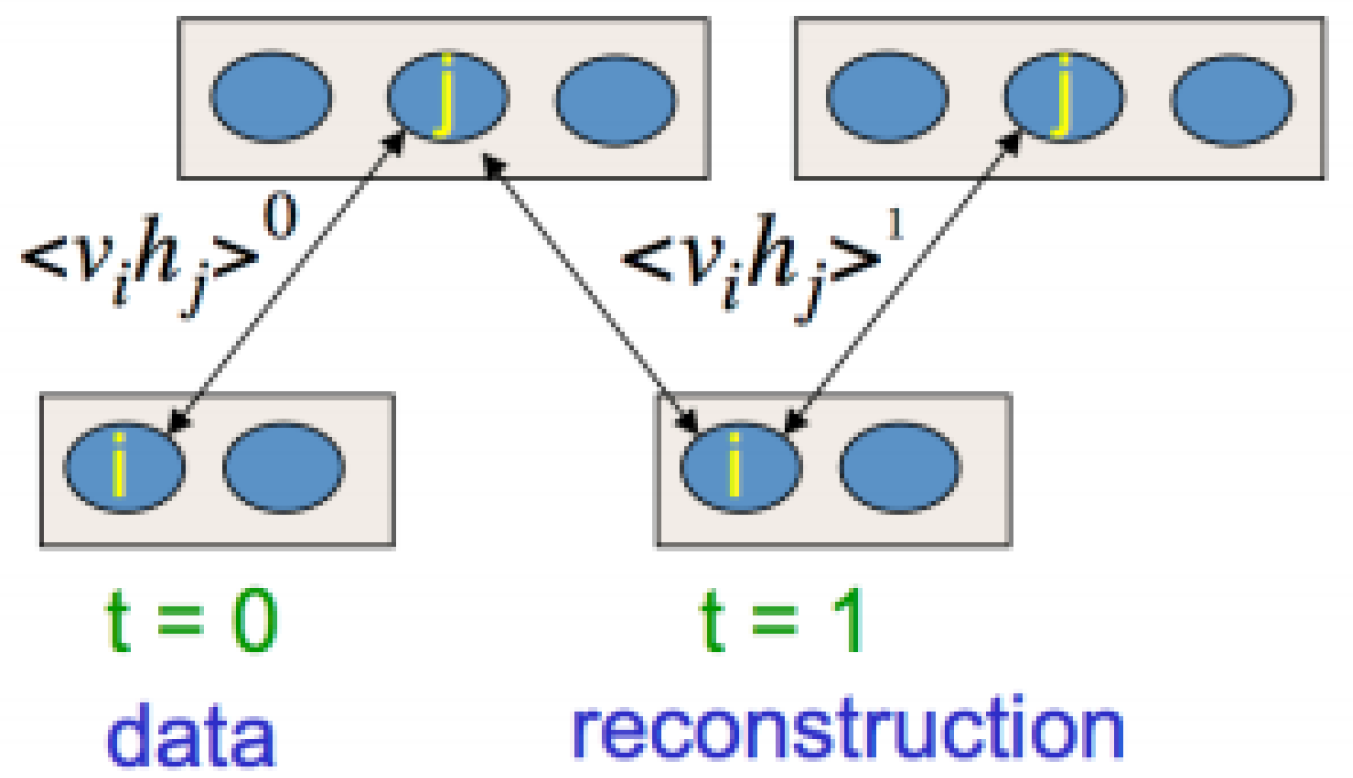
2.1. Restricted Boltzmann Machines
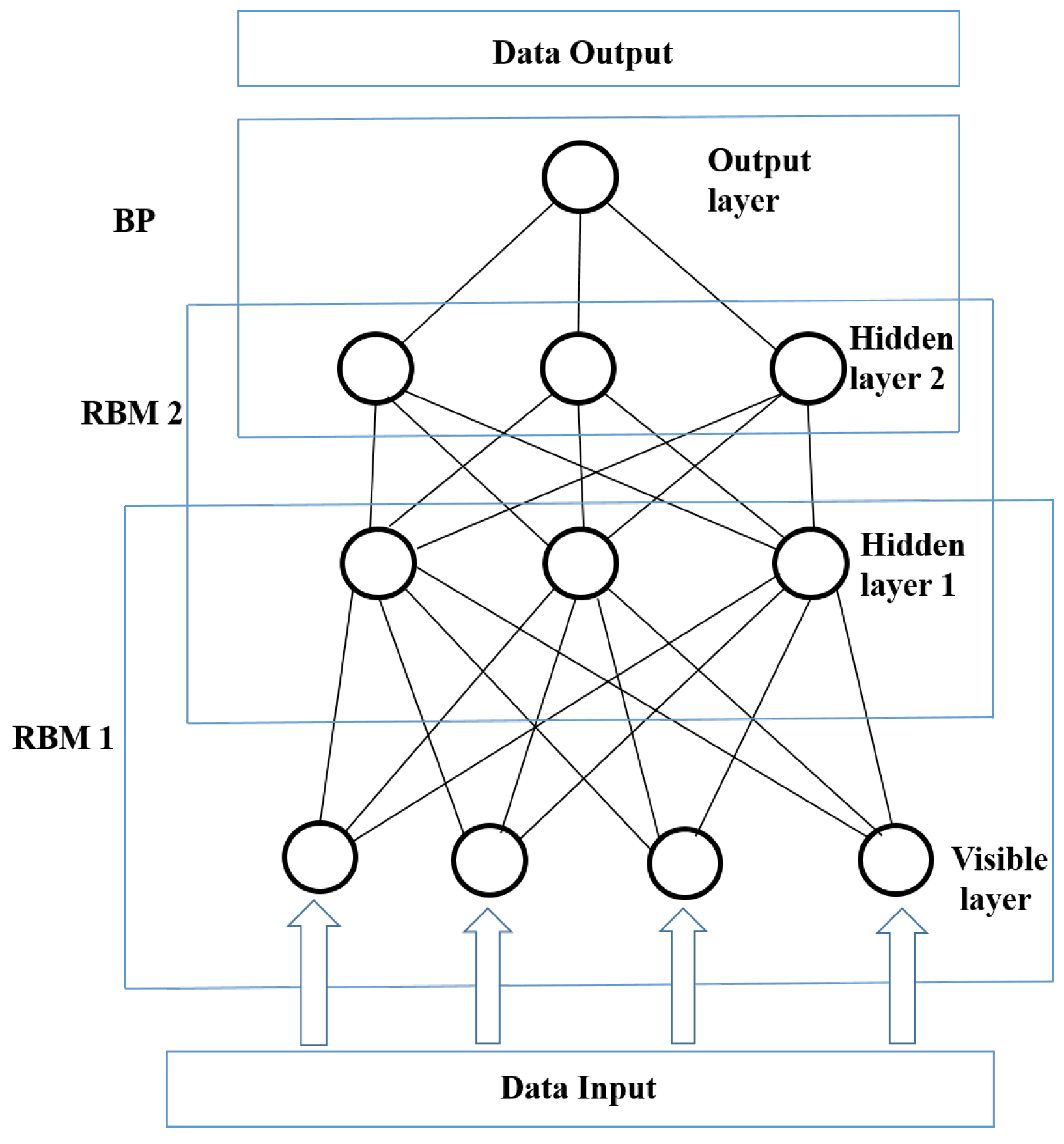
2.2. Deep Belief Network
- set initial states to the training data set (visible units);
- sample in a back-and-forth process
- update all of the hidden units in parallel starting with visible units, reconstruct visible units from the hidden units, and finally update the hidden units again;
- repeat with all training examples and update the weights using Equation (9).
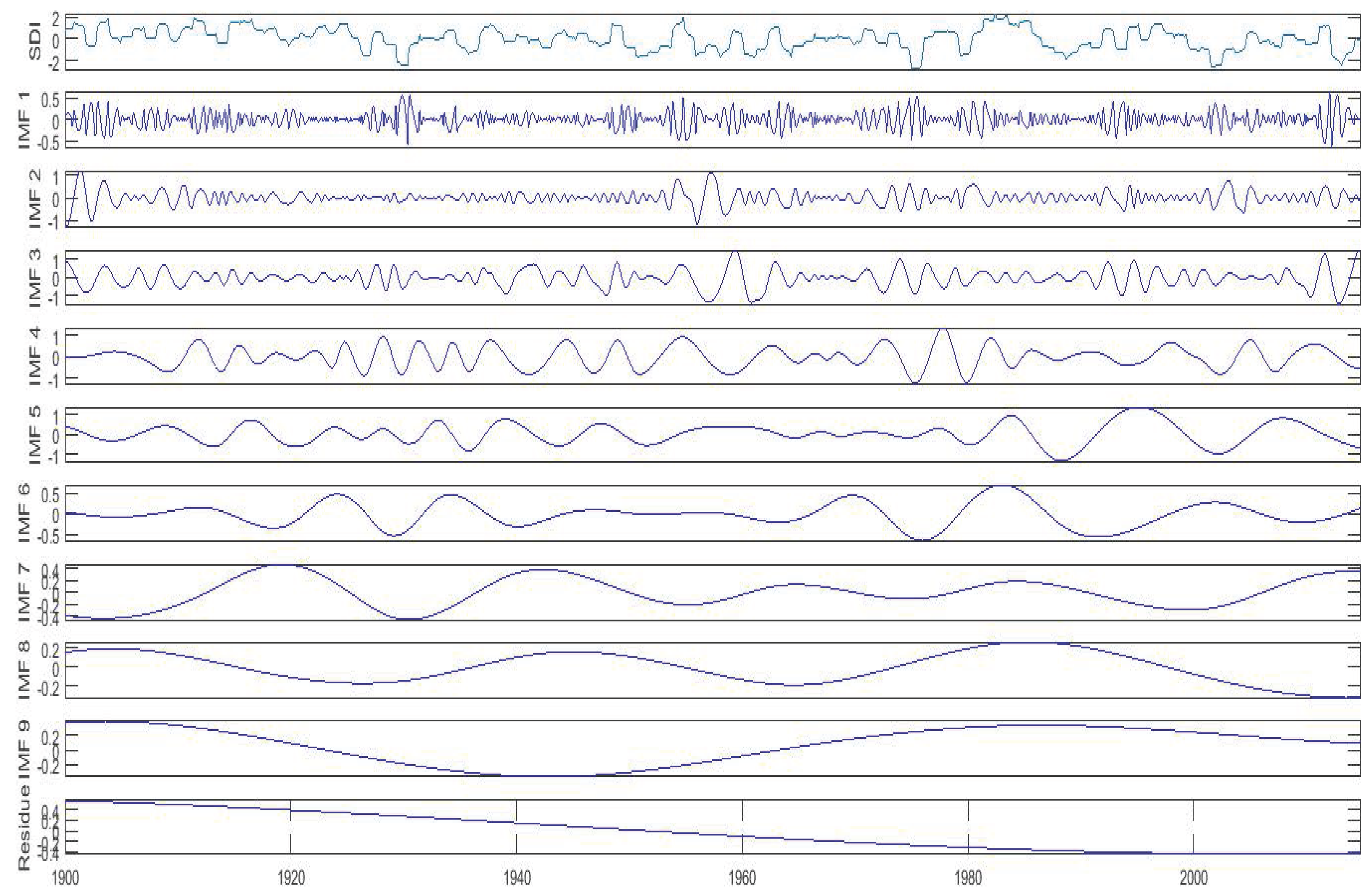
2.3. Empirical Mode Decomposition
- an IMF has only one extremum between two subsequent zero crossings—i.e., the number of local extrema and zero crossings differs at most by one;
- the local average of the upper and lower envelopes of an IMF has to be zero.
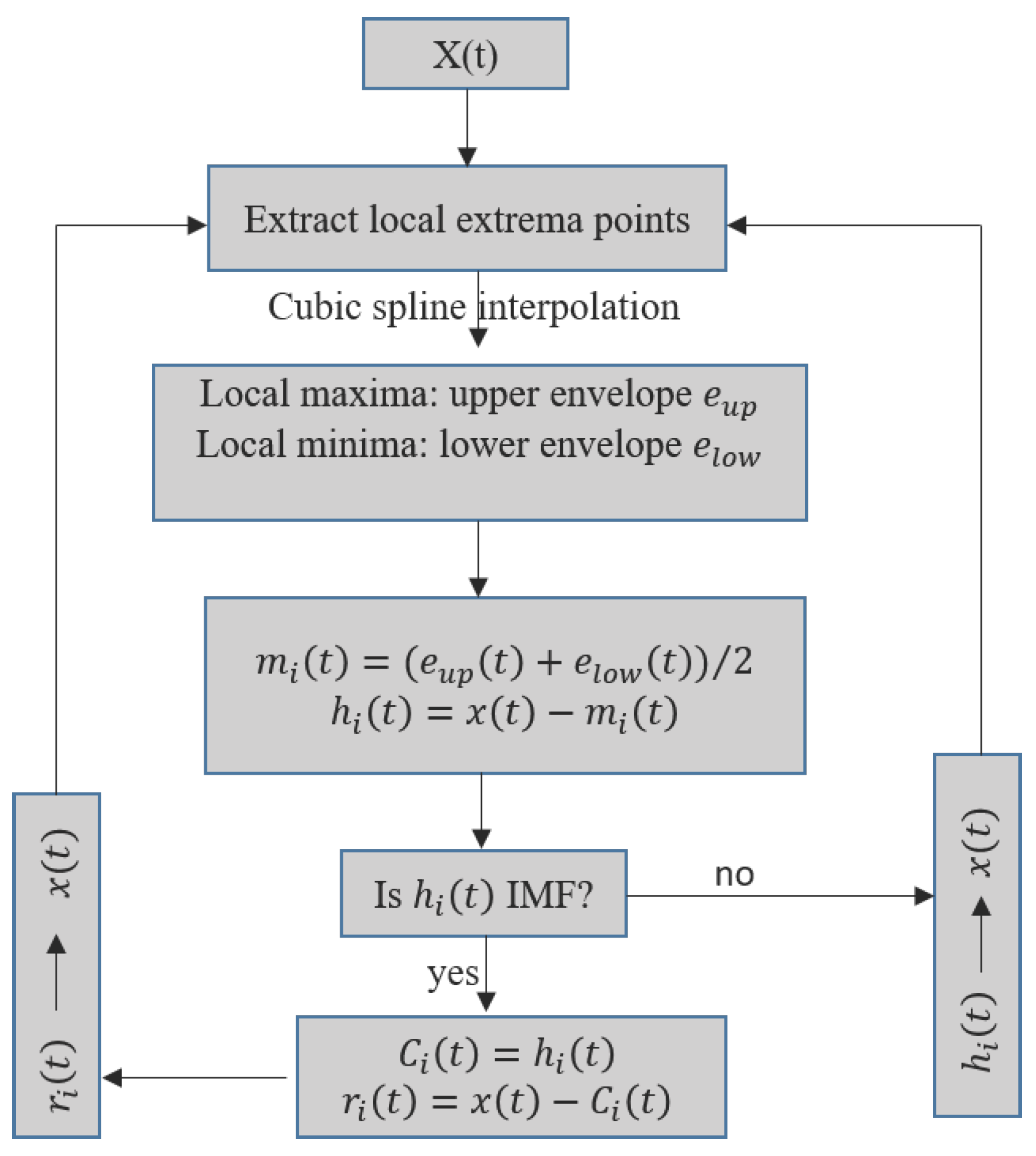
2.4. The EMD Algorithm
- identify all of the local extrema of ;
- create the upper envelope and the lower envelope by the cubic spline interpolation, respectively;
- compute the mean value of the upper and lower envelopes: ;
- extract the mean envelope from the signal , where the difference is defined as : ;
- check the properties of :
- (a)
- if d(t) satisfies the requirements of IMF Conditions (1) and (2), then is denoted as the ith IMF, and is replaced with the residual ; the ith IMF is denoted as , and i is the order number of the IMF;
- (b)
- if is not an IMF, replace with ;
- repeat Steps 1–5 until the residue becomes a monotonic function or the number of extrema is less than or equal to one, from which no further IMF can be extracted.
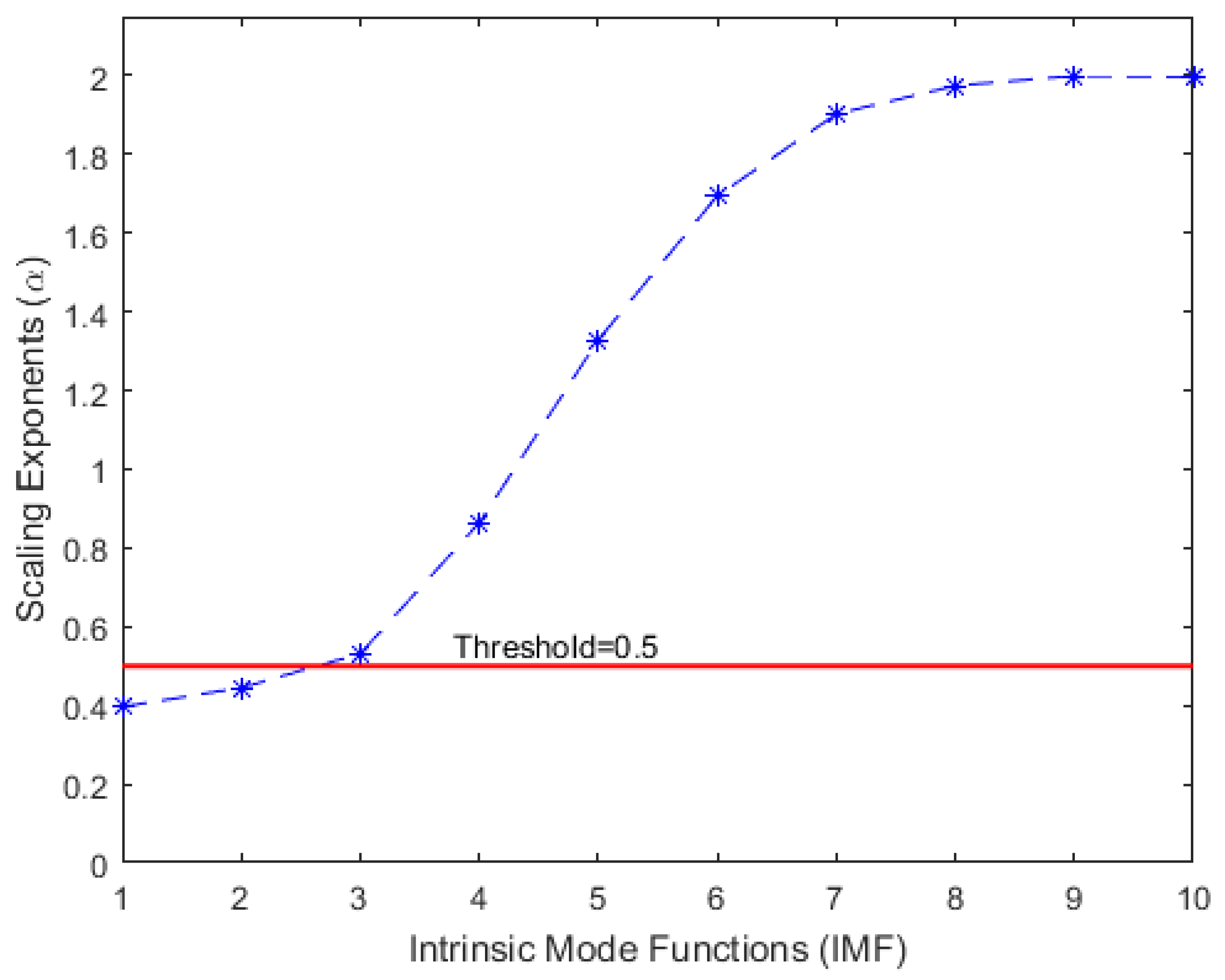
2.5. Detrended Fluctuation Analysis
- for a given time series with length L, divide it into d subseries of length n;
- for each subseries ,
- (a)
- Create a cumulative time series for
- (b)
- Fit a least squares line to {}
- (c)
- Calculate the root mean square fluctuation (i.e. standard deviation) of the integrated and detrended time series:
- (d)
- Finally, calculate the mean value of the root mean square fluctuation for all subseries of length n
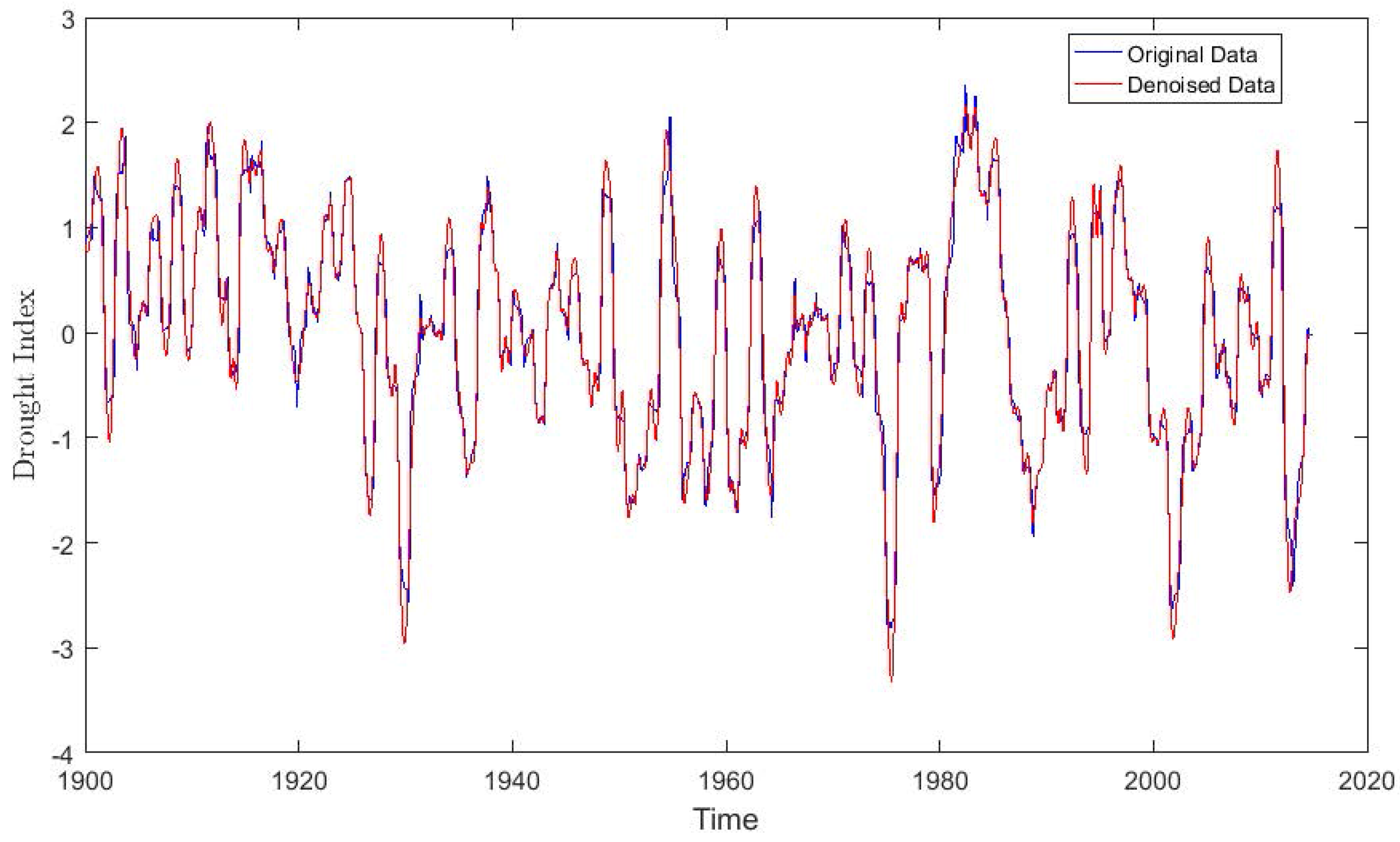
2.6. EMD-Based Denoising Using DFA
3. Study Area and Observed Dataset
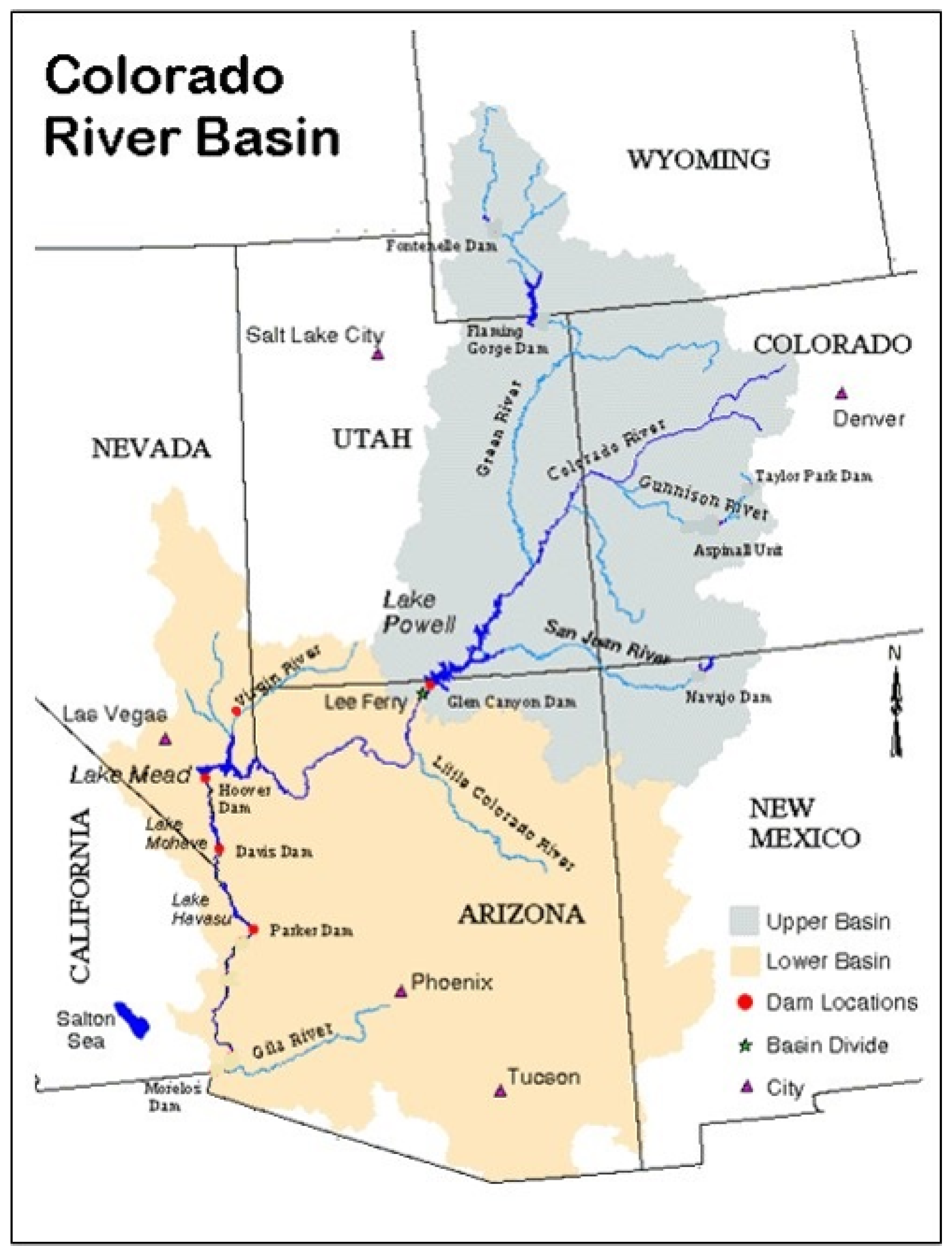
3.1. Study Area
3.2. Standardized Streamflow Index
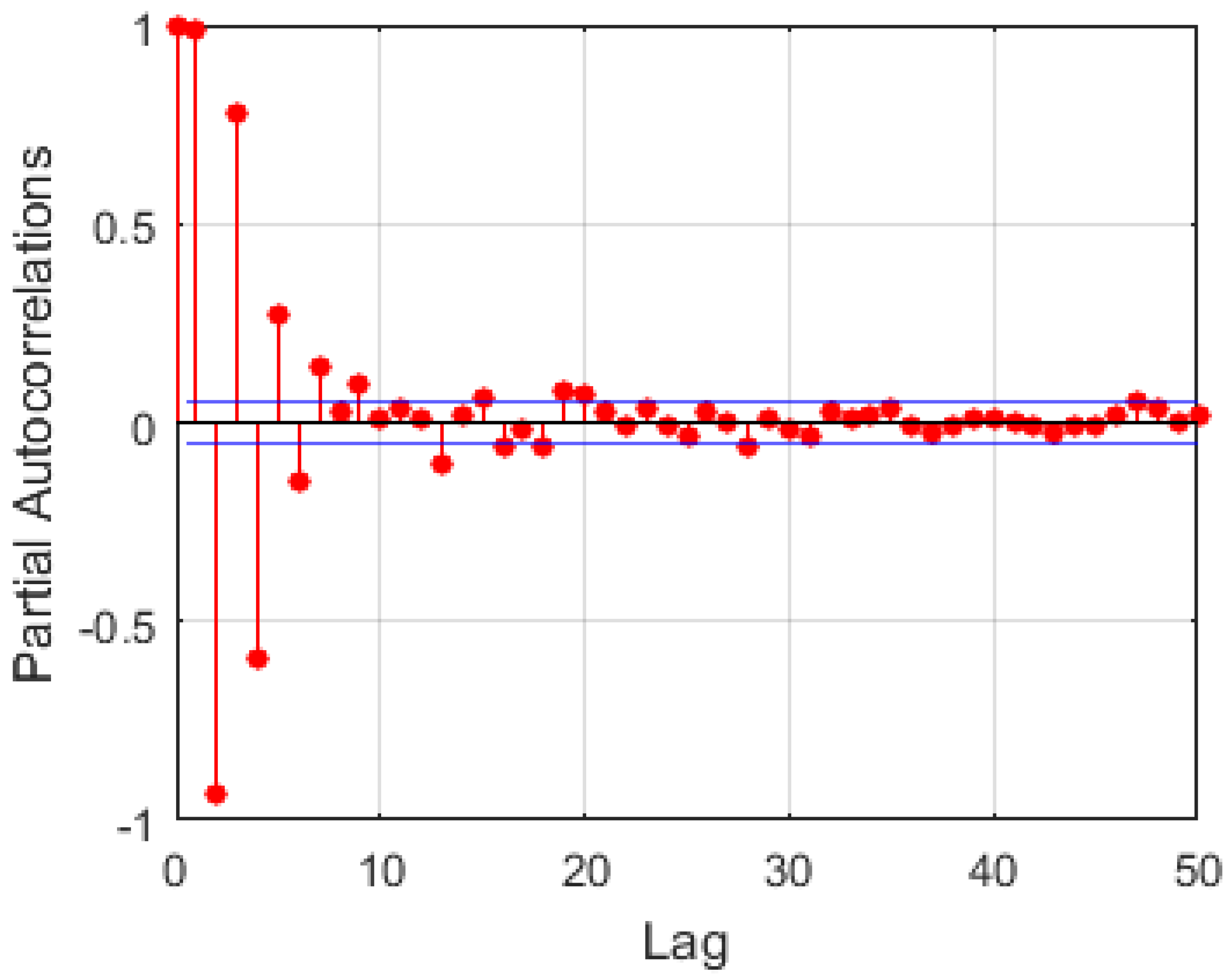
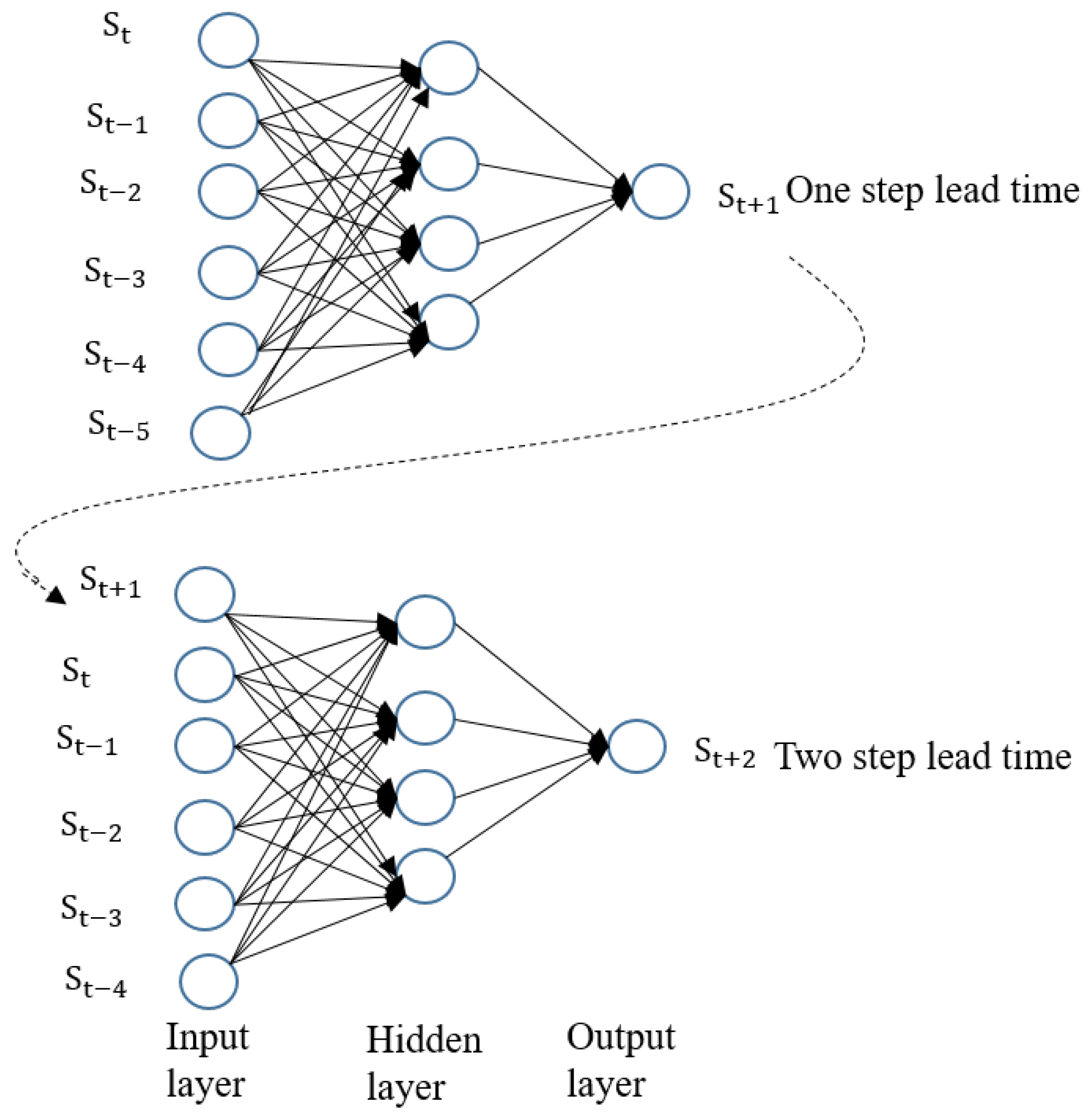
3.3. Feature Extraction
3.4. Evaluation of Model Performances
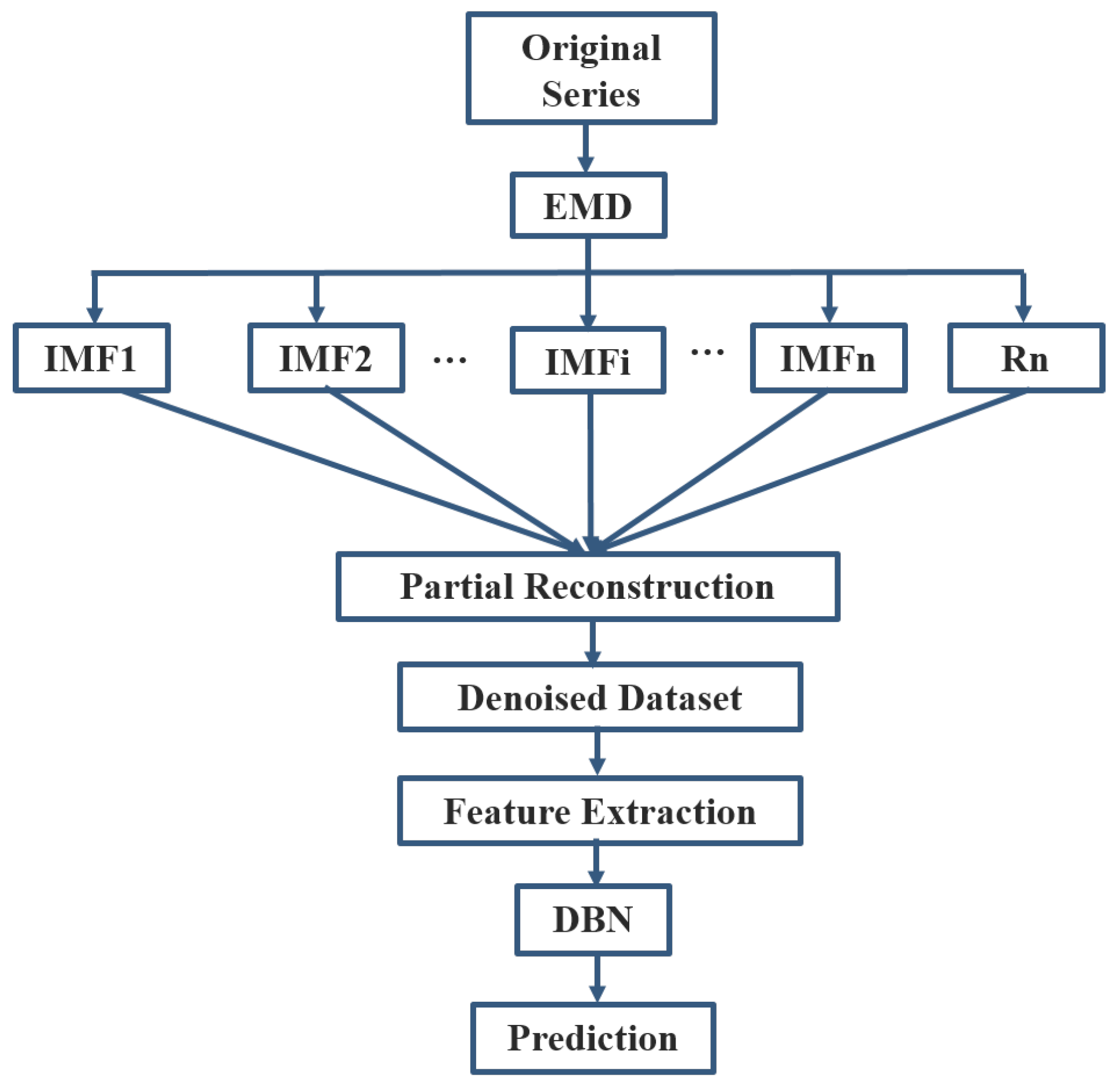
3.5. Summary of the Proposed EMD based Predictive Deep Belief Network
- obtain the different time-scale SSI (SSI 12 in this case);
- decompose the time series data into several IMFs and a residue (Rn) using EMD;
- reconstruct the original data using only relevant IMF components;
- divide the data into training and testing sets (80% for training and 20% for testing);
- construct one training matrix as the input for the DBN;
- select the appropriate model structure and initialize the parameters of the DBN (two hidden layers are used);
- using the training data, pre-train the DBN through unsupervised learning;
- fine-tune the parameters of the entire network using the back-propagation algorithm;
- perform predictions with the trained model using the test data.
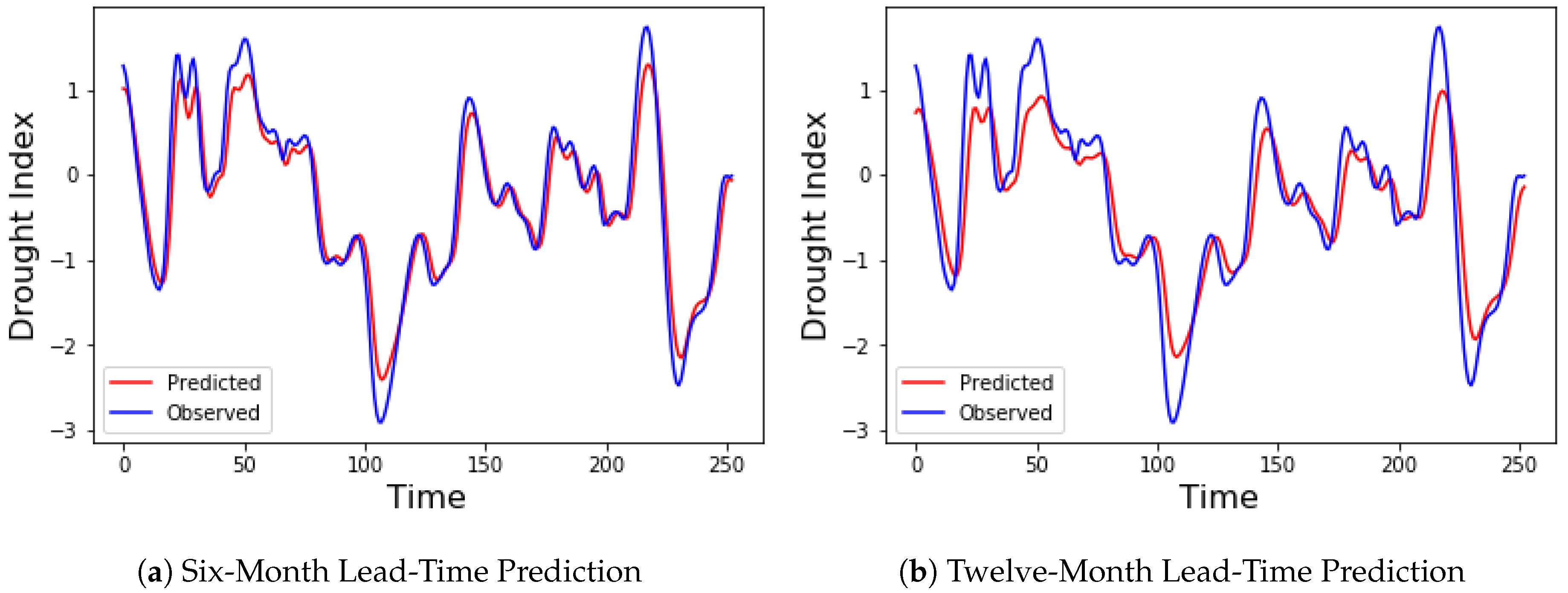
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wilhite, D.A.; Hayes, M.J. Drought planning in the united states: Status and future directions. In The Arid Frontier; Springer: Dordrecht, The Netherlands, 1998; pp. 33–54. [Google Scholar]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Smith, A.B.; Katz, R.W. Us billion-dollar weather and climate disasters: Data sources, trends, accuracy and biases. Nat. Hazards 2013, 67, 387–410. [Google Scholar] [CrossRef]
- Changnon, S.A.; Pielke, R.A., Jr.; Changnon, D.; Sylves, R.T.; Pulwarty, R. Human factors explain the increased losses from weather and climate extremes. Bull. Am. Meteorol. Soc. 2000, 81, 437. [Google Scholar] [CrossRef]
- Ross, T.; Lott, N. A Climatology of 1980–2003 Extreme Weather and Climate Events; US Department of Commerece, National Ocanic and Atmospheric Administration, National Environmental Satellite Data and Information Service, National Climatic Data Center: Asheville, NC, USA, 2003.
- Nielsen-Gammon, J.W. The 2011 texas drought. Texas Water J. 2012, 3, 59–95. [Google Scholar]
- Hoerling, M.; Eischeid, J.; Kumar, A.; Leung, R.; Mariotti, A.; Mo, K.; Schubert, S.; Seager, R. Causes and predictability of the 2012 great plains drought. Bull. Am. Meteorol. Soc. 2014, 95, 269–282. [Google Scholar] [CrossRef]
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 california drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef]
- Dutra, E.; Magnusson, L.; Wetterhall, F.; Cloke, H.L.; Balsamo, G.; Boussetta, S.; Pappenberger, F. The 2010–2011 drought in the horn of africa in ecmwf reanalysis and seasonal forecast products. Int. J. Climatol. 2013, 33, 1720–1729. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Nakhjiri, N.; Farahmand, A. Global integrated drought monitoring and prediction system. Sci. Data 2014, 1, 140001. [Google Scholar] [CrossRef] [PubMed]
- Madadgar, S.; Moradkhani, H. A bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685–1705. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using feed-forward recursive neural network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Mehr, A.D.; Kahya, E.; Özger, M. A gene–wavelet model for long lead time drought forecasting. J. Hydrol. 2014, 517, 691–699. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term spi drought forecasting in the awash river basin in ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P. Drought forecasting using a hybrid stochastic and neural network model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. Adv. Neural Inf. Process. Syst. 2007, 19, 153. [Google Scholar]
- Blenkinsop, S.; Fowler, H.J. Changes in drought frequency, severity and duration for the british isles projected by the prudence regional climate models. J. Hydrol. 2007, 342, 50–71. [Google Scholar] [CrossRef]
- Chun, K.P.; Wheater, H.; Onof, C. Prediction of the impact of climate change on drought: an evaluation of six uk catchments using two stochastic approaches. Hydrol. Processes 2013, 27, 1600–1614. [Google Scholar] [CrossRef]
- Liu, T. A novel text classification approach based on deep belief network. In Proceedings of the International Conference on Neural Information Processing, Sydney, Australia, 22–25 November 2010; Springer: Berlin, Germany, 2010; pp. 314–321. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Shen, F.; Zhao, J. A model with fuzzy granulation and deep belief networks for exchange rate forecasting. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 366–373. [Google Scholar]
- Chen, J.; Jin, Q.; Chao, J. Design of deep belief networks for short-term prediction of drought index using data in the huaihe river basin. Math. Probl. Eng. 2012, 2012, 235929. [Google Scholar] [CrossRef]
- Kuremoto, T.; Kimura, S.; Kobayashi, K.; Obayashi, M. Time series forecasting using a deep belief network with restricted boltzmann machines. Neurocomputing 2014, 137, 47–56. [Google Scholar] [CrossRef]
- Di, C.; Yang, X.; Wang, X. A four-stage hybrid model for hydrological time series forecasting. PLoS ONE 2014, 9, e104663. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 1998; Volume 454, pp. 903–995. [Google Scholar]
- Labate, D.; la Foresta, F.; Occhiuto, G.; Morabito, F.C.; Lay-Ekuakille, A.; Vergallo, P. Empirical mode decomposition vs. wavelet decomposition for the extraction of respiratory signal from single-channel ecg: A comparison. IEEE Sens. J. 2013, 13, 2666–2674. [Google Scholar] [CrossRef]
- Premanode, B.; Vonprasert, J.; Toumazou, C. Prediction of exchange rates using averaging intrinsic mode function and multiclass support vector regression. Artif. Intell. Res. 2013, 2, 47. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C.; Saidi, Z. Emd-based signal noise reduction. Int. J. Signal Process. 2004, 1, 33–37. [Google Scholar]
- Yaslan, Y.; Bican, B. Empirical mode decomposition based denoising method with support vector regression for time series prediction: A case study for electricity load forecasting. Measurement 2017, 103, 52–61. [Google Scholar] [CrossRef]
- Weron, R. Estimating long-range dependence: Finite sample properties and confidence intervals. Phys. A Stat. Mech. Appl. 2002, 312, 285–299. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of dna nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Tieleman, T. Training restricted boltzmann machines using approximations to the likelihood gradient. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 1064–1071. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Computat. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Agana, N.A.; Homaifar, A. A deep learning based approach for long-term drought prediction. In Proceedings of the SoutheastCon, Charlotte, NC, USA, 30 March–2 April 2017; pp. 1–8. [Google Scholar]
- Agana, N.A.; Homaifar, A. A hybrid deep belief network for long-term drought prediction. In Proceedings of the Workshop on Mining Big Data in Climate and Environment (MBDCE 2017), 17th SIAM International Conference on Data Mining (SDM 2017), Houston, TX, USA, 27–29 April 2017; pp. 1–8. [Google Scholar]
- Salakhutdinov, R. Learning deep generative models. Annu. Rev. Stat. Appl. 2015, 2, 361–385. [Google Scholar] [CrossRef]
- Kisi, O. Wavelet regression model for short-term streamflow forecasting. J. Hydrol. 2010, 389, 344–353. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M.; Mano, A. A multivariate ann-wavelet approach for rainfall–runoff modeling. Water Resour. Manag. 2009, 23, 2877. [Google Scholar] [CrossRef]
- Sang, Y.-F. Improved wavelet modeling framework for hydrologic time series forecasting. Water Resour. Manag. 2013, 27, 2807–2821. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [PubMed]
- Mert, A.; Akan, A. Detrended fluctuation thresholding for empirical mode decomposition based denoising. Dig. Signal Process. 2014, 32, 48–56. [Google Scholar] [CrossRef]
- Qian, X.; Gu, G.; Zhou, W. Modified detrended fluctuation analysis based on empirical mode decomposition for the characterization of anti-persistent processes. Phys. A Stat. Mech. Appl. 2011, 390, 4388–4395. [Google Scholar] [CrossRef][Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; American Meteorological Society Boston: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Cacciamani, C.; Morgillo, A.; Marchesi, S.; Pavan, V. Monitoring and forecasting drought on a regional scale: Emilia-romagna region. In Methods and Tools for Drought Analysis and Management; Springer: Dordrecht, The Netherlands, 2007; pp. 29–48. [Google Scholar]
- Wu, C.L.; Chau, K.W.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part i—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moreira, E.E.; Pires, C.L.; Pereira, L.S. Spi drought class predictions driven by the north atlantic oscillation index using log-linear modeling. Water 2016, 8, 43. [Google Scholar] [CrossRef]


| Station | Metric | DBN | EMD-DBN | MLP | EMD-MLP | SVR | EMD-SVR |
|---|---|---|---|---|---|---|---|
| Lee’s Ferry | RMSE | 0.03609 | 0.00892 | 0.05063 | 0.03638 | 0.03673 | 0.00918 |
| MAE | 0.022118 | 0.00647 | 0.03157 | 0.02745 | 0.02104 | 0.00667 | |
| NSE | 0.96323 | 0.99686 | 0.93207 | 0.96323 | 0.96504 | 0.99766 | |
| Paria | RMSE | 0.056349 | 0.0103 | 0.066744 | 0.025649 | 0.056196 | 0.008668 |
| MAE | 0.035205 | 0.007753 | 0.046733 | 0.018784 | 0.032271 | 0.006369 | |
| NSE | 0.89618 | 0.99655 | 0.84850 | 0.97231 | 0.89359 | 0.99683 | |
| Little C R | RMSE | 0.055215 | 0.0119 | 0.078347 | 0.060729 | 0.063625 | 0.012007 |
| MAE | 0.034330 | 0.00899 | 0.05710 | 0.049367 | 0.046197 | 0.00925 | |
| NSE | 0.87431 | 0.99408 | 0.81794 | 0.95161 | 0.86324 | 0.99403 | |
| C R Canyon | RMSE | 0.036122 | 0.00814 | 0.050631 | 0.034439 | 0.036642 | 0.009173 |
| MAE | 0.022646 | 0.006386 | 0.031531 | 0.026860 | 0.034869 | 0.006455 | |
| NSE | 0.96486 | 0.99853 | 0.93248 | 0.96803 | 0.96463 | 0.99842 | |
| Virgin R | RMSE | 0.048079 | 0.00817 | 0.053033 | 0.024385 | 0.046524 | 0.007942 |
| MAE | 0.027074 | 0.005180 | 0.033781 | 0.017263 | 0.025161 | 0.005616 | |
| NSE | 0.95914 | 0.99852 | 0.95262 | 0.98986 | 0.96421 | 0.99892 | |
| C R Hoover | RMSE | 0.038824 | 0.00686 | 0.045099 | 0.019594 | 0.039546 | 0.006937 |
| MAE | 0.018958 | 0.004499 | 0.021003 | 0.011846 | 0.015699 | 0.003347 | |
| NSE | 0.95193 | 0.99827 | 0.93280 | 0.98445 | 0.94833 | 0.99830 | |
| C R Davies | RMSE | 0.035912 | 0.00865 | 0.051219 | 0.034183 | 0.036535 | 0.008977 |
| MAE | 0.022693 | 0.006081 | 0.032272 | 0.026294 | 0.022015 | 0.006652 | |
| NSE | 0.96658 | 0.99722 | 0.93299 | 0.96613 | 0.96590 | 0.99780 | |
| Williams R | RMSE | 0.035366 | 0.00844 | 0.049666 | 0.03132 | 0.035801 | 0.006914 |
| MAE | 0.022378 | 0.006385 | 0.031253 | 0.024498 | 0.021475 | 0.005218 | |
| NSE | 0.96553 | 0.99748 | 0.93463 | 0.97234 | 0.96603 | 0.99801 | |
| C R Parker | RMSE | 0.035261 | 0.00875 | 0.048665 | 0.031484 | 0.037417 | 0.008185 |
| MAE | 0.022174 | 0.007089 | 0.030343 | 0.024622 | 0.021004 | 0.006305 | |
| NSE | 0.96085 | 0.99757 | 0.93435 | 0.96991 | 0.96451 | 0.99796 | |
| C R Imperial | RMSE | 0.035366 | 0.00844 | 0.049666 | 0.03132 | 0.035801 | 0.006914 |
| MAE | 0.022378 | 0.006385 | 0.031253 | 0.024498 | 0.021475 | 0.005218 | |
| NSE | 0.96245 | 0.99756 | 0.93617 | 0.96832 | 0.96540 | 0.99815 |
| Station | Metric | DBN | EMD-DBN | MLP | EMD-MLP | SVR | EMD-SVR |
|---|---|---|---|---|---|---|---|
| Lee’s Ferry | RMSE | 0.03760 | 0.01298 | 0.06858 | 0.04391 | 0.03830 | 0.01797 |
| MAE | 0.02314 | 0.01010 | 0.05181 | 0.03321 | 0.02454 | 0.01328 | |
| NSE | 0.95719 | 0.99540 | 0.87426 | 0.94605 | 0.96204 | 0.99118 | |
| Paria | RMSE | 0.05824 | 0.01177 | 0.07267 | 0.05547 | 0.05828 | 0.017298 |
| MAE | 0.04367 | 0.00924 | 0.05958 | 0.04810 | 0.04053 | 0.01344 | |
| NSE | 0.88405 | 0.99423 | 0.81943 | 0.87183 | 0.88386 | 0.98754 | |
| Little C R | RMSE | 0.06628 | 0.01693 | 0.07549 | 0.04769 | 0.07102 | 0.02833 |
| MAE | 0.04955 | 0.01332 | 0.06079 | 0.03727 | 0.04859 | 0.02094 | |
| NSE | 0.77706 | 0.98729 | 0.71083 | 0.89925 | 0.77409 | 0.96444 | |
| C R Canyon | RMSE | 0.03742 | 0.01114 | 0.06501 | 0.03640 | 0.03674 | 0.01447 |
| MAE | 0.02547 | 0.00815 | 0.04493 | 0.02718 | 0.03057 | 0.01067 | |
| NSE | 0.95384 | 0.99668 | 0.89088 | 0.95201 | 0.94519 | 0.99440 | |
| Virgin R | RMSE | 0.04420 | 0.01053 | 0.05337 | 0.03919 | 0.07664 | 0.03023 |
| MAE | 0.02765 | 0.00775 | 0.03703 | 0.03276 | 0.03963 | 0.01838 | |
| NSE | 0.94665 | 0.99810 | 0.92137 | 0.97376 | 0.89972 | 0.98438 | |
| C R Hoover | RMSE | 0.04997 | 0.01049 | 0.06616 | 0.04582 | 0.05298 | 0.02021 |
| MAE | 0.03089 | 0.00654 | 0.03266 | 0.04188 | 0.02707 | 0.01010 | |
| NSE | 0.89898 | 0.99483 | 0.82291 | 0.90135 | 0.88644 | 0.98080 | |
| C R Davies | RMSE | 0.03705 | 0.01395 | 0.05359 | 0.02945 | 0.04048 | 0.01529 |
| MAE | 0.02655 | 0.01060 | 0.03440 | 0.02330 | 0.02898 | 0.01128 | |
| NSE | 0.94084 | 0.99476 | 0.92770 | 0.97102 | 0.93875 | 0.99370 | |
| Williams R | RMSE | 0.033984 | 0.01035 | 0.06008 | 0.02838 | 0.03689 | 0.01502 |
| MAE | 0.02843 | 0.00780 | 0.03661 | 0.02559 | 0.02966 | 0.01119 | |
| NSE | 0.94899 | 0.99501 | 0.91175 | 0.95620 | 0.92468 | 0.99376 | |
| C R Parker | RMSE | 0.03713 | 0.01237 | 0.05935 | 0.02911 | 0.03905 | 0.01311 |
| MAE | 0.02493 | 0.00920 | 0.03715 | 0.02408 | 0.02535 | 0.01010 | |
| NSE | 0.93004 | 0.99538 | 0.90386 | 0.96657 | 0.92454 | 0.99480 | |
| C R Imperial | RMSE | 0.03601 | 0.01230 | 0.05998 | 0.02802 | 0.03729 | 0.01455 |
| MAE | 0.02424 | 0.00832 | 0.03834 | 0.02366 | 0.02590 | 0.01063 | |
| NSE | 0.94935 | 0.99561 | 0.90469 | 0.97006 | 0.95316 | 0.99386 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agana, N.A.; Homaifar, A. EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting. Hydrology 2018, 5, 18. https://doi.org/10.3390/hydrology5010018
Agana NA, Homaifar A. EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting. Hydrology. 2018; 5(1):18. https://doi.org/10.3390/hydrology5010018
Chicago/Turabian StyleAgana, Norbert A., and Abdollah Homaifar. 2018. "EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting" Hydrology 5, no. 1: 18. https://doi.org/10.3390/hydrology5010018
APA StyleAgana, N. A., & Homaifar, A. (2018). EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting. Hydrology, 5(1), 18. https://doi.org/10.3390/hydrology5010018




