Trends and Changes in Recent and Future Penman-Monteith Potential Evapotranspiration in Benin (West Africa)
Abstract
1. Introduction
2. Study Area, Data and Methods
2.1. Study Area and Data
2.2. Methods
2.2.1. PET computing
2.2.2. PET Inter-Annual Variability Assessment
2.2.3. Mann-Kendall Test
2.2.4. Bias Correction
2.2.5. Changes Rates
3. Results and Discussion
3.1. Recent Inter-Annual Variability of PET
3.2. PET Trends Analysis
3.3. Bias Correction Performances
3.4. Rates of Changes Related to the Baseline Period
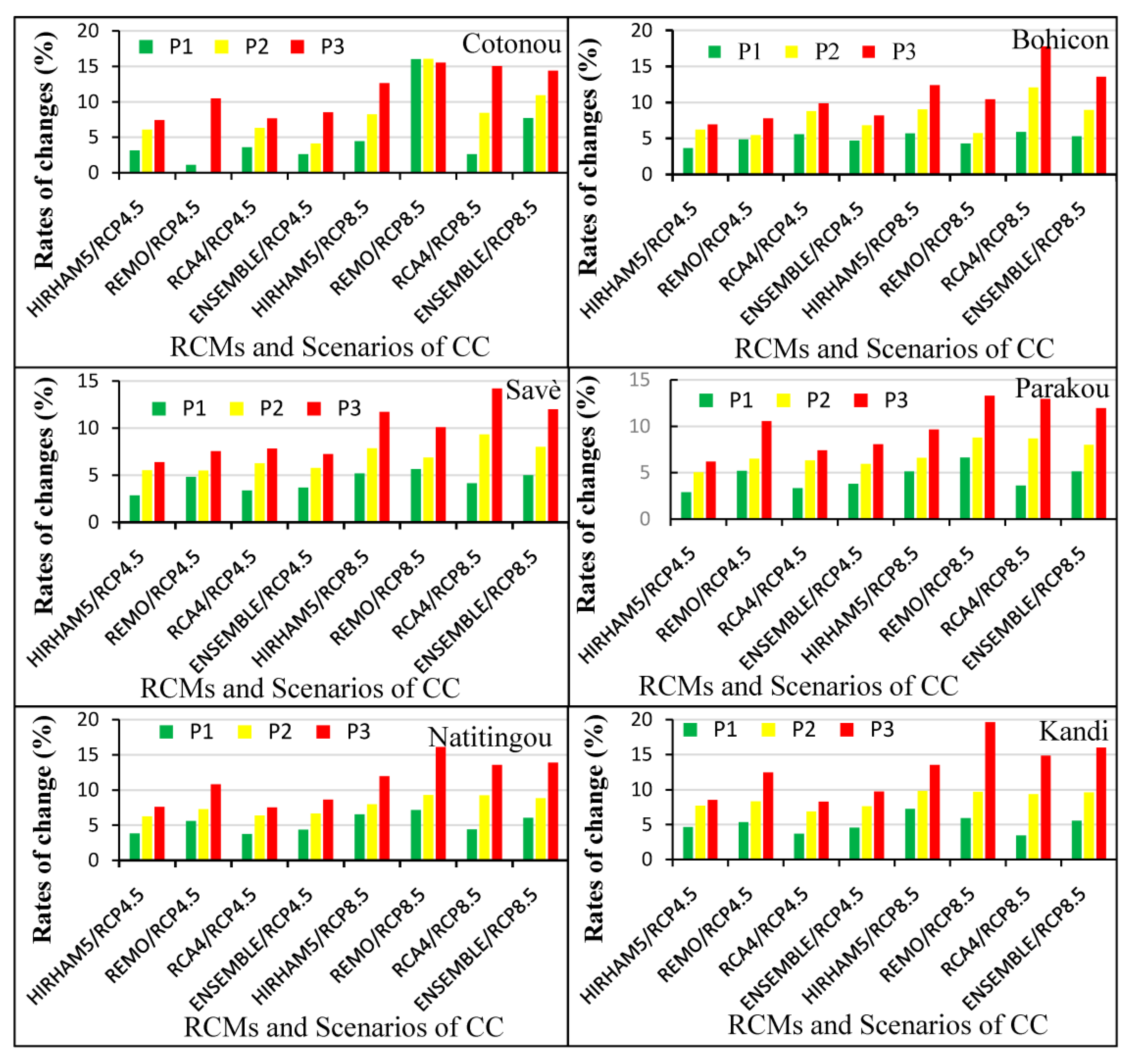
3.4.1. Annual Changes
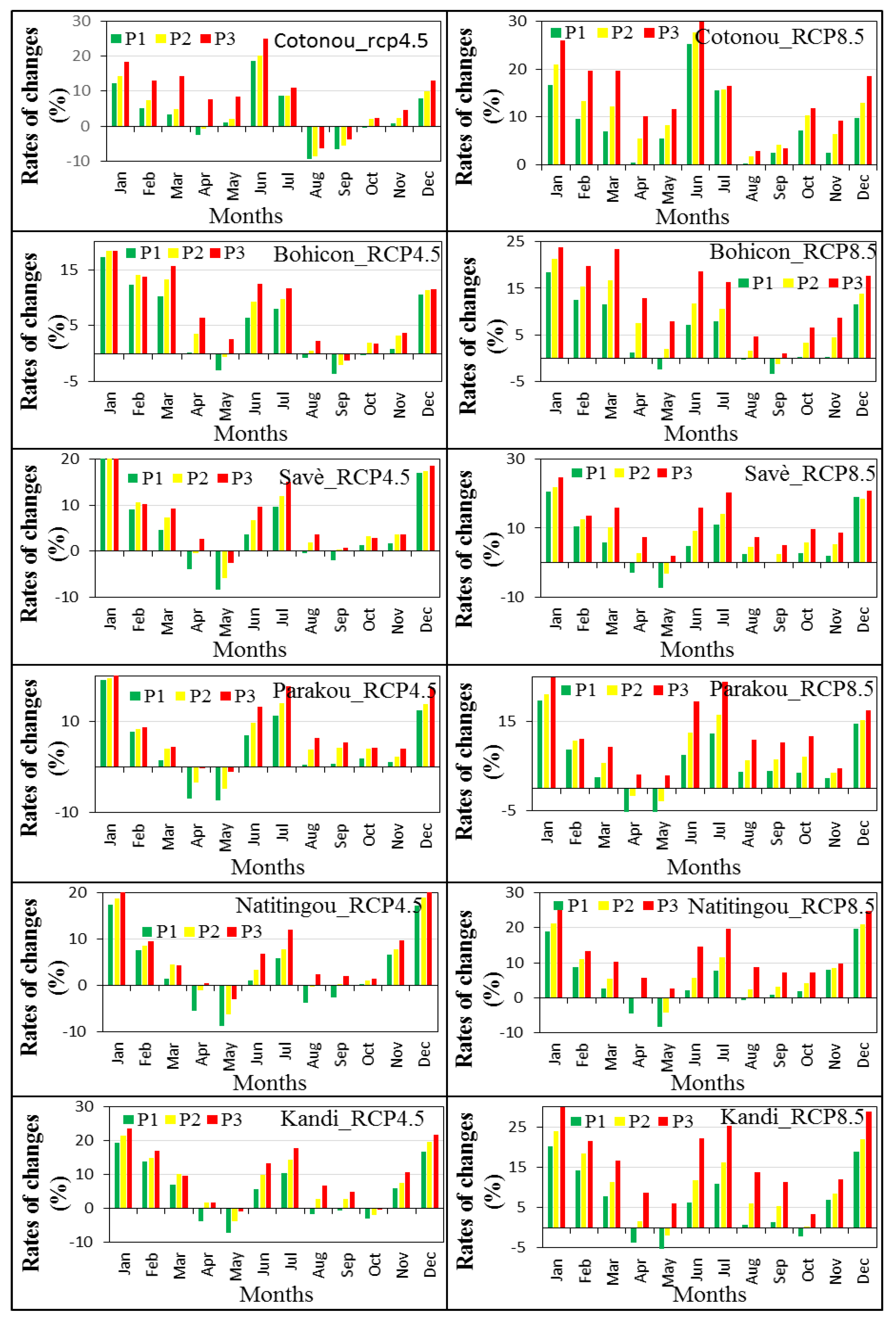
3.4.2. Monthly Changes
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Liu, X.M.; Luo, Y.; Zhang, D.; Zhang, M.; Liu, C. Recent changes in pan-evaporation dynamics in China. Geophys. Res. Lett. 2011, 38, L13404. [Google Scholar] [CrossRef]
- McVicar, T.R.; Van Niel, T.G.; Li, L.T.; Hutchinson, M.F.; Mu, X.M.; Liu, Z.H. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007, 338, 196–220. [Google Scholar] [CrossRef]
- Gu, S.; Tang, Y.; Cui, X.; Du, M.; Zhao, L.; Li, Y.; Xu, S.; Zhou, H.; Kato, T.; Qi, P.; et al. Characterizing evapotranspiration over a meadow ecosystem on the Qinghai-Tibetan Plateau. J. Geophys. Res. 2008, 113, D08118. [Google Scholar] [CrossRef]
- Van der Velde, Y.; Lyon, S.W.; Destouni, G. Data-driven regionalization of river discharges and emergent land cover-evapotranspiration relationships across Sweden. J. Geophys. Res. Atmos. 2013, 118, 2576–2587. [Google Scholar] [CrossRef]
- Xu, Y.P.; Pan, S.; Fu, G.; Tian, Y.; Zhang, X. Future potential evapotranspiration changes and contribution analysis in Zhejiang Province, East China. J. Geophys. Res. Atmos. 2014, 118, 2174–2192. [Google Scholar] [CrossRef]
- Allen, R.; Periera, L.; Raes, D.; Smith, M. FAO Irrigation and Drainage: Crop Evapotranspiration (Guidelines for Computing Crop Water Requirements); Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1996; p. 56. [Google Scholar]
- Xu, C.; Gong, L.; Jiang, T.; Chen, D. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Bashir, M.; Tanakamaru, H.; Tada, A. Remote sensing-based estimates of evapotranspiration for managing scarce water resources in the Gezira Scheme, Sudan. J. Environ. Inform. 2009, 13, 86–92. [Google Scholar]
- Li, Z.; Zheng, F.; Liu, W. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its projected changes during 2011–2099 on the Loess Plateau of China. Agric. For. Meteorol. 2012, 154–155, 147–155. [Google Scholar] [CrossRef]
- Fan, Z.X.; Thomas, A. Spatiotemporal variability of reference evapotranspiration and its contributing climatic factors in Yunan Province, SW China, 1961–2004. Clim. Chang. 2013, 116, 309–325. [Google Scholar] [CrossRef]
- Alemu, H.; Senay, G.B.; Kaptue, A.T.; Kovalskyy, V. Evapotranspiration variability and its association with vegetation dynamics in the Nile Basin, 2002–2011. Remote Sens. 2014, 6, 5885–5908. [Google Scholar] [CrossRef]
- Valipour, M. Ability of Box-Jenkins Models to Estimate of Reference Potential Evapotranspiration (A Case Study: Mehrabad Synoptic Station, Tehran, Iran). IOSR J. Agric. Vet. Sci. 2012, 1, 1–11. [Google Scholar] [CrossRef]
- Valipour, M. Application of new mass transfer formulae for computation of evapotranspiration. J. Appl. Water Eng. Res. 2014, 2, 33–46. [Google Scholar] [CrossRef]
- Valipour, M. Study of different climatic conditions to assess the role of solar radiation in reference crop evapotranspiration equations. Arch. Agron. Soil Sci. 2014, 61, 679–694. [Google Scholar] [CrossRef]
- Valipour, M.; Gholami Sefidkouhi, M.A. Temporal analysis of reference evapotranspiration to detect variation factors. Int. J. Glob. Warm. 2017, in press. [Google Scholar] [CrossRef]
- Valipour, M. Importance of solar radiation, temperature, relative humidity, and wind speed for calculation of reference evapotranspiration. Arch. Agron. Soil Sci. 2015, 61, 239–255. [Google Scholar] [CrossRef]
- IPCC. Climate Change: The Climate Change. Contribution of the Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Valipour, M. Use of surface water supply index to assessing of water resources management in Colorado and Oregon, US. Adv. Agric. Sci. Eng. Res. 2013, 3, 631–640. [Google Scholar]
- Valipour, M. Global experience on irrigation management under different scenarios. J. Water Land Dev. 2017, 32, 95–102. [Google Scholar] [CrossRef]
- Trenberth, K.E. Atmospheric Moisture Residence Times and Cycling: Implications for Rainfall Rates and Climate Change. Clim. Chang. 1998, 39, 667–694. [Google Scholar] [CrossRef]
- Labat, D.; Goddéris, Y.; Probst, J.L.; Guyot, J.L. Evidence for Global Runoff Increase Related to Climate Warming. Adv. Water Res. 2004, 27, 631–642. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for Intensification of the Global Water Cycle: Review and Synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Burt, T.P.; Shahgedanova, M. An historical record of evaporation losses since 1815 calculated using long-term observations from the Radcliffe Meteorological Station, Oxford, England. J. Hydrol. 1998, 205, 101–111. [Google Scholar] [CrossRef]
- Kay, A.L.; Bell, V.A.; Blyth, E.M.; Crooks, S.M.; Davies, H.N.; Reynard, N.S.A. Hydrological perspective on evaporation: Historical trends and future projections in Britain. J. Water Clim. Chang. 2013, 4, 193–208. [Google Scholar] [CrossRef]
- Onyutha, C. Statistical analyses of potential evapotranspiration changes over the period 1930–2012 in the Nile River riparian countries. Agric. For. Meteorol. 2016, 226–227, 80–95. [Google Scholar] [CrossRef]
- Ibrahim, B. Caractérisation des Saisons de Pluies au Burkina Faso Dans un Contexte de Changement Climatiques sur le Bassin de Nakambé. Thèse de Doctorat, Institut International d’Ingénierie de l’Eau et de l’Environnement (2iE), l’Université Pierre et Marie Curie, 2012; 234p. [Google Scholar]
- Jhajharia, D.; Pandey, P.K.; Dabral, P.P.; Kumar, R.; Choudhary, R. Variability in Temperature and Potential Evapotranspiration over West Siang in Arunachal Pradesh. Jour. Ind. Geil. Cong. 2015, 7, 37–43. [Google Scholar]
- Chattopdhyay, N.; Hulme, M. Evaporation and Potential Evapotranspiration in India under Conditions of Recent and Future Climate Change. Agric. For. Meteorol. 1997, 87, 55–73. [Google Scholar] [CrossRef]
- Moonen, A.C.; Ercoli, L.; Mariotti, M.; Masoni, A. Climate Change in Italy Indicated by Agro-meteorological Indices over 122 Years. Agric. For. Meteorol. 2002, 111, 13–27. [Google Scholar] [CrossRef]
- Chen, S.B.; Lui, Y.F.; Axel, T. Climatic change on the Tibetan Plateau: Potential evapotranspiration trends from 1961–2000. Clim. Chang. 2006, 76, 291–319. [Google Scholar]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. Evaluation and generalization of radiation-based methods for calculating evaporation. Hydrol. Process. 2001, 15, 305–319. [Google Scholar] [CrossRef]
- Trajkovic, S. Temperature-based approaches for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 316. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Nandagiri, L.; Kovoor, G. Performance evaluation of reference evapotranspiration equations across a range of Indian climates. J. Irrig. Drain. Eng. 2006, 132, 238. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G. Modeling reference evapotranspiration over complex terrains from minimum climatological data. Water Resour. Res. 2007, 43, W05444. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Judex, M.; Thamm, H.P. IMPETUS Atlas Benin Research Results 2000–2007, 3rd ed.; IMPETUS Project: Bonn, Germany, 2008. [Google Scholar]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Clarke, L.; Edmonds, J.; Jacoby, H.; Pitcher, H.; Reilly, J.; Richels, R. CCSP Synthesis and Assessment Product 2.1, Part A: Scenarios of Greenhouse Gas Emissions and Atmospheric Concentrations; US Government Printing Office: Washington, DC, USA, 2007; 154p.
- Fujino, J.; Nair, R.; Kainuma, M.; Masui, T.; Matsuoka, Y. Multi-gas mitigation analysis on stabilization scenarios using AIM global model. Multigas Mitigation and Climate Policy. Energy J. 2006, 3, 343–353. [Google Scholar]
- Riahi, K.; Gruebler, A.; Nakicenovic, N. Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol. Forecast. Soc. Chang. 2007, 74, 887–935. [Google Scholar] [CrossRef]
- Christensen, O.B.; Drews, M.; Christensen, J.H. The HIRHAM Regional Climate Model Version 5. Available online: http://orbit.dtu.dk/fedora/objects/orbit:118724/datastreams/file_8c69af6e-acfb-4d1aaa53–73188c001d36/content (accessed on 15 February 2017).
- Jacob, D.; Bärring, L.; Christensen, O.B.; Christensen, J.H.; Hagemann, S.; Hirschi, M.; Kjellström, E.; Lenderink, G.; Rockel, B.; Schär, C.; et al. An inter-comparison of regional climate models for Europe: Design of the experiments and model performance. Clim. Chang. 2007, 81, 31–52. [Google Scholar] [CrossRef]
- Samuelsson, P.; Jones, C.G.; Willén, U.; Ullerstig, A.; Gollvik, S.; Hansson, U.; Kjellström, E.; Nikulin, G.; Wyser, K. The Rossby Centre regional climate model RCA3: Model description and performance. Tellus A 2011, 63, 4–23. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Oxford University Press: Oxford, UK, 1948. [Google Scholar]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, G.; Zhao, W.; Yan, T.; Yuan, X. Analysis of Precipitation and Drought Data in Hexi Corridor, Northwest China. Hydrology 2017, 4, 29. [Google Scholar] [CrossRef]
- Wetterhall, F.; Pappenberger, F.; He, Y.; Freer, J.; Cloke, H. Conditioning model output statistics of regional climate model precipitation on circulation patterns. Nonlinear Process. Geophys. 2012, 19, 623–633. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of precipitation and temperature extreme over France in an anthropogenic scenario: Model results and statistical correction according to observed values. Glob. Planet Chang. 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Sennikovs, J.; Bethers, U. Statistical downscaling method of regional climate model results for hydrological modelling. In Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009. [Google Scholar]
- Michelangeli, P.A.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution function. Geophys. Res. Lett. 2009, 36, L11708. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Trenberth, K.; Dai, A.; Rasmussen, R.; Parsons, D. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Shuttleworth, W.J.; Blyth, E.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. Creation of the WATCH Forcing Data and Its use to assess global and regional reference crop evaporation over land during the twentieth century. J. Hydrometeorol. 2011, 12, 823–848. [Google Scholar] [CrossRef]
- Thomas, A. Spatial and temporal characteristics of potential evapotranspiration trends over China. Int. J. Climatol. 2000, 20, 381–396. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Zhao, D. Past and future spatiotemporal changes in evapotranspiration and effective moisture on the Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 10850–10860. [Google Scholar] [CrossRef]
- Arnell, N.W. Uncertainty in the relationship between climate forcing and hydrological response in UK catchments. Hydrol. Earth Syst. Sci. 2011, 15, 897–912. [Google Scholar] [CrossRef]
- Fowler, H.J.; Tebaldi, C.; Blenkinsop, S. Probabilistic estimates of climate change impacts on flows in the river Eden, Cumbria. In Proceedings of the British Hydrological Society 10th National Hydrology Symposium, Exeter, UK, 15–17 September 2008. [Google Scholar]
- Scheff, J. Reference Evapotranspiration from Standard Archived GCM Output: A Proof of Concept. 2011. Available online: www.atmos.washington.edu/~jack/PotEvapGCM.ps (assessed on 18 April 2017).
- King, D.A.; Bachelet, D.M.; Symstad, A.J.; Ferschweiler, K.; Hobbins, M. Estimation of potential evapotranspiration from extraterrestrial radiation, air temperature and humidity to assess future climate change effects on the vegetation of the Northern Great Plains, USA. Ecol. Model. 2015, 297, 86–97. [Google Scholar] [CrossRef]
- Scheff, J.; Frierson, D.M. Scaling potential evapotranspiration with greenhouse warming. J. Clim. 2013, 27, 1539–1558. [Google Scholar] [CrossRef]
- Feng, S.; Fu, Q. Expansion of global dry lands under warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- Ekstrom, M.; Jones, P.D.; Fowler, H.J.; Lenderink, G.; Buishand, T.A.; Conway, D. Regional climate model data used within the SWURVE project 1: Projected change in seasonal patterns and estimation of PET. Hydrol. Earth Syst. Sci. 2007, 11, 1069–1083. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.; Ju, H.; Garré, S. Impact of climate change on potential evapotranspiration under a historical and future climate scenario in the Huang-Huai-Hai Plain, China. Theor. Appl. Climatol. 2017, 1–15. [Google Scholar] [CrossRef]
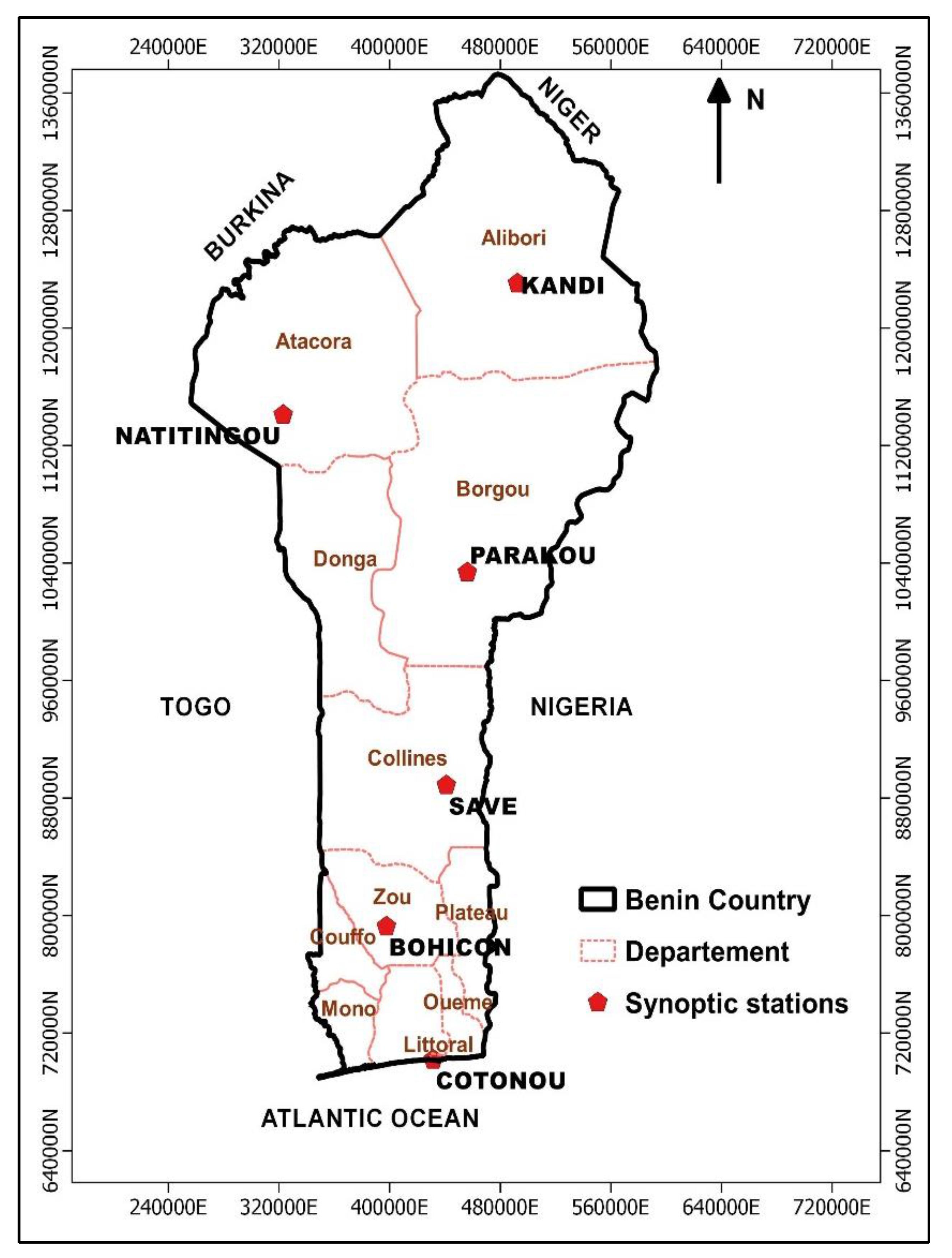
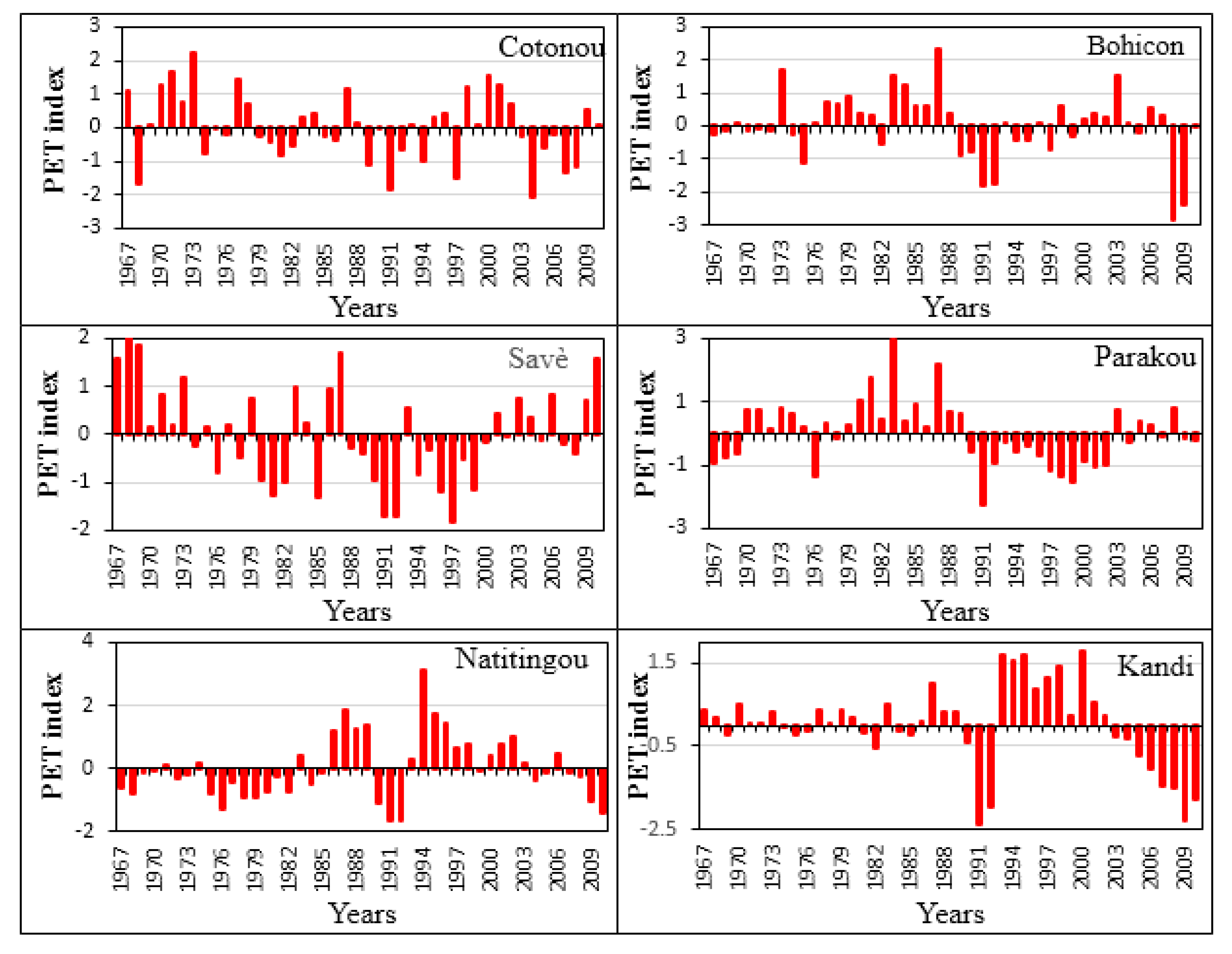
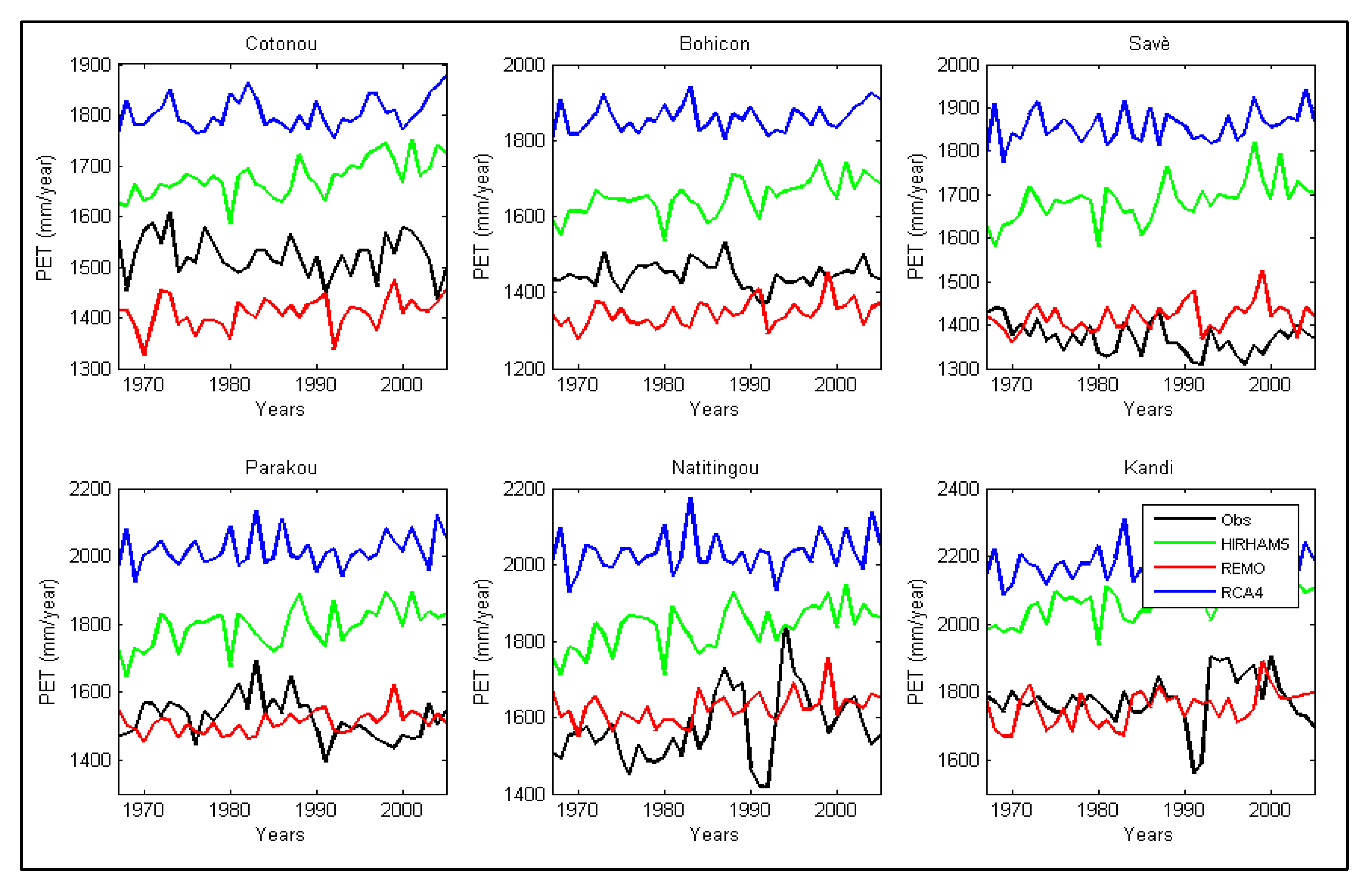

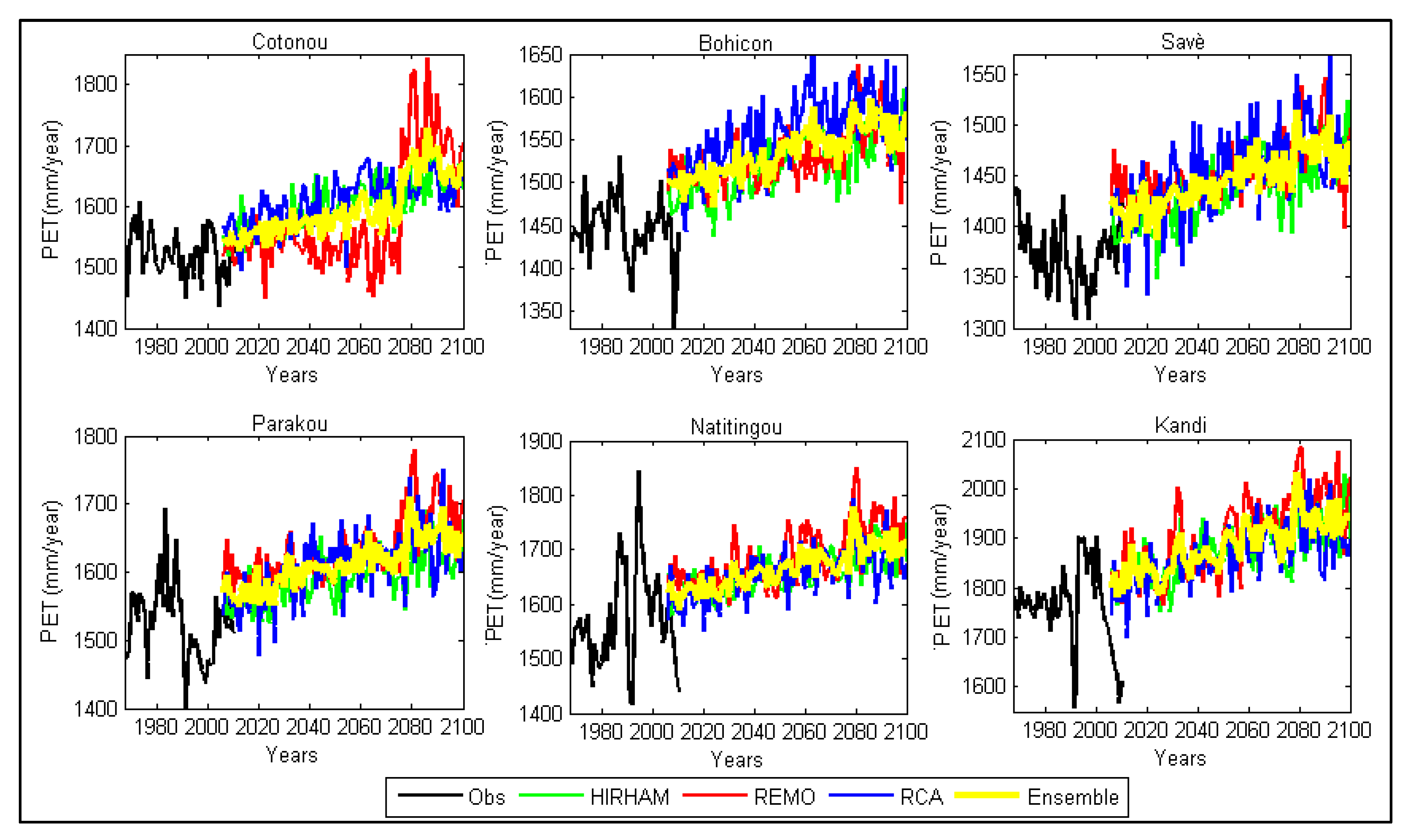

| Station | Longitude (°C) | Latitude (°C) | Elevation (m) |
|---|---|---|---|
| Cotonou | 2.38 | 6.35 | 4 |
| Bohicon | 2.07 | 7.17 | 166 |
| Savè | 2.47 | 8.03 | 198 |
| Parakou | 2.6 | 9.35 | 392 |
| Natitingou | 1.38 | 10.32 | 460 |
| Kandi | 2.93 | 11.13 | 290 |
| Model (RCM) | Institution | Driving GCM | Horizontal Resolution | No. of Vertical Levels | Simulation Period | Reference |
|---|---|---|---|---|---|---|
| HIRHAM5 | DMI | GFDL-ESM2M | 50 km | 31 | 1951–2100 | [43] |
| REMO | CSC | MPI-ESM-LR | 50 km | 27 | 1951–2100 | [44] |
| RCA4 | SMHI | EC-EARTH | 50 km | 40 | 1951–2100 | [45] |
| Month | Cotonou | Bohicon | Savè | Parakou | Natitingou | Kandi | |
|---|---|---|---|---|---|---|---|
| January | −0.07 | −1.75 | −0.64 | −1.57 | −0.14 | −0.57 | |
| February | +0.57 | −1.78 | +0.39 | −1.68 | −0.54 | −0.61 | |
| March | −0.21 | −1.43 | +0.39 | −2.50 * | −0.82 | −0.86 | |
| April | −2.14 * | −1.53 | −0.50 | −3.21 * | −0.46 | −1.21 | |
| May | −0.82 | −0.89 | −1.07 | −2.11 * | −1.11 | −2.00 * | |
| June | −0.82 | −2.18 * | +1.36 | −1.14 | −0.68 | −2.32 * | |
| July | +1.43 | +1.43 | +2.71 * | +0.93 | −0.46 | −2.03 * | |
| August | +0.86 | −0.75 | −0.21 | −0.96 | −1.11 | −2.71 * | |
| September | +1.71 | −0.39 | +1.36 | −0.29 | −0.96 | −2.11 * | |
| October | −0.86 | −0.82 | +2.28 * | −0.14 | −0.50 | −1.82 | |
| November | −0.36 | −0.11 | +2.78 * | +0.46 | −1.07 | −0.61 | |
| December | +3.00 * | +2.32 * | +2.39 * | +1.00 | −0.32 | +0.54 | |
| Annual | +0.18 | −0.96 | +1.53 | −1.71 | −0.96 | −1.71 | |
| Calibration | Validation | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HIRHAM 5 | REMO | RCA4 | HIRHAM 5 | REMO | RCA4 | |||||||||||||
| Station | Raw | Scaling | EQM | Raw | Scaling | EQM | Raw | Scaling | EQM | Raw | Scaling | EQM | Raw | Scaling | EQM | Raw | Scaling | EQM |
| MAE | ||||||||||||||||||
| Cotonou | 0.91 | 0.85 | 0.80 | 0.90 | 0.89 | 0.77 | 0.96 | 0.74 | 0.77 | 0.95 | 0.85 | 0.80 | 0.89 | 0.89 | 0.77 | 1.01 | 0.75 | 0.79 |
| Bohicon | 1.02 | 0.90 | 0.70 | 1.00 | 1.01 | 0.65 | 1.21 | 0.72 | 0.62 | 1.09 | 0.93 | 0.72 | 1.00 | 1.03 | 0.66 | 1.27 | 0.73 | 0.61 |
| Savè | 1.16 | 0.91 | 0.72 | 1.09 | 1.08 | 0.70 | 1.38 | 0.77 | 0.70 | 1.25 | 0.92 | 0.73 | 1.12 | 1.10 | 0.70 | 1.45 | 0.76 | 0.67 |
| Parakou | 1.10 | 0.96 | 0.80 | 0.95 | 0.96 | 0.73 | 1.39 | 0.86 | 0.82 | 1.27 | 1.03 | 0.85 | 1.00 | 1.03 | 0.78 | 1.56 | 0.87 | 0.82 |
| Natitingou | 1.29 | 1.12 | 0.86 | 1.06 | 1.04 | 0.8 | 1.44 | 0.94 | 0.87 | 1.31 | 1.15 | 0.9 | 1.02 | 1.01 | 0.81 | 1.39 | 0.96 | 0.89 |
| Kandi | 1.34 | 1.16 | 0.98 | 0.99 | 0.99 | 0.87 | 1.32 | 0.97 | 1.04 | 1.39 | 1.18 | 1.03 | 1.02 | 1.02 | 0.92 | 1.34 | 1.01 | 1.07 |
| RMSE | ||||||||||||||||||
| Cotonou | 0.36 | 0.00 | 0.00 | 0.34 | 0.00 | 0.00 | 0.74 | 0.00 | 0.00 | 0.52 | 0.16 | 0.16 | 0.26 | 0.07 | 0.07 | 0.81 | 0.07 | 0.08 |
| Bohicon | 0.49 | 0.00 | 0.02 | 0.32 | 0.00 | 0.01 | 1.11 | 0.00 | 0.00 | 0.67 | 0.18 | 0.16 | 0.21 | 0.11 | 0.09 | 1.17 | 0.07 | 0.06 |
| Savè | 0.79 | 0.00 | 0.01 | 0.09 | 0.00 | 0.00 | 1.30 | 0.00 | 0.00 | 0.99 | 0.20 | 0.17 | 0.20 | 0.11 | 0.10 | 1.39 | 0.10 | 0.09 |
| Parakou | 0.61 | 0.00 | 0.01 | 0.13 | 0.00 | 0.01 | 1.27 | 0.00 | 0.00 | 0.94 | 0.33 | 0.31 | 0.12 | 0.25 | 0.24 | 1.49 | 0.22 | 0.22 |
| Natitingou | 0.72 | 0.00 | 0.01 | 0.16 | 0.00 | 0.01 | 1.30 | 0.00 | 0.00 | 0.72 | 0.00 | 0.03 | 0.11 | 0.05 | 0.07 | 1.19 | 0.11 | 0.11 |
| Kandi | 0.76 | 0.00 | 0.01 | 0.08 | 0.00 | 0.01 | 1.09 | 0.00 | 0.00 | 0.85 | 0.09 | 0.07 | 0.03 | 0.05 | 0.04 | 1.05 | 0.04 | 0.04 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obada, E.; Alamou, E.A.; Chabi, A.; Zandagba, J.; Afouda, A. Trends and Changes in Recent and Future Penman-Monteith Potential Evapotranspiration in Benin (West Africa). Hydrology 2017, 4, 38. https://doi.org/10.3390/hydrology4030038
Obada E, Alamou EA, Chabi A, Zandagba J, Afouda A. Trends and Changes in Recent and Future Penman-Monteith Potential Evapotranspiration in Benin (West Africa). Hydrology. 2017; 4(3):38. https://doi.org/10.3390/hydrology4030038
Chicago/Turabian StyleObada, Ezéchiel, Eric Adéchina Alamou, Amedée Chabi, Josué Zandagba, and Abel Afouda. 2017. "Trends and Changes in Recent and Future Penman-Monteith Potential Evapotranspiration in Benin (West Africa)" Hydrology 4, no. 3: 38. https://doi.org/10.3390/hydrology4030038
APA StyleObada, E., Alamou, E. A., Chabi, A., Zandagba, J., & Afouda, A. (2017). Trends and Changes in Recent and Future Penman-Monteith Potential Evapotranspiration in Benin (West Africa). Hydrology, 4(3), 38. https://doi.org/10.3390/hydrology4030038





