Revisiting Cent-Fonts Fluviokarst Hydrological Properties with Conservative Temperature Approximation

Abstract

We assess the errors produced by considering temperature as a conservative tracer in fluviokarst studies. Heat transfer that occurs between karstic Conduit System (CS) and Porous Fractured Matrix (PFM) is the reason why one should be careful in making this assumption without caution. We consider the karstic aquifer as an Open Thermodynamic System (OTS), which boundaries are permeable to thermal energy and water. The first principle of thermodynamics allows considering the enthalpy balance between the input and output flows. Combined with a continuity equation this leads to a two-equation system involving flows and temperatures. Steady conditions are approached during the recession period or during particular phases of pumping test experiments. After a theoretical study of the error induced by the conservative assumption in karst, we have applied the method to revisit the data collected during a complete campaign of pumping test. The method, restricted to selected data allowed retrieving values of base flow, mixing of flow, intrusions of streams, and aquifer answer to drawdown. The applicability of the method has been assessed in terms of propagation of the temporal fluctuations trough the solving but also in terms of conservative assumption itself. Our results allow retrieving the main hydrological properties of the karst as observed on field (timed volumetric samplings, geochemical analyses, step pumping test and allogenic intrusion of streams). This consistency argues in favor of the applicability of the conservative temperature method to investigating fluviokarst systems under controlled conditions.

1. Introduction and Presentation of Cent-Fonts Fluviokarst

This paper addresses the issue of using the water temperature as a conservative tracer for karstic functioning studies. Whereas costly investments are often necessary to evaluate the potential of karstic aquifers, temperature records may bring cheap method for obtaining complementary information. However underground flows undergo heat transfers with the embedding rocks by advection and by conduction. Despite of this difficulty several studies used temperature as a mixing tracer. Several works [1,2] study the water exchanges between underground flows and surface stream. Others [3] retrieved aquifer recharges solving heat transport equation constrained by measurements of vertical temperature. Slow and rapid equilibrations between ground water and aquifer rocks have been analyzed [4] to study the dynamics of exchanges in fractured carbonate systems. Genthon et al. [5] determined the deep preferential path of rainfall water in caves from annual temperature variations of spring. This author also used temperature to determine limestone drainage in lagoon by removing the tidal component and emphasizing its poor correlation with rain temperature [6]. This short list is far to be exhaustive.

As mentioned in the following theoretical part of this work, the formal applicability of the conservative temperature approximation depends on the existence steady conditions that are never perfectly verified in nature. The question consists of estimating the outcome of this assumption. Indeed, our work is not the first to address this problem. In spite of disturbances due to meteorological conditions, Karanjac and Altug [7] used temperature records to characterize the recharge area, transmissivity and hydraulic regime of karst. Following Stonestrom and Constantz [8], O’Driscoll and DeWalle [9] studied the stream-ground water temperature interactions from stream-air temperature fluctuations. They used weekly averaging and equilibrium temperature concepts [10,11,12]. All these studies rely on damping of diurnal or seasonal variations of temperature records. This is done either by time averaging [13] or by natural damping of temperature fluctuations by depth [14,15]. It is clear that the method presented in this work is not adapted to transient flow or rapidly varying water conditions. Conversely, many situations as recession in karst undergo naturally damping of the temporal fluctuations both for temperatures and flows.

These preliminary considerations justify the interest to study the karst systems as an Open Thermodynamic Systems (OTS), that is to say a “black box” that exchanges water and heat energy with its surrounding environment. However, let us try to describe the thread of this paper. The following part of the present Section 1 recalls the hydrological description of the Cent-Fonts site and its consistency with the White’s fluviokarst model. Thus, we benefit of an exceptional set of high quality data recorded during the 2005 Cent-Font pumping tests and preliminary studies. This will provide a fair opportunity to test the method. Section 2 displays theory and resulting equations on a reduced form of the White’s model considered as an OTS. Section 3 describes the available data that will be revisited and Section 4 illustrates the application of the method to these selected data. The results are discussed in the “Summary and discussion” Section 5.

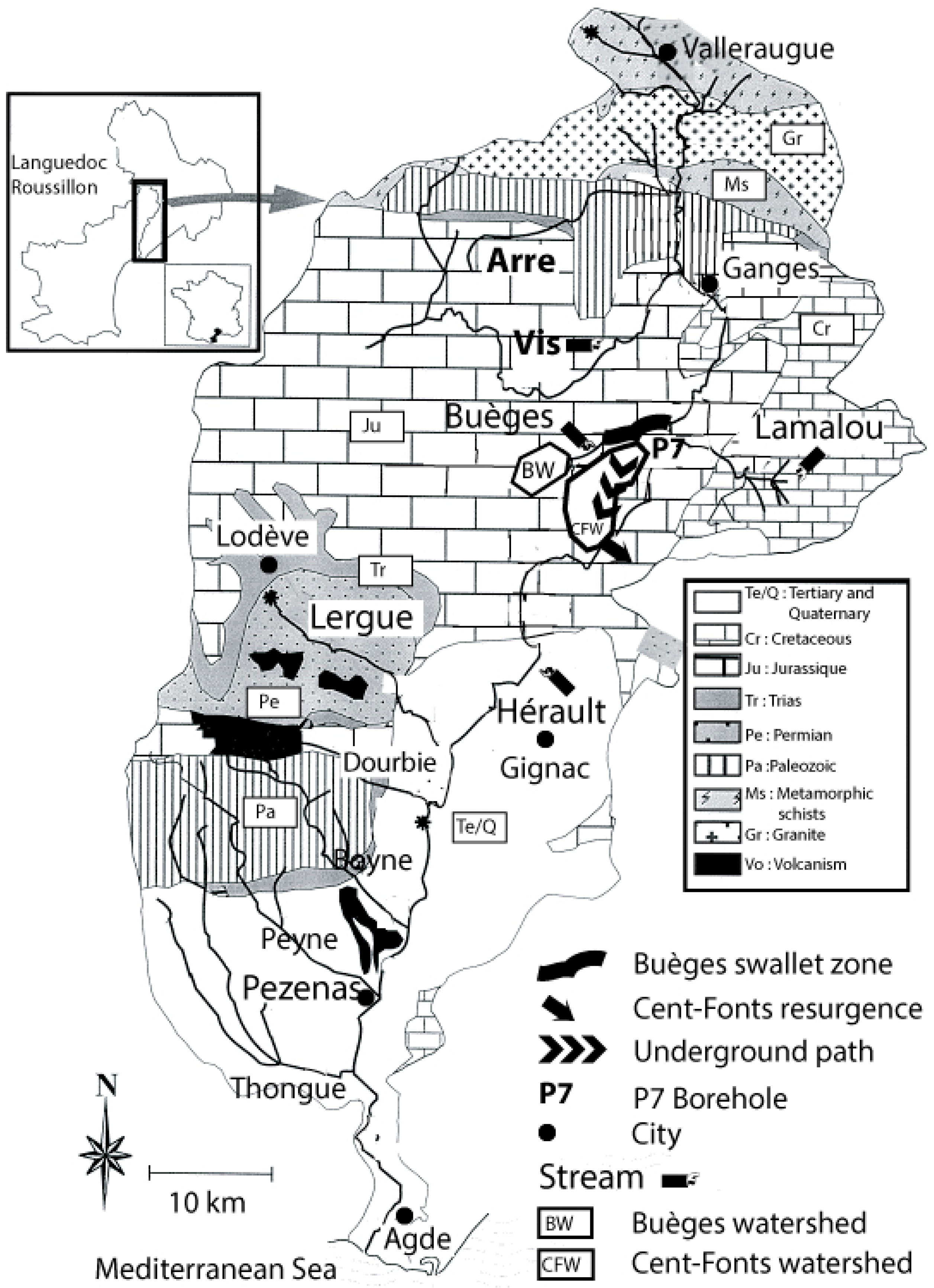
The Cents-Fonts resurgence is the only free-flowing of an underground drainage basin that covers 40 km² in the median part of Hérault River (Figure 1). The surface of the watershed reaches 60 km² considering the Buèges stream. It stretches in outcrops of thick calcareous and dolomite massifs (Middle and Upper Jurassic). Since several decades, many geological, geochemical and hydrological studies focused on the potential spring water production of this site (i.e., [16,17,18,19,20,21,22,23,24,25,26,27]).

The Buèges stream and the Cévennes fault mark the boundaries of the watershed to the north and northwest, while the altitude of the Hérault River matches the karstic base level to the southeast (Figure 1). Morphologically, the area is a plateau, uplifted of 200 to 500 m during the late Quaternary and eroded during Oligocene. The watershed drains rainfalls through an epikarstic transition zone that supplies the Cent-Fonts resurgence base flow [22]. To the north, Buèges stream flows permanently on Triassic low permeability outcrops however it disappears à few kilometers after Saint-Jean de Buèges where the course crosses a Bathonian, calcareous dolomite swallow zone. After this area, the Buèges stream course follows a valley that remains dry most of the year except after major rainfalls. Then a surface course catches up with Hérault River at a confluence point north of Lamalou stream (Figure 1). Tracing experiments have confirmed the underground path of Buèges stream intrusion from swallow zone to the Cent-Fonts resurgence [17,20].

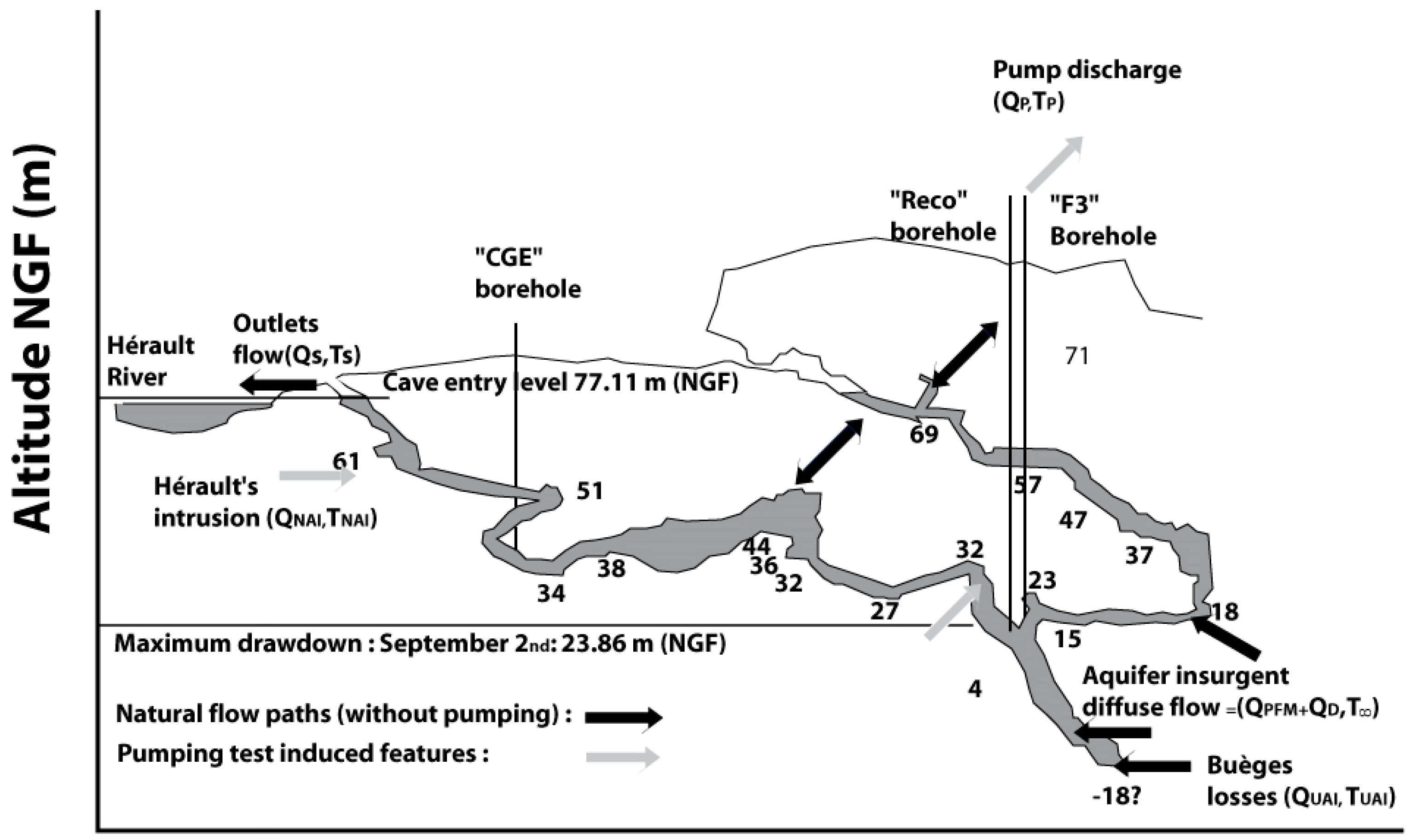
Bathonian, dolomitic layers of Middle Jurassic between 150 and 300 m thick embed the saturated zone of the Cent Fonts fluviokarst near the resurgence. The aquifer also possibly meets an underlying Aalenian-Bajocien layer. The near spring, Conduit System (CS) of the resurgence (Figure 2) has been explored thank to speleological diving that reached 107 m below the base level (Hérault River) [28]. The terminal part of the CS displays an outlet cave, roughly “Y” shaped, with two sub-horizontal branches joining above a deep sub-vertical chimney. The two ends of the “Y” branches open outside. These caves are seldom active except during peak flows. Most of the time, the Cent-Fonts resurgence flows into Hérault River through a shallow network of springs that gush out a few tens of centimeters above the base level. A spring also arises directly through the bottom of the Hérault River bed [20].

The Cent-Fonts karst matches precisely the fluviokarst idea depicted by Smart [29]. Following his definition, fluviokarst consist: in “karst landscapes where the dominant landforms are valleys cut by surface rivers. Such original surface flow may relate either to low initial permeability before caves (and hence underground drains) had developed, or to reduced permeability due to ground freezing in a periglacial environment. In both cases the valleys become dry as karstification improves underground drainage” [30]. 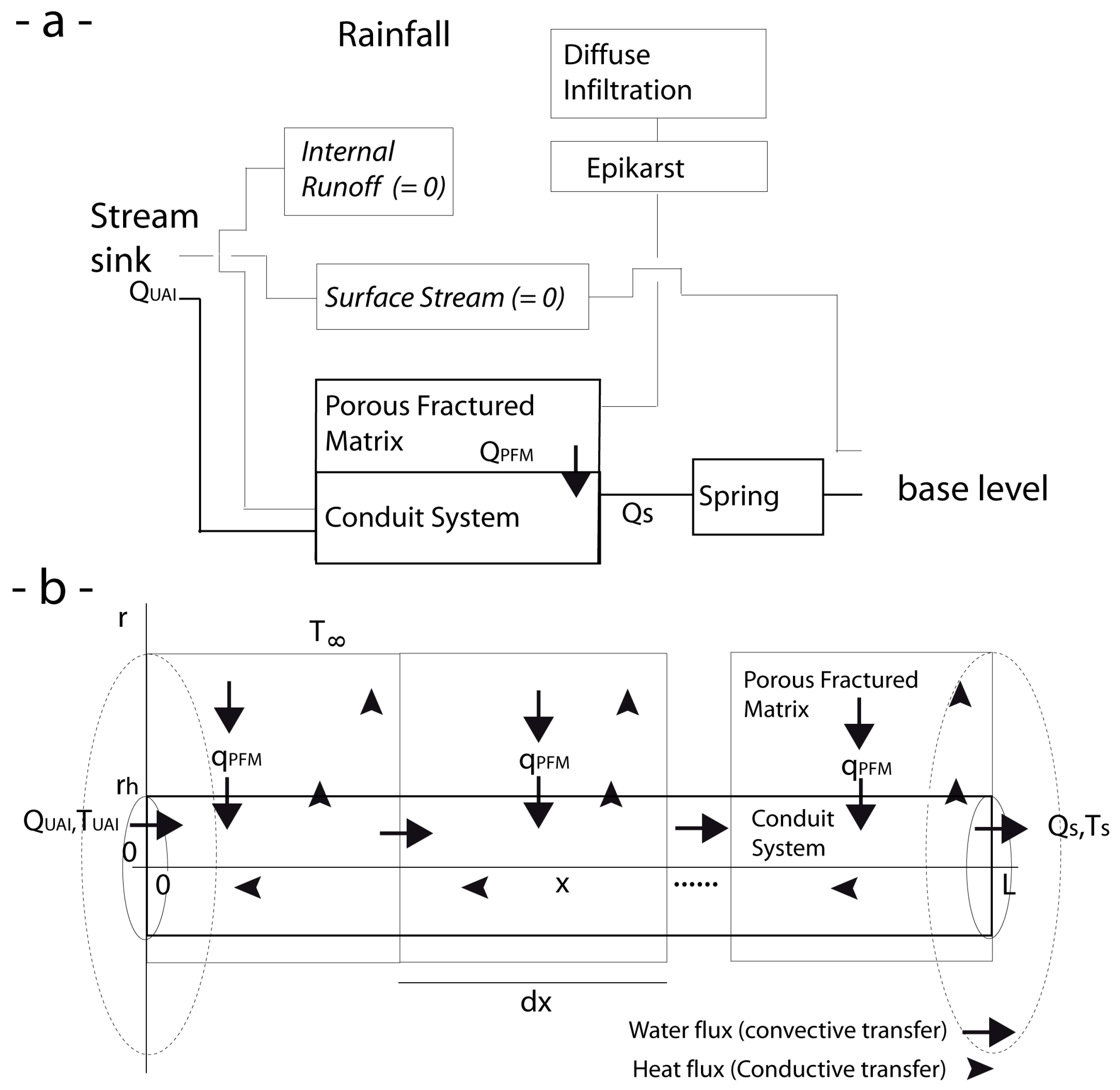White [31,32] proposed a model where the hydrological behaviors are forced by the external boundary conditions. The various recharges in the CS are Allogenic Intrusions, internal Run-off and Porous Fractured Matrix flows. Intrusions of neighbor streams cause the first category of flows. The second results from sporadically floods that occur after heavy rainfalls. The third category gathers percolation flows through soils and epikarstic layer that reach the CS as a Diffuse Infiltration through the fractured and porous rocks of the aquitard (Figure 3a). In the local context of the Cent-Font watershed, the permanent course of Buèges stream matches the Upper Allogenic Stream. Later, at the swallow zone, the Buèges splits into a Surface Stream and an Upper Allogenic Intrusion. The Surface stream forms a non-perennial flow that joins the Hérault River north of Lamalou confluence. The Upper Allogenic Intrusion, Q_UAI, joins the CS after an underground journey.

Table 1. Chronology of pumping test phases and periods.

Periods	Pumping Operation	Beginning mm/dd (hh:mm)	Ending	Revisited Periods
a	Pre-pumping phase	1992	07/27 (07:25)	07/14 (00:00)–07/18 (23:55)
b	Step drawdown	07/27 (07:30)	07/30 (12:40)	-
c	Constant pumping	08/01 (07:10)	08/09 (07:20)	-
d	Recovering test	08/09 (07:20)	08/09 (13:00)	-
e	Constant pumping	08/09 (13:05)	09/02 (07:15)	08/13 (00:00)–09/31 (23:55)
f	Recovering	09/02 (07:20)	09/03 (07:40)	-
g	Equilibrium-pumping	09/03 (07:45)	09/06 (06:00)	09/04 (12:00)–09/05 (11:55)

recalls the notations and acronyms of this article. This model also considers the Diffuse Infiltration that percolates through the CS wall. The only output flow of the fluviokarst is the spring, Q_S, that falls into the Hérault River at the karstic base level.

As mentioned above, the Cent-Fonts resurgence has received much attention since decades (see Ladouche et al. [23] for a review). In September 1992, Cge and the city of Montpellier organized a series of pumping tests but heavy rainfalls and resulting runoff force to stop the experiments after only 16 days. This short time prevents reaching significant aquifer drawdowns despite the high rate of pumping (0.5 m³/s). Thus, this experimentation failed to assess the hydrological properties of the karst and let believe in a high water production potential [33].

Many field observations, such as gauging data of the spring, of the Hérault River and of the Buèges stream have been recorded for several years before the summer 2005 pumping test experiments. New boreholes were drilled. New records of temperatures and discharges were collected in Buèges and Hérault. Temperatures and hydraulic heads were also recorded in the “P7” (Figure 1), “Reco”, “Cge” and “F3” boreholes (Figure 2). The 2005 pumping test campaign started with a sequence of step-drawdown tests. Heavy pumping sequences followed with a high constant rate pumping and a drawdown constant pumping (see Table 1 for accurate chronology). The drawdown induced during these heavy pumping allowed speleological explorations of the Cent-Fonts chimney. It also opened the possibility of in situ timed volumetric gauging and geochemical sampling of Hérault River intrusions in the CS. This rich set of data has been extensively analyzed already [26,34]. The present work aims to revisit part of these data to assess the accuracy of conservative tracer assumption for water temperature. In the following, we will consider that two error sources mainly affect the applicability of the method: (1) The natural temporal instabilities that affect the data series; (2) the effect of conservative temperature assumption itself according to our previous work [35,36].

The next section of the paper recalls the theoretical context of Open Thermodynamic System for fluviokarst. Section 3 describes the data chosen from the 2005 pumping test campaign, Section 4 presents their analysis and accuracy assessments. The results are summarized and discussed in Section 5.

2. Theoretical Context

An Open Thermodynamic System (OTS) does not require a precise knowledge of the locations and shapes of its boundaries to study the balance of the fluxes that enter or quit its Control Volume (CV). In that sense, CS of fluviokarsts are similar to CV of OTS (Figure 3b). We will benefit of this analogy to study the balance of fluxes and energy in the Cent-Fonts fluviokarst CV despite the inaccurate knowledge of its boundaries [35].

In our previous work [36] we assessed the error resulting, in OTS, of conservative temperature assumption within the theoretical context of White’s fluviokarst model. This analysis relied on two successive numerical solving of thermal behavior. The first considered the temperature as a conservative tracer, while the second, following works by Covington et al. [37,38] solved the complete set of energy equations including convective, diffusive and dispersive terms. The amplitude of differences between both results shows the first order of the error due to the conservative assumption. We drew abacus curves of this error versus thermal diffusivity ratio and the Peclet numbers, Prandtl numbers and Reynolds numbers of the CS. The error remains less than 1 percent in the dimensionless space and converges to zero for the most extremes values of karst features. This dimensionless error needs to be rescaled for each singular fluviokarst to calculate its physical amplitude.

In our study, we consider water as a Boussinesq fluid with constant thermal capacity, thermal expansion and density. As a result, water motion forms a zero divergence velocity field in the PFM and in the CS (Equation (1)).

$$div(\overrightarrow{v})=0$$

(1)

It is possible to convert the volume integrals over fluviokarst CS in flux integrals over the PFM boundaries and hydraulic sections of conduits entering or leaving the CS. Then, the terms of Equation (2) are equal to the input flows into the CS (positive algebraic values, q_i) and to the flows escaping from the CS (negative algebraic values, q_o). Therefore, the continuity equation leads to the mass conservation equation that links the various flows.

$${\displaystyle \sum _{input}{q}_i}+{\displaystyle \sum _{output}{q}_o}=0$$

(2)

The first law of thermodynamics stipulates that the internal energy change of the CV (Equation (3)) corresponds to the balance of the energy differences between all the incoming and outgoing flows (index j) and considering the work done. Thus, the internal energy change (δE) is equal to the summation of: the enthalpy by unit of mass (h_j), the potential energy (e_{pot j}), the kinetic energy (e_{cin j}), the external heat transfer (δΦ_j) and the work exchanges (δW_j) with the surrounding [39,40].

$$\delta E={\displaystyle \sum _j(h_j}+e_{pot,j}+e_{cin,j})d{m}_j+{\displaystyle \sum _j\delta {\Phi }_j}+{\displaystyle \sum _j\delta W_j}$$

(3)

In the following, we will consider no chemical contribution to enthalpy and flow transfers with negligible exchange between heat and work. We also will consider steady flux conditions in the CV (we discuss this point later). These hypotheses cancel the internal energy change but also the potential energy and kinetic energy changes. Then, Equation (3) becomes a balance between the specific enthalpies by unit of time of the flows entering (h_i) and escaping (h_o) the CS (Equation (4)).

$${\displaystyle \sum _i{h}_i}{\rho }_i{q}_i+{\displaystyle \sum _o{h}_o}{\rho }_o{q}_o=0$$

(4)

Now, specific enthalpy depends only on thermal capacity (Cp) and temperature (referred to an arbitrary value T_a) (Equation (5)).

$$h_j=C{p}_j(T_j-T_a)$$

(5)

Combination of Equations (4) and (5) leads to the enthalpy balance (Equation (6)).

$${\displaystyle \sum C{p}_i(T-Ta)}{\rho }_i{q}_i+{\displaystyle \sum C{p}_o(T_o-Ta)}{\rho }_o{q}_o=0$$

(6)

Finally, with constant density and thermal capacity Equation (6) reduces to a classical mixing equation (Equation (7)) that links temperatures (°K or °C) and mass transfers in the CS.

$${\displaystyle \sum _{input}{q}_i{T}_i}+{\displaystyle \sum _{output}{q}_o{T}_o}=0$$

(7)

Equations (2) and (7) form the basis of a linear system able to discover two unknown flows in the CS (so-called Q_k and Q_l in Equation (8)).

$$\begin{array}{l}{q}_k{T}_k+q_l{T}_l=-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o{T}_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i{T}_i}\\ q_k+q_l=-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i}\end{array}$$

(8)

Thus, these the two unknown flows are (Equation (9)).

$$\begin{array}{l}{q}_k=\frac{1}{(T_k-T_l)}\left|\begin{array}{cc}-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o{T}_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i{T}_i}& T_l\\ -{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i}& 1\end{array}\right|=\frac{-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o(T_o-T_l)}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i(T_i-T_l)}}{(T_k-T_l)},\\ q_l=-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}{q}_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}{q}_i}-q_k.\end{array}$$

(9)

As mentioned above, we will use the theoretical results of Machetel and Yuen [36] to quantify the sensitivity of the model to the conservative enthalpy assumption. However since we assumed that no other sources of heat are present (neither chemical heat, nor work conversion to heat), enthalpy conservation comes down on to temperature conservation. We will also use the differential form (Equation (10)) of Equation (9) to assess the effects of temperature and discharge uncertainties solving Equation (9).

$$\begin{array}{l}\delta q_k=\frac{1}{(T_k-T_l)}\left[\begin{array}{l}-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}\left[\delta q_o(T_o-T_l)-q_o\left((\delta T_o-\delta T_l)-\frac{(\delta T_k-\delta T_l)(T_o-T_l)}{(T_k-T_l)}\right)\right]}\\ -{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}\left[\delta q_i(T_i-T_l)+q_i\left((\delta T_i-\delta T_l)-\frac{(\delta T_k-\delta T_l)(T_i-T_l)}{(T_k-T_l)}\right)\right]}\end{array}\right]\\ \delta q_l=-{\displaystyle \sum _{\begin{array}{l}o\ne k\\ o\ne l\end{array}}\delta q_o}-{\displaystyle \sum _{\begin{array}{l}i\ne k\\ i\ne l\end{array}}\delta q_i}-\delta q_k\end{array}$$

(10)

The applicability of the method developed above depends on a “reasonably” steady CS. This is never the case in nature where temperature and flow variations due to human activities or diurnal or meteorological cycles disrupt steadiness. This is a recurring problem for hydrological studies. It can be significantly with careful choice of working periods and a 24-h moving averaging of data impacted by diurnal effects [10,11,12]. The thermal inertia of soil also damps the meteorological or seasonal effects with deepening [14,15].

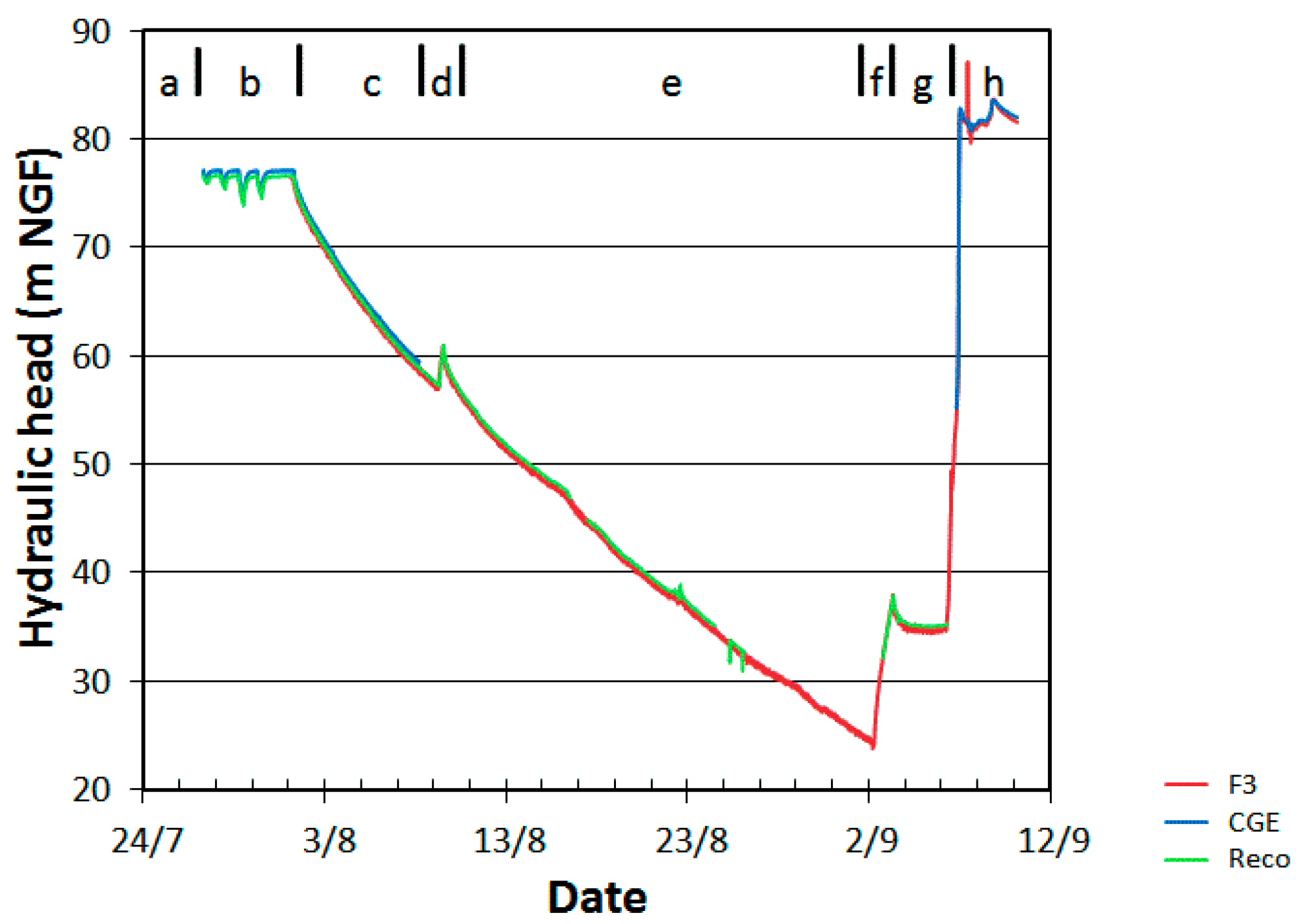
However, we also have to trust on the common sense of operators and analysts to “instinctively” avoid the most unstable periods for data collection. Thus, the conservative temperature assumption is unsuitable for runoff flow studies or all other kinds of events that imply transient and unstable thermal or water fluxes in the CS. This is why, the present work use a restriction of the White’s model to the recession period, with no run-off flow, and with a complete loss of the Upper Allogenic Stream (no surface stream). The 2005 Cent-Fonts pumping tests take place during the summer season when rainfalls are scarce on the watershed. However, even during that time, we focused the method on “steadiest” periods for water temperatures and flows. This is also why, despite available data until November, we stopped our analyses on 6 September (16:55) when a runoff due to a heavy thunderstorm flooded the boreholes (Figure 4).

3. Presentation of the Cent-Fonts Pumping Test Data

3.1. Period (a): Data Collected Prior the Beginning of the Pumping Test

Several years of flows and water temperatures have been recorded at the karst spring and in Buèges since 1997 to study the recession of the base flows during dry periods. This knowledge is essential to understand the answers of the aquifer during the pumping tests. The base flow (Q_S) gathers the upper allogenic intrusion of Buèges stream (Q_UAI) and the diffuse infiltration (Q_PFMB). The study of the karst recession conducted from 1997 to 2001 used a modified Mangin method to distinguish the parts played by Q_PFMB and Q_UAI to the base flow [23]. Q_S is described thank to three terms calculated from a Maillet homographic function [41]. Hence, two recession coefficients appear that characterizes the respective recession evolutions of Q_PFMB or Q_UAI. Ladouche et al. [23] calculated recession coefficients of 0.0080 (1998); 0.0088 (2000) and 0.0088 (day⁻¹) (2001) for the Q_PFMB contribution to the base flow [23] (p. 64).

Complementary flows and water temperatures have been recorded in the weeks preceding the step-drawdown sequence on 27 July (see Table 1 for an accurate chronology of the pumping tests). Figure 4 presents the far field (T_∞), the Upper Allogenic Intrusion (T_UAI, Buèges), the Neighbor Allogenic Intrusion (T_NAI, Hérault) and the CS (T_CS, in Cge borehole) temperatures recorded from 1 July to 6 September. During the pumping tests, Cge’s devices provided CS hydraulic heads and temperatures until their disconnection by drawdown. T_CS temperature was also recorded in the F3 borehole at the output of the pump (see Figure 2 and Figure 4).

3.2. Period (b): Data Collected during the Step-Drawdown Sequence (27 to 30 July)

Step-drawdown sequences are one of the most often performed pumping test to find out the behavior of wells and aquifer features. For the Cent-Fonts pumping test campaign, the pump has been placed directly inside a large CS conduit. The hydraulic heads recorded in F3, Reco and Cge will display such close curves they will be undistinguishable at the Figure 5 scale despite the bottleneck between Cge and F3 boreholes (Figure 2 and Figure 5). This superposition of curves reveals the hydraulic connectivity in this final part of the CS. Thus, the step-drawdown sequence will efficiently find out the resurgence yield by overestimating or underestimating the rate of pumping drying the spring.

Table 2. Step drawdown pumping, Q_PFMB from Equation (13), Q_UAI recorded at Buèges, total recovering.

Step-Drawdown Phase	Mean QP (m3/s)	Outlets Drying [26]	Mean QPFMB (m3/s)	Mean QUAI (m3/s)	QPFMB + QUAI (m3/s)
07/27 (07:30–13:20)	0.203	Partial drying of outlet n°4 No drying of other outlets	0.305	0.042	0.347
07/28 (06:35–12:00)	0.301	Drying of outlets except outlet n°4 (partial drying)	0.303	0.034	0.337
07/29 (06:20–12:20)	0.500	Drying of all outlets	0.300	0.031	0.331
07/30 (06:30–12:35)	0.402	Drying of all outlets	0.297	0.033	0.330

recalls the step-drawdown chronology, the pumping rates and the drying effects on griffons. Q_P of 0.2 and 0.3 m³/s did not achieve the completed drying of griffons while it was reached for 0.4 and 0.5 m³/s [26] (pp. 55–59). These results allow inferring that between 27 July and 30 July the base flow of the resurgence spring (that is Q_PFMB + Q_UAI) was ranging between 0.3 and 0.4 m³/s.

Four “coma-shaped” events (due to sudden deepening followed by recovering) occurred on the hydraulic head for each pumping of the step-drawdown sequence (Figure 5, Period (b)). During that time, the CS temperature remains constant to a few tens of degree while, on the opposite, T_UAI (Buèges) and T_NAI (Hérault) display diurnal temperature oscillations that reach 1 to 3 degrees (Figure 4). These diurnal temperature variations oscillate over 4 degrees, of meteorological trend that affect both T_UAI and T_NAI between 11 July and 30 July. The meteorological trend has the same amplitude on T_UAI and T_NAI. The amplitude of T_UAI diurnal oscillations remains lower than those of T_NAI because of shortness Buèges course and its low emergence temperature (12.5 °C). The stability of T_CS despite these oscillations results from the damping effects of soils and 10 days underground transfer from the losses area to the Cent-Font resurgence [20].

3.3. Period (c): Constant High Rate Pumping (1 to 9 August)

Long high rate pumping is used to assess the answer of the aquifer to drawdown. From 1 August to 9 August, the hydraulic head in the CS increases linearly with time (note that to avoid concave curves in Figure 5, the data are not plotted versus the log of time as usual). However, the drawdown induces a reversal of the hydraulic head that triggers the intrusion of Hérault in the CS and a new contribution that adds to the base flow Q_PFMB coming from the PFM. Two new flows, Q_NAI and Q_PFMD are added to Q_PFMB and Q_UAI while spring drying let Q_P be the only discharge of the CS. During that time, T_UAI and T_NAI display diurnal and meteorological variations while T_∞, recorded 25 m below the surface in the P7 borehole, remains remarkably constant (Figure 4, Period (c)).

T_CS is recorded both in the Cge and F3 boreholes. The first is measured close to the arrival of the neighbor allogenic intrusion of Hérault (Figure 2). The second T_CS is recorded deeper, close to the arrivals of Q_UAI and Q_PFMB. These two flows carry temperatures T_UAI and T_∞ lower than this of T_NAI. Thus, the values of the two T_CS series diverge rapidly as soon as the drawdown triggers arriving of hot intrusive Hérault water in the CS branch near the Cge borehole. T_CS (Cge recorded) increases rapidly a few hours after the starting of the high rate constant pumping from its 13.7 °C constant value since 2 August, 12h05. After a few days of transient evolutions, the temperatures in Cge and F3 boreholes stabilize respectively around 20 and 15 °C. Their temporal variations are correlated with the meteorological and diurnal trends observed for T_NAI and T_UAI (Figure 4, Period (c)).

The second series of T_CS records (F3) stabilizes rapidly around 15 °C. It displays diurnal oscillating changes that are clearly due to the mixing of hot Q_NAI with the cold Q_PFMB, Q_PFMD and Q_UAI in the vicinity of the pump. This stabilization of the T_CS increase indicates that Q_NAI acts like an almost constant vadose flow despite the increase of the hydraulic head between the water table and Hérault [26] (p. 191).

According to Maréchal et al. [34] we will considerer in the following the dewatering of the conduit network as a supplementary outgoing flow from the CS, Q_CS.

3.4. Period (d): Recovering Test (9 August)

The 6 h pump stop of 9 August allowed a recovering of 3.43 m (Figure 5, Period (d), and [26] (p. 65). During the interruption, Q_NAI brought warm water of Hérault that accumulated in the chimney above the pump. After pump re-starting, the temperature, T_P displayed a short peak 9 August, 13h05 consecutive to the rapid extraction of this warm water. Similar phenomena occurred at the restarting 22 August, 13h30 and 3 September, 07h45 (Figure 4, Periods e and g).

3.5. Period (e): Constant High Rate Pumping (9 August to 2 September)

After 6 h of recovering, high rate pumping has been restarted from 9 August until 2 September. During Period (e), the hydraulic head decreased almost linearly with a slope similar to the one of Period (c). On 13 August at 12h15, the drawdown reached the level of the temperature probe in Cge borehole (51.6 m NGF), causing its disconnection and the loss of the T_CS signal recorded there. At the end of Period (e), the drawdown approached the level of the pump in F3 that caused its stopping (Table 1).

As mentioned above for Period (c), two diurnal and meteorological trends are noticeable in the T_NAI and T_UAI temperature records. These variations are also present in the last part of T_CS (Cge recorded) and in T_CS (F3 recorded) (Figure 4, Period (e)).

From the beginning of August, the drawdown allowed speleological explorations of the resurgence branches (Figure 6). Surprisingly, while significant Q_PFMD infiltrations were expected in CS, no water was apparently percolating through the chimney wall (Figure 6a–c). However, several cascading vadose flows were observed between marks 657–658 of the lifeline (Figure 6d) and mark 670 (Figure 6e). Partial catchments of these Hérault intrusions at point 657 collect 0.045 to 0.050 m³/s [26] (p. 40). This value gives a rough lower bound value of Q_NAI since other hidden or deeper entries were probably active. These speleological explorations also opened the opportunity to collect geochemical samples to quantify the mixing of Hérault intrusion in the CS.

Water samples were collected 1 September at the above intrusion points. We used PP^® bottles previously washed with chlorydric acid, then bromydric acids, to prevent contamination [42]. Bottles and corks have been rinsed four times on site. The solutions have been filtered, acidified and prepared in two dilutions for analysis. Complementary samples were collected the same day at the Buèges spring, in Hérault and at the pump.

The samples were analyzed for the Rb, Sr, and Ba on the VG Plasmaquad II turbo ICPMS of Montpellier 2 University (

Table 3. CS1 and CS2: Hérault intrusions in CS, HR: Hérault, BS: Buèges, PO: Pump output.

ppB	CS1	CS2	HR	PO	BS	CS1	CS2	HR	PO	BS
Rb	1.054	1.131	1.582	0.460	0.193	1.157	1.166	1.366	0.443	0.188
Sr	76.854	82.443	91.054	58.334	52.596	83.390	81.500	77.440	58.510	53.551
Ba	52.231	52.577	94.786	12.723	3.736	55.773	52.676	80.564	12.935	3.791

and Figure 7). Sr, Rb, and Ba have been chosen as field tracers for water circulation and mixing [4] Petelet et al. 2003). Figure 7 shows the alignment of the samples in a (Ba/Sr) vs. (Rb/Sr) graph. The alignment of point denotes a mixing between two poles [43]. According to the regression curves and the rate of pumping Q_P = 0.4 m³/s, Q_NAI ranges from 0.039 to 0.048 m³/s for Ba, from 0.060 to 0.083 m³/s for Sr, and from 0.077 to 0.087 m³/s for Rb. However, the lower values of the Ba/Sr ratio may reflect a sorption effect onto mineral-water interfaces [44]. The averaged value of these six measures gives Q_NAI = 0.066 m³/s.

3.6. Period (f): Recovering Test (2 September to 3 September)

A second stop of the pump lasts 24 hours and 25 minutes, from 2 September to 3 September, that induced a 13.49 m recovering in the chimney (Figure 5).

3.7. Period (g): Drawdown Constant Pumping (3 September to 6 September)

The equilibrium-pumping (Period (g)) followed one month of constant pumping at constant rate that resulted in an important drawdown. After the recovering of Period (f), the equilibrium-pumping aimed to assess the dynamics of aquifer answer to hydraulic head. It started on 3 September at 7h45 with Q_P = 0.324 m³/s. The pumping rate has been dropped to Q_P = 0.304–0.305 m³/s a few hours later to stabilize the hydraulic head at 35.0 ± 0.1 m NGF (Figure 5).

Since, this value is around 40 m deeper than the karst base level the Hérault intrusion remained active (the first intrusion of Hérault occurred for 76.7 m NGF on 1 August at 07h10).

4. Revisiting the 2005 Pumping Test Data

The challenge of studying temperature as a conservative tracer also faces the natural complexity of karsts, which CS mixes water coming from low resistance conduits and low permeability PFM. A few decades ago, studies were often considering medium where CS was not disrupting the aquifer but continuous models were unsatisfactorily. Since a few years, improved analytical models take better into account for the different behavior of the two types of reservoirs [34] or even three reservoirs [45]. However, despite the importance of calibration for the models, temperature has not been used probably because of the non-conservative character of this signal [26,34]. In the following we will take benefit of particular periods of the pumping test to get new constraints for the models.

Our process consists, firstly, to revisit the data of Period (a) to recalculate the base flow Q_PFMB that forms the background over which the assessment of Q_PFMD is possible. Secondly, we benefit of the base flow knowledge to reevaluate the intrusion of Hérault, Q_NAI, on Period (g). Thirdly, relying on Q_PFMB and Q_NAI, we re-assess Q_PFMD, the answer of the aquifer to drawdown, during the constant pumping (Periods (c) and (e)).

4.1. Revisiting Q_PFMB from Period (a)

4.1.1. Revisiting the Data

Unlike Maréchal et al. [34], but following the results of [26] (p. 64), we consider that the recession of the Cent-Fonts base flow is better described separating the Buèges contribution Q_UAI. Then, the recession of Q_PFMB is calculated using Equation (11) in which we need to set the amplitude coefficient Q_PFMB(t_o).

$$Q_{PFMB}(t)=Q_{PFMB}(t_0)e^{-0.0088(t-t_0)}$$

(11)

Without pumping, the only flow leaving the CS is the one of the spring. In July 2005, as the surface course of Buèges fully disappears, and since no pumping affects the resurgence, no drawdown occurs in the CS. Under these natural conditions Q_S gathers Q_UAI and Q_PFMB and the water table in CS sits on top of the base level by a few centimeters. This weak hydraulic head is enough to prevent Hérault to intrude.

Then, replacing q_k = Q_PFMB, T_k = T_∞, q_l = −Q_S, T_l = T_CS, q_i = Q_UAI and T_i = T_UAI in Equation (8) leads to the Equation (12) below where the spring discharge Q_S and the base flow Q_PFMB are unknowns.

$$\begin{array}{l}{Q}_{PFMB}=\frac{Q_{UAI}(T_{UAI}-T_{CS})}{(T_{CS}-T_{\infty })}\\ Q_S=Q_{PFMB}+Q_{UAI}\end{array}$$

(12)

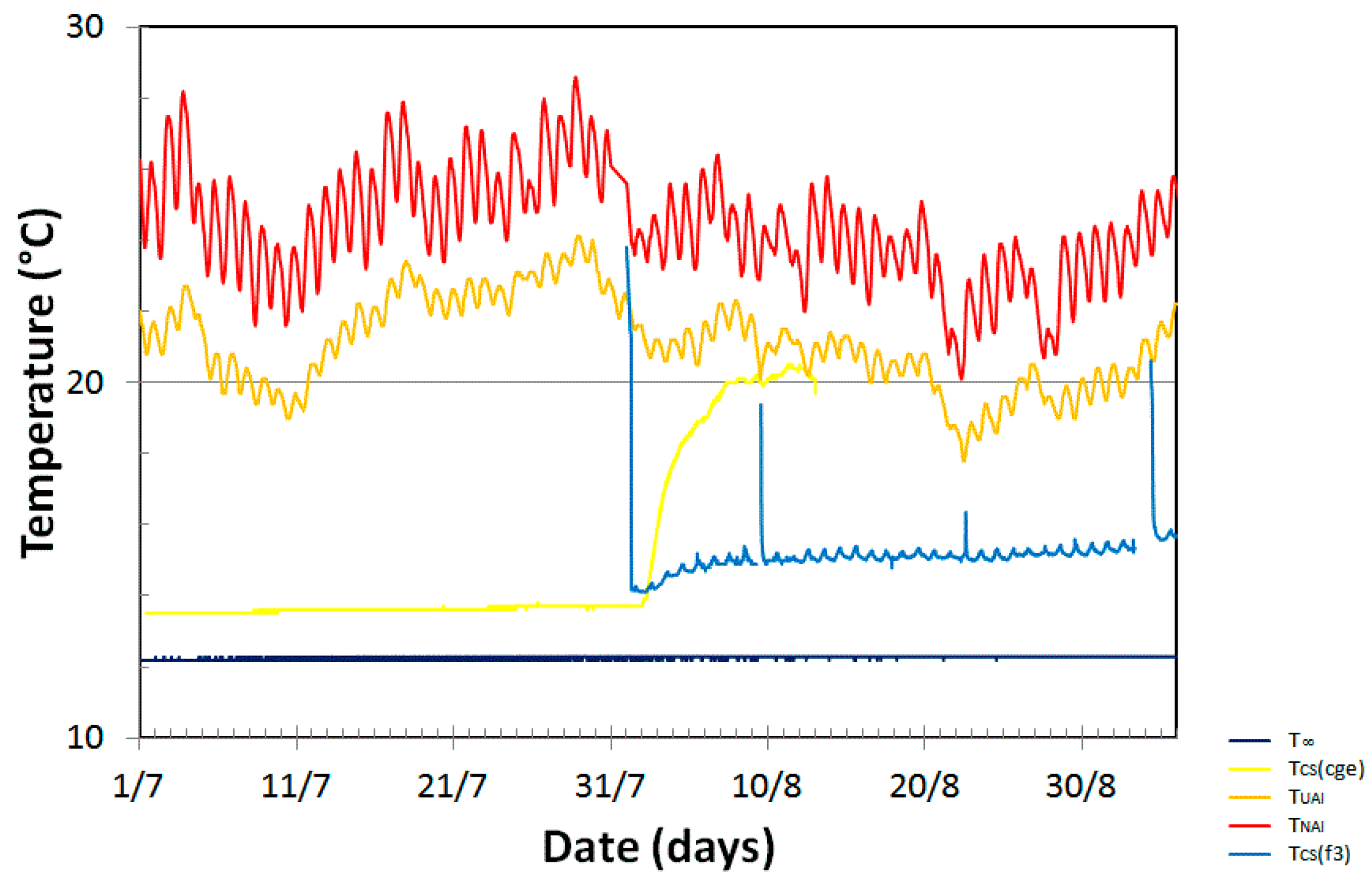
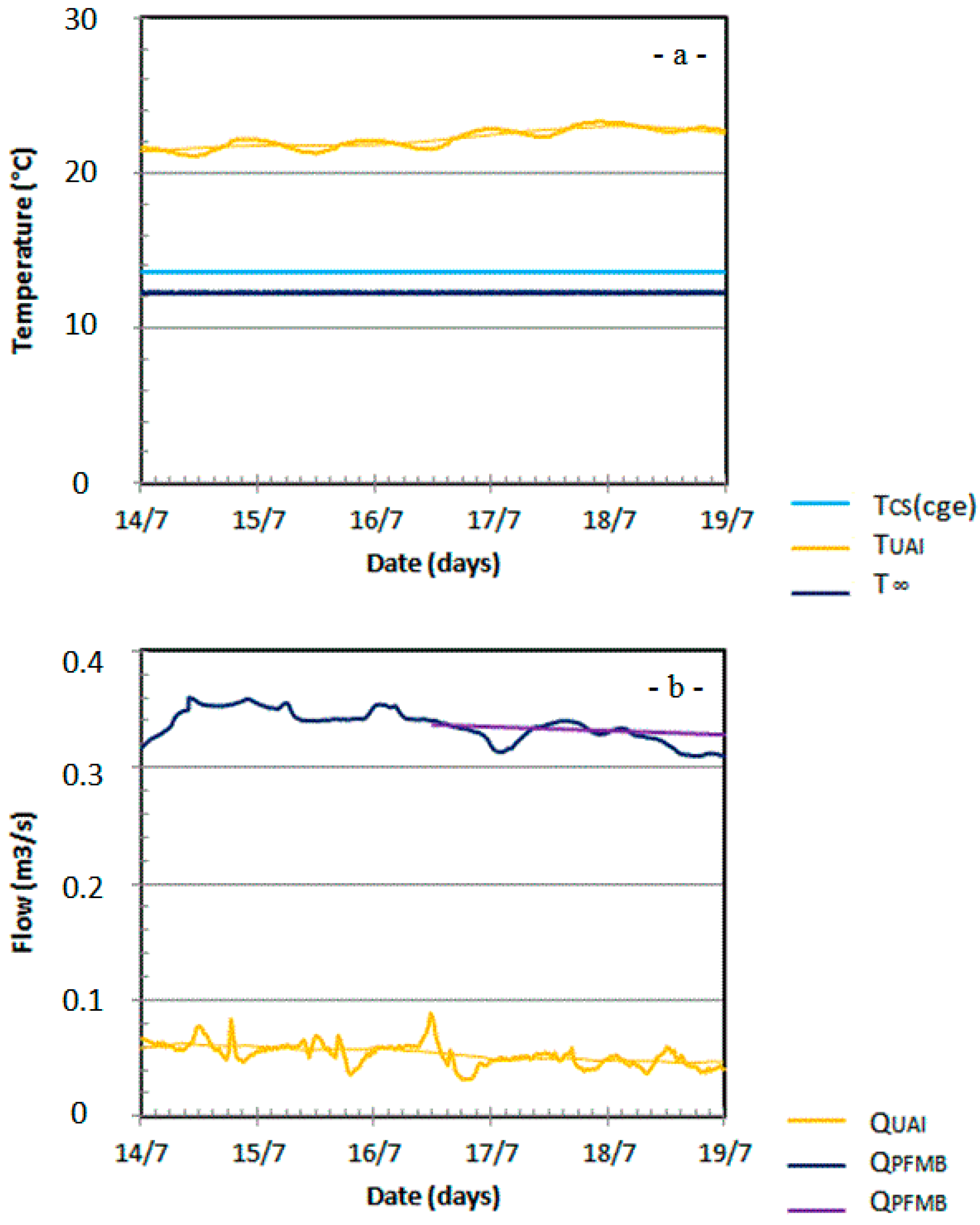
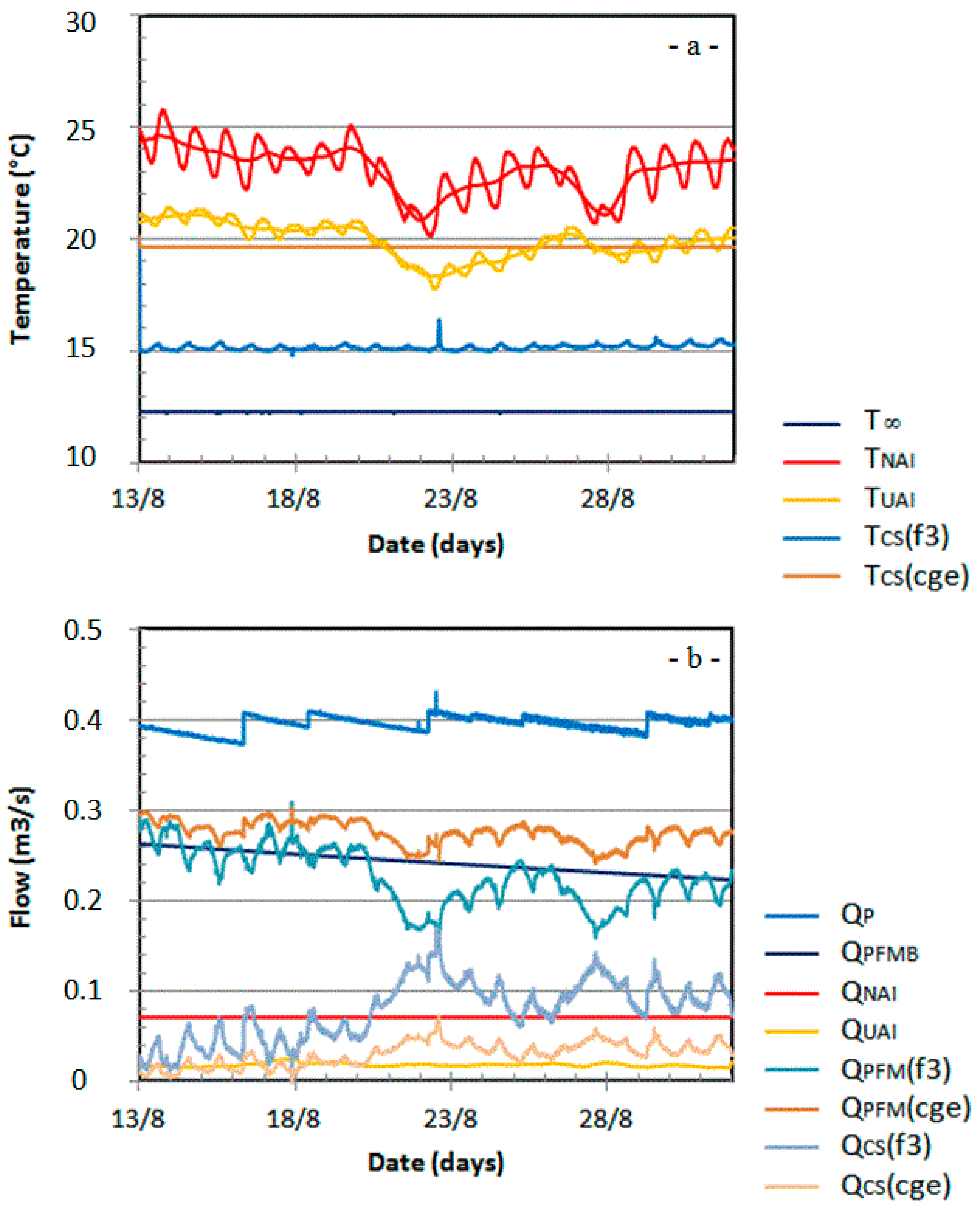
It is, therefore, possible to fix Q_PFMB(t_o) in the recession curve with the values Q_UAI, T_UAI, T_CS and T_∞ recorded for several weeks. Figure 8 displays an enlargement of these records from 14 July (00:00) to 19 July (23:55). T_UAI displays diurnal oscillations of 0.2 to 0.4 °C around its 24-h moving averaging and a small meteorological increasing trend of a few degrees (Figure 8, top). In bottom panel of Figure 8, Q_UAI also displays diurnal oscillations due to the water catchments upstream of the swallow zone. Concurrently, T_∞ and T_CS remain remarkably stable (Figure 8, top). The Q_PFMB curve in the bottom panel of Figure 8 displays the results of Equation (12) solving. We calculated its mean values (0.336 m³/s) and affected it at the median time to = 16 July (12:00) to extrapolate the PFM base flow for the remainder of our study (Equation (13)).

$$Q_{PFMB}(t)=0.336e^{-0.0088(t-t_0)}$$

(13)

4.1.2. Assessment of Error Due to Data Variability

Two kinds of inaccuracy may affect the measures and, therefore, the use of Q_UAI, T_UAI, T_CS and T_∞ for the method described in this article. The first are the precisions of the measures while the second relate to the difference between the steady state and the physical conditions in the CV. In the following, we will consider that modern thermometers result in negligible errors (less than 0.1 °C) in front of those resulting of unsteady behaviors. For Buèges gauging, the level error δQ_UAI at the swallow zone is not explicitly mentioned [26]. However, it is reduced by the total swallowing that limits it to the one of the zone entry. It is also reduced by the low flow context that allows more accurate gauging [46]. Therefore, without better assessment of this error, it seems reasonable to consider that it remains lower than a few liters by second. This level matches the one of standard errors induced by the diurnal variations (

Table 4. Error assessments: Parameter, Status (M)easured, (E)xtrapolated or (C)alculated; Figure or Equation; Mean value; Standard Error; Max Error; Standard Error 24 h averaging, Min Error.

Periods	Q, T	Status	Figure	Mean	SE	Error	24mSE	24mError
(a)	TCS	M	4, 8	13.6	0	-	0	-
	QUAI	M	8	0.053	0.010	-	0.005	-
	TUAI	M	8	22.3	0.64	-	0.55	-
	T∞	M	4, 8	12.2	0	-	0	-
	QPFMB	C	8	0.336	-	0.086%–25.6%	-	0.052%–15.5%
	QS	C	8	0.391	-	0.096%–24.7%	-	0.057%–14.7%,
(g)	QP	M	9	0.304	0	-	0	-
	TP	M	9	15.73	0	-	0	-
	T∞	M	4, 9	12.2	0	-	0	-
	QUAI	M	9	0.015	-	-	-	-
	TUAI	M	9	22.0	-	-	-	-
	TNAI	M	9	25.1	0.52	-	-	-
	QNAI	C	9	0.070	-	0.004%–5.7%
	QPFM	C	9	0.219	-	0.003%–1.4%		-
(e)	QP	M	10	0.396	0.008	-	-	-
	TP	M	10	15.16	0.015	-	-	-
	T∞	M	4, 10	12.2	0	-	-	-
	QUAI	M	10	0.0184	0.006	-	0.002	-
	TUAI	M	10	20.1	0.89	-	0.84	-
	QNAI	E	9, 10	0.070	-	-	-	-
	TNAI	M	10	23.2	1.21	-	0.97	-
	TCS	E	4	TP	-	-	-	-
	QPFMB	E	Equation (13)	var.	-	-	-	-
	QPFM	C	10	0.248	-	0.016%–5.7%		0.014%–5%
	QCS	C	10	0.278	-	0.029%–97%		0.021%–70%

).

Equation (10) provides a powerful tool to assess how errors spread through the solving. According our preceding comments, and considering the stability of T_CS and T_∞, we have reported δT_∞ = 0 and δT_CS = 0 in Equation (10). The differential form of Equation (9) becomes Equation (14), for which the numerical coefficients have been calculated by using the mean values and the Standard Errors of temperatures and flows.

$$\begin{array}{l}\delta Q_{PFMB}=\frac{1}{(T_{CS}-T_{\infty })}\left[(T_{UAI}-T_{\infty })\delta Q_{UAI}+Q_{UAI}\delta T_{UAI}\right]\\ \delta Q_S=\delta Q_{PFMB}+\delta Q_{UAI}\\ \delta Q_{PFMB}=6.21\delta Q_{UAI}+0.038\delta T_{UAI}\end{array}$$

(14)

More realistic physical conditions have been searched for in the CS by operating 24-h moving averaging on the diurnal variations of raw data (Table 4, columns 6 and 8). Such numerical process accounts for the natural thermal and kinetic inertia acting along underground water flows and allows damping the error that could arise from their neglecting. Thus, over a few days, a meteorological trend increases the temperature recorded at the Buèges swallow zone by one to two °C (Figure 8). However, the final standard error remain limited to 0.64 °C on raw data (Table 4, column 6) and to 0.55 °C after 24-h averaging of the data (Table 4, column 8). The natural damping of temperature fluctuations that affects Q_UAI during its underground travel to the CS prompts to consider the standard error as an upper bound.

Equation (14) shows that 1 °C of error on T_UAI induces 38 L/s (liters by second) of error on Q_PFMB; and that one L/s of error on Q_UAI induces 7 L/s on the final result. We can therefore expect that Q_PFMB is obtained to a few tens of L/s (around 20%) (Table 4, columns 7 and 9). This is consistent with the step drawdown tests that revealed a spring flow Q_PFMB + Q_UAI comprised between 0.3 and 0.4 m³/s.

4.1.3. Assessment of Error due the Conservative Temperature Assumption

Another way to explore the effects of non-stationarity on the solutions consists in confronting karst numerical models that consider (or not) temperature as a conservative tracer. This has been done in a previous study where several numerical models have been calculated over very broad ranges of karst morphological and hydrological parameters. According to Equation (15) of [36] a first order of the error induced by the conservative temperature assumption is reached by the following Equation (15):

$$\delta T=\epsilon ’\left[(T_{CS}+\frac{T_{\infty }}{\left(T_{UAI}-T_{\infty }\right)})\right]$$

(15)

The error, ε’, is calculated versus the hydrological and morphological properties as thermal diffusivity ratio (9.93), Conduit Peclet number (1.5 × 10⁸), Prandtl number (6.99) and Conduit Reynolds number (4.29 × 10⁴). Table 1 and

Table 5. Assessment of error due the conservative temperature assumption. Period, characteristic length, hydraulic radius, characteristic velocity, Dimensionless thermal diffusivity, Peclet number, Prandtl number, Conduit Reynolds number, dimensionless error, rescaled thermal error.

Periods	L (m)	r (m)	V(m/s)	D	Pe	Pr	Red	ε	δT
(a)	5 × 103	5	4.29 × 10−3	9.93	1.5 × 108	6.99	4.29 × 104	0.00613	1.93
(c, e, g)	2 × 102	5	2.78 × 10−3	9.93	3.9 × 106	6.99	2.78 × 104	0.002	0.62

recall the form and the physical values compatible with the Cent-Fonts karst. Then, the abacus curves of Figure 4 of [36] indicate ε’ = 0.00613 at the exit of the CS. With ε’ = 0.00613, T_CS = 286.75 K, T_UAI = 295.45 K and T_∞ = 285.35 K (Table 4, Period (a)) the first order of the error δT = 1.93 °C. Coming back to Equation (14), we can see that it may induce 0.073 m³/s of error for Q_PFMB. This result is higher but remains consistent with the previous estimate and the results of the step drawdown tests.

4.2. Revisiting Q_NAI from Périod (g)

4.2.1. Revisiting the Data

As recalled above, the equilibrium-pumping that started on 3 September (7h45) and ended on 6 September (6h00) followed one month of constant pumping and a one day recovering. After a few hours, the initial rate Q_P = 0.324 m³/s has been lowered to Q_P = 0.304–0.305 m³/s that stabilized the hydraulic head at 35.0 ± 0.1 m NGF (Figure 5). This hydraulic head is around 40 m deeper than the base level Hérault. Consequently, the Hérault intrusion Q_NAI remained fully active during all the equilibrium-pumping.

During Period (g), the incoming flows in the CS are Q_UAI, Q_NAI and both basic and drawdown induced PFM contribution Q_PFM = Q_PFMB + Q_PFMD. These input flows equilibrate the output flow Q_P while the stabilization of the hydraulic implies that the dewatering of the CS stops (Q_CS = 0). Hence, Equation (9) can be rewritten as Equation (16) to calculate Q_NAI, and Q_PFM.

$$\begin{array}{l}{Q}_{NAI}=\frac{Q_P(T_P-T_{\infty })-Q_{UAI}(T_{UAI}-T_{\infty })}{(T_{NAI}-T_{\infty })}\\ Q_{PFM}=\frac{Q_P(T_{NAI}-T_P)-Q_{UAI}(T_{NAI}-T_{UAI})}{(T_{NAI}-T_{\infty })}\end{array}$$

(16)

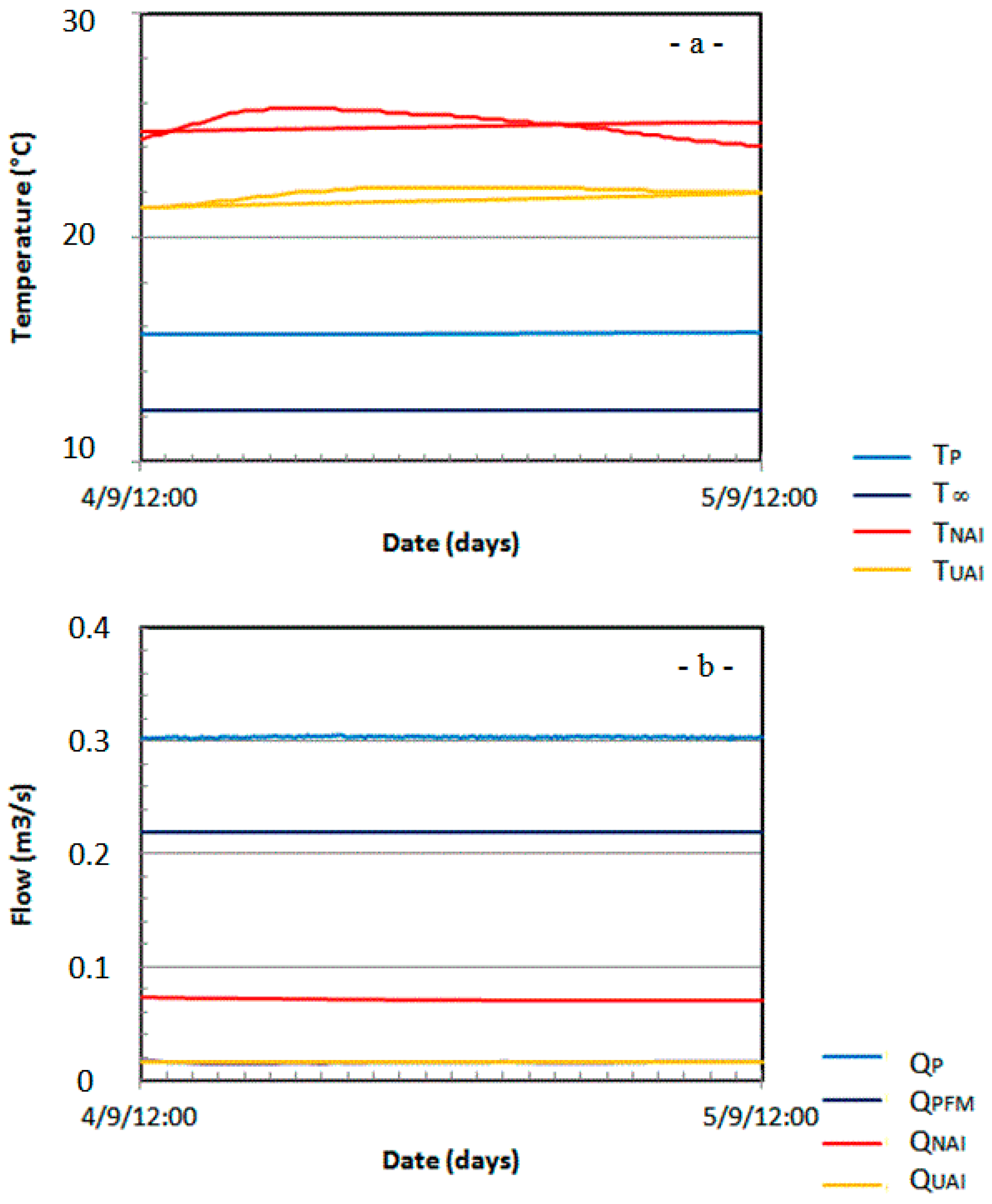
We focus on a remarkably stable 24-h data range from 4 September (12:00) to 5 September (12:00) (Figure 9). Indeed, the sinusoidal shapes of T_UAI and T_NAI are fully damped by the 24-h moving averaging, while T_∞, T_P, and Q_UAI remain rather constant.

The bottom panel of Figure 9 displays the results obtained for Q_NAI and Q_PFM. They lead to mean values of Q_NAI = 0.070 m³/s and Q_PFM = 0.219 m³/s. The first agrees well with the geochemical results presented in Section 3 while the second is only a few L/s higher than the base flow Q_PFMB = 0.216 m³/s obtained from Equation (11) for t = 5 September (00:00). This seems indicate that, a few hours after stabilization of the hydraulic head, the PFM contribution due to drawdown, Q_PFMD, is very low.

4.2.2. Assessment of Error Due to Data Variability

A procedure similar to the one described in Period (a) has been applied to Period (g) assessing the error due to data variability. The mean values of the parameters obtained on this interval have been introduced in the reduced form of Equation (10) to calculate the propagation of these errors through the resolution process (Equation (17)).

$$\begin{array}{l}\delta Q_{NAI}=\frac{1}{{(T_{NAI}-T_{\infty })}^2}\left[\begin{array}{l}(Q_{UAI}(T_{UAI}-T_{\infty })-Q_P(T_P-T_{\infty }))\delta T_{NAI}\\ -\delta Q_{UAI}(T_{UAI}-T_{\infty })(T_{NAI}-T_{\infty })\\ -Q_{UAI}(T_{NAI}-T_{\infty })\delta T_{UAI}\end{array}\right]\\ \delta Q_{NAI}=-0.0056\delta T_{NAI}-0.760\delta Q_{UAI}-0.0012\delta T_{UAI}\\ \delta Q_{PFM}=0.0056\delta T_{NAI}-0.240\delta Q_{UAI}+0.0012\delta T_{UAI}\end{array}$$

(17)

In this analysis, we will consider that pump gauging error δQ_P is negligible in front of δQ_UAI. Equation (17) shows that 1 °C of error on T_NAI induces 5.6 L/s of error on Q_NAI or Q_PFM; that of 1 L/s on Q_UAI results in 0.760 L/s; and that 1 °C on T_UAI induces 1.2 L/s. When the standard error of Table 4 are introduced in Equation (17), the error falls to a few L/s (a few %) (Table 4, Period (g)).

4.2.3. Assessment of Error Due the Conservative Temperature Assumption

During the equilibrium pumping, but also during constant pumping, most of the CS mixing occurs near the pump, in the top part of the chimney just beside Hérault (Figure 2). This proximity causes the diurnal oscillation of TP that occur with a delay of 20 h (Figure 4). The drawdown changes significantly the configuration of the CV with a mixing zone close to Hérault. The distance between the river and the chimney that contains the pump is less than 200 m. We have to take these consequences of the drawdown to assess the error due to the conservative temperature approximation during heavy pumping. Therefore, using these delay and distance to estimate the properties of the CV, the CS Peclet number and the Conduit Reynolds number fall respectively to Pe = 3.9 × 10⁶ and Re = 2.78 × 10⁴ (Table 5). The ratio of (PFM to Water) thermal diffusivities and the Prandtl number remain unchanged. We will use this new dimensionless configuration revisiting the data on Periods (e) and (g). (With these new values the abacus curves of Figure 4 of [36] tell that ε’ reaches around 0.002 at the exit of the CS.

$$\delta T=\epsilon ’\left[(T_P+\frac{T_{\infty }}{\left(T_{NAI}-T_{\infty }\right)})\right]$$

(18)

With ε’ = 0.002, T_P = 288.88 K, T_NAI = 298.25 K and T_∞ = 285.35 K (Table 4, Period (g)) δT reaches 0.62 °C. Through Equation (17), it induces a 0.003 m³/s error for Q_PFM. Similarly to the comparison of error on Period (a), both methods of error assessment lead to consistent results.

4.3. Revisiting Q_PFMD from Period (e)

4.3.1. Revisiting the Data

The knowledge of Q_PFMB and Q_NAI makes possible a backward analysis of the data recorded during Periods (c) and (e). Indeed, Q_PFMB forms the background over which it is possible to assess Q_PFMD. On the other hand, the vadose character of the Hérault intrusion results in a constant amplitude despite an increasing drawdown [26] (p. 191). These two previous results bring two “corner stones” situations separated by the constant pumping sequence. This allows us calculating two unknown flows: Q_PFM that includes the drawdown induced contribution Q_PFMD and the dewatering of the CS (Q_CS). The linear increase of the hydraulic head with time over Periods (c) and (e) (Figure 5) suggests a constant dewatering rate, bolstering us to assume a near steady CV situation. The input flows are Q_UAI, Q_NAI, Q_PFMB, Q_PFMD and the output flows are Q_CS and Q_P.

In order to maintain these “constant” conditions at best, our data processing skipped the data 24 h before and after the stopping. This allowed avoiding the transient phenomena observed at the restarting of the pump for temperature (Figure 4) and discharges. Consequently, we focused our analysis from 10 August (00:00) to 1 September (19:10). Within the context, Equation (9) can be rewritten as Equation (17).

$$\begin{array}{l}{Q}_{PFM}=\frac{Q_P(T_P-T_{CS})-Q_{UAI}(T_{UAI}-T_{CS})-Q_{NAI}(T_{NAI}-T_{CS})}{(T_{\infty }-T_{CS})}\\ Q_{CS}=\frac{Q_P(T_{\infty }-T_P)-Q_{UAI}(T_{\infty }-T_{UAI})-Q_{NAI}(T_{\infty }-T_{NAI})}{(T_{\infty }-T_{CS})}\end{array}$$

(19)

The brutal increase of the temperature records in the Cge borehole shows that, as soon as Hérault intrudes through the horizontal shallow branch of the CS, T_CS(Cge) is less representative of the dewatering temperature T_CS. Therefore, we will alternatively consider that the temperature recorded at the pump may represents another assessment T_CS(f3). This assumption seems reasonable since T_CS(f3) is only a few degrees higher than the T_CS temperature obtained on Period (a) before the mixing with the hot Hérault water.

The results of calculations for Q_PFM and Q_CS are presented on the lower diagram of Figure 10. From Q_PFM and Q_PFMB (Equation (13)), it is easy to calculate Q_PFMD. For both T_CS(Cge) and T_CS(f3) assumptions, Q_PFMD(Cge) and Q_PFMD(f3) curves display diurnal oscillations but do not display clear increasing trends despite of drawdown deepening. Figure 10 shows that Q_PFMD(Cge), Q_PFMD(f3), Q_CS(Cge) and Q_CS(f3) are clearly affected by the diurnal and meteorological oscillations on Q_NAI and Q_UAI. Considering the most advantageous situation T_CS(Cge), Q_PFMD ranges between 0.030 and 0.050 m³/s. However, this drawdown induced contribution is probably overestimated because of a too hot dewatering temperature assumption T_CS. Indeed, the calculation forces the system to equilibrate on the pump temperature. This will increase the low temperature contribution Q_PFM at the expense of the hot dewatering Q_PFM. On the other hand Q_PFMD(f3), computed taking the pump temperature as T_CS seems really too low since it would induces a zero or even negative contribution of Q_PFM to drawdown. In any case, these results seem consistent with short transient flows coming with the increase of the hydraulic head. These conclusions are consistent with the ones of Maréchal et al. [34], and consistent with the shortness of the flows observed at the beginning of the equilibrium-pumping phase.

4.3.2. Assessment of Error Due to Data Variability

Following the same procedure, the mean values of the parameter over this interval (Table 4—Period (e)) have been introduced into the reduced form of Equation (10) to establish the formal and numerical forms of Equation (20).

$$\begin{array}{l}\delta Q_{PFM}=\frac{1}{{(T_{CS}-T_{\infty })}^2}\left[\begin{array}{l}\delta T_{CS}(Q_P(T_P-T_{\infty })-Q_{UAI}(T_{UAI}-T_{\infty })-Q_{NAI}(T_{NAI}-T_{\infty }))\\ -\delta Q_{UAI}(T_{UAI}-T_{CS})(T_{\infty }-T_{CS})-\delta T_{UAI}{Q}_{UAI}(T_{\infty }-T_{CS})\\ -\delta Q_{NAI}(T_{NAI}-T_{CS})(T_{\infty }-T_{CS})-\delta T_{NAI}{Q}_{NAI}(T_{\infty }-T_{CS})\end{array}\right]\\ \delta Q_{PFM}=0.0044\delta T_{\infty }+0.039\delta Q_{UAI}+0.0024\delta T_{UAI}+0.447\delta Q_{NAI}+0.0092\delta T_{NAI}\\ \delta Q_{CS}=-0.0044\delta T_{\infty }-1.289\delta Q_{UAI}-0.0024\delta T_{UAI}-1.697\delta Q_{NAI}-0.0092\delta T_{NAI}\end{array}$$

(20)

One °C of error on T_CS value induces 4.4 L/s of error for Q_PFM. Finally, 1 °C of error on T_UAI induces 2.4 L/s of error and one °C on T_NAI results in 9.2 L/s of error. The introduction of the Standard error (24SE—Table 4) in Equation (20) leads to 14 to 21 L/s of error on Q_PFM and on Q_CS. Thus, small amplitude of Q_PFMD makes the error is of the same order than Q_MCD itself.

4.3.3. Assessment of Error due to the Conservative Temperature Assumption

As mentioned above, we consider that the hydrological configuration induced by drawdown is the same the one of Period (g). Then, the CS Peclet number and the Conduit Reynolds number remain the same and, ε’ keeps the same value around 0.002 at the exit of the CS.

$$\delta T=\epsilon ’\left[(T_P+\frac{T_{\infty }}{\left(T_{NAI}-T_{\infty }\right)})\right]$$

(21)

Therefore, the error on temperature balance due to the conservative approximation δT remains of the order 0.62 °C. Such temperature error would induce several tens liters by second of errors.

5. Summary and Discussion

The heat and matter exchanges occurring through the karstic boundaries impose a consideration of the Open Thermodynamic System (OTS). Within this framework, the first principle of thermodynamics leads to an enthalpy balance between flows entering and leaving the CV. Combining this property with mass conservation leads to systems of two equations involving the flows and temperatures. If formal physical conditions (steady states) are never achieved in nature, they are approached during particular periods as recession or certain phases of the pumping tests. These periods have been used these to calculate “corner stones” descriptions of the hydraulic regime between which we extend the results. The restriction of our model to the quietest part of the recession period cuts off the risk of disruption an approximate steady state by flooding and the possibility of reverse flow from CS to PFM. That way the periods of data revisiting were chosen outside of the recovering and the analysis has been stopped as soon as the flood event of 6 September occurred.

Revisiting the data recorded during these three periods with our theoretical analyses leads to a recalculation of consistent hydrological behavior of the karstic system. Thus, the speleological, hydrological or geochemical observations validated by previous studies [26,34] are not refuted despite of a less optimistic yield of the resurgence. This is particularly the case for spring drying during the step drawdown sequence, the results of geochemical analyses or the base flow recession of the resurgence.

Even though it is never perfectly reached in nature, the steady state approximation is necessary to use the method. While such state is assumed, temperatures equilibrate at the PFM/Conduit interface. However, this situation does not mean cancelling of embedding rocks/water heat transfer at the interface. Indeed, as shown in Machetel and Yuen 2015, PFM temperature gradient is maintained by the advection of cold, far field, water that counteracts the heat diffusion from CS to PFM through the wall. During the recession period, mixing of intrusive flows hotter than far field temperature, results in CS temperature hotter than in PFM. However, when a steady state is reached (or approached), all these local conductive effects (inside PFM and CS but also between PFM and CS) are taken into account by the final enthalpy balance. This is the most interesting property of the OTS approach that refers to the comparison of integrated incoming and leaving external heat sources and not on the local thermal properties inside of the “black box”. It is clear that what we called “conservative temperature assumption” may better be called as “conservative enthalpy approximation”. However since we assumed that no other sources of heat are present (neither chemical heat, nor work conversion to heat); enthalpy conservation comes down on to temperature conservation.

Thus, the application of the method to the first period (before pumping) of the Cent-Fonts pumping test experiments allowed assessing the basic recession flow of the resurgence. Then, the equilibrium-pumping allowed assessing the Hérault intrusion and the supplementary contribution induced by drawdown. The analysis shows that errors induced by unsteadiness reach a few tens of liters by second. They are of the same order of magnitude than the errors induced by conservative approximation itself.

In conclusion, we have confirmed the validity for using the thermometric method by the field observations that never contradict the results. It would be advantageous; insofar data exists, to check the method on other sites. It could also be interesting and of relatively low additional costs to develop recording and processing of temperature profiting of next pumping experiments. Indeed, as it does not require sophisticated equipment or procedures, the additional costs should remain low compared to drilling and pumping operations.

Our works may open the opportunity of using the steadiest part of the pumping test sequences to calibrate the global operating mode of complex resurgence system. Combining energy equation and mass conservation equations, temperature measurements in surface waters and boreholes may allow assessing the flow properties in borehole or mixing in karst CS. It seems therefore constitute an efficient tool to separate and calculate the karstic properties and could be a promising tool worthwhile to apply on other sites.