Abstract
A method is presented to analyze the interaction between groundwater and Lake Linlithgow (Australia) as a case study. A simplistic approach based on a “node” representing the groundwater component is employed in a spreadsheet of water balance modeling to analyze and highlight the effect of groundwater on the lake level over time. A comparison is made between the simulated and observed lake levels over a period of time by switching the groundwater “node “on and off. A bucket model is assumed to represent the lake behavior. Although this study demonstrates the understanding of Lake Linlithgow’s groundwater system, the current model reflects the contemporary understanding of the local groundwater system, illustrates how to go about modeling in data-scarce environments, and provides a means to assess focal areas for future data collection and model improvements. Results show that this approach is convenient for getting first-hand information on the effect of groundwater on wetland or lake levels through lake water budget computation via a node representing the groundwater component. The method can be used anywhere and the applicability of such a method is useful to put in place relevant adaptation mechanisms for future water resources management, reducing vulnerability and enhancing resilience to climate change within the lake basin.
1. Introduction
When water demand exceeds water availability, water scarcity is inevitable. Climate change, population growth, and economic development add to water scarcity risks mainly in arid regions [1,2,3,4,5,6]. Concerted data collection efforts are usually lacking in developing countries, especially when it comes to groundwater systems. Many lake studies encountered difficulties in estimating groundwater or defining a plausible, appropriate conceptual model of the aquifer system at hand [7,8,9,10,11]. Prudent understanding of the (ground) water system forms a major inhibiting factor for effective water management. Water management based on such models may have unintended or even detrimental consequences.
Wetland’s importance has been recognized by the Ramsar convention due to the possible impacts it may have on people in the next decades and how its conservation can ameliorate poverty conditions. Recent research has been done to assess the relationship between groundwater and surface water, due to the dependability of ecosystems on groundwater contributions [12,13,14,15,16]. The pressure on groundwater resources by these activities has alerted the interest of environmental authorities, who need to assess the hydrodynamic between wetlands, adjacent groundwater, and surface water [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Many activities have been carried out to validate the hydrogeological conceptual model in the wetland vicinity. A group of observation wells installed around the wetland has enabled the assessment through non-linear Darcy’s expression to approximate volumes of recharge and discharge from the aquifer to the wetland.
Groundwater is important for understanding lake systems due to its influence on a lake’s water budget, nutrient budget, and acid buffering capacity [21,22]. As a result, groundwater flows to and from lakes have often been estimated using simple flow grids and one-dimensional Darcian calculations. Groundwater interaction with lakes can be spatially and temporally variable, however. Other water balance approaches have also been used that employed a representative groundwater head underneath the lake for calculating the flux over the entire lake area. The most sophisticated way of investigating lake–groundwater interactions is by explicitly including lakes in groundwater flow models [10,28,29,30]. Water resources managers rely on tools that assist with streamlining supply and demand [25,26,27,31,49].
Modeling lake–aquifer interaction is an essential milestone in limnological studies [32]. Groundwater is one of the most important hydrological variables of the water budget in lakes; however, this variable, due to its nature, cannot be addressed without uncertainties [32,33]. Many scientists, however, have tried to model the interaction between groundwater and surface water using various statistical, conceptual, or empirical models (e.g., Lohman [34]; Edelman [2]; Lewis et al. [35]; Post et al. [36]; Jakovovic et al. [37]; Yihdego et al. [38]).
The role of groundwater in wetland water budget is of great concern to ecologists, water managers, and environmental scientists [39]. Groundwater is critical for understanding most lake systems because it influences a lake’s water budget and nutrient budget [40]. Several studies have reported on the use of a mass balance approach to simulate lake levels from hydrological and meteorological data [41,42]. There have been many different empirical, analytical, and numerical approaches for simulating lake–groundwater interactions (e.g., fixed lake stages, High-K nodes, and LAK3 package through numerical modeling). The advantages and disadvantages of these approaches have been documented by many researchers. Many highly sophisticated models like LAK Package are not widely used due to data and resource constraints [17,35,43]. The limited use of LAK Package is attributable to the lack of standardization and associated graphical user interfaces, complex three-dimensional discretization and data needs, and spatial and temporal complexity inherent in including surface water features in a groundwater model. While sophisticated approaches offer more detail, their advantages may be offset by associated complexity and even instability of the solution procedure [44]. Consequently, a full-featured LAK package is not an automatic choice for practitioners, regulators, and the wider community; rather, the chosen method should depend on both the hydrogeological conditions and the modeling objectives [39,45,46,47,48].
Within the Glenelg Hopkins Catchment Management Authority area, Lake Linlithgow and the nearby shallow lakes are considered to be of environmental importance due to the drainage and/or degradation of many other wetlands throughout this region [32,52,53]. However, in recent years Lake Linlithgow has been affected by algal blooms and high lake salinities, and has become dry over the summer during most years since 2000. The normal seasonal fluctuation for Lake Linlithgow is 10,000 μS/cm in winter and spring, rising to 16,000 μS/cm in late autumn [60]. However, during 1999, the lowest salinity levels recorded were 27,000 μS/cm and they peaked at 58,000 μS/cm (seawater) in the autumn, before sharply increasing to 63,000 μS/cm prior to drying out in February 2000. Extensive research was carried out to characterize future changes in groundwater salinization within the basalt aquifers in the Hamilton area, including Lake Linlithgow, using hydrogeological, chemical, and isotopic techniques [14,32,50]. The aim of this study is to improve our understanding of lake–aquifer interaction through analyzing the groundwater component of Lake Linlithgow as a case study.
2. Study Area
Lake Linlithgow covers an area of 9.65 km2 and is the largest in a series of highly to moderately saline wetlands, located approximately 16 km east of Hamilton, western Victoria (Figure 1). The lake is fed by Boonawah Creek and there is no surface outlet. The catchment area for Lake Linlithgow is 85 km2. The volcanic plains surrounding Lake Linlithgow are topographically subdued, comprising a flat to undulating plain with average elevation of ~200 m Australian Height Datum (AHD), gently increasing in elevation from south to north (Figure 1). The plain is dotted with several prominent eruption points and a number of smaller low-relief volcanic cones. The volcanic plain is deeply dissected (up to 80 m) by streams on its western and southwestern margins.
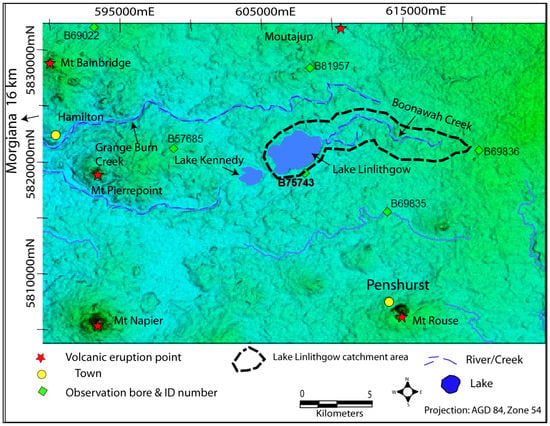
Figure 1.
Digital elevation model showing the relative elevation of the terrain surrounding Lake Linlithgow.
The pre-European vegetation comprised River Red Gum, Swamp Gum, Manna Gum, Blackwood, and Lightwood along moderately incised drainage lines, and Tea-tree, Silver Banksia, and Lightwood on the black self-mulching clays associated with the margins of swamps and lakes (i.e., Buckley Swamp) [55]. The poorly developed drainage lines associated with the headwaters of Grange Burn, Violet Creek, and Muddy Creek were often dominated by grasslands. Lake Linlithgow and Lake Kennedy (Figure 2) were presumably vegetated with salt-tolerant species such as plantain, Australian salt grass, and streaked arrow grass, and are relatively unaltered since European settlement.
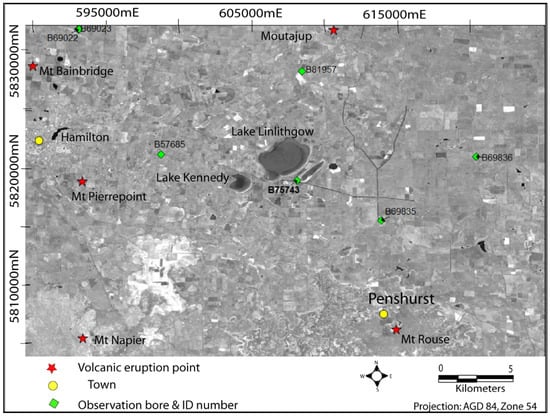
Figure 2.
Landsat imagery (taken in February 2004) showing the Lake Linlithgow area.
The most significant land use change occurred between 1900 and 1920, with the conversion to introduced pasture [55].
2.1. Hydrology
The average rainfall over the catchment is about 689 mm, recorded at Hamilton Research Centre. Rainfall records over the last 45 years clearly show that rainfall is highly variable, but over the last decade there has been a substantial drop, with annual rainfall below the long-term average. Maximum rainfall is received over winter (the wettest months are July and August) and exceeds or equals evaporation for May to September, when groundwater recharge is most likely to occur. June to September rainfall contributes 45% to the mean annual precipitation in the catchment; pan evaporation is highest from October to April and totals 1053 mm.
2.2. Geology
The basement geology of the area consists of Cambrian volcanics, Early Paleozoic turbidites, and Silurian sandstone, intruded by Devonian granites (Figure 3). These basement rocks do not outcrop around Lake Linlithgow.
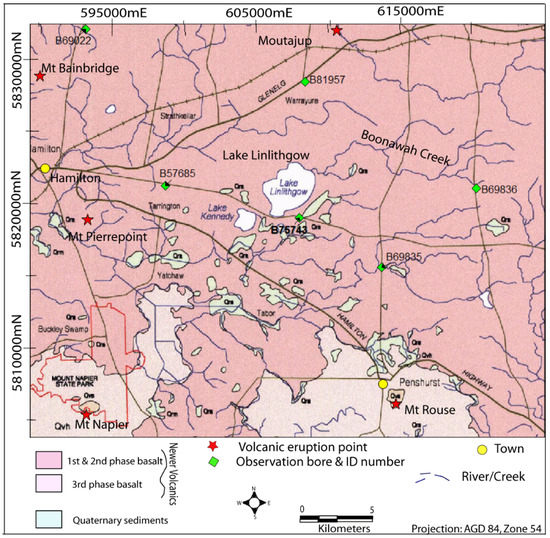
Figure 3.
Geological map of the area surrounding Lake Linlithgow.
The disruption of the drainage system by the basalt flows formed the lakes in the center of the catchment. Lake Linlithgow sits on first phase (~4 Ma) basalts, and is encircled by second phase (~2 Ma) basalt flows, forming a relatively flat lakebed with steep banks. Lunettes occur on the eastern and northeastern margin of the lake, ~4 m above the current maximum lake level [50]. There is a local groundwater flow system around Lake Linlithgow [32,55], and a regional to intermediate groundwater flow system in the surrounding volcanic plain (Figure 4).
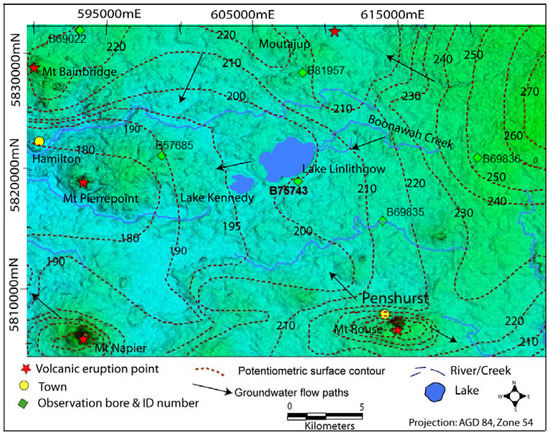
Figure 4.
Lake Linlithgow and associated wetlands (gray) and basalt aquifer potentiometric surface contours (m AHD).
Potentiometric surface contours for the Newer Volcanics aquifer indicate that Lake Linlithgow is a groundwater through-flow lake, with groundwater flow entering the lake from the east and leaving towards the west (Figure 4). Groundwater enters through a series of springs and seeps along the eastern lake margin, mostly from the second phase basalt aquifer, which terminates here [50,54,55,56]. Hydrographs from bores in the basalt aquifer surrounding Lake Linlithgow (Figure 5) show a strong correlation with the lake level. The declining trend of 20 cm/year from 1997 to 2001 is clearly a response to below-average rainfall [14]. The palaeosols lying between successive basalt phases hinder outflow from the lake and act as barriers to groundwater flow (Figure 6).
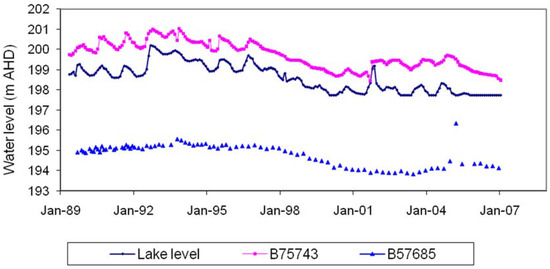
Figure 5.
Comparison of bore hydrographs with the lake level. The positions of the bores are shown in Figure 4; screened depth of B57685 is from 82.5 to 88.5 m.
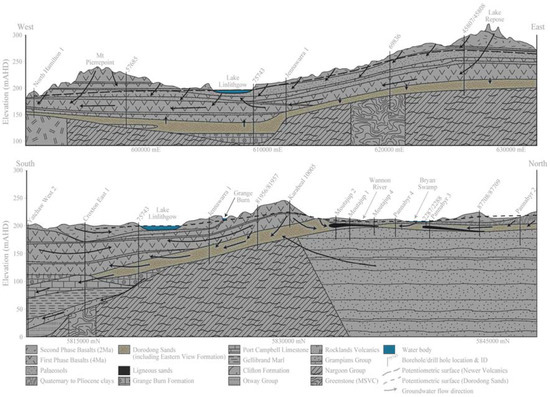
Figure 6.
West–East and South–North hydrogeological cross sections through Lake Linlithgow [50,55].
2.3. Lake Hydrology
Monthly lake level and salinity data are available for Lake Linlithgow from 1964 to 2007, when the lake dried out, although the salinity measurements are available only sporadically from 1964 to 1974 (Figure 7). Lake Linlithgow has a median depth of 1.45 m, but typically varies seasonally by up to 1 m (Figure 7). A graph of cumulative deviation of rainfall from the mean for Hamilton Research Station shows a strong correlation with lake levels; peaks in the lake level generally correspond to periods of above-average rainfall (Figure 7). In years of below-average rainfall, the lake dries out during summer, as occurred in January–April of 1983, 2000, and 2001, but after a succession of high rainfall years, lake levels rise substantially (Figure 7).
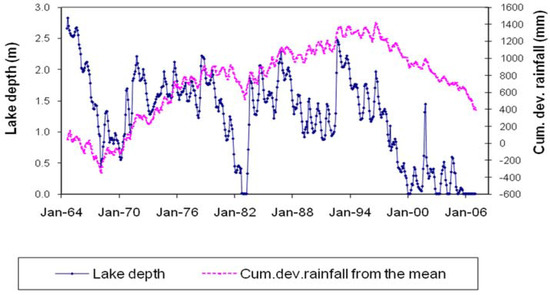
Figure 7.
Lake level with variation in rainfall.
Lake Linlithgow is typically saline (median 12400 μS/cm). The large seasonal variation in lake level is correlated with a substantial range in lake salinity (3300–98,900 μS/cm; Figure 8). There is a general tendency for Lake Linlithgow to become more saline until the lake dries out (Figure 8).
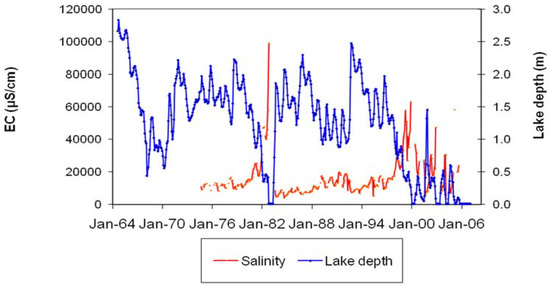
Figure 8.
Relationship between measured lake depth and salinity for the period 1964–2007.
3. Methodology
A spreadsheet model was employed to analyze for the current study [32]. An explanation of the model is given below.
3.1. Water Balance Model
Monthly time-step modeling of the lake water level was carried out using Excel spreadsheets, and the resulting water budget was used as input for the salt budget. The lake water balance is calculated by estimating all the lake’s water gains and losses, and the corresponding change in volume is expressed as:
where Qin is the groundwater inflow and Qout the groundwater outflow.
Volume change = Surface water inflow + Rainfall + Qin − Evaporation − Surface water outflow − Qout,
The net flux of the groundwater flow (Qin − Qout) can be calculated as:
where C is the conductance of the lakebed sediments (m2·month−1) and H is the water level in the lake and surrounding aquifer (m). Hydraulic conductivity can be expressed as
where K is the hydraulic conductivity of the lakebed sediments (m·month−1) and A and L are the lake area (m2) and lakebed sediment thickness (m), respectively. The formulation is similar to that used in the river (RIV) and lake packages, which specifies the flux through the riverbed or lakebed as a function of stage, potentiometric head in the connected cells, and the riverbed or lakebed conductance in which the lakebed conductance, COND, at each cell is either specified by the user in the lake package input file, or calculated from the lakebed geometry and hydraulic conductivity. As with the river package, flow from the lake to the groundwater in the LAK package is limited when the head in a cell falls below the lakebed bottom. Also, if the stage of the lake is below the top of the lakebed, the lake cell is dry and seepage into the groundwater is cut off for that cell. In this spreadsheet model, a similar procedure was applied to formulate the boundary conditions that control the solution of potentiometric head.
Q = C (Hlake − Haquifer) in m3·month−1,
C = K×A/L in m2·month−1,
The temporal area is estimated from the lake stage–area–volume relationship built in [42], while the lakebed sediment is estimated using the soil erosion model of the catchment. The water level in the surrounding aquifer is updated (Haquifer-new) using the inflow and outflow calculated for the previous month (Haquifer-pre) is
where A is the surface area of the interacting aquifer and Sy is the specific yield of the aquifer. The model requires known hydrometeorological data (inflow from the rivers, rainfall on the lake surface, aquifer area, and evaporation from the lake) and estimates the unknown net groundwater flux due to interaction of the lake with the surrounding aquifer by comparing the simulated and recorded lake levels and calculating a residual. The model was calibrated using solver and iteration. The net groundwater component is represented as a node in the equation to switch on and off and assess the significance of the groundwater in the overall lake water budget, as explained through the fluctuation and lake level trend over time.
Haquifer-pre = Q/A × Sy (m)
Haquifer-new = Hin-old + Hin (m),
3.2. Lake Water Budget and Model Parameters
3.2.1. Lake Storage
Bathymetry data are not available for the lake; however, the area–depth relationship was estimated. The lake area was measured from 12 Landsat images taken between 1972 and 2004 and correlated with the measured lake depth in the month when the images were taken (Figure 9). The lake area was estimated using ENVI software (with threshold method and grow button); this is more accurate than the GIS (vector) method used by [50] because it finds similar pixels selected for the water body and thereby better identifies the natural boundary. The line of best fit (with r2 = 0.99) to the area/depth data gives the relationship for Lake Linlithgow as:
A(t) = 1.545(D(t))5 − 23.09(D(t))4 + 135.9(D(t))3 − 393.7(D(t)2 + 561.1(D(t) − 305.8.

Figure 9.
Relationship between lake area derived from Landsat imagery and measured lake depth.
The polynomial relationship between lake area (A(t)) and lake depth (D(t)) is due to the lake’s relatively flat lakebed and steep banks, and gives a better fit for the depth–area relationship than the logarithm function used by [50], which had a smaller r2 value.
The lake volume at the beginning of a given month can therefore be calculated from the depth and area at the end of the preceding month. The lake depth must be first adjusted, because the minimum reading on the base of the lake level gauge is ~1.3 m. Thus, this value is deducted from the recorded lake level to get the true lake depth. For the modeling, the initial volume in September 1964 was calculated from the measured water depth in that month (2.79 m).
3.2.2. Precipitation on Lake
Monthly precipitation is taken from the nearest rainfall station (Hamilton Research Centre), which lies approximately 13 km southwest of Lake Linlithgow, and is multiplied by the lake area to give the volume of direct rainfall into the lake. The precipitation data are only available up until 2001; values for the subsequent time period have been extrapolated from the rainfall at Carinya station (~65 km from Hamilton Research Centre) using the correlation between rainfall at Hamilton Research Centre and Carinya.
3.2.3. Surface Flow to the Lake
Surface inflow to Lake Linlithgow is received through Boonawah Creek, for which there are no gauging data available. Surface inflows can, however, be estimated by the tanh cumulative surplus rainfall approach [42] using the Grange Burn flow, which is gauged at Morgiana (gauge no. 238219; Figure 1), because the Grange Burn and Lake Linlithgow catchments are adjacent and have similar topography, soil type, vegetation, land use, and rainfall. The tanh cumulative surplus rainfall approach provides a tool with which runoff in Grange Burn can be predicted for any given monthly precipitation/evaporation (Figure 10). Using area scaling, this can be converted to a flow in Boonawah Creek; the catchment areas for Boonawah Creek (at Lake Linlithgow) and Grange Burn at Morgiana are 85 km2 and 997 km2, respectively.
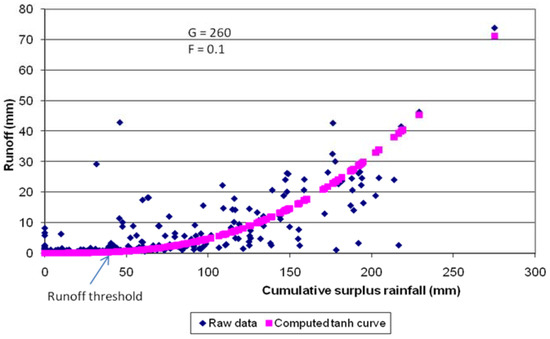
Figure 10.
Stream flow modeling for the Grange Burn at Morgiana (gauge no. 238219). The location of the gauge station is shown in Figure 1.
3.2.4. Outflow from the Lake
The evaporation from Lake Linlithgow is estimated using monthly evaporation data at Hamilton Research Station, where pan evaporation was measured from 1968 to June 2000. The evaporation data from July 2000 has been extrapolated from White Swan Reservoir station by establishing a correlation between pan evaporation at Hamilton Research Centre and White Swan Reservoir. Evaporation data from 1964 to 1968 are lacking at White Swan Reservoir, so evaporation for this period was estimated from the correlation of evaporation at the Hamilton Research Centre with that at the Melbourne regional office. A local calibration coefficient was used to adjust the seasonal pan evaporation data from Hamilton Research Centre for the best fit of the model. The optimized local calibration coefficient is 1.18; this takes into account the spatial variation in position, elevation, and storage effect between Hamilton Research Centre and Lake Linlithgow.
3.2.5. Groundwater Inflow and Outflow Estimation
Groundwater inflow/outflow was initially estimated using Darcy’s Law. The widths of the groundwater inflow and outflow zones along the lake perimeter are ~6.1 km and 3.6 km respectively. The cross-sectional area is calculated by multiplying the width of the groundwater inflow/outflow zone by the saturated thickness (8 m) of the first phase basalt aquifer in hydraulic contact with the lake. The average hydraulic conductivity of the basalt aquifer (0.09 m/day) is derived from groundwater flow rates calculated using groundwater radiocarbon ages by Bennetts [50]. The hydraulic gradient either side of the lake, derived directly from the potentiometric contours, is 3.7 × 10−3 (Figure 4). Similar to Lake Burrumbeet, an average value of 0.000864 m/d has been chosen for the permeability of the lake floor in order to estimate the groundwater outflow through the lakebed. Using these figures, the monthly groundwater outflow and inflow from/to the lake were estimated as ~0.29 ML and ~0.48 ML, respectively.
Model calibration, carried out by adjusting input parameters so that the simulated lake levels fit the observed lake level, gives the net groundwater flow estimation. In this case the optimized lake–aquifer conductance (C) value is 2.71 × 103 m2/day, which is equivalent to a hydraulic conductivity value of lake shore sediments of about 7 m/day; this falls within the range of previous hydraulic conductivity estimates for these sand beaches. The optimized specific yield and aquifer area are 0.1 and 45 km2, respectively [32].
The optimized specific yield compares reasonably with previous specific yield estimates of the basalt aquifer, which range up to 0.18 [51]. The aquifer area in hydraulic contact with the lake (45 km2) is significant compared with the catchment area of Lake Linlithgow (85 km2), indicating that lake level fluctuations directly impact about half of the basalt aquifer in the catchment area.
The best possible fit of the water budget model was attained at ~0.37 × 106 L and 3.1 × 106 L monthly average groundwater outflow and inflow, with the exception of dry periods. The value of optimized groundwater outflow compares closely with the initial estimate.
4. Results and Discussion
4.1. Lake Water Levels
The predicted lake levels show good agreement with the measured lake level data (Figure 11), with an r2 value of ~0.85 (Figure 12). The sum of the squared differences did not exceed 0.4 m, except for a few outliers (Figure 13).
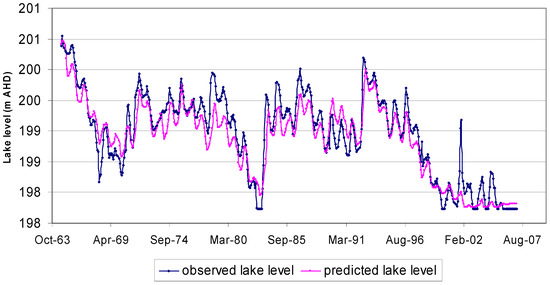
Figure 11.
Lake Linlithgow measured water levels and a comparison to modeled results for the period 1964–2007.
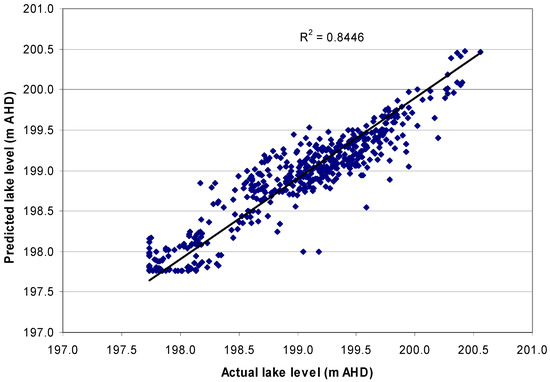
Figure 12.
Correlation between observed and calculated lake elevation in AHD m.
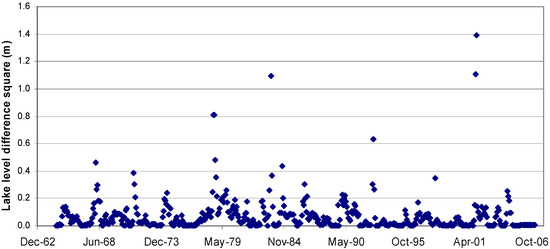
Figure 13.
Temporal distribution of square difference between observed and calculated lake levels.
The water balance shows that the major influence on lake levels is evaporation (Table 1), accounting for an average of 54% of the total water budget. It has the greatest influence in summer, reaching up to 99% of the total budget, but decreased during dry periods, because it is proportional to the lake area [32]. Groundwater inflow contributes about 1% of the lake water budget. Even though groundwater outflow is minor (0.1%), it dominates the lake water losses during early winter (June), a time when evaporation is very small (Figure 14).

Table 1.
Average long-term (1964–2007) monthly contribution (in percent) of each Lake Linlithgow water budget component to the overall lake water budget.
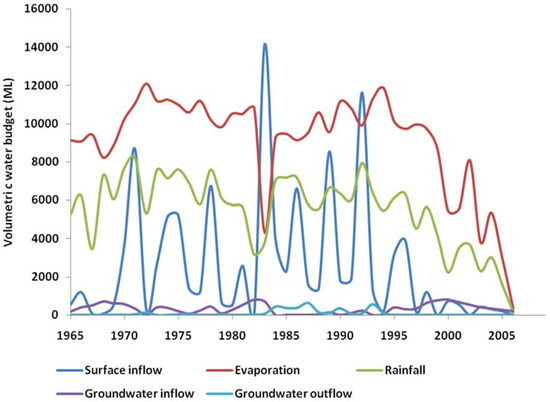
Figure 14.
Annual water balance of Lake Linlithgow (1965–2006).
Thus, Lake Linlithgow is a groundwater through-flow lake, and the lake–groundwater interaction is important since it affects the environmental health of this major wetland.
4.2. Water Budget Errors and Sensitivity Analysis
A sensitivity analysis shows that the model is most sensitive to evaporation and precipitation (Figure 15), and surface inflow to a lesser extent. However, the most likely source of error within the model is estimating the ungauged surface inflow (i.e., Boonawah Creek) by the tanh relationship from Grange Burn; this could be in error if the threshold value at which cumulative surplus rainfall becomes runoff in Grange Burn at Morgiana is different to that of the smaller catchment of Boonawah Creek.
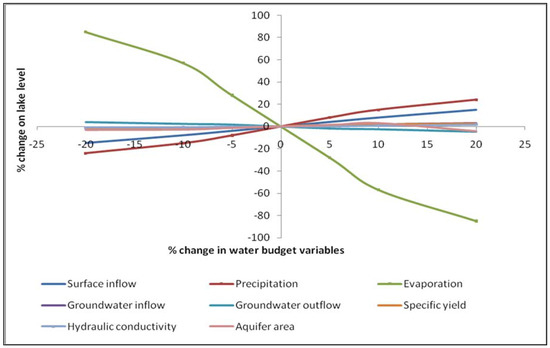
Figure 15.
Relative sensitivity of Lake Linlithgow water balance model to changes in the water budget components.
4.3. Interpretation
To assess the effect of groundwater component, which is the main objective of this paper, further analysis was carried out through a second model run without a groundwater component. The calculated water levels followed the same trend as observed lake levels, but were on average lower than the observed values. The lower calculated lake level implies that the total observed lake storage is lower than would be expected if the lake did not have groundwater inflow (Figure 16).
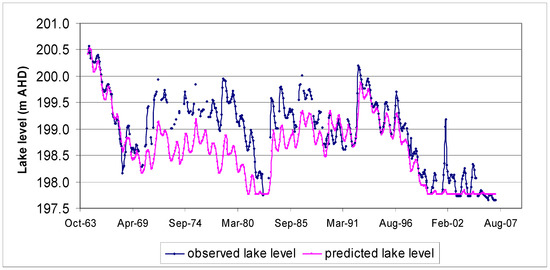
Figure 16.
Observed and simulated lake level (deactivating the groundwater node from the model).
The effect of groundwater is evident from the graph. The simulated volumetric component of the groundwater of the lake water budget is shown in Figure 17. The base flow is estimated (G = 260) (Figure 10) using the tanh cumulative surplus rainfall approach. This simplistic model seems a reliable and modest tool to see the lake–groundwater relationship at a glance and will be useful if constrained by the mass balance and reliable estimate of parameters [9,32,51]. This approach could be adopted for much wetland management. This model will give insight into the groundwater–surface water relationship and guide our future data gathering from sensitive parameters. The parameters used are small and convenient for management practice.
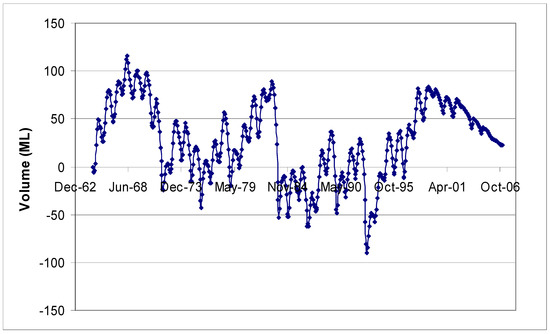
Figure 17.
Volumetric groundwater component in the Lake Linlithgow water budget.
The need for study of the interaction of lakes and groundwater stems from the fact that groundwater is commonly ignored or is the residual term in lake water. Because all variables in a lake water budget are rarely measured, it is impossible to adequately evaluate the errors or the residual.
Even if groundwater is included as part of a lake water balance study, improper placement of wells can lead to a misunderstanding of the interaction between lakes and groundwater. No matter how many wells are used to define the water table in the settings, the maps shows a gradient towards the lake, and there would be no way to detect the out-seepage that occurs. If only one or a few wells are placed near a lake, the groundwater flow system would not be adequately defined and would be subject to misinterpretation [16,55,58].
Over a long period of falling lake levels from 1968 up to the drought period 1982/3, the simulated lake levels are more than one meter lower than the observed levels due to the lack of groundwater inflow. However, there is a good match between the simulated and actual lake levels during a period of rising lake levels, indicating that the groundwater outflow from Lake Linlithgow recharging the aquifer is very small. When the groundwater component is added to the model, it accurately follows the observed levels (Figure 11).
Groundwater is an important component of the water balance of Lake Linlithgow, and its flow is influenced by the lake level. If the lake level rises, groundwater outflow and therefore lake recharge into the surrounding aquifer will increase. If the lake level decreases, groundwater discharge from the aquifer into the lake will increase. This interaction causes inertia in the lake–groundwater system, delaying reactions to external (meteorological) stresses (Figure 17). This phenomenon can be shown using the lake water balance model. If the model is run with no groundwater components, it overshoots after periods of rise or recession (Figure 16).
5. Conclusions
This paper aims at an understanding of the groundwater system in wetlands, via a case study at Lake Linlithgow, Australia.
When the model was run based on surface water balance components (via switching the “node” off, i.e., in the absence of groundwater), there was a progressive separation between observed and calculated lake levels. The calculated levels imply that the lake should accumulate more storage than is actually observed. This separation could not be attributed to systematic errors in surface runoff, precipitation, and evaporation measurements. Rather, it is an indication of subterranean water fluxes (i.e., groundwater).
The results of such analysis lead to a better understanding of the groundwater system within a lake/wetland ecosystem.
Uncertainties associated with the groundwater component of the lake water budget increase unpredictability and unreliability and further complicate the future management of wetlands. No matter how many wells are used to define the water table in the settings, the groundwater flow system would not be adequately defined and would be subject to misinterpretation. The present method gives a better way of studying surface water–groundwater interaction, which is in great demand in the current strategy for better wetland and integrated water resources management. The result underscores the need to put in place relevant adaptation mechanisms to reduce vulnerability and enhance resilience to climate change within the lake basin.
Acknowledgments
We would like to thank the anonymous reviewers. The manuscript has benefitted from the reviewers’ and editors’ comments.
Author Contributions
Y.Y. and J.W. conceived and designed the research; Y.Y. performed the research; Y.Y. and J.W. analyzed the data; B.V. contributed analysis tools; Y.Y. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dausman, A.M.; Doherty, J.; Langevin, C.D.; Dixon, J. Hypothesis testing of buoyant plume migration using a highly parameterized variable-density groundwater model. Hydrogeol. J. 2010, 18, 147–160. [Google Scholar] [CrossRef]
- Edelman, J.H. Groundwater Hydraulics of Extensive Aquifers (No. 13); International Livestock Research Institute, Wageningen University: Wageningen, The Netherlands, 1983. [Google Scholar]
- Yihdego, Y.; Drury, L. Mine water supply assessment and evaluation of the system response to the designed demand in a desert region, central Saudi Arabia. Environ. Monit. Assess. J. 2016, 188, 619. [Google Scholar] [CrossRef] [PubMed]
- Yihdego, Y.; Drury, L. Mine dewatering and impact assessment: Case of Gulf region. Environ. Monit. Assess. J. 2016, 188, 634. [Google Scholar] [CrossRef] [PubMed]
- Yihdego, Y.; Paffard, A. Predicting open mine inflow and recovery depth in the Durvuljin soum, Zavkhan Province, Mongolia. In Mine Water and the Environment; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–10. [Google Scholar]
- Yihdego, Y.; Paffard, A. Hydro-engineering solution for a sustainable groundwater management at a cross border region: Case of Lake Nyasa/Malawi basin, Tanzania. Int. J. Geo-Eng. 2016, 7, 23. [Google Scholar] [CrossRef]
- Christensen, S.; Doherty, J. Predictive error dependencies when using pilot points and singular value decomposition in groundwater model calibration. Adv. Water Resour. 2008, 31, 674–700. [Google Scholar] [CrossRef]
- Tonkin, M.; Doherty, J. Calibration-constrained Monte Carlo analysis of highly-parameterized models using subspace techniques. Water Resour. Res. 2008, 45, 12. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. Hydrogeological constraints on the hydrology of Lake Burrumbeet, southwestern Victoria, Australia. In 21st VUEESC Conference, Victorian Universities Earth and Environmental Sciences Conference; Hagerty, S.H., McKenzie, D.S., Yihdego, Y., Eds.; Abstracts No 88, 12; Geological Society of Australia: Sydney, Australia, 2007. [Google Scholar]
- Yihdego, Y. Three Dimensional Groundwater Model of the Aquifer around Lake Naivasha Area, Kenya. Master’s Thesis, Department of Water Resources, ITC, University of Twente, Enschede, The Netherlands, March 2005. [Google Scholar]
- Yihdego, Y.; Webb, J.A. Characterizing groundwater dynamics in Western Victoria, Australia using Menyanthes software. In Proceedings of the 10th Australasian Environmental Isotope Conference and 3rd Australasian Hydrogeology Research Conference, Perth, Australia, 1–3 December 2009.
- Rosenberry, D.O.; Lewandowski, J.; Meinikmann, K.; Nützmann, G. Groundwater-the disregarded component in lake water and nutrient budgets. Part 1: Effects of groundwater on hydrology. Hydrol. Process. 2015, 29, 2895–2921. [Google Scholar] [CrossRef]
- Scibek, J.; Allen, D.M.; Cannon, A.J.; Whitfield, P.H. Groundwater–surface water interaction under scenarios of climate change using a high-resolution transient groundwater model. J. Hydrol. 2007, 333, 165–181. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. Modeling of bore hydrographs to determine the impact of climate and land use change in a temperate subhumid region of southeastern Australia. Hydrogeol. J. 2011, 19, 877–887. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A.; Leahy, P. Response to Parker: Rebuttal: ENGE-D-13-00994R2 “Modelling of lake level under climate change conditions: Lake Purrumbete in south eastern Australia”. Environ. Earth Sci. J. 2016, 75, 1–4. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. Assessment of wetland hydrological dynamics in a modified catchment basin: Case of Lake Buninjon, Victoria, Australia. Water Environ. Res. J. 2017, 89, 144–154. [Google Scholar] [CrossRef] [PubMed]
- Doherty, J.; Hunt, R.J. Response to comment on “Two statistics for evaluating parameter identifiability and error reduction”. J. Hydrol. 2010, 380, 489–496. [Google Scholar] [CrossRef]
- Doherty, J.; Johnston, J.M. Methodologies for calibration and predictive analysis of a watershed model. J. Am. Water Resour. Assoc. 2003, 39, 251–265. [Google Scholar] [CrossRef]
- Yihdego, Y. Drought and Pest Management Initiatives (Book chapter 11). In Handbook of Drought and Water Scarcity (HDWS): Vol. 3: Management of Drought and Water Scarcity; Eslamian, S., Eslamian, F.A., Eds.; Francis and Taylor, CRC Group: Burlington, MA, USA, 2016. [Google Scholar]
- Yihdego, Y. Drought and Groundwater Quality in Coastal Area (Book chapter 15). In Handbook of Drought and Water Scarcity (HDWS): Vol. 2: Environmental Impacts and Analysis of Drought and Water Scarcity; Eslamian, S., Eslamian, F.A., Eds.; Francis and Taylor, CRC Group: Burlington, MA, USA, 2016. [Google Scholar]
- Lewandowski, J.; Meinikmann, K.; Nützmann, G.; Rosenberry, D.O. Groundwater–the disregarded component in lake water and nutrient budgets. Part 2: Effects of groundwater on nutrients. Hydrol. Process. 2015, 29, 2922–2955. [Google Scholar] [CrossRef]
- Shaw, G.D.; White, E.S.; Gammons, C.H. Characterizing groundwater–lake interactions and its impact on lake water quality. J. Hydrol. 2013, 492, 69–78. [Google Scholar] [CrossRef]
- Yihdego, Y.; Al-Weshah, R. Hydrocarbon assessment and prediction due to the Gulf War oil disaster, North Kuwait. J. Water Environ. Res. 2016. [Google Scholar] [CrossRef]
- Yihdego, Y.; Al-Weshah, R. Gulf war contamination assessment for optimal monitoring and remediation cost –benefit analysis, Kuwait. Environ. Earth Sci. 2016, 75, 1–11. [Google Scholar] [CrossRef]
- Gallagher, M.R.; Doherty, J. Predictive error analysis for a water resource management model. J. Hydrol. 2007, 34, 513–533. [Google Scholar] [CrossRef]
- Hunt, R.J.; Doherty, J.; Tonkin, M.J. Are models too simple? Arguments for increased parameterization. Ground Water 2007, 45, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Yihdego, Y.; Eslamian, S. Drought Management Initiatives and Objectives (Book chapter 1). In Handbook of Drought and Water Scarcity (HDWS): Vol. 3: Management of Drought and Water Scarcity; Eslamian, S., Eslamian, F.A., Eds.; Francis and Taylor, CRC Group: Burlington, MA, USA, 2016; p. 41. [Google Scholar]
- Shaw, G.D.; Mitchell, K.L.; Gammons, C.H. Estimating groundwater inflow and leakage outflow for an intermontane lake with a structurally complex geology: Georgetown Lake in Montana, USA. Hydrogeol. J. 2016, 1–15. [Google Scholar] [CrossRef]
- Skahill, B.; Doherty, J. Efficient accommodation of local minima in watershed model calibration. J. Hydrol. 2006, 329, 122–139. [Google Scholar] [CrossRef]
- Tonkin, M.; Doherty, J. A hybrid regularised inversion methodology for highly parameterized models. Water Resour. Res. 2005, 41, W10412. [Google Scholar] [CrossRef]
- Yihdego, Y. Data visualization tool as a framework for groundwater flow and transport models. In Proceedings of the International Conference on “MODFLOW and more 2013”, Translating Science into Practice; Integrated Groundwater Modelling Centre (IGWMC), Colorado School of Mines, University: Golden, CO, USA, 2013. [Google Scholar]
- Yihdego, Y.; Webb, J.A. Modelling of seasonal and long-term trends in lake salinity in south-western Victoria, Australia. J. Environ. Manag. 2012, 112, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, M.R.; Doherty, J. Parameter estimation and uncertainty analysis for a watershed model. Environ. Model. Softw. 2006, 22, 1000–1020. [Google Scholar] [CrossRef]
- Lohman, S.W. Ground-Water Hydraulics; US Government Printing Office: Washington, DC, USA, 1972; p. 70.
- Lewis, M.A.; Cheney, C.S.; ÓDochartaigh, B.E. Guide to Permeability Indices; CR/06/160N; British Geological Survey, Natural Environmental Council: London, UK, 2006. [Google Scholar]
- Post, V.; Kooi, H.; Simmons, C. Using hydraulic head measurements in variable-density ground water flow analyses. Ground Water 2007, 45, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Jakovovic, D.; Werner, A.D.; de Louw, P.G.; Post, V.E.; Morgan, L.K. Saltwater upcoming zone of influence. Adv. Water Resour. 2016, 94, 75–86. [Google Scholar] [CrossRef]
- Yihdego, Y.; Reta, G.; Becht, R. Hydrological analysis as a technical tool to support strategic and economic development: Case of Lake Navaisha, Kenya. Water Environ. J. 2016, 30, 40–48. [Google Scholar] [CrossRef]
- Yihdego, Y.; Reta, G.; Becht, R. Human impact assessment through a transient numerical modelling on The UNESCO World Heritage Site, Lake Navaisha, Kenya. Environ. Earth Sci. 2017, 76, 9. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. Validation of a model with climatic and flow scenario analysis: Case of Lake Burrumbeet in Southeastern Australia. Environ. Monit. Assess. 2016, 188, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.N.; McMahon, T.A.; Bowler, J.M. Modelling historical lake levels and recent climate change at three closed lakes, Western Victoria, Australia (c.1840–1990). J. Hydrol. 2001, 246, 159–180. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. An empirical water budget model as a tool to identify the impact of land-use change on stream flow in southeastern Australia. Water Resour. Manag. 2012, 27, 4941–4958. [Google Scholar] [CrossRef]
- James, S.C.; Doherty, J.; Eddebarh, A.A. Post-calibration uncertainty analysis: Yucca Mountain, Nevada, USA. Ground Water 2009, 47, 851–869. [Google Scholar] [CrossRef] [PubMed]
- Tonkin, M.; Doherty, J.; Moore, C. Efficient nonlinear predictive error variance analysis for highly parameterized models. Water Resour. Res. 2007, 43, 7. [Google Scholar] [CrossRef]
- Doherty, J.; Skahill, B. An advanced regularization methodology for use in watershed model calibration. J. Hydrol. 2006, 327, 564–577. [Google Scholar] [CrossRef]
- Doherty, J. Groundwater model calibration using pilot points and regularization. Ground Water 2003, 41, 170–177. [Google Scholar] [CrossRef]
- Moore, C.; Doherty, J. The cost of uniqueness in groundwater model calibration. Adv. Water Resour. 2006, 29, 605–623. [Google Scholar] [CrossRef]
- Yihdego, Y.; Becht, R. Simulation of lake–aquifer interaction at Lake Navaisha, Kenya using a three-dimensional flow model with the high conductivity technique and a DEM with bathymetry. J. Hydrol. 2013, 503, 111–122. [Google Scholar] [CrossRef]
- Yihdego, Y.; Al-Weshah, R. Engineering and environmental remediation scenarios due to leakage from the Gulf War oil spill using 3-D numerical contaminant modellings. J. Appl. Water Sci. 2016. [Google Scholar] [CrossRef]
- Bennetts, D. Hydrology, Hydrogeology and Hydro-Geochemistry of Groundwater Flow Systems within the Hamilton Basalt Plains, Western Victoria, and Their Role in Dry Land Salinisation. Ph.D. Thesis, Department of Earth Sciences, La Trobe University, Melbourne, Australia, September 2005. [Google Scholar]
- Yihdego, Y.; Webb, J.A. Use of a conceptual hydrogeological model and a time variant water budget analysis to determine controls on salinity in Lake Burrumbeet in southeast Australia. Environ. Earth Sci. 2015, 73, 1587–1600. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A.; Leahy, P. Modelling of lake level under climate change conditions: Lake Purrumbete in southeastern Australia. Environ. Earth Sci. 2015, 73, 3855–3872. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A.; Leahy, P. Modelling water and salt balances in a deep, groundwater-throughflow lake—Lake Purrumbete, southeastern Australia. Hydrol. Sci. J. 2016, 61, 186–199. [Google Scholar] [CrossRef]
- Yihdego, Y. Modelling of Lake Level and Salinity for Lake Purrumbete in Western Victoria, Australia; A Co-Operative Research Project between La Trobe University and EPA Victoria; EPA Victoria: Melbourne, Australia, 2010. [Google Scholar]
- Yihdego, Y. Modelling Bore and Stream Hydrograph and Lake Level in Relation to Climate and Land Use Change in Southwestern Victoria, Australia. Ph.D. Thesis, Faculty of Science, Technology and Engineering, Melbourne, La Trobe University, Melbourne, Australia, May 2010. [Google Scholar]
- Yihdego, Y.; Webb, J.A. Characterizing groundwater dynamics using Transfer Function-Noise and auto-regressive modelling in Western Victoria, Australia. In Proceedings of the 5th IASME/WSEAS International Conference on Water Resources, Hydraulics and Hydrology (WHH ’10), Cambridge, UK, 23–25 February 2010.
- Yihdego, Y.; Al-Weshah, R. Assessment and prediction of saline sea water transport in groundwater using using 3-D numerical modelling. Environ. Process. J. 2016. [Google Scholar] [CrossRef]
- Winter, T.C. Effects of water table configuration on seepage through lakebeds. Limnol. Oceanogr. 1981, 26, 925–934. [Google Scholar] [CrossRef]
- Yihdego, Y. Evaluation of Flow Reduction due to Hydraulic Barrier Engineering Structure: Case of Urban Area Flood, Contamination and Pollution Risk Assessment. J. Geotech. Geol. Eng. 2016, 34, 1643–1654. [Google Scholar] [CrossRef]
- Al-Weshah, R.; Yihdego, Y. Modelling of Strategically Vital Fresh Water Aquifers, Kuwait. Environ. Earth Sci. 2016, 75, 1315. [Google Scholar] [CrossRef]
- Yihdego, Y.; Danis, C.; Paffard, A. 3-D numerical groundwater flow simulation for geological discontinuities in the Unkheltseg Basin, Mongolia. Environ. Earth Sci. J. 2015, 73, 4119–4133. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A. Characterizing groundwater dynamics in Western Victoria, Australia using Menyanthes software. In Proceedings of the 10th Australasian Environmental Isotope Conference and 3rd Australasian Hydrogeology Research Conference, Perth, Australia, 1–3 December 2009.
- Yihdego, Y.; Webb, J.A. Modelling of Seasonal and Long-term Trends in Lake Salinity in Southwestern Victoria, Australia. J. Environ. Manag. 2012, 112, 149–159. [Google Scholar]
- Yihdego, Y. Engineering and enviro-management value of radius of influence estimate from mining excavation. J. Appl. Water Eng. Res. 2017. [Google Scholar] [CrossRef]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).