Abstract
Investigations of groundwater resources in order to understand aquifer system behavior are vital to the inhabitants of the Klela Basin, Mali, because groundwater is the only permanent water resource and is used for drinking water and irrigation. Due to climate change, this vital resource is being threatened. Therefore, MODFLOW was applied in this study to simulate groundwater dynamics. The aim of this study was to evaluate the impact of climate change on groundwater resources in the Klela basin using the RCP4.5 (Representative Concentration Scenario 4.5 W/m2) climate scenario. Climatological, geological, hydrogeological, hydraulic and demographic data were collected and used as model input data. Groundwater recharge was estimated to be approximately 165.3 mm/year using the EARTH (Extended model for Aquifer Recharge and soil moisture Transport through the unsaturated Hardrock) model. Recharge was then used as groundwater model input. The sandstone aquifer in the study area was simulated in steady and transient conditions. The results showed that hydraulic conductivity values varied from 1.1 to 13.9 m/day. The model was used for scenario quantification after model calibration and verification using three different piezometer data sets. The results of the simulated MODFLOW model showed a decrease in groundwater levels over time.
1. Introduction
Groundwater resources provide important sources of drinking water throughout the world, especially in developing countries where most human activities (e.g., domestic water use, small-scale irrigation, etc.) depend on groundwater. The investigated basin in Mali is an agriculture zone, growing cotton and rice during the rainy season and potatoes during the dry season. The surface area used for agriculture has been extended in the basin to assure food security for the growing population. In addition, most of the rural population uses water from traditional wells that are recharged by rainfall and dry out a few months after the recharge period. Moreover, water sustainability in the town of Sikasso’s supply system remains a challenge due to groundwater exploitation in the context of increased water demand and climate variability and change. Therefore, better understanding and management of this vital resource are the principal requirements of responsible water use. Because of the growing population and climate change, a scientific tool should be used to assess present and future difficulties related to water supply and demand in the study area. MODFLOW is one of the most popular hydrologic models in the world and can achieve the objectives of this study. MODFLOW is a modular, three-dimensional finite-difference groundwater model that was developed by the United States Geological Survey (USGS) []. It uses the groundwater flow equation, which is a combination of the continuity equation and Darcy’s law []. Over the past few years, the application of MODFLOW to describe and predict aquifer system behavior has increased significantly []. MODFLOW has been used by many authors [,,,] throughout the world to simulate groundwater dynamics; however, few studies have been conducted in West Africa, especially in Mali, where some studies [,] have predicted rainfall decreases. For example, Bricquet et al. [] showed a reduction in groundwater storage in the Bani basin (which contains several subbasins, including the Klela basin) due to decreases in rainfall and runoff. Additionally, Bokar et al. [] demonstrated that groundwater levels decreased from 2 to 15 cm per year from 1940 to 2008 in the Kolondieba catchment, a subbasin of the Bani basin. The interaction between surface water and groundwater has been the topic of many discussions [,,] in Mali, which have concluded that the river system drains the aquifer in the southern part of the country. Until now, no study has been performed in the Klela basin to confirm or refute these results or to quantify groundwater storage.
The partitioning of rainfall into groundwater (recharge) and the interaction between surface water and groundwater is unknown in the Klela basin. However, knowledge of these processes is required to facilitate water resources management in the Klela basin in the context of climate change.
Therefore, the purpose of this study is to evaluate the impact of climate change on groundwater resources in the Klela basin using the RCP4.5 climate scenario. EARTH (Extended model for Aquifer Recharge and soil moisture Transport through the unsaturated Hardrock) and PMWIN 5.3 (Processing MODFLOW for Windows) developed by Chiang and Kinzelbach [] is applied to estimate groundwater recharge and simulate groundwater behavior under steady and transient state conditions.
Study Area
The Klela basin is located in the Sikasso Region in southern Mali, with a small part located in western Burkina Faso. Situated between 5°55′58.8″ and 5°16′12″ longitude and 11°40′58.8″ and 10°59′45.6″ latitude, it covers approximately 3680 km2. The elevation of the Klela Basin decreases from south to north, from 748 m above sea level (masl; south) to 305 masl (north) (Figure 1). The main river of the area is the Lotio River, which has periodic flows and is a tributary of the Banifing, which is a tributary of the Bani River basin. The only assured water supply is groundwater, and all the inhabitants depend directly or indirectly on this resource. The minimum monthly temperature varies from 12.3 °C to 26.8 °C, the maximum temperature ranges from 28.8 °C to 39.9 °C and the average temperature is 27.4 °C (Figure 2). The climate belongs to the Soudano-Sahelian zone and is characterized by a dry season (November–May) dominated by a dry wind from the Sahara (harmattan) and a rainy season (June–October) with a wet wind from the Guinean Gulf (monsoon) []. The mean annual precipitation is approximately 1131 mm/year. The average annual potential evapotranspiration is approximately 2060 mm/year (Figure 2) based on the Blaney-Criddle method. The geology of the study area is mainly constituted by sandstone and dolerite formations (Figure 3). However, the Tabular Infra-Cambrian fractured sandstone formation is predominant. Groundwater can be found in the fractured bedrock at depths of up to 100 m. The recent formations that cover the sandstone bedrock are constituted by clay, sand and laterite, with a maximum covering thickness of 64 m.
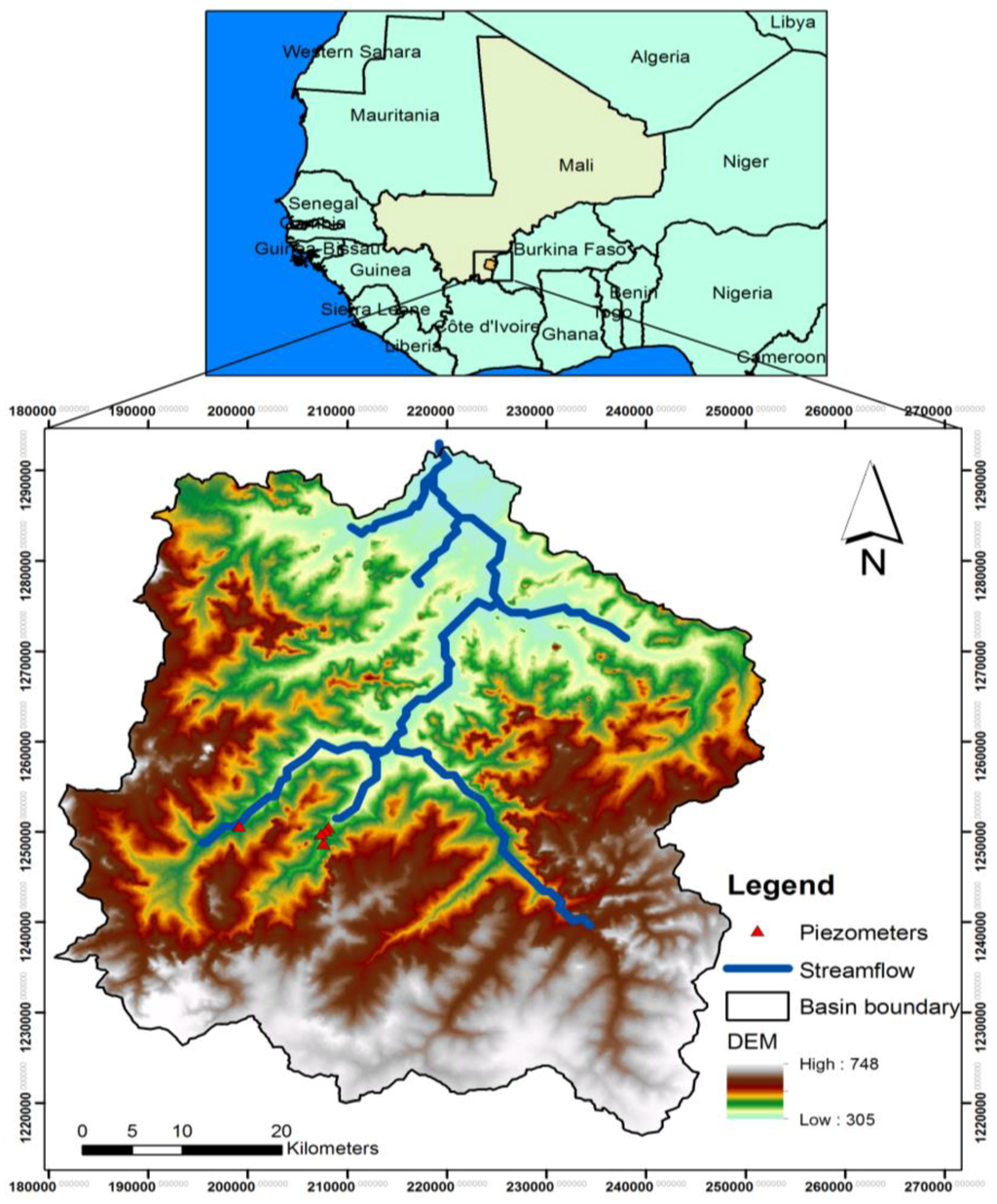
Figure 1.
Geographical location of the Klela Basin in southern Mali.
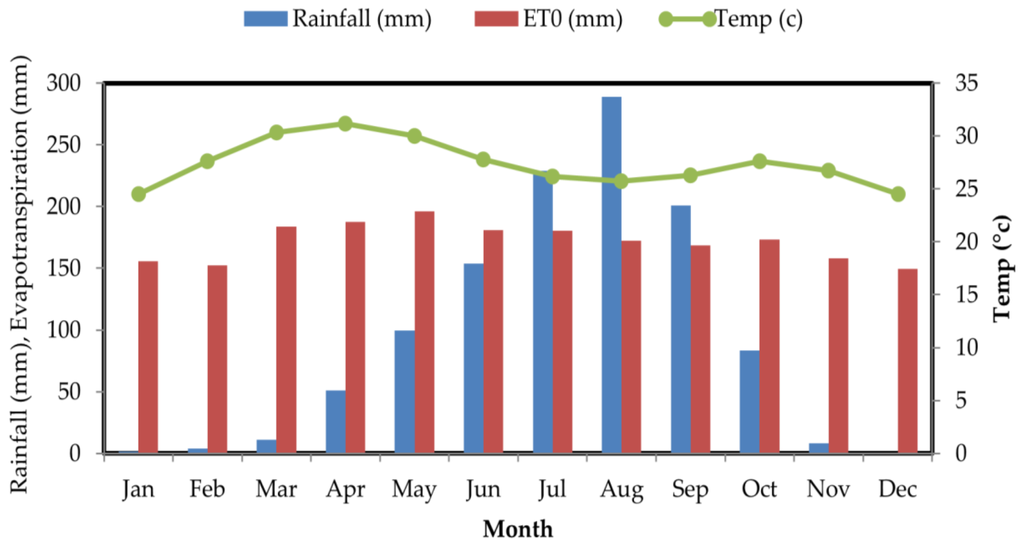
Figure 2.
Monthly average rainfall (mm) (blue bars), potential evapotranspiration ET0 (mm) (red bars) and temperature (green line) in the Klela Basin from 1970–2013 (data Source from DNM []).
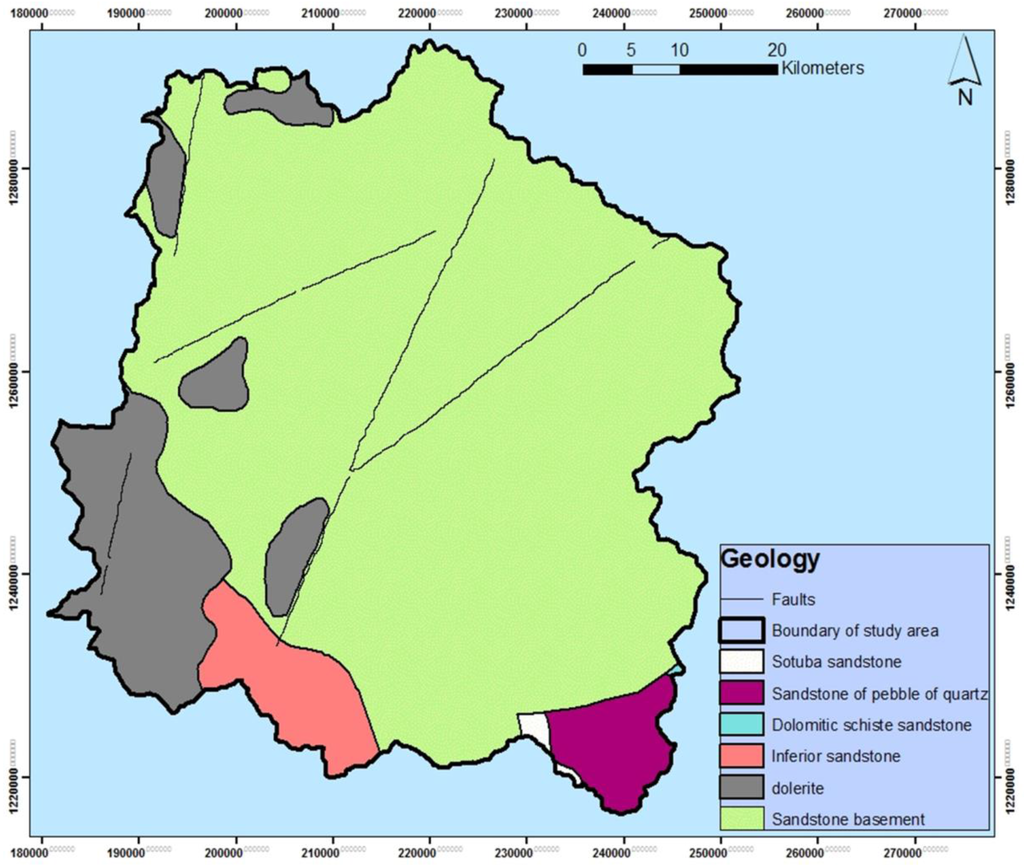
Figure 3.
Geologic map of the Klela basin (adapted from DNH []).
2. Methodology
The data and methods used in this modeling study are summarized in Figure 4.
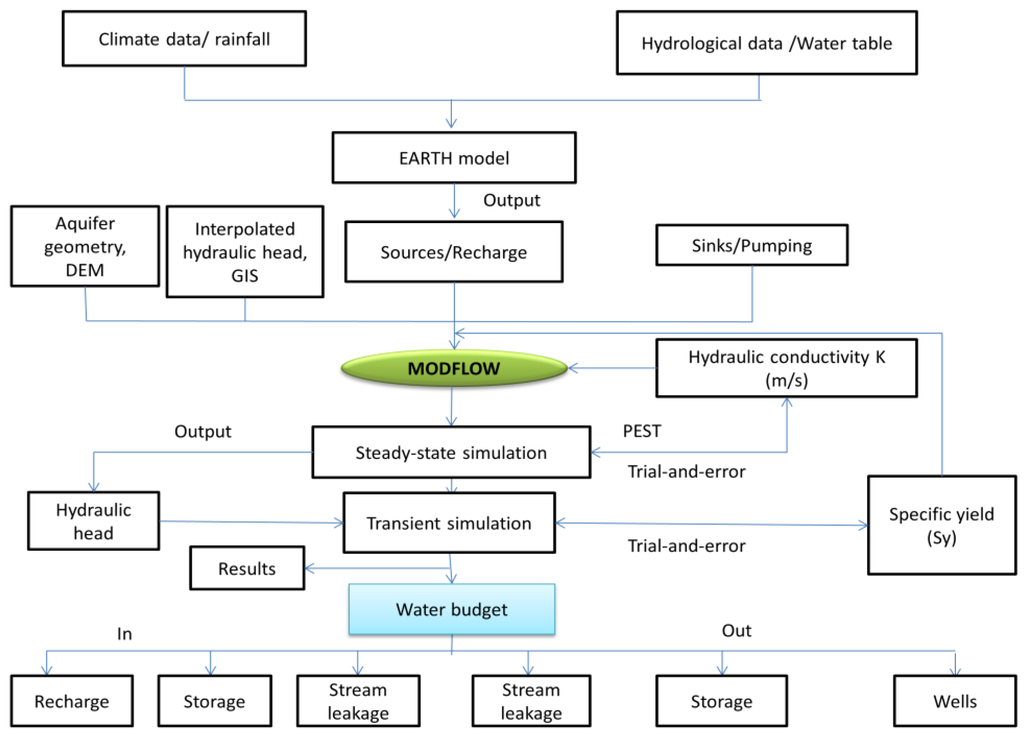
Figure 4.
Methodology and data used in this study.
The hydrogeological data (e.g., drilling logs, pumping tests, water levels, etc.) were provided by the DRH (Direction Regionale de l’Hydraulique de Sikasso), and climate data are from the DNM (Direction Nationale de la Meteorologie). GIS was used to draw all the maps and interpolate data using spatial analysis. PMWIN version 5.3 was used to model the aquifer behavior in the study area.
2.1. EARTH Model
EARTH (Extended model for Aquifer Recharge and soil moisture Transport through the unsaturated Hardrock) is a lumped parametric model that can be used to estimate groundwater recharge. It was developed by van der Lee et al. in 1989 in a project in Botswana and tested under different climate conditions []. It is a one-dimensional model designed for semi-arid areas. EARTH combines direct and indirect methods. The direct method describes the recharge process from the atmosphere to the soil zone. The indirect method uses groundwater level fluctuations as indicators of the recharge process. The direct method determines recharge using physical processes above the groundwater table, whereas the indirect method calculates the groundwater level that results from recharge estimated by the direct method []. The EARTH model has five modules: MAXIL, SOMOS, LINRES, SUST and SAFLOW (Figure 5). MAXIL, SOMOS and LINRES comprise the direct part of the model and simulate recharge in the unsaturated zone. They can be calibrated with measured time series of soil moisture data. SATFLOW is the indirect part of the model and calculates the water level from the recharge simulated by the direct part. SUST calculates the surface runoff.
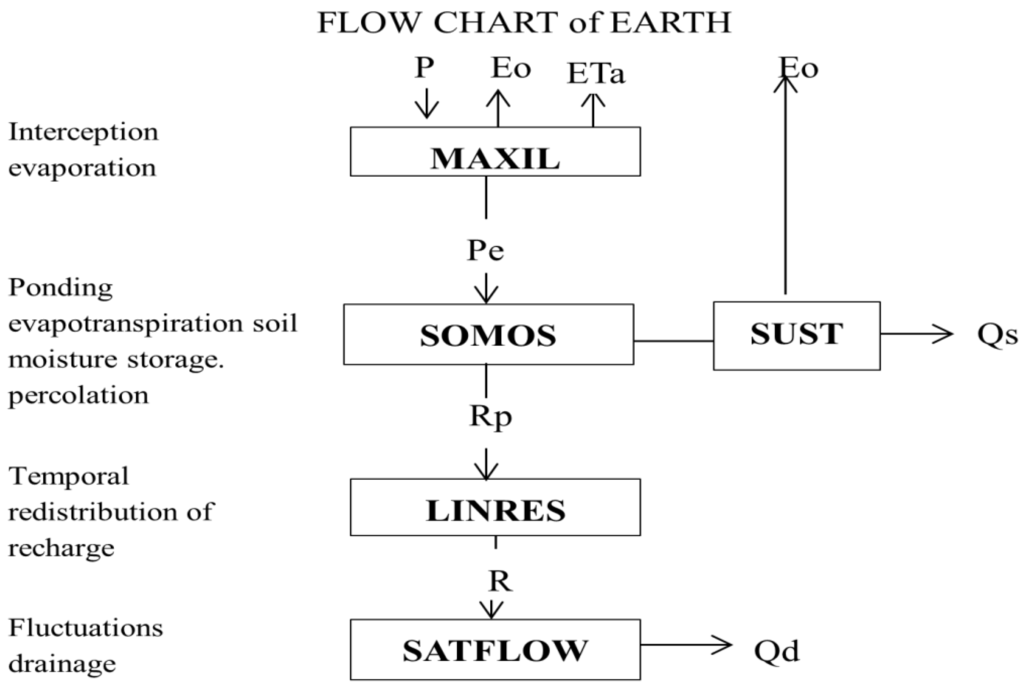
Figure 5.
Flow chart of the EARTH model (modified from []). E0 = potential evapotranspiration, ETa = actual evapotranspiration, P = precipitation, Pe = precipitation excess, Rp = percolation, R = recharge, Qs = surface runoff, and Qd = drainage runoff.
Details of the five modules are given by van der Lee and Gehrels [] and are briefly described as follows:
- MAXIL (Maximal Interception Loss) estimates the water intercepted by the Earth`s surface.
- SOMOS (Soil Moisture Storage) describes water storage in the root zone and calculates changes in soil moisture storage by removing actual evapotranspiration, percolation, evaporation and surface runoff to determine the infiltrated precipitation.
- SUST (Surface Storage) calculates ponding and runoff. It uses SUSTmax, which is the maximum ponding volume that can be stored at the surface. If the amount of ponding is greater than SUSTmax, then runoff occurs.
- LINRES (Linear Reservoir Routing) redistributes percolation (output of SOMOS) over time in the unsaturated hard rock or soil beneath the root zone using the parametric transfer function.
- SATFLOW (Saturated Flow) is the last part of the EARTH model. It is a simple one-dimensional parametric model that uses the outputs from the previous modules. SATFLOW calculates the groundwater level using the recharge estimated by the direct part of the model.
A general mathematical explanation of the EARTH model derived from the equation of de Vries 1974 cited in [] is given by [], as follows:
where ∂h/∂t is the change in water level head during one month (m/month), h is groundwater level (m), DR is the drainage resistance (a lumped, site-specific parameter), R is the recharge (m/month) and S is the specific yield.
The numerical solution of Equation (1) (linear transfer function) yields Equation (2):
where DR = drainage resistance (L2/βT), L = length of flow path, β = 2 for radial flow or β = 4 for parallel flow and T = transmissivity.
Monthly observed groundwater levels from two piezometers and rainfall data were used as model inputs. Groundwater levels collected during two years (2012–2013) at wells were used for calibration.
2.2. Groundwater Model
In MODLFOW, the three-dimensional movement of groundwater with constant density through porous media is described by the following partial-differential equation []:
where Kxx, Kyy, and Kzz are of the hydraulic conductivities in the x-, y- and z-directions (LT−1); h is potentiometric head (L); w is a volumetric flux per unit volume and represents sources and/or sinks of water (T−1); Ss is the specific storage of the porous material (L−1); and t is time (T).
2.2.1. Spatial Discretization
In numerical groundwater modeling, an aquifer system is replaced by a discretized domain consisting of an array of nodes and associated finite difference blocks (cells). In PMWIN, the model domain is divided into a rectangular mesh comprising columns, rows and layers [].
In this study, the model area was discretized into 239 columns and 256 rows, resulting in a total grid cell number of 61,184, with a grid size of 300 m × 300 m, taking into account the aquifer extension and hydrogeological data availability. The total number of active grid cells describing the active model domain was 40,992. The aquifer of the study area was modeled under an unconfined condition represented by a single numerical layer.
2.2.2. Aquifer Geometry
The aquifer geometry step establishes the top and bottom of an aquifer. Determination of aquifer geometry is critical in numerical modeling because it influences model calibration results []. Drilling log data and an SRTM-based Digital Elevation Model (DEM) from HydroSHED.org were used to estimate the top and bottom of the aquifer and aquifer thickness in the study area. The DEM was used as the aquifer top and the aquifer thickness was arbitrarily set to 300 m.
A scatter plot of surface elevation vs water table (Figure 6) shows that in most wells, the water table is up to 20 m below ground level. This assumes a possible strong interaction between groundwater and surface water bodies within the basin.
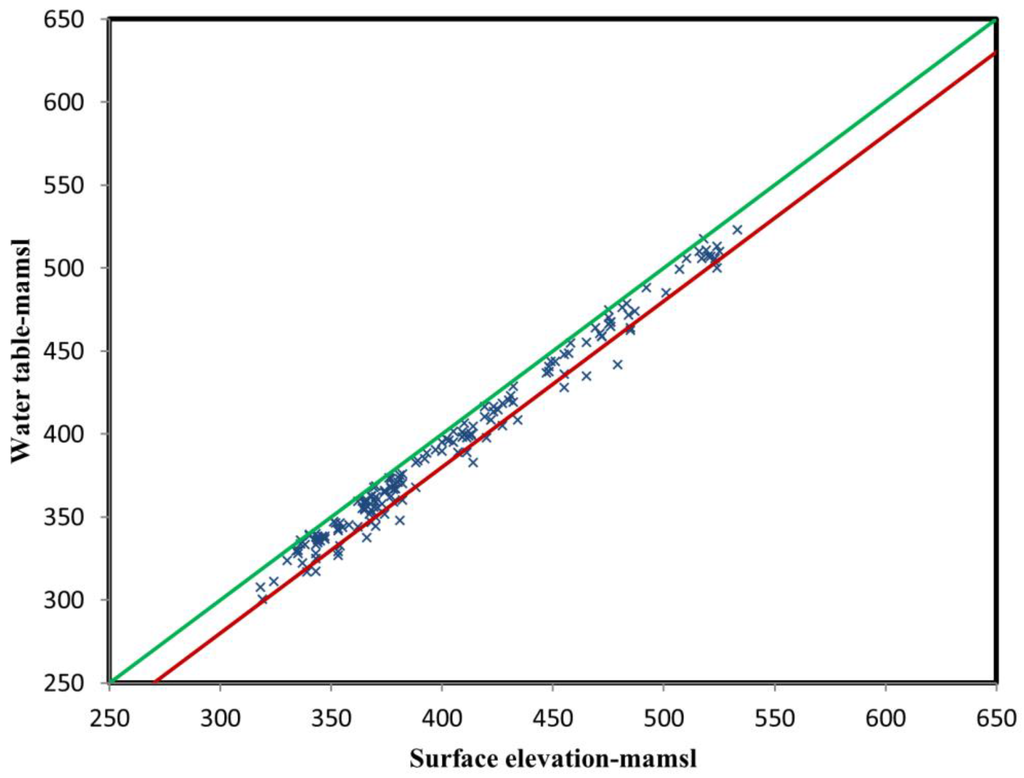
Figure 6.
Scatter plot between surface elevation and water table. The blue stars are water table field data, the green line represents surface elevation and the red line corresponds to surface elevation minus 20 m.
2.2.3. Aquifer Properties
The hydraulic properties of the aquifer, including transmissivity, hydraulic conductivity and storativity, determine water movement through the aquifer as well as storage in the aquifer. In this study, the horizontal hydraulic conductivity value was calibrated until a good correlation between simulated and observed heads was obtained. For this reason, the model domain was divided into six hydraulic conductivity zones.
Storativity data were not available in the study area. Therefore, specific yield data were estimated using the Cooper-Jacob method [] and used for transient calibration.
2.2.4. Boundary Conditions
Boundary conditions specify how an aquifer interacts with the environment outside the model domain []. Selection of boundary conditions is a key step in model design because they significantly control flow patterns [,]. Because there is not enough hydrogeological information in the study area, the topographical divide was considered a no-flow boundary condition. Thus, there was no hydrogeological interaction between the aquifer inside and outside the basin. Drainage of the basin was limited to groundwater–surface water interaction.
2.2.5. Initial Hydraulic Head
Historical water level data from more than 100 boreholes and data interpolated using the Kriging method were assigned to the model as initial hydraulic heads in the steady-state simulation. The head distribution computed using the calibrated steady-state simulation was used as the starting head distribution in the transient simulation.
2.2.6. Groundwater Sources/Sinks
As previously explained, the average recharge value (0.00044 m/day) estimated by the EARTH model was assigned to the entire model domain.
Groundwater abstraction was based on household (population and livestock) water consumption and irrigation water needs from pumping wells.
2.2.7. Streamflow Routing
In this study, the streamflow-routing package [] was used to simulate the exchange of fluxes (sources and sinks) between groundwater and surface water. The Streamflow-Routing package is designed to account for the amount of flow in streams and to simulate the interactions between surface streams and groundwater []. This package requires parameters such as streambed hydraulic conductance, elevation of the streambed top, elevation of the streambed bottom, width of the stream channel, slope of the stream channel, manning`s roughness coefficient, etc. For more details, see [].
In MODFLOW, the flow from streams to an aquifer (losing stream) or from an aquifer to streams (gaining stream) is calculated depending on the groundwater and streamwater tables. When groundwater table is above the streamwater table, the volumetric flux between streams and an aquifer is calculated using Equation (4) []:
where (L3/T) is the volumetric flux, (L2/T) is streambed hydraulic conductance, (L/T) is hydraulic conductivity, (L) is the length of the river within a cell, (L) is the width of the stream, (L) is the thickness of the streambed, (L) is the head in the stream and (L) is the groundwater head.
When the groundwater table h is below the elevation of the streambed bottom, the volumetric infiltration flux from the river to the aquifer is calculated using Equation (5).
The value of was determined to be 500 m2/day. The hydraulic conductivity of the streambed is unknown; therefore, it was set to 0.5 m/day based on the dominant soil material in the study area. The length L within the cell is 300 m, the width is 10 m, and the streambed thickness is 3 m.
3. Results and Discussion
3.1. EARTH Model
The calibrated results in both piezometers are shown in Figure 7. The correlation coefficients (R2) exhibit a good correlation between simulated and observed groundwater levels. A trial and error calibration process was performed as follows. First, the specific yield was fixed and the other parameters, such as drainage resistance and percentage of rainfall (%R), were adjusted to obtain the best estimation between the observed and simulated groundwater levels (Table 1). To evaluate the model quality, three efficiency criteria were used, namely, the correlation coefficient, root mean square error (RMSE) and Nash-Sutcliffe coefficient (Table 2).
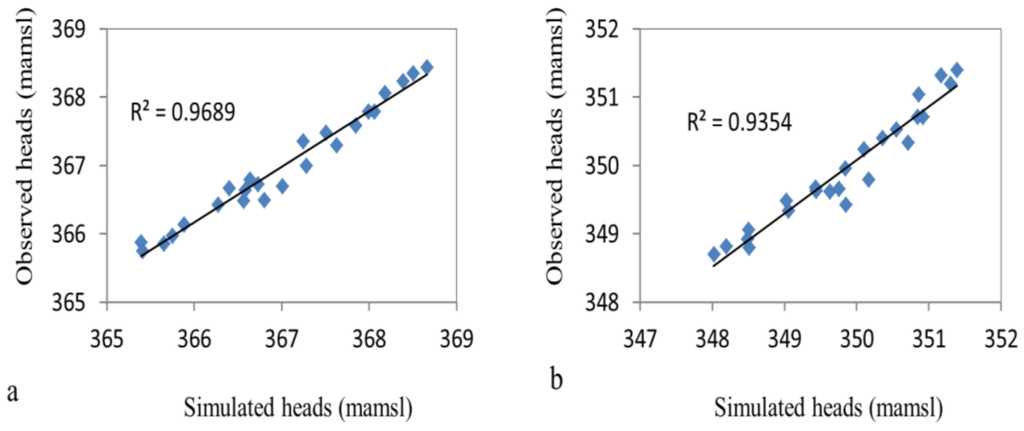
Figure 7.
Correlation between observed and simulated groundwater levels in meters above mean sea level (mamsl) at (a) piezometer F7 and (b) piezometer F15.

Table 1.
The values used to calibrate the model (%R: Percentage of rainfall).

Table 2.
EARTH model performance evaluation (R2: Correlation coefficient; RMSE: Root mean square error; Nr: Nash-Sutcliffe efficiency).
3.2. MODFLOW
3.2.1. Calibration
During the calibration process, model input parameters are changed so that the model output matches measured values []. Model calibration can be performed under steady-state and transient conditions. In this study, a two-step procedure was applied. In the first step, a steady-state simulation was used to analyze the system and generate consistent initial conditions for the dynamic simulation, which are required to perform the climate change impact study.
3.2.2. Steady-State Simulation
Mean water table data collected by the DRH Sikasso in 1985 (Direction Regionale de l`Hydraulique de Sikasso) and data measured in the field in 12 boreholes in 2014 were used to calibrate the steady-state simulation model. This calibration was first performed via a trial-and-error procedure. Then, the output was optimized using the PEST code integrated in PMWIN. The model performance yielded R2 = 0.98, RMSE = 5.67, and Nr = 0.86, exhibiting a good calibration. The scatter plot comparison between simulated and observed groundwater levels is shown in Figure 8. The output heads generated by the model (Figure 9) were used as initial conditions in the transient simulation. The calibration result show that hydraulic conductivity varies from 1.1 m/day to 13.9 m/day.
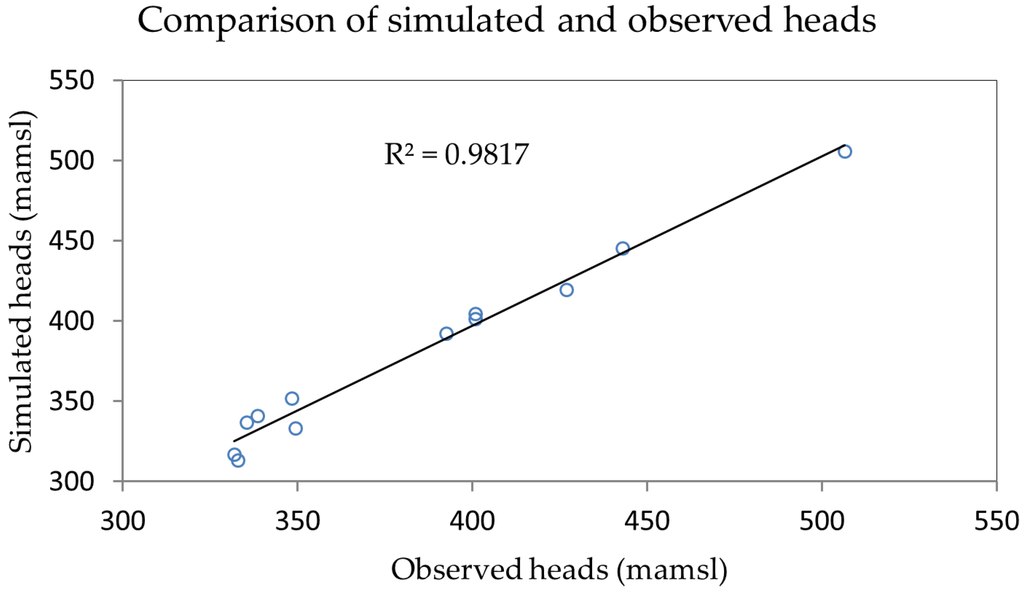
Figure 8.
Simulated and observed hydraulic heads in meters above mean sea level based on the steady-state calibration in the Klela basin.
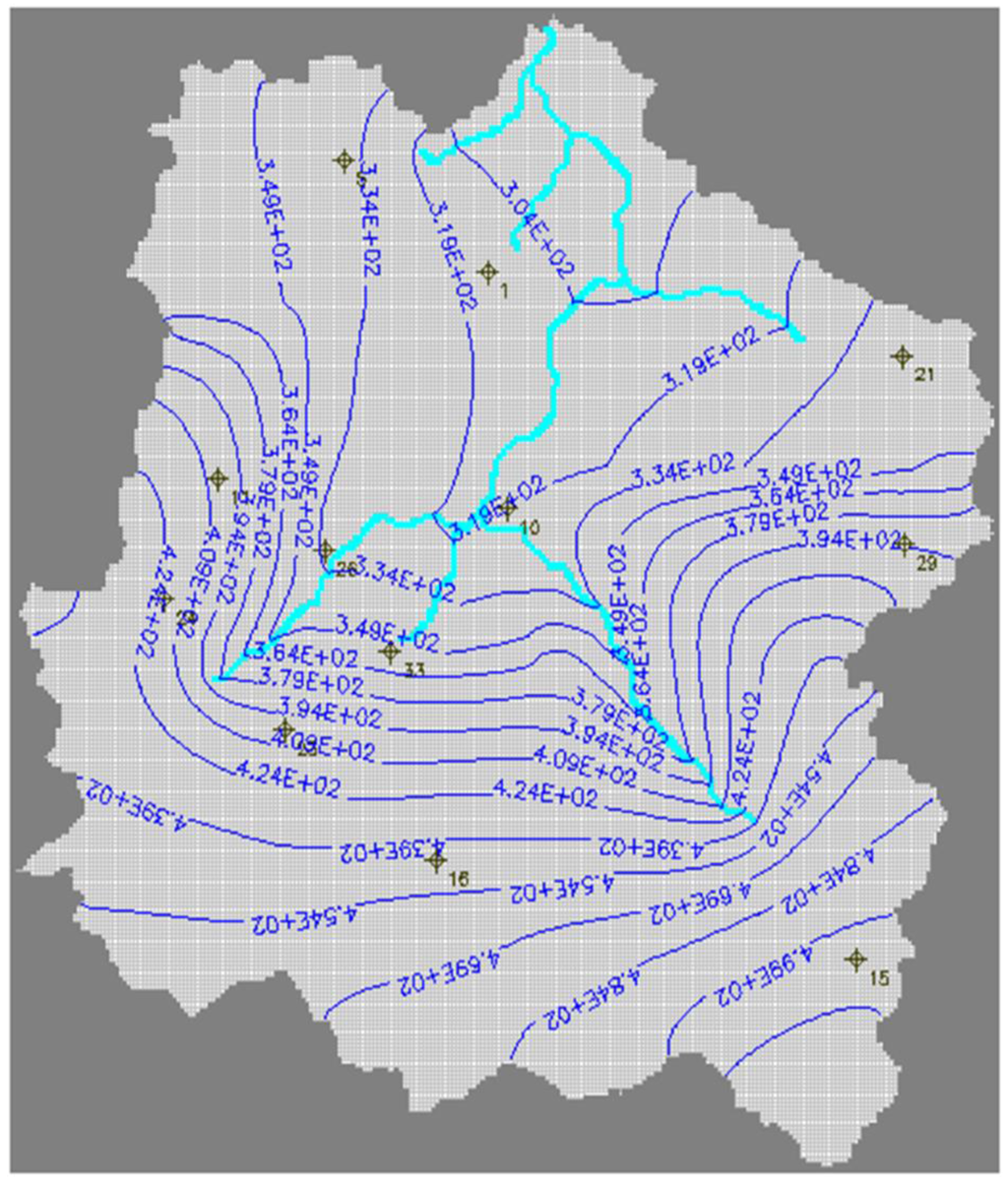
Figure 9.
Calculated hydraulic heads (mamsl) in the steady-state simulation, with borehole locations used to calibrate the model.
3.2.3. Transient Simulation
Only the trial and error method was used in the transient simulation due to technical problems with PEST. The groundwater level of the steady-state simulation was used as the initial hydraulic head in the transient simulation (Figure 9). For the transient calculations, the streamflow-routing package was used to simulate the interactions between streams and groundwater. In the same manner, sources (recharge) and sinks (wells) were introduced into the model. Specific yield was set to 0.06 for the whole model domain.
The model was run from November 2010 to November 2014 (48 months). Therefore, the simulation time was divided into 48 stress periods (with 32 dry and 16 wet periods), and each stress period represents one month. The length of a stress period was divided into days, resulting in total time steps over 48 months and a total simulation time of 1,460 days.
Mean monthly groundwater table data from three piezometers (F7, F15 and F18) were used to calibrate the model. In total, five piezometers were monitored weekly in the study area, but only three were chosen for modeling purposes. This choice was based on the data quality and data length. The quality of the calibration results is shown in Figure 10. Four efficiency criteria (Mean Absolute Error (MAE), Root Mean Square Error (RMSE), the Nash-Sutcliffe coefficient (E) and the Correlation Coefficient (R2)) (Table 3) were used to evaluate the model accuracy. The model efficiency results reflect an acceptable model calibration. However, F7 is not as well simulated as the others.
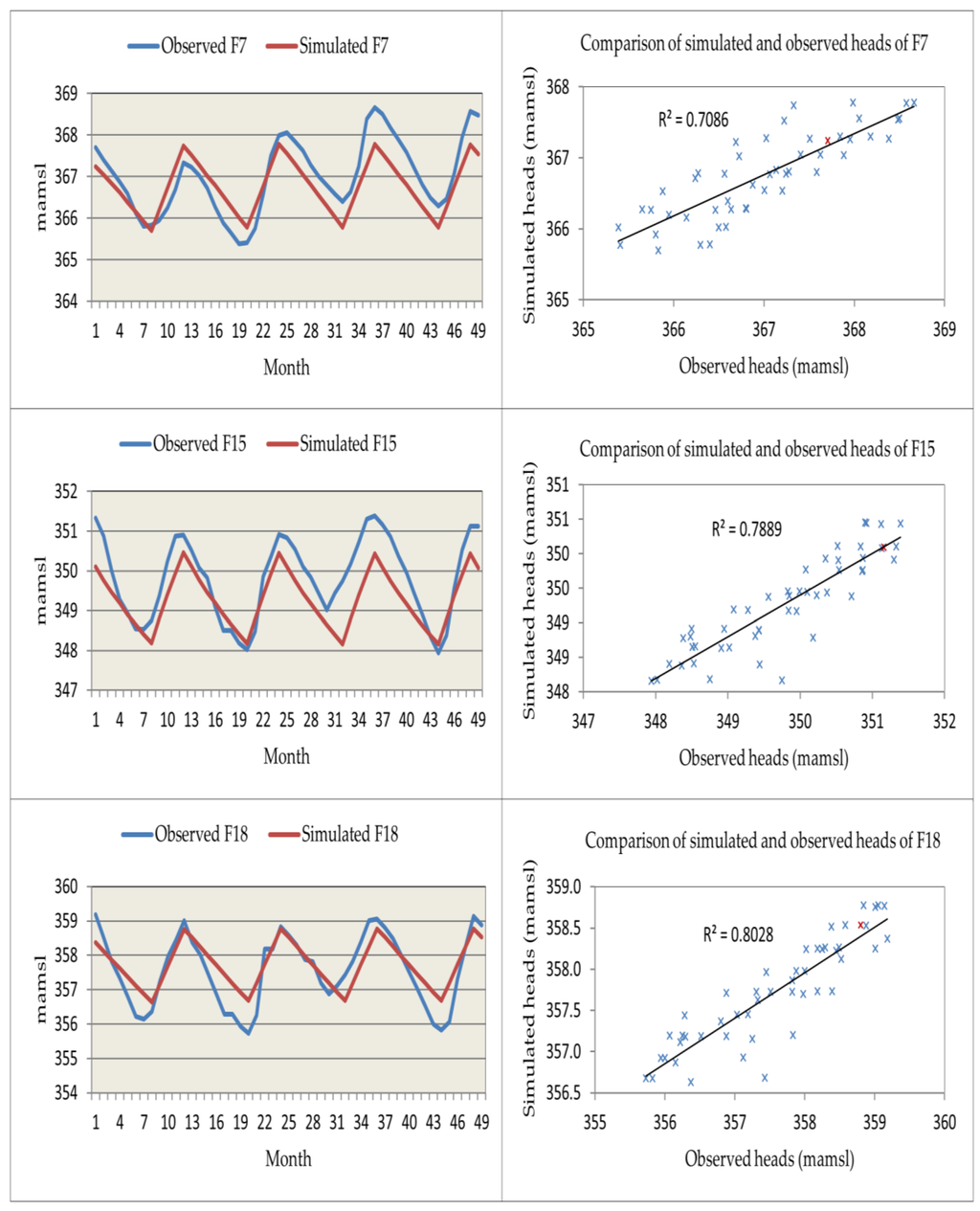
Figure 10.
Simulated and observed heads during the transient calibration in the Klela basin from November 2010-November 2014.

Table 3.
Summary of calibration errors in the transient simulation (MAE: Mean Absolute Error; RMSE: Root Mean Square Error; E: Nash-Sutcliffe coefficient and R2: Correlation Coefficient).
3.2.4. Water Budget
One of the best ways to assess model simulation quality is by analyzing the water budget. Although a good water balance cannot guarantee a good simulation, a bad water balance indicates problems in the model []. In this study, the percentage discrepancy in all the stress periods of the model is nearly zero. Thus, the model equations have been correctly solved []. The average annual water budget is summarized in Table 4.

Table 4.
Mean annual groundwater budget in m3/year in the Klela basin from November 2010 to November 2014.
Because the boundary condition is a no flow boundary, the only water source entering the aquifer is recharge. The annual recharge is slightly greater than groundwater seepage (Table 4), i.e., the amount of water that is entering the aquifer is almost the same as the amount exiting the aquifer and entering surrounding streams, which are the discharge points of the study area. According to the boundary condition, groundwater can leave the catchment only via the stream interaction. Inflow from the stream is calculated from the interaction between surface water and groundwater throughout the river system. The mean annual water budget shows that groundwater storage is slightly decreasing by 39,169,133 m3/year (approximately 10.6 mm/year) (calculated from Table 4).
The seasonal recharge from July to October was constant and represented the important water inflow entering the aquifer. The stream leakage that is leaving the aquifer and entering streams decreases during the dry season and increases during the rainy season (Figure 11). Figure 12 shows that during the dry season, groundwater storage decreases. It then increases during the rainy season. The maximum value of storage occurs in November.
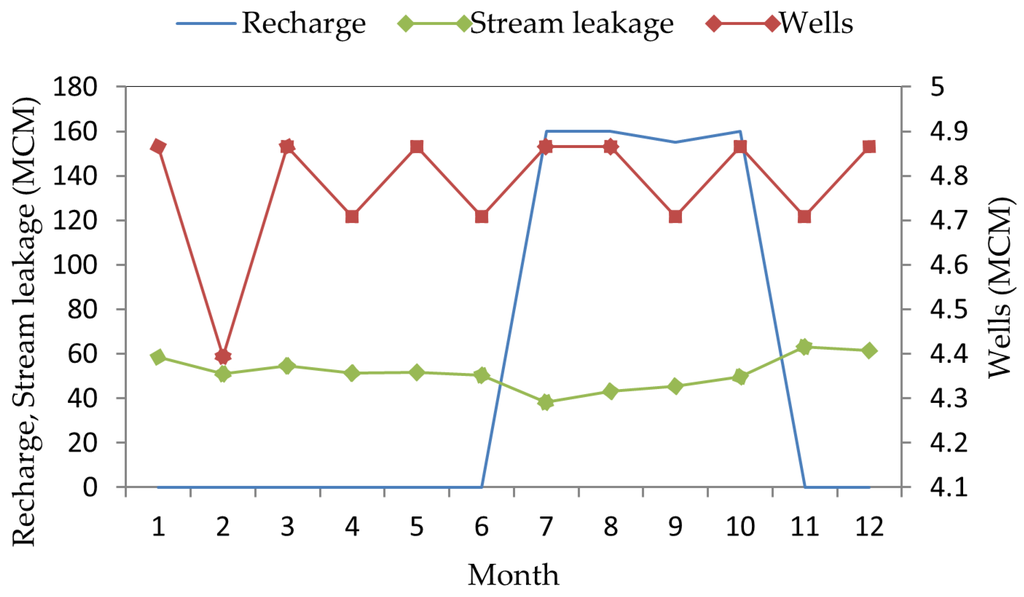
Figure 11.
Monthly average water budget in the Klela Basin in Mm³/month.
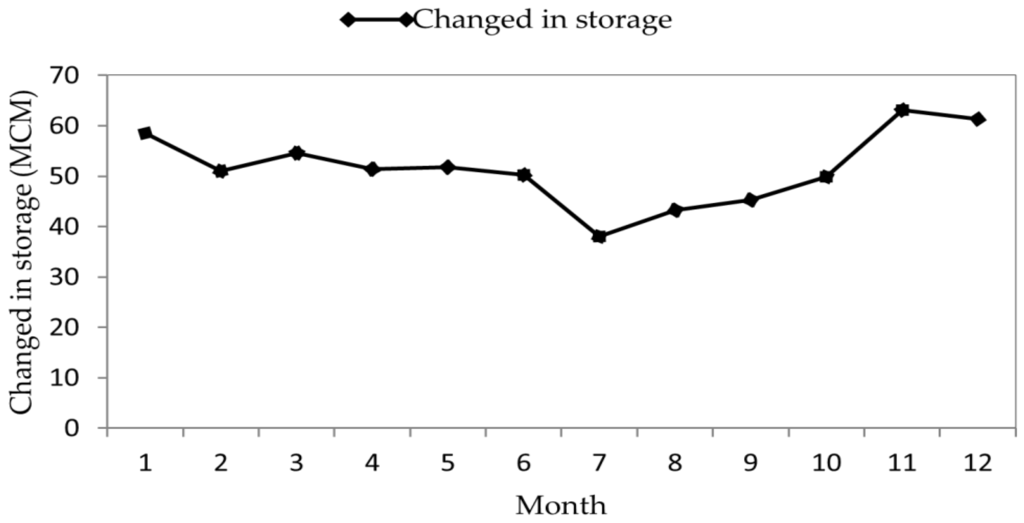
Figure 12.
Monthly change in groundwater storage (Mm3/month) in the Klela Basin.
3.2.5. Scenario Quantification
One of the most important objectives of our groundwater modeling study is to use the scenario data to predict the future behavior of the aquifer system. Thus, the model was used to quantify groundwater levels considering scenario data after model calibration and verification using three different piezometer data sets.
Monthly precipitation data from the RCP4.5 (Representative Concentration Scenario 4.5 W/m2) scenario were taken from the GCM ECHAM, downscaled to a 0.44° resolution by the Swedish Meteorological Service (Sveriges Meteorologiska och Hydrologiska Institute, SMHI) and provided by the CORDEX (Coordinated Regional Climate Downscaling Experiment) initiative. They were used to calculate the groundwater recharge (Figure 13), which was used as model input to quantify future groundwater levels in the Klela basin from June 2010 to November 2050. RCP4.5 is an intermediate pathway and a stabilization scenario based on the assumption that all countries around the world implement emissions mitigation policies [,].
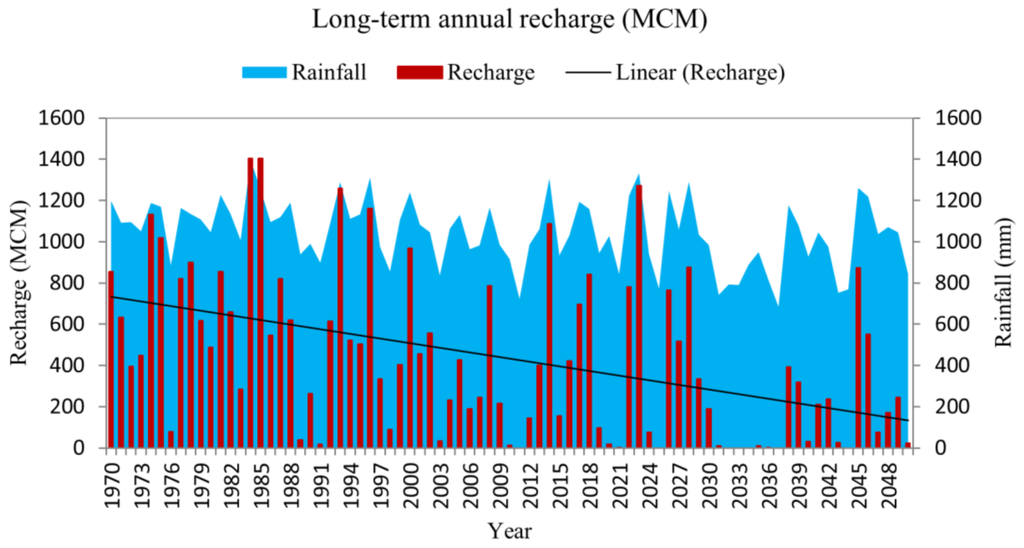
Figure 13.
Long-term groundwater recharge in million cubic meters (MCM) calculated using historical and future climate data from the RCP4.5 scenario based on the Thornthwaite Monthly Water Balance and rainfall (mm) from 1970 to 2050.
The Thornthwaite Monthly Water Balance model [], which is based on monthly temperature and rainfall data, was used for this recharge estimation. The model was calibrated to fit the groundwater recharge previously simulated using EARTH. To calibrate this model, direct runoff was set to zero because local scale surface runoff infiltrates on the way to the river system. There is no direct runoff contribution to the discharge of the basin. The soil moisture storage capacity was calibrated to be 375 mm by comparing the groundwater recharge of the two models (EARTH and Thornthwaite). All other parameters were unchanged. More details on this model can be found in []. After calibration, the model was applied to simulate groundwater recharge in the past (1970–2010) and the future (2010–2050). The overall result shows that recharge decreases from 1970 to 2050 and severe droughts occur from 2030 to 2037 (Figure 13).
The results of the simulated MODFLOW model reveal a decrease in groundwater level (GWL) over time (Figure 14). From June 2010 to November 2050, GWL decreases from 365 mamsl to 348 mamsl, or to approximately 17 m, in piezometer F7. During the same period, F18 decreases from 356 mamsl to 338 mamsl, or approximately 18 m. F15 decreases from 348 mamsl to 336 mamsl, or approximately 11 m. The overall mean of all the piezometer drops was approximately 15 m. Furthermore, an important decline in groundwater storage in the 2030s was modeled in all the piezometers considered in this study. Groundwater level reductions may intensify if water extraction increases over time.
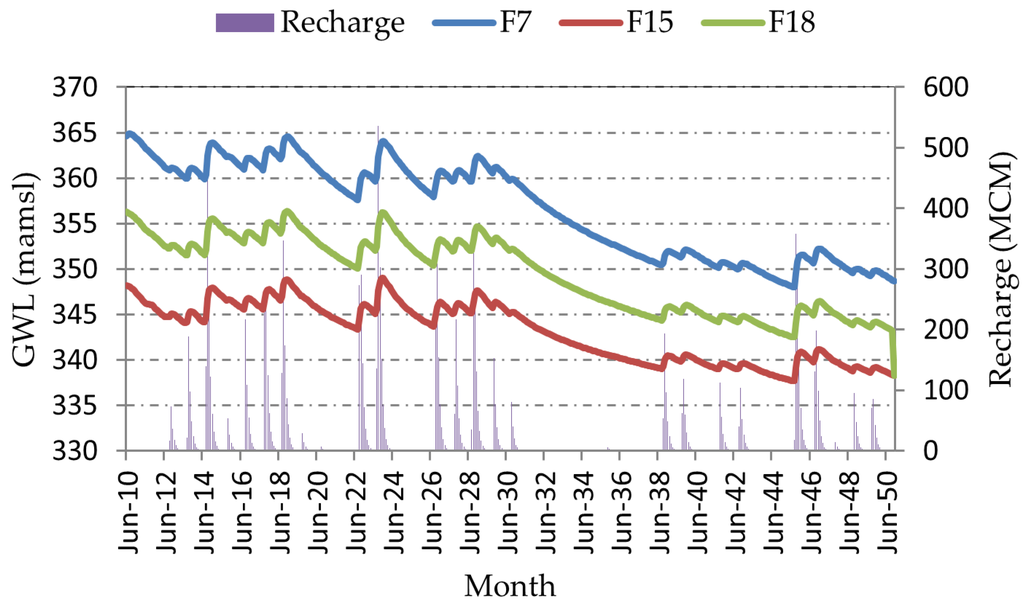
Figure 14.
Long-term monthly groundwater level in meters above mean sea level and groundwater recharge (MCM) in the Klela basin calculated using RCP4.5 climate data from June 2010 to November 2050.
Comparing the results of the EARTH model in this study to others carried out throughout the world in arid and semi-arid areas, the results are reasonably similar. For example, Usher et al. [] applied the EARTH model in a fractured sandstone aquifer in South Africa (Kalkveld area) and obtained a recharge rate of 7.4% of the mean annual precipitation of 559 mm. In a similar study, Baalousha [] applied the same model in Palestine in calcareous sandstone and sand aquifers and computed the recharge to be 36.95% of the average annual rainfall of 321 mm. Values between 7.2% and 26.5% of mean annual rainfall were also noted by Wang et.al. [] in China in unsaturated sand, with rainfall ranging from 511 to 557 mm. No previous studies have been conducted in the Klela basin using the EARTH model; however, Henry [] applied the HELP (Hydrologic Evaluation of Landfill Performance) model in southern Mali, including the Klela basin, and obtained an annual recharge of 12.6% of the mean rainfall of 1049 mm.
Regarding the MODFLOW results, despite a lack of hydrogeological data, they appear to be acceptable based on the model performance evaluation results. One of the most important uncertainties in this modeling is the establishment of boundary conditions. In this study, the boundary conditions were set as no flow boundaries. In reality, this is very difficult to prove. For example, Belay [] applied the PMWIN model to establish a water balance for Lake Beseka in Ethiopia and concluded that the choice of boundary conditions has a larger effect on the dynamics than does precipitation. Therefore, neglecting lateral outflow in groundwater modeling may affect the water balance.
4. Conclusions and Recommendations
The behavior of groundwater in the Klela basin has been evaluated in the context of climate change. This evaluation was performed using the RCP4.5 scenario data and applying the groundwater model MODFLOW and the Thornthwaite model for groundwater recharge. In this scenario, groundwater storage will decrease by approximately 10.6 mm/year. Furthermore, hydraulic heads generated by the model displayed a reduced groundwater level, increasing groundwater availability stresses in areas where agriculture is the main activity. By considering the scenario analysis in which the groundwater recharge decreases significantly compared to past recharge, the reduction of groundwater storage is important, especially in the 2030s, when severe drought events are simulated due to climate change effects. These events threaten access to groundwater for irrigation, agriculture and domestic use.
Groundwater recharge, the most important parameter in groundwater modeling, calculated using the EARTH model could have been over- or underestimated in some areas of the basin because the piezometers were not spatially distributed in a way that adequately allowed determination of spatial recharge patterns. Moreover, the true boundary of the basin was not known, potentially increasing the uncertainties in the results of this study. Despite these shortcomings, the results are reliable and can serve as a basis for watershed management.
In conclusion, a focus should be placed on determination of the hydrogeological situation in future studies. More piezometers should be implemented in the Klela basin to permit permanent monitoring of groundwater resources in the context of global change.
This study also shows that MODFLOW, which is widely used to model groundwater resources, can be applied in the Klela basin to quantify the influence of climate change on groundwater resources and can support water resources management.
Acknowledgments
This work was funded by the German Federal Ministry of Education and Research (BMBF). It is part of the WASCAL (West African Science Service Center on Climate Change and Adapted Land Use) project, which is available online at www.wascal.org. The authors thank all the National Directions in Mali for providing hydrological and climate data in the DRH of Sikasso, DNM. The authors also want to thank Wolfgang Kinzelbach and Lamine Baba Sy for helping to understand the PMWIN software.
Author Contributions
Adama Toure was responsible for this current research article in the framework of his Ph.D. program and initially wrote the manuscript. Bernd Diekkrüger directed the study by helping to interpret the results and improving the quality of the manuscript. Adama Mariko helped collect field data and correct the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McDonald, M.G.; Harbaugh, A.W. A modular three-dimensional finite-difference groundwater flow model. In Techniques of Water-Resources Investigations; Book 6, Chapter A1; U.S. Geological Survey: Reston, VA, USA, 1988; p. 586. [Google Scholar]
- Council, G.W. A Lake Package for MODFLOW (LAK2), Documentation and User’s Manual Version 2.2; HSI GEOTRANS, A Tetra Tech Company: Pasadena, CA, USA, 1999. [Google Scholar]
- AL-Fatlawi, A.N. The application of the mathematical model (MODFLOW) to simulate the behavior of groundwater flow in Umm Er Radhuma unconfined aquifer. Euphrates J. Agric. Sci. 2011, 3, 1–16. [Google Scholar]
- Saatsaz, M.; Chitsazan, M.; Eslamian, S.; Sulaiman, W.N.A. The application of groundwater modelling to simulate the behaviour of groundwater resources in the Ramhormooz Aquifer, Iran. Int. J. Water 2011, 6, 29–42. [Google Scholar] [CrossRef]
- Valerio, A.M. Modeling Groundwater-Surface Water Interactions in an Operational Setting by Linking Riverware with MODFLOW. Ph.D. Thesis, University of Colorado, Fort Collins, CO, USA, 2008. [Google Scholar]
- Banning, R.O.B. Analysis of the Groundwater/Surface Water Interactions in the Arikaree River Basin of Eastern Colorado. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2010. [Google Scholar]
- Sehatzadeh, M. Groundwater Modelling in the Chikwawa district, lower Shire area of southern Malawi. Master’s Thesis, University of Oslo, Oslo, Norway, 2011. [Google Scholar]
- Taylor, C.M.; Lambin, E.F.; Stephenne, N.; Harding, R.J.; Essery, R.L.H. The Influence of Land Use Change on Climate in the Sahel. J. Clim. 2002, 15, 3615–3629. [Google Scholar] [CrossRef]
- Funk, C.; Rowland, J.; Adoum, A.; Eilerts, G.; White, L. A Climate Trend Analysis of Mali. Available online: http://pubs.usgs.gov/fs/2012/3105/fs2012-3105.pdf (accessed on 27 November 2015).
- Bricquet, J.P.; Bamba, F.; Mahe, G.; Toure, M.; Olivry, J.C. Évolution récente des ressources en eau de l’Afrique atlantique. Rev Sci Eau. 1997. (In French) [Google Scholar] [CrossRef]
- Bokar, H.; Mariko, A.; Bamba, F.; Diallo, D.; Kamagaté, B.; Dao, A. Impact Of Climate Variability On Groundwater Resources in Kolondieba Catchment Basin, Sudanese Climate Zone in Mali. Int. J. Eng. Res. Appl. 2012, 2, 1201–1210. [Google Scholar]
- Mahe, G. Surface/groundwater interactions in the Bani and Nakambe rivers, tributaries of the Niger and Volta basins, West Africa. Hydrol. Sci. J. 2009, 54, 704–712. [Google Scholar] [CrossRef]
- Mahé, G.; Olivry, J.C.; Dessouassi, R.; Orange, D.; Bamba, F.; Servat, E. Relations eaux de surface-eaux souterraines d’une rivière tropicale au Mali. Sci Terre Planetes. 2000, 330, 689–692. (In French) [Google Scholar] [CrossRef]
- WWAP. Rapport national sur la mise en valeur des ressources en eau: Mali. 2006. Available online: http://unesdoc.unesco.org/images/0014/001472/147267f.pdf (accessed on 27 November 2015). (In French)
- Chiang, W.-H.; Kinzelbach, W. Processing Modflow A Simulation System for Modeling Groundwater Flow and Pollution. 1998. Available online: https://www.researchgate.net/publication/238774706_Processing_MODFLOWa_Simulation_System_for_Modelling_Groundwater_Flow_and_Pollution (accessed on 27 November 2015).
- USAID. Plan de sécurité alimentaire commune rurale de Klela. 2006. Available online: http://fsg.afre.msu.edu/mali_fd_strtgy/plans/sikasso/sikasso/psa_klela.pdf (accessed on 27 November 2015). (In French)
- Direction Nationale de la Meteorologie du Mali. Departement de gestion des donnees. 2014. Available online: http://www.linguee.com/french-english/translation/direction+nationale+de+la+m%C3%A9t%C3%A9orologie.html (accessed on 27 November 2015). (In French)
- Direction Nationale de l`Hydraulique du Mali. Projet Mali Sud II. Bibliotheque. 1987. Available online: http://documentation.2ie-edu.org/cdi2ie/opac_css/index.php?lvl=notice_display&id=15175 (accessed on 27 November 2015). (In French)
- Van der Lee, J.; Gehrels, J. Modeling Aquifer Recharge, Introduction to Lumped Parameter Model EARTH; Hydrological Report; Free University of Amsterdam: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Nyende, J. Application of isotopes and recharge analysis in investigating surface water and groundwater in fractured aquifer under influence of climate variability. J. Earth Sci. Clim. Change 2013, 4. [Google Scholar] [CrossRef]
- Tonder, G.V.; Yongxin, X. A guide for the Estimation of Groundwater Recharge in South Africa. 2000. Available online: http://www.uovs.ac.za/igs (accessed on 1 September 2014).
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2005. [Google Scholar]
- Middlemis, H. Groundwater flow Modeling Guideline; Murray-Darling Basin Commission: Canberra, Australia, 2001.
- Cooper, H.H.; Jacob, C.E. A generalized graphical method of evaluating formation constants and summarizing well-field history. Am. Geophys. Union Trans. 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Owais, S.; Atal, S.; Sreedevi, P. Governing Equations of Groundwater Flow and Aquifer Modelling Using Finite Difference Method. In Groundwater Dynamics in Hard Rock Aquifers; Ahmed, S., Jayakumar, R., Salih, A., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 201–218. [Google Scholar]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press Incorporated: Cambridge, MS, USA, 1992; p. 406. [Google Scholar]
- Ahern, J.A. Ground-Water Capture-Zone Delineation: Method Comparison in Synthetic Case Studies and a Field Example on Fort Wainwright, Alaska. Ph.D. Thesis, University of Alaska Fairbanks, Fairbanks, AK, USA, 2005. [Google Scholar]
- Prudic, D.E.; Konikow, L.F.; Banta, E.R. A New Streamflow-Routing (SFR1) Package to Simulate Stream-Aquifer Interaction with MODFLOW-2000; Open-File Report 2004–1042; U.S. Geological Survey: Reston, VA, USA, 2004; p. 95.
- Prudic, D.E. Documentation of a Computer Program to Simulate Stream-Aquifer Relations Using a Modular, Finite Difference, Ground-Water Flow Model; Open File Report; U.S. Geological Survey: Reston, VA, USA, 1989; pp. 88–729.
- Brunner, P.; Simmons, C.T.; Cook, P.G.; Therrien, R. Modeling Surface Water-Groundwater Interaction with MODFLOW: Some Considerations. Ground Water 2010, 48, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: with Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; p. 455. [Google Scholar]
- Jackson, J.M. Hydrogeology and Groundwater Flow Model, Central Catchment of Bribie Island, Southeast Queensland. Master’s Thesis, Queensland University of Technology, Queensland, Australia, 2007. [Google Scholar]
- Moss, R.; Babiker, M.; Brinkman, S.; Calvo, E.; Carter, T.; Edmonds, J.; Elgizouli, I.; Emori, S.; Erda, L.; Hibbard, K.; et al. (Eds.) Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies: Intergovernmental Panel on Climate Change; UNISDR: Geneva, Switzerland, 2008; p. 132.
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Chang. 2011, 109, 77–94. [Google Scholar] [CrossRef]
- McCabe, G.J.; Markstrom, S.L. A Monthly Water-Balance Model Driven by a Graphical User Interface; U.S. Geological Survey: Reston, VA, USA, 2007.
- Usher, B.; Pretorius, J.; van Tonder, G. Management of a Karoo fractured-rock aquifer system—Kalkveld Water User Association (WUA). Available online: http://www.wrc.org.za (accessed on 4 February 2015).
- Baalousha, H.M. Risk Assessment and Uncertainty Analysis in Groundwater Modelling. Ph.D. Thesis, Westfälischen Technischen Hochschule Aachen University, Aachen, Germany, 2003. [Google Scholar]
- Wang, B.; Jin, M.; Liang, X. Using EARTH model to estimate groundwater recharge at five representative zones in the Hebei Plain, China. J. Earth Sci. 2015, 26, 425–434. [Google Scholar] [CrossRef]
- Henry, C.M. An Integrated Approach to Estimating Groundwater Recharge and Storage Variability in Southern Mali, Africa. Ph.D. Thesis, Simon Fraser University, Vancouver, BC, Canada, 2011. [Google Scholar]
- Belay, E.A. Growing lake with Growing Problems: Integrated Hydrogeological Investigation on Lake Beseka, Ethiopia. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2009. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).