Abstract
Crop water use (ETc) is typically estimated as the product of crop evapotranspiration (ETo) and a crop coefficient (Kc). However, the estimation of ETo requires various meteorological data, which are often unavailable or of poor quality, particularly in countries such as Guinea-Bissau, where the maintenance of weather stations is frequently inadequate. The present study aimed to assess alternative approaches, as outlined in the revised FAO56 guidelines, for estimating ETo when only temperature data is available. These included the use of various predictors for the missing climatic variables, referred to as the Penman–Monteith temperature (PMT) approach. New approaches were developed, with a particular focus on optimizing the predictors at the cluster level. Furthermore, different gridded weather datasets (AgERA5 and MERRA-2 reanalysis) were evaluated for ETo estimation to overcome the lack of ground-truth data and upscale ETo estimates from point to regional and national levels, thereby supporting water management decision-making. The results demonstrate that the PMT is generally accurate, with RMSE not exceeding 26% of the average daily ETo. With regard to shortwave radiation, using the temperature difference as a predictor in combination with cluster-focused multiple linear regression equations for estimating the radiation adjustment coefficient (kRs) yielded accurate results. ETo estimates derived using raw (uncorrected) reanalysis data exhibit considerable bias and high RMSE (1.07–1.57 mm d−1), indicating the need for bias correction. Various correction methods were tested, with the simple bias correction delivering the best overall performance, reducing RMSE to 0.99 mm d−1 and 1.05 mm d−1 for AgERA5 and MERRA-2, respectively, and achieving a normalized RMSE of about 22%. After implementing bias correction, the AgERA5 was found to be superior to the MERRA-2 for all the studied sites. Furthermore, the PMT outperformed the bias-corrected reanalysis in estimating ETo. It was concluded that PMT-ETo can be recommended for further application in countries with limited access to ground-truth meteorological data, as it requires only basic technical skills. It can also be used alongside reanalysis data, which demands more advanced expertise, particularly for data retrieval and processing.
1. Introduction
An accurate estimation of the reference crop evapotranspiration (ETo) is critical for agricultural water resources planning and management [1,2,3]. ETo quantifies the natural loss of water to the atmosphere, incorporating an approximation that accounts for both evaporation and transpiration from a reference surface [1,2]. The FAO-PM ETo was parametrized for a hypothetical reference crop with specific characteristics in terms of height (0.12 m), albedo that reflects 23% and absorbs 77% of the incoming radiation under standard conditions, and a fixed surface resistance of 70 s m−1 [1]. ETo is essential for estimating crop water use (ETc) as it represents the climatic demand conditions. Crop ET is commonly estimated using the FAO approach, which involves multiplying ETo by a crop coefficient (Kc). The latter considers the differences in characteristics of the crop under study relative to the reference crop. Therefore, it enables the quantification of water use by any agroecosystem, landscape, wetland, or riparian ecosystem [4]. Under water or salinity stress, crop ET decreases [1,5,6,7].
The FAO-PM ETo requires data on several weather variables, including maximum and minimum temperature, shortwave or net radiation, relative humidity or dew point temperature, and wind speed. The FAO 56 guidelines [1], which have recently been revised [2], describe alternative approaches for estimating missing weather variables data, namely when using temperature data only (FAO-PMT), making these tools particularly valuable in regions with insufficient weather stations or low maintenance capabilities [1,2]. To improve the accuracy of the ETo PMT estimates, the calibration of the predictors may be performed for local conditions [8,9,10,11] or, alternatively, simplifications to the method can be adopted [2,12]. The accuracy of the PMT approach has been demonstrated in several studies conducted across Africa [13,14,15,16,17], although in many of these cases, adequate observed weather datasets were not available for a consolidated assessment of alternative approaches. Another commonly used approach that uses temperature data only for ETo estimation is the Hargreaves–Samani (HS) equation, earlier developed for the Senegal River Basin [18] and later commonly used [12,19,20,21]. The ETo estimates with HS can also be used with the FAO Kc-ETo approach despite the need for adjustments.
Various heuristic approaches have also been used to estimate ETo with minimal data availability, with machine learning (ML) algorithms being among the most widely used. However, as discussed by Pereira et al. [3], these approaches do not use the fundamental physics underlying the FAO-PM ETo equation, which is considered relevant when selecting alternative approaches to calculate ETo when weather datasets are incomplete. These algorithms leverage training data to model variables for specific regions or sites [22]. However, they have limited applicability as they are generally not transferable and are only effective for the sites for which they were developed. Examples of these approaches include support vector machines (SVMs) and random forest (RF), which are renowned for their accuracy in predictions using limited input data [23,24].
Alternative sources of weather data are those based on observational data with different spatial and temporal resolutions and different available weather variables. Examples include the Climate Research Unit Time Series (CRU) [25] and WorldClim for the globe [26], E-OBS for Europe [27], PRISM climate data for the USA [28], Iberia01 [29] for the Iberian Peninsula, or those provided by [30] for Brazil. For given weather variables, such as shortwave radiation, satellite data can be obtained, e.g., data provided by the geostationary Meteosat Second Generation (MSG) system, which includes the Satellite Application Facility for Land Surface Analysis (LSA-SAF) [31,32,33].
Other sources of weather data include reanalysis gridded data obtained by integrating observations from various sources, including ground-based weather stations, ocean buoys, ships, aircraft, and satellite sensors [34,35]. This integration is carried out by modeling and data assimilation systems, which provide accurate and continuous estimates of climate and meteorological variables [36,37]. Their temporal resolution can be hourly, daily, or monthly. The spatial resolution varies, depending on the data source. One of the most widely used sources is the ERA5 reanalysis, made available by the European Centre for Medium-Range Weather Forecasts (ECMWF) [36,38]. The AgERA5 dataset, which focuses on agriculture, is derived from this dataset. This dataset provides hourly data with a spatial resolution of 0.1° [39,40]. Another often-used reanalysis dataset is MERRA-2 version 2, an atmospheric reanalysis developed by NASA (National Aeronautics and Space Administration). MERRA-2 provides a reanalysis of global climatic and weather information [41]. Another reanalysis-based dataset is that provided by the National Centers for Environmental Prediction–National Center for Atmospheric Research (NCEP/NCAR) [42]. Reanalysis data have been used in several studies to estimate ETo and assess its spatial distribution [40,43,44,45,46]. One of the key advantages of using reanalysis data is that they provide all the weather variables required to calculate ETo without any gaps [47,48]. However, many studies have found that these gridded datasets require bias corrections, such as additive bias correction [32,49], simple regional bias correction [50,51], and Kalman filtering for temperature modeling [52], as well as adequate downscaling methods [53], to improve their quality.
The above-cited studies emphasize the critical importance of bias correction, particularly in regions lacking baseline meteorological information, such as many tropical areas [36], including part of Africa. This is the case of Guinea-Bissau (GB), located in West Africa, with an economy based primarily on agriculture. GB has limited economic resources, which has led to a decline in government investment in meteorological and agricultural information after independence. Although long-term weather records exist at three sites in the country (Bissau, Bafata, and Bolama), they are incomplete due to the loss of documents during the civil war (1998–1999), poor resources for digitizing the data and maintaining the weather stations, and a lack of financial resources for purchasing new sensors [54,55]. However, these sites only cover a small part of the country as they exclude the most important agricultural areas, regions in the north affected by drought, humid zones in the south, and the archipelago of Bijagós [56,57,58]. This hinders the spatial quantification of ETo across the country, particularly in agricultural water management studies [59,60], and highlights the need for easy-to-use approaches to cope with reduced weather datasets.
Therefore, the main objective of this study is to evaluate different approaches for estimating FAO-PM ETo using only temperature data (PMT). In addition, the study aims to assess the accuracy of AgERA5 and MERRA-2 reanalysis weather datasets to support the scaling of ETo estimates from field level to regional and national levels. This is the first study of its kind conducted in Guinea-Bissau, and its novelty lies in the combined use of ground-truth meteorological observations and reanalysis datasets. The methodologies developed will be made accessible to GB technical staff, who have diverse skills levels, namely relative to the use modeling tools aimed at improving water management in mangrove rice cultivation. Furthermore, the results of the current study are expected to enhance water resource management across different spatial scales and may contribute to improved water governance, particularly under conditions of climate variability and freshwater increasing scarcity.
2. Materials and Methods
2.1. Climate
The study was conducted in GB, West Africa (Figure 1). The study sites were located mainly in the coastal region (Figure 1), where, according to the Köppen–Geiger classification [61,62], the climate is of equatorial savannah with dry winter (Aw) but with different life zones as per the Holdridge classification [63,64]. The aridity index (AI, Table S2 in Supplemental Material), as defined by [65], is the ratio of the long-term mean annual precipitation (P, mm) [66] to the mean annual climatic evaporation index (CEITH, mm). The northern part of GB is classified as moist sub-humid (AI ≈ 0.7), while the south of the country has AI > 1.0.
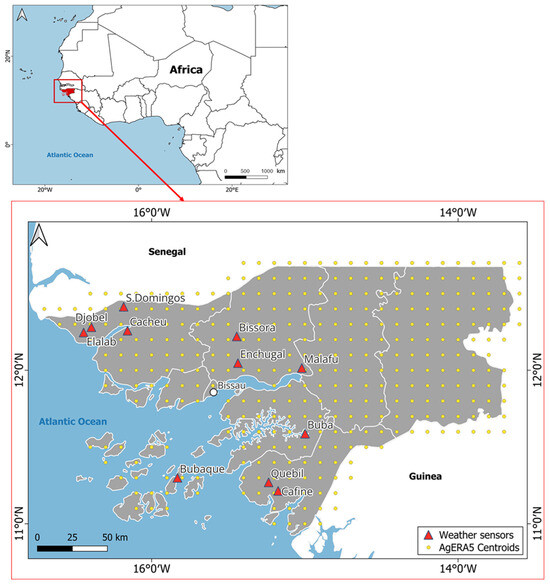
Figure 1.
Location of Guinea-Bissau in West Africa (top), reanalysis grid points within the country, and distribution of weather stations (bottom).
2.2. Data
2.2.1. Ground-Truth Weather Data
Automatic weather stations were installed over well-watered grass at various locations across the country (Table 1, Figure 1), situated in open areas, away from trees and buildings. The ATMOS 41 weather stations (Meter Environment Products, Pullman, WA, USA) were mounted on metal poles at a height of two meters above ground level, oriented northward according to the installation guidelines. Data were recorded every 30 min using ZL6 data loggers (Meter Group, Pullman, WA, USA). The stations were regularly maintained to ensure data quality, including the removal of Saharan dirt and dust, inspection of battery levels, and cleaning of the solar panels on the data loggers, typically every two months or whenever malfunctions were detected. Detailed information on weather station locations (Figure 1) and data collection periods is provided in Table 1.

Table 1.
Geographic coordinates, elevation, and data recording periods of the weather stations in Guinea-Bissau.
This study was carried out using the daily weather data recorded at each weather station. Thirty-minute measurements were processed to obtain daily values of maximum and minimum temperature (Tmax, Tmin, °C), maximum and minimum relative humidity (RHmax, RHmin, %), wind speed at 2 m height (u2, m s−1), and short wave solar radiation (Rs, MJ m−1). In line with common practices in several meteorological services, the RH measured at 9 a.m. (RH9) was taken to represent the mean daily conditions (RHmean). Rainfall (mm) data at 30 min intervals (mm) were also available from all weather stations.
2.2.2. Reanalysis Weather Data
Reanalysis datasets were obtained from two sources: the European Center for Medium-Range Weather Forecasts (ECMWF), platform AgrERA5, part of the Copernicus project [67], and the Global Modeling and Assimilation Office (GMAO), platform MERRA-2.
AgERA5 is a daily reanalysis dataset provided by ECMWF, available from 1979 to the present, with a focus on providing data for agricultural and agroecological studies [68,69]. It is provided at a spatial resolution of 0.1° × 0.1° (approximately 11 km × 11 km) [67] and is derived by forcing hourly ECMWF ERA5 data at the surface level. AgERA5 includes a wide range of atmospheric and surface variables. For this study, the following variables were downloaded from the Copernicus Climate Change Service (C3S) Climate Data Store (CDS) website: Rs (J m−2 d−1), Tmin and Tmax (K), dew point temperature (Tdew, K), RH9 (%), and wind speed measured at 10 m height (u10, m s−1).
MERRA also has a version tailored for agricultural studies, known as (AgMERRA). However, this dataset was not used in the present study due to its limited temporal coverage (1980–2010) [70,71]. Instead, the more recent product MERRA-2, developed by NASA to replace the original MERRA using a fixed assimilation system [41], was used, as it spans from 1980 to the present. MERRA-2 provides daily weather data at a spatial resolution of 0.5° × 0.625° [72,73]. All variables required for the calculation of FAO-PM ETo were downloaded: Tmin (K), Tmax (K), Tdew (K), RH9 (%), u10 (m s−1), Rs (J m−2 d−1), and vapor pressure (hPa). The appropriate conversion of units was therefore performed on both datasets, with the wind speed at 10 m adjusted to 2 m in accordance with the recommendation of FAO 56 [1]. Further details on the data assimilation system and performance metrics for AgrERA5 are reported by [74] and for MERRA-2 by [75].
The datasets were accessed using a script written in Python version 3.11 [76]. The MERRA-2 reanalysis data featured fewer grid centroids (36) compared to the AgERA5 (356), due to differences in spatial resolution between the two datasets. Both datasets were organized to cover the same period as the observed weather data, from January 2021 to May 2024 (Table 1). The Euclidean distance (straight line between two points) was calculated between each grid centroid and the weather station locations [77]. A filtering process was applied, and each grid centroid was classified based on its proximity to the weather stations. Following other approaches in the literature, the nearest grid point to each station was selected for use in this study [32,78,79,80]. Although other methods exist, e.g., multiple linear regression [49] or triangle-based bi-linear interpolation method [81], these approaches have not been shown to outperform the simpler and widely adopted method of using the nearest grid point to the targeted station.
2.3. Computation of the FAO-Penman Monteith ETo
The FAO Penman–Monteith equation is the most widely used method in agriculture for estimating the reference crop evapotranspiration (PM-ETo) [1,2]. It allows for an accurate determination of the climatic demand conditions as it integrates various meteorological variables. The daily ETo is estimated as follows:
where is the slope vapor pressure curve (kPa °C−1); Rn is the net radiation at the crop surface (MJ m−2 d−1); G is the soil heat flux density (MJ m−2 d−1), which is negligible at daily steps; T is the air temperature at 2 m height (°C); u2 is the wind speed at 2 m height (m s−1); es is the saturation vapor pressure (kPa); ea is the actual vapor pressure (kPa); es − ea is the vapor pressure deficit (kPa); and γ is the psychrometric constant (kPa °C−1).
The net radiation at the crop surface (Rn, MJ m−2 d−1) is calculated as the difference between the net shortwave radiation (Rns, MJ m−2 d−1) and the net longwave radiation (Rnl, MJ m−2 d−1), where Rns is calculated as (1 − α) Rs, assuming an albedo (α) value of 0.23 for the green grass reference crop, and Rnl is calculated as follows:
where is the Stefan–Boltzmann constant (4.903 × 10−9 MJ K−4 d−1), and Tmax and Tmin are the daily maximum and minimum temperatures (K), respectively. The mean es for a day is calculated as the average of the vapor pressure at the maximum and minimum temperature, while ea is estimated from the RHmax and RHmin as follows:
where eo (Tmin) (kPa) and eo (Tmax) (kPa) are the saturation vapor pressure at the daily minimum and maximum air temperature, respectively, and RHmax (%) and RHmin (%) are the maximum and minimum relative humidity, respectively.
The wind speed data (u2, m s−1) at the standard height of two meters above the ground level is obtained from that measured at height z (m) through the following logarithmic transformation:
where uZ is the wind speed measured at z meters above the ground surface (m s−1), and z is the height of the measurement above the ground surface (m).
2.4. Calculation of ETo Using Only Temperature Data (FAO-PMT)
Several approaches were used to estimate Tdew, u2, and Rs to overcome missing data or data with poor quality. The predictors and the combination of approaches used in the current study are detailed in Figure 2. For ea computation, and therefore the prediction of Tdew, the first approach used was straightforward and assumed Tmin as the best predictor for Tdew [1,2]. A second approach used either Tmin (for moist sub-humid sites), or the Tmean − aD (for humid sites) with aD = 2, both depending on the location aridity index (AI) [2,32,82]. Therefore, the first step was to calculate the already mentioned AI for each location. The third approach consisted of the numerical optimization of the value of aD by minimizing the root mean squared error (RMSE) using the “L-BFGS-B” algorithm (See Supplementary Material S1). To overcome the missing u2 data, two predictors were used, the average local or regional (u2 avg) or the world average value (u2 def = 2 m s−1) [1,2].
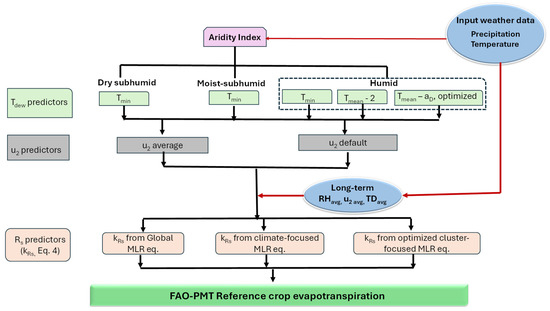
Figure 2.
Flowchart of the approach used to estimate reference crop evapotranspiration using the FAO-PM method based on temperature only (PMT). (MLR—multiple linear regression).
The shortwave radiation was estimated using the following equation [83]:
where kRs is the empirical adjustment coefficient (°C−0.5), Tmax and Tmin are the maximum and minimum air temperature (°C), and Ra is the extraterrestrial radiation (MJ m−2 d−1).
The estimation of kRs was carried out using three different approaches (Figure 2). The first two were based on the use of pre-established multiple linear regression (MLR) equations derived from long-term data collected from 555 weather stations across the Mediterranean. These MLR equations were derived by testing the average daily temperature difference (TDavg), the daily average local or regional wind speed (u2 avg), and the daily average relative humidity (RHavg) as predictors of kRs using a set of goodness-of-fit indicators, as detailed by Paredes et al. [12]. Therefore, one MLR global application across all climate types (global), and the other tailored to specific climate conditions (climate-focused), based on the AI [2,12,84] as follows:
Climate focused equations:
where TDavg is the average daily temperature difference Tmax − Tmin, u2 avg is the daily average local or regional wind speed, and RHavg is the daily average relative humidity, all computed using a long-term dataset.
The third approach was developed to improve kRs estimates and, consequently, the ETo PMT estimates. New adjusted MLR equations were derived at the cluster level (cluster-focused) using the same kRs predictors as in the previous approaches (TD avg, HRavg, u2 avg). The optimization was performed using the “L-BFGS-B” algorithm with the aim of minimizing the root mean square error (RMSE) between the ETo and the ETo PMT (see Supplementary Material S1). Therefore, kRs was considered a cluster-specific constant of proportionality, derived through MLR using long-term mean values of the referred predictors. Due to the relatively short weather dataset (<20 years), it was divided into calibration and validation subsets, comprising 70% and 30% of the data, respectively.
All the approaches were applied at two levels: individually at each site and across groups of sites as defined by the cluster analysis (Section 2.5).
2.5. Data Quality Assurance and Quality Checking (QAQC)
All the weather datasets used in this study were subjected to prior quality assurance and control procedures to ensure consistency, integrity, and quality for ETo calculations. This step is mandatory to avoid error propagation into ETo calculations. To this end, a custom script was developed to analyze data behavior through visual diagnostic tools, including Q-Q plots and normal probability plots (qqnorm), to identify data patterns and trends. Given the tropical location of the study, outliers were removed by applying a threshold of 3.5 times the interquartile range (IQR) below the first quartile (Q1) and above the third quartile (Q3) [85,86]. This procedure aimed to exclude extreme values likely resulting from measurement errors that could significantly bias the analysis. Subsequently, the datasets were tested for mean homogeneity, trend, and variance homogeneity tests, following established statistical procedures [2,87,88,89].
Wind speed data were specifically examined for prolonged periods of nearly constant and low values (≤0.5 m s−1), which may indicate anemometer malfunction or a numerical ‘offset’ in the sensor calibration.
Shortwave radiation data (Rs, MJ m−2 d−1) were evaluated following the procedure recommended by [87,90]. The Rs values were compared with estimated clear-sky solar radiation (Rso, MJ m−2 d−1) for each location, with Rso calculated as follows [1,2]:
where Ra is the extraterrestrial radiation (MJ m−2 d−1), and z is the weather station altitude (m) (Table 1). Ra calculation method is detailed in [1].
The Rs/Rso ratio was calculated as the highest recorded observation within each 15-day period. This ratio was then used to adjust the remaining Rs observations by dividing each observed Rs by the ratio calculated for the highest record in that period. This procedure was systematically applied across the entire dataset for each weather station. All calculations and analyses were carried out using R statistical software version 2025.05.1 +513 [91]. This tool performs functions similar to those of the agweather-qaqc software [92].
Relative humidity values were plotted against air temperature throughout the day to check for inverse behavior. RHmax values were inspected to determine whether they approached saturation or were no more than 3–5% higher in the early morning or during rain events, indicating the need to recalibrate the sensors. In addition, RH records were evaluated for consistency on rainy days, when RH values should typically exceed 95%.
A rigorous data filtering process was applied, retaining only those dates with complete records for all variables required for ETo estimation (Equation (1)). This ensured homogeneity across all sites. Once homogenized, the data were subjected to the Shapiro–Wilk test to assess the normality of distributions for subsequent analyses. To identify relationships between sites, a comparative analysis of climatic variables was performed using the non-parametric Kruskal–Wallis test [93,94], followed by pairwise comparisons using the Bonferroni method using a significance level of 0.01 (α = 0.01 indicates a 1% maximum probability of committing a Type I error across all comparisons when performing multiple statistical tests). This approach provided a robust evaluation of whether significant differences existed among sites. The same data filtering process was applied for the cluster analysis, ensuring that only data common to all sites were used. The sites were then normalized and grouped, and a distance matrix was calculated. A dendrogram based on site altitude guided the selection of site groups [95]. The optimal number of clusters was determined using the Elbow method, which suggested K = 5 (K represents the number of clusters into which the data was divided), indicating that the data naturally grouped into five distinct clusters [96,97]. Hierarchical clustering then identified the four final site groups.
2.6. Bias Correction of Reanalysis-Based ETo Estimates
To improve the accuracy of ETo estimates derived from reanalysis data (ETo rean) at both individual sites and cluster levels and to support the subsequent application of gridded data for regional ETo estimation [59,60,98,99], four correction methods were implemented. Rather than adjusting the underlying meteorological variables used in the calculation of ETo, these correction techniques were applied directly to the reanalysis-based ETo estimates [49]. The correction methods included linear model (LM) adjustment, slope correction, robust linear modeling, and simple bias correction. Each correction was applied at both the individual site level and across groups of sites defined by the cluster analysis. Further details on each correction method are provided below:
- (A)
- The adjusted linear model correction (ALMc) involved fitting a linear regression between ETo rean () and ETo obs () as follows:where β0 is the regression intercept, β1 is the slope, and represents the random error term [100].The resulting intercept and slope values were then used to adjust the ETo for each site. The ETo rean values were corrected for both systematic bias and scale error [89] by subtracting the intercept and dividing by the slope.
- (B)
- The slope correction (Sc) method involved fitting a simple linear regression (LM) model between the ETo rean and ETo obs values, with the intercept of 0 (). Once the model was fitted, the slope was calculated and applied as a correction factor. Each ETo rean value was adjusted by dividing it by the estimated slope (ETo/slope = ETo rean_adjusted) [100]. This correction was applied individually to each site and aimed to compensate for systematic bias identified in the relationship between reanalysis and observed data.
- (C)
- The robust linear model correction (RLMc) followed a similar principle to the slope correction but employed a robust linear regression instead of the ordinary least squares method. Unlike standard linear regression, which minimizes the sum of squared residuals, RLMc minimizes a loss function that is less sensitive to large deviations [100,101]. In this study, the Huber M-estimator was used, implemented through the ‘rlm’ function in the R software version 2025.05.1 +513. Fitting was carried out using integrated weighted least squares (IWLS). The Huber function addresses a convex optimization problem and provides parameter estimates that are more robust in the presence of outliers. As with the slope correction, the new (means the updated or robust slope coefficient obtained from this Huber-based fitting procedure) was used to fit ETo rean, reducing the influence of extreme values on the correction process, which are common in tropical regions. Therefore, the corrected ETo rean is estimated as follows:
- (D)
- A simplified bias correction was applied to adjust ETo rean at different sites. The simplified BIAS correction (BIASc) was calculated as follows:where n is the number of observations per site, represents the reanalysis values for the i-th observation, and is the corresponding observed value. The new estimated ETo rean_corrBIAS was calculated by subtracting BIASc from each daily ETo rean value. This correction aimed to eliminate systematic deviations inherent to the original estimates.
2.7. Accuracy Assessment
To assess the accuracy of the tested approaches, a set of goodness-of-fit indicators [3,32] was employed to compare the observed (Oi = ETo obs) and estimated (Pi = ETo PMT or ETo REAN) values. The regression coefficient (b0) of a forced-to-the-origin (FTO) linear regression was used to assess the proportionality between the estimated and observed ETo values. A value of b0 close to 1.0 indicates that the estimated and observed ETo values are statistically similar. A b0 < 1 suggests underestimation, while a b0 > 1 suggests overestimation. The coefficient of determination (R2) from an ordinary least squares (OLS) linear regression was used to assess the degree of dispersion of the Oi and Pi pairs along the regression line. R2 represents the proportion of variance in the observed data that is explained by the estimation approach. Values of R2 approaching 1 indicate a strong linear relationship between the observed and predicted values and hence a better model fit. To quantify estimation errors, the root mean square error (RMSE) was calculated, providing an overall measure of the differences between Oi and Pi. Additionally, the normalized root mean square error (NRMSE, %) was calculated as the RMSE divided by the mean of the observations (). Lower RMSE and/or NRMSE values indicate greater estimation accuracy. Two further indicators were used to assess the systematic bias of the estimates, the BIAS and the percentage bias (PBIAS, %). BIAS was calculated as the average difference between the observed and predicted values, while PBIAS was obtained by dividing BIAS by the sum of the Oi. The positive values of BIAS and PBIAS indicate a tendency toward overestimation, whereas negative values indicate underestimation. Values close to zero suggest lower systematic bias in the model’s predictions [89]. All goodness-of-fit indicators were calculated using R statistical software [91].
2.8. Spatial Variability of ETO in Guinea-Bissau
As Figure 1 clearly shows, there are few weather stations in the country, most of which are in western Guinea-Bissau. Furthermore, the distribution of stations varies greatly between regions. Following a thorough evaluation of the two reanalysis datasets, the one demonstrating superior performance was selected to estimate ETo at all gridded centroids across the country, to overcome this lack of data.
Initially, ETo was calculated using the raw reanalysis data. These values were subsequently corrected using the most appropriate method identified in the study, with adjustments applied to each centroid based on its proximity to the most influential weather station. The mean annual cumulative ETo for the period 2021–2023 was then estimated and mapped using ordinary kriging. Spatial autocorrelation analysis was conducted using the Global Moran’s I statistic, together with Z-score and p-value calculations for the annual ETo (Table S8), following a methodology similar to that used for soil salinity mapping by [99]. All special analyses were carried out using ArcMap 10.8.2 and the Geostatistical Analyst (GS+) tool. In addition, RStudio version 2025.05.1 +513 was used to compute the goodness-of-fit indicators for the interpolated maps.
3. Results and Discussion
3.1. QAQC Assessment
The results of the tests for mean homogeneity, trend, and variance homogeneity of the ground-truth data relative to Tmax and Tmin, RH, and u2 are shown in Table 2. The results of the Mann–Kendall test showed that none of the variables exhibited statistically significant trends, as the z-values were close to zero and the p-values were greater than 0.05. The Wilcoxon rank-sum test was then used to compare the central tendencies of the data from different locations. All variables yielded p-values above the 0.05 significance threshold, indicating that there were no significant differences in median values between the locations being compared. The analysis of the equality of variances across different locations (Levene’s test) showed that all p-values exceeded 0.05, suggesting homoscedasticity (equal variances) across the dataset. Overall, the results of the statistical tests demonstrate that the analyzed meteorological variables are stable over time and comparable between locations. They also show that the variables exhibit consistent variability and are unaffected by outliers or measurement errors at all sites. Therefore, they can be used to estimate ETo.

Table 2.
Statistical tests applied—mean homogeneity (Mann–Kendall test), trend analysis (Wilcoxon rank-sum test), and variance homogeneity (Levene’s test)—for weather variables used in for calculation of the ETo in Guinea-Bissau.
Additionally, Rs was checked and corrected as necessary, and examples of this correction are presented in Figure 3. These examples demonstrate the need for Rs correction due to inadequate pyranometer sensor calibration.
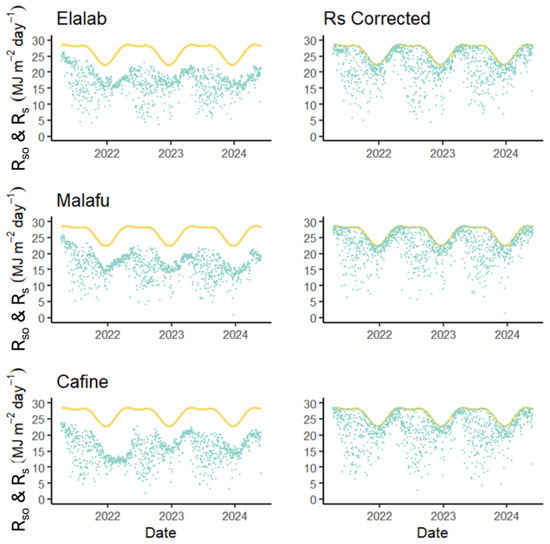
Figure 3.
Examples of daily shortwave radiation (Rs) measured data (●) and estimated Rso dynamics (▬) before and after correction in different locations of Guinea-Bissau—Elalab (north), Malafu (central), and Cafine (south).
3.2. Meteorological Characteristics of the Studied Sites
A high variability in the different weather variables used for the calculation of ETo was observed among the different sites in GB (Table 3). The sites with the significantly (α = 0.01) highest temperatures were Bissora, Cacheu, and Buba. The sites with the lowest temperatures were Bissora, Cacheu, and Malafu. The results indicate that Bissora and Cacheu have the highest thermal amplitude among the studied locations, while Bubaque has the lowest thermal amplitude significantly (α = 0.01). This trend was similar when the average daily temperature difference (TD) was analyzed. From one perspective, the site with the significantly (α = 0.01) highest RH value was Cafine, which was the most humid site in the country. On the other hand, Bissora had significantly lower RH values (RHmin: 49.9% and RHavg: 67.3%; α = 0.01) and was therefore considered the least humid site compared to the others. Buba presented contrasting humidity conditions. Djobel was the windiest location (u2 avg = 2.1 m s−1), while Bissora was the least windy location (u2 avg = 0.7 m s−1), both with significant differences (α = 0.01) relative to the other sites.

Table 3.
Weather characterization of various locations in Guinea-Bissau based on the mean daily maximum (Tmax), minimum (Tmin), and average temperature difference (TDavg); maximum (RHmax), minimum (RHmin), and average (RHavg) relative humidity; and average wind speed (u2 avg) for the period 2021–2023.
The dendrogram generated by the cluster analysis identified three distinct groups based on the accumulated precipitation and ETo at each site (Figure 4). These groups were formed according to their position in the dendrogram and the geographical proximity of the sites. The first cluster included Buba and Cafine; the second included Malafu, Cacheu, and Enchugal; and the third included Elalab, Djobel, and S. Domingos. These clusters represent the southern, central, and northern regions, respectively. As mentioned above, Bissora presented contrasting weather conditions and did not fit into any cluster within the analysis. Its inland-like location resulted in distinct weather characteristics. Bubaque was also not included in the cluster analysis as it is located on an island. Quebil was excluded from the cluster analysis due to a lack of observations relating to sensor malfunction problems, which began in mid-2022. However, it was included in the ETo estimates using the available weather data.
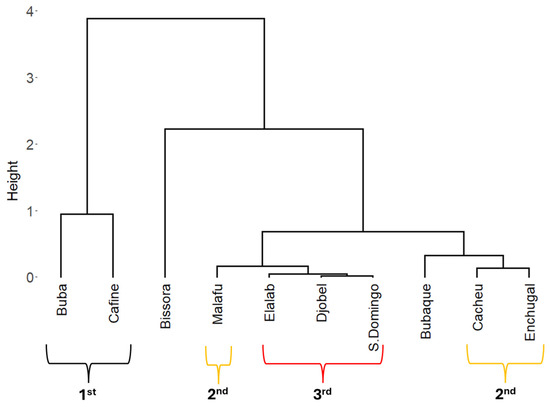
Figure 4.
Dendrogram of hierarchical clustering of the selected sites. Clustering was performed using cumulative rainfall and ETo for 2021–2023, and site elevation considering their spatial distribution in Guinea-Bissau.
In Guinea-Bissau, there is considerable climatic variability between different sites, and this study demonstrated sensitivity in identifying moist sub-humid and humid areas, regions with greater thermal amplitude, and sites with variable wind patterns (Table 2). Tropical climates are variable because they are frequently influenced by tropical storms [102,103]. These regions typically experience two well-defined seasons, namely the rainy season and the dry season, but with high interannual variability [104]. Subsistence agriculture is highly dependent on the behavior of the rainy season, particularly for the Mangrove Swamp Rice production in the country [59,105,106]. However, this seasonality is becoming increasingly unpredictable, with global warming exacerbating variability, particularly in rainfall distribution patterns and intensity [107,108]. As a result, these areas are becoming increasingly vulnerable, making sustainable agricultural production more challenging [98,109]. Appropriate management of water resources is therefore necessary.
3.3. FAO-PM ETo Using Temperature Data Only
As previously stated, one of the new approaches for humid climates consisted of optimizing the aD value used in the prediction of Tdew from Tmean. The results showed that aD values ranged from 2.5 °C to 5.0 °C, depending on the location, with an average aD of 4.8 °C when used alongside with u2 avg. When the u2 def was used instead, the optimized aD values ranged from 1.5 to 5.0 °C, with an average of 4.5 °C. These results are consistent with those reported by [110] for humid climates in China, with aD values of 5.14 ± 1.33 °C. Similarly, ref. [11] reported aD values ranging from 1.5 °C to 4 °C for the humid oceanic islands of the Azores, Portugal.
The new cluster-focused MLR equations, which were derived from observed weather datasets by minimizing RMSE, are presented in Table 4. The statistical indicators related to the test and validation datasets are presented in Table S3 of the Supplemental Material. All the considered variables (TDavg, u2 avg, and HRavg) contribute differently to the estimation of kRs but play complementary roles. As with the global (Equation (6)) and climate-focused MLR equations (Equations (7a) and (7b)), and in line with the findings of [84], TDavg has a negative regression coefficient associated with the loss of long-wave radiation when TDavg is high. The impact of u2 avg on kRs values is positive and may be related to the transport of air moisture masses in windy conditions, leading to a clearer atmosphere. The impact of RHavg on the kRs value is negative, representing the influence of cloudiness and air moisture. This is consistent with previous findings in other parts of the world [2,10,11,84]. It should be noted that the cluster-focused MLR regression to the origin presents a small range of 0.409–0.416, while the regression coefficients are relatively similar among the clusters (Table 4). The other two locations, which were not within the three clusters, present slightly different regression coefficients. Table 4 shows the kRs values estimated for each cluster.

Table 4.
Cluster-focused optimized predictive multi-linear regression equations for estimating kRs values and respective values.
The goodness-of-fit indicators for the different approaches tested for estimating ETo using ground-truth temperature and u2 data, i.e., the FAO-PMT ETo approach, are shown in Table 5, and the ranges of each indicator are presented in Table S4. It was found that the climate type of the site influenced the results. For the moist sub-humid locations, i.e., those sites located in the north of GB, the best predictor for kRs was, as expected, the value derived from the optimized LMR value (Table 5); for u2, the best predictor was the regional/local average u2 (u2 avg) value. This combination resulted in no tendency to over- or underestimation of ETo (b0 = 0.98) and yielded acceptable errors in estimates, with RMSE of 0.80 mm d−1 and NRMSE of 16.5%. However, small and no significant differences in estimates were found when u2 def was used as a predictor, with RMSE of 1.08 mm d−1 and NRMSE of 22.5%.

Table 5.
Goodness-of-fit indicators used to compare PM-ETo with ETo PMT when using Tmin or Tmean as a predictor of Tdew, when kRs was calibrated for each site, when computed with the global Equation (6) or with the climate-focused Equations (7a) and (7b), and when using the default or the average local u2 value, for the eleven sites of Guinea-Bissau.
The second-best approach was to use either the global (Equation (6)) or the climate-focused MLR (Equations (7a) and (7b)) to estimate kRs in combination with the u2 def. For this set of sites, there was no significant difference (p < 0.05) between using the climate-focused equations and using the global MLR, with RMSE of 1.04 mm d−1 and 1.00 mm d−1, and NRMSE of 21.5% and 20.5%, respectively (Table 5). The results also showed that using u2 avg did not improve predictions of kRs when either global or climate-focused MLR equations were used. This is because it led to an increase in RMSE and NRMSE, which was not only statistically significant but also resulted in a large underestimation of ETo, with b0 values decreasing to 0.82 and 0.79 when the global and climate-focused MLR equations were used, respectively.
The results for the humid sites (Table 5) showed that, similarly to the moist sub-humid sites, the best predictor was the one resulting from the optimized MLR combined with the u2 avg. However, there was no significant difference (p < 0.05) in the RMSE values using the tested Tdew predictors, i.e., Tmin or the adjusted Tmean with either aD = 2 or calibrated aD value, with RMSE of 0.68 mm d−1, 0.71 mm d−1, and 0.67 mm d−1, respectively. When analyzing the results in terms of NRMSE, using the adjusted aD value led to statistically different values, but there were few improvements in the results: NRMSE was 14.3%, compared to 14.6% with Tmin and 15.1% with Tmean-2. There were also few differences in the other goodness-of-fit indicators, except for b0, which showed a clear tendency toward underestimation when u2 avg was used with either the global or the climate-focused MLR. These results showed that optimizing the predictors leads to very good results, but this approach is only possible when a good dataset is available, hence uncommonly. Moreover, for the optimization approach (L-BFGS-B) applied in all the studied sites (Supplementary S1), there was a general tendency for slight underestimation when using u2avg, distinguishing these results from other studies that relied on trial-and-error calibration of the Tdew and Rs predictors [9,12,82].
The global LMR and the u2 deaf results showed the advantage of optimizing the aD value when using Tmean-aD as Tdew predictor in relation to the use of the aD = 2 °C, as the latter led to a clear underestimation of ETo (b0 = 0.88) and higher RMSE (0.89 mm d−1 vs. 0.71 mm d−1). The use of Tmin as the Tdew predictor also revealed good results, with an RMSE of 0.83 mm d−1. Overall, the results for the humid climates showed a limited advantage in adjusting the Tmean as a Tdew predictor, when combined with the use of the global or climate-focused equations using the u2 default value, with NRMSE ranging from 16.6% to 23.8% and 15.3% to 21.1%, respectively.
The results of using the climate-focused LMR equations showed that these had an advantage over the global equation, but it was not statistically significant (α > 0.05). This advantage resulted from a decrease in the underestimation, as well as in the RMSE and NRMSE. In such cases, it is beneficial to use Tmean rather than Tmin as the Tdew predictor considering that there are lower errors in the ETo estimates. As with the global LMR, there was a slight advantage in adjusting the aD value. However, the improvements were not significant, and therefore, the Tmin should be used as a predictor of Tdew in humid climates, with these findings agreeing with those of FAO56rev [2].
Selected examples of comparison results between ETo PMT and PM-ETo when the analysis focused at the cluster level are shown in Figure 5 and Table S5. Examples also include the locations that were excluded from, the clusters Bissora (moist sub-humid) and Bubaque (humid). The scatter plots in Figure 5 demonstrate the strong correlation between ETo PMT using u2 def and the various MLR equations, as well as PM-ETo. The plots show that ETo PMT slightly underestimates PM-ETo in Clusters 1 and 2, as well as in Bissora, when either the global or climate-focused equations are used to predict kRs. Furthermore, using the cluster-focused equations did not offer any advantages in these locations as the RMSEs were higher. Conversely, Cluster 3 and Bubaque show high underestimation when using the same predictors for kRs estimation, demonstrating the advantage of using cluster-focused equations in this case.
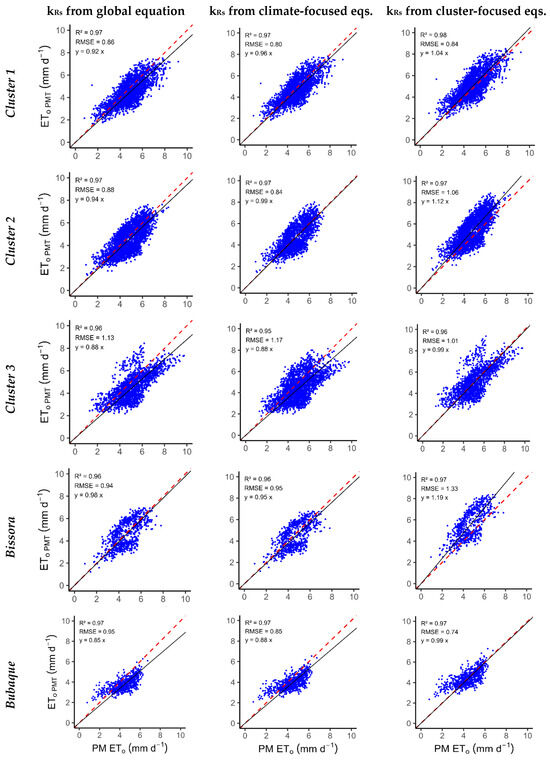
Figure 5.
Comparing ETo PMT with PM-ETo for each cluster and location when using Tdew = Tmin, the default u2 value, and the different MLR equations for estimating kRs. Included are the FTO regression equation, the OLS determination coefficient R2, and the RMSE.
Table S5 provides the results of the goodness-of-fit indicators for all approaches when the analysis was performed at the cluster level. The results showed, as in the previous analysis, that the best approach was to optimize the predictors of Tdew and kRs (i.e., aD and cluster-focused MLR). Therefore, the results are discussed with a focus on the previous simplified approaches.
The first cluster included only locations with humid climates, and the results showed that using Tmin relative to Tmean-2 as a predictor of Tdew was advantageous. Additionally, there was a clear advantage from using the climate-focused MLR alongside u2 def. For the second cluster, which included both humid and moist sub-humid locations, the results showed that the best approach was to use Tdew predictors according to the AI, along with the climate-focused MLR equations and u2 def. The use of u2 avg yielded a higher RMSE and a stronger tendency to underestimate ETo. The third cluster comprised only moist sub-humid locations and showed the poorest results in terms of errors of all the clusters. In this case, the second-best approach was to use u2 def alongside either the global or climate-focused MLR, as there were no significant differences. For Bissora (moist sub-humid), the second-best approach was to use the climate-focused equation with u2 def, while for Bubaque, despite being classified as humid, Tmin was a better predictor of Tdew, with u2 def being the best predictor over u2 avg.
As mentioned previously, the cluster-focused optimized MLR equations using numerical models outperformed the global and climate-focused MLR equations for the set of sites, whether considering individual sites or clusters (Figure 6). Some sites exhibited similar RMSE values when using the climate-focused MLR and the global equation. However, the box-and-whiskers plot revealed variations where the metrics overlapped, indicating that while these standard approaches may be effective for certain sites, they are not suitable for most of them (Figure 6). The metrics indicate that the best adjustments for estimating ETo using temperature alone were achieved by applying either Tdew = Tmin or Tdew = Tmean − aD criterion with optimized aD, u2 def, and using the cluster-focused MLR to estimate kRs for each site or group of sites. The results for Tmin showed a wider spread of RMSE values (Figure 6), possibly because humid and moist sub-humid sites were considered together. In contrast, for the other two predictors using Tmean, the spread was smaller, because only humid sites were considered.
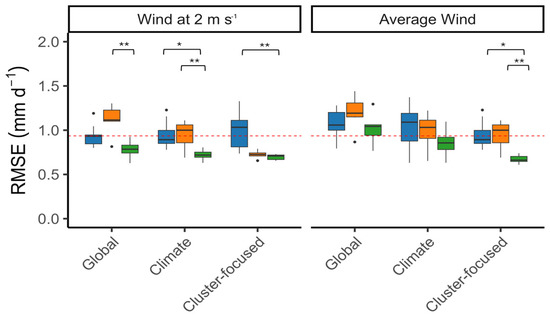
Figure 6.
Box-and-whiskers plots of the root mean square errors of ETo estimations using the PMT approach with different predictors for Tdew (Tmin (blue), Tmean-2 (orange), or Tmean-aD with aD optimized (green)), using either the default 2 m s−1 or the local average wind speed as predictors, and using as the kRs predictor either the global, climate-focused or the cluster-focused equations, for the various sites in Guinea-Bissau. Means followed by an asterisk (*) are significantly different (α < 0.05) and those followed by two asterisks (**) are highly significantly different (α < 0.01) according to the Kruskal–Wallis test.
The results of the current study when using any of the MLR equations were within the range of those reported for several sites in Africa, such as the study performed by [13] in Tanzania and Kenya when using the PMT approach with u2 avg and the default predictors of Tdew and Rs (RMSE ranging 0.64 mm d−1 to 1.09 mm d−1). A study performed in Côte d’Ivoire [15] reported RMSE ranging from 0.43 mm d−1 to 0.89 mm d−1 when using PMT with the default values for the different predictors [1]. A study performed at several sites in Ghana [16], reported RMSE values ranging from 0.58 to 1.11 mm d−1 when using PMT, while RMSE decreased when using artificial neural networks (ANNs) and gene expression programming (GEP) to 0.53–0.84 mm d−1 and 0.51–0.79 mm d−1, respectively. The study performed in humid climates of Uganda by [14] tested several approaches to cope with missing data and reported that the PMT with default values for the predictors of kRs and Tdew and u2 avg outperformed the other approaches with an RMSE ranging from 0.69 mm d−1 to 1.34 mm d−1. Better results were reported in a study applied to Burkina Faso with an RMSE 0.53 mm d−1 and a tendency to overestimate ETo (PBIAS = 6%) when the PMT approach was used, optimizing the Rs and Tdew predictors and using the u2avg value [17]. The globally applied study by [10] reported an RMSE of 0.63 mm d−1 for Aw of climates as in GB when using the default predictors for Tdew and u2 and calibrated or default kRs values. In the current study, using the same approach, RMSE was 0.79 mm d−1 and 0.85 mm d−1 for humid and moist sub-humid sites, respectively. Trajkovic et al. [111] reported a wide range of RMSE for several humid locations in Hungary, ranging from 0.10 mm d−1 to 0.81 mm d−1 when using the default kRs and Tdew predictors values with u2 avg. Other studies such as those by [9,82] for sub-humid and humid climates in the Mediterranean basin and in Iran, respectively, also reported better results when calibrating kRs, u2 avg, and using the different Tdew predictors. Furthermore, the results of the current study when using the LMR equations with the PMT approach are in line with those reported in [12] for humid and moist sub-humid climates.
Enhancing the accuracy of ETo estimation can be challenging, particularly when analyzing sites with high climate variability and limited weather data availability. The FAO-PMT ETo approach, which uses global and climate-focused MLR equations, showed good accuracy, particularly when considering each site individually, demonstrating that there is no significant advantage in developing cluster-focused MLR equations or optimizing aD. However, when performing the analysis at the cluster level, there was a consistent trend toward improved performance with this optimization, despite the robustness of the approach needing to be further tested using a wider set of weather data. Overall, due to the simplicity of the approach, the use of the global and/or climate-focused LMRs as predictors of kRs is advocated despite their tendency to underestimate ETo, in combination with the u2 default when it leads to less underestimation. Furthermore, these approaches demonstrated their potential as valuable tools for improving water use efficiency in the absence of accurate data, as they can serve as a baseline for estimating water and salt balances using different models [7,59,60,112]. Future applications of the method would benefit from enhanced ground observation networks, particularly in data-scarce regions like central and eastern GB, to strengthen calibration and reduce potential uncertainties.
3.4. ETo Estimation Using Different Reanalysis Datasets
Analysis of wind speed data from AgERA5 (u2 ERA5) and MERRA-2 (u2 MERRA) revealed significant discrepancies with u2 observations (results not shown), as reported in previous studies assessing reanalysis data [46,49]. This led to ETo estimation using reanalysis data that excluded this variable. Two approaches were then used: one replaced u2 ERA5 and u2 MERRA with the u2 def value, while the other used the u2 avg value. The results show that the estimation of ETo using raw AgERA5 reanalysis data (ETo ERA5) exhibited significant variability compared to the ETo values calculated from ground-truth (observed, ETo OBS) data (Figure 7 and Figure S7), particularly when the default u2 was used in the ETo ERA5 estimations.
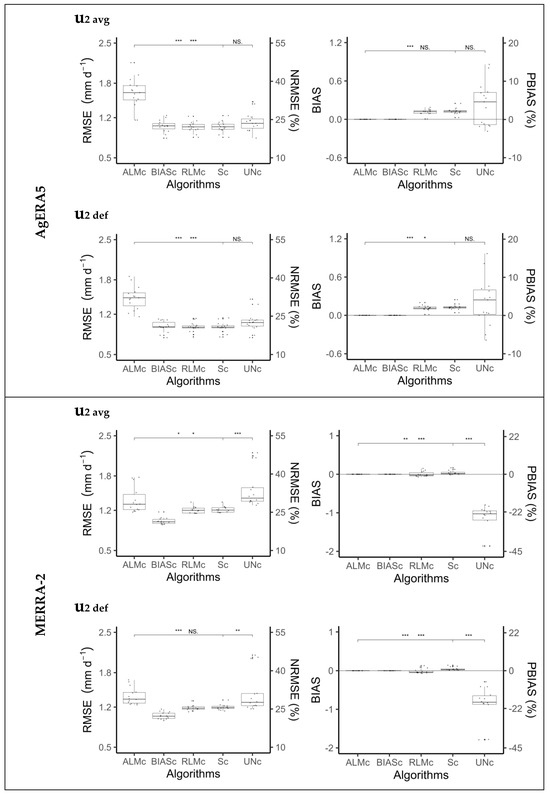
Figure 7.
Comparison of ETo estimated with ground-truth (observed) data and with AgERA5 and MERRA-2 reanalysis datasets when raw (UNc) data were used and after using the diverse bias correction methods (Sc, RLMc, Biasc, and ALMc). The local average (u2 avg) or the default value of 2 m s−1 (u2 def) was used instead of the reanalysis wind speed data. (UNc—uncorrected bias; bias correction methods: Sc—slope, RLMc—robust linear model; Biasc—bias; ALMc—adjusted linear model). Means followed by an asterisk (*) are significantly different (α < 0.05) and those followed by two or three asterisks (** or ***) are highly significantly different (α < 0.01) according to the Kruskal–Wallis test, NS = not statistically significant.
Using raw (uncorrected) reanalysis data with u2 avg to estimate ETo yielded a wide range of regression coefficients b0 (0.90–1.18) (Table S6) and PBIAS (−7.72–21.14) (Figure 7), but most sites did not show an under- or overestimation tendency (b0 near 1.0 and PBIAS near 0%) (Figure S7). When u2 def was used, however, the b0 and PBIAS values varied in a wider range, with two groups of sites, one with an underestimation tendency (b0 < 0.90, PBIAS) and the other with an overestimation tendency (b0 > 1.10, PBIAS). In both approaches, R2 was generally above 0.95, showing that ETo ERA5 was able to explain most of the ETo OBS variance. When analyzing the errors due to using u2 avg, the RMSE ranged from 0.84 to 1.48 mm d−1. This value decreased slightly when u2 def was used instead (RMSE from 0.80 to 1.46 mm d−1), corresponding to NRMSE ranging from 17.9% to 31.9% and 17.9% to 31.8%, respectively.
After applying different bias correction methods to the ETo ERA5 data, the results showed a general decrease in the RMSE values and, as expected, in PBIAS and BIAS (Figure 7) and as well as in b0 (Table S6). The analysis of the BIAS and PBIAS metrics revealed that BIASc and ALMc effectively removed the under- and overestimation of the ETo ERA5 data. However, the ALMc ability to explain the variability in the data was lower than that of the other bias correction methods, suggesting lower predictive performance. This is evident in the decrease in R2 from 0.96 to 0.90 and 0.92 when using u2 avg or u2 def, respectively (Table S6). Although ALMc removed the bias of the reanalysis data, it failed to reduce the estimation errors.
Analyzing the set of goodness-of-fit indicators (Figure 7 and Table S6), it was found that the different bias correction methods exhibited further differences in accuracy, with the simple BIASc method performing the best. The average RMSE values were very similar for BIASc (1.05 mm d−1 or 0.99 mm d−1 when using u2 avg and u2 def, respectively), RLMc (1.04 mm d−1 or 0.97 mm d−1), and Sc (1.04 mm d−1 or 0.98 mm d−1). This small difference in NRMSE indicated that these bias correction methods were not significantly different (α <0.05). Similarly, the mean NRMSE values were 22.0%, 21.7%, and 21.7%, respectively (Table S6). For ALMc, the bias correction was successfully applied; however, the RMSE was higher (>1.3 mm d−1) than that of the other correction methods in both AgERA5 and MERRA-2, indicating lower accuracy. Using the u2 def value resulted in slightly higher accuracy for all bias correction methods, but this was not statistically significant (NS). Overall, the BIASc was the simplest and most effective, leading to significant differences (α = 0.05) compared to using raw data. This makes it a practical option for calculating ETo using AgERA5 and MERRA-2 data with either u2 avg or u2 def.
Using raw MERRA-2 data to estimate ETo (ETo MERRA) produced greater variability, a marked underestimation (Figure 7), and less precision (Table S6). Comparing the two datasets (Figure 7), the superiority of using raw AgERA5 becomes evident, i.e., the results indicate that MERRA-2 underperforms compared to AgERA5. Similar results were reported by [78] for the estimation of annual ETo in Greece. The differences in performance between the reanalysis datasets may be due to the coarser resolution of the MERRA-2 dataset, which makes it difficult to adequately capture climate variability within GB. When u2 avg and u2 def were used, the latter performed slightly better but did not reach statistical significance.
The results show that, for operational use, the ETo MERRA needs to be bias-corrected (see Figure 7). As with ETo ERA5, the results also highlight that ALMc and BIASc were the only methods that effectively removed the bias. The RMSE was 1.57 mm d−1 when raw data were used, and it decreased to 1.38 mm d−1 with the ALMc method and to 1.01 mm d−1 with the BIASc method. As with the AgERA5 data, ALMc’s ability to explain the variability in the data was lower than that of the other bias correction methods, showing a smaller reduction in RMSE (see Table S6). BIASc was the best bias correction method, as it improved all accuracy indicators.
The results of the current study using raw reanalysis data are comparable to those reported in the literature. Tiruye et al. [113] reported a tendency for overestimation when using ERA5-Land for the Tana Basin in Ethiopia, which has a subtropical climate, with RMSE ranging from 0.54 mm d−1 to 1.82 mm d−1. Lopez-Guerrero et al. [114] reported RMSE values ranging from 0.49 mm d−1 to 0.88 mm d−1 for Egypt, Morocco, and Tunisia. Nouri et al. [43] reported an NRMSE ranging from 11% to 20% for ETo estimates on a monthly timescale for the humid sites of Iran. Various studies have been carried out for Italy and Portugal. For example, [80] reported an NRMSE ranging from 15% to 47% when using two ERA5 products, depending on the time scale. Other studies carried out in Italy using ERA5-Land datasets reported a tendency toward underestimation and generally lower RMSE; for instance, Pelosi et al. [51] reported an RMSE ranging from 0.44 to 1.04 mm d−1, with NRMSE values lower than 14%, and [115] reported RMSE ranging from 0.42 to 1.26 mm d−1. Paredes et al. [49] reported better results using ERA-Interim for mainland Portugal, with RMSE > 0.75 mm d−1 for most sites, combined with a tendency of underestimation. After simple bias correction, the RMSE decreased to a range of 0.50–0.75 mm d−1 for most sites [49].
There are few studies in the literature that have used MERRA-2 to estimate ETo. The results of the current study are comparable with those reported by [43], with lower NRMSE values ranging from 10 to 20% at humid sites in Iran.
Overall, the results of the analysis of the gridded datasets emphasize the need for bias correction to enhance the accuracy of ETo estimates derived from reanalysis products in data-scarce regions. Furthermore, a comparison of the results from AgERA5 and MERRA-2 (Figure 7, Table S6) with the FAO-PMT approach (Section 3.2, Table 5) shows that the latter performs better and therefore can be used to estimate ETo when temperature data is available.
The results of the current study suggest that AgERA5 data could be used with caution for estimating ETo, particularly when the observed weather data are unavailable. Further caution is needed, particularly for studying climate variability and change, as previously reported [107,108,116]. To allow for a more thorough evaluation of the gridded dataset’s accuracy, it is advisable to continue collecting meteorological data over a longer period and across different regions. The method can be adapted to other regions but local ground data are key for improving accuracy. Further long-term studies are encouraged, particularly in areas with limited station coverage, where expanding or recovering weather observations could reduce uncertainties.
3.5. ETo Mapping
Figure 8 shows the spatial variability of the mean annual ETo ERA5 in the country after applying the best bias correction method (BIASc). The results show that the spatial distribution of the annual ETo presents strong spatial coherence and continuity (Table S8). The fitted exponential variogram with a nugget of 10 mm, sill of 17.8 km, and an extensive range of 240.3 km indicates a well-structured spatial dependence on the regional scale. Autocorrelation results support this, with a Global Moran’s I of 0.84, a Z-score of 20.71, and p < 0.001, confirming significant spatial clustering of ETo values. The model achieved excellent annual accuracy, with errors less than 2.5% of the observed NRMSE mean and minimal bias (BIAS = 0.14, negligible PBIAS). These values indicate both high precision and negligible systematic errors in the estimation. The high R2 (0.87) and Spearman correlation (ρ = 0.94) further validate the model’s reliability across spatial domains.
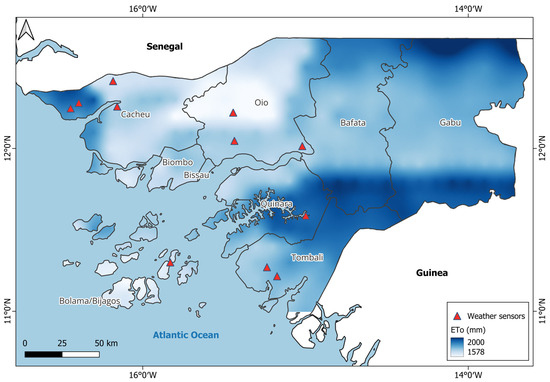
Figure 8.
Spatial distribution of annual ETo estimated using bias-corrected AgERA5 data, in Guinea-Bissau.
In practice, the ETo map is consistent with the observed patterns in the country, where southern areas have higher temperatures and ETo, while some inland locations have lower ETo values. This reflects the typical variability observed in tropical regions, where climatic and topographic conditions contribute to significant spatial differences in ETo. The results of this study highlight the value of gridded climate datasets such as AgERA5, after appropriate bias correction, for regional-scale agroclimatic applications. For regions of Guinea-Bissau where ground-based meteorological data are sparse, corrected satellite-derived ETo maps can provide important support for water management planning, drought monitoring, and sustainable agricultural management. However, it is advisable to collect more observational data to further support the findings of the current study.
4. Conclusions
The approach developed in this study is an important tool for Guinea-Bissau (GB), where limited government investment in sensors hinders the rapid acquisition of accurate meteorological data. The findings of the present study underscore that the PMT approach yielded more accurate ETo estimates than either of the reanalysis products, even after its bias correction. However, in the absence of observed temperature data, AgERA5 data could be used as an alternative source, although caution is advised due to known biases and uncertainties associated with ETo estimation from this reanalysis product. When using the PMT approach, it can be concluded that Tmin is an adequate predictor of Tdew in both moist sub-humid and humid climates. Therefore, there is no need to use corrected Tmean to predict Tdew, as this does not significantly affect ETo estimates. Furthermore, the u2 default value of 2 m s−1 was found to be the best predictor when coupled with either the global or the climate-focused equations for estimating ETo. The newly proposed cluster-focused equations improve the accuracy of ETo compared to the global or climate-focused equations but require further validation for GB. More broadly, this study demonstrates the suitability of the user-friendly approaches outlined in FAO56rev, particularly in regions where access to comprehensive weather information is limited.
The study provides a robust framework for enhancing agricultural practices and fostering resilience in areas grappling with climatic and environmental challenges. In the case of GB specifically, the approximate datasets and tools provided by the developed approaches could greatly benefit organizations working to improve the country’s social and food security, such as international cooperation projects and GB’s development ministries.
However, the approach explored in this study could be further enhanced by expanding the ground-truth database to include more years of observations. It is important to test the global and climate-focused equations with more data from tropical countries, especially those with high rainfall and climate variability. This is particularly relevant for regions between 0° and 20° N latitude, which experience the greatest climate variability and have not been the focus of previous studies. Overall, it is essential to refine the tools further to improve the estimation of ETo in regions where investment in specialized equipment is low. Nevertheless, this work provides a foundation for calculating water and salt balances in MSR production in Guinea-Bissau and other West African countries where this system exists.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/hydrology12070161/s1, Supplementary S1: Numerical method for deriving the cluster-focused multiple linear regression (MLR) equations to estimate kRs; Table S2: Aridity index for GB calculated with data from FAO CLIMWAT 2.0 weather data; Tables S3–S5: Goodness of fit indicators and standard deviation for predicting ETo in sites; Table S6: Correlation between ETo estimated with weather observations and with AgeERA5 and MERRA-2 reanalysis data; Figure S7: Comparing ETo estimated with observed weather data and with AgERA5 after bias correction for the eleven sites in Guinea Bissau; Table S8: Geostatistical parameters used to calculate the interpolation annual ETo with AgERA5 in GB.
Author Contributions
Conceptualization: G.G. and P.P.; methodology: G.G., P.P. and L.S.P.; software: G.G. and J.C.; validation, G.G.; formal analysis: G.G. and P.P.; investigation: G.G.; data curation: G.G.; writing—original draft preparation: G.G.; review: T.B.R., M.d.R.C., M.T., L.S.P. and P.P.; visualization: G.G. and P.P.; supervision, P.P., T.B.R. and M.d.R.C.; funding: M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research article was made possible thanks to the financial support provided by the European Union through the DeSIRA program Titled “Mangroves, Mangrove Rice and Mangrove People: Sustainably Improving Rice Production, Ecosystem, and Livelihoods” (Grant Contract FOOD/2019/412-700) (https://www.malmon-desira.com, accessed on 18 April 2025).
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors acknowledge the support of the Fundação para a Ciência e a Tecnologia, Portugal, through the grant attributed to the research unit Forest Research Centre (CEF) UIDB/00239/2020, as well as the project LEAF—Linking Landscape, Environment, Agriculture and Food Research Centre (UIDB/04129/2020) of Associate Laboratory TERRA. Additionally, this research received support from the University of Costa Rica. Sincere thanks are also due to Orlando Mendes, Merlin Leunda, Filipa Zacarias, Viriato Cossa, Matilda Merkohasanaj, Joseph Sandoval, Eduino Mendes, Adriano Barbosa, Alqueia Intchama, Adinane Jalo, and Juvinal Santos for their invaluable support, data availability, and dedicated work in the villages of Guinea-Bissau.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Available online: https://www.fao.org/4/x0490e/x0490e00.htm (accessed on 10 August 2024).
- Pereira, L.S.; Allen, R.; Paredes, P.; López-Urrea, R.; Raes, D.; Smith, M.; Kilic, A.; Salman, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements; FAO Irrig. Drain. Pap. 56rev; FAO: Rome, Italy, 2025; 395p. (In Press) [Google Scholar]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Espírito-Santo, D. Crop coefficients of natural wetlands and riparian vegetation to compute ecosystem evapotranspiration and the water balance. Irrig. Sci. 2024, 42, 1171–1197. [Google Scholar] [CrossRef]
- Rosa, R.; Ramos, T.; Pereira, L. The dual Kc approach to assess maize and sweet sorghum transpiration and soil evaporation under saline conditions: Application of the SIMDualKc model. Agric. Water Manag. 2016, 177, 77–94. [Google Scholar] [CrossRef]
- Liu, M.; Shi, H.; Paredes, P.; Ramos, T.B.; Dai, L.; Feng, Z.; Pereira, L.S. Estimating and partitioning maize evapotranspiration as affected by salinity using weighing lysimeters and the SIMDualKc model. Agric. Water Manag. 2022, 261, 107362. [Google Scholar] [CrossRef]
- Liu, M.; Paredes, P.; Shi, H.; Ramos, T.B.; Dou, X.; Dai, L.; Pereira, L.S. Impacts of a shallow saline water table on maize evapotranspiration and groundwater contribution using static water table lysimeters and the dual Kc water balance model SIMDualKc. Agric. Water Manag. 2022, 273, 107887. [Google Scholar] [CrossRef]
- Popova, Z.; Kercheva, M.; Pereira, L.S. Validation of the FAO methodology for computing ETo with limited data. Application to south Bulgaria. Irrig. Drain. 2006, 55, 201–215. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Almorox, J.; Senatore, A.; Quej, V.H.; Mendicino, G. Worldwide assessment of the Penman–Monteith temperature approach for the estimation of monthly reference evapotranspiration. Theor. Appl. Clim. 2018, 131, 693–703. [Google Scholar] [CrossRef]
- Paredes, P.; Fontes, J.C.; Azevedo, E.B.; Pereira, L.S. Daily reference crop evapotranspiration with reduced data sets in the humid environments of Azores islands using estimates of actual vapor pressure, solar radiation, and wind speed. Theor. Appl. Clim. 2018, 134, 1115–1133. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.; Almorox, J.; Darouich, H. Reference grass evapotranspiration with reduced data sets: Parameterization of the FAO Penman-Monteith temperature approach and the Hargeaves-Samani equation using local climatic variables. Agric. Water Manag. 2020, 240, 106210. [Google Scholar] [CrossRef]
- Djaman, K.; Tabari, H.; Balde, A.B.; Diop, L.; Futakuchi, K.; Irmak, S. Analyses, calibration and validation of evapotranspiration models to predict grass-reference evapotranspiration in the Senegal river delta. J. Hydrol. Reg. Stud. 2016, 8, 82–94. [Google Scholar] [CrossRef]
- Djaman, K.; Rudnick, D.; Mel, V.C.; Mutiibwa, D.; Diop, L.; Sall, M.; Kabenge, I.; Bodian, A.; Tabari, H.; Irmak, S. Evaluation of Valiantzas’ Simplified Forms of the FAO-56 Penman-Monteith Reference Evapotranspiration Model in a Humid Climate. J. Irrig. Drain. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Koudahe, K.; Djaman, K.; Adewumi, J.K. Evaluation of the Penman–Monteith reference evapotranspiration under limited data and its sensitivity to key climatic variables under humid and semiarid conditions. Model. Earth Syst. Environ. 2018, 4, 1239–1257. [Google Scholar] [CrossRef]
- Landeras, G.; Bekoe, E.; Ampofo, J.; Logah, F.; Diop, M.; Cisse, M.; Shiri, J. New alternatives for reference evapotranspiration estimation in West Africa using limited weather data and ancillary data supply strategies. Theor. Appl. Clim. 2018, 132, 701–716. [Google Scholar] [CrossRef]
- Yonaba, R.; Tazen, F.; Cissé, M.; Mounirou, L.A.; Belemtougri, A.; Ouedraogo, V.A.; Koïta, M.; Niang, D.; Karambiri, H.; Yacouba, H. Trends, sensitivity and estimation of daily reference evapotranspiration ET0 using limited climate data: Regional focus on Burkina Faso in the West African Sahel. Theor. Appl. Clim. 2023, 153, 947–974. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Hargreaves, G.H.; Riley, J.P. Irrigation Water Requirements for Senegal River Basin. J. Irrig. Drain. Eng. 1985, 111, 265–275. [Google Scholar] [CrossRef]
- Musa, A.A.; Elagib, N.A. Extra Dimensions to the Calibration of Hargreaves-Samani Equation Under Data-Scarce Environment. Water Resour. Manag. 2025, 1–18. [Google Scholar] [CrossRef]
- Moratiel, R.; Bravo, R.; Saa, A.; Tarquis, A.M.; Almorox, J. Estimation of evapotranspiration by the Food and Agricultural Organization of the United Nations (FAO) Penman–Monteith temperature (PMT) and Hargreaves–Samani (HS) models under temporal and spatial criteria—A case study in Duero basin (Spain). Nat. Hazards Earth Syst. Sci. 2020, 20, 859–875. [Google Scholar] [CrossRef]
- Abdulsalam, M.K.; Akpootu, D.O.; Aliyu, S.; Isah, A.K. A Comparative Study for Estimating Reference Evapotranspiration Models over Kano, Nigeria. J. Energy Res. Rev. 2023, 15, 12–25. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Zereg, S.; Belouz, K. Modeling daily reference evapotranspiration using SVR machine learning algorithm with limited meteorological data in Dar-el-Beidha, Algeria. Acta Geophys. 2023, 72, 2009–2025. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, H.; Ma, X.; Fan, J.; Zhang, F. Daily reference evapotranspiration prediction based on hybridized extreme learning machine model with bio-inspired optimization algorithms: Application in contrasting climates of China. J. Hydrol. 2019, 577, 123960. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Anwar, S.A.; Malcheva, K.; Srivastava, A. Estimating the potential evapotranspiration of Bulgaria using a high-resolution regional climate model. Theor. Appl. Clim. 2023, 152, 1175–1188. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Clim. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Herrera, S.; Cardoso, R.M.; Soares, P.M.; Espírito-Santo, F.; Viterbo, P.; Gutiérrez, J.M. Iberia01: A new gridded dataset of daily precipitation and temperatures over Iberia. Earth Syst. Sci. Data 2019, 11, 1947–1956. [Google Scholar] [CrossRef]
- Xavier, A.C.; Scanlon, B.R.; King, C.W.; Alves, A.I. New improved Brazilian daily weather gridded data (1961–2020). Int. J. Clim. 2022, 42, 8390–8404. [Google Scholar] [CrossRef]
- Trigo, I.F.; de Bruin, H.; Beyrich, F.; Bosveld, F.C.; Gavilán, P.; Groh, J.; López-Urrea, R. Validation of reference evapotranspiration from Meteosat Second Generation (MSG) observations. Agric. For. Meteorol. 2018, 259, 271–285. [Google Scholar] [CrossRef]
- Paredes, P.; Trigo, I.; de Bruin, H.; Simões, N.; Pereira, L.S. Daily grass reference evapotranspiration with Meteosat Second Generation shortwave radiation and reference ET products. Agric. Water Manag. 2021, 248, 106543. [Google Scholar] [CrossRef]
- Gebremedhin, M.A.; Lubczynski, M.W.; Maathuis, B.H.; Teka, D. Deriving potential evapotranspiration from satellite-based reference evapotranspiration, Upper Tekeze Basin, Northern Ethiopia. J. Hydrol. Reg. Stud. 2022, 41, 101059. [Google Scholar] [CrossRef]
- Demchev, D.M.; Kulakov, M.Y.; Makshtas, A.P.; Makhotina, I.A.; Fil’cHuk, K.V.; Frolov, I.E. Verification of ERA-Interim and ERA5 Reanalyses Data on Surface Air Temperature in the Arctic. Russ. Meteorol. Hydrol. 2020, 45, 771–777. [Google Scholar] [CrossRef]
- ECMWF Fact Sheet: Earth System Data Assimilation. Available online: https://www.ecmwf.int/en/about/media-centre/focus/2020/fact-sheet-earth-system-data-assimilation (accessed on 4 December 2024).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Toreti, A.; Maiorano, A.; De Sanctis, G.; Webber, H.; Ruane, A.; Fumagalli, D.; Ceglar, A.; Niemeyer, S.; Zampieri, M. Using reanalysis in crop monitoring and forecasting systems. Agric. Syst. 2019, 168, 144–153. [Google Scholar] [CrossRef]
- Xue, C.; Niu, L.; Wu, H.; Jiang, X.; Fan, D. Drought Assessment in Belt and Road Area Based on ERA5 Reanalyses. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July—2 August 2019; pp. 7737–7740. [Google Scholar]
- Brown, D.; de Sousa, K.; van Etten, J. ag5Tools: An R package for downloading and extracting agrometeorological data from the AgERA5 database. SoftwareX 2023, 21, 101267. [Google Scholar] [CrossRef]
- Kruger, J.A.; Roffe, S.J.; van der Walt, A.J. AgERA5 representation of seasonal mean and extreme temperatures in the Northern Cape, South Africa. South Afr. J. Sci. 2024, 120, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Kistler, R.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Kalnay, E.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP–NCAR 50–Year Reanalysis: Monthly Means CD–ROM and Documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–267. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M. Reference crop evapotranspiration for data-sparse regions using reanalysis products. Agric. Water Manag. 2022, 262, 107319. [Google Scholar] [CrossRef]
- Xi, X.; Zhuang, Q.; Kim, S.; Gentine, P. Evaluating the Effects of Precipitation and Evapotranspiration on Soil Moisture Variability Within CMIP5 Using SMAP and ERA5 Data. Water Resour. Res. 2023, 59, e2022WR034225. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, G.; Chen, C.; Shen, L.; Xiao, B. Population Exposure to Compound Droughts and Heatwaves in the Observations and ERA5 Reanalysis Data in the Gan River Basin, China. Land 2021, 10, 1021. [Google Scholar] [CrossRef]
- Martins, D.S.; Paredes, P.; Raziei, T.; Pires, C.; Cadima, J.; Pereira, L.S. Assessing reference evapotranspiration estimation from reanalysis weather products. An application to the Iberian Peninsula. Int. J. Clim. 2017, 37, 2378–2397. [Google Scholar] [CrossRef]
- Meng, X.; Guo, H.; Cheng, J.; Yao, B. Can the ERA5 Reanalysis Product Improve the Atmospheric Correction Accuracy of Landsat Series Thermal Infrared Data? IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; Reig, F.; Tomas-Burguera, M.; Peña-Angulo, D.; Latorre, B.; Beguería, S.; Rabanaque, I.; Noguera, I.; Lorenzo-Lacruz, J.; et al. A global drought monitoring system and dataset based on ERA5 reanalysis: A focus on crop-growing regions. Geosci. Data J. 2023, 10, 505–518. [Google Scholar] [CrossRef]
- Paredes, P.; Martins, D.S.; Pereira, L.S.; Cadima, J.; Pires, C. Accuracy of daily estimation of grass reference evapotranspiration using ERA-Interim reanalysis products with assessment of alternative bias correction schemes. Agric. Water Manag. 2018, 210, 340–353. [Google Scholar] [CrossRef]
- Gourgouletis, N.; Gkavrou, M.; Baltas, E. Comparison of Empirical ETo Relationships with ERA5-Land and In Situ Data in Greece. Geographies 2023, 3, 499–521. [Google Scholar] [CrossRef]
- Pelosi, A.; Terribile, F.; D’urso, G.; Chirico, G.B. Comparison of ERA5-Land and UERRA MESCAN-SURFEX Reanalysis Data with Spatially Interpolated Weather Observations for the Regional Assessment of Reference Evapotranspiration. Water 2020, 12, 1669. [Google Scholar] [CrossRef]
- Pelosi, A.; Medina, H.; Bergh, J.V.D.; Vannitsem, S.; Chirico, G.B. Adaptive Kalman Filtering for Postprocessing Ensemble Numerical Weather Predictions. Mon. Weather Rev. 2017, 145, 4837–4854. [Google Scholar] [CrossRef]
- Viggiano, M.; Busetto, L.; Cimini, D.; Di Paola, F.; Geraldi, E.; Ranghetti, L.; Ricciardelli, E.; Romano, F. A new spatial modeling and interpolation approach for high-resolution temperature maps combining reanalysis data and ground measurements. Agric. For. Meteorol. 2019, 276–277, 107590. [Google Scholar] [CrossRef]
- Ferreira, P.M. GUINEA-BISSAU. Afr. Secur. Rev. 2004, 13, 44–56. [Google Scholar] [CrossRef]
- Kovsted, J.; Tarp, F. Guinea-Bissau: War, Reconstruction and Reform; UNU-WIDER: Helsinki, Finland, 1999; Available online: https://www.wider.unu.edu/sites/default/files/wp168.pdf (accessed on 10 August 2024).
- Republic of Guinea Bissau Framework Convention on Climate Change; National Communication: Bissau, Guinea Bissau, 2018; Available online: https://unfccc.int/sites/default/files/resource/TCN_Guinea_Bissau.pdf (accessed on 10 August 2024).
- Republic of Guinea Bissau Fifth National Report to the Convention on Biological Diversity; Secretary of State for Environment and Tourism: Bissau, Guinea Bissau, 2014; Available online: https://www.cbd.int/doc/world/gw/gw-nr-05-en.pdf (accessed on 10 August 2024).
- Samuel, N.; Lonatchedná, J.; Mendes, O.; Mendes, C. A Comparative Investigation of Evapotranspiration (ET) Obtained from Two Methods and Determining a Best Cultivation Period. Case of Bafata—Guinea Bissau. Int. J. Curr. Res. 2019, 11, 1468–1470. Available online: https://www.journalcra.com/article/comparative-investigation-evapotranspiration-et-obtained-two-methods-and-determining-best (accessed on 10 June 2025).
- Garbanzo, G.; Cameira, M.D.R.; Paredes, P.; Temudo, M.; Ramos, T.B. Modeling soil water and salinity dynamics in mangrove swamp rice production system of Guinea Bissau, West Africa. Agric. Water Manag. 2025, 313, 109494. [Google Scholar] [CrossRef]
- Garbanzo, G.; Céspedes, J.; Sandoval, J.; Temudo, M.; Paredes, P.; Cameira, M.D.R. Moving toward the Biophysical Characterization of the Mangrove Swamp Rice Production System in Guinea Bissau: Exploring Tools to Improve Soil- and Water-Use Efficiencies. Agronomy 2024, 14, 335. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Harris, S.A. Comments on the Application of the Holdridge System for Classification of World Life Zones as Applied to Costa Rica. Arct. Alp. Res. 2014, 5, A187–A191. [Google Scholar] [CrossRef]
- Holdridge, L.R. Determination of World Plant Formations From Simple Climatic Data. Science 1947, 105, 367–368. [Google Scholar] [CrossRef] [PubMed]
- Middleton, N.; Thomas, D. World Atlas of Desertification; UNEP, United Nations: London, UK, 1997. [Google Scholar]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- C3S. ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 10 August 2024).
- Chevuru, S.; de Wit, A.; Supit, I.; Hutjes, R. Copernicus global crop productivity indicators: An evaluation based on regionally reported yields. Clim. Serv. 2023, 30, 100374. [Google Scholar] [CrossRef]
- Van Tricht, K.; Degerickx, J.; Gilliams, S.; Zanaga, D.; Battude, M.; Grosu, A.; Brombacher, J.; Lesiv, M.; Bayas, J.C.L.; Karanam, S.; et al. WorldCereal: A dynamic open-source system for global-scale, seasonal, and reproducible crop and irrigation mapping. Earth Syst. Sci. Data 2023, 15, 5491–5515. [Google Scholar] [CrossRef]
- Ruane, A.C.; Goldberg, R.; Chryssanthacopoulos, J. Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation. Agric. For. Meteorol. 2015, 200, 233–248. [Google Scholar] [CrossRef]
- Galmarini, S.; Solazzo, E.; Ferrise, R.; Srivastava, A.K.; Ahmed, M.; Asseng, S.; Cannon, A.; Dentener, F.; De Sanctis, G.; Gaiser, T.; et al. Assessing the impact on crop modelling of multi- and uni-variate climate model bias adjustments. Agric. Syst. 2024, 215, 103846. [Google Scholar] [CrossRef]
- Global Modeling and Assimilation Office (GMAO). MERRA-2 statD_2d_slv_Nx: 2d, Daily, Aggregated Statistics, Single-Level, Assimilation, Single-Level Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. Available online: https://disc.gsfc.nasa.gov/datasets/M2SDNXSLV_5.12.4/summary (accessed on 10 December 2024).
- Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1_2d_flx_Nx: 2d, 1-Hourly, Time-Averaged, Single-Level, Assimilation, Surface Flux Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. Available online: https://disc.gsfc.nasa.gov/datasets/M2T1NXFLX_5.12.4/summary (accessed on 10 December 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009; ISBN 1441412697. [Google Scholar]
- Mardia, K.V.; Kent, J.T.; Bibby, J.M. Multivariate Analysis; Academic Press: London, UK; New York, NY, USA, 1979; ISBN 0124712525. [Google Scholar]
- Soulis, K.; Dosiadis, E.; Nikitakis, E.; Charalambopoulos, I.; Kairis, O.; Katsogiannou, A.; Gravani, S.P.; Kalivas, D. Assessing AgERA5 and MERRA-2 Global Climate Datasets for Small-Scale Agricultural Applications. Atmosphere 2025, 16, 263. [Google Scholar] [CrossRef]
- Pelosi, A.; Chirico, G. Regional assessment of daily reference evapotranspiration: Can ground observations be replaced by blending ERA5-Land meteorological reanalysis and CM-SAF satellite-based radiation data? Agric. Water Manag. 2021, 258, 107169. [Google Scholar] [CrossRef]
- Vanella, D.; Longo-Minnolo, G.; Belfiore, O.R.; Ramírez-Cuesta, J.M.; Pappalardo, S.; Consoli, S.; D’urso, G.; Chirico, G.B.; Coppola, A.; Comegna, A.; et al. Comparing the use of ERA5 reanalysis dataset and ground-based agrometeorological data under different climates and topography in Italy. J. Hydrol. Reg. Stud. 2022, 42, 101182. [Google Scholar] [CrossRef]
- Pelosi, A. Performance of the Copernicus European Regional Reanalysis (CERRA) dataset as proxy of ground-based agrometeorological data. Agric. Water Manag. 2023, 289, 108556. [Google Scholar] [CrossRef]
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference evapotranspiration estimate with limited weather data across a range of Mediterranean climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating Potential Evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L. Computing FAO56 reference grass evapotranspiration PM-ETo from temperature with focus on solar radiation. Agric. Water Manag. 2019, 215, 86–102. [Google Scholar] [CrossRef]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008. [Google Scholar]
- D’Enza, A.I.; Greenacre, M. Multiple Correspondence Analysis for the Quantification and Visualization of Large Categorical Data Sets. In Advanced Statistical Methods for the Analysis of Large Data-Sets; Di Ciaccio, A., Coli, M., Angulo Ibanez, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 453–463. ISBN 978-3-642-21036-5. [Google Scholar]
- Allen, R.G. Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Levene, H. Robust Tests for the Equality of Variance. In Contributions to Probability and Statistics; Olkin, I., Ed.; Stanford University Press: Paolo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 5th ed.; John Wiley & Sons, Inc.: Sedona, AZ, USA, 2011. [Google Scholar]
- Allen, R. Quality Assessment of Weather Data and Micrometeological Flux-Impacts on Evapotranspiration Calculation. J. Agric. Meteorol. 2008, 64, 191–204. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 30 March 2024).
- Dunkerly, C.; Huntington, J.L.; McEvoy, D.; Morway, A.; Allen, R.G. agweather-qaqc: An Interactive Python Package for Quality Assurance and Quality Control of Daily Agricultural Weather Data and Calculation of Reference Evapotranspiration. J. Open Source Softw. 2024, 9, 6368. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Alvo, M.; Yu, P.L.H. A Parametric Approach to Nonparametric Statistics; Springer Series in the Data Sciences; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-94152-3. [Google Scholar]
- Kassambara, A. Multivariate Analysis. Practical Guide To Cluster Analysis in R. Unsupervised Machine Learning; Sthda: Marseille, France, 2017. [Google Scholar]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration K-Means Clustering Method and Elbow Method For Identification of The Best Customer Profile Cluster. IOP Conf. Ser. Mater. Sci. Eng. 2018, 336, 012017. [Google Scholar] [CrossRef]
- Thorndike, R.L. Who Belongs in the Family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Céspedes, J.; Garbanzo, G.; Cabral, A.; Temudo, M.; Campagnolo, M. An Approach to Monitoring Rice Development in the Mangrove Swamp Rice Production System of Guinea-Bissau. Int. J. Appl. Earth Obs. Geoinf. 2025. submitted. [Google Scholar]
- Garbanzo, G.; Céspedes, J.; Temudo, M.; Cameira, M.D.R.; Paredes, P.; Ramos, T. Advances in soil salinity diagnosis for mangrove swamp rice production in Guinea Bissau, West Africa. Sci. Remote Sens. 2025, 11, 100231. [Google Scholar] [CrossRef]
- Bapat, R.B. Linear Algebra and Linear Models, 3rd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Huber, P.; Ronchetti, E. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Broccoli, A.J.; Manabe, S. Can existing climate models be used to study anthropogenic changes in tropical cyclone climate? Geophys. Res. Lett. 1990, 17, 1917–1920. [Google Scholar] [CrossRef]
- Hartshorn, G.S. Tropical Forest Ecosystems. In Encyclopedia of Biodiversity; Elsevier: Amsterdam, The Netherlands, 2013; pp. 269–276. [Google Scholar]
- Frank, W.M.; Young, G.S. The Interannual Variability of Tropical Cyclones. Mon. Weather Rev. 2007, 135, 3587–3598. [Google Scholar] [CrossRef]
- Linares, O.F. African rice (Oryza glaberrima): History and future potential. Proc. Natl. Acad. Sci. USA 2002, 99, 16360–16365. [Google Scholar] [CrossRef] [PubMed]
- Garbanzo, G.; Cameira, M.D.R.; Paredes, P. The Mangrove Swamp Rice Production System of Guinea Bissau: Identification of the Main Constraints Associated with Soil Salinity and Rainfall Variability. Agronomy 2024, 14, 468. [Google Scholar] [CrossRef]
- Mendes, O.; Fragoso, M. Assessment of the Record-Breaking 2020 Rainfall in Guinea-Bissau and Impacts of Associated Floods. Geosciences 2023, 13, 25. [Google Scholar] [CrossRef]
- Mendes, O.; Correia, E.; Fragoso, M. Variability and trends of the rainy season in West Africa with a special focus on Guinea-Bissau. Theor. Appl. Clim. 2025, 156, 242. [Google Scholar] [CrossRef]
- Temudo, M.P.; Cabral, A.I.R. Climate change as the last trigger in a long-lasting conflict: The production of vulnerability in northern Guinea-Bissau, West Africa. J. Peasant Stud. 2023, 50, 315–338. [Google Scholar] [CrossRef]
- Qiu, R.; Li, L.; Kang, S.; Liu, C.; Wang, Z.; Cajucom, E.P.; Zhang, B.; Agathokleous, E. An improved method to estimate actual vapor pressure without relative humidity data. Agric. For. Meteorol. 2021, 298–299, 108306. [Google Scholar] [CrossRef]
- Trajkovic, S.; Gocic, M.; Pongracz, R.; Bartholy, J.; Milanovic, M. Assessment of Reference Evapotranspiration by Regionally Calibrated Temperature-Based Equations. KSCE J. Civ. Eng. 2020, 24, 1020–1027. [Google Scholar] [CrossRef]
- Ramos, T.B.; Gonçalves, M.C.; van Genuchten, M.T. Soil salinization in Portugal: An in-depth exploration of impact, advancements, and future considerations. Vadose Zone J. 2024, 23, e20314. [Google Scholar] [CrossRef]
- Tiruye, A.; Ditthakit, P.; Linh, N.T.T.; Wipulanusat, W.; Weesakul, U.; Thongkao, S. Comparing WaPOR and ERA5-Land: Innovative Estimations of Precipitation and Evapotranspiration in the Tana Basin, Ethiopia. Earth Syst. Environ. 2024, 8, 1225–1246. [Google Scholar] [CrossRef]
- Lopez-Guerrero, A.; Cabello-Leblic, A.; Fereres, E.; Vallee, D.; Steduto, P.; Jomaa, I.; Owaneh, O.; Alaya, I.; Bsharat, M.; Ibrahim, A.; et al. Developing a Regional Network for the Assessment of Evapotranspiration. Agronomy 2023, 13, 2756. [Google Scholar] [CrossRef]
- Ippolito, M.; De Caro, D.; Cannarozzo, M.; Provenzano, G.; Ciraolo, G. Evaluation of daily crop reference evapotranspiration and sensitivity analysis of FAO Penman-Monteith equation using ERA5-Land reanalysis database in Sicily, Italy. Agric. Water Manag. 2024, 295, 108732. [Google Scholar] [CrossRef]
- Mendes, O.; Fragoso, M. Recent changes in climate extremes in Guinea-Bissau. Afr. Geogr. Rev. 2024, 44, 166–184. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).