Impact of Spatio-Temporal Variability of Droughts on Streamflow: A Remote-Sensing Approach Integrating Combined Drought Index
Abstract
1. Introduction
| Reference | Description of Drought Impact |
|---|---|
| World Health Organization [7] | Every year, globally, 55 million people are affected by droughts. Water shortages affect 40% of the world’s population, and by 2030, there is a high risk that 700 million people will be displaced due to drought occurrences. |
| World Meteorological Organization [2] | Between 1970 and 2019, about 650,000 lives were tragically lost due to drought-related impacts. |
| Food and Agriculture Organization [3] | From 2008 to 2018, 34% of crop and livestock production was lost due to droughts, which is estimated at USD 37 billion in the least-developed and low- and middle-income nations. |
| Zaveri et al. [8] | In low- or middle-income countries, moderate and severe droughts reduce their Gross Domestic Product growth by 0.39% and 0.85%, respectively. |
| Asian Development Bank [5] Naumann et al. [6] Seneviratne et al. [16] | In South Asia, the occurrence of drought events may become more frequent over the 21st century, with a current 1-in-100-year event potentially happening once every 40 to 50 years if global temperatures rise by 1.5 °C to 2 °C and approximately every 20 years with a 3 °C rise in temperatures. |
| Asian Development Bank [5] | Sri Lanka has about a 4% annual risk of experiencing severe meteorological drought, as indicated by a Standardized Precipitation Evaporation Index (SPEI) of less than −2. |
| Food and Agriculture Organization [4] | In 2016 and 2017, Sri Lanka experienced a widespread drought that severely affected cultivation, leading to a 40% drop in rice production and affecting about 900,000 people. |
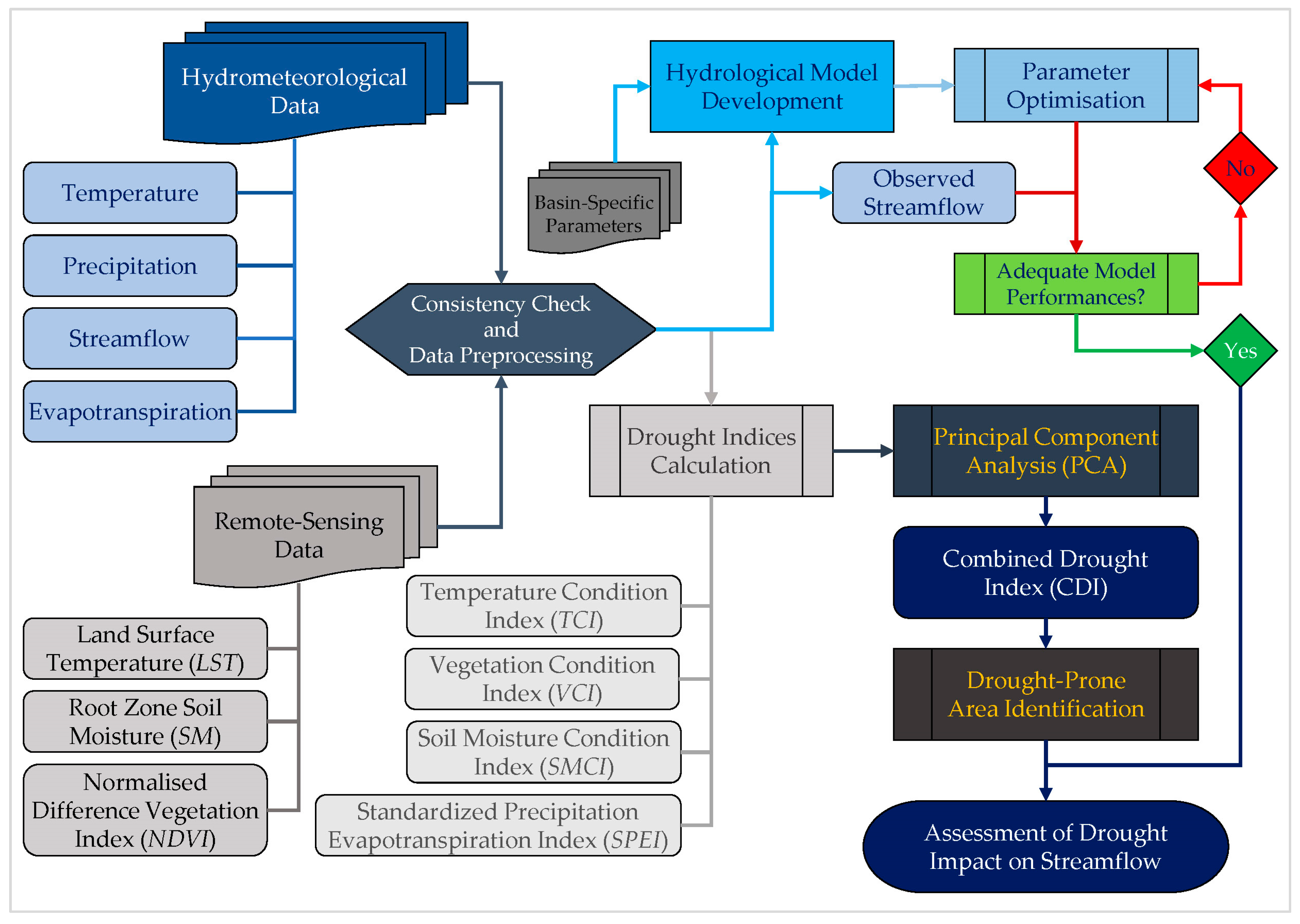
2. Materials and Methods
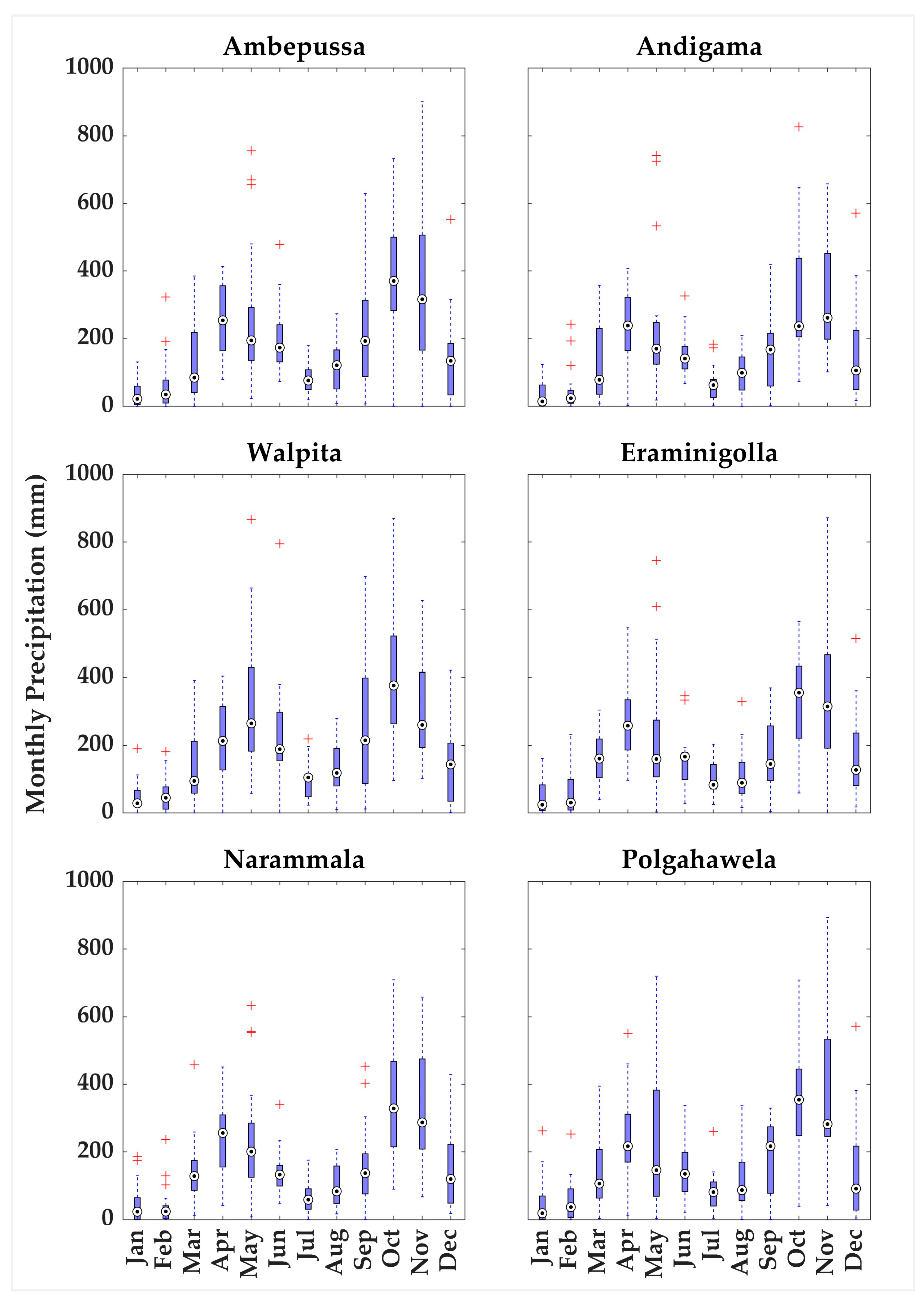
2.1. Study Area
2.2. Hydro-Meteorological and Remote-Sensing Data Collection
2.3. Development of the Combined Drought Index
2.3.1. Standardized Precipitation Evapotranspiration Index (SPEI)
2.3.2. Temperature Condition Index (TCI)
2.3.3. Vegetation Condition Index (VCI)
2.3.4. Soil Moisture Condition Index (SMCI)
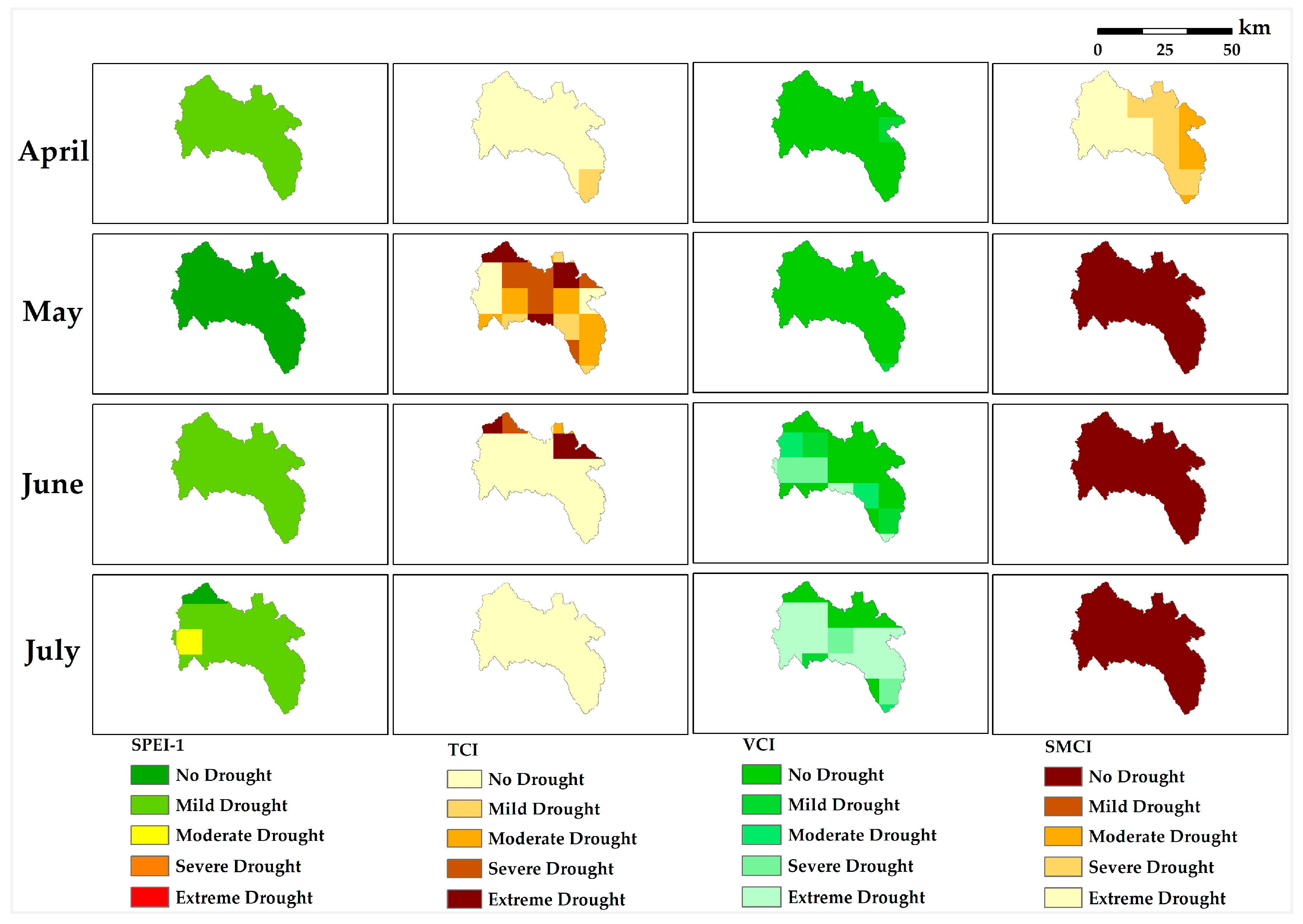
2.3.5. Spatial Dynamics of Drought Parameters
2.3.6. Formulating Combined Drought Index (CDI)
2.4. Hydrological Model Setup, Calibration, and Validation
2.5. Evaluation of the Impact of Spatial Drought Variation on Streamflow
3. Results
3.1. Relationship Between Individual Drought Parameters and Streamflow
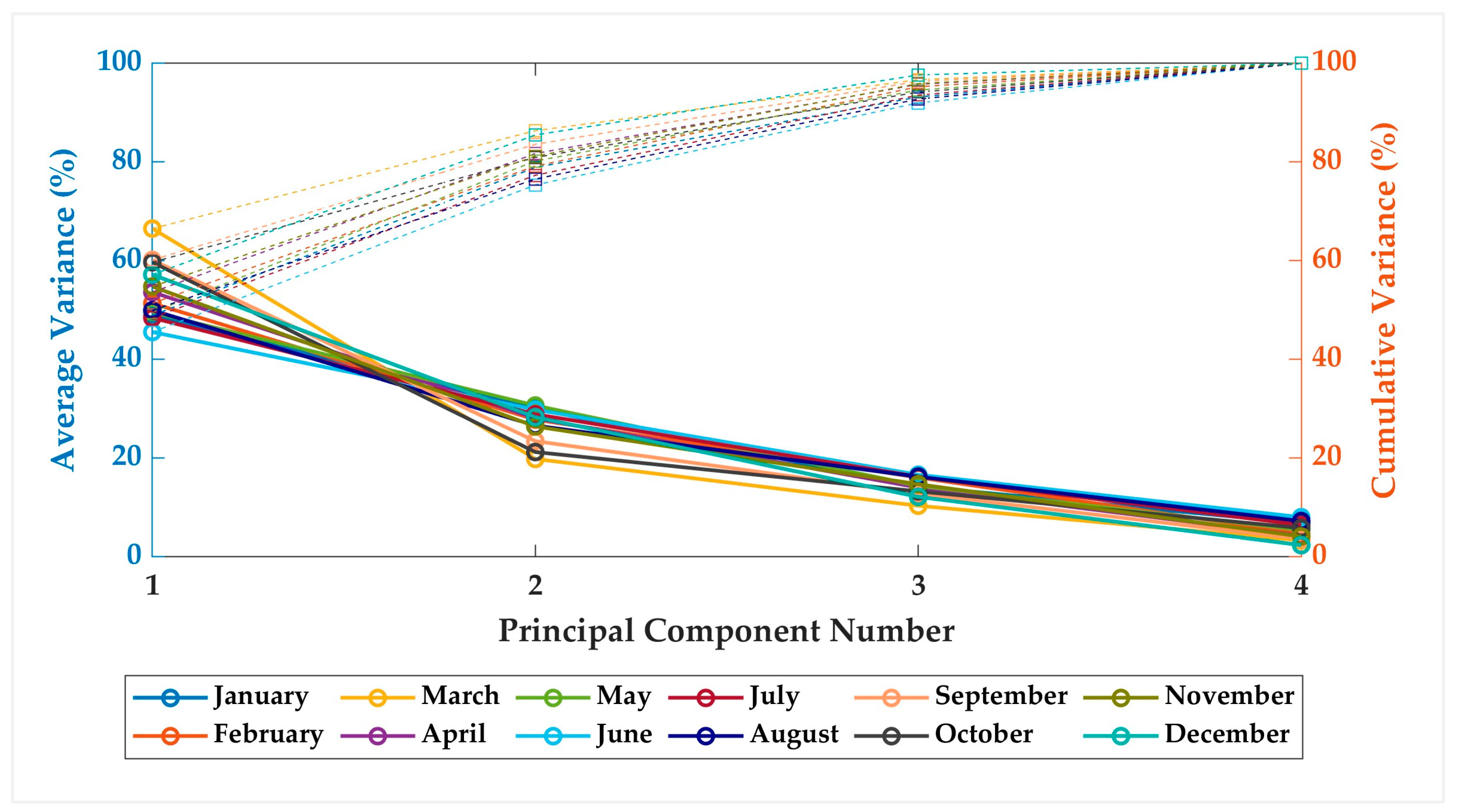
3.2. Principal Component Analysis (PCA)
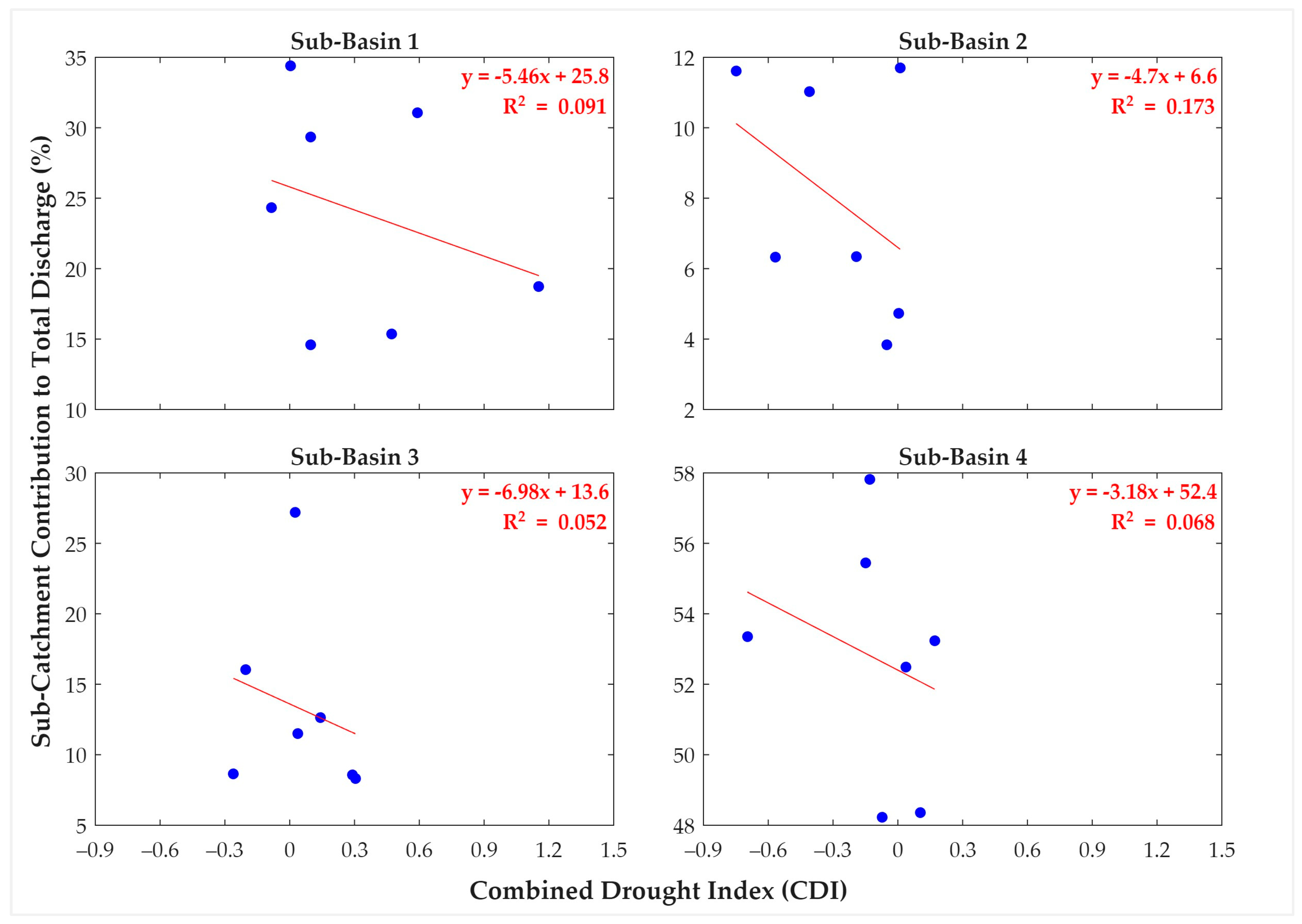
3.3. Correlation of the Combined Drought Index (CDI) with Component Indices
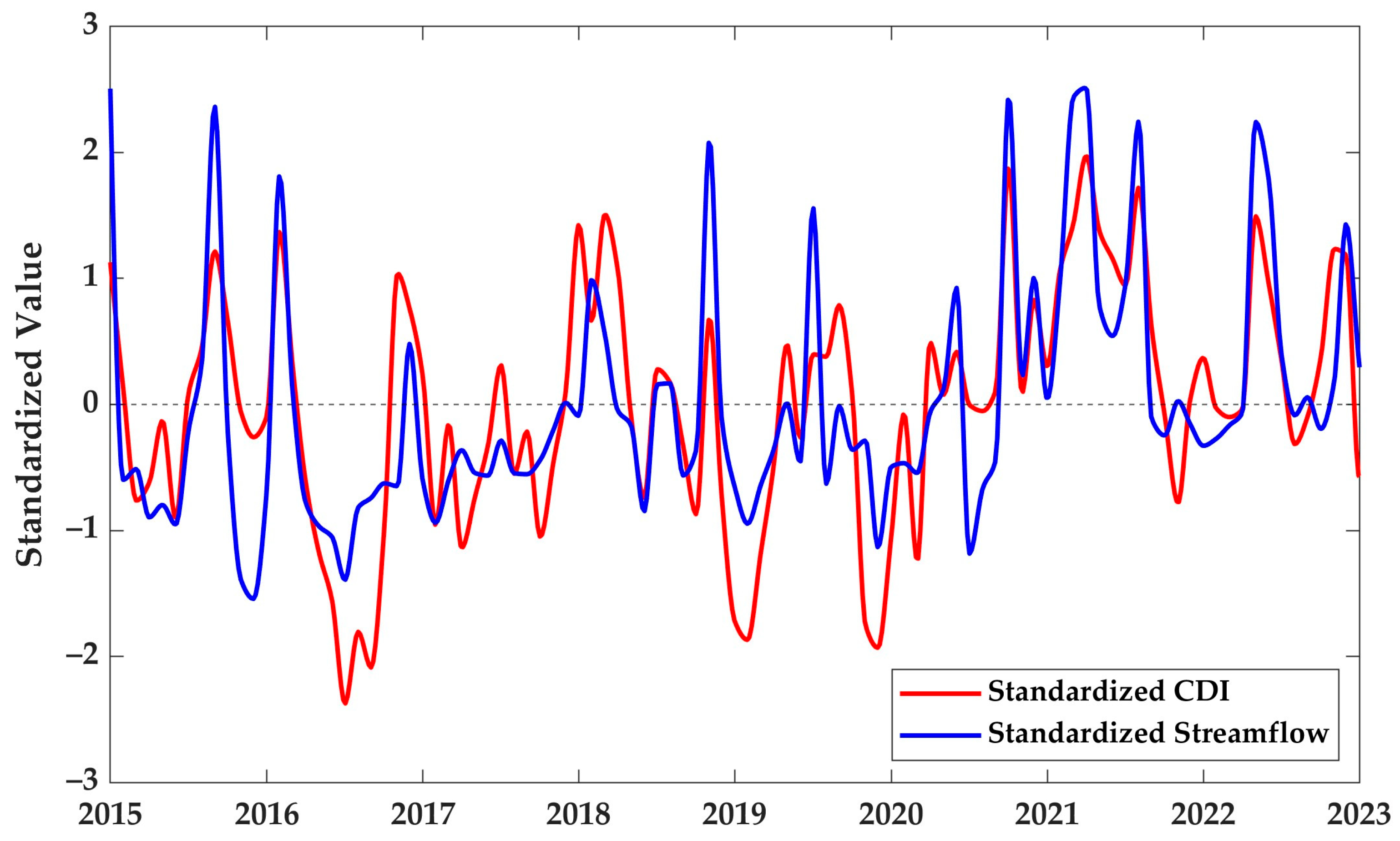
3.4. Combined Drought Index (CDI) and Validation with Streamflow
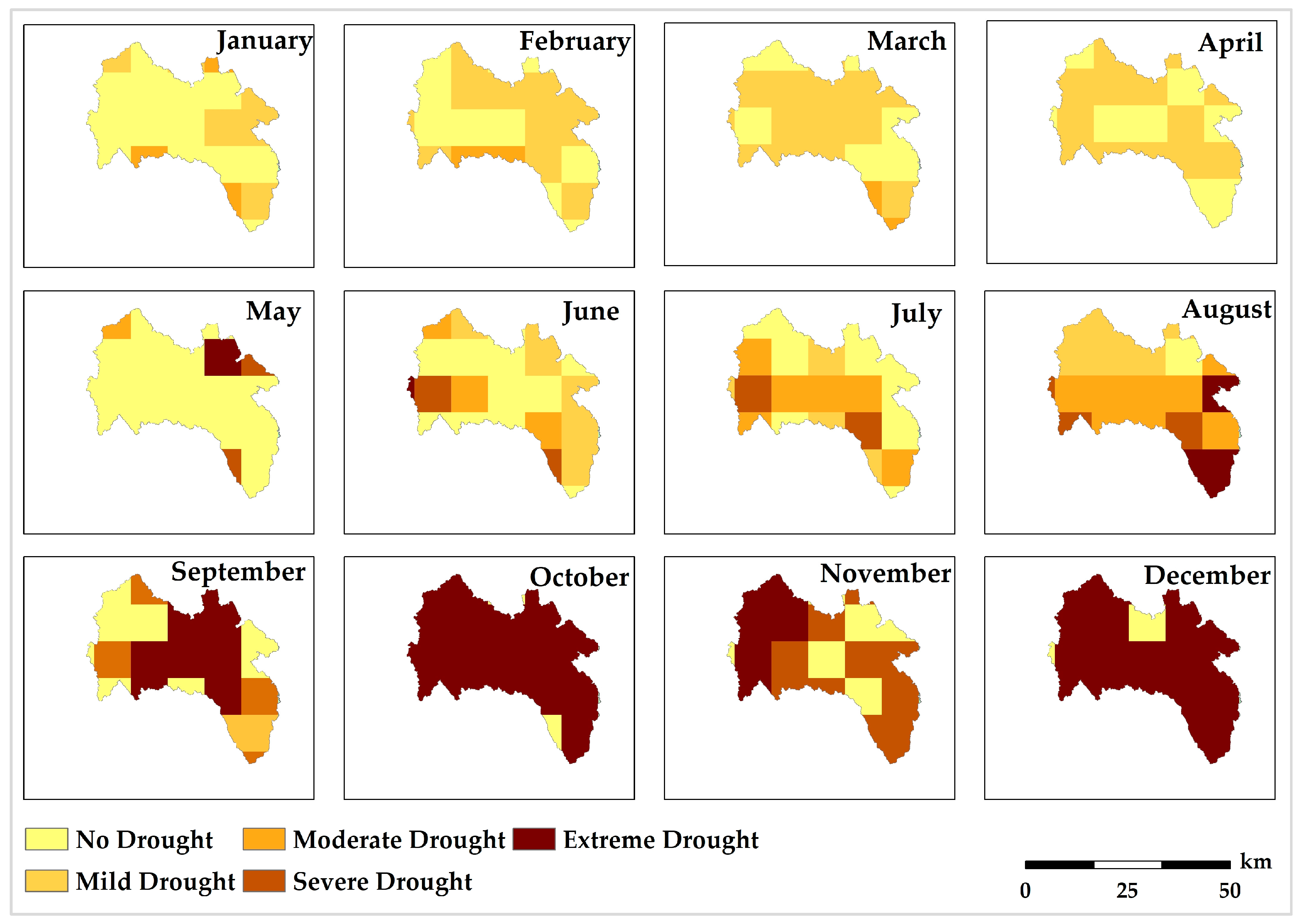
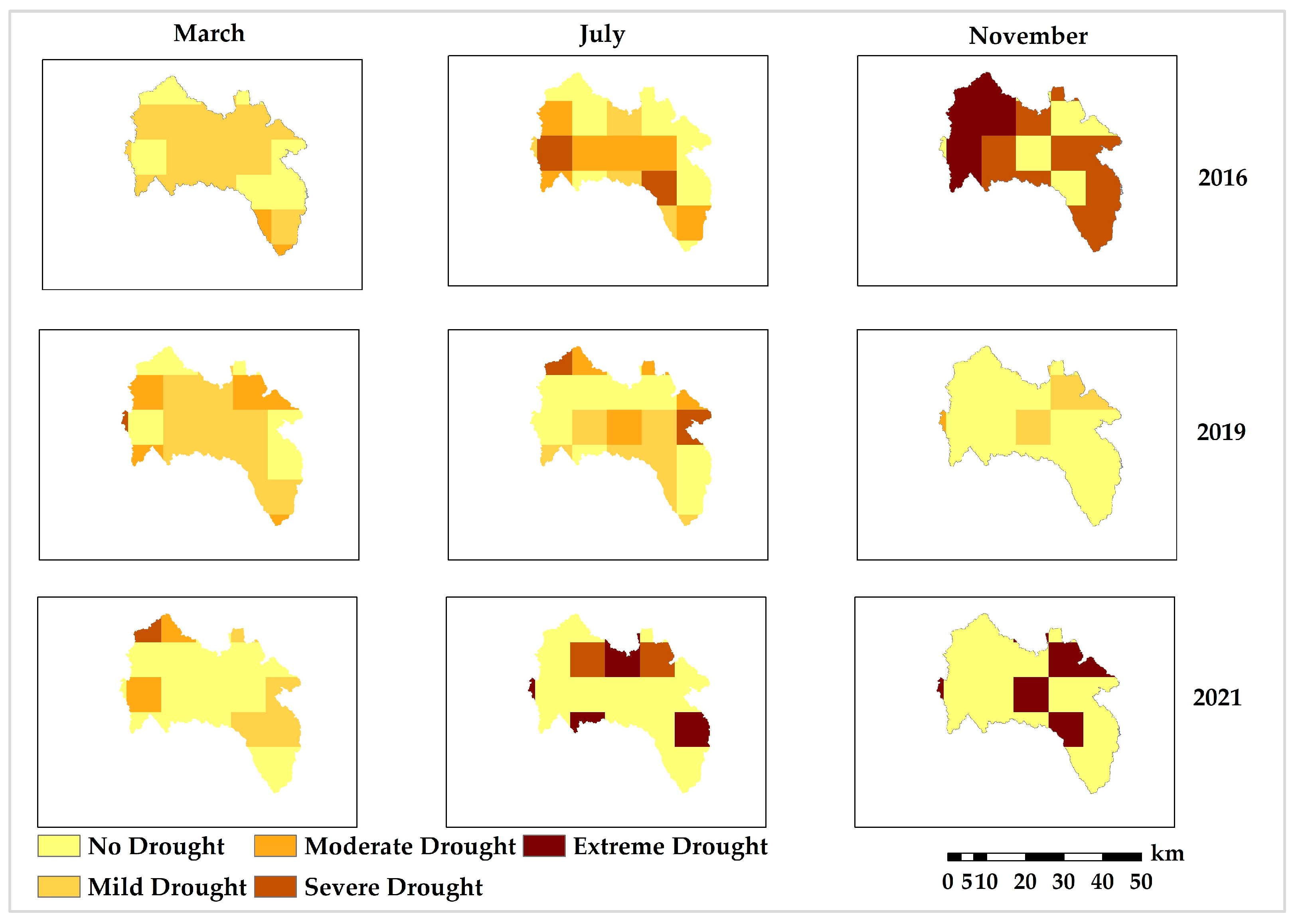
3.5. Spatial and Temporal Dynamics of Drought
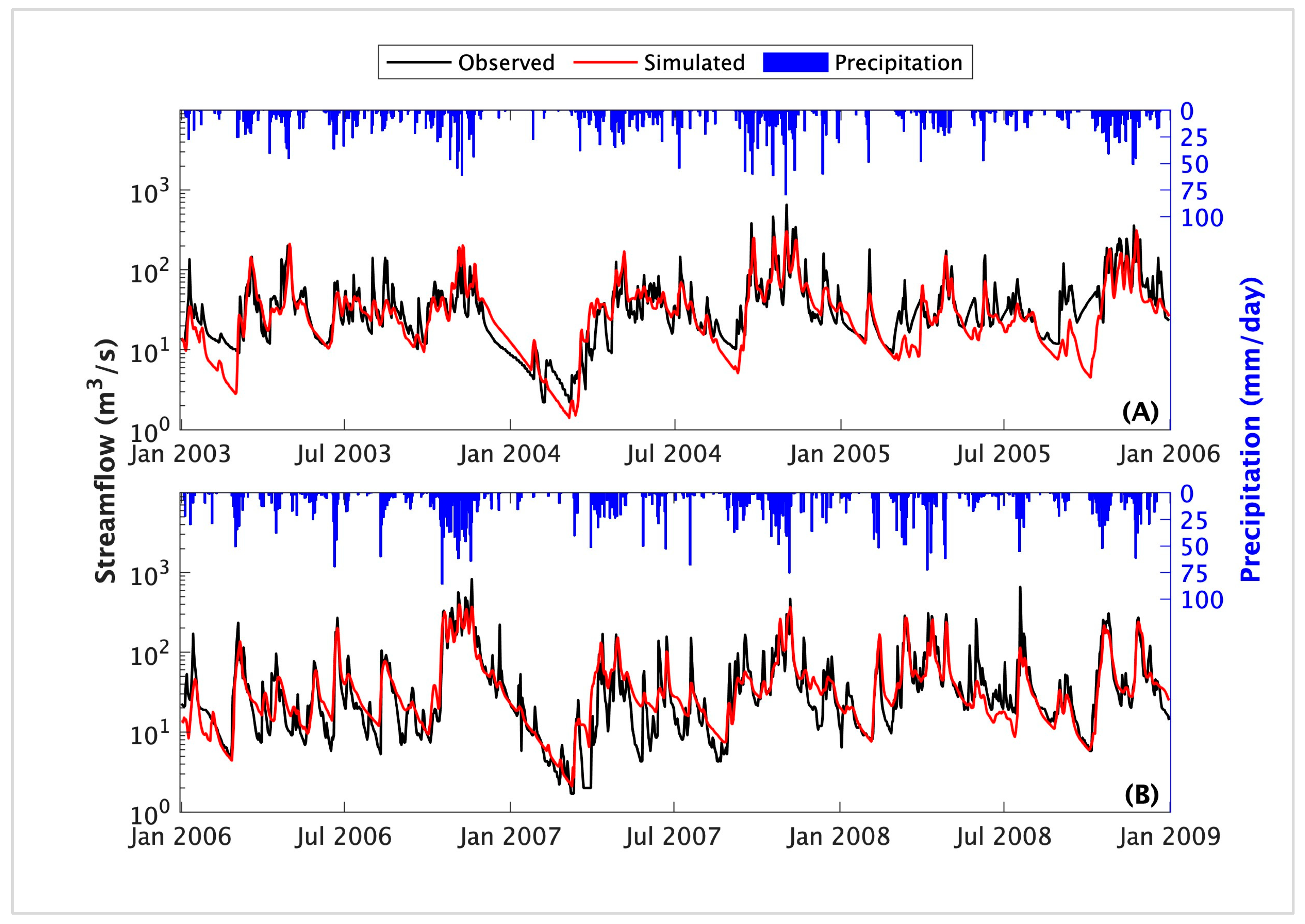
3.6. Hydrological Model Performance and Streamflow Simulation
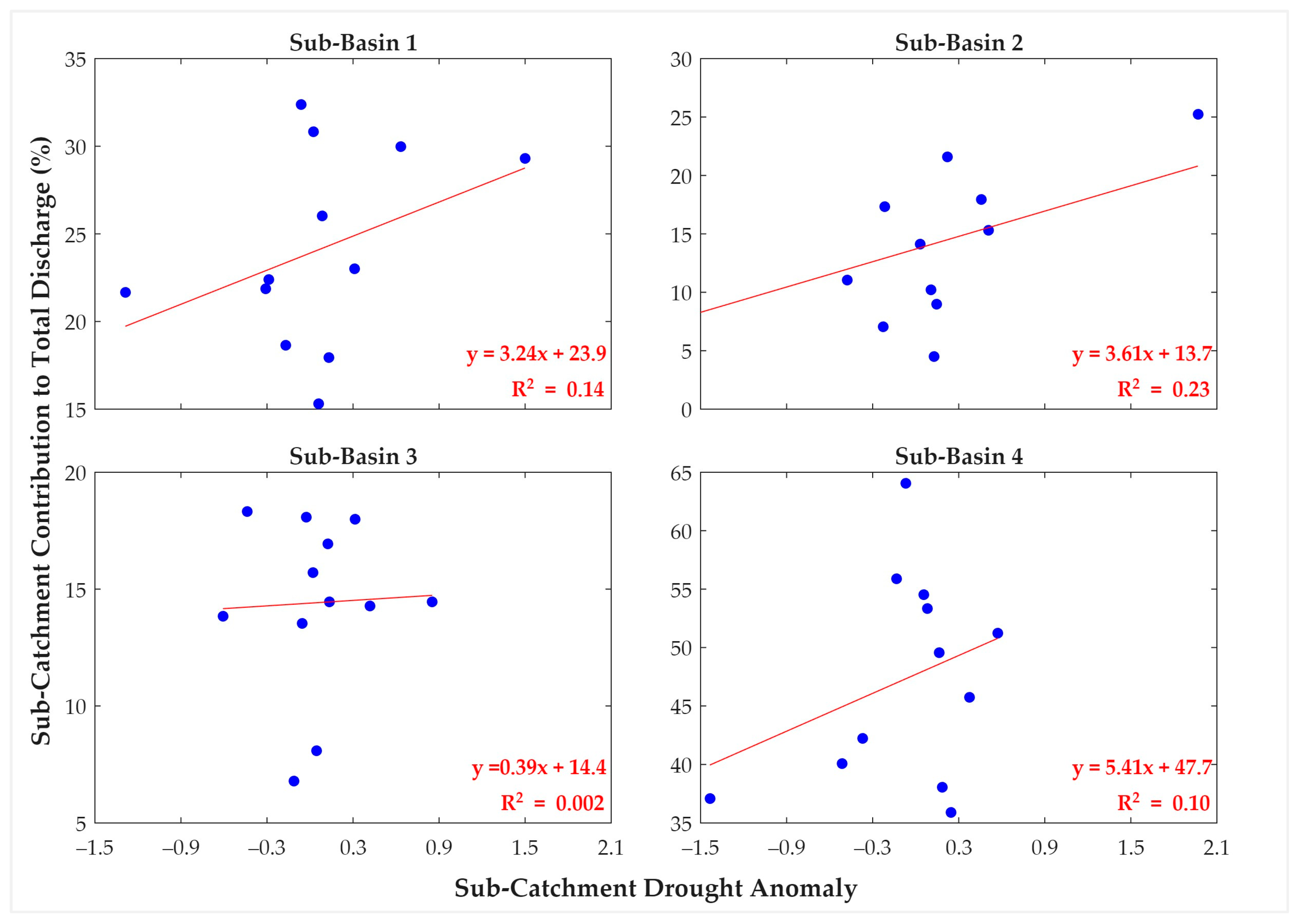
3.7. Impact of Spatial Drought Variation on Streamflow
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Drought Classes | Range |
|---|---|
| Extreme Drought | ≤−2 |
| Severe Drought | −2 to −1.5 |
| Moderate Drought | −1.5 to −1 |
| Mild Drought | −1 to 0 |
| No Drought | 0 to 3 |
| Drought Classes | Range |
|---|---|
| Extreme Drought | <0.1 |
| Severe Drought | 0.1–0.2 |
| Moderate Drought | 0.2–0.3 |
| Mild Drought | 0.3–0.4 |
| No Drought | >0.4 |
| Drought Classes | Range |
|---|---|
| Extreme Drought | CDI ≤ −1.7 |
| Severe Drought | −1.3 ≤ CDI <−1.7 |
| Moderate Drought | −0.8 ≤ CDI < −1.3 |
| Mild Drought | 0 ≤ CDI < −0.8 |
| No Drought | CDI > 0 |
| Criteria | Parameter | Sub-Basin 01 | Sub-Basin 02 | Sub-Basin 03 | Sub-Basin 04 |
|---|---|---|---|---|---|
| Canopy—Simple canopy | Initial Storage (%) | 0.27 | 0.27 | 0.10 | 2.26 |
| Max Storage (mm) | 5 | 5 | 10 | 10 | |
| Crop Coefficient | 0.64 | 0.50 | 1.49 | 1.49 | |
| Surface—Simple Surface | Initial Storage (%) | 1.7 | 1.3 | 2.9 | 3.3 |
| Max Storage (mm) | 8 | 10 | 11 | 14 | |
| Loss—Soil Moisture Accounting | Soil (%) | 4.6 | 5.7 | 1.2 | 5.0 |
| Groundwater 1 (%) | 3.1 | 5.0 | 5.3 | 4.1 | |
| Groundwater 2 (%) | 5.1 | 3.2 | 3.1 | 4.1 | |
| Maximum Infiltration (mm/h) | 9 | 10 | 10 | 8 | |
| Impervious (%) | 6 | 6 | 6 | 6 | |
| Soil Storage (mm) | 102 | 120 | 142 | 105 | |
| Tension Storage (mm) | 25 | 36 | 44 | 51 | |
| Soil Percolation (mm/h) | 5 | 4 | 2 | 0.5 | |
| Groundwater 1 Storage (mm) | 154 | 151 | 52 | 51 | |
| Groundwater 1 Percolation (mm/h) | 2.9 | 2.9 | 1.8 | 0.4 | |
| GW1 Coefficient (h) | 51 | 83 | 117 | 207 | |
| Groundwater 2 Storage (mm) | 300.76 | 300.26 | 300.94 | 300 | |
| Groundwater 2 Percolation (mm/h) | 1.0 | 1.4 | 1.8 | 0.3 | |
| GW2 Coefficient (h) | 155 | 162 | 277 | 299 | |
| Transform—SCS Unit Hydrograph | Lag Time (min) | 166 | 150 | 118 | 158 |
| Base flow—Linear Reservoir | GW 1 Initial (m3/s) | 1.7 | 2.0 | 1.7 | 2.0 |
| GW 1 Fraction | 0.5 | 0.5 | 0.5 | 0.5 | |
| GW 1 Reservoirs | 2 | 2 | 2 | 2 | |
| GW 2 Initial (m3/s) | 1.5 | 1.2 | 2.0 | 1.4 | |
| GW 2 Fraction | 0.3 | 0.3 | 0.3 | 0.3 | |
| GW 2 Reservoirs | 1 | 1 | 1 | 1 | |
| Routing—Muskingum | Muskingum K (h) | 15.4 | 22.9 | 16.2 | |
| Muskingum X | 0.20 | 0.27 | 0.47 |
References
- World Meteorological Organization. Drought Monitoring and Early Warning: Concepts, Progress and Future Challenges Weather and Climate Information for Sustainable Agricultural Development; World Meteorological Organization: Geneva, Switzerland, 2006. [Google Scholar]
- World Meteorological Organization. Weather-Related Disasters Increase over Past 50 Years, Causing More Damage but Fewer Deaths. Available online: https://wmo.int/news/media-centre/weather-related-disasters-increase-over-past-50-years-causing-more-damage-fewer-deaths (accessed on 26 March 2025).
- Food and Agriculture Organization of the United Nations. Agriculture on the Proving Grounds: Damage and Loss. Available online: https://www.fao.org/interactive/disasters-in-agriculture/en/ (accessed on 16 April 2025).
- Food and Agriculture Organization of the United Nations. Sri Lanka’s Food Production Hit by Extreme Drought Followed by Floods|FAO in Sri Lanka|Food and Agriculture Organization of the United Nations. Available online: https://www.fao.org/srilanka/news/detail-events/en/c/897464/ (accessed on 24 March 2025).
- Asian Development Bank. Sri Lanka Climate Risk Country Profile; Asian Development Bank: Mandaluyong City, Philippines, 2020. [Google Scholar]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global Changes in Drought Conditions Under Different Levels of Warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- World Health Organization. Drought. Available online: https://www.who.int/health-topics/drought#tab=tab_1 (accessed on 26 April 2025).
- Zaveri, E.D.; Damania, R.; Engle, N. Droughts and Deficits: The Global Impact of Droughts on Economic Growth; Policy Research Working Paper; Water Global Practice, The World Bank: Washington, DC, USA, 2023. [Google Scholar]
- Jing, F.; Baisha, W.; Cheng, Z.; Qing, W. The Recognition of Drought and Its Driving Mechanism Based on “Natural-Artificial” Dual Water Cycle. Procedia Eng. 2012, 28, 580–585. [Google Scholar] [CrossRef]
- Ndayiragije, J.M.; Li, F. Effectiveness of Drought Indices in the Assessment of Different Types of Droughts, Managing and Mitigating Their Effects. Climate 2022, 10, 125. [Google Scholar] [CrossRef]
- Cavus, Y.; Aksoy, H. Critical Drought Severity/Intensity-Duration-Frequency Curves Based on Precipitation Deficit. J. Hydrol. 2020, 584, 124312. [Google Scholar] [CrossRef]
- Hong, S.; Deng, H.; Zheng, Z.; Deng, Y.; Chen, X.; Gao, L.; Chen, Y.; Liu, M. The Influence of Variations in Actual Evapotranspiration on Drought in China’s Southeast River Basin. Sci. Rep. 2023, 13, 21336. [Google Scholar] [CrossRef]
- Mishra, V.; Aadhar, S.; Asoka, A.; Pai, S.; Kumar, R. On the Frequency of the 2015 Monsoon Season Drought in the Indo-Gangetic Plain. Geophys. Res. Lett. 2016, 43, 12,102–12,112. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Rajeevan, M. Trends in the Rainfall Pattern over India. Int. J. Climatol. 2008, 28, 1453–1469. [Google Scholar] [CrossRef]
- Chen, Y.; Teo, F.Y.; Wong, S.Y.; Chan, A.; Weng, C.; Falconer, R.A. Monsoonal Extreme Rainfall in Southeast Asia: A Review. Water 2024, 17, 5. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Weather and Climate Extreme Events in a Changing Climate. In Climate Change 2021—The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1513–1766. [Google Scholar]
- Martínez-Sifuentes, A.R.; Trucíos-Caciano, R.; Rodríguez-Moreno, V.M.; Villanueva-Díaz, J.; Estrada-Ávalos, J. The Impact of Climate Change on Evapotranspiration and Flow in a Major Basin in Northern Mexico. Sustainability 2023, 15, 847. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Sorensson, A.A.; Almazroui, M.; Dosio, A.; Gutowski, W.J.; Haarsma, R.; Hamdi, R.; Hewitson, B.; Kwon, W.-T.; Lamptey, B.L.; et al. Linking Global to Regional Climate Change. In Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Mishra, V.; Kumar, R.; Shah, H.L.; Samaniego, L.; Eisner, S.; Yang, T. Multimodel Assessment of Sensitivity and Uncertainty of Evapotranspiration and a Proxy for Available Water Resources under Climate Change. Clim. Change 2017, 141, 451–465. [Google Scholar] [CrossRef]
- Sanogo, N.D.M.; Dayamba, S.D.; Renaud, F.G.; Feurer, M. From Wooded Savannah to Farmland and Settlement: Population Growth, Drought, Energy Needs and Cotton Price Incentives Driving Changes in Wacoro, Mali. Land 2022, 11, 2117. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, W.; Jin, Z.; Yan, J.; Lü, Y.; Li, S.; Yu, Q. Rapid Urbanization and Agricultural Intensification Increase Regional Evaporative Water Consumption of the Loess Plateau. J. Geophys. Res. Atmos. 2020, 125, e2020JD033380. [Google Scholar] [CrossRef]
- Eyring, V.; Gillett, N.P.; Achuta Rao, K.M.; Barimalala, R.; Barreiro Parrillo, M.; Bellouin, N.; Cassou, C.; Durack, P.J.; Kosaka, Y.; McGregor, S.; et al. Human Influence on the Climate System. In Climate Change 2021—The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 423–552. [Google Scholar]
- Tran, H.T.; Campbell, J.B.; Wynne, R.H.; Shao, Y.; Phan, S.V. Drought and Human Impacts on Land Use and Land Cover Change in a Vietnamese Coastal Area. Remote Sens. 2019, 11, 333. [Google Scholar] [CrossRef]
- Khan, M.; Chen, R. Assessing the Impact of Land Use and Land Cover Change on Environmental Parameters in Khyber Pakhtunkhwa, Pakistan: A Comprehensive Study and Future Projections. Remote Sens. 2025, 17, 170. [Google Scholar] [CrossRef]
- Gupta, R.; Yan, K.; Singh, T.; Mo, D. Domestic and International Drivers of the Demand for Water Resources in the Context of Water Scarcity: A Cross-Country Study. J. Risk Financ. Manag. 2020, 13, 255. [Google Scholar] [CrossRef]
- Tzanakakis, V.A.; Paranychianakis, N.V.; Angelakis, A.N. Water Supply and Water Scarcity. Water 2020, 12, 2347. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite Remote Sensing for Water Resources Management: Potential for Supporting Sustainable Development in Data-Poor Regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Van Rooy, M.P. A Rainfall Anomaly Index (RAI), Independent of the Time and Space. Notos 1965, 14, 43–48. [Google Scholar]
- Bajracharya, S.; Gunawardhana, L.N.; Sirisena, J.; Bamunawala, J.; Rajapakse, L.; Odara, M.G.N. Unlocking the Mysteries of Drought: Integrating Snowmelt Dynamics into Drought Analysis at the Narayani River Basin, Nepal. Nat. Hazards 2025, 121, 5267–5291. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Narasimhan, B.; Srinivasan, R. Development and Evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for Agricultural Drought Monitoring. Agric. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Shafer, B.A.; Dezman, L.E. Development of a Surface Water Supply Index (SWSI) to Assess the Severity of Drought Conditions in Snowpack Runoff Areas. In Proceedings of the Western Snow Conference, Reno, Nevada, 19–23 April 1982; pp. 164–175. [Google Scholar]
- Alahacoon, N.; Edirisinghe, M.; Ranagalage, M. Satellite-Based Meteorological and Agricultural Drought Monitoring for Agricultural Sustainability in Sri Lanka. Sustainability 2021, 13, 3427. [Google Scholar] [CrossRef]
- Sirisena, J.; Augustijn, D.; Nazeer, A.; Bamunawala, J. Use of Remote-Sensing-Based Global Products for Agricultural Drought Assessment in the Narmada Basin, India. Sustainability 2022, 14, 13050. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, Y.; Chang, J.; Zhou, S.; Guo, A. Spatial and Temporal Evolution of Drought Characteristics across the Yellow River Basin. Ecol. Indic. 2021, 131, 108207. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.; Olivares, B.O.; Movil-Fuentes, Y.; Arevalo-Groening, J.; Gil, A. Assessing the Spatiotemporal Patterns and Impacts of Droughts in the Orinoco River Basin Using Earth Observations Data and Surface Observations. Hydrology 2023, 10, 195. [Google Scholar] [CrossRef]
- Houmma, I.H.; Hadri, A.; Boudhar, A.; Karaoui, I.; Oussaoui, S.; El Khalki, E.M.; Chehbouni, A.; Kinnard, C. Analysis of the Propagation Characteristics of Meteorological Drought to Hydrological Drought and Their Joint Effects on Low-Flow Drought Variability in the Oum Er Rbia Watershed, Morocco. Remote Sens. 2025, 17, 281. [Google Scholar] [CrossRef]
- Raczynski, K.; Dyer, J. Variability of Annual and Monthly Streamflow Droughts over the Southeastern United States. Water 2022, 14, 3848. [Google Scholar] [CrossRef]
- Central Environment Authority. Water Quality Monitoring of Ma Oya. Available online: https://www.cea.lk/web/en/water?id=158 (accessed on 20 November 2024).
- Imbulana, K.A.U.S.; Wijesekera, N.T.S.; Neupane, B.R. Sri Lanka National Water Development Report; UNESCO & Ministry of Agriculture, Irrigation and Mahaweli Development: Colombo, Sri Lanka, 2006. [Google Scholar]
- World Meteorological Organization, WMO Guidelines on the Calculation of Climate Normals; World Meteorological Organization: Geneva, Switzerland, 2017.
- Pabasara, K.; Gunawardhana, L.; Bamunawala, J.; Sirisena, J.; Rajapakse, L. Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka. Hydrology 2024, 11, 116. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Carrillo-Carrillo, M.; Ibáñez-Castillo, L.; Arteaga-Ramírez, R.; Arévalo-Galarza, G. Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City. Atmosphere 2025, 16, 202. [Google Scholar] [CrossRef]
- Parviz, L. Determination of Effective Indices in the Drought Monitoring through Analysis of Satellite Images. J. Agric. For. 2016, 62, 305–324. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Zhou, J.; Zhou, L.; Xie, B.; Li, C. Monitoring Drought Dynamics in China Using Optimized Meteorological Drought Index (OMDI) Based on Remote Sensing Data Sets. J. Environ. Manag. 2021, 292, 112733. [Google Scholar] [CrossRef]
- Kogan, F.N. Remote Sensing of Weather Impacts on Vegetation in Non-Homogeneous Areas. Int. J. Remote Sens. 1990, 11, 1405–1419. [Google Scholar] [CrossRef]
- Reichle, R.; De Lannoy, G.; Koster, R.D.; Crow, W.T.; Kimball, J.S.; Liu, Q. SMAP L4 Global 3-hourly 9 km EASE-Grid Surface and Root Zone Soil Moisture Geophysical Data. (SPL4SMGP, Version 4). [Data Set]. NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction. Disaster Risk Reduction in Sri Lanka; United Nations Office for Disaster Risk Reduction: Nairobi, Kenya, 2019. [Google Scholar]
- Cai, S.; Zuo, D.; Wang, H.; Xu, Z.; Wang, G.; Yang, H. Assessment of Agricultural Drought Based on Multi-Source Remote Sensing Data in a Major Grain Producing Area of Northwest China. Agric. Water Manag. 2023, 278, 108142. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, S.; Zhang, H.; Bai, Y.; Zhang, J. Monitoring Drought Using Composite Drought Indices Based on Remote Sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef]
- Suo, N.; Xu, C.; Cao, L.; Song, L.; Lei, X. A Copula-Based Parametric Composite Drought Index for Drought Monitoring and Applicability in Arid Central Asia. Catena 2024, 235, 107624. [Google Scholar] [CrossRef]
- Başakın, E.E.; Stoy, P.C.; Demirel, M.C.; Ozdogan, M.; Otkin, J.A. Combined Drought Index Using High-Resolution Hydrological Models and Explainable Artificial Intelligence Techniques in Türkiye. Remote Sens. 2024, 16, 3799. [Google Scholar] [CrossRef]
- Pandya, P.; Gontia, N.K.; Parmar, H.V. Development of PCA-Based Composite Drought Index for Agricultural Drought Assessment Using Remote-Sensing. J. Agrometeorol. 2022, 24, 384–392. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.F.; Hastie, T.; D’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal Component Analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Vithanage, R.; Gunawardhana, L. Integrating Remote Sensing Data with Hydrological Modeling for Drought Analysis. In Proceedings of the 2024 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 8–10 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 187–192. [Google Scholar]
- Hydrologic Engineering Center. HEC-HMS Technical Reference Manual. 2023. Available online: https://www.hec.usace.army.mil/confluence/hmsdocs/hmstrm (accessed on 29 January 2025).
- International Federation of Red Cross and Red Crescent Societies. Sri Lanka: Floods and Landslides—Final Report (MDRLK012); International Federation of Red Cross and Red Crescent Societies: Geneva, Switzerland, 2022. [Google Scholar]
- Kulkarni, S.; Sawada, Y.; Bayissa, Y.; Wardlow, B. Global Assessment of Socio-Economic Impacts of Subnational Droughts: A Comparative Analysis of Combined Versus Single Drought Indicators. Hydrol. Earth Syst. Sci. Discuss. 2024. in review. [Google Scholar]
- Hendawitharana, S.U.; Priyasad, M.K.D.D.; Rajapakse, R.L.H.L. Comparative Study of Spatial and Temporal Variation of Drought Using Remotely Sensed Data—A Case Study for Kirindi Oya Basin. In ICSBE 2018; Springer: Singapore, 2020; pp. 116–130. [Google Scholar]
- Wu, H.; Xiong, D.; Liu, B.; Zhang, S.; Yuan, Y.; Fang, Y.; Chidi, C.L.; Dahal, N.M. Spatio-Temporal Analysis of Drought Variability Using CWSI in the Koshi River Basin (KRB). Int. J. Environ. Res. Public Health 2019, 16, 3100. [Google Scholar] [CrossRef]
- Dahlmann, H.; Stephan, R.; Stahl, K. Upstream-Downstream Asymmetries of Drought Impacts in Major River Basins of the European Alps. Front. Water 2022, 4, 1061991. [Google Scholar] [CrossRef]
- Liu, Q.; Liang, L.; Sun, T.; Wang, X.; Yan, D.; Li, C. Hydrological Response of Drought Impacts across Catchments Worldwide. Sci. Total Environ. 2024, 931, 172912. [Google Scholar] [CrossRef] [PubMed]
- Fernando, R.; Ratnasooriya, H.; Bamunawala, J.; Sirisena, J.; Nipuni Odara, M.G.; Gunawardhana, L.; Rajapakse, L. Assessing Climate-Change-Driven Impacts on Water Scarcity: A Case Study of Low-Flow Dynamics in the Lower Kalu River Basin, Sri Lanka. Water 2024, 16, 1317. [Google Scholar] [CrossRef]

| Dataset | Resolution | Source |
|---|---|---|
| Rainfall | Daily | Meteorology Department, Sri Lanka |
| Temperature | Daily | Meteorology Department, Sri Lanka |
| Evapotranspiration | Monthly | 2005/06 and 2016/17 Hydrological Annual Reports, Irrigation Department, Sri Lanka |
| Streamflow | Daily | Irrigation Department, Sri Lanka |
| Land Surface Temperature (MOD21C3.061) | Monthly (5.6 km × 5.6 km) | NASA Land Processes Distributed Active Archive Center (NASA LP DAAC) |
| Normalized Difference Vegetation Index (MOD13A3) | Monthly (1 km × 1 km) | NASA Land Processes Distributed Active Archive Center (NASA LP DAAC) |
| SMAP L4 Root Zone Soil Moisture | 3 hourly (9 km × 9 km) | National Snow and Ice Data Centre Distributed Active Archive Center (NSIDC DAAC), USA |
| Digital Elevation Model | 30 m × 30 m | United States Geological Survey (USGS) Shuttle Radar Topography Mission (SRTM) 1 Arc-second Global Data |
| Land Use/Land Cover | 10 m × 10 m | Environmental Systems Research Institute (Esri) Sentinel-2 10 m Land Use/Land Cover (2017–2018) |
| Month | Variance (%) | Month | Variance (%) |
|---|---|---|---|
| January | 48.9 | July | 48.4 |
| February | 51.4 | August | 50.0 |
| March | 66.5 | September | 60.1 |
| April | 53.6 | October | 59.7 |
| May | 49.5 | November | 54.8 |
| June | 45.5 | December | 57.2 |
| Metrics | Calibration | Validation |
|---|---|---|
| NSE | 0.60 | 0.74 |
| NSElog | 0.61 | 0.81 |
| PBIAS | 15.5% | 11.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srimali, A.; Gunawardhana, L.; Bamunawala, J.; Sirisena, J.; Rajapakse, L. Impact of Spatio-Temporal Variability of Droughts on Streamflow: A Remote-Sensing Approach Integrating Combined Drought Index. Hydrology 2025, 12, 142. https://doi.org/10.3390/hydrology12060142
Srimali A, Gunawardhana L, Bamunawala J, Sirisena J, Rajapakse L. Impact of Spatio-Temporal Variability of Droughts on Streamflow: A Remote-Sensing Approach Integrating Combined Drought Index. Hydrology. 2025; 12(6):142. https://doi.org/10.3390/hydrology12060142
Chicago/Turabian StyleSrimali, Anoma, Luminda Gunawardhana, Janaka Bamunawala, Jeewanthi Sirisena, and Lalith Rajapakse. 2025. "Impact of Spatio-Temporal Variability of Droughts on Streamflow: A Remote-Sensing Approach Integrating Combined Drought Index" Hydrology 12, no. 6: 142. https://doi.org/10.3390/hydrology12060142
APA StyleSrimali, A., Gunawardhana, L., Bamunawala, J., Sirisena, J., & Rajapakse, L. (2025). Impact of Spatio-Temporal Variability of Droughts on Streamflow: A Remote-Sensing Approach Integrating Combined Drought Index. Hydrology, 12(6), 142. https://doi.org/10.3390/hydrology12060142









