Future Dynamics of Drought in Areas at Risk: An Interpretation of RCP Projections on a Regional Scale
Abstract
1. Introduction
2. Materials and Methods
2.1. Area of Study
2.2. Precipitation Dataset
2.3. Bias Adjusting
2.4. Calculation of Pluviometric Deficit
3. Results and Discussion
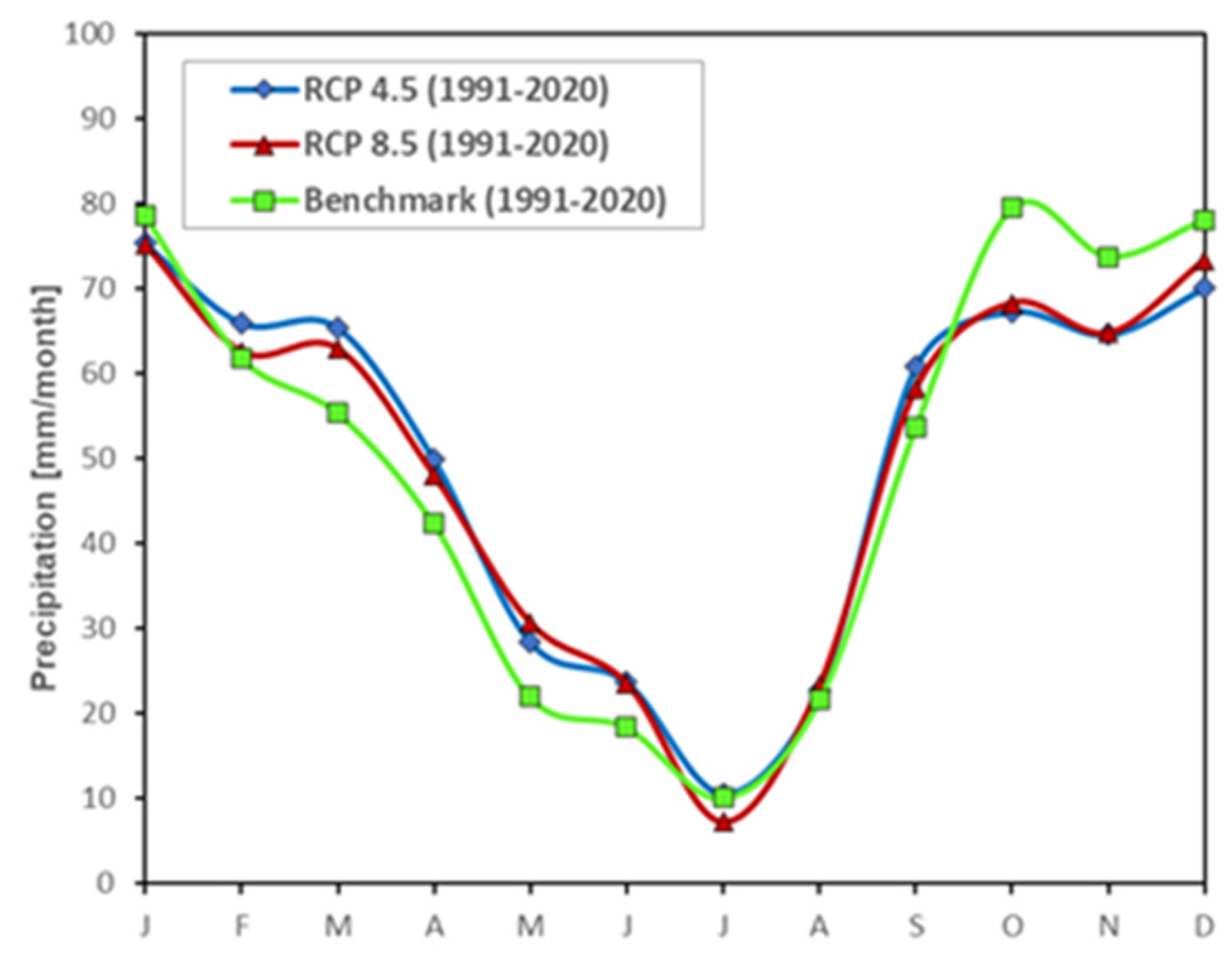
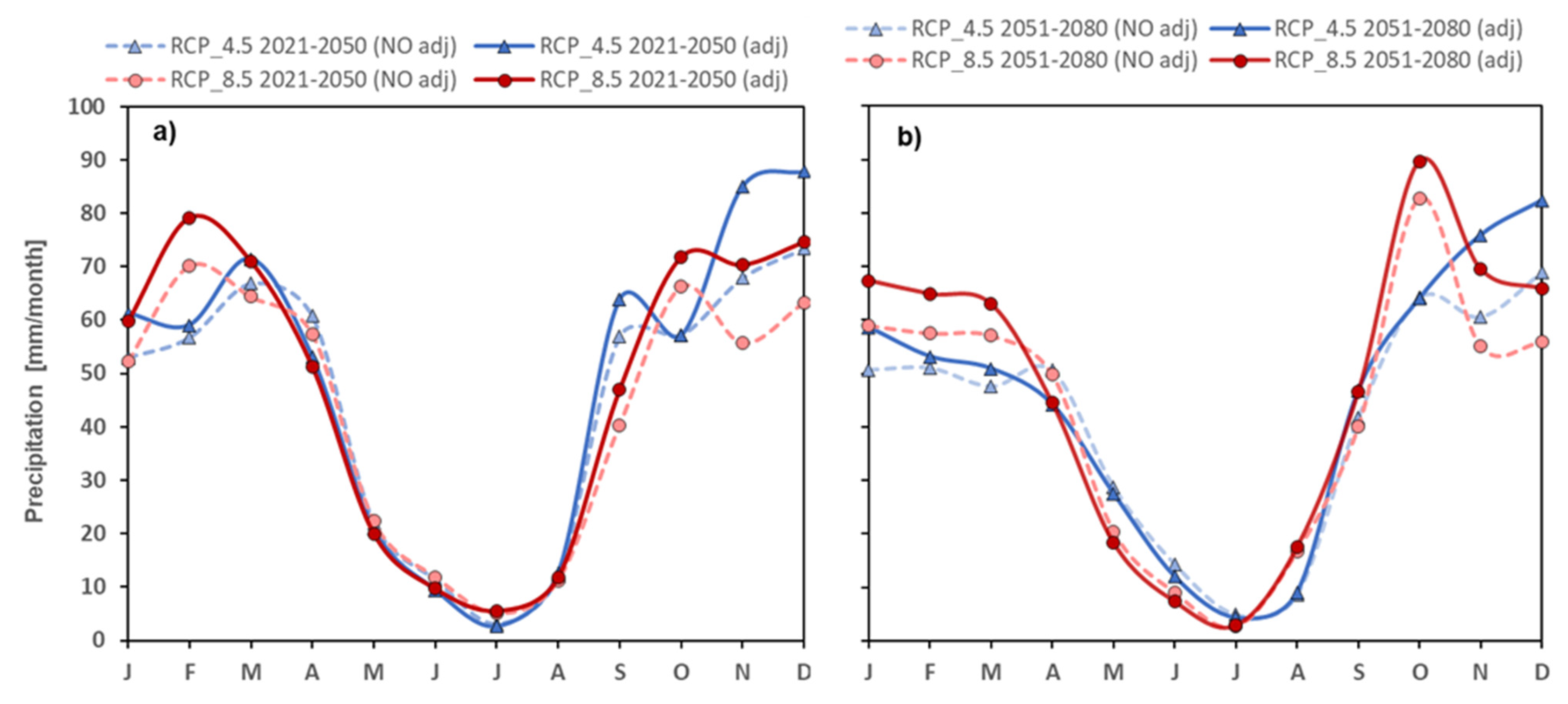
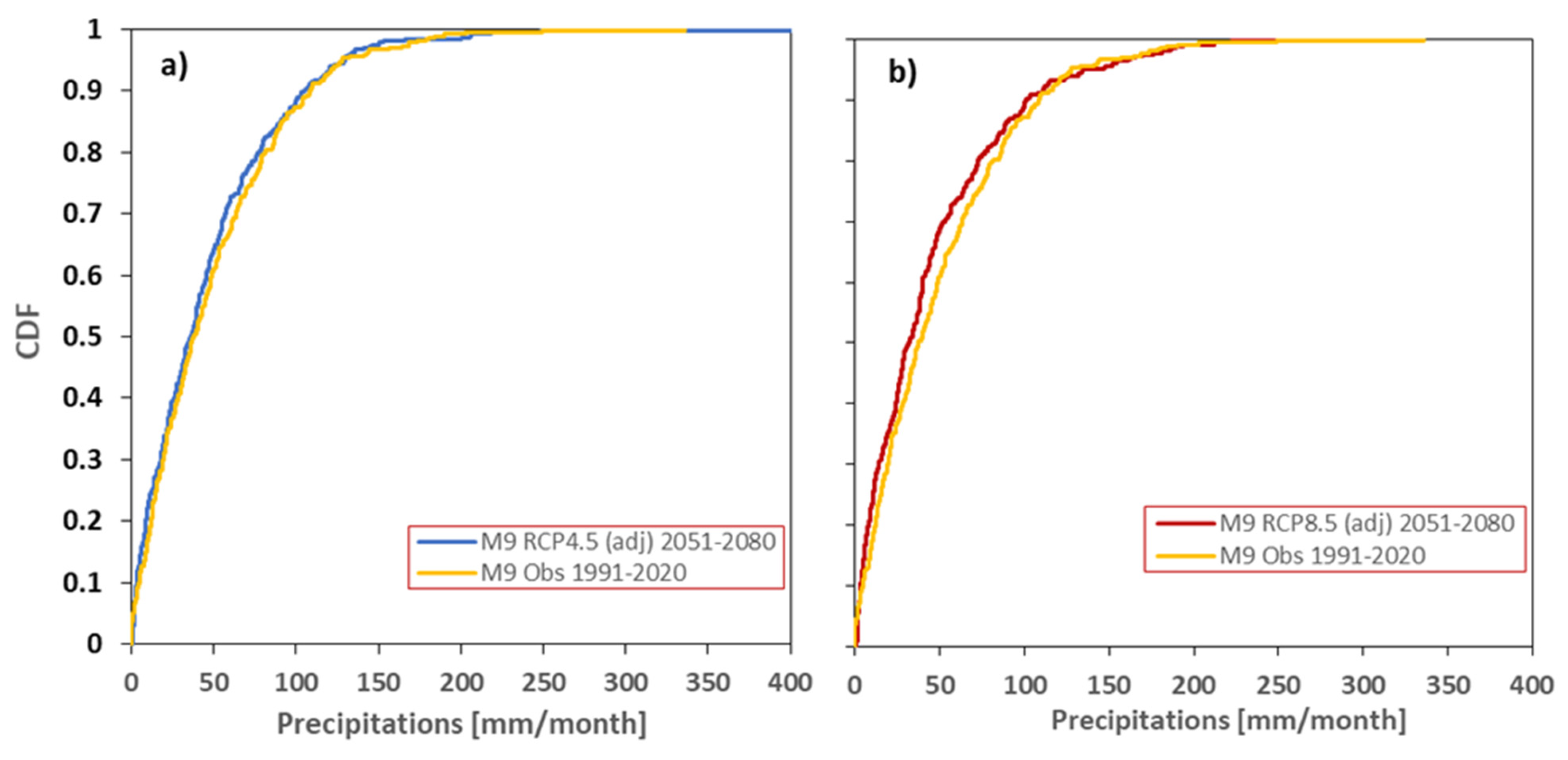
3.1. Climatic Normal Values and Adjustment
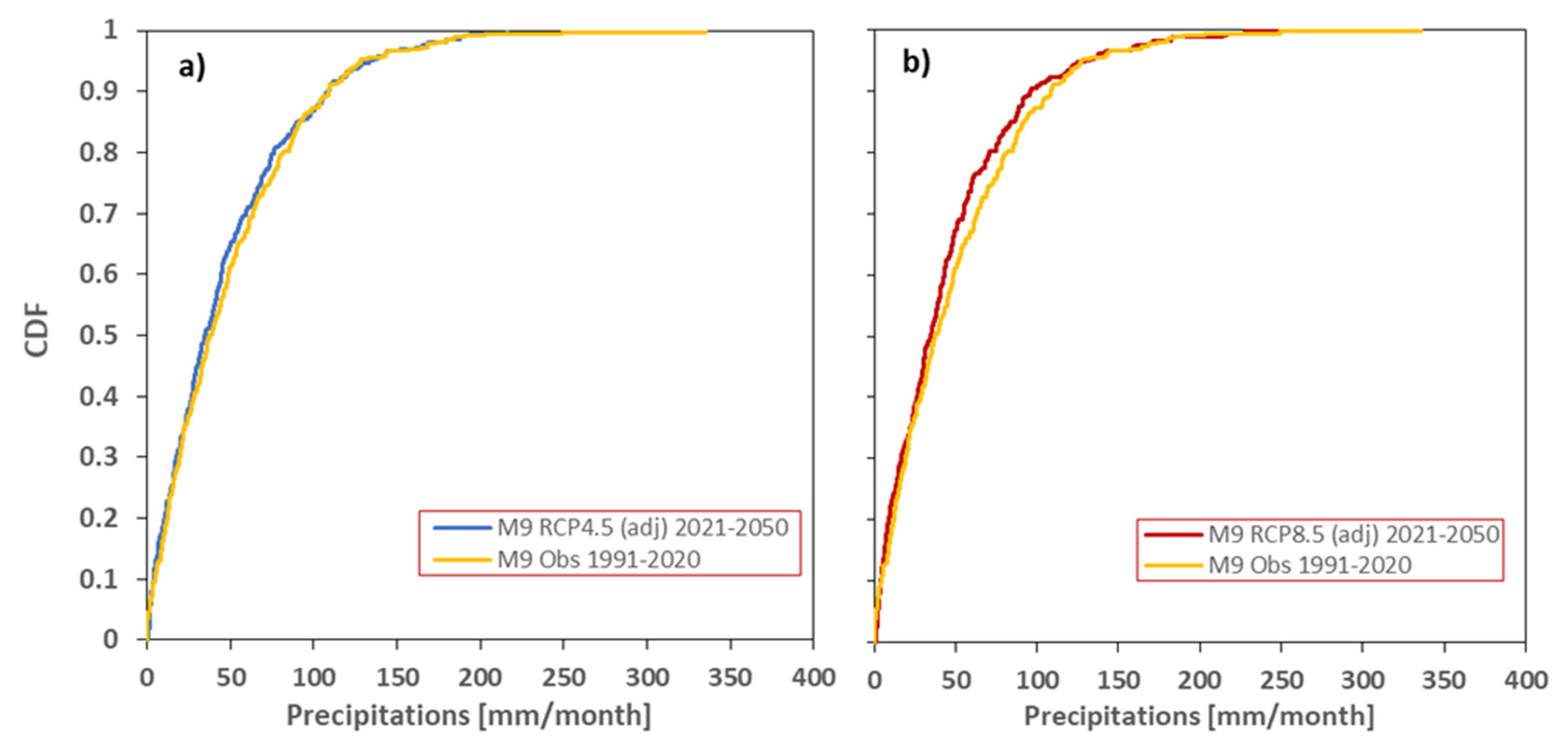
3.2. Kolmogorov–Smirnov Test Interpretation
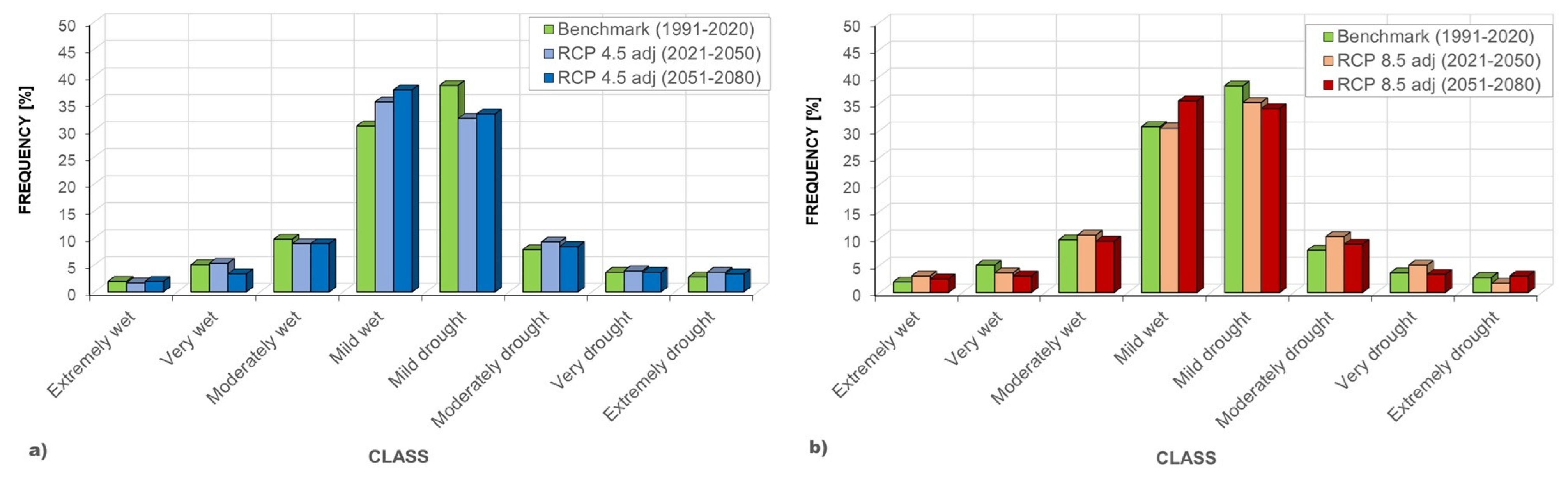
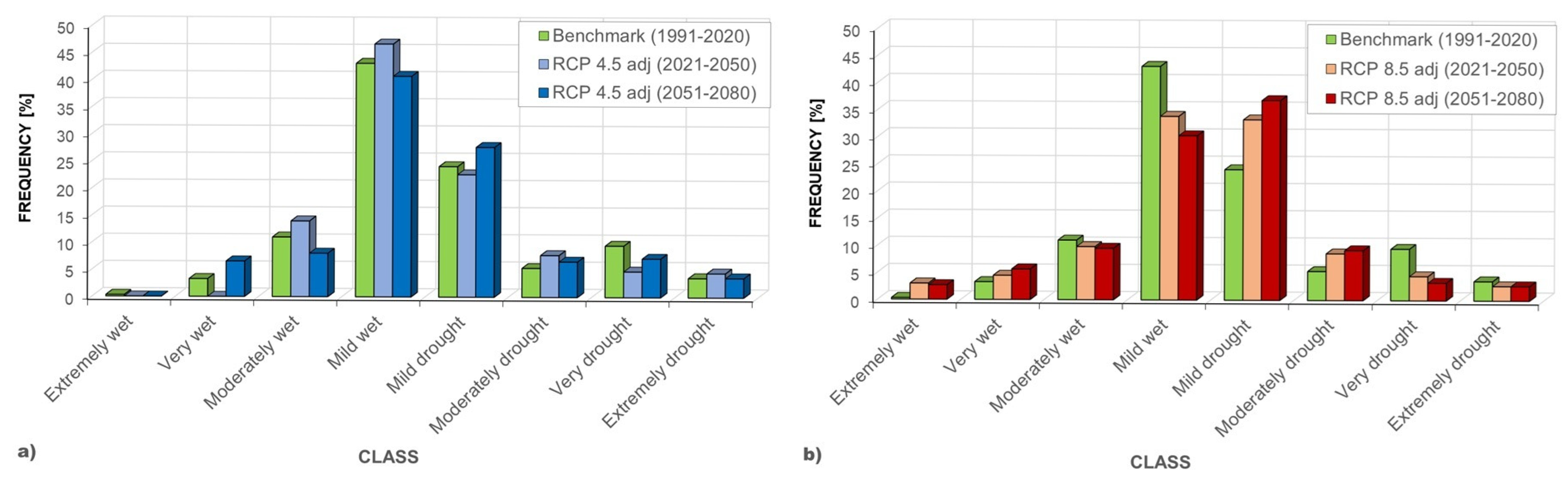
3.3. SPI Class Frequency Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kushabaha, A.; Scardino, G.; Sabato, G.; Miglietta, M.M.; Flaounas, E.; Monforte, P.; Marsico, A.; De Santis, V.; Borzì, A.M.; Scicchitano, G. ARCHIMEDE—An innovative Web-GIS platform for the study of medicanes. Remote Sens. 2024, 16, 2552. [Google Scholar] [CrossRef]
- Monforte, P.; Ragusa, M.A. Evaluation of bioclimatic discomfort trend in a central area of the mediterranean sea. Climate 2022, 10, 146. [Google Scholar] [CrossRef]
- Wilhite, D.A. Planning for Drought: A Methodology. In Drought Assessment, Management, and Planning: Theory and Case Studies; Springer: Boston, MA, USA, 1993; pp. 87–108. [Google Scholar]
- Vogt, J.V.; Niemeyer, S.; Somma, F.; Beaudin, I.; Viau, A.A. Drought monitoring from space. In Drought and Drought Mitigation in Europe; Springer: Berlin/Heidelberg, Germany, 2000; pp. 167–183. [Google Scholar]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Vogt, J.V.; Barbosa, P.; Cammalleri, C.; Carrão, H.; Lavaysse, C. Drought risk management: Needs and experiences in Europe. In Drought and Water Crises, Integrating Science, Management, and Policy; CRC Press: Boca Raton, FL, USA, 2017; pp. 385–407. [Google Scholar]
- Colombo, T.; Pelino, V.; Vergari, S.; Cristofanelli, P.; Bonasoni, P. Study of temperature and precipitation variations in Italy based on surface instrumental observations. Glob. Planet. Change 2007, 57, 308–318. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T. Changes in total precipitation, rainy days and extreme events in northeastern Italy. Int. J. Climatol. A J. R. Meteorol. Soc. 2001, 21, 861–871. [Google Scholar] [CrossRef]
- Homar, V.; Ramis, C.; Romero, R.; Alonso, S. Recent trends in temperature and precipitation over the Balearic Islands (Spain). Clim. Change 2009, 98, 199–211. [Google Scholar] [CrossRef]
- de Luis, M.; Brunetti, M.; Gonzalez-Hidalgo, J.C.; Longares, L.A.; Martin-Vide, J. Changes in seasonal precipitation in the Iberian Peninsula during 1946–2005. Glob. Planet. Change 2010, 74, 27–33. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Matzneller, P.; Ventura, F.; Gaspari, N.; Pisa, P.R. Analysis of climatic trends in data from the agrometeorological station of Bologna-Cadriano, Italy (1952–2007). Clim. Change 2010, 100, 717–731. [Google Scholar] [CrossRef]
- Brusca, S.; Famoso, F.; Lanzafame, R.; Messina, M.; Monforte, P. Placement optimization of biodiesel production plant by means of centroid mathematical method. Energy Procedia 2017, 126, 353–360. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. A J. R. Meteorol. Soc. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Tsesmelis, D.E.; Leveidioti, I.; Karavitis, C.A.; Kalogeropoulos, K.; Vasilakou, C.G.; Tsatsaris, A.; Zervas, E. Spatiotemporal application of the standardized precipitation index (SPI) in the eastern Mediterranean. Climate 2023, 11, 95. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Appl. Meteorol. Climatol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Ampitiyawatta, A.D.; Wimalasiri, E.M. Review of Drought Characterization Indices. Sri Lankan J. Agric. Ecosyst. 2023, 5, 86–112. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.M.; Church, J.A.; Cubasch, U.; Emori, S.; et al. Technical summary. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2013; pp. 33–115. [Google Scholar]
- Monforte, P.; Ragusa, M.A. Temperature trend analysis and investigation on a case of variability climate. Mathematics 2022, 10, 2202. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Trend analysis of monthly mean values and extreme indices of daily temperature in a region of southern Italy. Int. J. Climatol. 2017, 37, 284–297. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies. Int. J. Clim. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Droughts; Routledge: London, UK, 2016; pp. 3–18. [Google Scholar]
- World Meteorological Organization. WMO Guidelines on the Calculation of Climate Normals (WMO-No.1203); World Meteorological Organization: Geneva, Switzerland, 2017; pp. 1–18. [Google Scholar]
- World Meteorological Organization. Technical Regulations: WMO-No. 49; World Meteorological Organization: Geneva, Switzerland, 2019. [Google Scholar]
- Littmann, T. An empirical classification of weather types in the Mediterranean Basin and their interrelation with rainfall. Theor. Appl. Climatol. 2000, 66, 161–171. [Google Scholar] [CrossRef]
- Salata, F.; Golasi, I.; Treiani, N.; Plos, R.; Vollaro, A.d.L. On the outdoor thermal perception and comfort of a Mediterranean subject across other Koppen-Geiger’s climate zones. Environ. Res. 2018, 167, 115–128. [Google Scholar] [CrossRef] [PubMed]
- Fratianni, S.; Acquaotta, F. The climate of Italy. In Landscapes and Landforms of Italy; Springer: Berlin/Heidelberg, Germany, 2017; pp. 29–38. [Google Scholar]
- Bordi, I.; Fraedrich, K.; Petitta, M.; Sutera, A. Extreme value analysis of wet and dry periods in Sicily. Theor. Appl. Climatol. 2007, 87, 61–71. [Google Scholar] [CrossRef]
- Weisse, A.K.; Bois, P. Topographic effects on statistical characteristics of heavy rainfall and mapping in the French Alps. J. Appl. Meteorol. 2001, 40, 720–740. [Google Scholar] [CrossRef]
- Wilhere, G.F. Adaptive management in habitat conservation plans. Conserv. Biol. 2002, 16, 20–29. [Google Scholar] [CrossRef]
- Tramblay, Y.; Neppel, L.; Carreau, J. Brief communication Climatic covariates for the frequency analysis of heavy rainfall in the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2011, 11, 2463–2468. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.; Best, M.; Gomes, S.; Viterbo, P.; Hagemann, S.; Haerter, J. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Kurnik Blaž, L.; Bogataj, K.; Ceglar, A. Correcting mean and extremes in monthly precipitation from 8 regional climate models over Europe. Clim. Past Discuss. 2012, 8, 953–986. [Google Scholar]
- Estévez, J.; Llabrés-Brustenga, A.; Casas-Castillo, M.C.; García-Marín, A.P.; Kirchner, R.; Rodríguez-Solà, R. A quality control procedure for long-term series of daily precipitation data in a semiarid environment. Theor. Appl. Climatol. 2022, 149, 1029–1041. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; García-Marín, A.P. Data validation procedures in agricultural meteorology–a prerequisite for their use. Adv. Sci. Res. 2011, 6, 141–146. [Google Scholar] [CrossRef]
- You, J.; Hubbard, K.G.; Nadarajah, S.; Kunkel, K.E. Performance of quality assurance procedures on daily precipitation. J. Atmos. Ocean. Technol. 2007, 24, 821–834. [Google Scholar] [CrossRef]
- Dunn, R.J.; Donat, M.G.; Alexander, L.V. Comparing extremes indices in recent observational and reanalysis products. Front. Clim. 2022, 4, 989505. [Google Scholar] [CrossRef]
- Tebaldi, C.; Armbruster, A.; Engler, H.P.; Link, R. Emulating climate extreme indices. Environ. Res. Lett. 2020, 15, 074006. [Google Scholar] [CrossRef]
- Ibebuchi, C.C. The impact of horizontal resolution on the representation of atmospheric circulation types in Western Europe using the MPI-ESM model. Int. J. Climatol. 2023, 43, 6450–6462. [Google Scholar] [CrossRef]
- Ibebuchi, C.C. Circulation type analysis of regional hydrology: The added value in using CMIP6 over CMIP5 simulations as exemplified from the MPI-ESM-LR model. J. Water Clim. Change 2022, 13, 1046–1055. [Google Scholar] [CrossRef]
- Yulan, L.; Gong, H.; Chen, W.; Wang, L. Contribution of internal variability to the Mongolian Plateau summer precipitation trends in MPI-ESM large-ensemble model. Glob. Planet. Change 2024, 240, 104544. [Google Scholar]
- Zhuk, E. Using GIS technology for visualizing marine environmental data in netCDF format. In Proceedings of the Ninth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2023), Ayia Napa, Cyprus, 3–5 April 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12786. [Google Scholar]
- Piani, C.; Haerter, J.C.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Change 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Aryal, A.; Kawaike, K.; Yamanoi, K.; Nakagawa, H.; Bhatta, B.; Karki, S.; Thapa, B.R. Evaluation of precipitation elasticity using precipitation data from ground and satellite-based estimates and watershed modeling in Western Nepal. J. Hydrol. Reg. Stud. 2021, 33, 10. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Lanzante, J.R. Testing for differences between two distributions in the presence of serial correlation using the Kolmogorov–Smirnov and Kuiper’s tests. Int. J. Clim. 2021, 41, 6314–6323. [Google Scholar] [CrossRef]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index: User Guide; World Meteworological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Panofsky, H.A.; Brier, G.W. Some Applications of Statistics to Meteorology; Pennsylvania State University: University Park, PA, USA, 1968. [Google Scholar]
- Edwards, D.C.; McKee, T.B. Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Colorado State University: Collins, CO, USA, 1997. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17. [Google Scholar]
- Nimisha, K.; Arunkumar, R. Meteorological drought analysis under climate change scenario using SPI index. In Proceedings of the International Conference on Emerging Trends in Engineering, Yukthi-2023, Kozhikode, India, 10–12 April 2023; Department of Civil Engineering, Government Engineering College: Kozhikode, India, 2023; pp. 394–400. [Google Scholar]
- Addor, N.; Rohrer, M.; Furrer, R.; Seibert, J. Propagation of biases in climate models from the synoptic to the regional scale: Implications for bias adjustment. J. Geophys. Res. Atmos. 2016, 121, 2075–2089. [Google Scholar] [CrossRef]
- Dosio, A.; Paruolo, P. Bias correction of the ENSEMBLES high-resolution climate change projections for use by impact models: Evaluation on the present climate. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Pavan, V.; Antolini, G.; Barbiero, R.; Berni, N.; Brunier, F.; Cacciamani, C.; Torrigiani Malaspina, T. High resolution climate precipitation analysis for north-central Italy, 1961–2015. Clim. Dyn. 2019, 52, 3435–3453. [Google Scholar] [CrossRef]
- Avanzi, F.; De Michele, C.; Gabriele, S.; Ghezzi, A.; Rosso, R. Orographic signature on extreme precipitation of short durations. J. Hydrometeorol. 2015, 16, 278–294. [Google Scholar] [CrossRef]
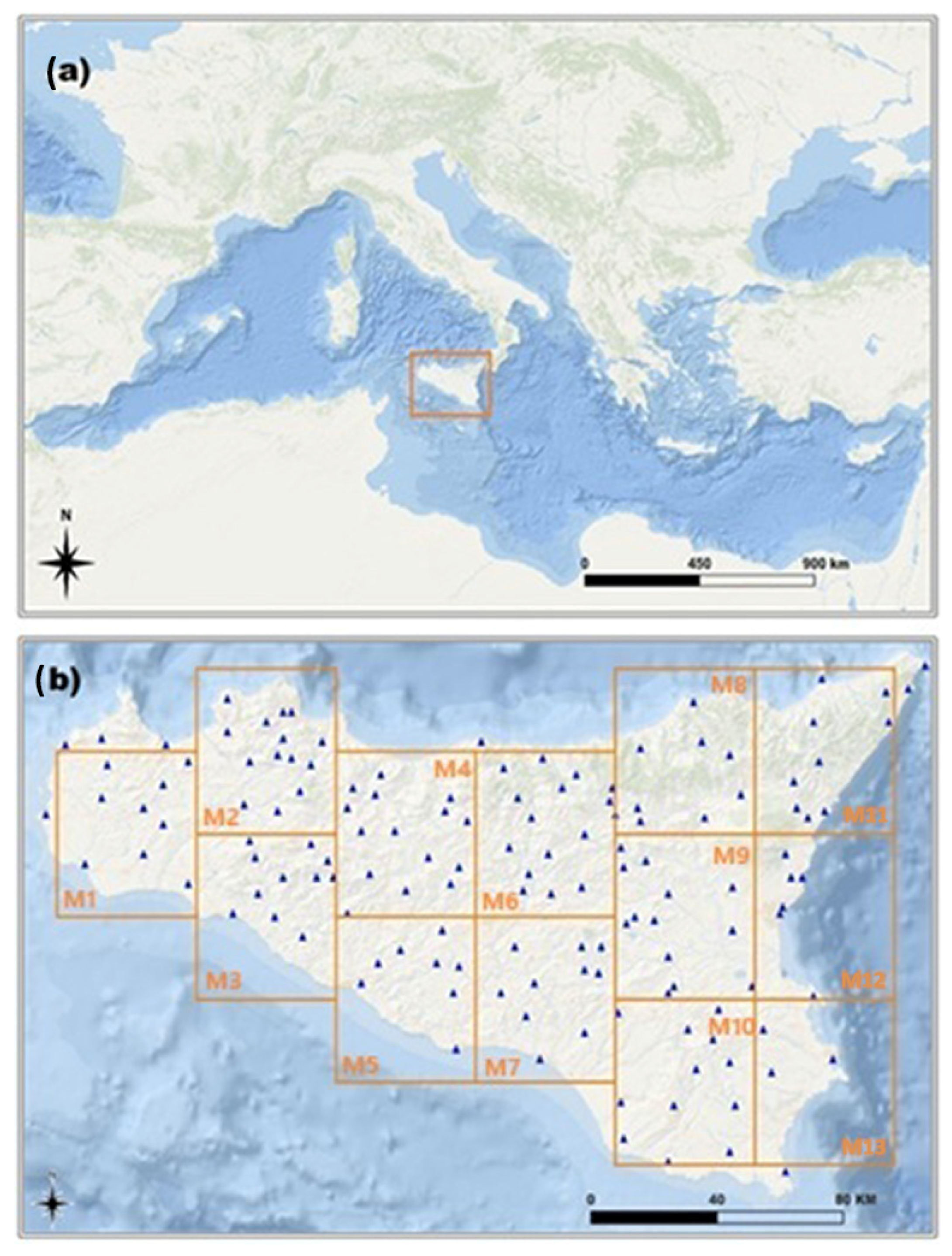

| Mesh | Latitude [N] | Longitude [E] |
|---|---|---|
| M1 | 38.00°–37.50° | 13.00°–12.50° |
| M2 | 38.25°–37.75° | 13.50°–13.00° |
| M3 | 37.75°–37.25° | 13.50°–13.00° |
| M4 | 38.00°–37.50° | 14.00°–13.50° |
| M5 | 37.50°–37.00° | 14.00°–13.50° |
| M6 | 38.00°–37.50° | 14.50°–14.00° |
| M7 | 37.50°–37.00° | 14.50°–14.00° |
| M8 | 38.25°–37.75° | 15.00°–14.50° |
| M9 | 37.75°–37.25° | 15.00°–14.50° |
| M10 | 37.25°–36.75° | 15.00°–14.50° |
| M11 | 38.25°–37.75° | 15.50°–15.00° |
| M12 | 37.75°–37.25° | 15.50°–15.00° |
| M13 | 37.25°–36.75° | 15.50°–15.00° |
| SPI Value | Classification |
|---|---|
| 2.0 < SPI ≤ max | Extremely wet |
| 1.5 < SPI ≤ 2.0 | Very wet |
| 1.0 < SPI ≤ 1.5 | Moderately wet |
| 0.0 < SPI ≤ 1.0 | Mildly wet |
| −1.0 < SPI ≤ 0.0 | Mildly dry |
| −1.5 < SPI ≤ 1.0 | Moderately dry |
| −2.0 < SPI ≤ 1.5 | Very dry |
| min < SPI ≤ −2.0 | Extremely dry |
| Obs—RCP 4.5(adj) | Obs—RCP 8.5(adj) | ||||||
|---|---|---|---|---|---|---|---|
| Id. Mesh | D | p-Value | Test Interpretation | Id. Mesh | D | p-Value | Test Interpretation |
| M1 | 0.075 | 0.264 | Acept H0 | M1 | 0.078 | 0.226 | Acept H0 |
| M2 | 0.053 | 0.698 | Acept H0 | M2 | 0.067 | 0.401 | Acept H0 |
| M3 | 0.058 | 0.573 | Acept H0 | M3 | 0.078 | 0.226 | Acept H0 |
| M4 | 0.078 | 0.226 | Acept H0 | M4 | 0.099 | 0.052 | Acept H0 |
| M5 | 0.078 | 0.226 | Acept H0 | M5 | 0.097 | 0.067 | Acept H0 |
| M6 | 0.056 | 0.635 | Acept H0 | M6 | 0.061 | 0.513 | Acept H0 |
| M7 | 0.067 | 0.401 | Acept H0 | M7 | 0.083 | 0.164 | Acept H0 |
| M8 | 0.067 | 0.401 | Acept H0 | M8 | 0.081 | 0.193 | Acept H0 |
| M9 | 0.056 | 0.635 | Acept H0 | M9 | 0.083 | 0.164 | Acept H0 |
| M10 | 0.064 | 0.455 | Acept H0 | M10 | 0.067 | 0.401 | Acept H0 |
| M11 | 0.039 | 0.949 | Acept H0 | M11 | 0.050 | 0.760 | Acept H0 |
| M12 | 0.047 | 0.817 | Acept H0 | M12 | 0.067 | 0.400 | Acept H0 |
| M13 | 0.069 | 0.350 | Acept H0 | M13 | 0.069 | 0.350 | Acept H0 |
| Obs—RCP 4.5(adj) | Obs—RCP 8.5(adj) | ||||||
|---|---|---|---|---|---|---|---|
| Id. Mesh | D | p-Value | Test Interpretation | Id. Mesh | D | p-Value | Test Interpretation |
| M1 | 0.097 | 0.067 | Acept H0 | M1 | 0.100 | 0.056 | Acept H0 |
| M2 | 0.094 | 0.081 | Acept H0 | M2 | 0.072 | 0.305 | Acept H0 |
| M3 | 0.089 | 0.116 | Acept H0 | M3 | 0.108 | 0.029 | Reject H0 |
| M4 | 0.101 | 0.056 | Acept H0 | M4 | 0.103 | 0.045 | Reject H0 |
| M5 | 0.094 | 0.081 | Acept H0 | M5 | 0.119 | 0.012 | Reject H0 |
| M6 | 0.086 | 0.139 | Acept H0 | M6 | 0.103 | 0.045 | Reject H0 |
| M7 | 0.092 | 0.097 | Acept H0 | M7 | 0.133 | 0.003 | Reject H0 |
| M8 | 0.069 | 0.350 | Acept H0 | M8 | 0.092 | 0.097 | Acept H0 |
| M9 | 0.058 | 0.573 | Acept H0 | M9 | 0.092 | 0.097 | Acept H0 |
| M10 | 0.086 | 0.139 | Acept H0 | M10 | 0.106 | 0.036 | Reject H0 |
| M11 | 0.044 | 0.870 | Acept H0 | M11 | 0.058 | 0.573 | Acept H0 |
| M12 | 0.053 | 0.698 | Acept H0 | M12 | 0.056 | 0.635 | Acept H0 |
| M13 | 0.067 | 0.400 | Acept H0 | M13 | 0.069 | 0.350 | Acept H0 |
| Scenario | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 | M11 | M12 | M13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Extremely Wet | ΔRCP 4.5(21–50) | +0.3 | +0.7 | −1.4 | +0.6 | −2.0 | −1.1 | −1.4 | +0.8 | −0.3 | +0.0 | −2.5 | −0.3 | −1.1 |
| ΔRCP 4.5(51–80) | +0.3 | +0.6 | −1.1 | +0.8 | +0.8 | −0.6 | −1.4 | +0.6 | 0.0 | +0.8 | −2.5 | −1.1 | −1.4 | |
| ΔRCP 8.5(21–50) | +0.8 | +0.6 | −0.6 | 0.0 | −0.8 | −1.1 | −1.7 | +1.1 | +1.1 | −0.3 | −2.8 | +0.3 | −1.7 | |
| ΔRCP 8.5(51–80) | +1.1 | +0.5 | +0.8 | +1.3 | +0.3 | −0.3 | 0.0 | +0.6 | +0.6 | +0.6 | −2.0 | −0.3 | −0.5 | |
| Very Wet | ΔRCP 4.5(21–50) | −0.8 | −2.0 | +3.1 | −3.6 | +0.6 | +0.8 | −0.6 | +1.4 | +0.3 | −1.7 | +1.7 | +1.7 | −2.5 |
| ΔRCP 4.5(51–80) | −1.1 | −2.8 | +0.8 | −2.8 | −3.4 | +1.4 | +0.6 | +1.1 | −1.7 | −3.1 | +0.8 | +0.3 | −1.4 | |
| ΔRCP 8.5(21–50) | +0.6 | −1.7 | +2.2 | −2.8 | +0.3 | +1.7 | +1.4 | +1.7 | −1.4 | −1.4 | +3.2 | +1.4 | −0.3 | |
| ΔRCP 8.5(51–80) | −1.1 | −2.2 | 0.0 | −4.5 | −2.0 | +0.3 | −0.3 | +0.8 | −2.0 | −0.6 | +1.4 | +2.0 | −4.1 | |
| Moderately Wet | ΔRCP 4.5(21–50) | +0.3 | +0.3 | −3.4 | +3.6 | +1.7 | 0.0 | +1.7 | −1.4 | −0.8 | −1.1 | −0.6 | −1.4 | +2.8 |
| ΔRCP 4.5(51–80) | −0.8 | −1.1 | −1.7 | −0.8 | +2.5 | −3.6 | −1.4 | −2.2 | −0.8 | −1.7 | −0.8 | −0.6 | +0.3 | |
| ΔRCP 8.5(21–50) | −1.4 | 0.0 | −4.7 | +1.4 | −0.3 | −2.2 | −0.6 | −3.4 | +0.8 | +0.3 | −0.6 | −2.0 | +3.9 | |
| ΔRCP 8.5(51–80) | −0.8 | −0.6 | −4.2 | +1.1 | +0.6 | −1.4 | −2.2 | −1.7 | −0.3 | −4.2 | +0.6 | −1.7 | +5.6 | |
| Mildly Wet | ΔRCP 4.5(21–50) | +1.1 | −0.8 | +4.5 | +2.0 | +0.6 | 0.0 | +3.4 | −1.4 | +4.5 | +5.3 | +2.2 | +3.6 | +3.9 |
| ΔRCP 4.5(51–80) | +3.6 | +3.9 | +3.9 | +6.7 | +1.1 | +3.4 | +4.5 | +3.9 | +6.7 | +4.5 | +3.9 | +6.1 | +7.5 | |
| ΔRCP 8.5(21–50) | −0.3 | −1.1 | +8.7 | +3.9 | +3.9 | +3.4 | +4.2 | +1.1 | −0.3 | +1.1 | −2.0 | 0.0 | −1.7 | |
| ΔRCP 8.5(51–80) | +1.4 | +0.3 | +6.1 | +4.7 | −0.8 | +2.8 | +3.1 | +2.0 | +4.7 | +4.7 | 0.0 | −1.7 | −2.1 | |
| Mildly Dry | ΔRCP 4.5(21–50) | −2.0 | +2.0 | −1.4 | −2.5 | +2.0 | +2.8 | −3.4 | +1.1 | −6.1 | −3.1 | −1.7 | −5.0 | −5.9 |
| ΔRCP 4.5(51–80) | −3.4 | −1.1 | 0.0 | −3.4 | +1.4 | +2.2 | −3.4 | −0.6 | −5.3 | +0.3 | −0.6 | −2.8 | −7.3 | |
| ΔRCP 8.5(21–50) | −0.6 | +0.8 | −7.5 | −5.3 | −4.5 | −1.7 | −8.4 | −0.6 | −3.1 | −0.3 | +0.8 | +0.3 | −2.5 | |
| ΔRCP 8.5(51–80) | −0.8 | +1.4 | −2.2 | −4.5 | +4.7 | +0.3 | −0.6 | −0.8 | −4.2 | +1.1 | +2.0 | +2.0 | +0.4 | |
| Moderately Dry | ΔRCP 4.5(21–50) | +1.4 | −1.1 | −2.8 | −0.6 | −2.8 | −4.7 | −0.8 | −1.7 | +1.4 | 0.0 | −2.0 | 0.0 | +1.7 |
| ΔRCP 4.5(51–80) | +2.2 | 0.0 | −3.4 | −1.7 | −2.0 | −5.3 | +0.6 | −3.4 | +0.6 | −1.4 | −2.8 | −3.4 | +2.5 | |
| ΔRCP 8.5(21–50) | +1.4 | +1.4 | +2.0 | +2.5 | +2.0 | −1.7 | +5.3 | −1.4 | +2.5 | +0.3 | −0.8 | −0.3 | +1.4 | |
| ΔRCP 8.5(51–80) | +0.6 | +0.3 | −0.8 | +2.2 | −2.2 | −3.1 | 0.0 | −1.1 | +1.1 | −2.2 | −3.9 | −2.0 | +1.4 | |
| Very Dry | ΔRCP 4.5(21–50) | +1.7 | +0.8 | +0.6 | −1.4 | −1.7 | +0.6 | +0.6 | +0.3 | +0.3 | −0.3 | +1.4 | +2.0 | +2.0 |
| ΔRCP 4.5(51–80) | +0.6 | −0.3 | +0.6 | 0.0 | −1.7 | +1.1 | +0.3 | −0.6 | 0.0 | −0.6 | +0.3 | −0.3 | −0.8 | |
| ΔRCP 8.5(21–50) | +0.6 | +1.1 | −0.8 | +0.3 | −0.6 | +1.1 | +0.8 | +1.4 | +1.4 | +0.3 | +0.8 | +0.8 | +2.5 | |
| ΔRCP 8.5(51–80) | −1.4 | −0.6 | +1.1 | +0.3 | +0.3 | +0.8 | −0.8 | +1.1 | +0.3 | +0.3 | +1.7 | −0.3 | −2.2 | |
| Extremely Dry | ΔRCP 4.5(21–50) | −2.0 | −1.1 | +0.8 | +2.0 | +1.7 | +1.7 | +0.6 | +0.8 | +0.8 | +0.8 | +1.4 | −0.6 | −0.8 |
| ΔRCP 4.5(51–80) | −1.4 | 0.0 | +0.8 | +1.1 | +1.1 | +1.4 | +0.3 | +1.1 | +0.6 | +1.1 | +1.7 | +1.7 | +0.6 | |
| ΔRCP 8.5(21–50) | −1.1 | −1.4 | +0.8 | 0.0 | 0.0 | +0.6 | −1.1 | 0.0 | −1.1 | 0.0 | +0.6 | −0.6 | −1.7 | |
| ΔRCP 8.5(51–80) | −1.4 | −0.6 | +1.1 | +0.3 | +0.3 | +0.8 | −0.8 | +1.1 | +0.3 | +0.3 | +1.7 | −0.3 | −2.2 |
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 | M11 | M12 | M13 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Extremely Wet | ΔRCP 4.5(21–50) | 0.0 | +0.9 | +0.8 | −1.4 | 0.0 | −3.4 | −0.3 | −0.6 | −0.3 | +0.3 | −4.3 | −3.2 | −0.9 |
| ΔRCP 4.5(51–80) | −2.3 | −1.1 | 0.0 | +0.3 | +2.0 | −2.3 | +1.4 | −2.0 | +1.4 | +2.0 | −5.7 | −2.0 | −1.4 | |
| ΔRCP 8.5(21–50) | +0.3 | +1.6 | +2.9 | +2.0 | +3.2 | −0.9 | 0.0 | −0.6 | +2.3 | +2.9 | −4.9 | +1.1 | 0.0 | |
| ΔRCP 8.5(51–80) | +3.2 | −1.1 | +2.6 | −0.9 | +5.2 | −1.1 | +4.0 | −1.7 | +2.3 | +3.7 | −3.2 | 0.0 | 0.0 | |
| Very Wet | ΔRCP 4.5(21–50) | −2.3 | −2.6 | −2.6 | −0.6 | +0.6 | +1.7 | −1.1 | +1.4 | −1.1 | −1.4 | +2.3 | +3.7 | +1.4 |
| ΔRCP 4.5(51–80) | −1.1 | −2.6 | +0.6 | −2.6 | +0.6 | −1.1 | −0.6 | −0.6 | −1.4 | −2.9 | +2.6 | +2.3 | +0.9 | |
| ΔRCP 8.5(21–50) | −1.4 | −2.6 | −3.2 | −2.3 | −2.6 | +0.3 | +1.1 | +2.6 | −1.1 | −2.9 | +2.6 | +1.1 | +2.0 | |
| ΔRCP 8.5(51–80) | −3.7 | +2.3 | 0.0 | +1.4 | +2.3 | +1.7 | +1.7 | +4.0 | −2.9 | −1.7 | +2.9 | 0.0 | −1.4 | |
| Moderately Wet | ΔRCP 4.5(21–50) | −0.9 | −0.9 | +0.9 | −0.9 | −0.3 | −2.6 | −0.3 | −5.2 | +0.9 | +1.1 | +1.4 | +2.6 | −2.6 |
| ΔRCP 4.5(51–80) | 0.0 | +2.3 | −4.0 | −0.6 | −6.0 | +0.3 | −3.4 | +1.1 | −1.7 | +0.3 | −0.9 | +0.3 | −1.1 | |
| ΔRCP 8.5(21–50) | +0.6 | −3.4 | −4.6 | −4.0 | −3.4 | −4.0 | −5.2 | −5.4 | +0.6 | −2.0 | +6.9 | −0.6 | −4.9 | |
| ΔRCP 8.5(51–80) | −1.4 | −2.6 | −6.3 | −3.4 | −10.3 | −2.0 | −8.9 | −2.3 | −0.6 | −3.7 | +0.9 | +2.6 | +2.9 | |
| Mildly Wet | ΔRCP 4.5(21–50) | +6.6 | +5.4 | +2.0 | +9.2 | 0.0 | +13.2 | +4.6 | +12.6 | −0.3 | +1.7 | +12.9 | +4.0 | +8.9 |
| ΔRCP 4.5(51–80) | +6.9 | +7.7 | +3.7 | +8.0 | +4.0 | +10.9 | +4.9 | +5.7 | +3.4 | +1.7 | +18.3 | +9.2 | +12.3 | |
| ΔRCP 8.5(21–50) | +2.9 | +9.2 | +5.7 | +6.6 | +1.4 | +9.2 | +4.9 | +5.7 | −8.9 | +5.2 | +3.4 | −0.3 | +10.6 | |
| ΔRCP 8.5(51–80) | 0.0 | +3.7 | +1.4 | +4.6 | −4.6 | +5.4 | −4.0 | +0.9 | −1.7 | −0.6 | +11.2 | −4.0 | +1.7 | |
| Mildly Dry | ΔRCP 4.5(21–50) | −5.7 | −4.3 | +2.6 | −3.2 | +0.9 | −7.2 | +0.3 | −5.4 | −2.6 | −1.7 | −14.6 | −6.6 | −11.7 |
| ΔRCP 4.5(51–80) | −2.9 | −4.0 | +2.6 | +1.4 | −0.3 | −6.6 | −0.9 | +0.6 | −5.2 | −1.4 | −16.6 | −12.9 | −14.6 | |
| ΔRCP 8.5(21–50) | −2.0 | −6.6 | +4.3 | +2.0 | +3.7 | −2.9 | +3.2 | −0.3 | +6.9 | −3.2 | −13.8 | −2.3 | −12.9 | |
| ΔRCP 8.5(51–80) | +1.4 | −3.4 | +1.7 | +0.6 | +7.7 | −3.7 | +6.3 | −1.7 | −0.6 | −0.9 | −18.6 | 0.0 | −6.3 | |
| Moderately Dry | ΔRCP 4.5(21–50) | −1.4 | +1.1 | −4.3 | −6.3 | −0.9 | −3.4 | −3.4 | −2.6 | +4.9 | −2.0 | 0.0 | −2.0 | +2.3 |
| ΔRCP 4.5(51–80) | −4.6 | −2.9 | −2.0 | −9.2 | +0.6 | −4.3 | −1.7 | −4.9 | +3.7 | −0.6 | −2.9 | +0.3 | +1.1 | |
| ΔRCP 8.5(21–50) | −4.3 | +0.3 | −5.2 | −4.3 | −1.4 | −2.0 | −3.2 | −1.4 | +1.7 | −0.3 | +2.6 | 0.0 | +2.6 | |
| ΔRCP 8.5(51–80) | −1.4 | +0.6 | +4.0 | −5.7 | +4.0 | −1.1 | +5.4 | −0.3 | +8.6 | +6.6 | +5.7 | +3.4 | +4.6 | |
| Very Dry | ΔRCP 4.5(21–50) | +2.9 | −1.1 | −1.7 | +0.6 | −2.3 | −1.1 | −2.3 | −2.0 | −0.9 | +0.9 | −0.3 | −0.9 | +2.0 |
| ΔRCP 4.5(51–80) | +0.9 | −3.4 | −3.4 | −0.6 | −0.3 | −0.3 | +0.3 | −2.9 | +0.9 | −0.6 | +1.4 | +0.9 | +2.3 | |
| ΔRCP 8.5(21–50) | +4.6 | −1.4 | −3.2 | −2.0 | −0.6 | −2.0 | −1.1 | −2.0 | +0.9 | −1.1 | +3.4 | +1.4 | +4.0 | |
| ΔRCP 8.5(51–80) | +3.7 | −1.1 | −2.9 | +2.0 | −0.6 | −0.3 | −0.6 | +2.0 | 0.0 | −0.3 | +1.4 | −0.9 | +0.9 | |
| Extremely Dry | ΔRCP 4.5(21–50) | −1.1 | +1.4 | +2.3 | +2.6 | +2.0 | +2.9 | +2.6 | +1.7 | −0.6 | +1.1 | +2.6 | +2.3 | +0.6 |
| ΔRCP 4.5(51–80) | +3.2 | +4.0 | +2.6 | +3.2 | −0.6 | +3.4 | 0.0 | +2.9 | −1.1 | +1.4 | +3.7 | +2.0 | +0.6 | |
| ΔRCP 8.5(21–50) | −0.6 | +2.0 | +3.2 | +2.0 | −0.3 | +2.3 | +0.3 | +1.4 | −2.3 | +1.4 | −0.3 | −0.6 | −1.4 | |
| ΔRCP 8.5(51–80) | −1.7 | +1.7 | −0.6 | +1.4 | −3.7 | +1.1 | −4.0 | −0.9 | −5.2 | −3.2 | −0.3 | −1.1 | −2.3 |
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 | M11 | M12 | M13 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Extremely Wet | ΔRCP 4.5(21–50) | +0.9 | −0.3 | 0.0 | 0.0 | 0.0 | −3.0 | 0.0 | −2.7 | −0.3 | 0.0 | −3.0 | −0.6 | −3.9 |
| ΔRCP 4.5(51–80) | +0.9 | +1.5 | +1.2 | +2.7 | 0.0 | −2.7 | 0.0 | −2.1 | −0.3 | 0.0 | −1.5 | −0.3 | −3.9 | |
| ΔRCP 8.5(21–50) | +0.3 | 0.0 | +2.1 | +2.4 | +1.2 | −1.8 | 0.3 | −2.7 | +2.7 | +0.9 | −2.7 | 0.0 | −4.2 | |
| ΔRCP 8.5(51–80) | +0.6 | −0.3 | +0.9 | +0.9 | +0.9 | −3.0 | +1.8 | −2.4 | +2.4 | +3.3 | −0.3 | −0.9 | −1.2 | |
| Very Wet | ΔRCP 4.5(21–50) | −2.7 | −2.4 | −0.6 | −6.8 | −5.3 | −4.2 | −5.3 | +0.9 | −3.3 | −0.9 | −0.9 | −5.0 | +2.1 |
| ΔRCP 4.5(51–80) | −4.5 | −1.8 | −1.5 | −3.3 | −0.3 | 0.0 | −2.4 | +3.9 | +3.3 | +1.5 | +1.2 | +1.2 | +2.7 | |
| ΔRCP 8.5(21–50) | −3.6 | +1.8 | −0.9 | −0.9 | −0.3 | +3.0 | −0.6 | +5.6 | +1.2 | +1.2 | +3.0 | +4.5 | +3.9 | |
| ΔRCP 8.5(51–80) | −0.9 | −0.6 | −3.6 | −3.0 | +5.6 | +4.2 | +3.9 | +6.8 | +2.4 | +2.7 | +3.6 | +3.3 | +2.1 | |
| Moderately Wet | ΔRCP 4.5(21–50) | −2.7 | 0.0 | −1.5 | +5.6 | +0.9 | +3.0 | +1.2 | +7.4 | +3.0 | −2.1 | −0.6 | +3.0 | +13.4 |
| ΔRCP 4.5(51–80) | −3.9 | −4.2 | −2.4 | −1.2 | −1.2 | +3.0 | +3.3 | +3.0 | −3.0 | −3.9 | −5.9 | −2.1 | +1.8 | |
| ΔRCP 8.5(21–50) | −1.2 | −8.0 | −2.7 | −3.9 | −2.4 | −6.5 | +6.2 | +1.2 | −1.2 | −3.3 | −3.3 | −5.0 | +8.0 | |
| ΔRCP 8.5(51–80) | −3.9 | +0.6 | −4.2 | +3.6 | −6.2 | +2.4 | +1.5 | +2.7 | −1.5 | −4.2 | −6.5 | −3.6 | +8.6 | |
| Mildly Wet | ΔRCP 4.5(21–50) | +18.4 | +14.5 | +7.1 | +6.5 | +11.6 | +15.4 | +7.4 | −5.6 | +3.6 | +7.4 | +2.4 | +8.6 | −11.3 |
| ΔRCP 4.5(51–80) | +13.9 | +11.9 | +4.5 | −0.3 | +6.2 | +4.2 | −2.7 | −9.2 | −2.4 | +2.7 | +9.8 | +3.9 | +5.9 | |
| ΔRCP 8.5(21–50) | +11.9 | +15.7 | +6.2 | 0.0 | −2.1 | +13.9 | −16.3 | 0.0 | −9.2 | −0.6 | +2.1 | −2.7 | −5.6 | |
| ΔRCP 8.5(51–80) | +3.6 | +5.0 | +1.5 | −7.7 | −10.7 | −0.9 | −14.2 | −14.5 | −12.8 | −9.5 | −1.8 | −5.6 | −16.0 | |
| Mildly Dry | ΔRCP 4.5(21–50) | −11.3 | −13.9 | −5.3 | +2.1 | −3.6 | −5.3 | +1.5 | +3.0 | −1.5 | −2.7 | +3.0 | −4.5 | −3.9 |
| ΔRCP 4.5(51–80) | −2.7 | −4.5 | −2.4 | +11.6 | −4.7 | 0.0 | +3.0 | +6.2 | +3.6 | −4.2 | −6.2 | +0.6 | −14.8 | |
| ΔRCP 8.5(21–50) | −7.1 | −8.9 | −8.0 | +8.9 | +3.0 | −3.6 | +12.5 | +2.4 | +9.2 | +2.4 | −0.3 | +8.6 | −6.5 | |
| ΔRCP 8.5(51–80) | −2.7 | −8.3 | −2.1 | +14.5 | +14.5 | +4.7 | +15.1 | +10.7 | +12.8 | +6.5 | +2.7 | +4.2 | +0.6 | |
| Moderately Dry | ΔRCP 4.5(21–50) | −2.4 | −1.2 | 0.0 | −9.5 | −2.4 | −11.3 | −0.9 | −0.3 | +2.4 | −2.1 | +2.7 | −2.1 | +5.3 |
| ΔRCP 4.5(51–80) | −5.0 | −6.5 | +3.3 | −12.2 | +1.8 | −10.1 | +3.0 | −0.6 | +1.2 | +5.3 | +0.3 | −5.6 | +5.0 | |
| ΔRCP 8.5(21–50) | −4.2 | −5.9 | +5.6 | −7.7 | +1.8 | −9.2 | +3.3 | −0.9 | +3.3 | −0.9 | +0.6 | −3.6 | +1.8 | |
| ΔRCP 8.5(51–80) | +2.7 | −2.7 | +4.7 | −11.3 | −3.9 | −10.4 | −1.5 | −0.6 | +3.9 | +3.3 | +3.3 | +5.3 | +7.1 | |
| Very Dry | ΔRCP 4.5(21–50) | −4.2 | 0.0 | −2.4 | −2.4 | −4.7 | +0.9 | −8.9 | −5.3 | −4.7 | +0.6 | −2.4 | −1.2 | −1.5 |
| ΔRCP 4.5(51–80) | −3.6 | +0.3 | −3.9 | −3.6 | −3.3 | +0.9 | −6.5 | −1.2 | −2.4 | −1.2 | −0.6 | +1.2 | +4.2 | |
| ΔRCP 8.5(21–50) | +0.6 | +3.0 | −3.0 | −2.7 | −1.5 | 0.0 | −8.6 | −5.3 | −5.0 | +0.9 | −3.0 | −2.4 | +3.0 | |
| ΔRCP 8.5(51–80) | −1.2 | +6.5 | +0.3 | −2.1 | +2.1 | −1.5 | −3.6 | −5.3 | −6.2 | +1.8 | −0.6 | −1.8 | +2.7 | |
| Extremely Dry | ΔRCP 4.5(21–50) | +5.6 | +3.3 | +2.7 | +4.5 | +3.6 | +3.5 | +5.0 | +2.1 | +0.9 | −0.3 | +3.0 | +1.8 | −0.3 |
| ΔRCP 4.5(51–80) | +4.7 | +3.3 | +1.2 | +6.2 | +1.5 | +4.7 | +2.4 | 0.0 | 0.0 | −0.3 | +3.0 | +1.2 | −0.9 | |
| ΔRCP 8.5(21–50) | +3.3 | +2.4 | +0.6 | +3.9 | +0.3 | +4.2 | +3.3 | +2.1 | −0.9 | −0.6 | +3.6 | +0.6 | −0.3 | |
| ΔRCP 8.5(51–80) | 0.0 | −0.3 | −1.8 | +5.0 | −2.4 | +4.5 | 0.0 | +2.7 | −0.9 | −3.9 | −0.3 | −2.7 | −3.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monforte, P.; Imposa, S. Future Dynamics of Drought in Areas at Risk: An Interpretation of RCP Projections on a Regional Scale. Hydrology 2025, 12, 143. https://doi.org/10.3390/hydrology12060143
Monforte P, Imposa S. Future Dynamics of Drought in Areas at Risk: An Interpretation of RCP Projections on a Regional Scale. Hydrology. 2025; 12(6):143. https://doi.org/10.3390/hydrology12060143
Chicago/Turabian StyleMonforte, Pietro, and Sebastiano Imposa. 2025. "Future Dynamics of Drought in Areas at Risk: An Interpretation of RCP Projections on a Regional Scale" Hydrology 12, no. 6: 143. https://doi.org/10.3390/hydrology12060143
APA StyleMonforte, P., & Imposa, S. (2025). Future Dynamics of Drought in Areas at Risk: An Interpretation of RCP Projections on a Regional Scale. Hydrology, 12(6), 143. https://doi.org/10.3390/hydrology12060143







