Next Article in Journal
Assessing the Effects of Bioenergy Cropping Scenarios on the Surface Water and Groundwater of an Intensively Agricultural Basin in Central Greece
Previous Article in Journal
Glacier, Wetland, and Lagoon Dynamics in the Barroso Mountain Range, Atacama Desert: Past Trends and Future Projections Using CA-Markov
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 12
Issue 4
10.3390/hydrology12040065
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Assessing Deep Learning Techniques for Remote Gauging and Water Quality Monitoring Using Webcam Images

by
Ruichen Xu
1 and
Binbin Wang
1,2,*
1
Department of Civil and Environmental Engineering, University of Missouri, Columbia, MO 65211, USA
2
Missouri Water Center, Columbia, MO 65211, USA
*
Author to whom correspondence should be addressed.
Hydrology 2025, 12(4), 65; https://doi.org/10.3390/hydrology12040065
Submission received: 16 February 2025 / Revised: 20 March 2025 / Accepted: 20 March 2025 / Published: 22 March 2025
Browse Figures
Versions Notes

Abstract

River and stream gauging and water quality monitoring are essential for understanding and managing freshwater resources. The U.S. Geological Survey (USGS) has been implementing and expanding the coverage of webcams across the U.S. stream gauges. A publicly available website has been established, known as the Hydrological Imagery Visualization and Information System (HIVIS). Motivated by routine webcam monitoring and recent advances in image-based machine learning research, in this technical paper, we evaluate three convolutional neural network (CNN) models including two deep neural network models (CNN3, VGG16, and ResNet50) in predicting river gauging, turbidity, dissolved oxygen, and dissolved organic matter in the Missouri River. We select the Missouri River due to the logistical challenges in field data collection. Our objective is to evaluate the predictability of the selected CNN and deep CNN models in inferring water surface elevation and water quality parameters from webcam images. The results show that the images can provide robust prediction for gauge height, a reasonable prediction for dissolved oxygen, and unsatisfactory prediction for turbidity or dissolved organic matter. The results demonstrate the potential use and limitation of using webcam images to remotely sense water quantity and quality data.

1. Introduction

River gauging and water quality monitoring are fundamental practices for comprehending and managing freshwater resources (e.g., [1,2,3]). The United States Geological Survey (USGS) operates one of the largest hydrological and hydraulic monitoring networks in the world, and provides essential historical and near-real-time data for managing water resources in the U.S. The data include gauge, discharge, and water quality parameters, including turbidity and dissolved oxygen at some monitoring stations [4]. These gauge data have provided essential hydrological parameters for water management and research, such as peak flow and flood prediction [5], water allocation and infrastructure design [6], and ecological studies [7,8,9].
In recent years, the USGS launched a Hydrological Imagery Visualization and Information System (HIVIS) (https://www.usgs.gov/tools/hydrologic-imagery-visualization-and-information-system-hivis), which offers enhanced visual monitoring at critical hydrological sites. As of 26 November 2024, 809 cameras in total and the associated data are available through the USGS HIVIS portal. The webcam imagery provides near-real-time or time-lapse images at the monitoring sites. These images are useful in providing visualization of ice formation [10], rainfall events, floods [11], and seasonal changes of water surface elevation. Some sites are paired with measured hydrological data, including gauge height, discharge, and other water quality parameters (e.g., turbidity and dissolved oxygen) [12,13,14]. The paired images and the continuously monitored hydrologic data provide an excellent data source for training machine learning (ML) models. In this paper, we explore deep learning (DL) approaches in predicting gauge and water quality parameters (i.e., turbidity, dissolved organic matter, and dissolved oxygen) using the time-lapse images along with the measured data for model training and testing.
Deep learning, a sub-class of ML, uses multiple layers of interconnected neurons known as deep neural networks to solve complex, high-dimensional problems by learning a hierarchical representation of data (e.g., [15,16]). Each layer in a deep neural network extracts increasingly abstract features, which enables the model to capture intricate patterns and relationships that traditional methods might miss. This approach is particularly powerful when dealing with images, time series, and spatial datasets (e.g., [17,18]). The methods include supervised learning, unsupervised learning, and reinforcement learning, which have been used in image generation, image and video processing, time series prediction, among others [19].
In hydraulics and water quality research, the applications of ML and DL have gained significant attention due to their ability to handle non-linear relationships within large datasets [20,21,22,23]. Convolutional neural network (CNN)-based DL methods are useful for extracting information from images. Eltner et al. [24] used two CNN-based DL methods for the segmentation of a water body, which was used to infer gauge heights based on a pre-determined photogrammetry map at the measurement site. Vandaele et al. [25] applied inductive transfer learning based on water surface segmentation and a CNN to estimate water surface elevation. Vanden Boomen et al. [26] implemented a 16-layer CNN-based DL model, VGG16 [27], to successfully predict gauge heights for three rivers with drainage areas from approximately 100 to 600 square miles. The deep layer architecture allows for a trained, robust prediction model that can be deployed for the same river over several months after the training. DL methods have also been used in estimating water surface velocities [28] based on CNN-based learning algorithms to produce optical flow estimates [29]. In addition, ML and DL based on images, webcams, and satellite imageries have been widely explored for flood monitoring [30,31,32] and water quality prediction [33,34,35,36].
Although DL methods are rapidly advancing in the field of hydraulics, their potential for routine monitoring as a water management tool remains uncertain. In water quality studies, many reported applications rely on imaging water samples, which still require significant human effort. This study investigates the use of long-term deployed webcams within the HIVIS network for remote sensing of water level and water quality parameters. Building on the work of Vanden Boomen et al. [26], who demonstrated the effectiveness of VGG16 in predicting gauge heights for three rivers, we extend this approach to a larger system, the Missouri River, and compare it to two other CNN-based models: a basic 3-layer CNN (CNN3) and a 50-layer deep residual learning model (ResNet50) [37]. The Missouri River is selected due to challenges for in situ measurements compared to small rivers and streams [38]. In addition to gauge height predictions, we explore the potential of these models to predict water quality parameters that are visually influenced, including turbidity, dissolved organic matter, and dissolved oxygen concentrations. The goal of this technical paper is to assess the feasibility of routine remote sensing for water quantity and quality in the Missouri River using the growing HIVIS webcam network.

2. Methods

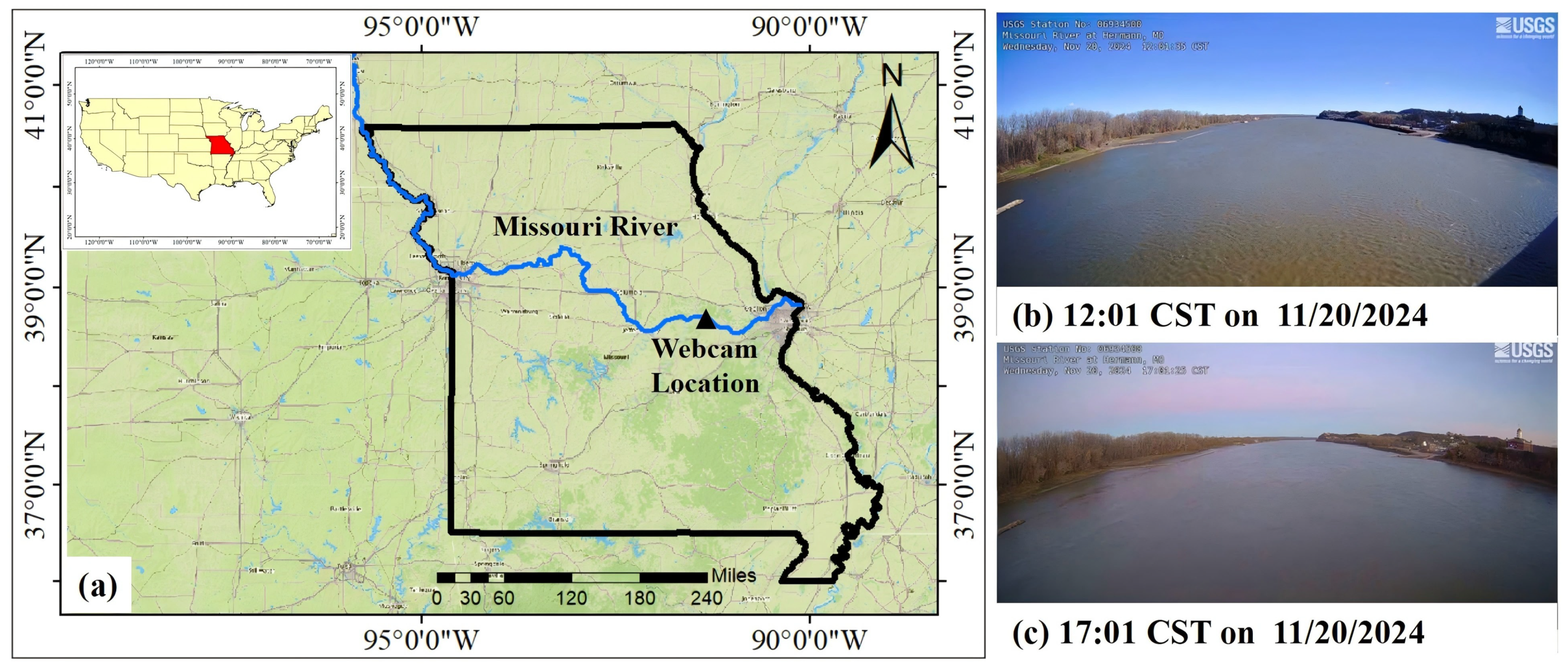
2.1. Image Data

The webcam images analyzed in this study are managed by the National Imagery Management System (NIMS) and can be visualized through the HIVIS portal. The data presented in this study are for the Missouri River, where a webcam was installed on a bridge at Hermann, Missouri. RGB images from this webcam have been available from 14 November 2022, with a recording interval of one hour, resulting in 24 images per day. Beginning 14 September 2024, the image collection policy was modified so that images were only stored during daylight hours, reducing the total number of images per day. To automate the retrieval of these images, we developed a customized Python (version 3.12.7) script that interacts with the NIMS API. This script systematically downloads and stores the image data for subsequent analysis. The images were saved in JPEG (‘.jpg’) format, with varying resolutions, including 2688 × 1520, 1280 × 960, and 1920 × 1080. Among these, the majority of images are available in 1920 × 1080. The timestamp was embedded in each image’s filename, allowing synchronization with water quality measurements from the gauging station. Figure 1 shows the location of our study site and an example of the webcam images at this site.

2.2. Gauging Data

The drainage area for the reach at Hermann on the Missouri River is 522,500 square miles. A nearby USGS gauging station (station ID 069345000) records hydrological parameters continuously, including the gauge height, temperature, and other water quality data. In this study, we select four parameters that are directly or indirectly related to the visualization of the water body. They are gauge height, turbidity, dissolved oxygen (DO), and fluorescent dissolved organic matter (fDOM).
The gauge height is a standard hydraulic parameter reported by the USGS, which indicates the elevation of the water surface and is used to estimate the discharge of the river and stream using the stage–discharge relationship (known as the rating curve method). The USGS routinely conducts field measurements to examine the temporal variation of the stage–discharge relationship, and applies a ‘shift’ correction to the established rating curve accordingly. Turbidity refers to the cloudiness of water caused by suspended particles, including sediments, algae, microorganisms, and organic or inorganic matter. At USGS gauge stations, turbidity is reported in formazin nephelometric units (FNU). It is included in this study because turbidity influences the visualization of water color, clarity, and opacity. DO and fDOM are not directly visible in images, but both are influenced by organic compounds in the water that absorb and emit light at specific wavelengths. Additionally, DO levels are affected by water turbidity, which impacts light penetration. These relationships make DO and fDOM potential candidates for DL-based image analysis. DO at USGS gauge stations is reported in milligrams per liter (mg/L), and fDOM is reported in micrograms per liter as quinine sulfate equivalents (QSE) [39].

2.3. CNN-Based Architectures

Three CNN-based models [40,41] were used in this study: a 3-layer classic CNN, a 16-layer VGG model, and a 50-layer ResNet model (Figure 2). For each model, the RGB channels of the webcam images were used as input, with a batch size of 32 for training. The images were normalized to a resolution of 224 × 224 pixels. To ensure robust model training and mitigate the effects of varying image distortions caused by camera movement and outdoor factors (e.g., temperature and humidity), a standardized preprocessing algorithm was applied to all images. This algorithm included random rotations up to 5 degrees in both clockwise and counterclockwise directions, random shifting by up to 4% of the image dimension, and random shearing by up to 0.5 degrees.
In the 3-layer CNN (CNN3) [42] architecture (Figure 2a), each input image was operated using 3 × 3 convolutional kernels, followed by ReLU activation and max pooling. After three convolutional layers, the data were flattened into a 1D tensor, passed through a fully connected layer, and further processed with a ReLU activation and a dropout layer. The final output layer produced the predicted gauge height or other targeted water quality parameters, which were used for regression.
VGG16 [27,43] has a deep CNN architecture (Figure 2b), including 13 convolutional layers and 3 fully connected layers. The three fully connected layers are followed by a softmax classifier. Similarly to CNN3, VGG16 uses 3 × 3 convolutional kernels with a stride of 1 and max-pooling layers with a 2 × 2 kernel to progressively reduce the spatial dimensions of the dataset. To customize the pre-trained VGG16 for regression problems, such as predicting gauge height, turbidity, and other water quality parameters, the softmax activation in the original VGG16 was removed, and the final fully connected layer was replaced with a new layer that has a single output unit, i.e., the training target parameter.
ResNet50 [37,44] is also a deep CNN-based model (Figure 2c), which uses residual blocks (Figure 2d) to more efficiently train models in better capturing small gradients in very deep networks, so-called “vanishing gradient problems” in traditional, very deep neural network models. ResNet models uses the ‘skip connection’ feature with fewer parameters; therefore, it is generally faster than VGG16 even though it has more network layers [37].

2.4. Model Training, Validation, and Deployment

Because the webcam images, river gauge, and all water quality data are timestamped, we interpolate the measured gauge and water quality data (turbidity and dissolved oxygen) onto the timestamp of the images. Since the gauge and water quality data were saved in a local time zone while the webcam images were saved in Coordinated Universal Time (UTC), we converted all timestamps of hydrological data to UTC before interpolation. This ensured that each image had a corresponding gauge height and water quality parameter for training regression-based DL models.
The webcam images (17,446 images) from 14 November 2022 to 31 August 2023 were used for model training and validation for all three CNN-based models. The entire dataset was split into 80% for training and 20% for validation. Mean squared error (MSE) was used as the loss function for all models and all parameters [45]. Due to the existence of sparse but orders-of-magnitude-larger peaks in the turbidity data, a logarithm operation was applied to turbidity before model training. The Adam optimizer was used with a learning rate of 0.0001 and a weight decay of 0.0001 to update the parameters. An early stopping mechanism was applied for effective and efficient model training if the validation loss did not improve for 10 consecutive epochs.
Once three optimal CNN and DL models were determined, we applied each model to the data outside the date range of training period, i.e., from 1 September to 31 December 2024. This allowed us to examine the model performance for hydrological prediction from ‘future’ images, the so-called deployment of ML models [25].

3. Results and Discussion

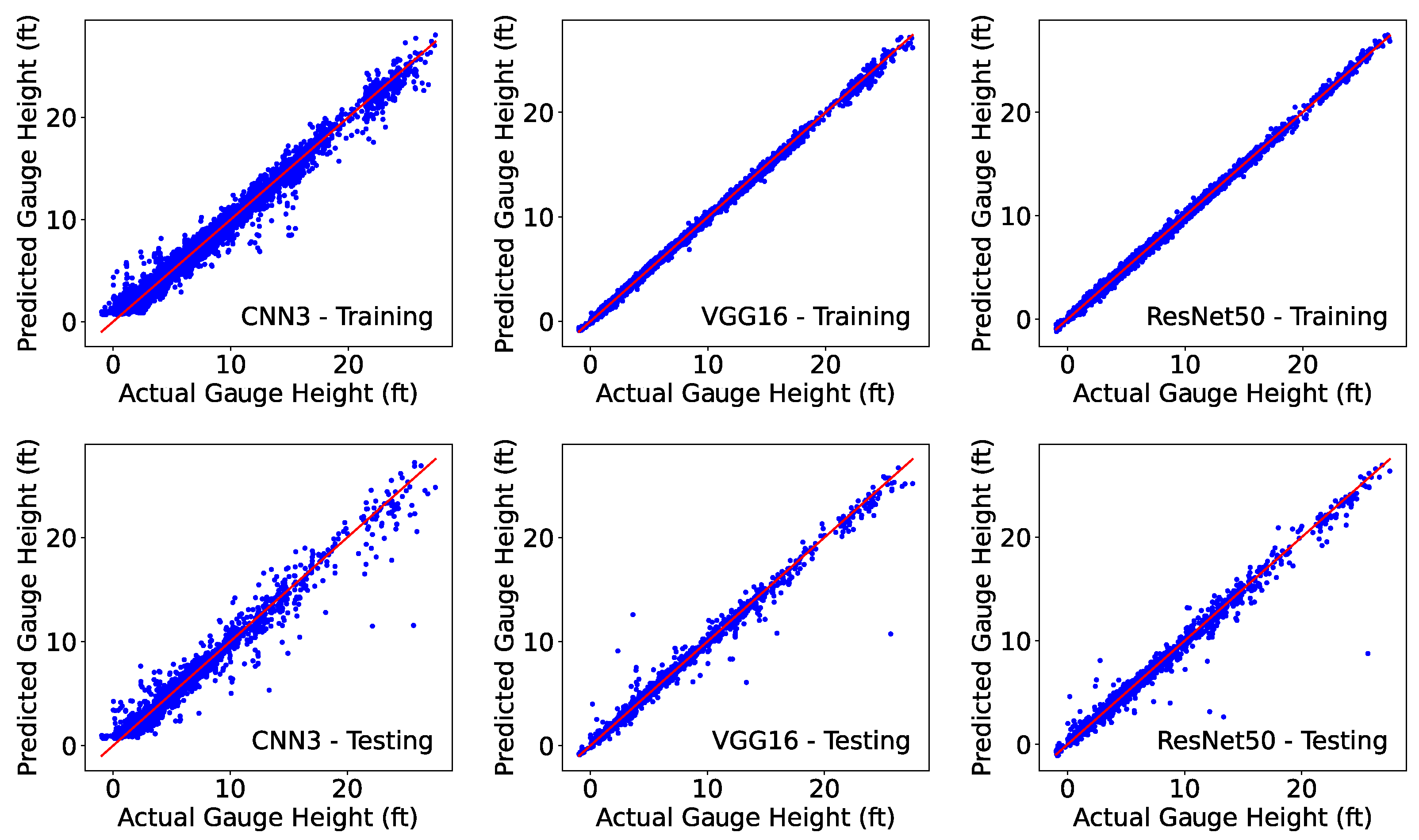
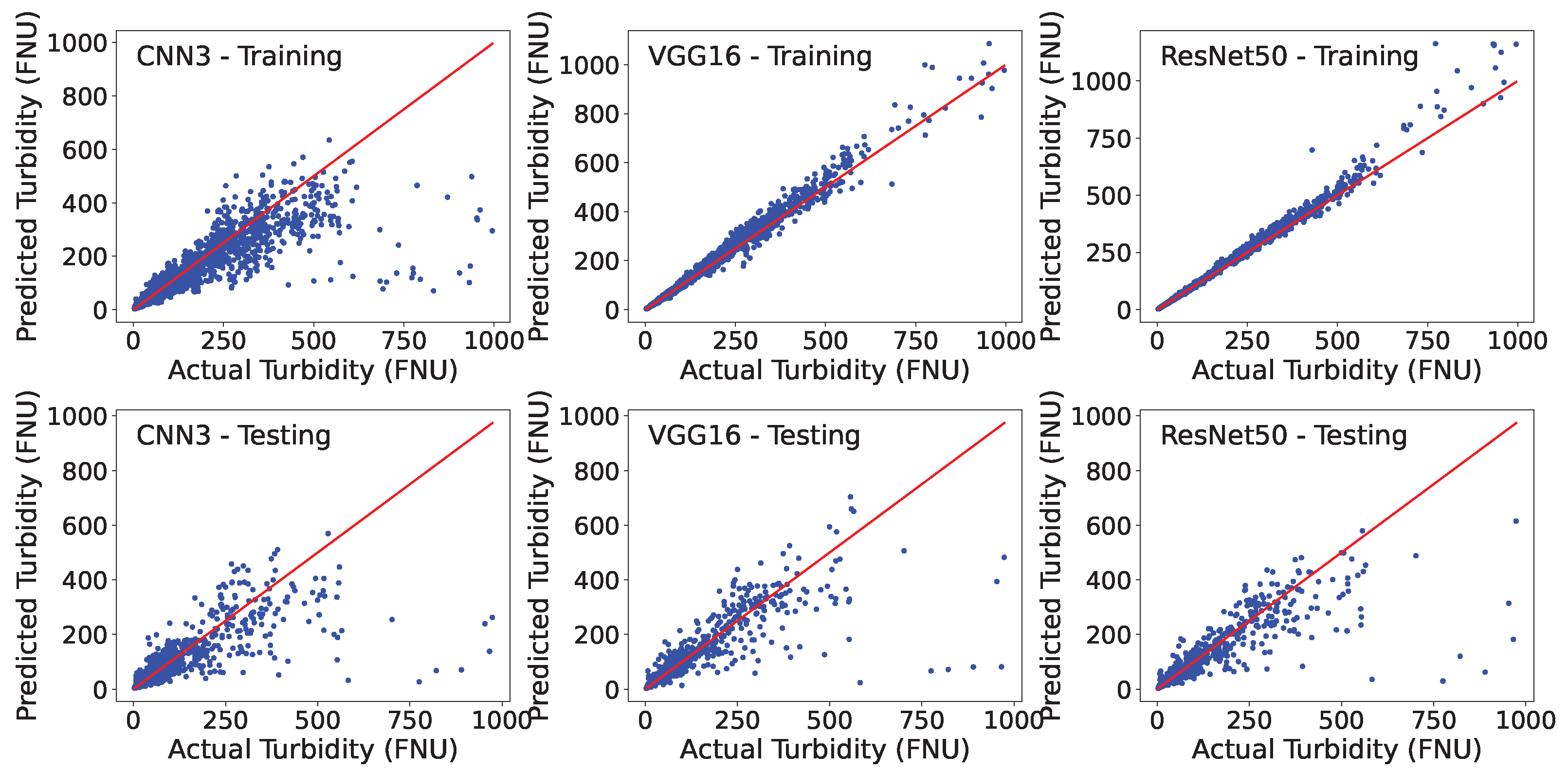
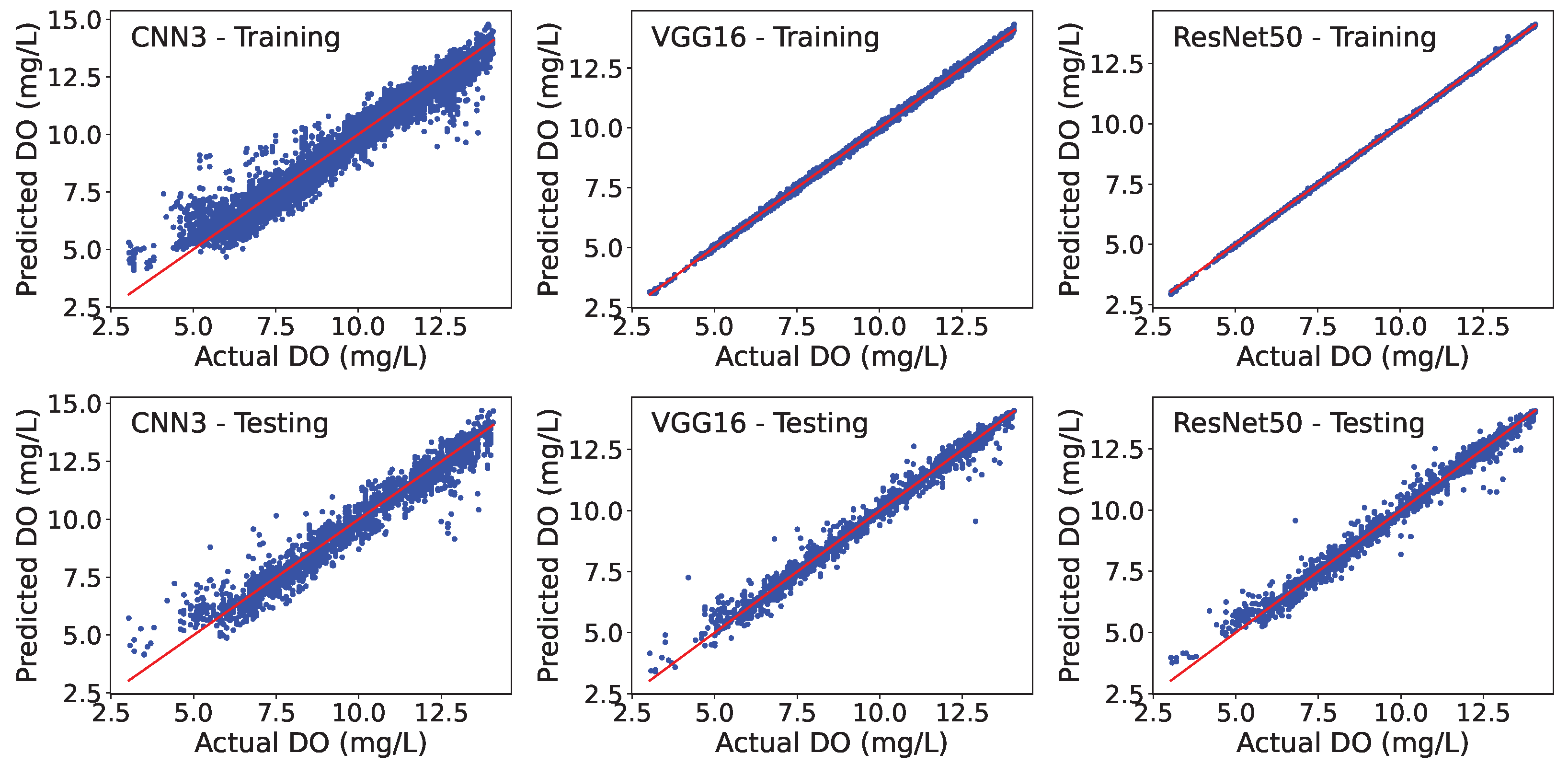
3.1. Modeling Training and Testing

For gauge height estimation, a simple three-layer CNN model achieved strong performance, with an R2 of 0.981 during training and 0.959 during testing (Table 1, Figure 3). Deeper neural architectures in VGG16 and ResNet50 significantly enhance the capture of nonlinear relationships between image intensity values and gauge height, leading to further improvements in R2 for both training and testing (Table 1, Figure 3). While R2 indicates overall model fit, root-mean-square-error (RMSE) provides a more interpretable measure of performance. The CNN3 model yielded RMSE values of 0.58 ft for training and 0.86 ft for testing. Compared to the mean gauge height of 6.63 ft during the model training period, the RMSE values correspond to errors of 8.7% for training and 13.0% for testing. Among the DL models, VGG16 achieved an RMSE of 0.18 ft in training and 0.50 ft in testing. ResNet50 produced slightly higher RMSE values but benefited from a faster training period. Both VGG16 and ResNet50 demonstrated comparable testing errors to CNN3’s training error.
Compared to gauge height estimation, turbidity estimation is significantly more challenging. While model training maintained high R2 values, particularly in VGG16 and ResNet50, these values dropped substantially during testing (Table 1, Figure 4). This decline is expected, as turbidity is influenced by water color and opacity, which are also affected by sunlight, weather conditions, and webcam exposure [10]. These external factors interact with turbidity’s effect on water appearance, making it difficult to establish a clear quantitative relationship between images and turbidity, even when such a relationship exists. The results indicate that the RMSE for turbidity estimation using images ranges from 40 to 50 FTU (Table 1), which is lower than the mean turbidity value of 74.94 FTU. Therefore, turbidity estimation using DL models proved unsatisfactory.
DO and fDMO estimation show similar performance. During training, VGG16 and ResNet50 achieved near-perfect R2 values caused by over-fitting. This is evidenced by the nearly perfect 1:1 line in the training phase, contrasted with a more scattered prediction vs. actual plot during testing (Figure 5 and Figure 6). For both parameters, VGG16 and ResNet50 achieved testing RMSE values that were either smaller than or comparable to the training RMSE for CNN3. The results demonstrate improved model performance in the test phase, benefited from deeper neural layers.
Time series plots illustrate the temporal variation of hydraulic and water quality data, as well as how model predictions align with measured values (Figure 7, Figure 8, Figure 9 and Figure 10). The results indicate that DL models track measured data more closely than the simpler CNN3 model, demonstrating superior performance.
Here, we note that all model performance evaluations were conducted using testing data that temporally overlap with the training period. This overlap may lead to an overestimation of model accuracy, as the models could be benefiting from learned temporal patterns rather than generalizing to entirely unseen conditions. Consequently, examining the ability of these models for non-overlapping time periods would provide us with a more robust evaluation of model reliability.

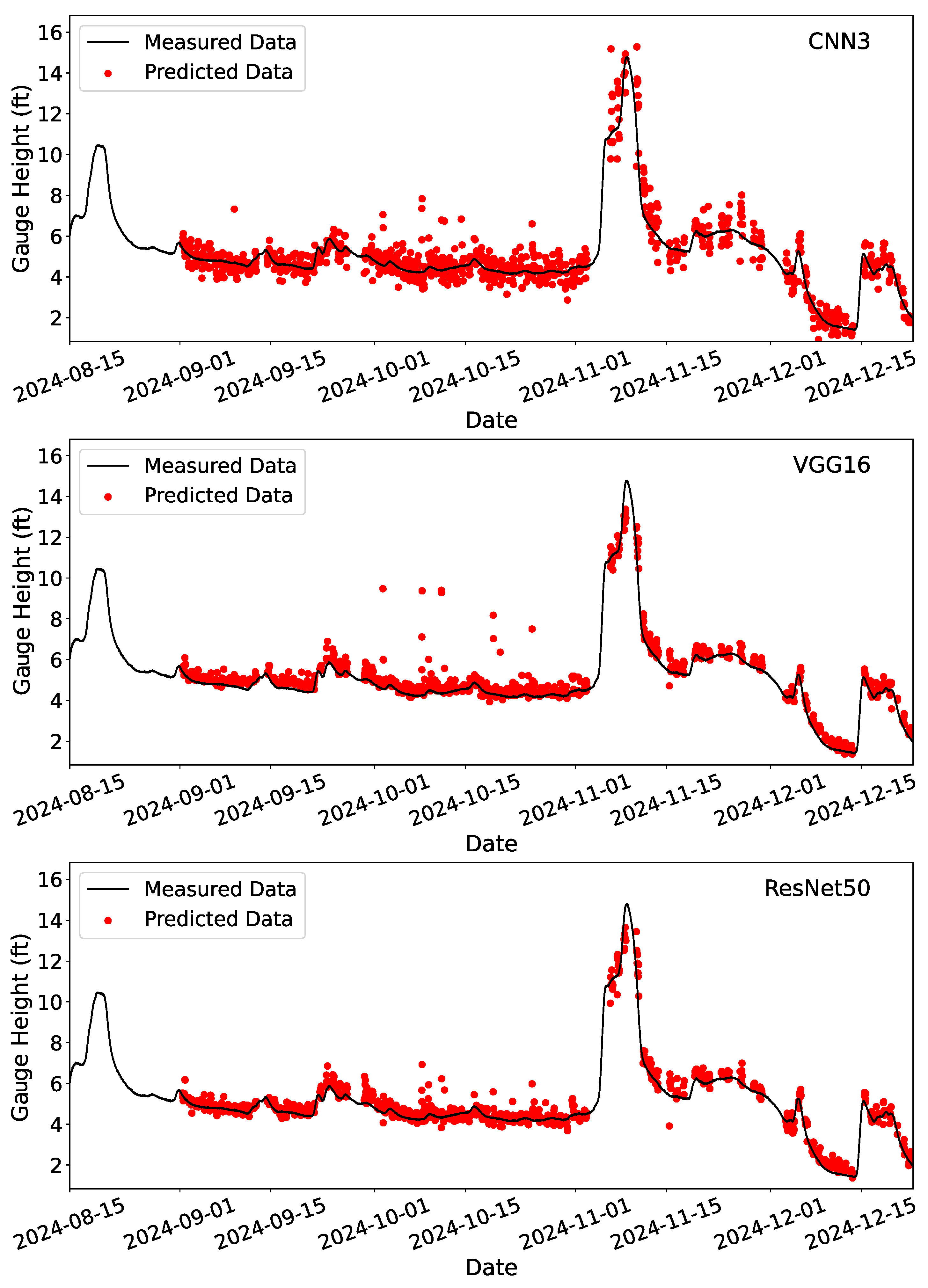
3.2. Deployment

The ML models show substantially different behaviors during the deployment stage, and vary differently among the four tested hydraulic and water quality parameters (Table 2, Figure 11). While DL models maintain superior performance to CNN3, the ability of all models in predicting ‘future’ suffers substantially due to unseen features. Among four parameters, ML models provide satisfactory prediction of gauge height, resulting in a slightly lower R2 than the model testing (Figure 12. The RMSE for VGG16 and ResNet50 is 0.56 and 0.4 ft, respectively, maintaining similar errors during the model testing (0.5 and 0.57 ft, respectively). This result shows that ML models are skilled in predicting gauging height, as demonstrated by Vanden Boomen et al. [26].
The agreement between the model predictions and the measured data is further illustrated in the time series plot (Figure 12). The results demonstrate that both VGG16 and ResNet50 effectively tracked the measured gauge height data when predicting ‘future’ and previously unseen conditions. Vanden Boomen et al. [26] applied saliency mapping to identify key image features that strongly influence predicted gauge height, such as shoreline and exposed land in shallow rivers. In our study, shoreline proved to be the most influential feature for gauge height prediction, ensuring robustness against data extrapolation to ‘future’ conditions.
The residuals (i.e., observed gauge height minus predicted gauge height) of all models are well distributed around zero, with median values of 0 ft during the training/testing period and −0.16 ft during the deployment period (Figure 13). The Pearson correlation coefficient between the residuals and gauge height is 0.08 for the training/testing period and −0.3 for the deployment period, indicating nearly no correlation (close to the value of 0) during the model training and a moderate negative correlation during the deployment. To further evaluate possible autocorrelation within the residuals, we performed the Durbin–Watson statistic test, yielding values of 2.01 for the training/testing period and 1.09 for the deployment period. This result indicates nearly no autocorrelation (close to the value of 2) during the training/testing period and positive autocorrelation in the deployment. The residual analysis suggests that these ML models perform excellently and produce largely unbiased predictions during training and testing. However, when deployed for future events, the models exhibit slight to moderate bias, potentially leading to discernible patterns in the residuals.
However, all three ML models failed to provide satisfactory predictions for turbidity and fDOM, yielding low R2 values based on direct prediction-versus-measurement comparisons (Table 2, Figure 11b,c). Nevertheless, this does not imply that the models lack predictive skill for these parameters. The time series plot of turbidity (Figure 14) shows that the models successfully captured the turbidity spike around 8 November 2024, with the two DL models performing particularly well in detecting this peak event. However, all models produced scattered predictions around the average turbidity for other periods and failed to capture the second peak on 15 December 2025. For fDOM, the time series plot indicates that none of the models accurately predicted the observed values (Figure 15). However, the measured fDOM range (7–13 µg/L) is only slightly narrower than the training range (5–17 µg/L), and the measured fDOM data exhibit high fluctuations. This inherent data uncertainty likely contributed to the poor performance of ML models.
Surprisingly, the ML-predicted DO concentrations align well with the measured data (Table 2, Figure 11d). Although the model predictions do not capture the day-to-day variations in DO caused by temperature effects on oxygen solubility, all ML models effectively track overall DO trends during the deployment period (Figure 16).
We note that different ML models may be suitable for different tasks in hydraulic and hydrological applications [46,47]. For instance, CNN3 might be suitable for simpler relationship, while deeper architectures in VGG16 and ResNet50 are better suited for more complex relationships. VGG16 has a uniform architecture, which can effectively learn the global patterns across images related to the characteristics of water quality. ResNet50 uses a skip-connection algorithm that can learn the long-range dependencies in images while mitigating the vanishing gradient problem. The ability of ML models to predict gauge height is quite intuitive, due to the direct relationship between images and water level changes. The effectiveness of ML models in predicting water quality parameters (e.g., DO) indicates that these models can also detect complex patterns or deeply encoded relationships within the images.
In addition, the strong performance during training and testing but reduced effectiveness during deployment indicates potential overfitting to training data. This is particularly evident in turbidity and fDOM predictions, where the ML models fail to generalize well to unseen conditions. In future research, we plan to explore regularization techniques, data augmentation, and ensemble learning to enhance model robustness.

4. Concluding Remarks

With the rapid expansion of webcam deployment in the U.S. Geological Survey (USGS) water information mission, this technical paper tests and evaluates three convolutional neural network (CNN)-based machine learning (ML) models, including two deep network-layer architectures, VGG16 and ResNet50. This study focuses on four hydrological and hydraulic parameters: gauge height, turbidity, fluorescent dissolved organic matter (fDOM), and dissolved oxygen (DO).
During the training and testing period, the machine learning (ML) models, particularly deep learning (DL) models, exhibited excellent performance in capturing complex nonlinear relationships between RGB images and the selected hydrological parameters. This is not surprising given the strong learning capabilities of deep neural networks.
During the deployment period for ‘future’ events, the results indicate that the simple three-layer model (CNN3) is effective in identifying patterns and trends in hydrological parameters but performs poorly in prediction. DL models, including VGG16 and ResNet50, exhibit similar predictive abilities across all four parameters. Both models achieve satisfactory predictions for gauge height and offer some insights into turbidity and fDOM, though their predictions for these parameters remain inadequate. Surprisingly, both models demonstrate reasonably accurate predictions for DO concentration in water.
Although pure image-based ML or DL approaches may not be ideal for routine water quality monitoring, model performance could be enhanced by incorporating additional constraints, such as time series information. For example, integrating a CNN with a long short-term memory (LSTM) algorithm could improve predictive accuracy by capturing both image features and temporal dependencies in water quality variations. This hybrid approach could lead to more robust and reliable prediction, particularly in dynamic aquatic environments where temporal patterns play a crucial role. Therefore, the development of hybrid models is subject to further research.

Author Contributions

Conceptualization, B.W.; methodology, R.X. and B.W.; validation, R.X. and B.W.; formal analysis, R.X. and B.W.; data curation, R.X.; writing—original draft preparation, R.X. and B.W.; writing—review and editing, R.X. and B.W.; supervision, B.W. All authors have read and agreed to the published version of the manuscript.

Funding

This publication was developed under Assistance Agreement no. EM-84065101 awarded by the US Environmental Protection Agency to the Missouri Water Center at the University of Missouri. It has not been formally reviewed by the EPA. The views expressed in this document are solely those of the authors and do not necessarily reflect those of the Agency. The EPA does not endorse any products or commercial services mentioned in this publication.

Data Availability Statement

The U.S. Geological Survey (USGS) gauging station data are available from the National Water Information System (https://waterdata.usgs.gov/monitoring-location/06934500), accessed on 10 January 2025.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CNNConvolutional neural network
DLDeep learning
DODissolved oxygen
fDOMFluorescent dissolved organic matter
FNUFormazin nephelometric units
HIVISHydrological Imagery Visualization and Information System
MLMachine learning
QSEQuinine sulfate equivalents
USGSU.S. Geological Survey

References

  1. Sutadian, A.; Muttil, N.; Yilmaz, A.; Perera, B.J.C. Development of river water quality indices—A review. Environ. Monit. Assess. 2016, 188, 58. [Google Scholar] [CrossRef]
  2. Nguyen, T.; Helm, B.; Hettiarachchi, H.; Caucci, S.; Krebs, P. The selection of design methods for river water quality monitoring networks: A review. Environ. Earth Sci. 2019, 78, 96. [Google Scholar] [CrossRef]
  3. Kuehne, L.; Dickens, C.; Tickner, D.; Messager, M.; Olden, J.; O’Brien, G.; Lehner, B.; Eriyagama, N. The future of global river health monitoring. PLoS Water 2023, 2, e0000101. [Google Scholar] [CrossRef]
  4. Falcone, J.A.; Carlisle, D.M.; Wolock, D.M.; Meador, M.R. GAGES: A stream gage database for evaluating natural and altered flow conditions in the conterminous United States. Ecology 2010, 91, 621. [Google Scholar] [CrossRef]
  5. Marti, M.; Heimann, D. Peak Streamflow Trends in Missouri and Their Relation to Changes in Climate, Water Years 1921–2020-F; U.S. Geological Survey Scientific Investigations Report 2023–5064, 50p; Chapter F of Peak Streamflow Trends and Their Relation to Changes in Climate in Illinois, Iowa, Michigan, Minnesota, Missouri, Montana, North Dakota, South Dakota, and Wisconsin; U.S. Geological Survey: Reston, VA, USA, 2024. [CrossRef]
  6. U.S. Geological Survey. A New Evaluation of the USGS Streamgaging Network; A Report to Congress; U.S. Geological Survey: Reston, VA, USA, 1998.
  7. Li, G.; Wang, B.; Elliott, C.M.; Call, B.C.; Chapman, D.C.; Jacobson, R.B. A three-dimensional Lagrangian particle tracking model for predicting transport of eggs of rheophilic-spawning carps in turbulent rivers. Ecol. Model. 2022, 470, 110035. [Google Scholar] [CrossRef]
  8. Li, G.; Elliott, C.M.; Call, B.C.; Chapman, D.C.; Jacobson, R.B.; Wang, B. Evaluations of Lagrangian egg drift models: From a laboratory flume to large channelized rivers. Ecol. Model. 2023, 475, 110200. [Google Scholar] [CrossRef]
  9. Xu, R.; Chapman, D.C.; Elliott, C.M.; Call, B.C.; Jacobson, R.B.; Wang, B. Ecological inferences on invasive carp survival using hydrodynamics and egg drift models. Sci. Rep. 2024, 14, 9556. [Google Scholar] [CrossRef]
  10. Tom, M.; Prabha, R.; Wu, T.; Baltsavias, E.; Leal-Taixé, L.; Schindler, K. Ice Monitoring in Swiss Lakes from Optical Satellites and Webcams Using Machine Learning. Remote Sens. 2020, 12, 3555. [Google Scholar] [CrossRef]
  11. Tedesco, M.; Radzikowski, J. Assessment of a Machine Learning Algorithm Using Web Images for Flood Detection and Water Level Estimates. GeoHazards 2023, 4, 437–452. [Google Scholar] [CrossRef]
  12. Bradley, E.S.; Toomey, M.P.; Still, C.J.; Roberts, D.A. Multi-scale sensor fusion with an online application: Integrating GOES, MODIS, and webcam imagery for environmental monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 497–506. [Google Scholar] [CrossRef]
  13. Helmrich, A.M.; Ruddell, B.L.; Bessem, K.; Chester, M.V.; Chohan, N.; Doerry, E.; Eppinger, J.; Garcia, M.; Goodall, J.L.; Lowry, C.; et al. Opportunities for crowdsourcing in urban flood monitoring. Environ. Model. Softw. 2021, 143, 105124. [Google Scholar]
  14. Richardson, A.D.; Jenkins, J.P.; Braswell, B.H.; Hollinger, D.Y.; Ollinger, S.V.; Smith, M.L. Use of digital webcam images to track spring green-up in a deciduous broadleaf forest. Oecologia 2007, 152, 323–334. [Google Scholar]
  15. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar]
  16. Tripathy, K.P.; Mishra, A.K. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions. J. Hydrol. 2024, 628, 130458. [Google Scholar]
  17. Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.L.; Chen, S.C.; Iyengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar]
  18. Sharifani, K.; Amini, M. Machine learning and deep learning: A review of methods and applications. World Inf. Technol. Eng. J. 2023, 10, 3897–3904. [Google Scholar]
  19. Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar]
  20. Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
  21. Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef]
  22. Kim, H.I.; Kim, D.; Mahdian, M.; Salamattalab, M.M.; Bateni, S.M.; Noori, R. Incorporation of water quality index models with machine learning-based techniques for real-time assessment of aquatic ecosystems. Environ. Pollut. 2024, 355, 124242. [Google Scholar] [CrossRef]
  23. Saravani, M.J.; Noori, R.; Jun, C.; Kim, D.; Bateni, S.M.; Kianmehr, P.; Woolway, R.I. Predicting Chlorophyll-a Concentrations in the World’s Largest Lakes Using Kolmogorov-Arnold Networks. Environ. Sci. Technol. 2025, 59, 1801–1810. [Google Scholar] [CrossRef]
  24. Eltner, A.; Bressan, P.O.; Akiyama, T.; Gonçalves, W.N.; Junior, J.M. Using Deep Learning for Automatic Water Stage Measurements. Water Resour. Res. 2021, 57, e2020WR027608. [Google Scholar] [CrossRef]
  25. Vandaele, R.; Dance, S.L.; Ojha, V. Deep learning for automated river-level monitoring through river-camera images: An approach based on water segmentation and transfer learning. Hydrol. Earth Syst. Sci. 2021, 25, 4435–4453. [Google Scholar] [CrossRef]
  26. Vanden Boomen, R.L.; Yu, Z.Y.; Liao, Q. Application of Deep Learning for Imaging-Based Stream Gaging. Water Resour. Res. 2021, 57, e2021WR029980. [Google Scholar] [CrossRef]
  27. Simonya, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
  28. Ansari, S.; Rennie, C.D.; Jamieson, E.C.; Seidou, O.; Clark, S.P. RivQNet: Deep Learning Based River Discharge Estimation Using Close-Range Water Surface Imagery. Water Resour. Res. 2023, 59, e2021WR031841. [Google Scholar] [CrossRef]
  29. Dosovitskiy, A.; Fischer, P.; Ilg, E.; Häusser, P.; Hazırbaş, C.; Golkov, V.; Smagt, P.v.d.; Cremers, D.; Brox, T. FlowNet: Learning Optical Flow with Convolutional Networks. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
  30. Lopez-Fuentes, L.; Rossi, C.; Skinnemoen, H. River segmentation for flood monitoring. In Proceedings of the IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 3746–3749. [Google Scholar] [CrossRef]
  31. Moy de Vitry, M.; Kramer, S.; Wegner, J.D.; Leitão, J.P. Scalable flood level trend monitoring with surveillance cameras using a deep convolutional neural network. Hydrol. Earth Syst. Sci. 2019, 23, 4621–4634. [Google Scholar] [CrossRef]
  32. Pally, R.; Samadi, S. Application of image processing and convolutional neural networks for flood image classification and semantic segmentation. Environ. Model. Softw. 2022, 148, 105285. [Google Scholar] [CrossRef]
  33. Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
  34. Gupta, A.; Ruebush, E. AquaSight: Automatic Water Impurity Detection Utilizing Convolutional Neural Networks. arXiv 2019, arXiv:1907.07573. [Google Scholar]
  35. Chen, J.; Zhang, D.; Yang, S.; Nanehkaran, Y.A. Intelligent monitoring method of water quality based on image processing and RVFL-GMDH model. IET Image Process. 2020, 14, 4646–4656. [Google Scholar] [CrossRef]
  36. Anand, V.; Oinam, B.; Wieprecht, S. Machine learning approach for water quality predictions based on multispectral satellite imageries. Ecol. Inform. 2024, 84, 102868. [Google Scholar] [CrossRef]
  37. He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
  38. Li, G.; Elliott, C.M.; Call, B.C.; Sansom, B.J.; Jacobson, R.B.; Wang, B. Turbulence near a sandbar island in the lower Missouri River. River Res. Appl. 2023, 39, 1857–1874. [Google Scholar] [CrossRef]
  39. Booth, A.; Fleck, J.; Pellerin, B.A.; Hansen, A.; Etheridge, A.; Foster, G.M.; Graham, J.L.; Bergamaschi, B.A.; Carpenter, K.D.; Downing, B.D.; et al. Field Techniques for Fluorescence Measurements Targeting Dissolved Organic Matter, Hydrocarbons, and Wastewater in Environmental Waters: Principles and Guidelines for Instrument Selection, Operation and Maintenance, Quality Assurance, and Data Reporting; U.S. Geological Survey Techniques and Methods, Book 1, Chap. D11, 41p; U.S. Geological Survey: Reston, VA, USA, 2023; 41p. [CrossRef]
  40. Dai, D. An introduction of cnn: Models and training on neural network models. In Proceedings of the 2021 International Conference on Big Data, Artificial Intelligence and Risk Management (ICBAR), Shanghai, China, 5–7 November 2021; pp. 135–138. [Google Scholar]
  41. Jing, Y.; Zhang, L.; Hao, W.; Huang, L. Numerical study of a CNN-based model for regional wave prediction. Ocean. Eng. 2022, 255, 111400. [Google Scholar] [CrossRef]
  42. Trang, N.T.H.; Long, K.Q.; An, P.L.; Dang, T.N. Development of an artificial intelligence-based breast cancer detection model by combining mammograms and medical health records. Diagnostics 2023, 13, 346. [Google Scholar] [CrossRef] [PubMed]
  43. Tammina, S. Transfer learning using vgg-16 with deep convolutional neural network for classifying images. Int. J. Sci. Res. Publ. (IJSRP) 2019, 9, 143–150. [Google Scholar] [CrossRef]
  44. Khan, M.A.; Ahmed, N.; Padela, J.; Raza, M.S.; Gangopadhyay, A.; Wang, J.; Foulds, J.; Busart, C.; Erbacher, R.F. Flood-ResNet50: Optimized Deep Learning Model for Efficient Flood Detection on Edge Device. In Proceedings of the 2023 International Conference on Machine Learning and Applications (ICMLA), Jacksonville, FL, USA, 15–17 December 2023; pp. 512–519. [Google Scholar]
  45. Prakash, S.; Sharma, A.; Sahu, S.S. Soil moisture prediction using machine learning. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 1–6. [Google Scholar]
  46. Luan, H.; Tsai, C.C. A review of using machine learning approaches for precision education. Educ. Technol. Soc. 2021, 24, 250–266. [Google Scholar]
  47. Lange, H.; Sippel, S. Machine learning applications in hydrology. In Forest-Water Interactions; Springer: Cham, Switzerland, 2020; pp. 233–257. [Google Scholar]
Hydrology 12 00065 g001
Figure 1. (a) Location of the webcam at the Missouri River at Hermann, Missouri. (b,c) Two sample images at two different times ((b): 12:01 CST; (c): 17:01 CST) on 11/20/2024, available on the HIVIS portal.
Figure 1. (a) Location of the webcam at the Missouri River at Hermann, Missouri. (b,c) Two sample images at two different times ((b): 12:01 CST; (c): 17:01 CST) on 11/20/2024, available on the HIVIS portal.
Hydrology 12 00065 g001
Hydrology 12 00065 g002
Figure 2. Architecture of the (a) CNN3 model; (b) VGG16 model; and (c) ResNet50 model. The residual network in the ResNet50 model is shown in subplot (d).
Figure 2. Architecture of the (a) CNN3 model; (b) VGG16 model; and (c) ResNet50 model. The residual network in the ResNet50 model is shown in subplot (d).
Hydrology 12 00065 g002
Hydrology 12 00065 g003
Figure 3. Comparison of gauge height prediction using ML with measured data.
Figure 3. Comparison of gauge height prediction using ML with measured data.
Hydrology 12 00065 g003
Hydrology 12 00065 g004
Figure 4. Comparison of turbidity prediction using ML with measured data.
Figure 4. Comparison of turbidity prediction using ML with measured data.
Hydrology 12 00065 g004
Hydrology 12 00065 g005
Figure 5. Comparison of dissolved oxygen prediction using ML with measured data.
Figure 5. Comparison of dissolved oxygen prediction using ML with measured data.
Hydrology 12 00065 g005
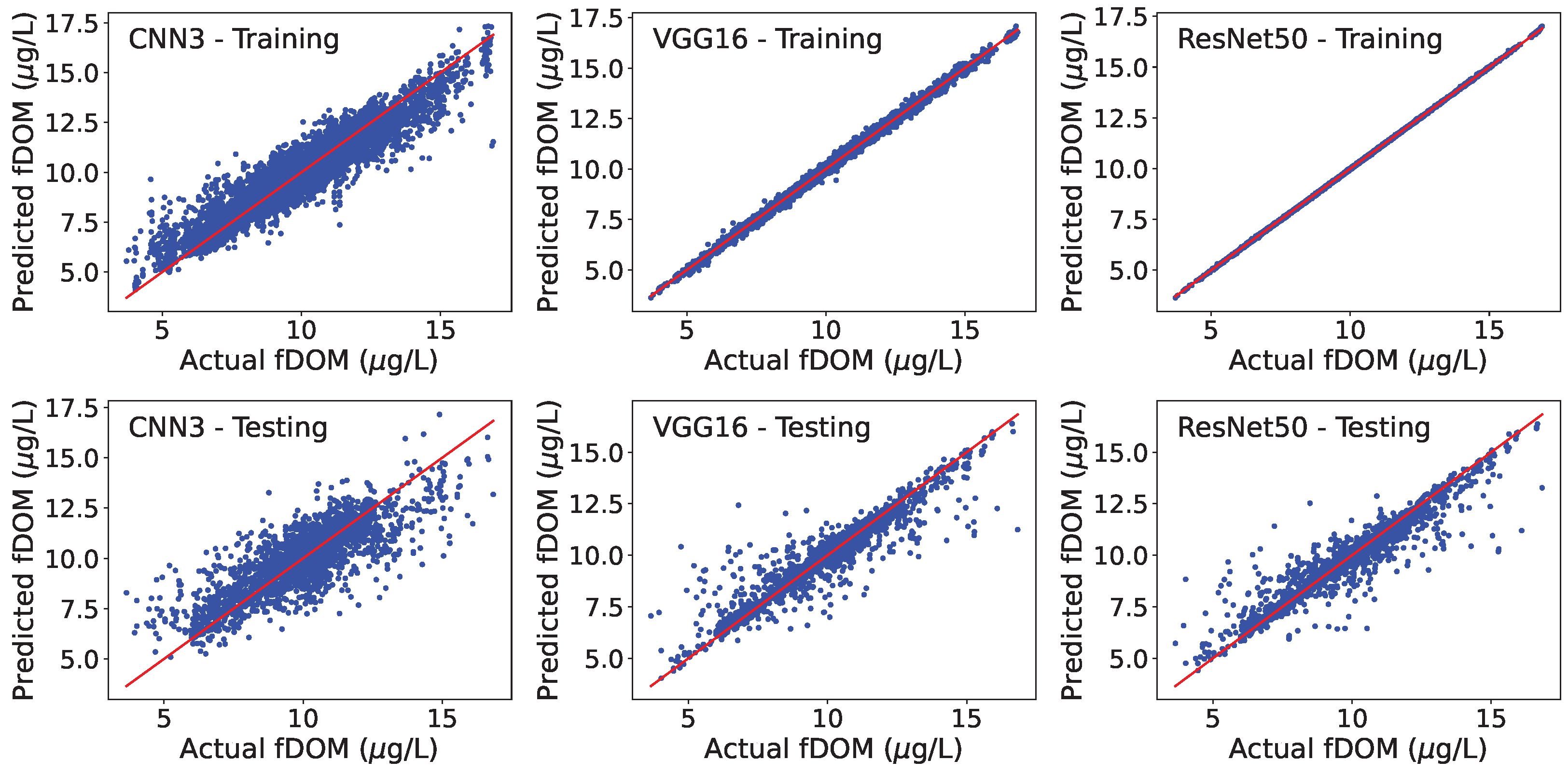
Hydrology 12 00065 g006
Figure 6. Comparison of fDOM prediction using ML with measured data.
Figure 6. Comparison of fDOM prediction using ML with measured data.
Hydrology 12 00065 g006
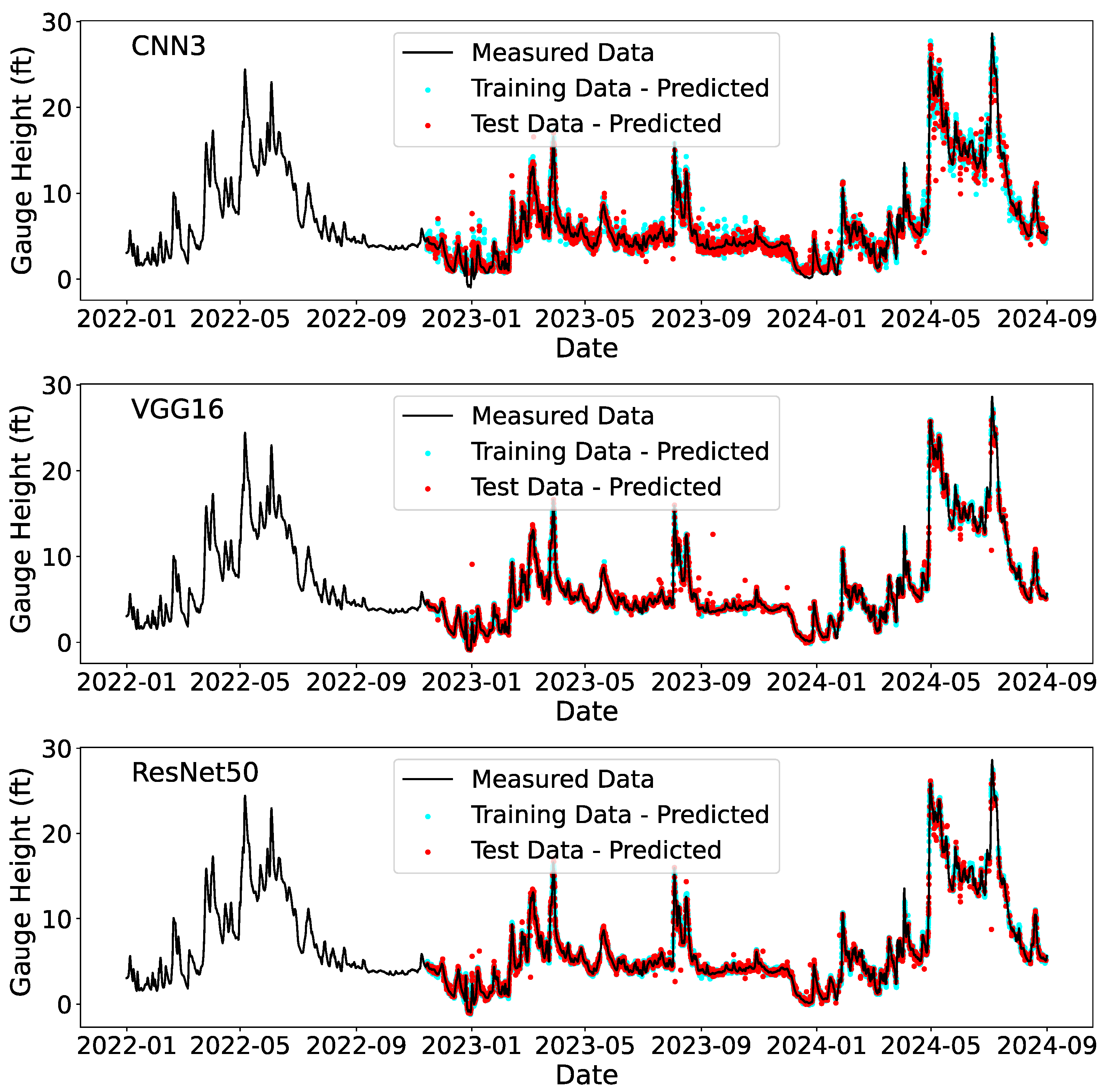
Hydrology 12 00065 g007
Figure 7. Time series of ML models predicted gauge height in comparison with measured data.
Figure 7. Time series of ML models predicted gauge height in comparison with measured data.
Hydrology 12 00065 g007
Hydrology 12 00065 g008
Figure 8. Time series of ML models’ predicted turbidity in comparison with measured data.
Figure 8. Time series of ML models’ predicted turbidity in comparison with measured data.
Hydrology 12 00065 g008
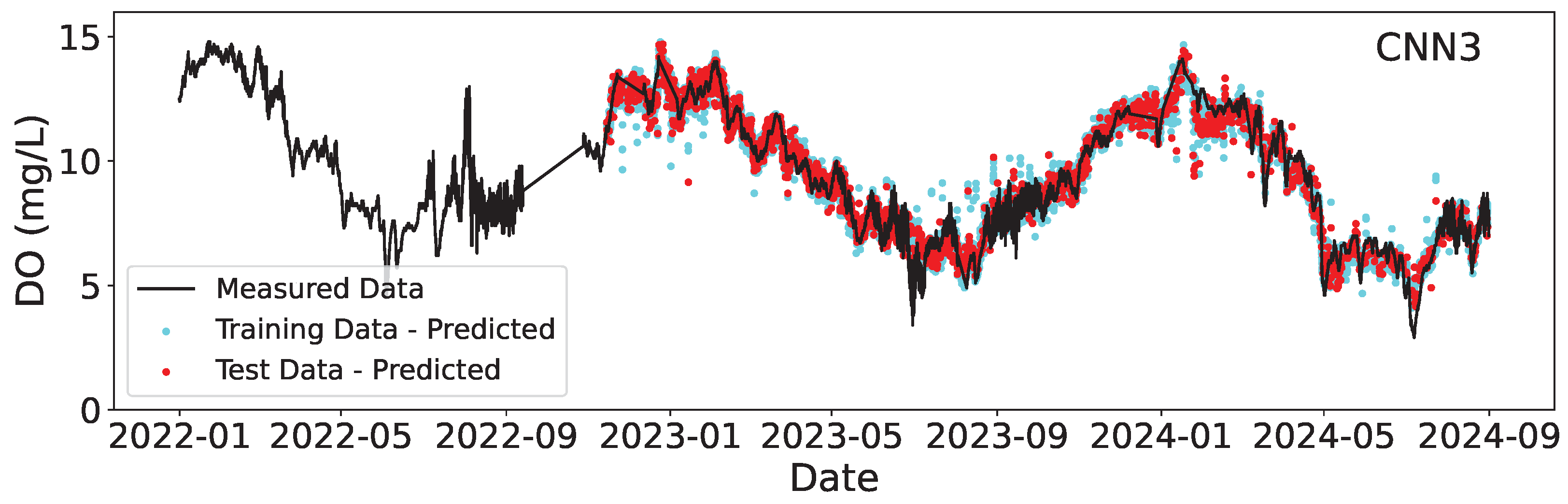
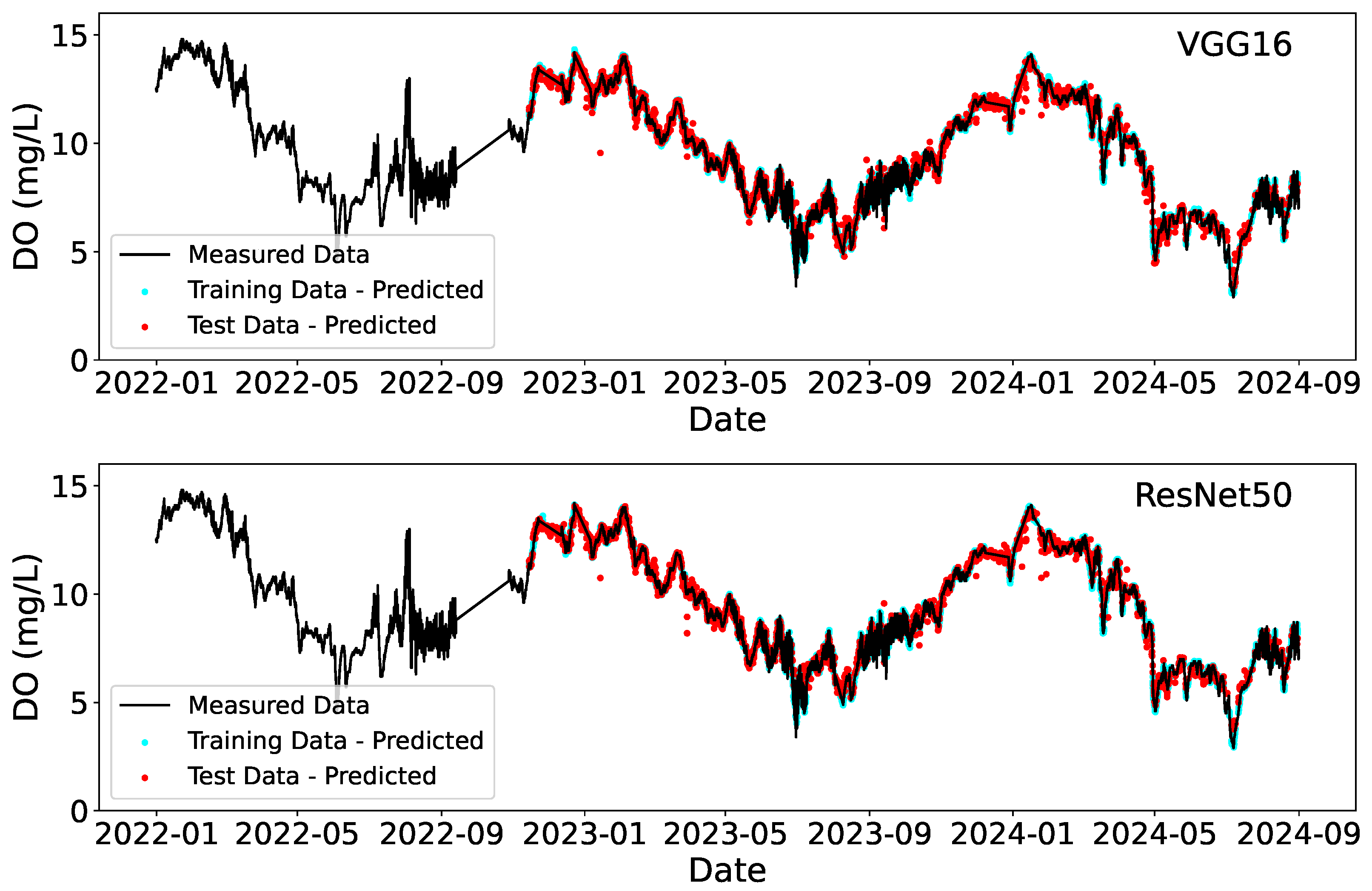
Hydrology 12 00065 g009aHydrology 12 00065 g009b
Figure 9. Time series of ML models’ predicted dissolved oxygen in comparison with measured data.
Figure 9. Time series of ML models’ predicted dissolved oxygen in comparison with measured data.
Hydrology 12 00065 g009aHydrology 12 00065 g009b
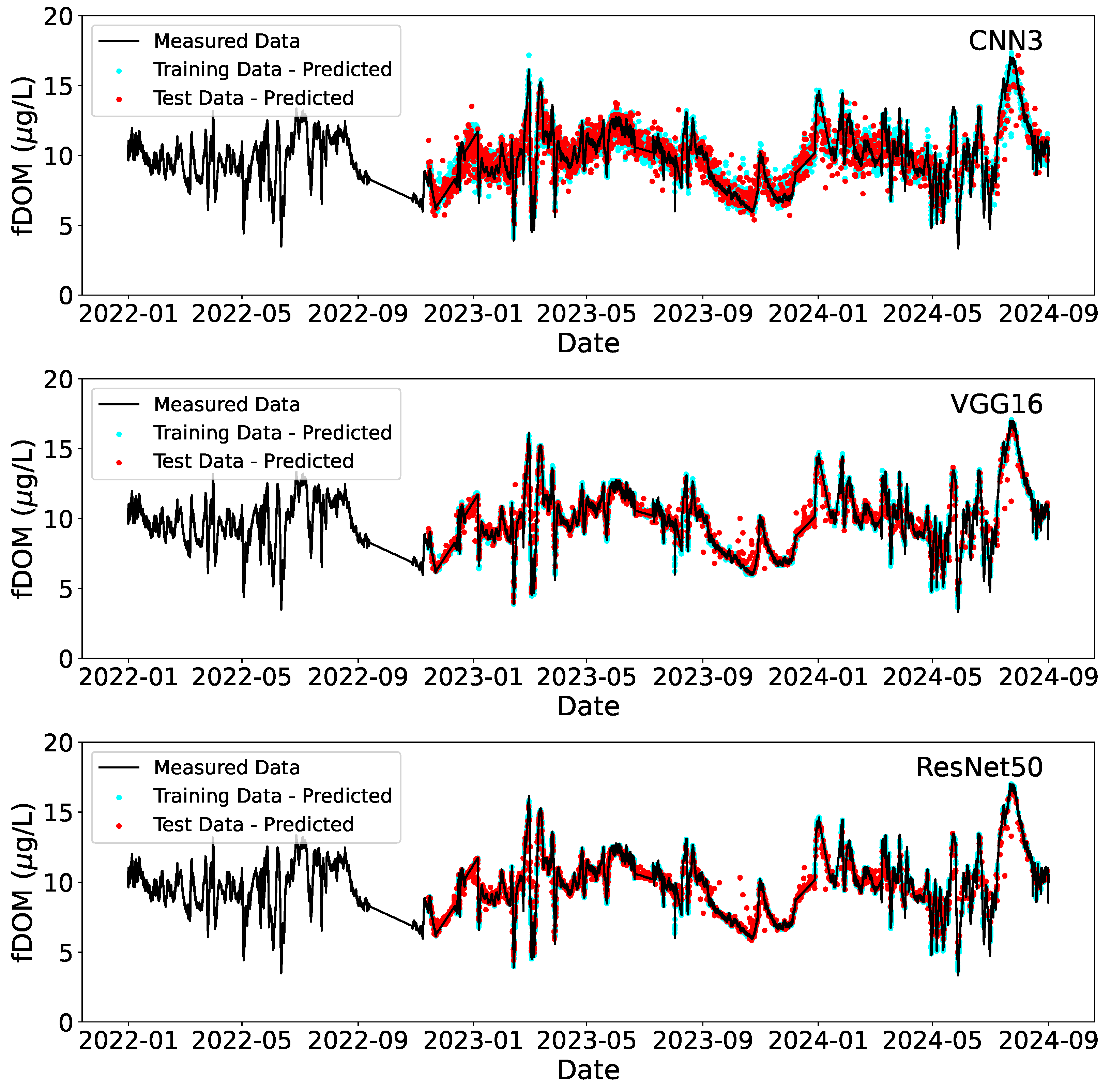
Hydrology 12 00065 g010
Figure 10. Time series of ML models’ predicted fDOM in comparison with measured data.
Figure 10. Time series of ML models’ predicted fDOM in comparison with measured data.
Hydrology 12 00065 g010
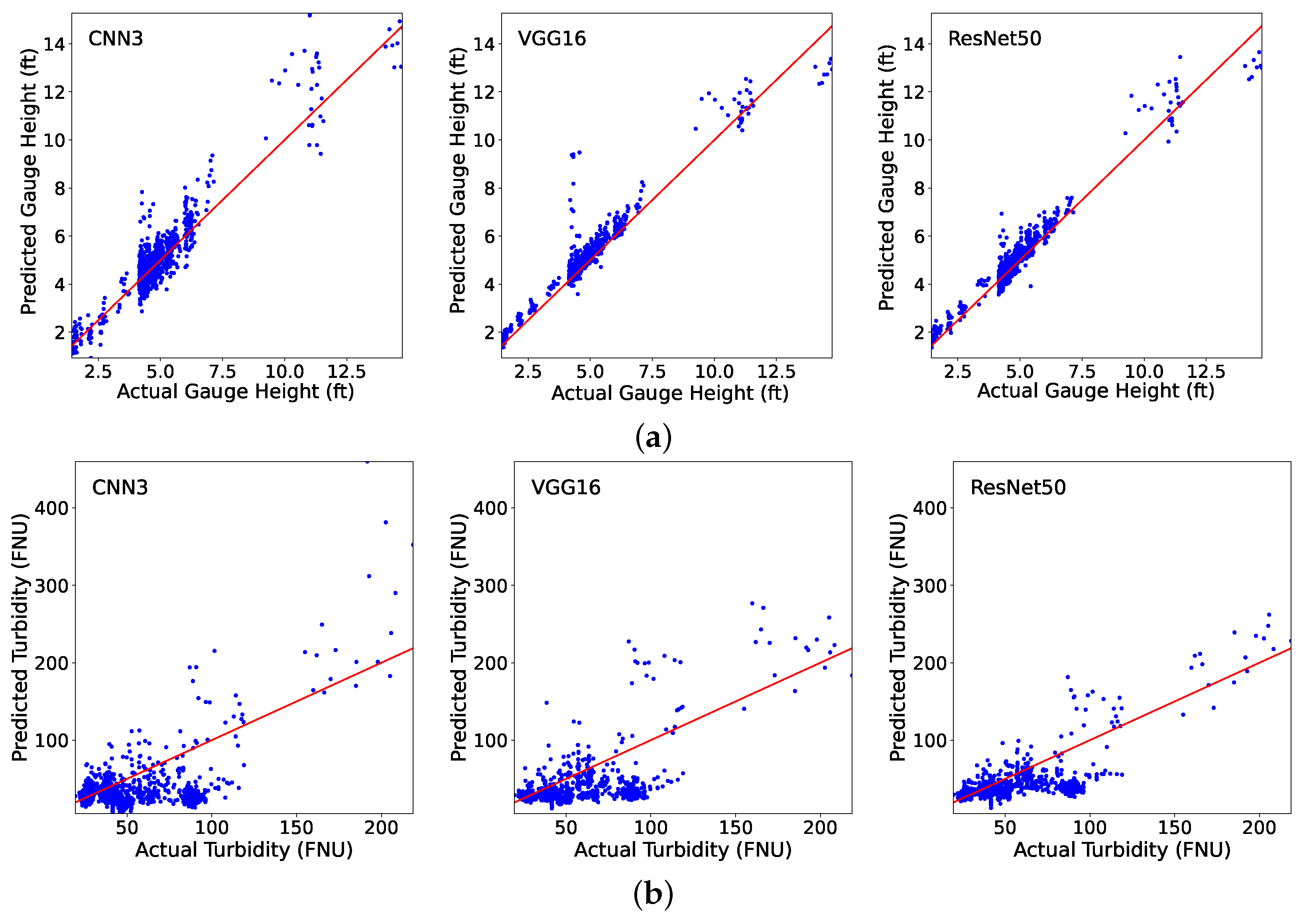
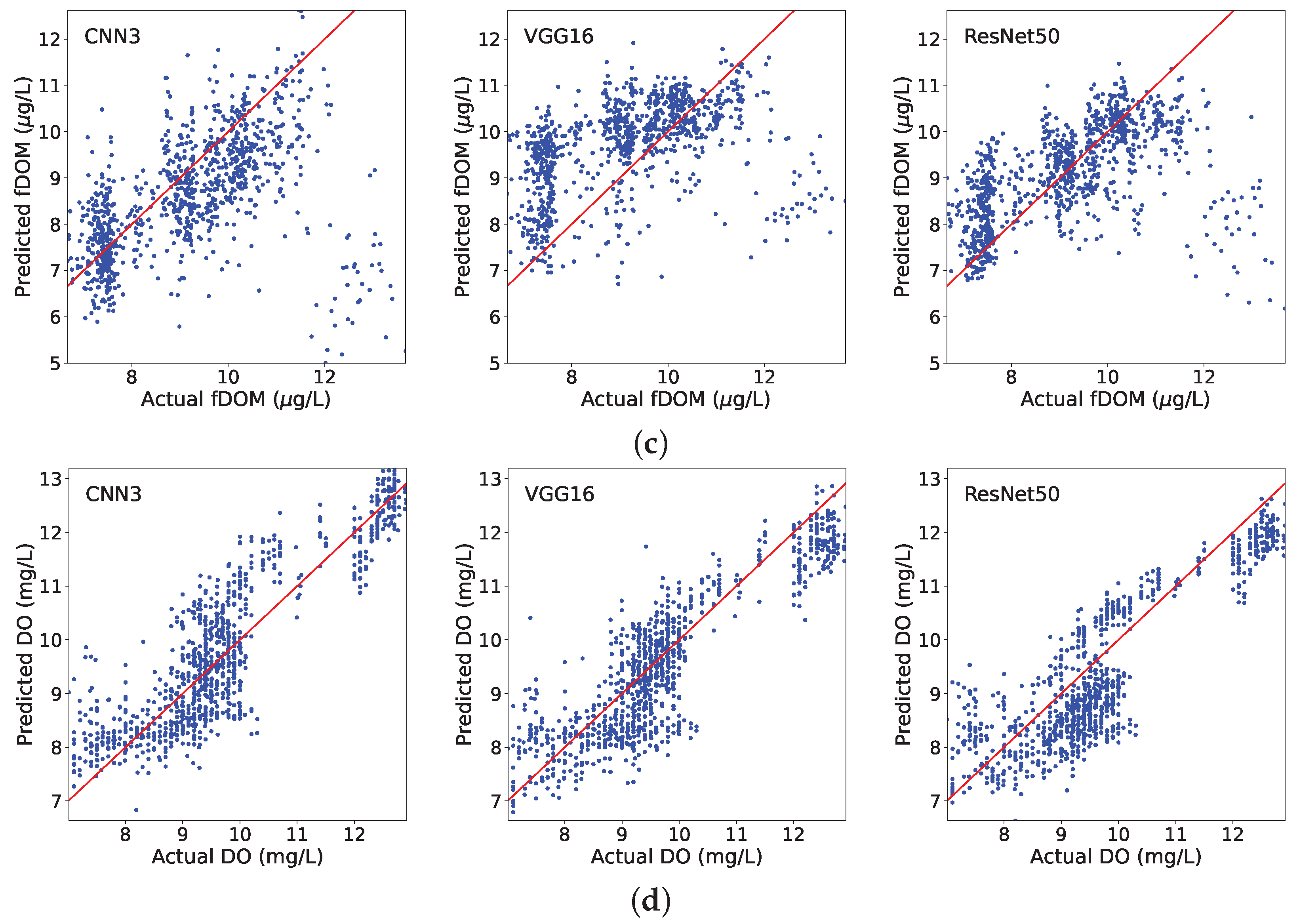
Hydrology 12 00065 g011aHydrology 12 00065 g011b
Figure 11. Comparison between three ML models with measured data during the deployment period: (a) gauge height; (b) turbidity; (c) fDOM; and (d) DO.
Figure 11. Comparison between three ML models with measured data during the deployment period: (a) gauge height; (b) turbidity; (c) fDOM; and (d) DO.
Hydrology 12 00065 g011aHydrology 12 00065 g011b
Hydrology 12 00065 g012
Figure 12. Time series of ML model-predicted gauge height with measured data during the deployment period.
Figure 12. Time series of ML model-predicted gauge height with measured data during the deployment period.
Hydrology 12 00065 g012
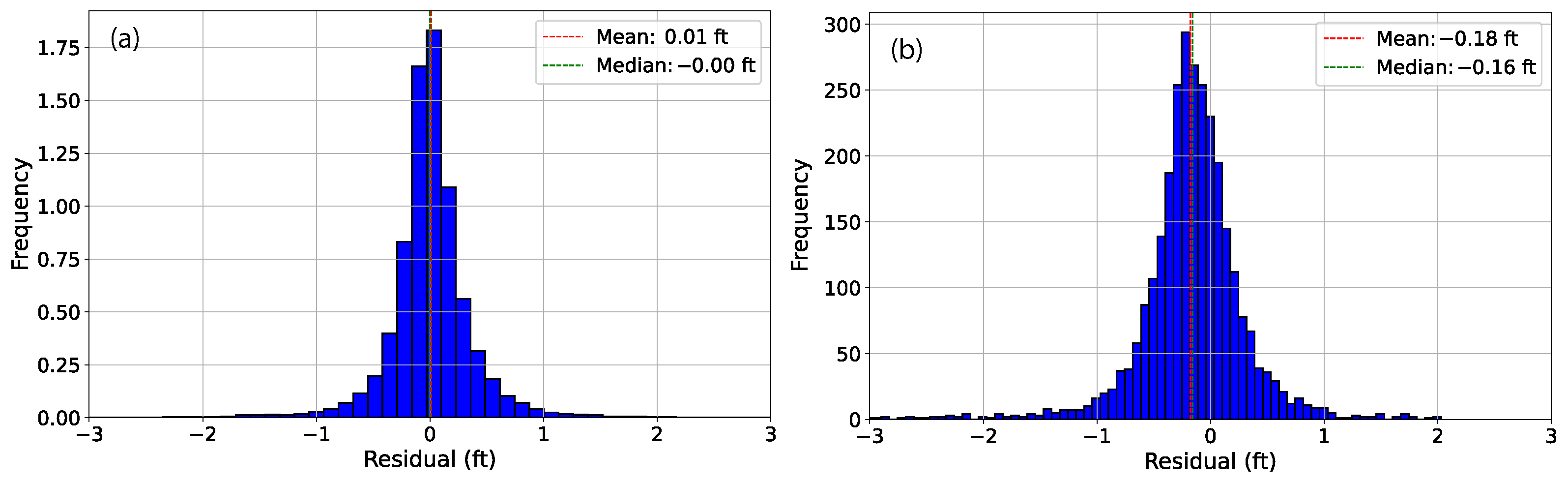
Hydrology 12 00065 g013
Figure 13. Histogram of residuals for all models during the period of (a) training and testing; (b) deployment.
Figure 13. Histogram of residuals for all models during the period of (a) training and testing; (b) deployment.
Hydrology 12 00065 g013
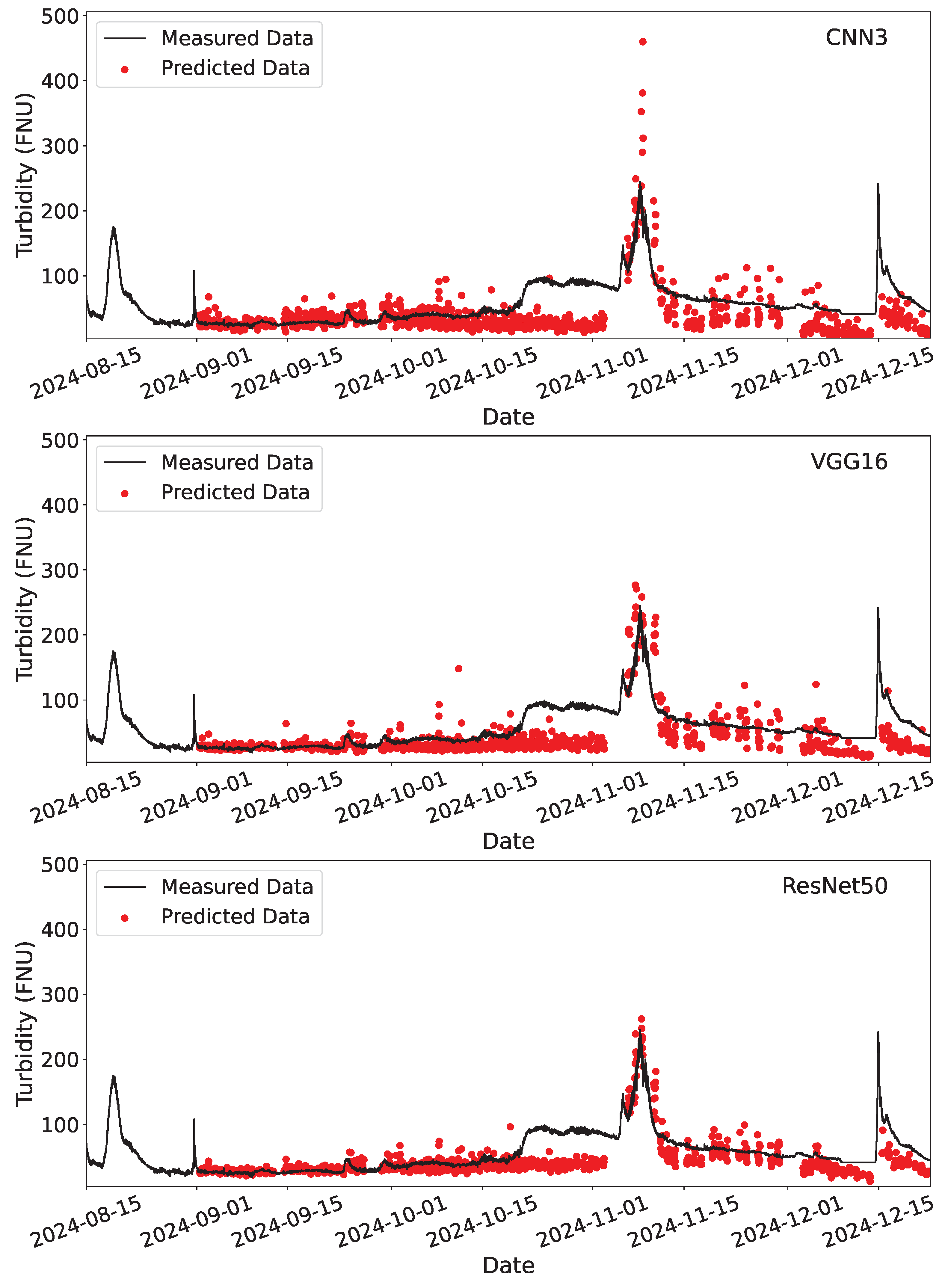
Hydrology 12 00065 g014
Figure 14. Time series of ML model-predicted turbidity with measured data during the deployment period.
Figure 14. Time series of ML model-predicted turbidity with measured data during the deployment period.
Hydrology 12 00065 g014
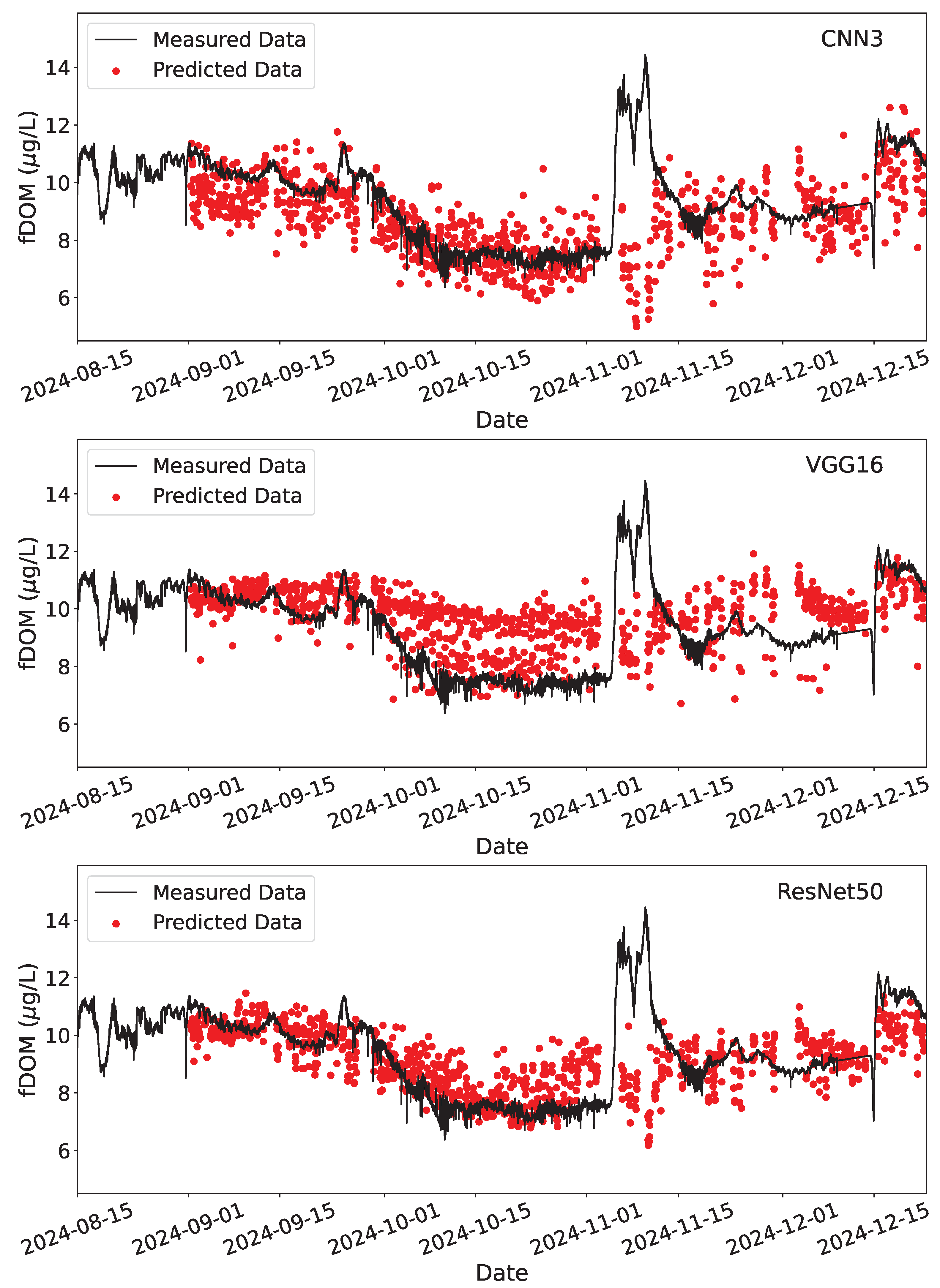
Hydrology 12 00065 g015
Figure 15. Time series of ML model-predicted fDOM with measured data during the deployment period.
Figure 15. Time series of ML model-predicted fDOM with measured data during the deployment period.
Hydrology 12 00065 g015
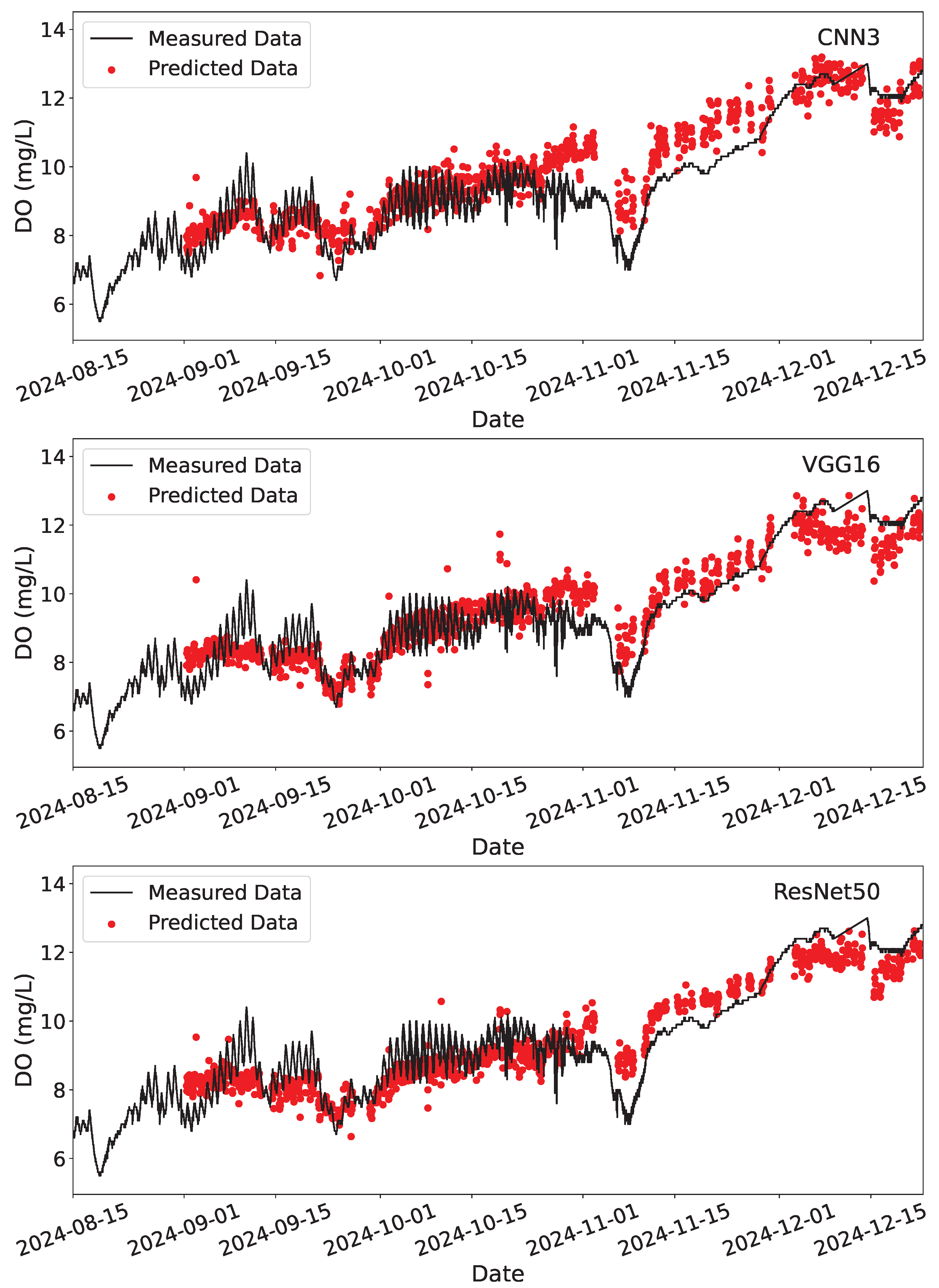
Hydrology 12 00065 g016
Figure 16. Time series of ML model-predicted DO with measured data during the deployment period.
Figure 16. Time series of ML model-predicted DO with measured data during the deployment period.
Hydrology 12 00065 g016
Table 1. Model performance during the training and testing for four hydrological parameters. RMSE indicates root-mean-square-error.
Table 1. Model performance during the training and testing for four hydrological parameters. RMSE indicates root-mean-square-error.
CNN3VGG16ResNet50
Gauge height (ft)R2Training0.9810.9980.998
R2Testing0.9590.9860.982
RMSETraining0.580.180.20
RMSETesting0.860.500.57
Turbidity (FNU)R2Training0.7910.9860.986
R2Testing0.6270.7280.743
RMSETraining41.0610.6510.47
RMSETesting56.5748.3148.99
fDOM (μg/L in QSE)R2Training0.8900.9971.000
R2Testing0.6750.8860.890
RMSETraining0.680.120.02
RMSETesting1.140.680.66
DO (mg/L)R2Training0.9540.9991.000
R2Testing0.9440.9860.987
RMSETraining0.510.070.03
RMSETesting0.570.280.28
Table 2. Model performance during the deployment for four hydrological parameters.
Table 2. Model performance during the deployment for four hydrological parameters.
CNN3VGG16ResNet50
Gauge height (ft)R20.8430.8920.945
RMSE0.670.560.40
Turbidity (FNU)R2−0.371−0.0770.315
RMSE34.0930.2224.11
fDOM (μg/L in QSE)R2−0.050−0.0150.227
RMSE1.521.491.30
DO (mg/L)R20.7520.7590.703
RMSE0.720.710.79
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xu, R.; Wang, B. Assessing Deep Learning Techniques for Remote Gauging and Water Quality Monitoring Using Webcam Images. Hydrology 2025, 12, 65. https://doi.org/10.3390/hydrology12040065

AMA Style

Xu R, Wang B. Assessing Deep Learning Techniques for Remote Gauging and Water Quality Monitoring Using Webcam Images. Hydrology. 2025; 12(4):65. https://doi.org/10.3390/hydrology12040065

Chicago/Turabian Style

Xu, Ruichen, and Binbin Wang. 2025. "Assessing Deep Learning Techniques for Remote Gauging and Water Quality Monitoring Using Webcam Images" Hydrology 12, no. 4: 65. https://doi.org/10.3390/hydrology12040065

APA Style

Xu, R., & Wang, B. (2025). Assessing Deep Learning Techniques for Remote Gauging and Water Quality Monitoring Using Webcam Images. Hydrology, 12(4), 65. https://doi.org/10.3390/hydrology12040065

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop