Stable Isotope Investigations of Icicle Formation and Evolution

Abstract

Icicles are elongated structures formed from water flowing over hangings and crystallizing in sub-freezing conditions. These features are ubiquitous in several parts of the world that experience severe to moderate winter seasons. It has been suggested that they could be a source of recharge to groundwater. Icicles are presumed to affect groundwater quality via incorporation of atmospheric and roof top contaminants. Relatively little attention has been paid to these wintry features, insofar as only a few theoretical models have attempted to describe their formation. Stable isotope measurements (δ¹⁸O and δ²H) of icicles that were melted stepwise into fractions are presented as support for the models that invoke the rapid formation of icicles. Icicles exhibit minimal fraction to fraction isotope variation, suggesting a lack of isotope equilibrium and that kinetic effects dominate the freezing process. Deviations from the Global Meteoric Water Line (GMWL), which is similar to the Local Meteoric Water Line (LMWL), indicate that post-depositional processes, namely sublimation, may occur throughout the freezing process. Isotopic evidence lends support to a “growth-cessation-growth” variation of the already proposed methods of rapid icicle formation, where a cessation period occurs between pulses of rapid freezing during icicle growth.

1. Introduction

Icicles are a picturesque feature commonly seen in regions that experience cold winter weather. These wintery features form whenever cold water, typically snowmelt, continuously flows over an overhang under subfreezing temperatures. The molten snow freezes as latent heat is lost to the colder atmosphere. Icicles may be found suspended from rock outcrops, roofs of buildings, ledges, tree branches, and power lines. These elongated structures (Figure 1) typically possess a slightly convex, carrot-like form that is distinct from a cone and can bear a striking resemblance to the stalactites that form in caves [1].

Despite their frequent occurrence, relatively little scientific attention has been paid to the physical processes that lead to the formation and subsequent growth of icicles. Indeed, several theoretical models have been suggested [1,2,3,4], but hardly any experimental studies have examined natural samples. A better understanding of the mechanisms of icicle formation can advance our knowledge of the general process of ice formation and melting of ice. It has also been suggested that they may add to the understanding of the growth of hailstones and groundwater and contaminant hydrology [5,6]. There are some obvious means by which icicles can be a carrier of contaminants to groundwater. Because they primarily form on roof tops and roofs are invariably coated with weather-resistant chemicals, with the passage of time, the chemicals are released and trapped inside of the icicles. In fact, several icicles do appear to be yellowish brown as a testimony to the trapping of materials from the roof. The same mechanism might operate in icicles that form in open areas or beneath natural rocks. Furthermore, the isotopic interactions involved in the melting and subsequent refreezing of ice may provide some insight into the dynamic processes involved in the basal ice of a glacier [7].

The basic processes involved in icicle growth have been well-explained [2,8]. When water supply is low and temperatures are well below freezing, icicles may form from the advancement of a uniform, horizontal freezing front. Hatakeyama and Nemoto [9] observed this process during the infant stage of icicle formation. The root of a pendant drop freezes, creating the uniform, horizontal freezing front. Subsequently, water flows down to the tip of the icicle, producing another pendant drop. This drop freezes entirely and lengthens the icicle, with each successive drop lowering the freezing boundary. When there is sufficient meltwater available to maintain a continuous pendant drop, icicles grow as the sides of the drop freeze, producing a thin ice shell [10]. This growth model is shown schematically in Figure 2.

A thin film of liquid water encompasses the ice shell and flows downward, continuously supplying the pendant drop with water. The thickness of this liquid film varies with supply rate, but it is typically less than 0.1 mm. The diameter of the icicle increases as portions of the liquid film freeze during downward flow. The icicle lengthens as the sides of the drop continue to freeze, simultaneously producing a narrow cylinder. This cylinder, usually about 5 mm in diameter, captures unfrozen water and extends several centimeters into the core of a growing icicle. The encompassed water column remains unfrozen until meltwater is no longer available, and icicle growth ceases. At this time, the liquid column can freeze, trapping many air bubbles within the core of the icicle. In any situation, the consequence is freezing of the water in “layers”. This latter method of icicle growth has received the majority of attention, in that few theoretical approaches have attempted to describe the mechanisms of growth [1,3,4]. However, the evolution of icicles has not been studied from the perspective of stable isotope effects during the freezing process.

The present paper reports the first stable isotope measurements from several natural icicles that formed during the winter of 2015 (February and March) in Kalamazoo (42.290° N, 85.586° W) in southwest Michigan, USA (Figure 3). Our experimental data provide evidence for the few theoretical models that have been suggested for the rapid growth of icicles. Furthermore, our data are in agreement with laboratory experiments that describe the isotopic fractionation that occurs during freezing, where diffusion-induced kinetic fractionation occurs through a boundary layer between the forming ice and the remaining water.

2. Materials and Methods

Icicles were sampled from the roof of a building on the campus of Western Michigan University, Kalamazoo, Michigan, where they were growing on the structures of an external ventilation system. This is analogous to a poorly insulated roof of a building, the most common place of icicle formation. Analysis of oxygen and hydrogen isotope ratios (δ¹⁸O and δ²H) was performed by melting the icicles at room temperature (25 °C ± 0.1) into several fractions and analyzing each fraction separately. It is a reasonable assumption that the stepwise melting process is the reverse of icicle formation in that each sample represents different “layers” of the icicle, as it has been shown that no isotope fractionation occurs during the melting of ice [7,11]. A total of 20 icicles were collected for sampling; however, only samples with at least 8 fractions are presented. Thus, data from a total of 8 icicles are presented in this work, taking into account the sample size available for analysis. Selection of these samples was dictated by the need to create cross-correlation plots and a “rule of thumb” suggesting at least 10 samples be used [12]. Aliquots of snowfall from a nearby location in Kalamazoo were periodically collected throughout the icicle sampling period and analyzed. Their isotope values were presumed to be the starting value of snow out of which the icicles were forming. Icicles were melted indoors (25 °C ± 0.1) using the device shown in Figure 4. The icicle samples are labeled A through H.

As melting proceeded, several water fractions were captured from below in 15 mL plastic vials as they dripped from the hanging icicle. Melted portions were collected at equal intervals of 10 min each for consistency. Each of the vials was capped and sealed to prevent evaporation. Samples were melted in fractions of varying volumes until the icicle was completely melted. Fractions collected per icicle ranged from 5 to 19 fractions; however, only samples with at least 10 fractions are presented in this work. Sample fractions were analyzed for their δ¹⁸O and δ²H values using a Los Gatos Research Triple Liquid Water Isotope Analyzer in the Stable Isotope Laboratory at Western Michigan University. Measurements are expressed in the conventional δ‰ notation and reference the international standard VSMOW, where

$$\delta \mathrm{‰}=\left({\displaystyle \frac{R_{sample}}{R_{standard}}}-1\right)\times 1000$$

(1)

R represents the ratio of heavy to light isotopes, i.e., ¹⁸O/¹⁶O and ²H/¹H. Results are presented with an analytical precision of 0.1‰ and 1‰ for oxygen and hydrogen, respectively, based on the repeated analysis of an internal standard [13].

3. Results

All of the isotope data are presented in Table S1 in the Supplementary Materials Section. We prefer to use the δ²H record of the samples analyzed as it is more sensitive than δ¹⁸O, although both are expected to arrive at the same conclusion. Based on our isotope studies, we look at two plausible models of icicle growth. First, we look at the δ²H–δ¹⁸O relationship.

3.1. δ²H–δ¹⁸O Relationship

Figure 5 presents the results of the analysis of all icicles in this study. The purpose of this plot is to compare the data with the Local Meteoric Water Line (LMWL) rather than comparing individual icicle samples. Chauvenet’s criterion could be applied to ensure that any outlier is still within acceptable analytical errors [14].

The slope (6.48) and the intercept (−19.49) of this plot deviate from the Global Meteoric Walter Line (GMWL), defined by Craig [15] as δ²H = 8 (δ¹⁸O) + 10. A very similar relationship, δ²H = 7.67 δ¹⁸O + 12.03, exists for the precipitation isotope ratio in the study area [16]. This deviation in the slope suggests that post-depositional processes, possibly sublimation, may have occurred after freezing. This lends support to the “growth-cessation-growth” model, in that the occurrence of sublimation is a possibility during the cessation period of icicle growth. We discuss these in the following sections.

3.2. Isotope Fractionation During Melting and Refreezing

The relative abundance of the stable isotopes of oxygen and hydrogen in precipitation varies spatially and seasonally due to a variety of factors [17]. Winter precipitation is generally more depleted in heavy isotopes when compared to summer precipitation, which is mostly driven by temperature. In Kalamazoo, Michigan, the site of the present study, earlier work has confirmed this seasonality [16,18]. The average δ¹⁸O and δ²H of precipitation collected during the sampling period (February–March 2015) were −20.1‰ (δ¹⁸O) and −141.7‰ (δ²H), respectively. Isotopic fractionation typically occurs with phase changes in water [7,11]. Furthermore, it has been suggested that isotopic fractionation does not occur during the melting of compact ice due to the low diffusion coefficient in ice [19]. During freezing, isotope fractionation does take place, such that ¹⁸O and ²H are preferentially incorporated into the solid phase, leaving the residual liquid depleted in heavy isotopes. Isotopic equilibrium processes largely govern fractionation during freezing. Under equilibrium conditions, the isotope fractionation factors (α) for oxygen and hydrogen, as reported, are 1.0028 and 1.0206, respectively [20]. Thus, the δ¹⁸O and δ²H values of ice are 2.8 and 20.6‰ more positive, respectively, than those of water, as also reported for a similar fractionation factor of 1.0208 for hydrogen [19,20]. However, non-equilibrium affects, such as diffusion through a boundary layer and the trapping of liquid water during crystal growth, do alter the distribution of isotopes in the freezing process. These kinetic effects usually result in lesser isotope fractionation than equilibrium effects [21,22]. Furthermore, if the freezing rate is too great, isotopic equilibrium cannot be attained, and the ice does not fractionate isotopes with respect to the water [23,24,25]. If the present icicles formed in isotopic equilibrium, this would result in a Rayleigh-type process. The first ice that formed would be enriched in the heavier isotopes relative to the snowmelt from which it formed. Subsequent ice crystallization would result in continuous depletion of the snowmelt reservoir and the forming ice. This process can be described by the Rayleigh distillation equation as

$$R=R_0{f}^{\alpha -1}$$

(2)

where R is the isotopic composition of the ice formed, R₀ is the original isotopic composition of the snowmelt prior to refreezing, f is the fraction of icicle formed, and α is the equilibrium fractionation factor. The value used for δ_snowmelt was −141.7 ± 7.3‰, which was derived from the average δ values for all of the snow collected during the sampling period. It is presumed that this is the snow out of which the icicles were formed. The rate of freezing would be reflected in the amount of isotope fractionation, as rapid freezing restricts fractionation. All of the isotope data are presented in Table S1 in the Supplementary Materials Section. We prefer to use the δ²H record of the samples analyzed as it is more sensitive than δ¹⁸O, although both are expected to arrive at the same conclusion. Based on our isotope studies, we look at two plausible models of icicle growth. Model 1 is a theoretical model that considers laminar heat flow and the role of gravity, while Model 2 uses the experimentally obtained isotope data to examine a new Rayleigh-process-based model.

3.3. Model 1

In this model, which we refer to as the “growth-cessation-growth” model, under favorable conditions, the collected basal snow melts, and, as it falls under gravity, it becomes frozen through the laminar heat flow, as the ambient temperature is very low [4]. In this scenario, there is no fractionation during the melting of the basal snow [7,11], and there is no fractionation when the snowmelt freezes too rapidly [15]. Icicle B exhibits the largest inter-fraction variations in δ²H (−161.0 ± 2.8 ‰) of all of the icicles. While the spread is outside of the analytical precision, we believe it is still within a narrow range, making this model a likely scenario for this particular icicle. The gist of this model is that the rapid growth of icicles prohibits isotopic equilibrium.

3.4. Model 2

Here, we explore the possibility that the icicles form via a Rayleigh distillation process and examine if the fractionation factors derived agree with the theoretical non-equilibrium process. In this model, it is proposed that the entire icicle formed out of one “reservoir” of snowmelt. The δ²H of this “reservoir” is taken to be the average δ²H of the snow that fell during the sampling period. Fractionation factors for each icicle fraction were calculated using the expanded form of the Rayleigh distillation equation, where

$$\left(\mathsf{\alpha }-1\right)\ln \mathrm{f}=\ln ({10}^3+{\mathsf{\delta }}^2{\mathrm{H}}_{\mathrm{i}\mathrm{c}\mathrm{e}})-\ln ({10}^3+{\mathsf{\delta }}^2{\mathrm{H}}_{\mathrm{s}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{t}})$$

(3)

The fraction f (Table S1) is calculated by dividing each volume of melt sample by the total amount of melt material. This is akin to the rain-out process where a given amount of vapor mass leaves the oceanic source and different fractions of the vapor mass are removed via rain-out as the vapor mass moves landwards.

The value used for δ_snowmelt was −141.7 ± 7.3‰, which was derived from the average δ for all snow collected during the sampling period. This is a very tightly spaced value, and the safe presumption is that this is the snow out of which the icicles were formed. The δ²H–δ¹⁸O plots representing this model are shown Figure 6. Note that the r² value of the regression coefficient may appear to be small. This is an artifact of the statistical method of regression when the variables have very close values [12]. This does not affect the interpretation of the regression.

The mean fractionation factor (α) for all icicle samples is 1.0005 + 0.0029.

Table 1. Fractionation factors for each icicle.

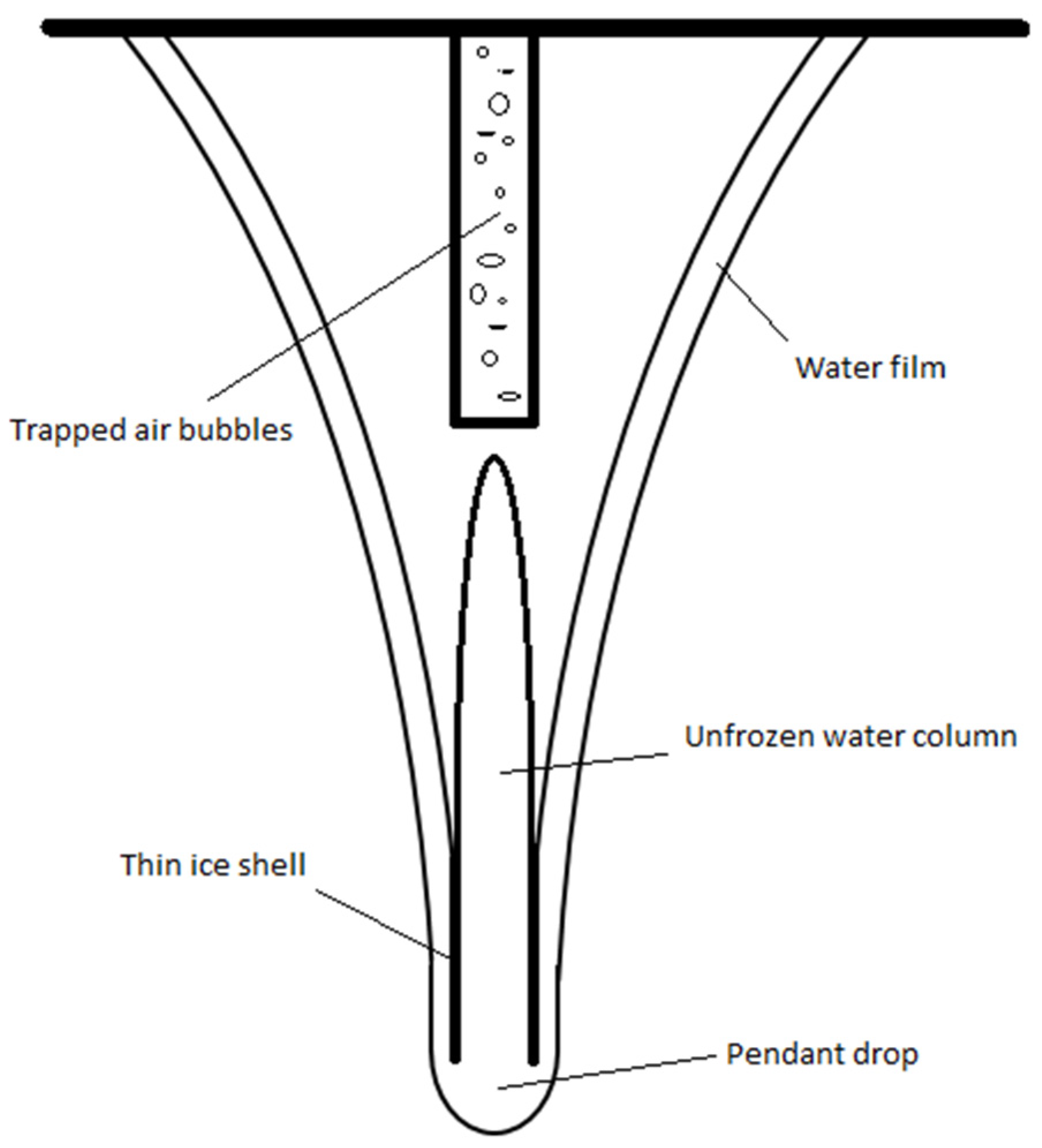
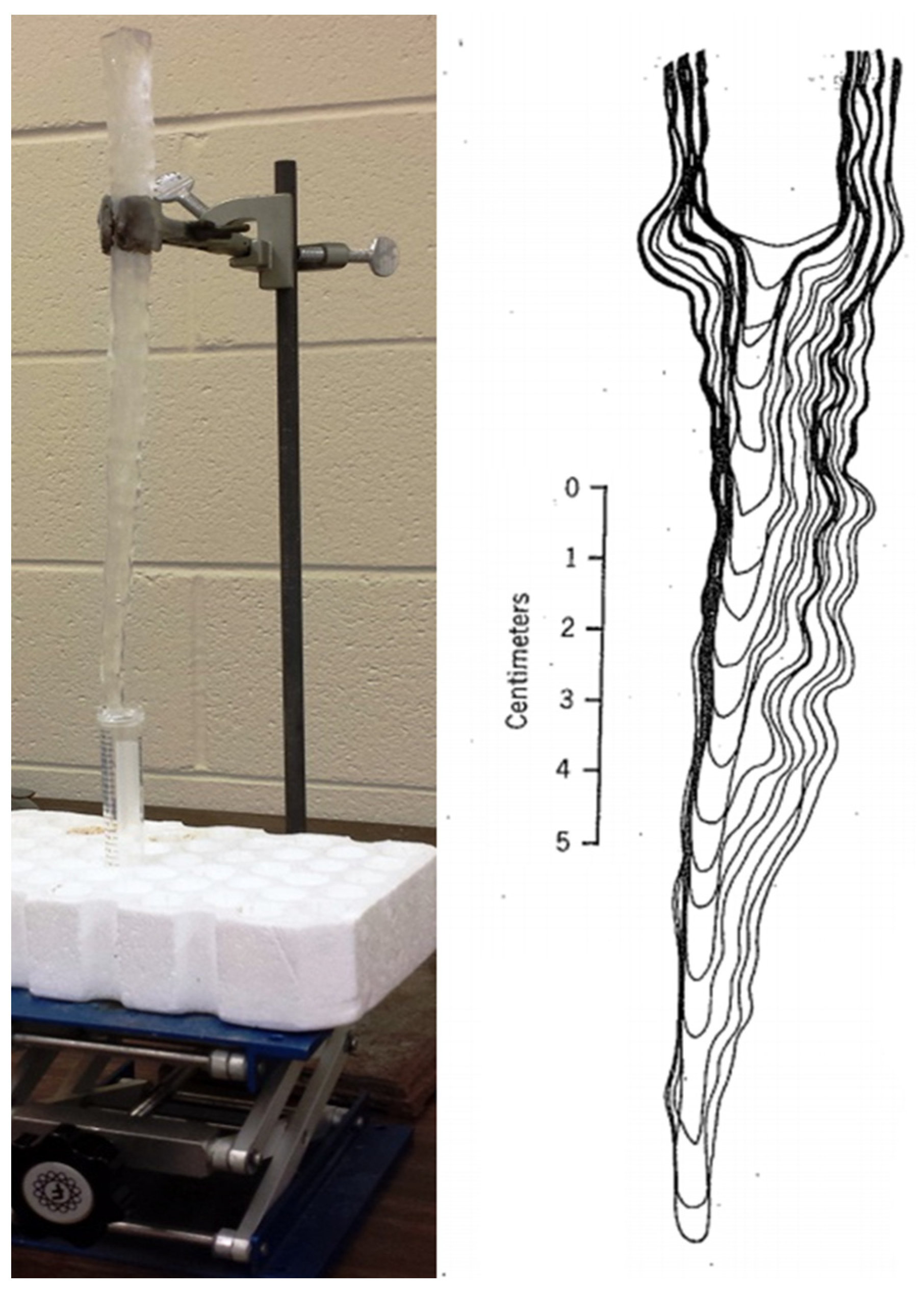
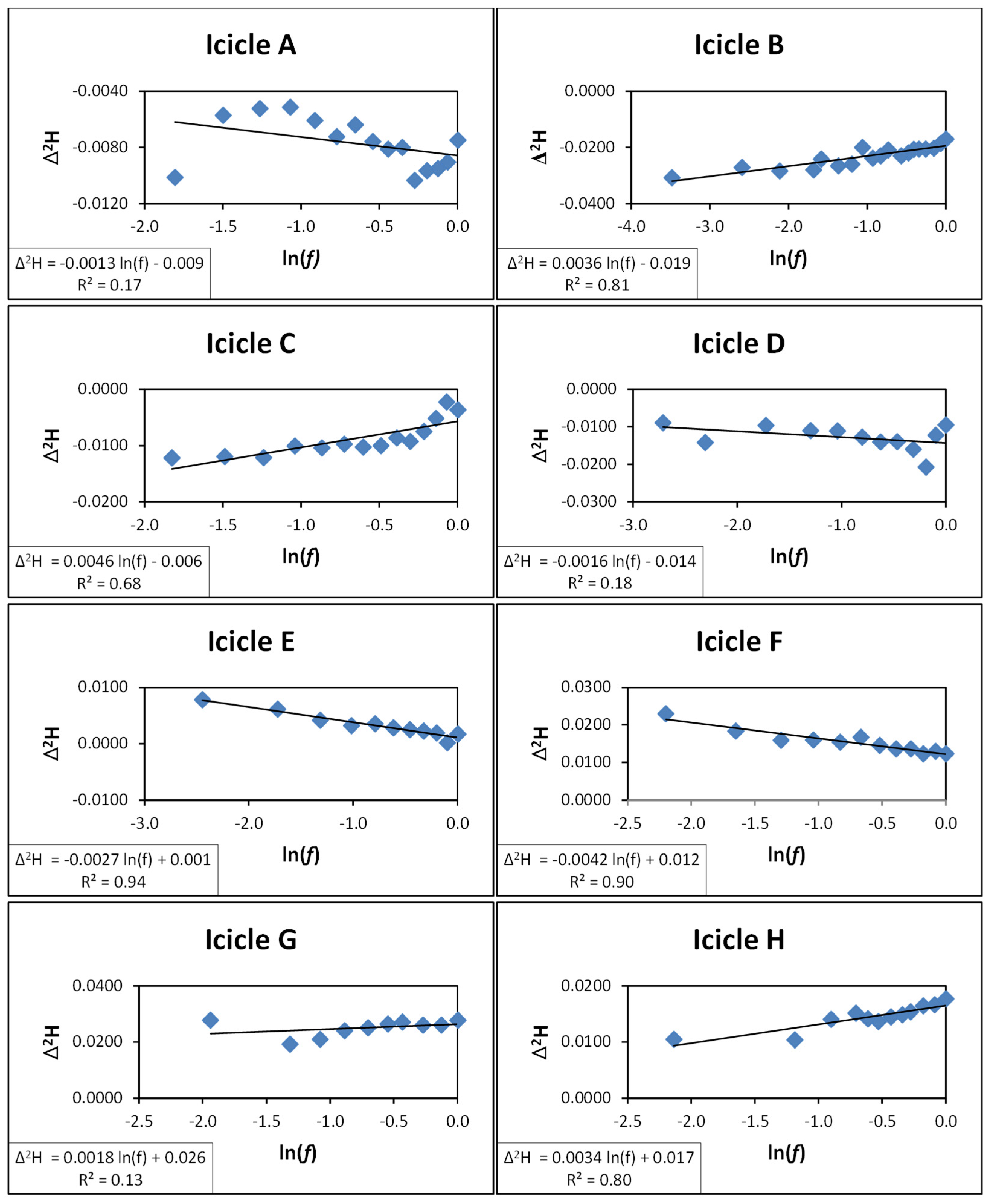
Icicle	Slope	α
A	−0.0013	0.9987
B	0.0036	1.0036
C	0.0046	1.0046
D	−0.0016	0.9984
E	0.0027	0.9973
F	0.0042	0.9958
G	0.0018	1.0018
H	0.0034	1.0034
Average	0.0005	1.0005

presents the fractionation factor for individual icicles.

Alternatively, if the ice formed under equilibrium conditions, a fractionation factor of 1.0208 is expected [19,20]. The deviation from equilibrium fractionation lends support to the theoretical models that suggest rapid growth of icicles where an isotopic equilibrium is not achieved. The outcome of these findings has implications for ground-water-management-related issues. In general, the isotopic ratio of groundwater reflects the mean isotope ratio of annual precipitation. However, in most cases, the groundwater isotope ratios deviate from the LMWL, indicating additional sources of groundwater recharge. An obvious source suggested is surface water. The results obtained here suggest that icicles can also be a good source of recharge source. Because icicle formation is very prominent in many parts of the world, a better survey of icicle isotope ratios can help quantify its contribution to local groundwater recharge.

4. Conclusions

Icicles are more abundant than generally assumed in many parts of the world with a severe winter season. They undergo melting and can be an important source of regional groundwater. These icicles can also contribute to groundwater contamination by incorporating contaminants during formation and post melting. The mechanism of icicle formation and its impact on the stable oxygen and hydrogen isotope ratio is critical in interpreting the stable isotope ratio of groundwater. The results of the δ¹⁸O and δ²H analyses of icicles in this study provide experimental support to the few theoretical models that suggest a rapid growth of icicles under the thin shell approach. In these models, molten water drips from an overhang and forms a pendant drop. Subsequently, the sides of the drop freeze to form a thin ice shell. A thin film of liquid supplies the pendant drop with continuous water, and the thin ice shell lengthens vertically as freezing continues, simultaneously entrapping a column of liquid water. Latent heat is lost from the film as it flows downward, resulting in rapid freezing and widening of the icicle.

Minimal isotope fractionation observed in melted icicle fractions suggests that non-equilibrium isotope effects, namely diffusion, governed the freezing process. The rate of freezing has been shown to be a major limiting factor in equilibrium effects, suggesting that the phase change was rapid. The slope of the δ²H and δ¹⁸O regression line shows significant deviation from the Global Meteoric Water Line. These data suggest that post-depositional processes occurred after freezing. The most likely process is sublimation. Obviously, more lab-based icicle research is warranted.