Refined Simulation of Old Urban Inundation and Assessment of Stormwater Storage Capacity Based on Surface–Pipe Network–Box Culvert–River Coupled Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Surface Runoff Generation
2.2. Pipe Network Flow Routing
2.3. 1D–2D Coupled Model
3. Study Area and Model Construction
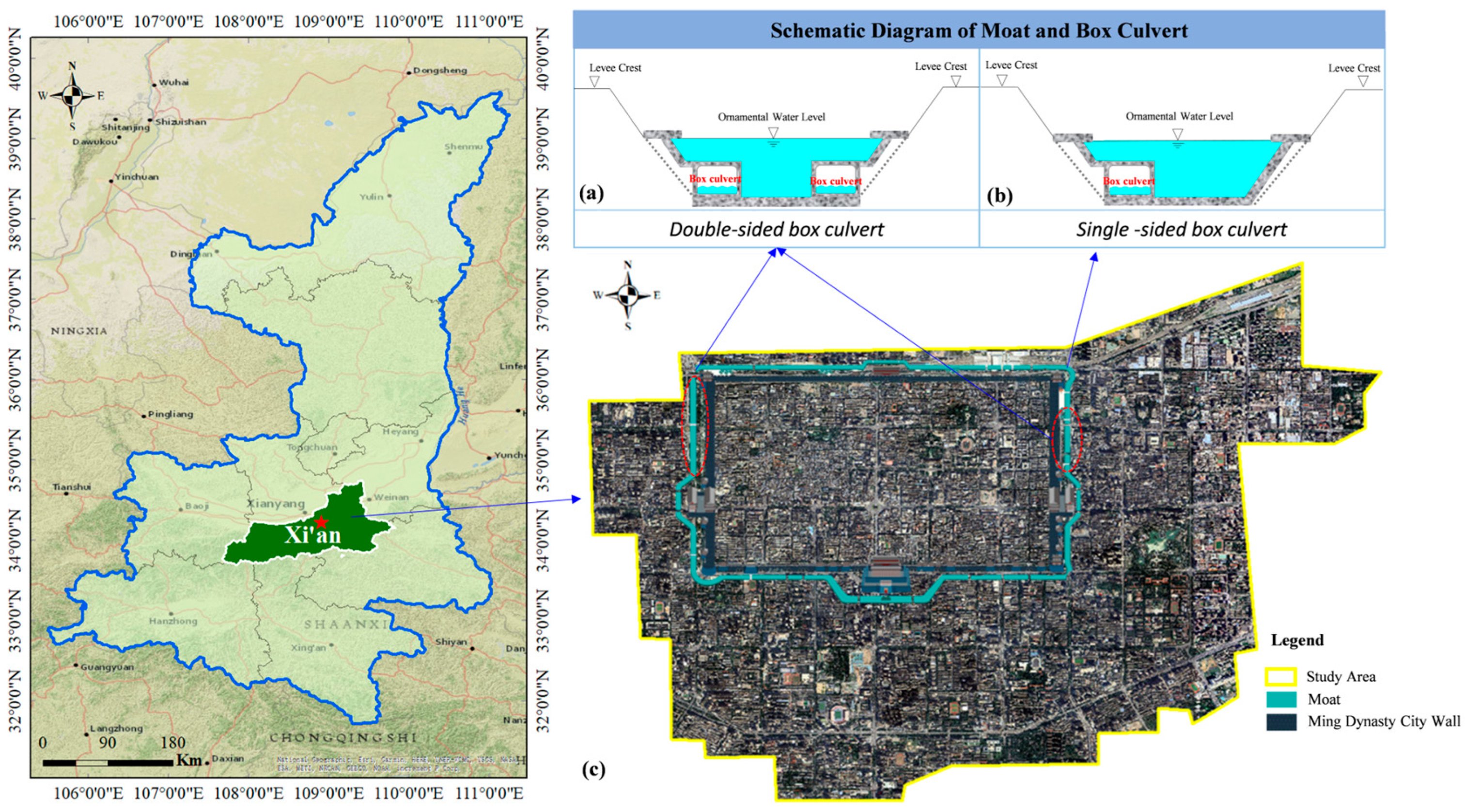
3.1. Study Area
3.2. Model Construction
3.2.1. Surface Runoff Model Construction
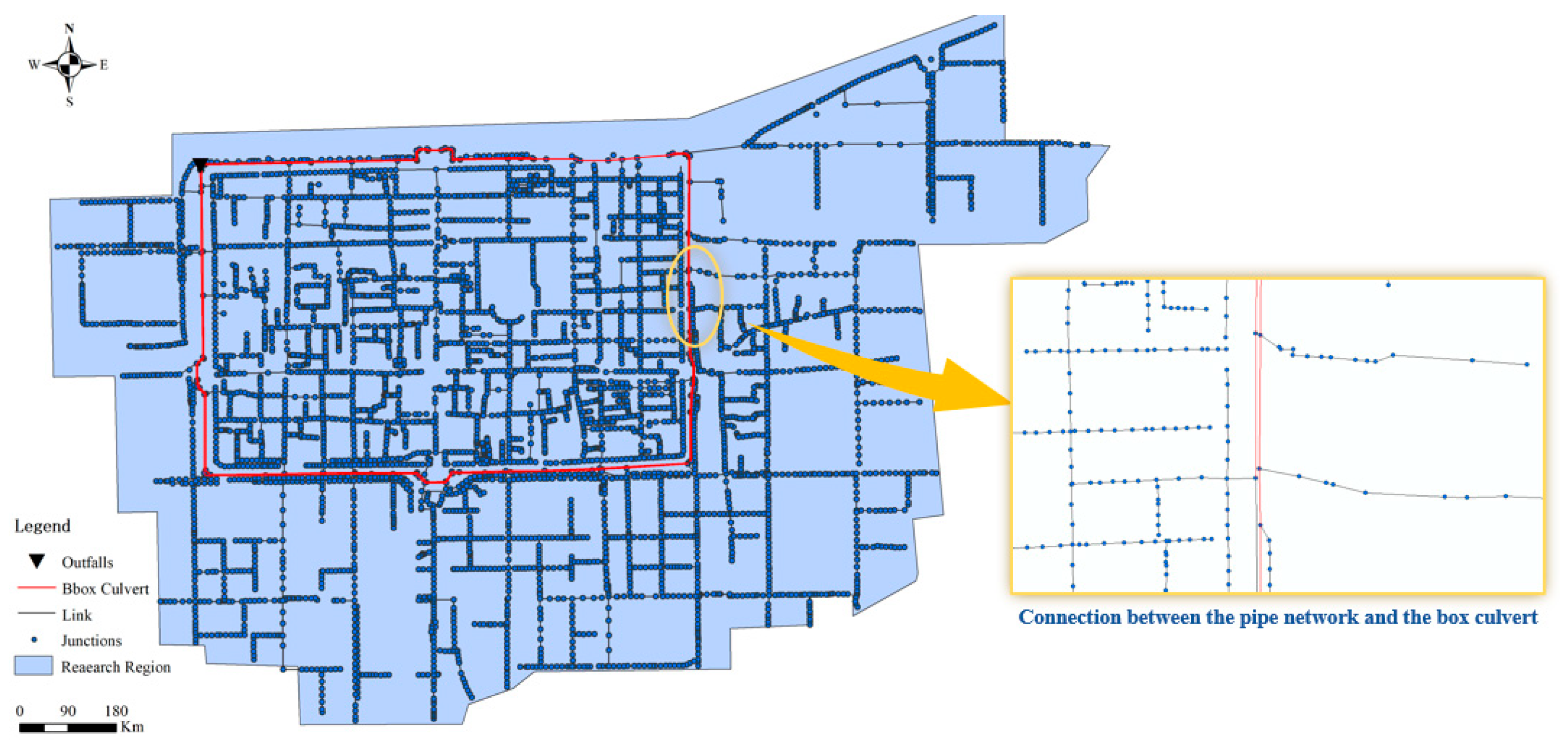
3.2.2. Drainage Network Routing Model Construction
3.2.3. 1D-2D Coupled Model Construction
3.3. Model Validation
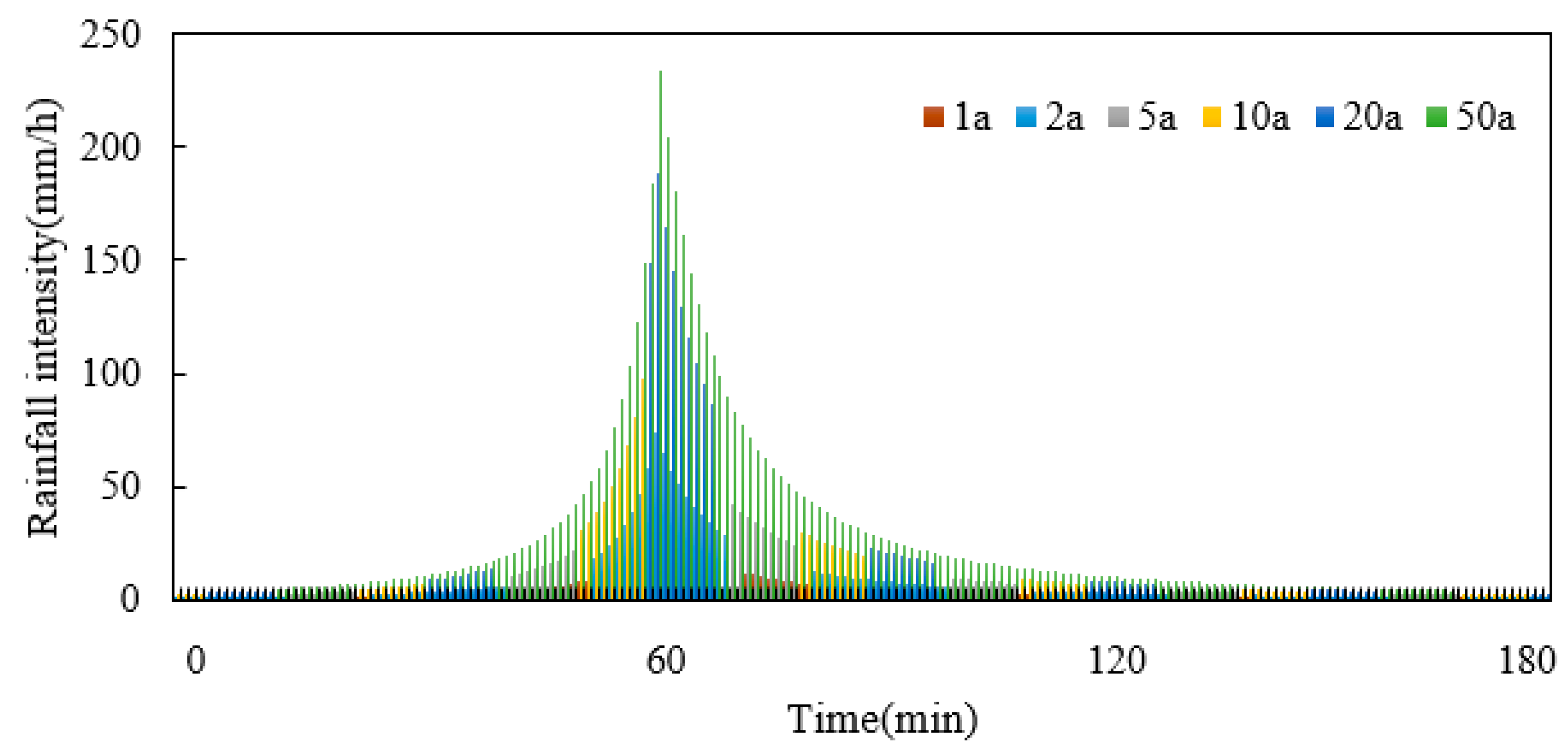
3.4. Rainfall Scenario Design
4. Results and Discussion
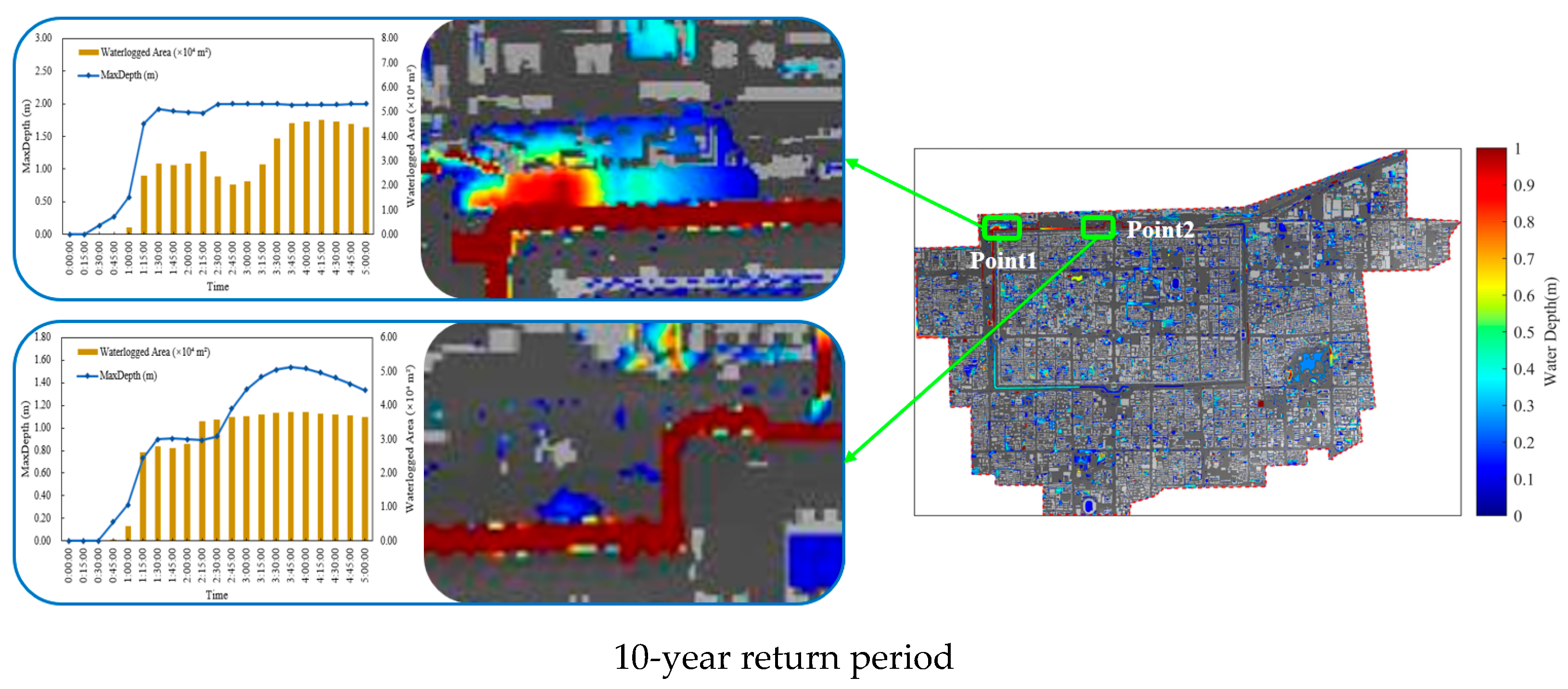
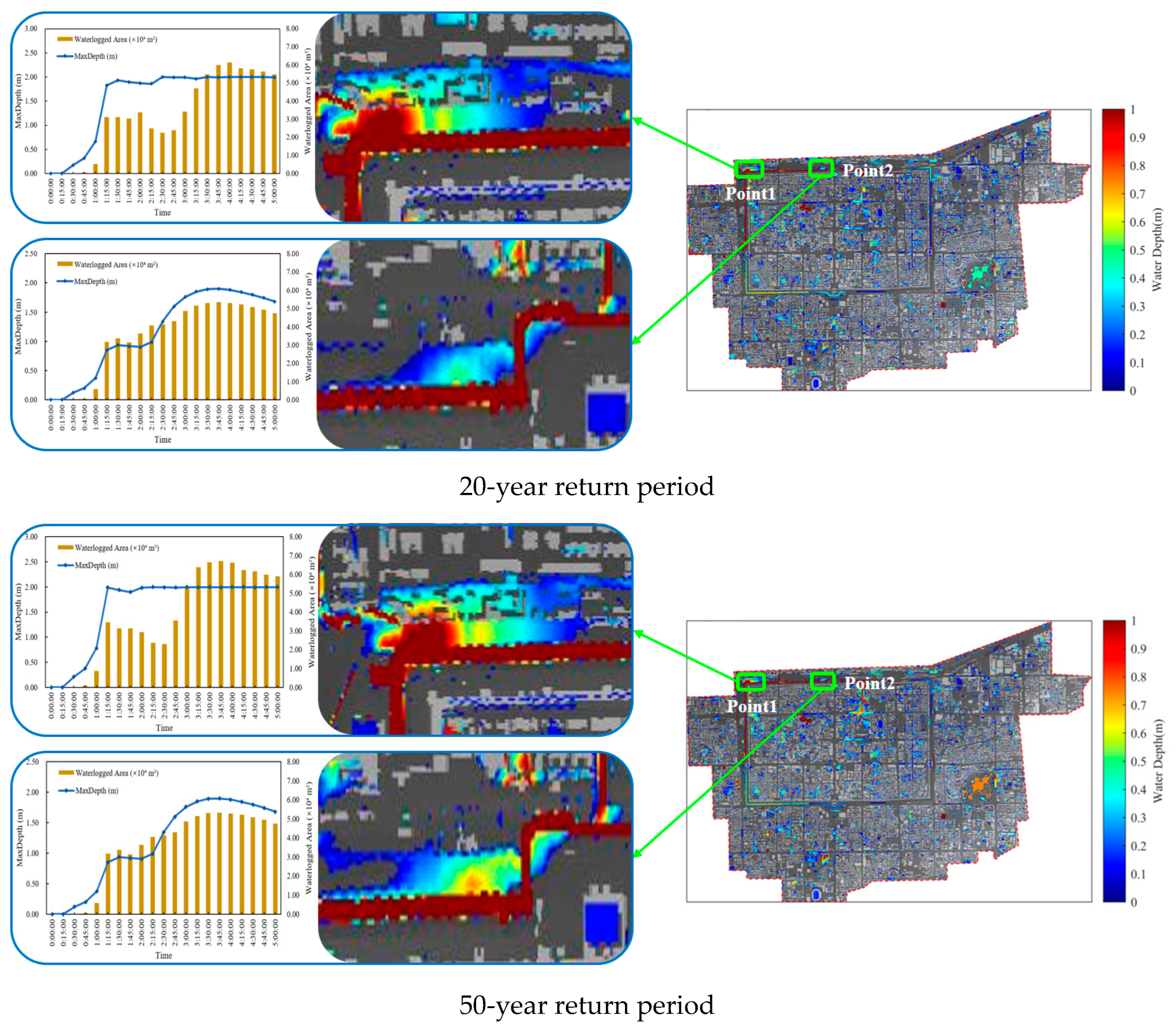
4.1. Detailed Simulation of Complex Drainage System
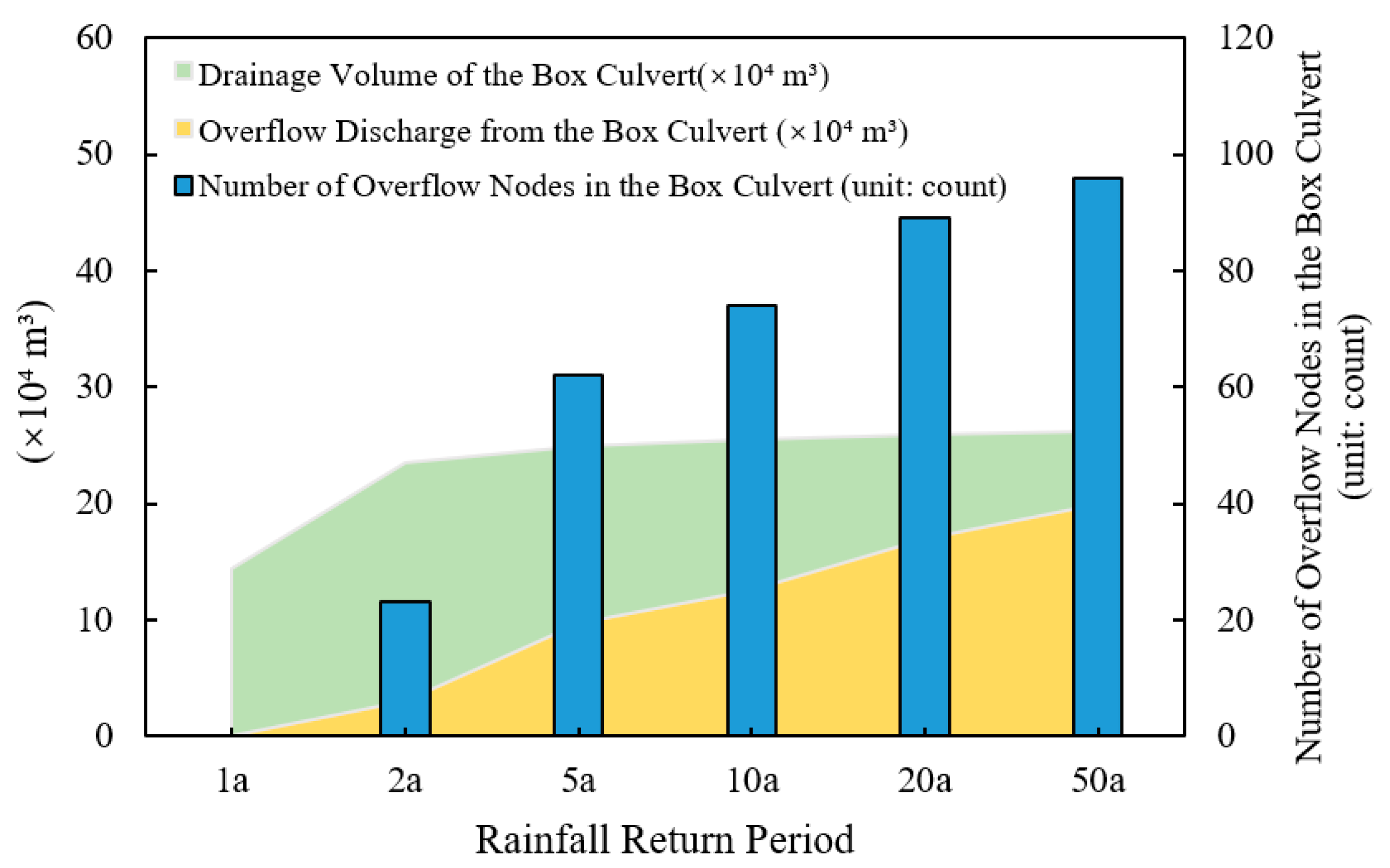
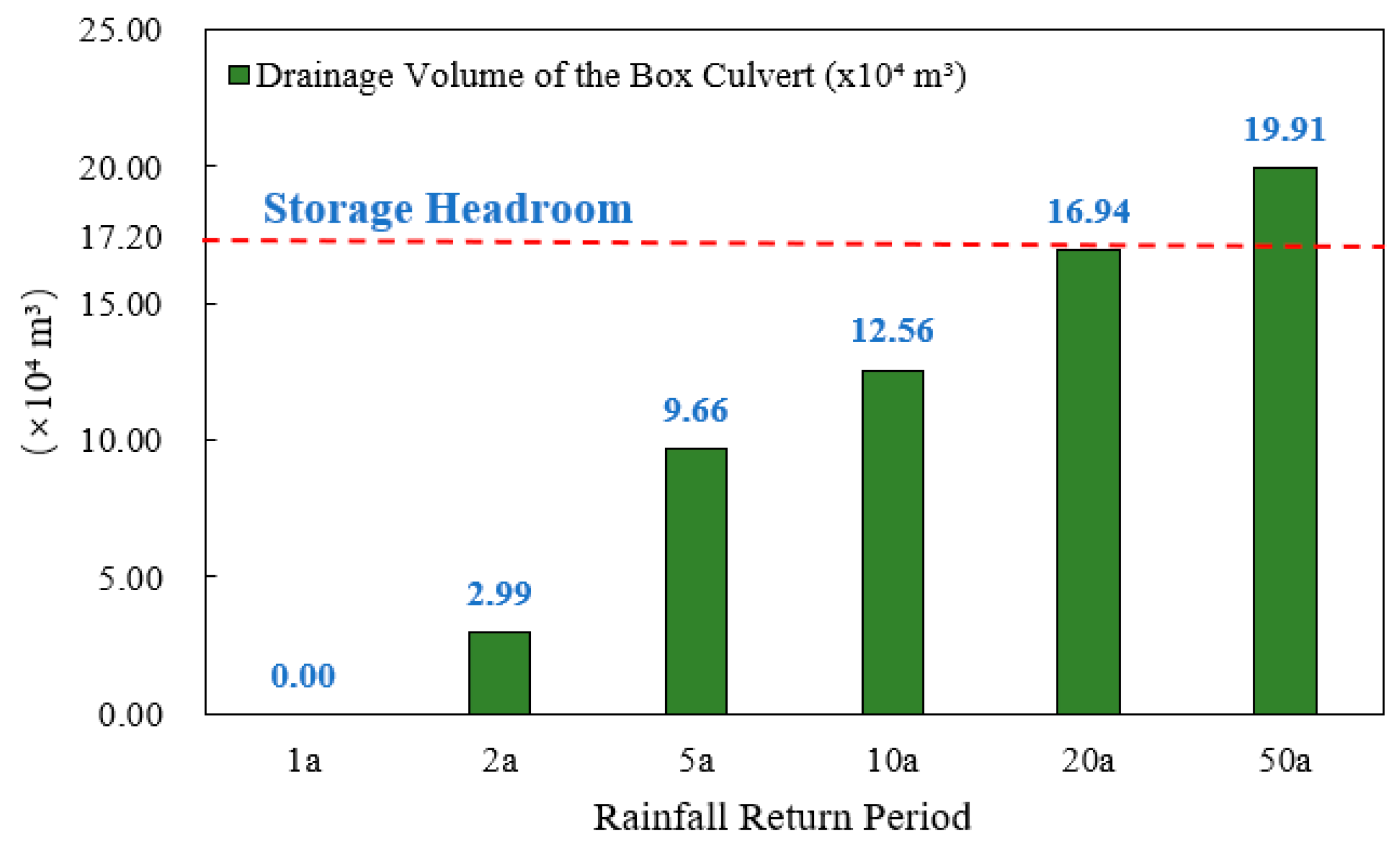
4.2. Flood Storage Capacity Analysis of Box Culverts
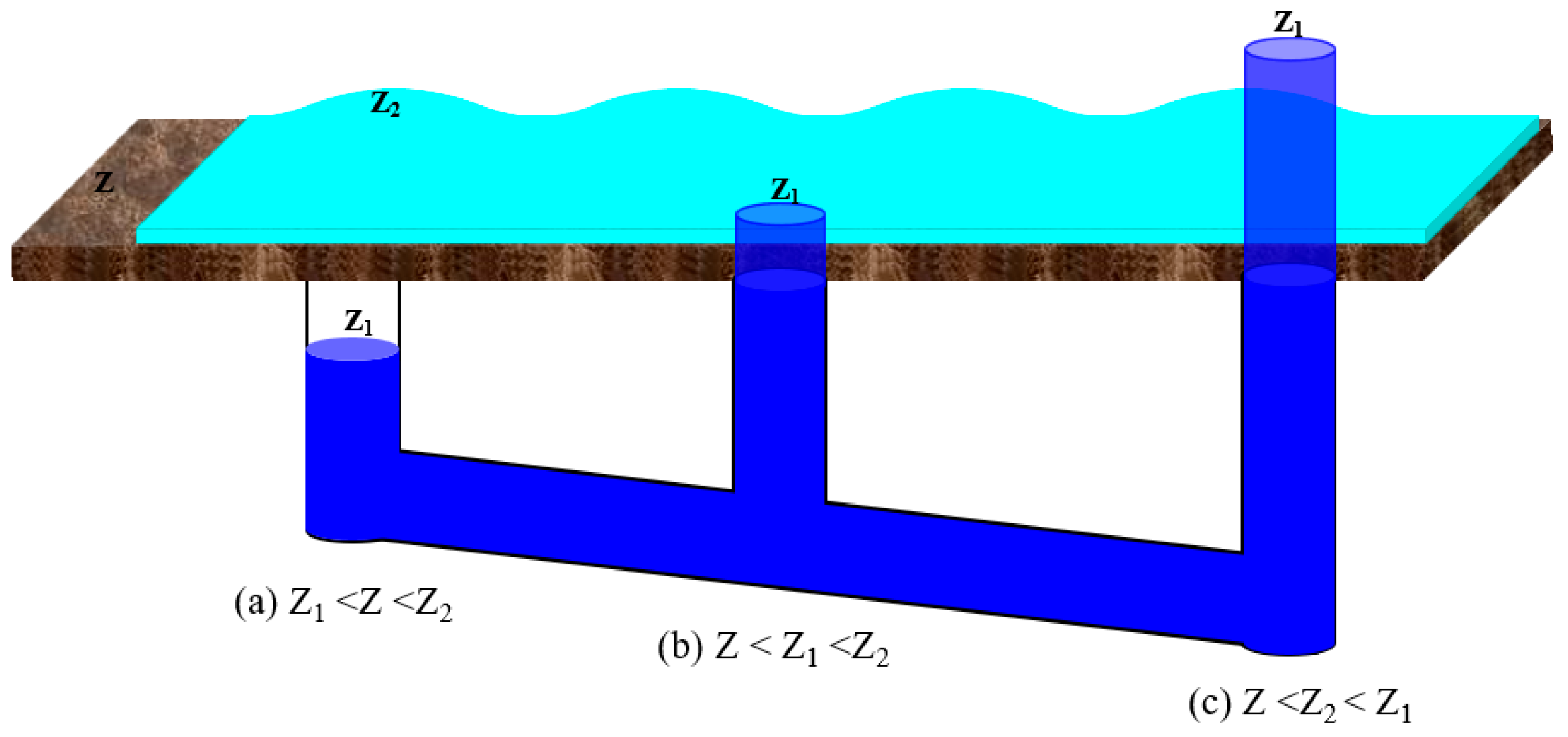
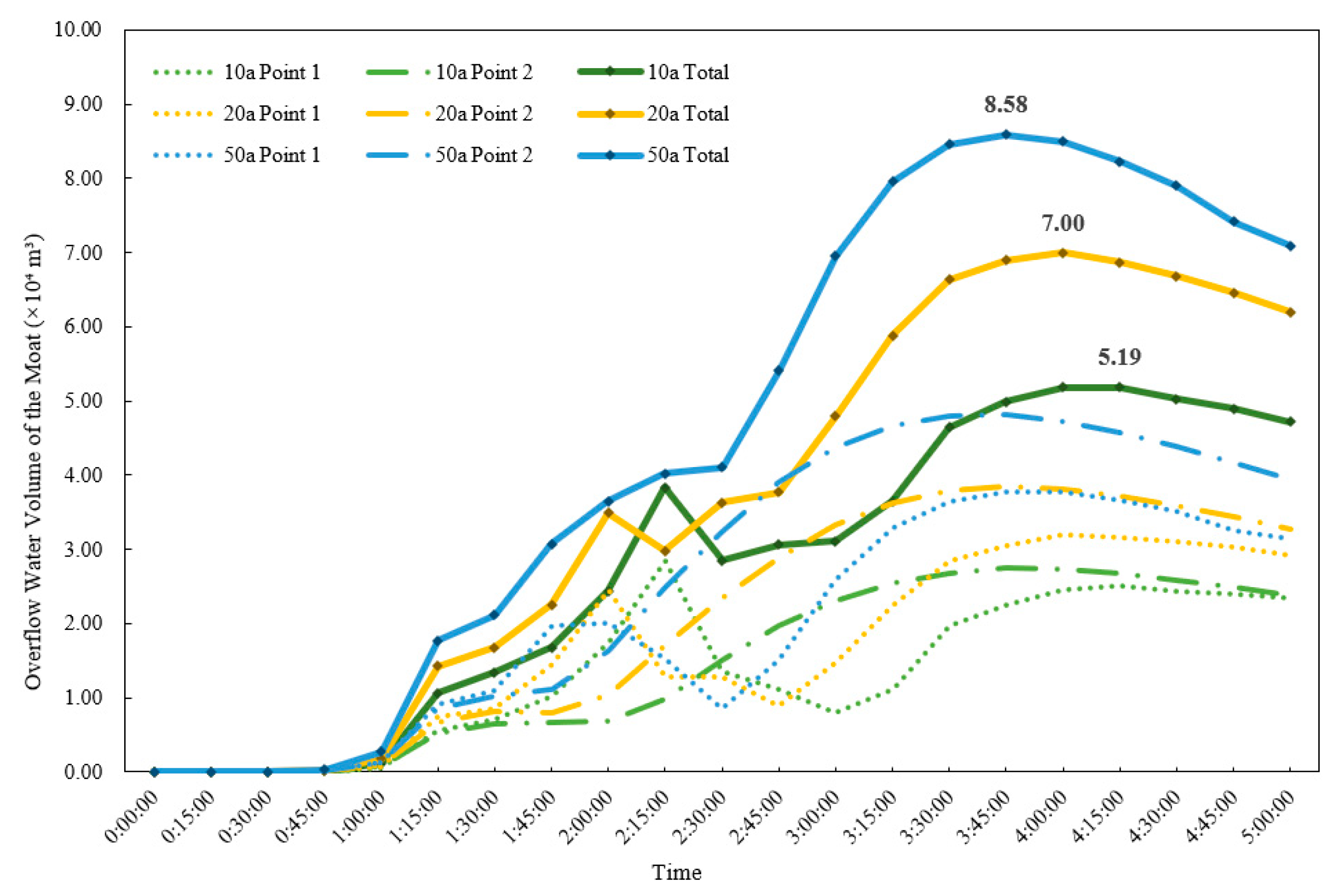
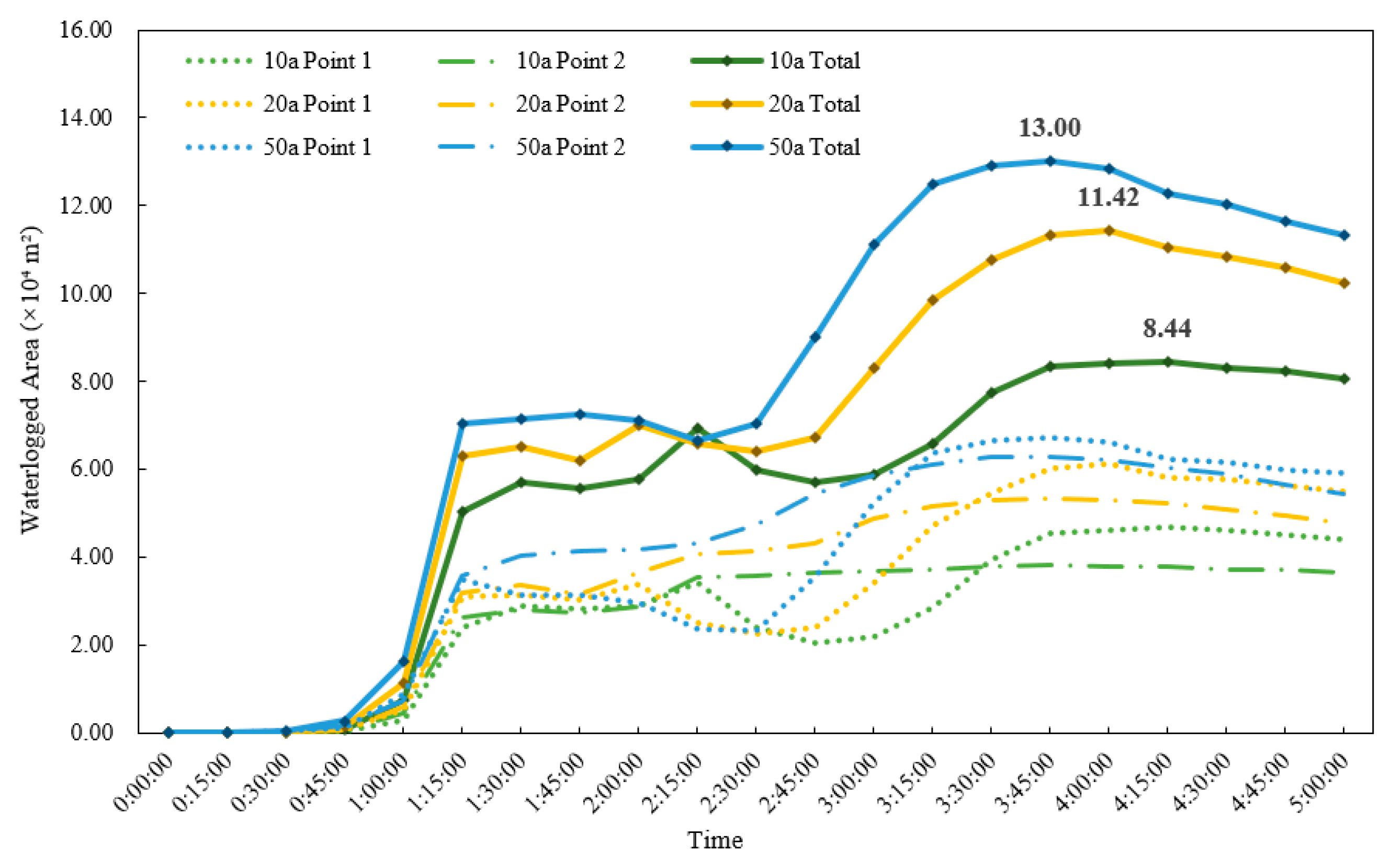
4.3. Dynamic Flood Storage Analysis of the Xi’an City Moat
5. Conclusions
- (1)
- The GAST–SWMM coupled model, incorporating the Surface–Pipe Network–Box Culvert–River framework, effectively reproduced the complete process, including rainfall, surface runoff generation, pipe network transport, and river network flow and overflow. The model demonstrated high accuracy in simulating complex urban hydrological and hydraulic processes, providing a reliable technical tool for urban flood risk assessment and infrastructure performance evaluation.
- (2)
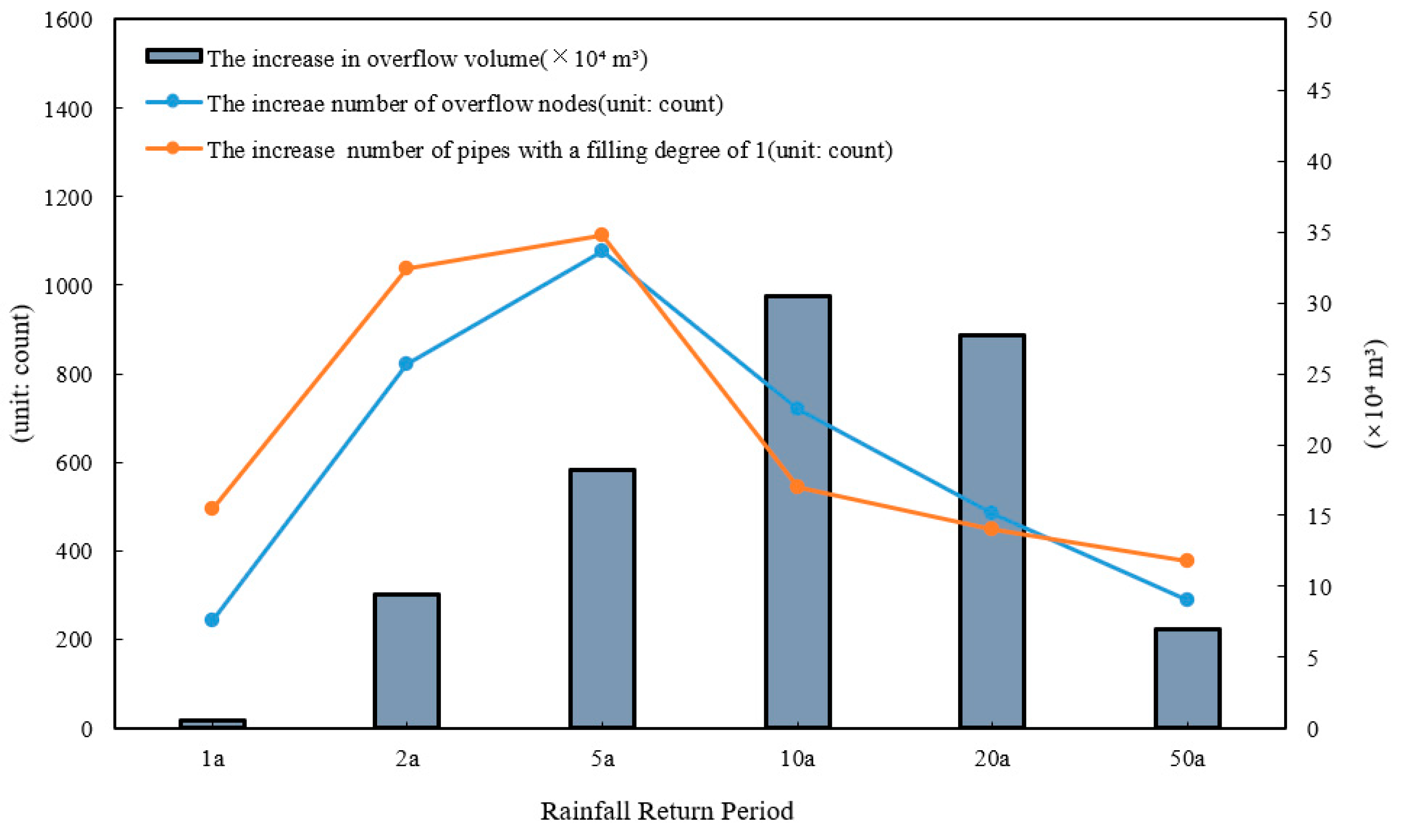
- The study performed a high-resolution simulation of the dynamic water exchange and hydrological–hydrodynamic response within the coupled “rainfall–surface–pipe–river network” system. The model captured the full hydrological and hydraulic processes under six design rainfall events with return periods from 1 to 50 years. Simulation results indicate that the total drainage volume in the study area increased from 14.99 × 104 m3 (1 year) to 33.18 × 104 m3 (50 years). The system load intensified continuously, with the proportion of fully filled pipes (fill ratio = 1) rising from 8.85% to 72.06%, and the percentage of overflow nodes increasing from 4.38% to 65.29%. The total overflow volume sharply increased from 0.57 × 104 m3 to 93.29 × 104 m3. The model accurately captured the spatiotemporal dynamics of surface runoff generation, convergence, infiltration, and surface–pipe water exchange, revealing the system’s dynamic response mechanisms under varying rainfall intensities.
- (3)
- The study revealed in detail the dynamic response and critical thresholds of the “rainfall–surface–pipe–river network” system. Simulation results indicate that the drainage capacity of the box culverts approaches saturation under the 2-year return period rainfall (23.52 × 104 m3), with their effective regulatory capacity limited to approximately the 1- to 2-year return periods. Beyond this standard, the overflow volume increases sharply (reaching 19.91 × 104 m3 under the 50-year return period), with the proportion of overflow nodes exceeding 80%. For the moat, when maintaining the landscape water level, the available storage capacity is 17.2 × 104 m3, corresponding to an effective regulation capacity of roughly the 5- to 10-year return period. Under the 10-year return period, the culvert overflow (12.56 × 104 m3) nearly reaches this regulation limit, and overtopping begins to occur.
6. Discussion and Outlook
6.1. Discussion
- (1)
- Assessment and optimization of drainage system capacity
- (2)
- Flood control scheduling and risk management for river channels
- (3)
- Enhancing overall system resilience
6.2. Outlook
- (1)
- Serving as a benchmark for simplified models
- (2)
- Developing a hierarchical and hybrid modeling strategy
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GSAT | GPU-accelerated Surface Water Flow and Associated Transport |
| SWMM | Storm Water Management Model |
References
- Ke, E.T.; Zhao, J.C.; Zhao, Y.L. Investigating the influence of nonlinear spatial heterogeneity in urban flooding factors using geographic explainable artificial intelligence. J. Hydrol. 2025, 648, 132398. [Google Scholar] [CrossRef]
- Song, J.Y.; Shao, Z.Y.; Zhan, Z.Y.; Chen, L. State-of-the-Art Techniques for Real-Time Monitoring of Urban Flooding: A Review. Water 2024, 16, 2476. [Google Scholar] [CrossRef]
- Wang, M.; Fu, X.P.; Zhang, D.Q.; Chen, F.R.; Liu, M.; Zhou, S.Q.; Su, J.; Tan, S.K. Assessing urban flooding risk in response to climate change and urbanization based on shared socio-economic pathways. Sci. Total Environ. 2023, 880, 163470. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Zhang, D.Q.; Wang, M.; Liu, Z.Y.; Gan, W.; Zhao, Z.C.; Xue, S.S.; Müller, B.; Zhou, M.M.; Ni, X.Q.; et al. Risk-driven composition decoupling analysis for urban flooding prediction in high-density urban areas using Bayesian-Optimized LightGBM. J. Clean. Prod. 2024, 457, 142286. [Google Scholar] [CrossRef]
- Li, J.G.; Yuan, L.N.; Hu, Y.C.; Xu, A.; Cheng, Z.X.; Song, Z.J.; Zhang, X.W.; Zhu, W.T.; Shang, W.B.; Liu, J.Y.; et al. Flood simulation using LISFLOOD and inundation effects: A case study of Typhoon In-Fa in Shanghai. Sci. Total Environ. 2024, 954, 176372. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.P.; Li, X.C.; Zhang, H.R. Research on urban waterlogging risk prediction based on the coupling of the BP neural network and SWMM model. Water Clim. Change 2023, 14, 3417–3434. [Google Scholar] [CrossRef]
- Li, X.; Yu, Y.; Wang, C.; Zheng, S.; Li, L.; Chen, G. Monitoring and characterization of the entire urban flooding process in the typical southern plain river network area. J. Hydraul. Eng. 2022, 53, 845–853. [Google Scholar]
- Hou, J.M.; Wang, N.; Guo, K.H.; Li, D.L.; Jing, H.X.; Wang, T.; Hinkelmann, R. Effects of the temporal resolution of storm data on numerical simulations of urban flood inundation. J. Hydrol. 2020, 589, 125100. [Google Scholar] [CrossRef]
- Xing, Y.; Shao, D.; Liang, Q.H.; Chen, H.L.; Ma, X.Y.; Ullah, I. Investigation of the drainage loss effects with a street view based drainage calculation method in hydrodynamic modelling of pluvial floods in urbanized area. J. Hydrol. 2022, 605, 127365. [Google Scholar] [CrossRef]
- Lazzarin, T.; Costabile, P.; Viero, D.P. An efficient physics-based modeling strategy for pluvial floods in urban areas with a subgrid scheme for the stormwater drainage network. J. Hydrol. 2025, 661, 133617. [Google Scholar] [CrossRef]
- Oberauer, M.; Lehmann, B. Enhanced 2D-models as alternative to dual-drainage systems for urban flood simulation. J. Hydrol. 2024, 645, 132198. [Google Scholar]
- Barreiro, J.; Santos, F.; Ferreira, F.; Neves, R.; Matos, J.S. Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land. Sustainability 2023, 15, 707. [Google Scholar] [CrossRef]
- Susetyo, C.; Idajati, H.; Navastara, A.M. Transformation of urban flood modelling from hydrodynamic to system dynamics approach. IOP Conf. Ser. Earth Environ. Sci. 2019, 340, 012013. [Google Scholar] [CrossRef]
- Montalvo, C.; Reyes-Silva, J.D.; Sañudo, E.; Cea, L.; Puertas, J. Urban pluvial flood modelling in the absence of sewer drainage network data: A physics-based approach. J. Hydrol. 2024, 634, 131043. [Google Scholar] [CrossRef]
- Caradot, N.; Rouault, P.; Clemens, F.; Cherqui, F. Evaluation of uncertainties in sewer condition assessment. Struct. Infrastruct. Eng. 2018, 14, 264–273. [Google Scholar] [CrossRef]
- Khaleghian, H.; Shan, Y.W. Developing a Data Quality Evaluation Framework for Sewer Inspection Data. Water 2023, 15, 2043. [Google Scholar] [CrossRef]
- Li, D.L.; Hou, J.M.; Zhou, Q.S.; Lyu, J.; Pan, Z.P.; Wang, T.; Sun, X.L.; Yu, G.L.; Tang, J.Y. Urban rainfall-runoff flooding response for development activities in new urbanized areas based on a novel distributed coupled model. Urban. Clim. 2023, 51, 101628. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.; Wang, H.; Wang, J.; Luo, J.; Wang, Z. Comprehensive review on the impact of spatial features of urban underlying surface on runoff processes. Adv. Water Sci. 2021, 32, 791–800. [Google Scholar]
- Yang, W.C.; Zheng, C.X.; Jiang, X.L.; Wang, H.; Lian, J.J.; Hu, D.; Zheng, A.R. Study on urban flood simulation based on a novel model of SWTM coupling D8 flow direction and backflow effect. J. Hydrol. 2023, 621, 129608. [Google Scholar] [CrossRef]
- Min, A.K.; Tashiro, T. Assessment of pluvial flood events based on monitoring and modeling of an old urban storm drainage in the city center of Yangon, Myanmar. Nat. Hazard. 2024, 120, 8871–8892. [Google Scholar] [CrossRef]
- Simone, A.; Cesaro, A.; Del Giudice, G.; Di Cristo, C.; Fecarotta, O. Potentialities of Complex Network Theory Tools for Urban Drainage Networks Analysis. Water Resour. Res. 2022, 58, e2022WR032277. [Google Scholar] [CrossRef]
- Francipane, A.; Pumo, D.; Sinagra, M.; La Loggia, G.; Noto, L.V. A paradigm of extreme rainfall pluvial floods in complex urban areas: The flood event of 15 July 2020 in Palermo (Italy). Nat. Hazards Earth Syst. Sci. 2021, 21, 2563–2580. [Google Scholar] [CrossRef]
- Mutua, B.M.; Miyazaki, Y. Two-dimensional longitudinal dynamic response of two-units box culvert on a liquefiable ground. Nat. Hazards Earth Syst. Sci. 2024, 10, 1295–1300. [Google Scholar]
- Willis, T.D.M. Systematic Analysis of Uncertainty in Flood Inundation Modelling. Ph.D. Thesis, University of Leeds, Leeds, UK, 2014. [Google Scholar]
- Hou, J.; Li, G.; Li, G.; Liang, Q.; Zhi, Z. Application of efficient high-resolution hydrodynamic model to simulations of flood propagation. J. Hydroelectr. Eng. 2018, 37, 96–107. [Google Scholar]
- Hou, J.; Wang, R.; Li, G.; Li, G. High-performance numerical model for high-resolution urban rainfall-runoff process based on dynamic wave method. J. Hydroelectr. Eng. 2018, 37, 40–49. [Google Scholar]
- Hou, J.M.; Simons, F.; Mahgoub, M.; Hinkelmann, R. A robust well-balanced model on unstructured grids for shallow water flows with wetting and drying over complex topography. Comput. Meth. Appl. Mech. Eng. 2013, 257, 126–149. [Google Scholar] [CrossRef]
- Liao, K.H. A Theory on Urban Resilience to Floods-A Basis for Alternative Planning Practices. Ecol. Soc. 2012, 17, 48. [Google Scholar] [CrossRef]
- Hou, J.M.; Wang, T.; Li, P.; Li, Z.B.; Zhang, X.; Zhao, J.H.; Hinkelmann, R. An implicit friction source term treatment for overland flow simulation using shallow water flow model. J. Hydrol. 2018, 564, 357–366. [Google Scholar] [CrossRef]
- Chen, G.Z.; Hou, J.M.; Wang, T.; Gao, X.J.; Yang, D.F.; Li, T. Analysis of the effect of rainfall center location on the flash flood process at the smallbasin scale. Water Clim. Change 2024, 15, 652–668. [Google Scholar] [CrossRef]
- Ma, L.; Hou, J.; Zhang, D.; Xia, J.; Li, B.; Ning, L. Study on 2-D numerical simulation coupling with breach evolution in flood propagation. J. Hydraul. Eng. 2019, 50, 1253–1267. [Google Scholar]
- Zhao, L.D.; Zhang, T.; Fu, J.; Li, J.Z.; Cao, Z.X.; Feng, P. Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data. Remote Sens. 2021, 13, 4381. [Google Scholar] [CrossRef]
- Zeng, Z.; Lai, C.; Wang, Z.; Wu, X.; Huang, G.; Hu, Q. Rapid simulation of urban rainstorm flood based on WCA2D and SWMM model. Adv. Water Sci. 2020, 31, 29–38. [Google Scholar]
- Li, X.; Hou, J.; Pan, Z.; Jing, J.; Fan, C.; Sun, X. Simulation study on dynamic response of rain and flood process in urban renewal: A case study of Yinchuan City. J. Hydraul. Eng. 2023, 54, 1347–1358. [Google Scholar]
- Zhang, H.P.; Wu, W.M.; Hu, C.H.; Hu, C.W.; Li, M.; Hao, X.L.; Liu, S. A distributed hydrodynamic model for urban storm flood risk assessment. J. Hydrol. 2021, 600, 126513. [Google Scholar] [CrossRef]
- Li, D.L.; Hou, J.M.; Zhang, Y.W.; Guo, M.P.; Zhang, D.W. Influence of Time Step Synchronization on Urban Rainfall-Runoff Simulation in a Hybrid CPU/GPU 1D-2D Coupled Model. Water Resour. Manag. 2022, 36, 3417–3433. [Google Scholar] [CrossRef]
- Pan, X.X.; Hou, J.M.; Chen, G.Z.; Li, D.L.; Zhou, N.; Imran, M.; Li, X.Y.; Qiao, J.; Gao, X.J. Rapid urban inundation prediction method based on numerical simulation and AI algorithm. J. Hydrol. 2025, 647, 132334. [Google Scholar] [CrossRef]
- Chen, G.Z.; Hou, J.M.; Zhou, N.E.; Yang, S.X.; Tong, Y.; Su, F.; Huang, L.; Bi, X. High-Resolution Urban Flood Forecasting by Using a Coupled Atmospheric and Hydrodynamic Flood Models. Front. Earth Sci. 2020, 8, 545612. [Google Scholar] [CrossRef]
- Hou, J.; Wang, Z.; Li, D.; Bu, L.; Chen, G.; Yang, Y.; Fang, Y. Simulation of the response of drainage capacity of pipe network to street inlet clogging and pipeline silting. Adv. Water Sci. 2025, 36, 122–131. [Google Scholar]
- Li, D.; Xu, Y.; Hou, J.; Liang, X.; Wang, Y.; Yang, Y.; Wu, F. Approximate simulation method for stormwater process in urban areas with missing data of fine pipe network. Adv. Water Sci. 2024, 35, 960–971. [Google Scholar]
- Yuan, J.; Chen, W.; Zhao, T.; Zhang, D.; Li, L. Dimension reduction simulation technology of pipeline network in rainstorm floods of high-density city for computational timeliness. Water Resour. Prot. 2024, 40, 69–77. [Google Scholar]
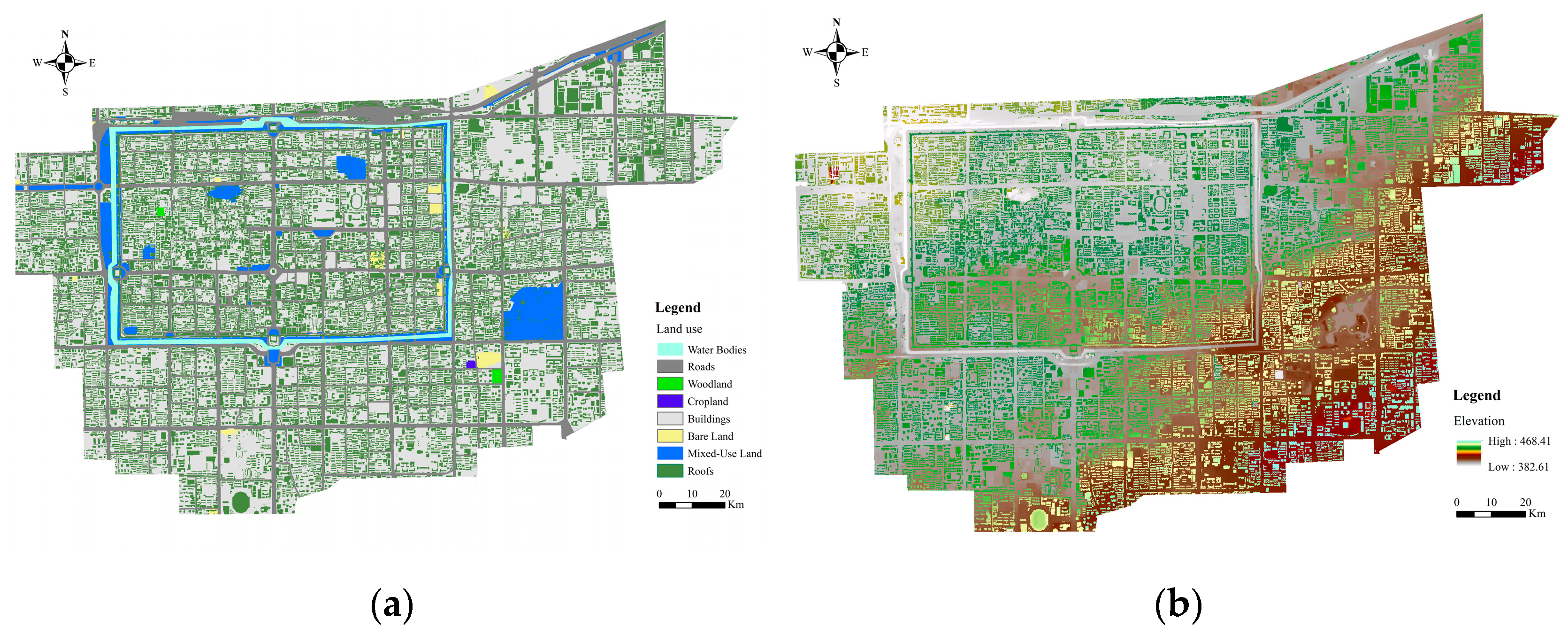
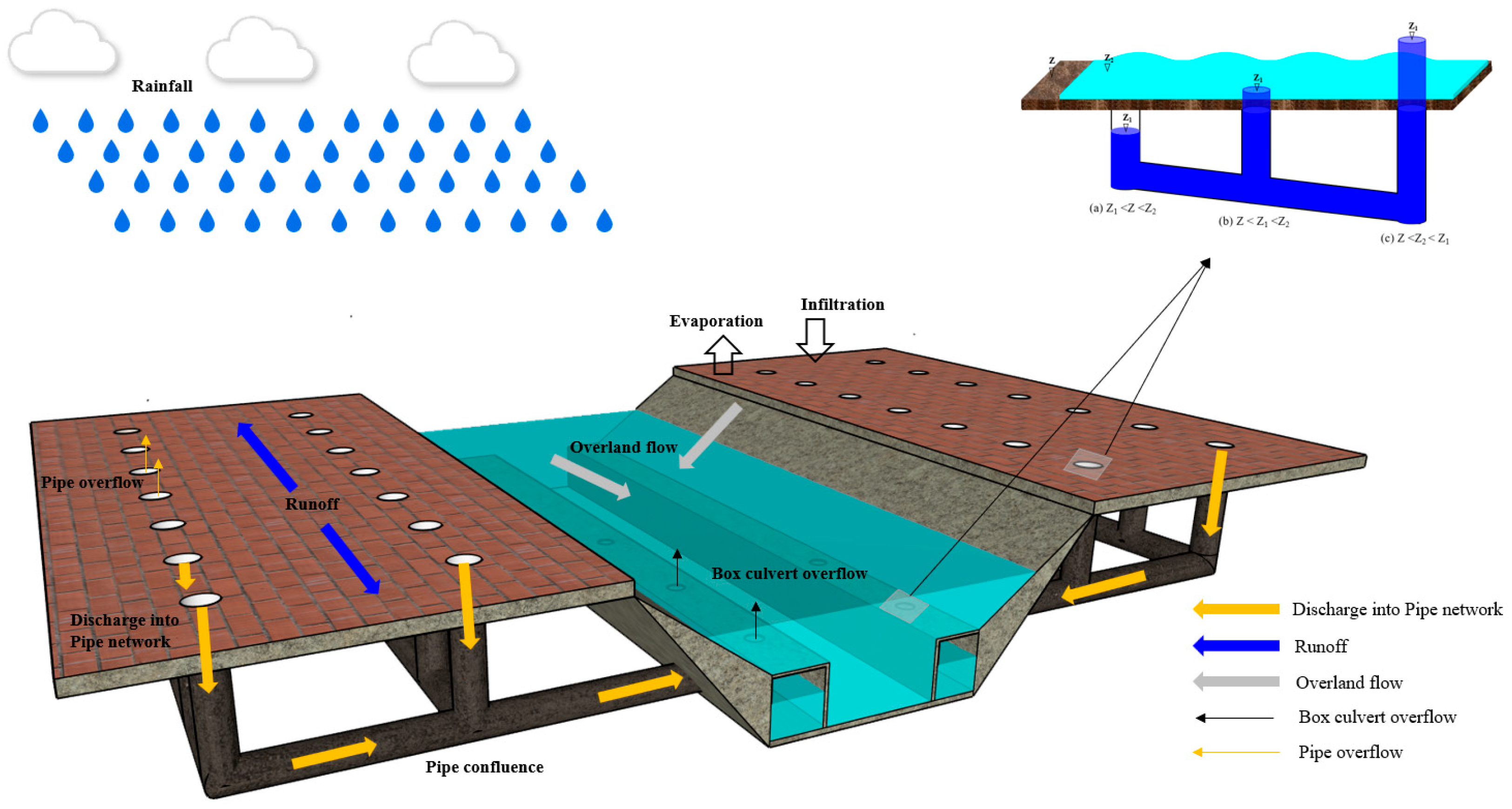

| Land Use Type | Manning Value | Steady Infiltration Rate (mm/h) |
|---|---|---|
| Water Bodies | 0.010 | 0 |
| Roads | 0.014 | 0 |
| Woodland | 0.200 | 37.55 |
| Cropland | 0.045 | 20 |
| Buildings | 0.014 | 0 |
| Bare Land | 0.030 | 19.43 |
| Mixed-Use Land | 0.025 | 5 |
| Roofs | 0.014 | 0 |
| Rainfall Event | Location | Name | Observed Water Depth (m) | Simulated Water Depth (m) | Relative Error | Average Relative Error |
|---|---|---|---|---|---|---|
| 11 September 2023 | A | Taiyi Road Interchange | 0.78 | 0.76 | 2.7% | 4.7% |
| B | Nanshaomen | 0.60 | 0.56 | 6.7% | ||
| 29 July 2024 | A | Taiyi Road Interchange | 0.70 | 0.63 | 10.0% | 5.8% |
| B | Nanshaomen | 0.45 | 0.43 | 4.4% | ||
| C | Youyi Road | 0.10 | 0.103 | 3.0% |
| Return Period | Rainfall Volume (×104 m3) | Total Drainage (×104 m3) | Number of Pipes at Full Capacity | Proportion of Pipes at Full Capacity | Total Overflow Nodes | Proportion of Overflow Nodes | Total Overflow Volume (×104 m3) |
|---|---|---|---|---|---|---|---|
| 1-year | 46.5 | 14.99 | 493 | 8.85% | 244 | 4.38% | 0.57 |
| 2-year | 87.35 | 24.69 | 1531 | 27.49% | 1064 | 19.11% | 9.95 |
| 5-year | 141.33 | 28.41 | 2644 | 47.48% | 2142 | 38.46% | 28.16 |
| 10-year | 182.18 | 30.47 | 3188 | 57.25% | 2862 | 51.39% | 58.66 |
| 20-year | 222.99 | 31.72 | 3637 | 65.31% | 3348 | 60.12% | 86.35 |
| 50-year | 276.97 | 33.18 | 4013 | 72.06% | 3636 | 65.29% | 93.29 |
| Return Period | Box Culvert Discharge (104 m3) | Box Culvert Overflow (104 m3) | Number of Overflow Nodes | Proportion of Overflow Nodes |
|---|---|---|---|---|
| 1-year | 14.38 | 0.00 | 0 | 0.00% |
| 2-year | 23.52 | 2.99 | 23 | 19.49% |
| 5-year | 24.89 | 9.66 | 62 | 52.54% |
| 10-year | 25.47 | 12.56 | 74 | 62.71% |
| 20-year | 25.85 | 16.94 | 89 | 75.42% |
| 50-year | 26.21 | 19.91 | 96 | 81.36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Ma, L.; Hou, J.; Wang, J.; Li, X.; Li, D.; Pan, X.; Cui, R.; Ren, Y.; Cheng, Y. Refined Simulation of Old Urban Inundation and Assessment of Stormwater Storage Capacity Based on Surface–Pipe Network–Box Culvert–River Coupled Modeling. Hydrology 2025, 12, 280. https://doi.org/10.3390/hydrology12110280
Li N, Ma L, Hou J, Wang J, Li X, Li D, Pan X, Cui R, Ren Y, Cheng Y. Refined Simulation of Old Urban Inundation and Assessment of Stormwater Storage Capacity Based on Surface–Pipe Network–Box Culvert–River Coupled Modeling. Hydrology. 2025; 12(11):280. https://doi.org/10.3390/hydrology12110280
Chicago/Turabian StyleLi, Ning, Liping Ma, Jingming Hou, Jun Wang, Xuan Li, Donglai Li, Xinxin Pan, Ruijun Cui, Yue Ren, and Yangshuo Cheng. 2025. "Refined Simulation of Old Urban Inundation and Assessment of Stormwater Storage Capacity Based on Surface–Pipe Network–Box Culvert–River Coupled Modeling" Hydrology 12, no. 11: 280. https://doi.org/10.3390/hydrology12110280
APA StyleLi, N., Ma, L., Hou, J., Wang, J., Li, X., Li, D., Pan, X., Cui, R., Ren, Y., & Cheng, Y. (2025). Refined Simulation of Old Urban Inundation and Assessment of Stormwater Storage Capacity Based on Surface–Pipe Network–Box Culvert–River Coupled Modeling. Hydrology, 12(11), 280. https://doi.org/10.3390/hydrology12110280






