Flood Frequency Analysis Using the Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals
Abstract
1. Introduction
2. Materials and Methods
2.1. Bivariate Logistic Model
2.2. Estimation of Bivariate Parameters
- univariate lengths of record before and after the common period
- common bivariate period
- variable with univariate record before the common period
- variable with univariate record after the common period
- variable with bivariate record during the common period
- indicator number such that = 1 if or = 0 if
- = parameter vector
2.3. Non-Stationary GEV Models and Covariates
2.4. Covariate Choice and Functional Form
2.5. Choice of Non-Stationary Model
2.6. Regional Homogeneity
3. Results
3.1. Data
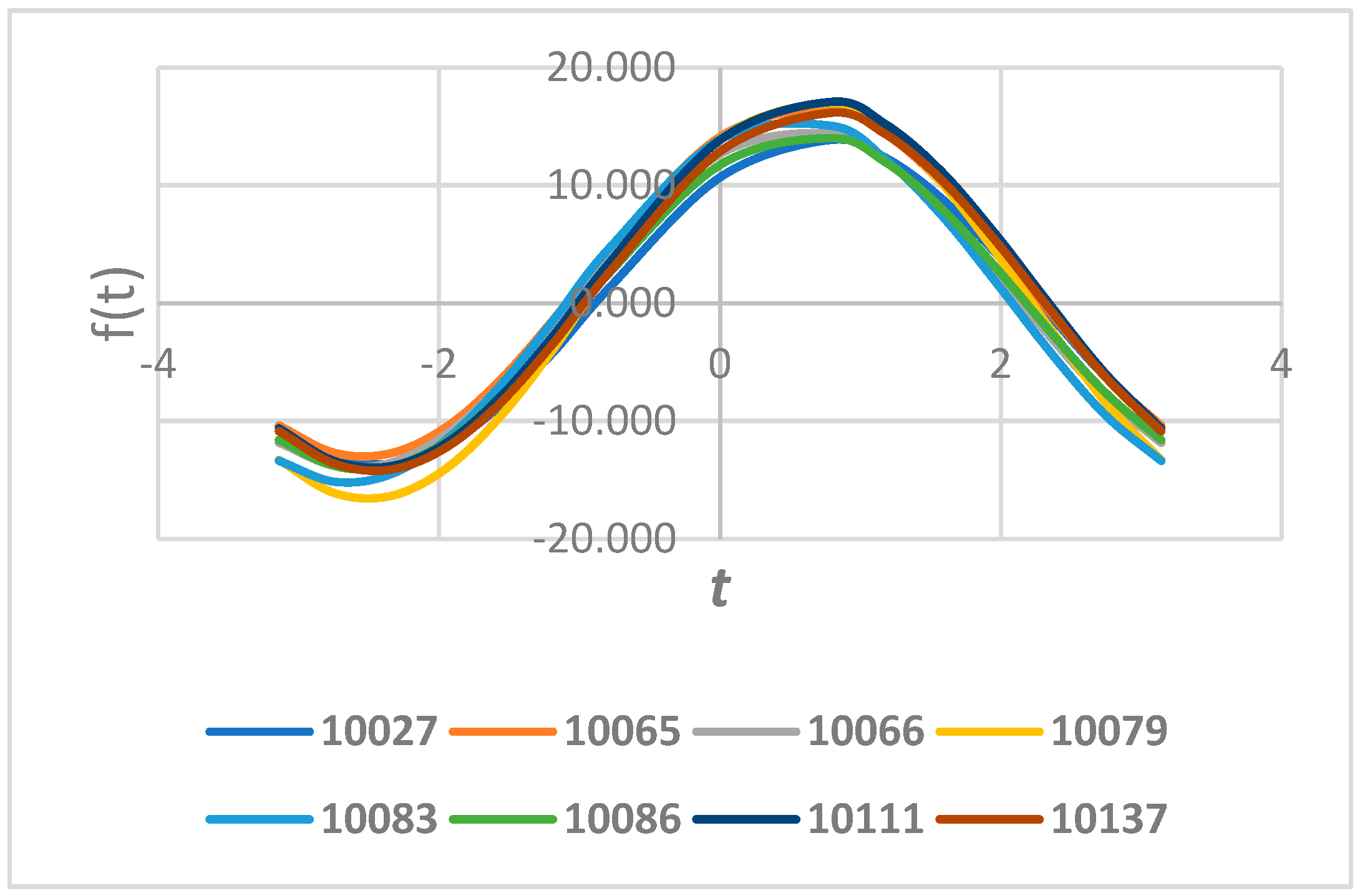
3.2. Delineation of Homogeneous Region
3.3. Frequency Analysis
4. Discussion
4.1. Performance of GEV and Gumbel Marginals
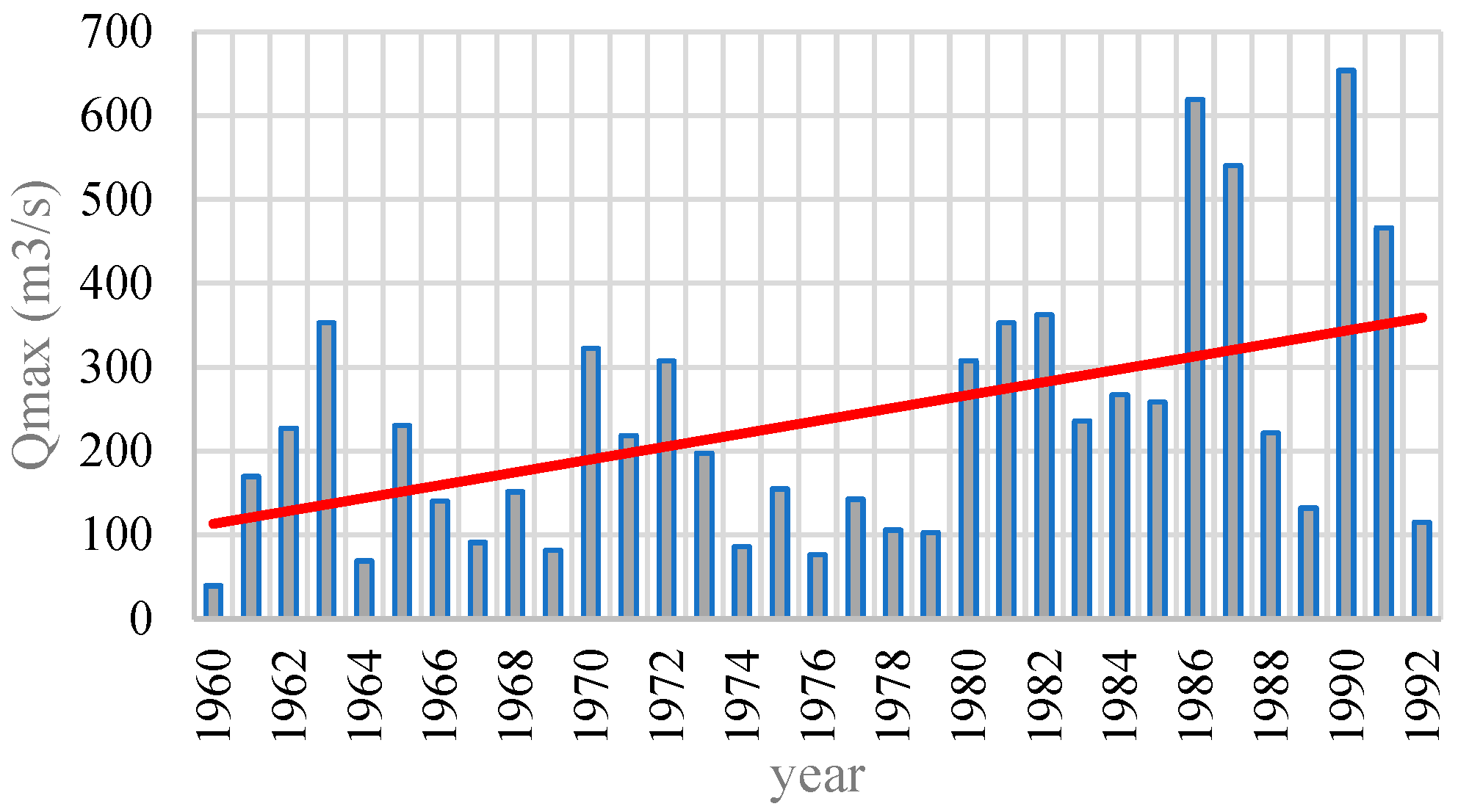
4.2. Case Study: Station 10086
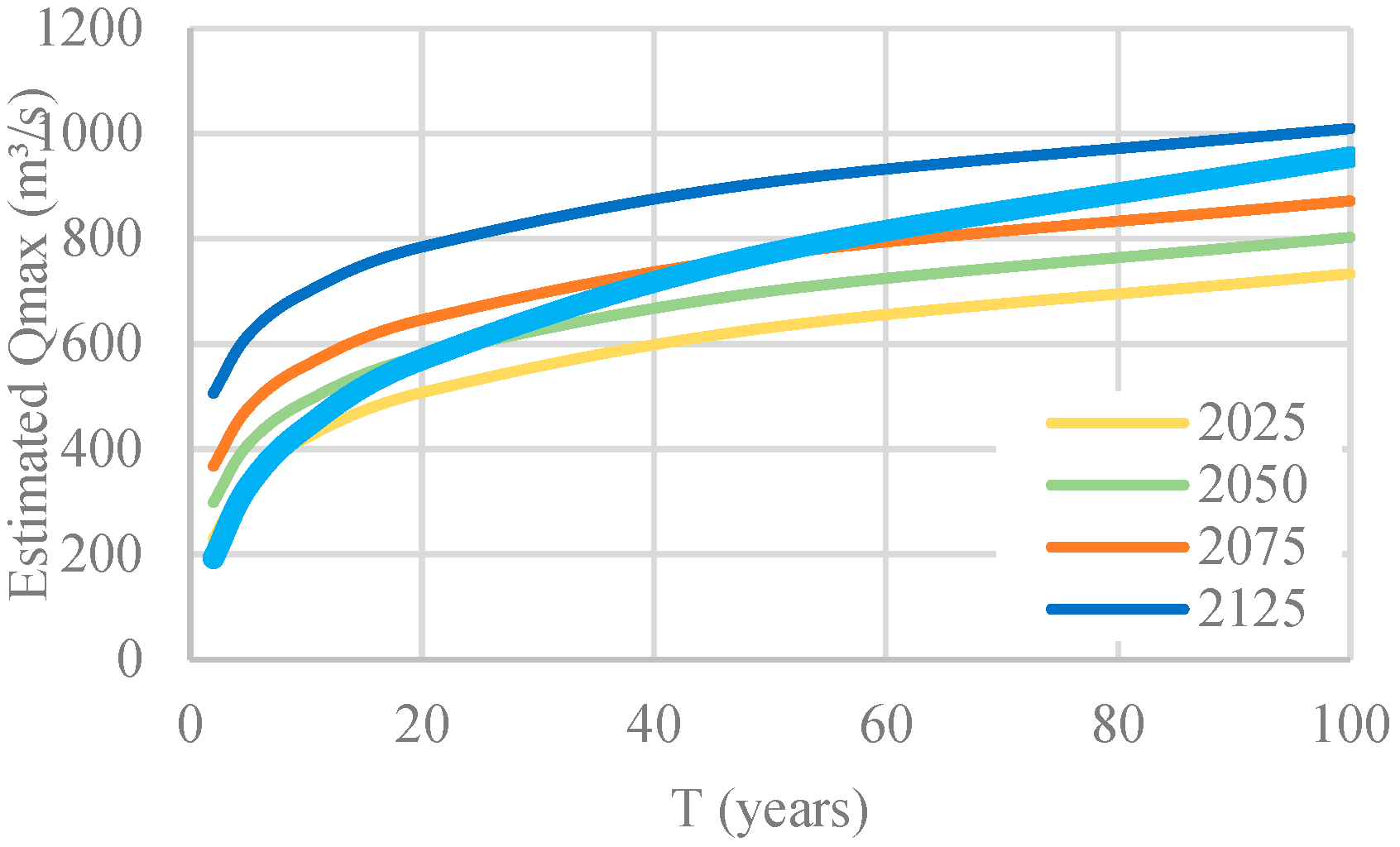
4.3. Practical and Policy Implications
4.4. Limitations of the Proposed Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Bivariate Extreme Value Distribution |
| FFA | Flood Frequency Analysis |
| GEV | Generalized Extreme Value |
| PDO | Pacific Decadal Oscillation |
| SOI | Southern Oscillation Index |
| T | Return period |
Appendix A. Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals
Appendix A.1. Probability Distribution and Density Functions for the BEV11 Distribution
Appendix A.2. Probability Distribution and Density Functions for the BEV12 Distribution
Appendix A.3. Probability Distribution and Density Functions for the BEV22 Distribution
Appendix A.4. Log-Likelihood Function for the BEV11 DistributionAppendix
Appendix A.5. Log-Likelihood Function for the BEV12 Distribution
Appendix A.6. Log-Likelihood Function for the BEV22 Distribution
Appendix A.7. Return Levels for the Gumbel and GEV Distributions
| Distribution | Function |
| Gumbel | |
| GEV | |
| Non-Stationary Gumbel | |
| Non-Stationary GEV |
References
- Genest, C.; Favre, A.-C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Salvadori, G.; Michele, C.D.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2007; Volume 56, ISBN 978-1-4020-4414-4. [Google Scholar]
- Zhang, L.; Singh, V.P. Copulas and Their Applications in Water Resources Engineering, 1st ed.; Cambridge University Press: Cambridge, UK, 2019; ISBN 978-1-108-56510-3. [Google Scholar]
- Coles, S.G.; Tawn, J.A. Modelling Extreme Multivariate Events. J. R. Stat. Soc. Ser. B Stat. Methodol. 1991, 53, 377–392. [Google Scholar] [CrossRef]
- Naveau, P.; Guillou, A.; Cooley, D.; Diebolt, J. Modelling Pairwise Dependence of Maxima in Space. Biometrika 2009, 96, 1–17. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Katz, R.W. Statistical Methods for Nonstationary Extremes. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2013; Volume 65, pp. 15–37. ISBN 978-94-007-4478-3. [Google Scholar]
- Serinaldi, F.; Kilsby, C.G. Stationarity Is Undead: Uncertainty Dominates the Distribution of Extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood Frequency Analysis for Nonstationary Annual Peak Records in an Urban Drainage Basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-Stationary Flood Frequency Analysis in Continental Spanish Rivers, Using Climate and Reservoir Indices as External Covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U.; Troy, T.; Devineni, N. A Hierarchical Bayesian GEV Model for Improving Local and Regional Flood Quantile Estimates. J. Hydrol. 2016, 541, 816–823. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgia, E. Frequency Analysis of Extreme Events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw Hill: New York, NY, USA, 1993; pp. 18.1–18.66. [Google Scholar]
- Yue, S.; Wang, C.Y. A Comparison of Two Bivariate Extreme Value Distributions. Stoch. Environ. Res. Risk Assess. 2004, 18, 61–66. [Google Scholar] [CrossRef]
- Gumbel, E.J. Bivariate Logistic Distributions. J. Am. Stat. Assoc. 1961, 56, 335–349. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments, 1st ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-43045-6. [Google Scholar]
- Viglione, A.; Laio, F.; Claps, P. A Comparison of Homogeneity Tests for Regional Frequency Analysis. Water Resour. Res. 2007, 43, 2006WR005095. [Google Scholar] [CrossRef]
- Andrews, D.F. Plots of High-Dimensional Data. Biometrics 1972, 28, 125. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Identification of Homogeneous Regions for the Purposes of Regionalisation. J. Hydrol. 1990, 121, 217–238. [Google Scholar] [CrossRef]
- Durocher, M.; Burn, D.H.; Mostofi Zadeh, S. A Nationwide Regional Flood Frequency Analysis at Ungauged Sites Using ROI/GLS with Copulas and Super Regions. J. Hydrol. 2018, 567, 191–202. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the Peaks-over-Threshold Method and the Annual Maximum Method for Flood Frequency Analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2001; ISBN 978-1-84996-874-4. [Google Scholar]
- Anderson, T.W. Maximum Likelihood Estimates for a Multivariate Normal Distribution When Some Observations Are Missing. J. Am. Stat. Assoc. 1957, 52, 200–203. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- CONAGUA Banco Nacional de Datos de Aguas Superficiales (BANDAS). Available online: https://app.conagua.gob.mx/bandas/ (accessed on 1 April 2024).
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for Assessing Water Infrastructure for Nonstationary Extreme Events: A Review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate Flood Frequency Analysis Using the Copula Method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: Salisbury South, Australia, 1975. [Google Scholar]
- Rootzén, H.; Katz, R.W. Design Life Level: Quantifying Risk in a Changing Climate: Design Life Level. Water Resour. Res. 2013, 49, 5964–5972. [Google Scholar] [CrossRef]
- Intergovernmental Panel On Climate Change (IPCC). Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, UK, 2021; ISBN 978-1-009-15789-6. [Google Scholar]

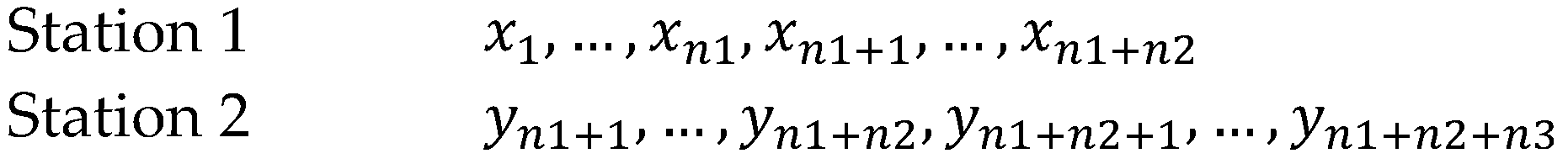

| Station | Period | Length of Record (Years) | Mean | Standard Deviation | Kurtosis | Skewness | Variation Coefficient |
|---|---|---|---|---|---|---|---|
| 10027 | 1938–1995 | 58 | 285.79 | 260.83 | 13.68 | 2.74 | 0.91 |
| 10065 | 1953–1999 | 47 | 1218.73 | 1081.76 | 13.59 | 2.84 | 0.89 |
| 10066 | 1955–2005 | 51 | 311.89 | 278.67 | 16.36 | 3.18 | 0.89 |
| 10079 | 1959–1999 | 41 | 1016.91 | 1642.41 | 19.86 | 3.74 | 1.62 |
| 10083 | 1960–1992 | 33 | 458.64 | 425.13 | 5.85 | 1.58 | 0.93 |
| 10086 | 1960–1992 | 33 | 236.33 | 156.80 | 4.48 | 1.19 | 0.66 |
| 10111 | 1958–2009 | 52 | 1315.93 | 1558.22 | 14.23 | 3.03 | 1.18 |
| 10137 | 1958–2008 | 51 | 1058.15 | 992.91 | 7.59 | 2.02 | 0.94 |
| Station | Independent? | Homogeneous? | Trend? | Increasing? |
|---|---|---|---|---|
| 10027 | Yes | Yes | No | Yes |
| 10065 | Yes | Yes | No | No |
| 10066 | Yes | No | No | No |
| 10079 | Yes | Yes | Yes | Yes |
| 10083 | Yes | Yes | No | Yes |
| 10086 | Yes | No | Yes | Yes |
| 10111 | Yes | Yes | No | No |
| 10137 | Yes | Yes | No | No |
| Station | A (km2) | MAP (mm) | DD (km/km2) |
|---|---|---|---|
| 10027 | 388.259 | 912.9 | 0.2135 |
| 10065 | 6102.181 | 871.5 | 0.2474 |
| 10066 | 1373.576 | 777.45 | 0.2471 |
| 10079 | 1010.891 | 1031.19 | 0.2746 |
| 10083 | 827.432 | 754.8 | 0.2750 |
| 10086 | 226.588 | 831.2 | 0.2356 |
| 10111 | 5277.521 | 993.5 | 0.2471 |
| 10137 | 3300.188 | 982.9 | 0.2396 |
| Station | Area (km2) | MAP (mm) | DD (km/km2) |
|---|---|---|---|
| 10027 | 0.169 | 8.855 | 10.579 |
| 10065 | 2.656 | 8.454 | 12.259 |
| 10066 | 0.598 | 7.542 | 12.244 |
| 10079 | 0.440 | 10.003 | 13.607 |
| 10083 | 0.360 | 7.322 | 13.626 |
| 10086 | 0.099 | 8.063 | 11.674 |
| 10111 | 2.297 | 9.637 | 12.244 |
| 10137 | 1.436 | 9.535 | 11.872 |
| Distribution | Covariate | M | AIC | D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gumbel | - | - | 168.54 | 108.89 | −203.88 | 411.75 | ||||||
| GEV | - | - | 155.56 | 96.66 | −0.235 | −204.12 | 414.23 | |||||
| BEV 21-10137 | - | 1.11 | 154.55 | 92.42 | −0.094 | 681.09 | 574.59 | −200.14 | 406.28 | |||
| BEV 21-10137 | Time | 1.10 | 105.82 | 2.77 | 86.74 | −0.123 | 745.27 | −2.45 | 573.55 | −198.55 | 405.11 | 11.13 |
| Distribution | Scenario | t | T (years) | |||||
|---|---|---|---|---|---|---|---|---|
| 2 | 5 | 10 | 20 | 50 | 100 | |||
| Gumbel | - | - | 208.45 | 331.86 | 413.58 | 491.96 | 593.42 | 669.44 |
| GEV | - | - | 192.55 | 329.32 | 442.08 | 570.59 | 772.66 | 955.82 |
| BEV 21-10137 | - | - | 189.01 | 303.43 | 386.20 | 471.27 | 590.31 | 686.62 |
| BEV 21-10137 non-stationary in time | 2025 | 66 | 320.99 | 431.32 | 513.29 | 599.33 | 722.62 | 824.71 |
| 2050 | 91 | 390.17 | 500.51 | 582.47 | 668.52 | 791.81 | 893.90 | |
| 2075 | 116 | 459.36 | 569.69 | 651.66 | 737.71 | 861.00 | 963.08 | |
| 2125 | 166 | 597.74 | 708.07 | 790.03 | 876.08 | 999.37 | 1101.46 | |
| Station | Best-Fitting Distribution | Covariate | M | AIC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10027 | BEV 21-10065 | SOI | 1.18 | 165.48 | −4.68 | 112.91 | −0.219 | 825.22 | −75.56 | 584.65 | −369.18 | 746.36 |
| 10065 | BEV 21-10027 | Time | 1.15 | 804.27 | −1.31 | 436.67 | −0.191 | 190.17 | −0.06 | 148.03 | −361.49 | 730.98 |
| 10066 | BEV 21-10079 | SOI | 1.07 | 192.23 | 4.25 | 103.89 | −0.236 | 527.80 | 26.00 | 637.16 | −320.53 | 649.06 |
| 10079 | BEV 21-10066 | Time | 1.10 | 337.40 | 1.80 | 270.49 | −0.478 | 257.48 | −1.57 | 142.75 | −301.79 | 611.58 |
| 10083 | BEV 21-10065 | Time | 1.34 | 186.50 | 0.59 | 155.50 | −0.455 | 909.26 | −2.88 | 584.78 | −223.72 | 455.45 |
| 10086 | BEV 21-10137 | Time | 1.10 | 105.82 | 2.77 | 86.74 | −0.123 | 745.27 | −2.45 | 573.55 | −198.55 | 405.11 |
| 10111 | BEV 21-10065 | Time | 2.05 | 800.38 | −6.16 | 338.99 | −0.485 | 943.79 | −2.84 | 626.07 | −395.48 | 798.95 |
| 10137 | BEV 21-10066 | SOI | 1.13 | 512.21 | −44.16 | 344.23 | −0.524 | 215.82 | −4.84 | 146.25 | −389.67 | 787.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berbesi-Prieto, L.; Escalante-Sandoval, C. Flood Frequency Analysis Using the Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals. Hydrology 2025, 12, 274. https://doi.org/10.3390/hydrology12110274
Berbesi-Prieto L, Escalante-Sandoval C. Flood Frequency Analysis Using the Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals. Hydrology. 2025; 12(11):274. https://doi.org/10.3390/hydrology12110274
Chicago/Turabian StyleBerbesi-Prieto, Laura, and Carlos Escalante-Sandoval. 2025. "Flood Frequency Analysis Using the Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals" Hydrology 12, no. 11: 274. https://doi.org/10.3390/hydrology12110274
APA StyleBerbesi-Prieto, L., & Escalante-Sandoval, C. (2025). Flood Frequency Analysis Using the Bivariate Logistic Model with Non-Stationary Gumbel and GEV Marginals. Hydrology, 12(11), 274. https://doi.org/10.3390/hydrology12110274





