Abstract
Groundwater contamination poses a major challenge to water supplies around the world. Assessing groundwater vulnerability is crucial to protecting human livelihoods and the environment. This research explores a machine learning-based variation of the classic DRASTIC method to map groundwater vulnerability. Our approach is based on the application of a large number of tree-based machine learning algorithms to optimize DRASTIC’s parameter weights. This contributes to overcoming two major issues that are frequently encountered in the literature. First, we provide an evidence-based alternative to DRASTIC’s aprioristic approach, which relies on static ratings and coefficients. Second, the use of machine learning approaches to compute DRASTIC vulnerability maps takes into account the spatial distribution of groundwater contaminants, which is expected to improve the spatial outcomes. Despite offering moderate results in terms of machine learning metrics, the machine learning approach was more accurate in this case than a traditional DRASTIC application if appraised as per the actual distribution of nitrate data. The method based on supervised classification algorithms was able to produce a mapping in which about 45% of the points with high nitrate concentrations were located in areas predicted as high vulnerability, compared to 6% shown by the original DRASTIC method. The main difference between using one method or the other thus lies in the availability of sufficient nitrate data to train the models. It is concluded that artificial intelligence can lead to more robust results if enough data are available.
1. Introduction
Groundwater vulnerability is a complex and manifold concept that escapes a univocal definition [1]. Broadly speaking, groundwater vulnerability represents how likely pollutants are to reach the saturated zone of an aquifer based on the features of the land surface and the vadose zone. It depends on the physical, chemical, and biological processes that govern the movement of a given contaminant. Suitably, different approaches to compute groundwater vulnerability have been proposed over the years. These can be classified into index-based, statistical, and process-based methods [2,3]. Index-based methods, including DRASTIC, rank among the most widely used [4,5,6]. DRASTIC is an acronym that stands for a series of factors that control groundwater vulnerability to contamination, namely, depth to the water table, recharge, aquifer media, soil, slope, hydraulic conductivity, and the effect of the vadose zone [7]. A variety of modifications have been proposed to the original DRASTIC approach, mostly to cater to different hydrogeological environments and site-specific considerations [8,9,10,11]. Changes to DRASTIC are frequently based on incorporating additional parameters—land use, geological lineaments, and altitude, among others—modifying the weights of the original parameters, or a combination of both [3,5].
By definition, groundwater vulnerability is constrained by spatially distributed variables. Thus, the outcomes of vulnerability studies are generally presented as maps [7,12]. A recurring issue with index-based methods is how to assign coefficients to each governing parameter so as to reflect spatial variability. In this regard, it is sometimes pointed out that DRASTIC can be used without giving due importance to validation, which may bring its outcomes under scrutiny [13]. The advent of machine learning (ML) techniques represents a two-fold advantage in terms of enhancing the credibility of vulnerability maps. For one, machine learning allows new ways to infer groundwater-related variables by training artificial intelligence algorithms within GIS environments [14]. This means that weights can be optimized on ground truth. Furthermore, the process of training supervised learning algorithms on contamination data contributes to improving the credibility of the outcomes.
Groundwater vulnerability studies have tested multiple machine learning approaches in recent years. Frequently used algorithms include logistic regression, random forests, artificial neural networks, and support vector machines, among others [15]. These studies deal with different target variables; some studies predict the groundwater vulnerability index by using DRASTIC parameters [16] or several parameters related to topography, meteorology, socio-economic, and geological variables [17]. In contrast, other studies define the target variable as a specific contaminant such as nitrate [18,19].
Regarding the performance of the different algorithms, some authors have found that random forest, and in general, the ensemble tree-based methods, often perform well in relation to other algorithm families [19,20]. Conceptually speaking, this could be due to the conditional logic underlying tree algorithms, which is equivalent in many respects to the rationale behind index-based vulnerability. For instance, ref. [21] compared neural networks, random forest regression, and support vector regression to evaluate vulnerability to nitrate contamination in alluvial aquifers of South Korea based on the DRASTIC-L method. DRASTIC-L is an evolution of the original DRASTIC method that incorporates the land use factor. These authors found that an ensemble random forest regression approach was best to depict the threat of contamination. Similarly, ref. [22] highlighted the random forest as the best-performing model against support vector machines, Naïve Bayes, and C4 classifiers when computing vulnerability in an aquifer of the United Arab Emirates, much like [23] found random forest to excel against other algorithms in an application of the classic DRASTIC method to a groundwater catchment in central Iran. For its side, ref. [19] performs a multi-class classification ML approach for groundwater vulnerability assessment by using the conventional DRASTIC-L method parameters and nitrates target variable. This work shows again the random forest model as the optimal choice. While other authors suggest that algorithms like categorical and adaptive boosting can outperform random forest in certain cases [24], the consensus seems to be that tree-based algorithms are naturally suited to address groundwater vulnerability. In this context, the first goal of our research is to provide a machine learning approach to optimize DRASTIC’s weighting system. We broaden the methodological scope in relation to previous studies by using an array of tree-based models instead of just one. This is because it is typically unfeasible to foretell which algorithm is likely to perform best on a given dataset. The better scoring algorithms are picked for ensuing analyses and, eventually, ensemble mapping. Another methodological insight consists of the elimination of the reclassification procedures of the continuous variables. This will allow to determine the weights of the DRASTIC method with the raw values of depth to the water table (D), recharge (R), and topographic slope (T).
2. Material and Methods
2.1. Study Area
The method is illustrated through its application to the aquifers of the Duero River basin (Figure 1). The Duero basin is shared by Spain and Portugal. With a surface area of 98,000 km2, it is the Iberian Peninsula’s largest river catchment. About 79,000 km2 are located within Spanish territory. The catchment is predominantly flat and takes up most of the northern part of the peninsula’s central plateau. The Duero is best described as a sedimentary basin made up of the accumulation of materials eroded from the Galician (northwest), Cantabrian (north), Central (south), and Iberian (east) mountain ranges. Altitude varies between 700 m.a.s.l. in the central part of the basin and 2600 m.a.s.l. in the mountains of the Central Range.
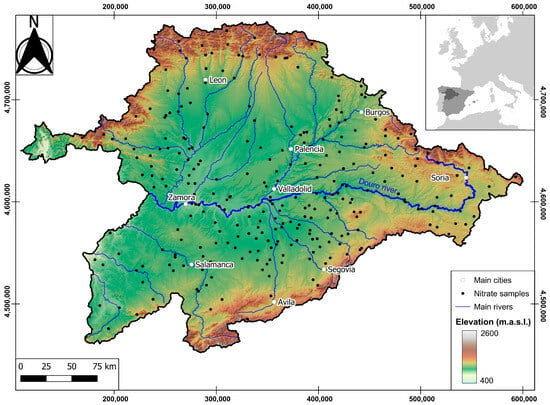
Figure 1.
The study area covers the aquifers of the Duero river basin within Spanish territory.
The climate is continental semiarid. Winters are long and cold, with mean temperatures in the order of 2 °C in the higher areas of León and along the northern and southern mountain ranges. Summers are comparatively shorter and milder, particularly in the higher altitude areas. Mean summer temperatures exceed 22 °C in the central part of the basin. Annual rainfall amounts to 610 mm but ranges widely, from 400 mm in the central part of the basin to 1800 mm in the northern and northwestern mountains.
Approximately 65% of the catchment surface consists of permeable rocks. For administrative purposes, these are classified in 31 different groundwater bodies that represent three major groundwater regions, namely, the Iberian range, the central tertiary basin, and the peripheral mountain massifs [25]. The Iberian range is characterized by the presence of calcareous materials that behave as productive regional aquifers when karstified and/or fissured. These are mostly recharged by rainfall and discharge through springs and rivers, as well as laterally into the tertiary region.
Tertiary aquifers are traditionally referred to as the main groundwater units in the catchment. This is largely due to their comparatively larger extension and storage capacity. Tertiary aquifers are further subdivided into shallow and deep systems. The shallow ones are unconfined, present limited thickness and storage capacity, and are dependent on recent rainfall. Conversely, deep tertiary aquifers take up most of the basin and behave as a single, heterogeneous, anisotropic system with confined and semiconfined sectors. As explained above, recharge in tertiary materials depends on lateral inflows from neighboring systems as well as on direct infiltration from rainfall and losing streams. Discharge takes place through gaining rivers, particularly the Duero River, as well as through pumping.
Aquifers in peripheral mountain massifs stem from the fracturing and weathering of igneous and metamorphic rocks. Peripheral aquifers present similar recharge and discharge conditions as the Iberian range aquifers. Though more limited in size and storage capacity, peripheral aquifers are often important for small rural communities.
Natural groundwater quality is suitable for most uses, though instances of geogenic arsenic have been reported towards the southeastern part of the basin. Arsenic mobilization is partially attributed to groundwater pumping [26]. Nitrate contamination due to agricultural activities is also widespread across the central area and perhaps represents the most important threat to groundwater quality in the region [27].
The Spanish sector of the Duero basin is home to 2.2 million people, about half of whom inhabit rural areas. Irrigation accounts for 93% of the basin’s water uses, while domestic supply amounts to 6%. Energy, industry, and other uses make up the remaining 1% [27]. Approximately 25% of the total domestic supply relies on groundwater, with aquifers being the main source of water for two-thirds of the municipalities. Additionally, 25% of irrigation (765 Mm3/yr) is groundwater-based. Finally, aquifers are important from an environmental perspective, as 30 to 35% of the total discharge of the Duero River is attributed to base flow. Groundwater also underpins numerous springs and wetlands [28].
2.2. Nitrate Data
Nitrate data from the official groundwater monitoring network was made available by the river basin authorities (Figure 1). The database comprises over four hundred observation boreholes, most time series spanning the 2006–2023 interval. Nitrate is measured at least once a year in each borehole, but some years in the series feature more than two readings in many monitoring points. The most comprehensive dataset in the recent past is the 2019 one, which encompasses 421 individual boreholes and over 1100 nitrate analyses. The dataset was created by selecting the maximum values of nitrate concentrations for each borehole for the corresponding period. Joint analysis of borehole depth and geological context led us to use exclusively those boreholes that are shallower than 100 m, which resulted in 294 sampling locations.
Because supervised classification algorithms attempt to predict a category, rather than a numerical outcome, known instances of nitrate contamination were reclassified prior to running the algorithms. The nitrate dataset is binary and classifies boreholes as “contaminated” (≥37.5 mg/L) or “uncontaminated” (<37.5 mg/L). The 37.5 value is the threshold that Spanish law currently establishes for groundwater to be considered “affected by nitrate” [29].
Adequately balancing input data is important to prevent algorithms from overfitting. Overfitting may result in spurious outcomes by, for instance, entirely ignoring a category in favor of the other while still obtaining good results from a mathematical perspective. There is no rule of thumb for balancing input data, except that the algorithms should have enough instances of each category to learn from and test for. In the case at hand, the largest category comprises just below two hundred instances, while the smallest one comprises slightly over one hundred. In the binary dataset, 74% of the 421 boreholes are in the “uncontaminated” category, and 26% are in the “contaminated” category. This split is considered sufficiently well balanced for artificial learning. Imbalanced datasets are usually those with a ratio higher than 1/10, and can be as high as 1/100 in the case of some binary approaches [30].
2.3. DRASTIC Inputs
The classic DRASTIC approach considers seven input parameters, namely, depth to the water table (D), recharge (R), aquifer media (A), soil (S), topographic slope (T), impact of the vadose zone (I), and hydraulic conductivity (C) [7]. We used a modification of the original method that incorporates land use (L) as an additional input parameter [31] because agricultural use was expected to be a driving factor explaining groundwater nitrate. All variables were compiled in map form into a QGIS 3 geographic database (Figure 2 and Figure 3). Some layers were subsequently reclassified based on DRASTIC’s original categories, while others were employed with the raw values, specifically depth to the water table, recharge, and topographic slope (Table 1). Layer weight was left as the parameter for machine learning algorithms to optimize.
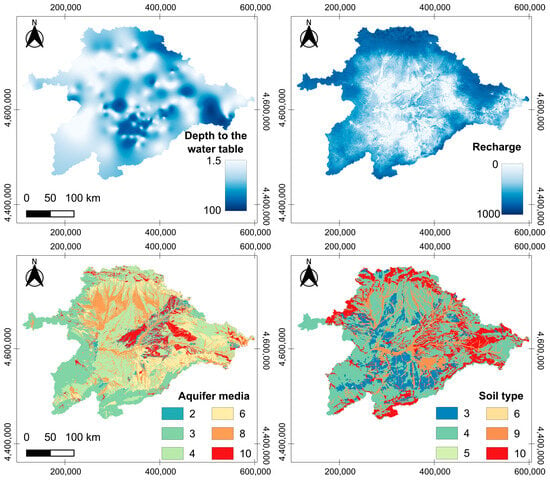
Figure 2.
Spatially distributed variables for the input parameters used in the DRASTIC method, namely, depth to the water table (D), recharge (R), aquifer media (A), and soil (S).
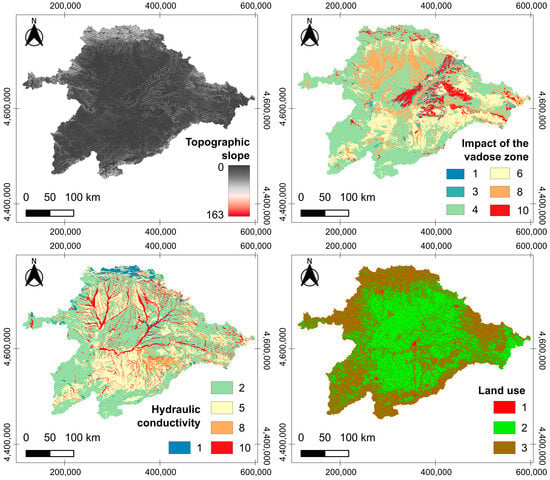
Figure 3.
Spatially distributed variables for the input parameters used in the DRASTIC method, namely, topographic slope (T), impact of the vadose zone (I), hydraulic conductivity (C), and land use (L).

Table 1.
Reclassification of layer information based on the classic DRASTIC method and machine learning algorithms.
Land topography was obtained directly from the 30 × 30 resolution digital elevation model of the Shuttle Radar Topography Mission [32,33]. Slope was then computed in percentage form by using the slope tool from QGIS 3.10.9 software. The combination of topographic information with groundwater elevation data from 232 boreholes allowed us to obtain a continuous map of the depth to the water table across all permeable units. The continuous map was obtained by using the multilevel B-spline interpolation tool from QGIS software. In the case of the tertiary aquifers that conform the central part of the basin, where vertical flows and confined layers exist, care was taken to distinguish between shallow and deep boreholes so as to give due consideration to hydrogeological constraints. Wet season piezometric readings were used preferentially in order to compute vulnerability under adverse conditions.
The recharge layer is an outcome of the SIMPA model [34]. SIMPA is a widely recognized rainfall-runoff code that computes the main hydrological variables for the whole of the Spanish national territory [35]. Long-term recharge is calculated at the 1:1,000,000 scale and refers to the mean annual aquifer recharge for the 1980/81–2005/06 interval.
The hydraulic conductivity of the aquifer, impact of the vadose zone, soil media, and aquifer media layers are reclassifications of the characteristics of the rock at different depths (Table 1). All four of them were downloaded from the intrinsic vulnerability information provided in the online dashboard of the Duero Basin Authority [36]. Finally, land use was depicted as per the 1:25,000 scale national cartography [37]. To aid the algorithms, the many categories that make up the official land use maps were reclassified in three categories, namely, urban/industrial, agricultural, and natural areas.
2.4. Machine Learning Software
MLMapper 2.0 uses a wide variety of algorithms from the Scikit Learn toolbox. These have been described in depth by [38], and include five tree-based machine learning models, Decision Tree Classifier (DTC), Random Forest Classifier (RFC), Gradient Boosting Classification (GBC), Ada-Boost Classifier (ABC), and Extra-Trees Classifier (ETC). The software incorporates standard machine learning routines such as collinearity checks, randomized-search parameter fitting, cross validation, and recursive feature elimination. It also enables the user to pick one or several among a set of scoring metrics. These comprise the raw test score, area under receiver operating characteristic curve (AUC), precision, recall, and F1-score.
Each algorithm samples the pixel value of each GIS layer corresponding to a known contamination outcome. Then, it uses the sets of pixel values associated with every borehole to find the combinations of explanatory variables that result in a given concentration level. Because every pixel value is known for every layer in the GIS database, the findings of the algorithms can be subsequently extrapolated in space to develop a validated predictive map. Parameter weights are computed during this process so as to find out which explanatory variables are more important in explaining nitrate content. This all represents an entirely alternative way to determine the extent to which each layer of the DRASTIC model controls vulnerability. Outcomes are then compared with a classic DRASTIC map to analyze the differences (Figure 4). Two well-known metrics in the field of machine learning have been used to validate the results. These are the F1 score and the area under the receiver operating characteristic curve (AUC). The F1 score is the harmonic mean of precision and recall. Precision is calculated as the ratio of true positives over the sum of true and false positives, while recall is the ratio of true positives over the sum of true positives and false negatives. The AUC score shows the performance of a classification model at all classification thresholds. The AUC is a probabilistic metric that evaluates the degree to which algorithms can distinguish between classes and rank on a scale of 0 to 1, with a higher score implying better performance.
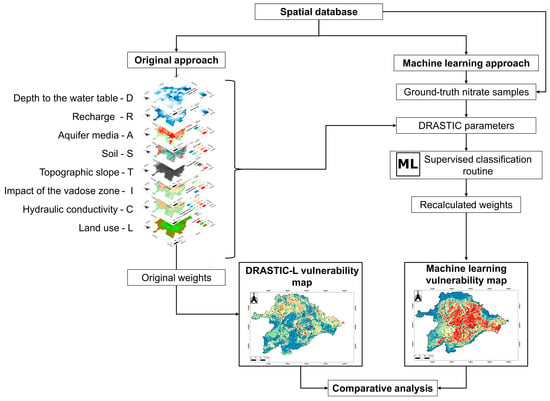
Figure 4.
Methodological flowchart.
MLMapper 2.0 uses a wide variety of algorithms from the Scikit Learn toolbox. These have been described in depth by [38] and include five tree-based machine learning models: Decision Tree Classifier, Random Forest Classifier, Gradient Boosting Classification, Ada-Boost Classifier, and Extra-Trees Classifier. The software incorporates standard machine learning routines such as collinearity checks, randomized-search parameter fitting, cross validation, and recursive feature elimination. It also enables the user to pick one or several among a set of scoring metrics. These comprise the raw test score, area under receiver operating characteristic curve (AUC), precision, recall, and F1-score.
3. Results
3.1. Model Performance
Figure 5 shows the area under the curve results for the best-performing models. The best performance was obtained by the Random Forest and ExtraTrees classifiers. Area under the curve scores of 0.76 and 0.73 for RFC and ETC, respectively, can be considered a measure of a reasonable predictive capability by these algorithms. The DTC, ABC, and GBC models show raw test scores below 0.67. The best-performing algorithms were also selected based on the F1 score values for both classes since it was observed that F1 values for the positive class were systematically lower than for the negative class. The RFC and ETC F1 scores exceeded those of the other algorithms, which barely reached 0.45, while these models exceeded 0.50.
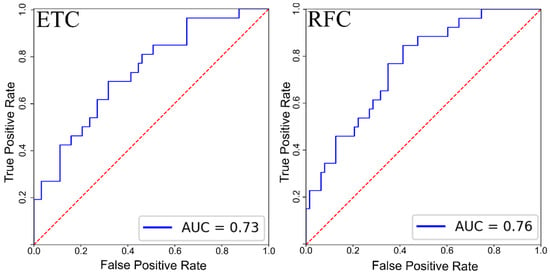
Figure 5.
Receiver operator curves (ROC) and area under curve (AUC) for the best-performing tree-based algorithms, ExtraTrees and Random Forest.
3.2. DRASTIC Recalculated Weights and Model Insights
Table 2 shows the DRASTIC recalculated weights obtained from the feature importance analysis for Random Forest and ExtraTrees classifiers. For each algorithm, the sum of the weights is equal to 1. The feature importance attribute of the ensemble tree-based models is computed as the mean and standard deviation of the accumulation of the impurity decrease within each tree. This means that the relative rank of an explanatory variable used as a decision node in a tree can be used to assess the relative importance of that feature in relation to the predictability of the target variable. The explanatory variables used at the upper part of the tree contribute to the final prediction decision for a larger fraction of the input samples. Therefore, the expected fraction of the samples to which they contribute can be used as an estimate of the relative importance of the features [38]. Then, ensemble recalculated weights were obtained by averaging the weight values for the two models. For comparison purposes, the original weights of the DRASTIC method were also included and normalized to 1. ETC and RFC agreed in giving more weight to the recharge and the aquifer media parameters. This is more acute in the case of ETC, which attributes weights of 0.210 and 0.300 for recharge and aquifer media, respectively. In the case of the RFC, the weight of recharge and aquifer media is 0.230 and 0.150, respectively, closer to the weight of the rest of the parameters, which ranges between 0.080 and 0.130.

Table 2.
DRASTIC recalculated weights from the feature importance for the best-performing algorithms, ETC and RFC. The original weights of the DRASTIC method were normalized to 1 for comparison purposes.
Comparison with the original DRASTIC weights shows that the supervised classification approach increases the importance of the recharge, aquifer media, soil media, and topography. In contrast, the depth to water table, impact of the vadose zone, hydraulic conductivity, and land use parameters experience a decrease in comparison to the original weights of the DRASTIC method.
3.3. Spatial Predictions
The spatial maps were computed for the two different approaches, namely the original DRASTIC approach (Figure 6) and the binary supervised classification approach (Figure 7). The original DRASTIC map and the one obtained with the binary approach are colored from blue to red, showing areas from less to more vulnerable to contamination. In Figure 6, the vulnerability index was computed using the weights from Table 1. Figure 7 shows the spatial prediction probability of exceeding 37.5 mg/L of nitrates according to the best-performing algorithms. This map was obtained by averaging pixel by pixel the probability for the RFC and ETC models of exceeding the 37.5 mg/L threshold.
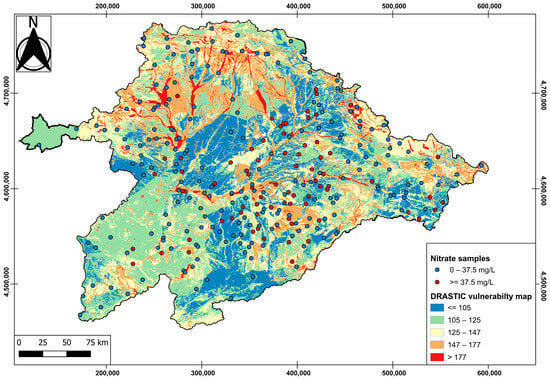
Figure 6.
DRASTIC vulnerability map using the original approach.
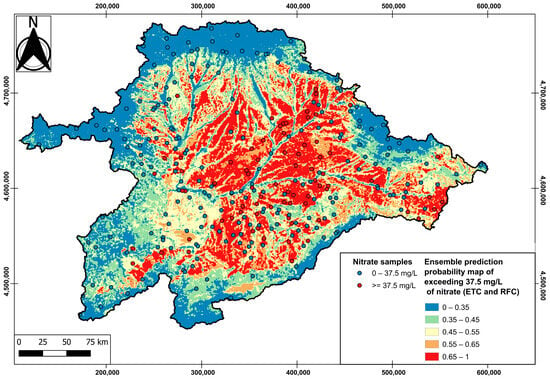
Figure 7.
Ensemble prediction probability map of exceeding 37.5 mg/L of nitrate when using the best-performing tree-based algorithms, ExtraTrees and Random Forest.
Figure 6 shows that the most vulnerable areas are generally located along the fluvial systems of the basin. This is consistent with the materials found in this geological context, which consist of sands and gravels with higher permeability values. Using the original DRASTIC weights thus leads to a higher vulnerability. Figure 7, on the other hand, shows the most vulnerable areas to be those associated with the sedimentary materials that filled up the basin but are not linked to the current rivers. This also applies to carbonate materials. From a regional perspective, the areas with the greatest vulnerability to contamination are located in the central part of the basin. The direction of groundwater flow throughout the region is directed from the outer edges of the basin and towards the center, where the Duero River flows. This hydrogeological behavior could explain why the pollutants infiltrated in the outermost areas of the basin end up concentrated in the central part of the basin. Unlike the map obtained using the original DRASTIC method, Figure 7 shows low vulnerability in the fluvial zones. This could be explained by the nature of the alluvial materials. As they are more permeable, nitrates from infiltration through the river channels connected to the aquifer can be evacuated more quickly to areas with lower permeability where the flow velocity decreases, such as the areas showing greater vulnerability.
Figure 6 and Figure 7 were used to analyze the spatial coherence of these maps in relation to ground-truth data. For this purpose, the ranges in Table 3 were used to assign a DRASTIC vulnerability class, from very low to very high, to the DRASTIC original map and the ensemble prediction probability map obtained by using the binary supervised classification approach. Table 4 shows the total number of points, the number of positive points (≥37.5 mg/L nitrate content), and the average nitrate concentration situated along these areas for the original DRASTIC approach and for each vulnerability class.

Table 3.
Reclassification of machine learning probability predictions and DRASTIC values into different vulnerability classes for analysis purposes.

Table 4.
Spatial analysis for the different DRASTIC vulnerability classes obtained with the original DRASTIC weights. The total number of points, number of positive points, and average nitrate concentration were computed for each class separately.
Table 4 shows that the “very high” vulnerability class zone has the fewest points compared to the other vulnerability classes in the case of the original DRASTIC approach, with the moderate class having the highest percentage of points. About 49% of the positive points (samples with nitrate concentration in excess of 37.5 mg/L) were located within the “very low” and “low” vulnerability class areas, while only 20.5% of the positive points were located within the “high” and “very high” vulnerability zones. Furthermore, the “very low” vulnerability class shows that positive points represent almost half of the total points found in these zones (47.1%). The “very high” and “high” vulnerability class zones show a very small percentage (<17% in both cases) of positive points with respect to the total points. The average nitrate concentration calculated for the different areas shows that the DRASTIC original method could not capture the nitrate spatial distribution as the average concentration was higher in the “very low” and “low” areas in comparison with the “high” and “very high” vulnerable areas.
This is consistent with Table 5, which reveals that the “moderate” vulnerability class zone has the highest number of points, while the “high” vulnerability zone shows the lowest percentage of total points when using the machine learning approach. The 44.9% of the positive points were located within the “very high” vulnerability class areas, and the 21.8% were located within the “high” vulnerability class areas. Moreover, only 8.9% of the positive points were located in the “very low” and “low” vulnerability class zones. In addition, the “very low” and “low” vulnerability class areas show that positive points account for a very limited percentage of the total number of points found in these areas (<8% in both cases), whereas the “very high” and “high” vulnerability class areas show that a large percentage of the points are positive. Finally, the average nitrate concentration calculated for the different class zones shows that the binary supervised classification approach captures the nitrate spatial distribution as the average concentration increased from the “very low” to the “very high” vulnerable zones.

Table 5.
Spatial analysis for the different DRASTIC vulnerability classes obtained with the tree-based machine learning algorithms. The total number of points, number of positive points, and average nitrate concentration were computed for each class separately.
4. Discussion
4.1. Machine Learning Approach: Performance, Advantages, and Limitations
In the case at hand, nitrate contamination was used as a proxy for groundwater vulnerability. Though there is a conceptual difference between vulnerability to contamination and actual contamination, which partly explains the differences between machine learning and DRASTIC results, we consider this assumption acceptable because human activity is widespread across the Duero basin and because monitoring points are well distributed in space, which implies that the algorithms have a sufficiently wide variety of explanatory variable combinations to learn from. In this context, it is also important to note that nitrate tends to be conservative. Once it reaches the unsaturated zone, it is bound to percolate into groundwater, so all aquifers in any given basin would be ultimately vulnerable except when overlain by impervious materials. In this context, evidence-based approaches such as the one we present in this paper might be better suited than index-based methods when trying to depict vulnerability to this kind of contamination.
Perhaps the main advantage of using machine learning is the reliance on ground truth. Instead of assigning a set of static weights and ratings to a fixed number of explanatory variables, machine learning uses an evidence-based approach. In other words, ground truth is the departure point to determine which spatially distributed variables explain the presence of contamination in groundwater [39]. As shown in Table 4 and Table 5, this results in a higher degree of agreement between machine learning and ground truth than between DRASTIC and ground truth.
Versatility is an additional benefit of machine learning over index-based methods. As opposed to DRASTIC, which relies on seven variables, predictive machine learning mapping may use as many variables as needed, and these may be different from one study site to another [40,41,42]. This may allow us to take into consideration the vulnerability to different kinds of contaminants simultaneously, as opposed to referring exclusively to the intrinsic vulnerability of aquifer systems. Exploring other combinations of explanatory variables was avoided altogether in this case because the specific goal was the optimization of DRASTIC weights based on artificial intelligence, but the literature demonstrates it to be possible [43,44].
The comparison at hand works with continuous variables, i.e., recharge, slope, and depth of the water table, in raw or unclassified format. This is because the reclassification promoted by the DRASTIC method is subject to the specific conditions under which the method was developed. Therefore, different climatic, topographic, or hydrogeological conditions may require different approaches to reclassification. Accordingly, using the raw values in the ML approach increases the degrees of freedom when generating the final mapping, thus better adjusting the results to the conditions of the study area.
From a practical standpoint, a major drawback of machine learning applications is the need for large datasets (typically a few hundred to a few thousand data points). Such detailed information is not always available, particularly when working at local scales. Thus, predictive machine learning mapping tends to be more applicable in regional contexts of well-monitored areas. In that kind of context, index-based methods such as DRASTIC emerge as the alternative of choice. The performance differences between the various algorithms are explained by differences in internal architecture and ensemble procedures specific to each algorithm, which generate variability in performance and results depending on the model used. As previously mentioned, the use of a series of tree-based models rather than a single one and then selecting the best-performing ones is an optimal strategy. The reason behind this is that it is often impossible to predict which algorithm will perform best on a specific database. Ref. [45] shows that the good performance usually offered by tree-based ensemble algorithms could be due to their nature as “interpolating” algorithms to “noise points”. This type of model, which is highly adaptive to ensemble training, is able to generate “spiked-smooth” decision boundaries. This feature gives it a higher robustness compared to other models.
There are some additional limitations to machine learning outcomes. Some of them pertain to input data, while others are related to the structure of the machine learning method. Regarding the former, the original dataset presents uncertainties of its own. For instance, field sampling does not necessarily reflect the distribution of nitrate in the vertical dimension, as there is one single reading for each date and borehole. Besides, potential information such as the depth of the well screen or the existence of pumping wells in the vicinity of each point was missing. More detailed field information would undoubtedly lead to more accurate results. Additionally, it is important to note the limitations associated with both the spatial distribution of the data and the temporal frequency of the data. As a predictive mapping approach, the final outcome will vary depending on the availability and heterogeneity of the data distribution from the spatial perspective. It is essential to have accurate information for all the geological environments and to have the greatest variability in terms of values of explanatory variables, in this case, the DRASTIC parameters, in order to obtain a sufficiently good generalization. In this line, the absence of sufficient data in a given context could lead to a high error of generalization due to the lack of information used during the training phase of the models. From a temporal point of view, the final map is a static picture of vulnerability to contamination according to the values used to train the algorithms, i.e., it is a groundwater vulnerability map to nitrate contamination for the maximum nitrate peak in 2019. Creating a continuous map over time would require a continuous database with regular sampling and, at the same time, comparable spatial distributions. However, factors that change over time, such as recharge, water table depth, and even land use, would need to be further elaborated again according to the time frame.
From the methodological perspective, the current version of MLMapper is designed to predict in space, not in time [20]. In other words, it does not take into consideration variables such as groundwater dynamics, which would need to be incorporated by means of proxy variables such as latitude and longitude. This is seen as a line of future research.
4.2. Practical Implications
The application of machine learning methods in real-world groundwater (GW) management has increased in recent times [46]. The application of these approaches ranges from GW monitoring network optimization [47] or decision-making for GW quality [48] to GW level forecasting/prediction [49] and GW potential mapping [14].
All these applications can be used to support groundwater management plans to improve all aspects, from groundwater prospecting to quality monitoring to water distribution for different uses. The present case illustrates how, through the application of a series of machine learning algorithms and the same parameters that are used in more rigid methods such as DRASTIC, an improvement can be obtained in groundwater contamination vulnerability studies. The final groundwater vulnerability map can be used by water management authorities to support different actions, from improving the quality monitoring network to conducting more detailed studies in areas of high vulnerability in order to solve or mitigate sources of contamination.
The main requirement for the application of this methodology is the availability of data to train the models. DRASTIC parameters are usually available in open data sources, and the MLMapper code, in its first version, is also publicly available (https://www.ucm.es/hidrogeologia/programas-software, accessed on 12 July 2024). The computational requirements for the application of these methods are not particularly large, and, in addition, open-source libraries are available and can be run both in a local environment and in online environments via external servers. The computational time will depend on the size of the database, but for databases containing up to 1000 samples, the computational time should not exceed 20 min.
5. Conclusions
Groundwater faces the threat of contamination in many regions of the world. While spatially distributed methods have long since been used to determine the vulnerability to contamination of this valuable resource, traditional approaches suffered from shortcomings such as the reliance on static or semi-static variables and weights. The advent of machine learning techniques represents a major breakthrough in water science that can contribute to overcoming these limitations. This research demonstrates the ability of machine learning algorithms to update coefficients on a case-by-case basis, as well as to optimally incorporate site-specific considerations into vulnerability studies. Thus, we advocate the use of a wide range of tree-based algorithms to maximize the potential of artificial intelligence to unravel hidden patterns in complex datasets and, ultimately, enhance vulnerability maps.
Comparison of the maps obtained using the original DRASTIC method and the artificial intelligence-based method with the real nitrate data shows the improvement of using this methodology compared to a simpler approach. The relative weight of the factors has varied considerably from one approach to another, which shows the need to adjust traditional approaches to local contexts.
Author Contributions
Conceptualization, P.M.-S.; methodology, V.G.-E. and P.M.-S.; software, VGE. PMS; validation, V.G.-E. and P.M.-S.; formal analysis, V.G.-E.; investigation, V.G.-E. and P.M.-S.; resources, V.G.-E. and P.M.-S.; data curation, V.G.-E.; writing—original draft preparation, V.G.-E. and P.M.-S.; writing—review and editing, V.G.-E. and P.M.-S.; visualization, V.G.-E. and P.M.-S.; supervision, P.M.-S.; project administration, P.M.-S.; funding acquisition, P.M.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded under research grant PID2021-124018OB-I00 of Spain’s Ministry of Science, Innovation and Universities and the European project STARS4Water. The STARS4Water project received funding from the European Union’s Horizon Europe research and innovation program under Grant Agreement No. 101059372. The authors thank the Duero Basin Authority for kindly making available the data of the official monitoring network. We would also like to thank the reviewers for their comments and suggestions that have improved this work.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vrba, J.; Zaporožec, A. Guidebook on mapping groundwater vulnerability. In International Association of Hydrogeologists; Heise, H., Ed.; The International Association of Hydrogeologists: Hannover, Germany, 1994. [Google Scholar]
- Katyal, D.; Tomer, T.; Joshi, V. Recent trends in groundwater vulnerability assessment techniques: A review. Int. J. Appl. Res. 2017, 3, 646–655. [Google Scholar]
- Goyal, D.; Haritash, A.K.; Singh, S.K. A comprehensive review of groundwater vulnerability assessment using index-based, modelling, and coupling methods. J. Environ. Manag. 2021, 296, 113161. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, F.A.L.; Pires, L.M.G.R.; Santos, R.M.B.; Sanches-Fernandes, L.F. Factor weighting in DRASTIC modeling. Sci. Total Environ. 2015, 505, 474–486. [Google Scholar] [CrossRef] [PubMed]
- Fannakh, A.; Farsang, A. DRASTIC, GOD, and SI approaches for assessing groundwater vulnerability to pollution: A review. Environ. Sci. Eur. 2022, 34, 77. [Google Scholar] [CrossRef]
- Patel, P.; Mehta, D.; Sharma, N. A review on the application of the DRASTIC method in the assessment of groundwater vulnerability. Water Supply 2022, 22, 5190–5205. [Google Scholar] [CrossRef]
- Aller, L.; Lehr, J.H.; Petty, R.; Bennett, T. DRASTIC—A Standardized System to Evaluate Groundwater Pollution Potential Using Hydrogeologic Setting. J. Geol. Soc. India 1987, 29, 23–37. [Google Scholar]
- Civita, M. La valutazione della vulnerabilità degli acquiferi all’inquinamamento. In Atti 1° Conv. Naz. “Protezione e Gestione delle Acque Sotterranee: Metodologie, Tecnologie e Obiettivi”; IRIS: Marano sul Panaro, Italy, 1990; Volume 3, pp. 39–86. [Google Scholar]
- Hernández-Espriú, A.; Reyna-Gutiérrez, J.A.; Sánchez-León, E.; Cabral-Cano, E.; Carrera-Hernández, J.; Martínez-Santos, P.; Falorni, G.; Colombo, D. DRASTIC-Sg Model, a new extension to the DRASTIC approach for mapping groundwater vulnerability in aquifers subject to differential land subsidence. Application to Mexico City. Hydrogeol. J. 2014, 22, 1469–1485. [Google Scholar] [CrossRef]
- Kazakis, N.; Voudouris, K.S. Groundwater vulnerability and pollution risk assessment of porous aquifers to nitrate: Modifying the DRASTIC method using quantitative parameters. J. Hydrol. 2015, 525, 13–25. [Google Scholar] [CrossRef]
- Barbulescu, A. Assessing Groundwater Vulnerability: DRASTIC and DRASTIC-Like Methods: A Review. Water 2020, 12, 1356. [Google Scholar] [CrossRef]
- Albinet, M.; Margat, J. Cartographie de la vulnerabilité a la pollution des nappes d’eau souterraine. Bull. Bur. Rech. Géologiques Minières 1970, 3, 13–22. [Google Scholar]
- Khosravi, K.; Sartaj, M.; Tsai, F.T.C.; Singh, V.P.; Kazakis, N.; Melesse, A.M.; Prakash, I.; Bui, D.T.; Pham, B.T. A comparison study of DRASTIC methods with various objective methods for groundwater vulnerability assessment. Sci. Total Environ. 2018, 642, 1032–1049. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Alcaide, S.; Martínez-Santos, P. Review: Advances in groundwater potential mapping. Hydrogeol. J. 2019, 27, 2307–2324. [Google Scholar] [CrossRef]
- Moges, S.S.; Dinka, M.O. Assessment of groundwater vulnerability mapping methods for sustainable water resource management: An overview. J. Water Land Dev. 2022, 52, 186–198. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Venkatramanan, S.; Selvam, S.; Ahemd, H.A.; Seo, Y.K.; Bhuyan, M.S.; Yassin, M.A. Novel machine learning algorithms to predict the groundwater vulnerability index to nitrate pollution at two levels of modeling. Chemosphere 2023, 314, 137671. [Google Scholar] [CrossRef]
- Raisa, S.S.; Sarkar, S.K.; Sadiq, M.A. Advancing groundwater vulnerability assessment in Bangladesh: A compre-hensive machine learning approach. Groundw. Sustain. Dev. 2024, 25, 101128. [Google Scholar] [CrossRef]
- Abba, S.I.; Yassin, M.A.; Jibril, M.M.; Tawabini, B.; Soupios, P.; Khogali, A.; Shah, S.M.H.; Usman, J.; Aljundi, I.H. Nitrate concentrations tracking from multi-aquifer groundwater vulnerability zones: Insight from machine learning and spatial mapping. Process Saf. Environ. Prot. 2024, 184, 1143–1157. [Google Scholar] [CrossRef]
- Subbarayan, S.; Thiyagarajan, S.; Karuppanan, S.; Panneerselvam, B. Enhancing groundwater vulnerability assessment: Comparative study of three machine learning models and five classification schemes for Cuddalore district. Environ. Res. 2024, 242, 117769. [Google Scholar] [CrossRef]
- Gómez-Escalonilla, V.; Martínez-Santos, P.; Martín-Loeches, M. Preprocessing approaches in machine-learning-based groundwater potential mapping: An application to the Koulikoro and Bamako regions, Mali. Hydrol. Earth Syst. Sci. 2022, 26, 221–243. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Senapathi, V.; Sekar, S.; Lee, S.Y.; Roy, P.D.; Hassan, A.; Sabarathinam, C. Comparative study of machine learning models for evaluating groundwater vulnerability to nitrate contamination. Ecotoxicol. Environ. Saf. 2022, 229, 113061. [Google Scholar] [CrossRef]
- Khan, Q.; Liaqat, M.U.; Mohamed, M.M. A comparative assessment of modeling groundwater vulnerability using DRASTIC method from GIS and a novel classification method using machine learning classifiers. Geocarto Int. 2021, 37, 5832–5850. [Google Scholar] [CrossRef]
- Motlagh, Z.K.; Derakhshani, R.; Sayadi, M.H. Groundwater vulnerability assessment in central Iran: Integration of GIS-based DRASTIC model and a machine learning approach. Groundw. Sustain. Dev. 2023, 23, 101037. [Google Scholar] [CrossRef]
- Tachi, S.E.; Bouguerra, H.; Benaroussi, O. Assessing the Risk of Groundwater Pollution in Northern Algeria through the Evaluation of Influencing Parameters and Ensemble Methods. Dokl. Earth Sci. 2023, 513, 1233–1243. [Google Scholar] [CrossRef]
- MOPTMA-MINER. Libro Blanco de las Aguas Subterráneas; Ministerio de Obras Publicas, Transportes y Medio Ambiente: Madrid, Spain, 1994; p. 136. [Google Scholar]
- Sahun, B.; Gómez, J.J.; Lillo, J.; Olmo, P. Arsénico en aguas subterráneas e interacción agua-roca: Un ejemplo en la cuenca terciaria del Duero (Castilla y León, España). Rev. De La Soc. Geológica De España 2004, 17, 137–155. [Google Scholar]
- CHD. Plan Hidrológico de la parte española de la Demarcación Hidrográfica del Duero. In Revisión de Tercer Ciclo (2022–2027); Technical Report; Confederación Hidrográfica del Duero: Segovia, España, 2022; 276p. [Google Scholar]
- López-Geta, J.A.; Barrio, V.; Vega, L. Explotación de las aguas subterráneas en el Duero: Los retos de la cuenca. In Congreso Homenaje al Douro/Duero y sus ríos. Memoria, Cultura y Porvenir; Fundación Nueva Cultura del Agua: Zamora, Spain, 2006. [Google Scholar]
- Ministerio de la Presidencia, Relaciones con las Cortes y Memoria Demo-crática. MPRCMD Real Decreto 47/2022, de 18 de enero, sobre protección de las aguas contra la contaminación difusa producida por los nitratos procedentes de fuentes agrarias. Boletín Of. Del Estado 2022, 17, 5664–5684. [Google Scholar]
- Kotsiantis, S.; Kanellopoulos, D.; Pintelas, P. Handling imbalanced datasets: A review. GESTS Int. Trans-Actions Comput. Sci. Eng. 2006, 30, 25–36. [Google Scholar]
- Alam, F.; Rashid, U.; Shakeel, A.; Dar, F. A new model (DRASTIC-LU) for evaluating groundwater vulnerability in parts of central Ganga Plain, India. Arab. J. Geosci. 2021, 2, 7. [Google Scholar] [CrossRef]
- Farr, T.G.; Kobrick, M. Shuttle Radar Topography Mission produces a wealth of data. Eos Trans. Am. Geophys. Union 2000, 81, 583. [Google Scholar] [CrossRef]
- NASA Shuttle Radar Topography Mission (SRTM) Global. Digital Elevation Model Dataset. 2013. [CrossRef]
- Estrela, T.; Quintas, L. El sistema integrado de modelización Precipitación-Aportación SIMPA. Ing. Civ. 1996, 104, 43–52. [Google Scholar]
- MITECO Recarga de acuíferos anual (Media período 1940/41-2005/06); Modelo SIMPA; Ministerio para la Transición Ecológica: Madrid, Spain, 2015.
- CHD Mirame Duero. Online Utility. Confederación Hidrográfica del Duero. 2023. Available online: https://mirame.chduero.es/chduero/public/home (accessed on 6 June 2024).
- IGN Sistema de Ocupación del Suelo de España. Digital Cartography. 1:25,000; Instituto Geográfico Nacional: Madrid, Spain, 2014.
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. Mach Learn Python. 2011, 12, 2825–2830. [Google Scholar]
- Díaz-Alcaide, S.; Martínez-Santos, P. Mapping fecal pollution in rural groundwater supplies by means of artificial intelligence classifiers. J. Hydrol. 2019, 577, 124006. [Google Scholar] [CrossRef]
- Haggerty, R.; Sun, J.; Yu, H.; Li, Y. Application of machine learning in groundwater quality modeling-A comprehensive review. Water Res. 2023, 233, 119745. [Google Scholar] [CrossRef] [PubMed]
- Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef]
- Podgorski, J.; Wu, R.; Chakravorty, B.; Polya, D.A. Groundwater arsenic distribution in India by machine learning geospatial modeling. Int. J. Environ. Res. Public Health 2020, 17, 7119. [Google Scholar] [CrossRef]
- Cardenas-Martinez, A.; Rodriguez-Galiano, V.; Luque-Espinar, J.A.; Mendes, M.P. Predictive modelling benchmark of nitrate Vulnerable Zones at a regional scale based on Machine learning and remote sensing. J. Hydrol. 2021, 603, 127092. [Google Scholar] [CrossRef]
- Podgorski, J.; Araya, D.; Berg, M. Geogenic manganese and iron in groundwater of Southeast Asia and Bangladesh–machine learning spatial prediction modeling and comparison with arsenic. Sci. Total Environ. 2022, 833, 155131. [Google Scholar] [CrossRef]
- Gómez-Escalonilla, V. Metodologías de Aprendizaje Automático para la Optimización de Campañas de Prospección Hidrogeológica y Mejora del Acceso al Agua en el Sahel. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2024; 376p. [Google Scholar]
- Zaresefat, M.; Derakhshani, R. Revolutionizing groundwater management with hybrid AI models: A practical review. Water 2023, 15, 1750. [Google Scholar] [CrossRef]
- Guo, X.; Luo, J.; Lu, W.; Dong, G.; Pan, Z. Optimal design of groundwater pollution monitoring network based on a back-propagation neural network surrogate model and grey wolf optimizer algorithm under uncertainty. Environ. Monit. Assess. 2024, 196, 132. [Google Scholar] [CrossRef]
- Trabelsi, F.; Bel Hadj Ali, S. Exploring machine learning models in predicting irrigation groundwater quality indices for effective decision making in Medjerda River Basin, Tunisia. Sustain. 2022, 14, 2341. [Google Scholar] [CrossRef]
- Khan, J.; Lee, E.; Balobaid, A.S.; Kim, K. A comprehensive review of conventional, machine leaning, and deep learning models for groundwater level (GWL) forecasting. Appl. Sci. 2023, 13, 2743. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).