1. Introduction
The National Water Model (NWM) is a hydrologic modeling framework that simulates and forecasts water flow over the continental United States [
1]. It provides useful information for water-resource management, flood prediction, and drought monitoring. Although the NWM excels in many inland areas, its hydrological code base lacks a direct connection to coastal water dynamics. This limitation is particularly evident in coastal regions where tidal and surge processes affect river discharge and storage. The absence of these coastal influences in the model may affect predictions of backwater effects, altering flow dynamics in a river’s lower reaches and impacting lateral flood processes and ultimate discharge [
2].
The latest operational implementation of the NWM (version 3.0) has made strides in addressing this limitation by coupling it to a hydrodynamic ocean model, the Semi-implicit Cross-scale Hydroscience Integrated System Model (SCHISM), to provide total water-level predictions [
3]. This one-way coupling represents an advancement where the NWM provides the SCHISM with upstream boundary conditions, driving the SCHISM to predict total water levels in coastal areas. However, this coupling is unidirectional—the hydrological component of the NWM does not receive updates from the SCHISM. In other words, there is no feedback mechanism from the SCHISM to the NWM to improve discharge or streamflow modeling and forecasting. The interaction between the NWM and the SCHISM remains one-way. This one-way coupling approach is common in most current hydrological–hydrodynamic model integrations. For instance, the ADCIRC Surge Guidance System (ASGS-STORM) [
4] and the coupling between the NWM, Advanced CIRCulation (ADCIRC), and WAVEWATCH III for the Delaware River Basin [
5] both employ similar one-way strategies.
The one-way coupling’s lack of feedback limits the NWM as it does not incorporate coastal processes to update the NWM’s streamflow modeling. A two-way coupling between the NWM and coastal hydrodynamic models like the SCHISM would offer benefits that extend far beyond merely improving the NWM’s streamflow predictions. Feedback from the SCHISM to the NWM’s streamflow calculations is important because the NWM’s streamflow serves as the foundation for numerous subproducts and downstream applications [
6,
7]. This improved streamflow modeling enhances soil moisture and groundwater representation in coastal areas, providing a more accurate picture of subsurface hydrology influenced by tidal and storm surge effects [
8,
9,
10,
11,
12]. It leads to more reliable long-term water-balance calculations and seasonal to subseasonal forecasting capabilities, offering valuable insights for water-resource planning and management [
12,
13]. The coupling allows for a more precise simulation of floodplain dynamics for flood-risk assessments in coastal regions [
5,
14,
15,
16]. By ensuring more accurate initial conditions for each forecast cycle, the model provides more reliable short-term predictions, which are vital for flood warning systems and emergency responses [
13]. Furthermore, improved streamflow data enhance water-quality modeling throughout the watershed, supporting ecosystem management efforts and pollution-control strategies [
6]. These wide-ranging improvements stem from the more accurate streamflow predictions and collectively lead to a more comprehensive understanding of coastal–riverine interactions, advancing the ability to manage water resources and predict hydrological events in these complex and vulnerable environments [
14,
17].
In this research, we aimed to design and implement a two-way coupling method between the NWM and the SCHISM. In this approach, the NWM would continue to drive the SCHISM, with the upstream streamflow as a boundary condition. The SCHISM’s total water modeling results would then be fed back to update the streamflow predictions in the NWM, creating a more comprehensive and dynamic modeling system.
This paper examines the gains in the NWM’s streamflow modeling accuracy and reliability resulting from this two-way coupling. We analyze how incorporating coastal influences improved predictions in various scenarios, including during storm events and tidal extremes. This analysis provides valuable insights into the benefits of integrated coastal–riverine modeling for water-resource management and flood predictions in coastal regions.
2. Methods
2.1. NWM–SCHISM Coupling
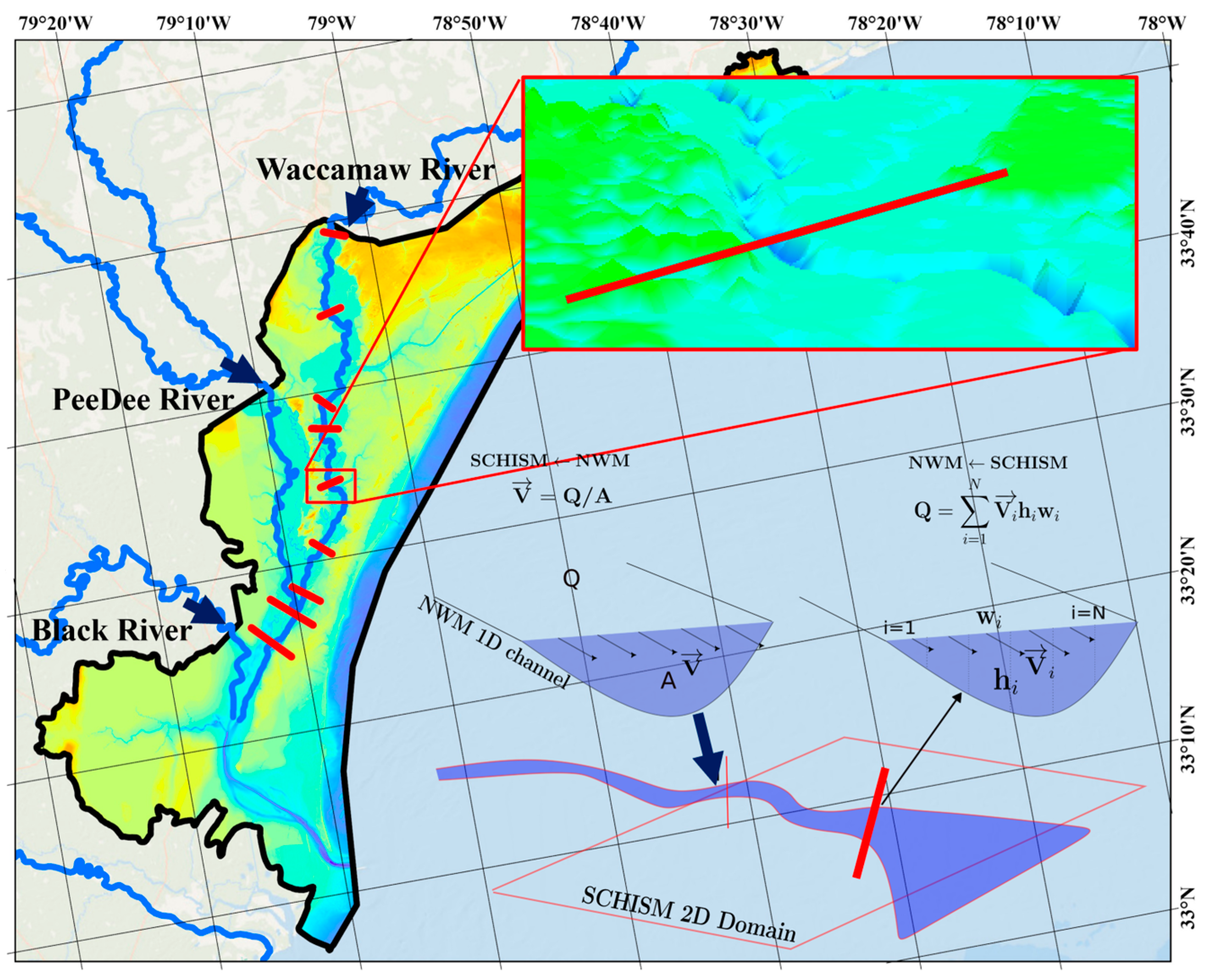
The two-way coupling between the NWM and the SCHISM was implemented through an iterative exchange of data, focusing on the conversion between discharge (Q) and velocity (V) at the interface of the two models (
Figure 1).
NWM to SCHISM (SCHISM ← NWM): The NWM computed the river discharge () for its one-dimensional channel. This discharge was then converted to velocity () for the SCHISM using the equation , where is the cross-sectional area of the channel at the boundary between the NWM and SCHISM domains.
SCHISM simulation: The SCHISM used the velocity input from the NWM as its upstream boundary condition and simulated water levels and velocities across its two-dimensional coastal domain.
SCHISM to NWM (NWM ← SCHISM): To feed information back to the NWM, the SCHISM’s 2D velocity field was converted back to a discharge value. This was performed by integrating the velocity across the bathymetry-defined cross-section of the SCHISM domain using the equation , where is the velocity, is the water depth, and is the width of each segment along the cross-section.
NWM update: The NWM then used this integrated discharge value from the SCHISM to update its flow calculations for the next time step.
The locations of the SCHISM-calculated discharge and the NWM channel nodes did not necessarily coincide as they were based on different spatial discretization methods. To address this spatial mismatch, a weighting coefficient, denoted as , was introduced. If the distance between the SCHISM discharge location and the NWM channel node was less than the specified radius , then the weighting coefficient was calculated as . Otherwise, the weighting coefficient was set to 0. In order to ensure smooth coupling, was set as 1000 m to include a few links nearby.
The weighting coefficient allowed for a smooth transition of the SCHISM-calculated discharge values to the NWM channel nodes based on their spatial proximity. This helped to mitigate potential discontinuities from differences in the spatial discretization between the models. By applying the weighting, the SCHISM feedback to the NWM channel was more seamless and reflected the underlying spatial relationships, potentially improving the overall model performance and consistency. However, in cases where the high-resolution SCHISM simulation had grid locations that matched the NWM channel nodes, the calculated discharge from the SCHISM could directly be used as the input to the NWM without the need for the weighting coefficient.
This process was repeated for each time step of the simulation, allowing for dynamic feedback between the inland river model (the NWM) and the coastal hydrodynamic model (the SCHISM). This two-way coupling enabled a more comprehensive representation of the interactions between riverine and coastal processes, particularly in areas where tidal influences and storm surges affected river discharge.
The two-way coupling method between the NWM and the SCHISM was implemented and tested using the CoastalApp framework. CoastalApp [
18] is a comprehensive modeling framework designed for coastal applications and regional forecasts, built upon the Earth System Modeling Framework (ESMF) [
19] to facilitate the coupling of various earth system model components to integrate coastal-zone simulations. This iterative coupling process focuses on the conversion between discharge (
) and velocity (
) at the interface of the two models, leveraging the Coastal App’s capabilities to integrate different environmental modeling components.
2.2. Study Area, Flood Events, and Model Set-Up
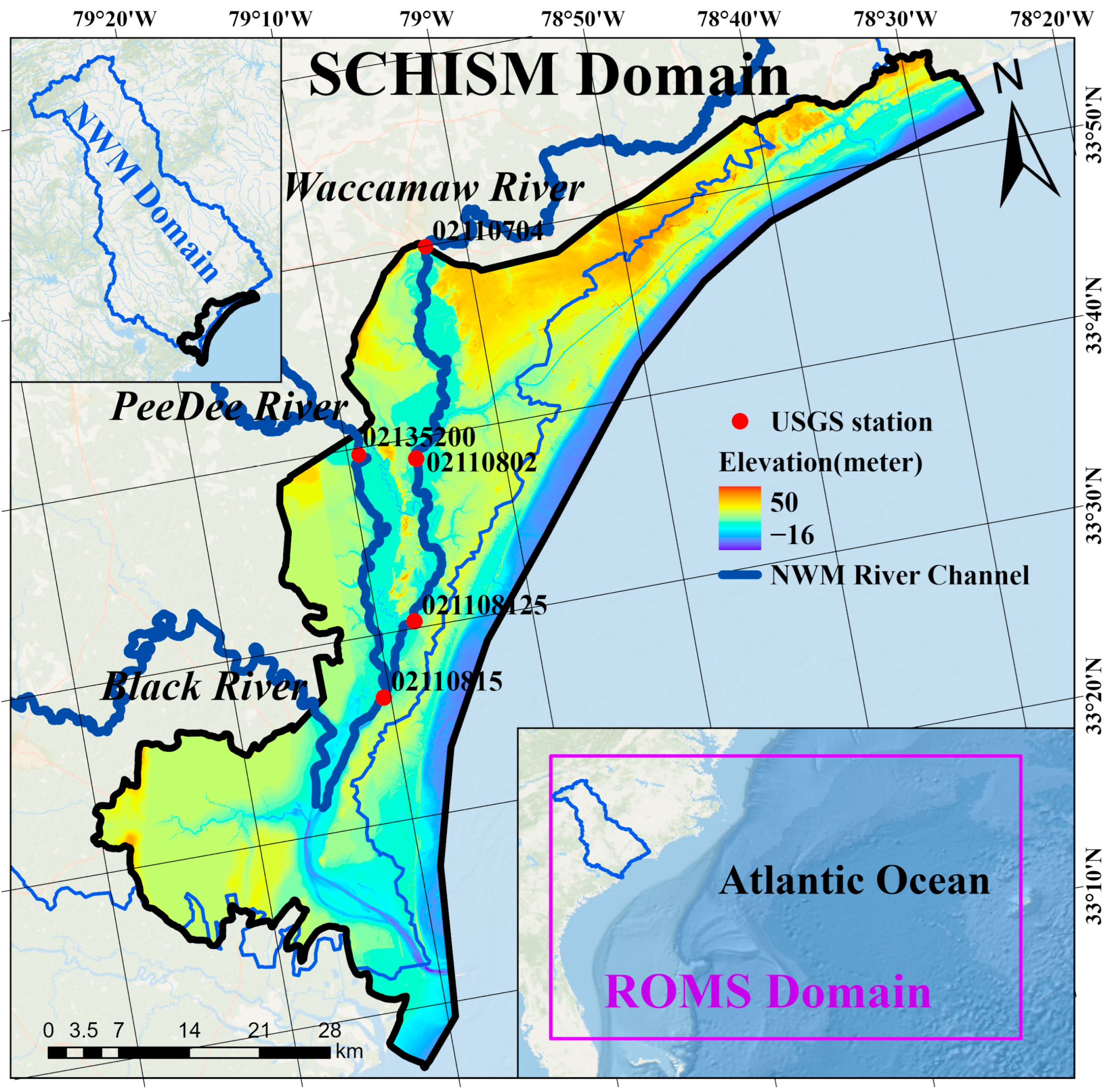
This study encompassed three distinct model domains, each serving a specific purpose in the coupled modeling system (
Figure 2). The SCHISM domain covered the northeastern coast of South Carolina, including three major rivers that flow into the Atlantic Ocean. This area, part of the South Carolina coastal plain, is frequently affected by hurricanes and storms.
The NWM domain extended to the entire Pee Dee watershed. This broader coverage was necessary to accurately simulate discharge in the lower reaches as it was influenced by upstream hydrological conditions. As illustrated in
Figure 2, the NWM domain overlapped the SCHISM domain, establishing the region where the model coupling occurred.
The Regional Oceanic Modeling System (ROMS) [
20]—a free-surface, terrainfollowing, primitive equation ocean model—is used to simulate oceanographic conditions in the northwestern Atlantic Ocean Basin offshore of the southeast U.S. coast. It provides downstream boundary conditions of water levels to the SCHISM to accurately represent tidal and surge effects in the coastal regions.
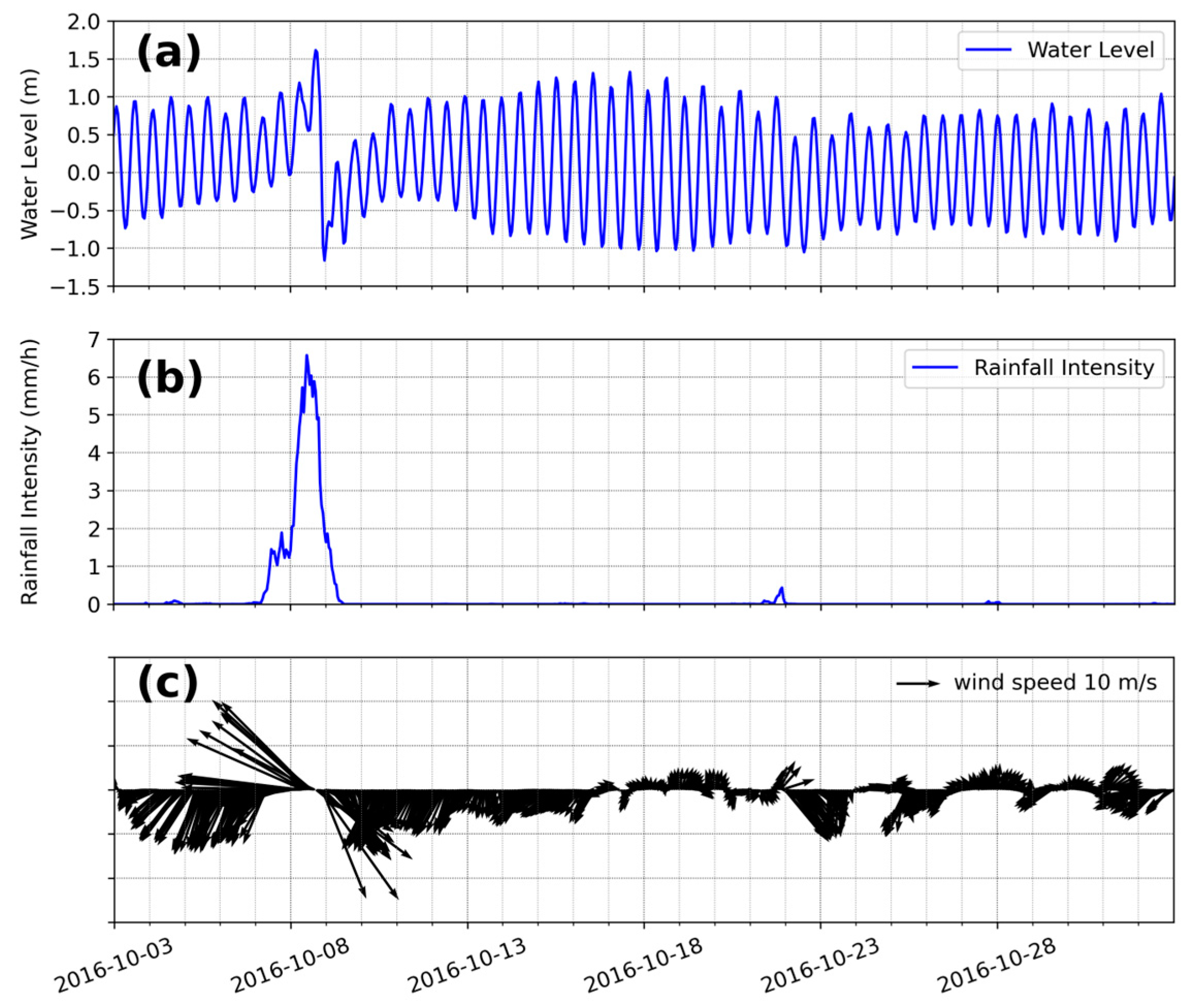
Hurricane Matthew, which made landfall in South Carolina on 8 October 2016, was selected as the case study to test the coupled model. From 7 October to 8 October, strong onshore winds drove storm surges into coastal areas. Subsequently, the wind direction shifted, causing offshore flow and lower water levels (negative storm surges) from 8 October to 9 October. Concurrently, heavy rainfall from 1 mm/h to 6 mm/h over 2 days led to severe inland flooding (
Figure 3). This combination of storm surge inundation and inland flooding damaged over 1 million structures, with estimated costs reaching approximately USD 10.3 billion [
21].
This extreme event provided an ideal scenario to evaluate the performance of the coupled modeling system in simulating complex coastal–riverine interactions during severe weather conditions.
This larger-scale ocean model operated at a temporal resolution of 30 s. The zonal and meridional spatial resolutions ranged from 2.70 to 8.69 km and 1.83 to 4.47 km, respectively.
The ROMS simulations were driven by atmospheric forcing data from NCEP CFSR [
22] and CFSv2 [
23] and included the longwave radiation, shortwave radiation, air pressure at the mean sea-surface level, air temperature at a 2 m height above the sea surface, relative humidity at a 2 m height above the sea surface, and a 10 m height wind. TPXO9 [
24] data were used as the tidal forcing data in the ROMS. Daily Copernicus Marine Environment Monitoring Service (CMEMS) Global Ocean Physics Reanalysis (GOPR) data [
25], with a spatial resolution of 1/12 degree, including the water temperature, salinity, current, and free-sea-surface level, were used to initialize the ROMS. The ROMS boundary schemes included the Chapman boundary condition for a free-sea-surface, the radiation lateral boundary condition for three-dimensional variables, and the Flather boundary condition [
26] for two-dimensional variables. The generic length scale turbulence closure scheme was used for the water mixing. The ROMS simulations were for the period from 1 September to 30 November 2016, fully encompassing the study period. Key outputs from the ROMS, the water levels, were used to force the open boundary of the SCHISM through a one-way coupling approach. This integration of the ROMS into the modeling framework was essential to capture the large-scale oceanic influences on the coastal study area, ensuring that the SCHISM accurately represented the complex interactions between offshore conditions and nearshore processes during extreme events like Hurricane Matthew.
A detailed model set-up is shown in
Table 1.
2.3. Experimental Design
The following three experiments were designed to test and validate the coupling method (
Table 2):
EXP1: two-way coupling between the SCHISM and the NWM, with the NWM providing upstream boundary conditions;
EXP2: no-coupled validation, with the SCHISM using USGS-observed discharge as upstream boundary conditions;
EXP3: one-way coupling from the NWM to the SCHISM, without feedback from the SCHISM to the NWM.
EXP1 represented the two-way coupling method where the NWM was updated with feedback from the SCHISM. EXP2 depicted the no-coupled validation. EXP3 served as a baseline, representing the one-way coupling method where the NWM operated without updates from the SCHISM.
In EXP1, the NWM provided the upstream boundary conditions, demonstrating the model’s performance under typical operational conditions. EXP2 used USGS-observed discharge data for upstream boundary conditions. This experiment served two purposes: it allowed for a model validation using reliable observational data and it provided a method to assess the model performance when given accurate input data, which was crucial when the NWM data might not have been sufficiently accurate.
The simulation period spanned from 1 September to 10 November, 2016. This timeframe encompassed the flood hydrograph duration of Hurricane Matthew as well as a “spin-up” period to ensure model stability prior to a flood event. The Manning roughness coefficient was set as 0.025 in the SCHISM. This value is used for flood plains with short grass [
27].
The results from these experiments were analyzed as follows:
EXP2 was primarily used for the model validation. The simulated water levels from the SCHISM were compared with the observed water levels to demonstrate the model’s robustness and accuracy when provided with reliable input data.
The streamflow results from EXP1 (two-way coupling) and EXP3 (one-way coupling) were compared to illustrate the benefits of the two-way coupling method. This comparison directly addressed the main objective of the study, demonstrating how the feedback mechanism improved the NWM’s performance in coastal regions.
These experiments and subsequent analyses provided comprehensive insights into the effectiveness of and potential improvements offered by the two-way coupling method in coastal hydrological modeling.
3. Results
3.1. Model Validation
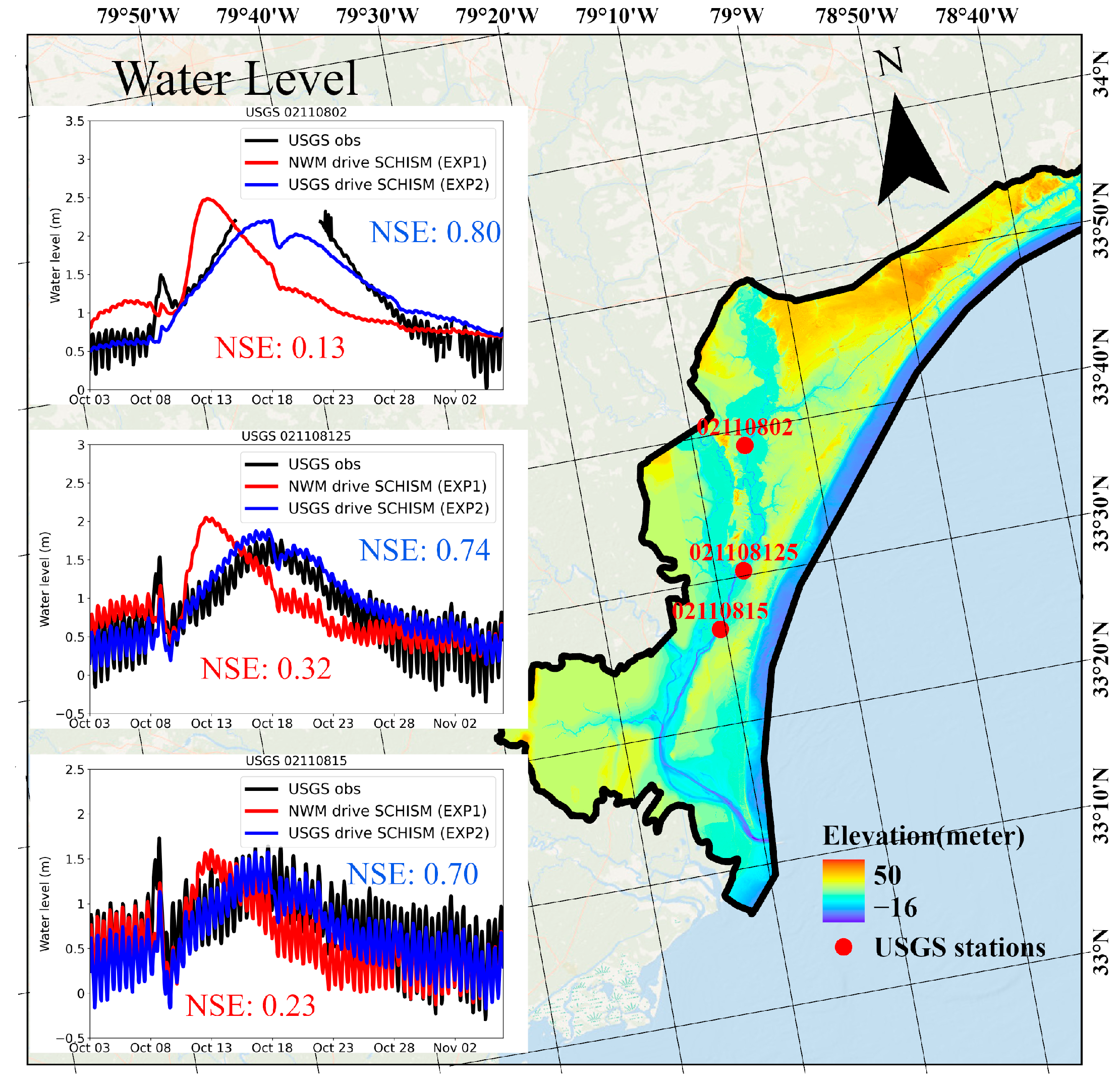
The SCHISM domain contained three water-level observation stations (as shown in
Figure 4), providing data for the model validation. However, no discharge observations were available within the domain, limiting the validation to water-level comparisons.
Given the data availability, we focused on validating the water levels in the coupled model runs. The primary goal of this validation was to establish confidence in the SCHISM simulations, which was essential for the credibility of the coupled modeling approach.
Experiment 2 (EXP2), driven by observed discharge at the three river inputs, was more suitable for validation purposes. In contrast, Experiment 1 (EXP1), driven by the NWM forecasts, introduced additional uncertainties that could complicate the validation process.
Figure 4 illustrates the comparison between the simulated water levels from EXP2 and the observed water levels. The results showed good agreement, with Nash–Sutcliffe efficiency (NSE) scores ranging from 0.70 to 0.80 across the observation stations. This strong performance built confidence in the SCHISM’s ability to accurately simulate coastal hydrodynamics when provided with reliable boundary conditions.
Overall, the peak water levels from the SCHISM matched well with the USGS observations. A 2 h timing bias existed in the current simulation results. This bias is not discernible in
Figure 4, but a closer examination of the data revealed it. According to the USGS observations, the peak water level caused by the storm surge occurred on 8 October at 17:00 UTC, 18:00 UTC, and 21:00 UTC for stations 02110815, 021108125, and 02110802, respectively. The SCHISM recorded the peak water level caused by the storm surge on 8 October at 19:00 UTC, 20:00 UTC, and 23:00 UTC for stations 02110815, 021108125, and 02110802, respectively. For the peak water level caused by upstream discharge, the USGS observations recorded peaks on 17 October at 15:00 UTC and 16:00 UTC for stations 02110815 and 021108125, respectively. The observation from station 02110802 during the peak water-level period was missing. According to the SCHISM results, the peak water levels at stations 02110815 and 021108125 occurred on 17 October at 17:00 UTC for both stations. The timing bias was within 2 h.
It is noteworthy that when the NWM forecasts were used as boundary conditions (EXP1), larger biases were observed in the water-level predictions. However, addressing these biases was beyond the scope of this study. The objective was to improve the NWM by incorporating ocean processes such as surges and tides, rather than correcting model deficiencies caused by upstream forecast inaccuracies.
This validation demonstrated that when the upstream boundary conditions were accurate, the coupled model performed well in simulating coastal water levels. This gave us confidence in using the model to study the impacts of incorporating oceanic processes into the NWM, even if the absolute accuracy of the predictions was limited by the quality of the NWM’s upstream forecasts.
3.2. Model Results
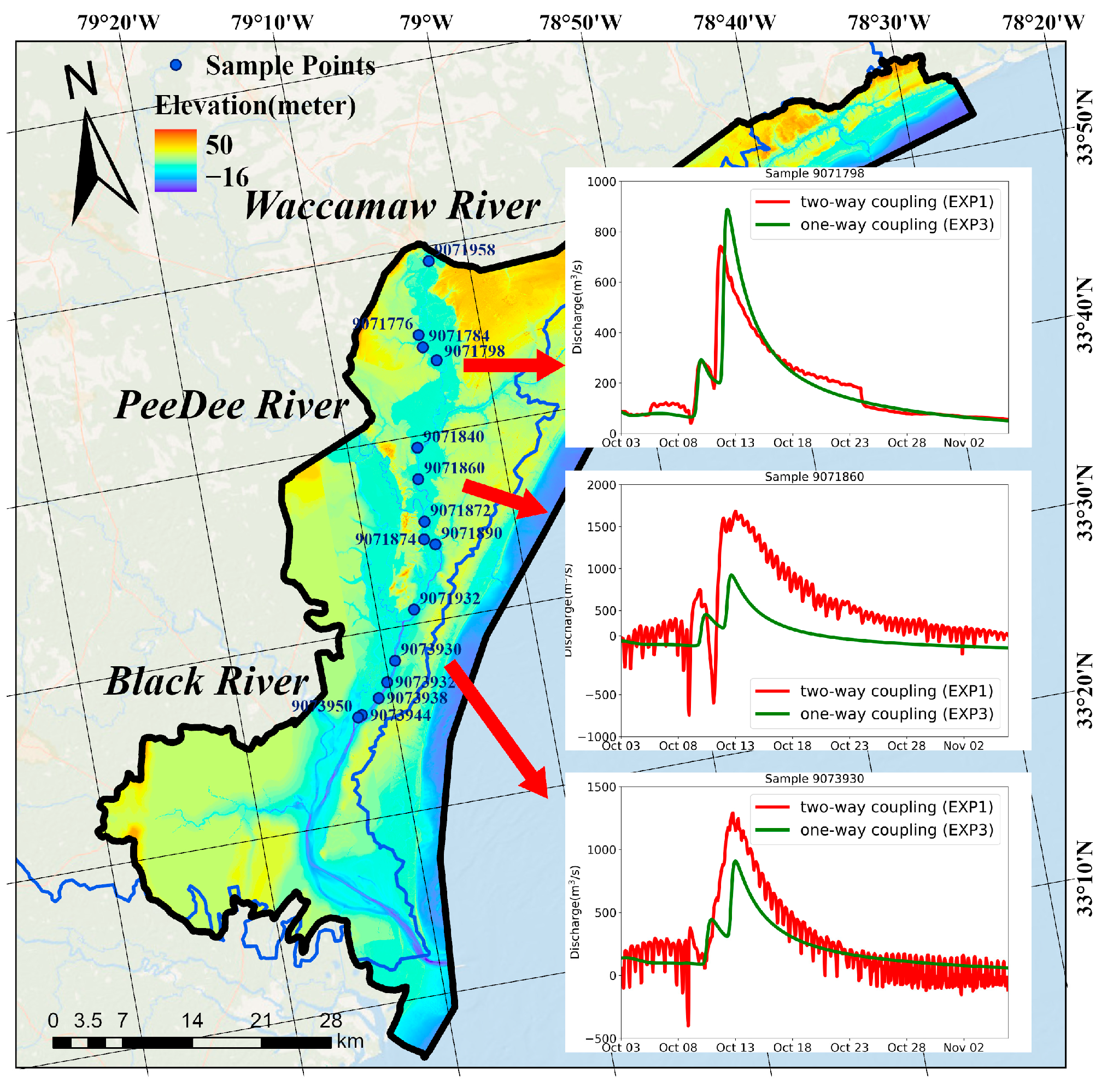
The two-way coupling between the NWM and the SCHISM showed improvements in modeling coastal river dynamics, particularly during extreme events like Hurricane Matthew. We compared the results from EXP1 (two-way coupling) with EXP3 (one-way coupling) to highlight these improvements (
Figure 5).
Tidal influence on river discharge: The coupled model successfully introduced tidal oscillations in river discharge, which were absent in the one-way-coupled NWM results. These oscillations decreased in amplitude moving upstream, accurately representing the spatial extent of the tidal influence. This attenuation of the tidal signal demonstrated the transition from coastal process dominance near the estuary to inland river system dominance further upstream. The performance of the coupled model reflected these changing dominant factors from estuary to inland regions.
Storm surge effects: EXP1 captured the storm surge impacts on river discharge, including flow reversals and backwater effects. Notably, backflows were observed at sampling points 9071860 and 9073930, with discharges of −213.8 m3/s and −399.4 m3/s, respectively, immediately following the storm surge on 8 October. This timing closely corresponded with the observed wind shift and water-level changes during Hurricane Matthew’s passage, demonstrating the model’s ability to capture the temporal relationship between meteorological forcing and the hydrological response. The one-way-coupled NWM (EXP3) could not represent these phenomena, showing only a positive discharge throughout the event.
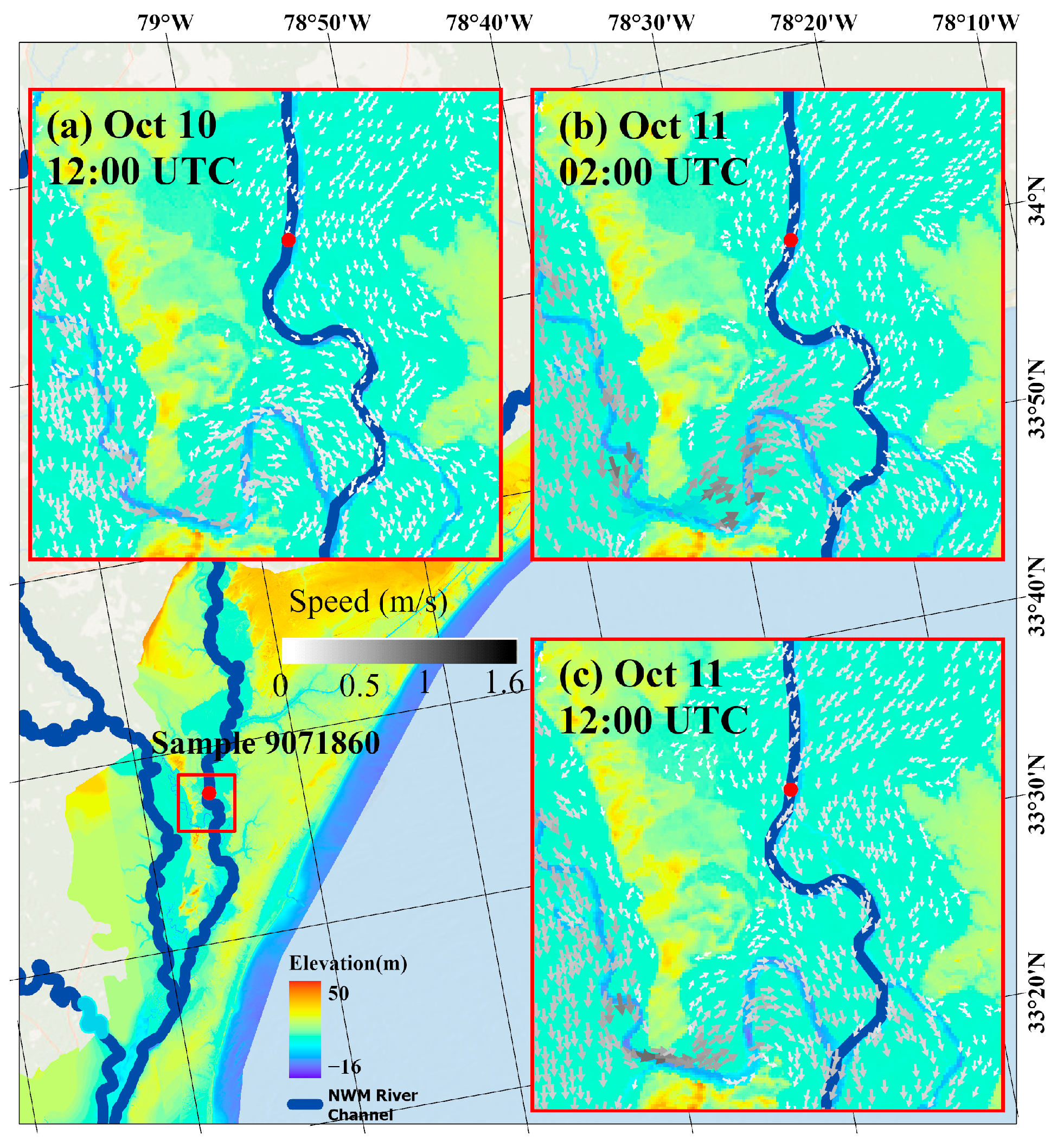
River–river interactions:
Figure 6 illustrates an important observation—the coupled model revealed complex interactions between the Pee Dee and Waccamaw Rivers not captured by the NWM. A small connecting branch, visible in the SCHISM’s high-resolution modeling, could alter the flow dynamics during flood events as follows:
- (a)
Under normal conditions (10 October, 12:00 UTC): the branch simply merged with the Waccamaw River;
- (b)
During peak flooding (11 October, 02:00 UTC): intense flow through this branch reversed the Waccamaw River flow, causing a backwater effect;
- (c)
Post-flood peak (11 October, 12:00 UTC): the flow patterns began to normalize. This phenomenon demonstrated the model’s ability to capture nuanced hydrodynamics for accurate flood prediction.
Timing and magnitude of peak discharge: The coupled model showed marked differences in the timing and magnitude of peak discharge compared with the one-way-coupled NWM. For example, at sampling point 9071860, EXP1 showed a peak discharge of 1683.1 m3/s on 13 October at 00:00, while EXP3 predicted 921.1 m3/s on 12 October at 15:00. Notably, the coupled model consistently showed higher discharge peaks at the two near-coast locations. This difference likely stemmed from the limitations of the NWM’s idealized 1D channel representation with predefined widths, which may have underestimated the discharge in coastal areas where the rivers widened into deltas. The SCHISM’s use of realistic bathymetry allowed for a more accurate representation of these widened channels and complex flows near the coast, capturing the flood dynamics that the simplified NWM structure might miss.
Water storage and release: EXP1 demonstrated an improved representation of temporary water storage in the coastal floodplain and its subsequent release. For instance, in EXP3 (one-way coupling), we observed a consistent propagation of peak discharge of 921.1 m3/s at point 9071860 and 908.9 m3/s at point 9073930. This represented only a 1% change in peak discharge between these two points. In contrast, EXP1 (two-way coupling) showed a significant reduction in peak discharge of 1683.1 m3/s at point 9071860 and 1289.3 m3/s at point 9073930. This represented a 23% decrease in peak discharge. This substantial decrease in peak discharge in EXP1 could be attributed to lateral flooding in the coastal floodplains. As a flood wave propagates downstream, a significant portion of the water is stored in these flat, low-lying areas adjacent to the main channel. The one-way-coupled model (EXP3) failed to adequately capture this process. The NWM used in EXP3 employed idealized river channels that did not account for the complex topography and storage capacity of coastal floodplains. As a result, it showed almost no change in peak discharge between the two points.
Spatial variations in coupling effects: The impact of coupling varies spatially, reflecting the transition from coastal to inland dominance. Upstream locations like point 9071798 showed similar flow patterns between EXP1 and EXP3, especially in terms of tide and storm surge signals related to backwater effects, indicating minimal coastal influence. However, the midstream (9071860) and downstream (9073930) points exhibited considerable differences, underscoring the importance of coupling in coastal regions where tidal and surge effects interact with riverine processes.
These results demonstrated that the two-way-coupled model captured complex coastal–riverine interactions that may improve flood forecasting, which are missed by traditional one-way-coupled or uncoupled hydrological models. The ability to represent phenomena like river–river interactions, tidal influences, and storm surge effects as well as the more realistic representation of coastal river morphology could enhance the capacity to model and predict coastal flooding events. This improved representation is particularly important in transitional zones where coastal and inland processes interact, offering a more nuanced and accurate picture of hydrodynamics during extreme events.
4. Discussion
The two-way coupling approach in this study represents an advancement of traditional one-way coupling methods. By allowing feedback from the coastal model (SCHISM) to the hydrological model (NWM), we captured complex interactions that may be typically overlooked in one-way coupling. This bidirectional exchange of information enabled the model to represent phenomena such as backwater effects, flow reversals, and the intricate interplay between tidal influences and river discharge. These improvements extend beyond merely enhancing hydrograph predictions; they provide a more comprehensive understanding of coastal hydrodynamics that can impact decision-making during extreme events.
The modeling capabilities offered by this two-way coupling approach have potential implications for coastal management and disaster responses. During extreme events like hurricanes, the improved representation of storm surge effects on inland water bodies can lead to more accurate flood forecasts, potentially saving lives and property. Moreover, the model’s ability to capture complex river–river interactions and tidal influences could inform long-term infrastructure planning, helping to design more resilient coastal communities. The detailed insights provided by this coupled model could also enhance ecological management strategies in coastal wetlands and estuaries where the balance between freshwater and saltwater intrusion is important.
Looking ahead, there are several promising directions for future research and applications of this coupled model. One area for improvement is the incorporation of more complex coastal processes such as sediment transport and coastal erosion. These processes affect long-term coastal evolution and could further enhance the model’s predictive capabilities. Additionally, exploring the integration of wave models could provide a more complete picture of coastal dynamics during storm events.
The potential applications of this coupled model extend to various coastal settings worldwide. For instance, it could be adapted to study the impacts of sea-level rise on deltaic regions where the interaction between river discharge and tidal influences is particularly complex. In urbanized coastal areas, the model could be used to assess the combined effects of land subsidence and changing hydrological patterns on flood risks. Furthermore, in regions with extensive coastal wetlands, this model could help to predict how changes in freshwater input and tidal regimes might affect ecosystem health and biodiversity.
Despite these advancements and promising future applications, the two-way coupling approach is not without its challenges. These challenges stem from fundamental differences in how hydrological and hydraulic models represent physical processes and variables as well as the computational complexities introduced by more detailed bidirectional data exchanges [
28,
29,
30].
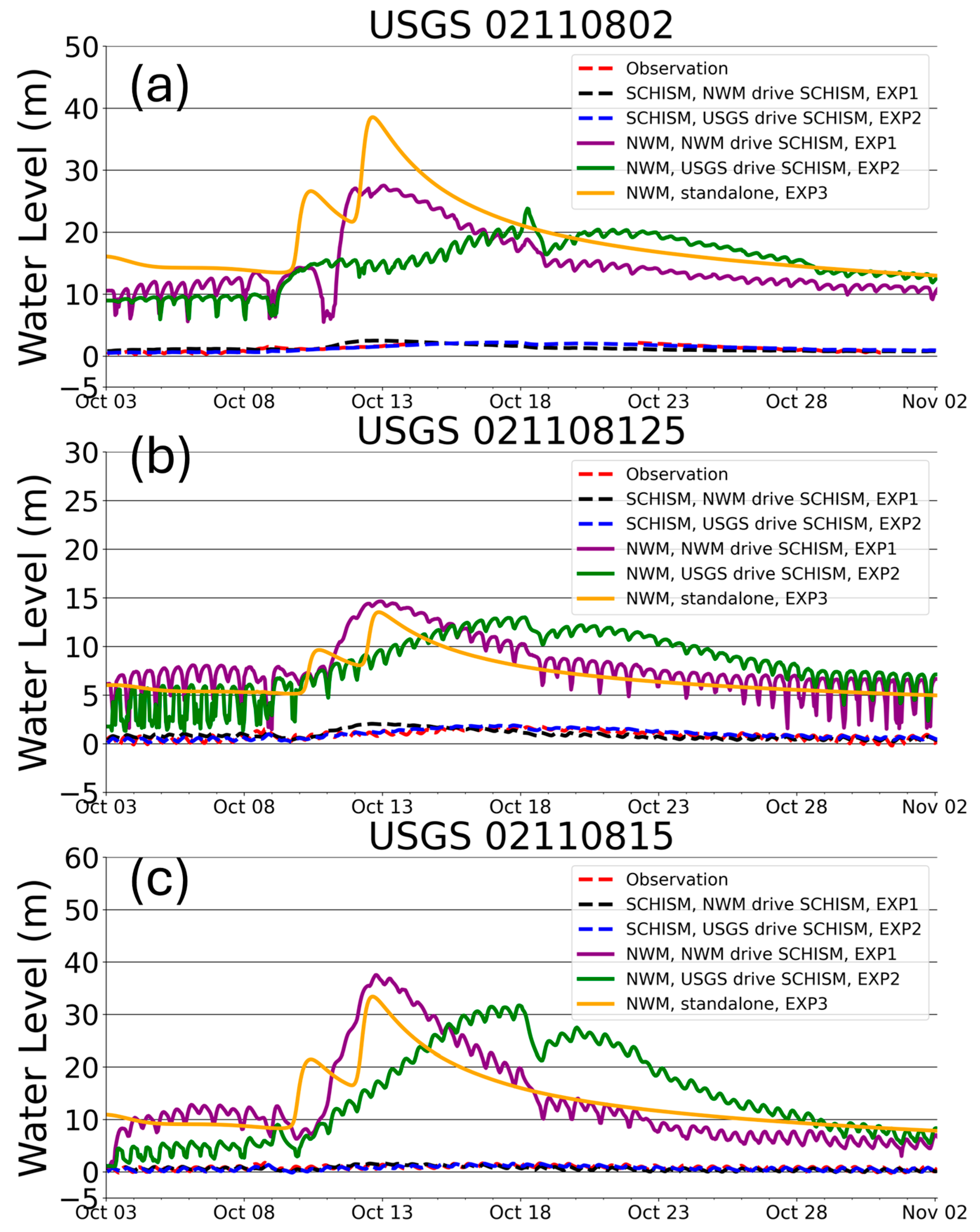
A critical barrier we identified in coastal model coupling—and more broadly, in hydrological and hydraulic model coupling—was the dissimilarity in variables between different types of models. Despite representing the same physical concept, variables such as water depth can exhibit significant differences in magnitude and timing between the NWM and the SCHISM, even for small natural events. This dissimilarity is evident in
Figure 7, which shows the discrepancies in water-level calculations between the two models, and represents a barrier in the two-way coupling of these models. Although the SCHISM’s water levels aligned better with the observed water levels, exhibiting smaller oscillations, the NWM’s water levels differed. The water level in the NWM was the sum of the variable “head” (the water depth above the river channel bottom) and the elevation from the input dataset [
1].
This dissimilarity arises from the different approaches used by the models. The NWM relies on an idealized trapezoidal river channel described by parameters, which simplifies calculations but fails to capture the complex coastal morphology. In contrast, the SCHISM hydraulic model provides a more detailed representation of water flows, leading to a more accurate depiction of water-level dynamics [
31].
The conflicts in the changing and timing of variables between the models can cause mismatches in the data exchange during the coupling process. This variable dissimilarity, even for small natural events, is a critical barrier in the two-way coupling of hydrological and hydraulic models.
To address this challenge, there is a need to improve the integration of a complex coastal morphology in hydrological models and standardize variable definitions and calculations across different modeling approaches. This would facilitate a more seamless coupling and enhance the accuracy of the integrated coastal–hydrological modeling system.
The enhanced ability of hydraulic models like the SCHISM to represent detailed water flows suggests that traditional hydrological models may benefit from adaptation for certain applications, particularly in complex coastal environments. This observation points to a need to develop hydrological models that can incorporate the level of detail provided by modern 2D and 3D datasets.
Moving forward, the focus should be on developing hydrological models capable of utilizing high-resolution multidimensional datasets. There is also a pressing need to improve the integration of complex coastal morphology in hydrological models. Standardizing variable definitions and calculations across hydrological and hydraulic models could facilitate a more seamless coupling.
In conclusion, the coupling of hydrological and hydraulic models represents a step forward in improving the understanding and prediction of coastal hydrodynamics. However, the path to fully integrated seamless coupling is still fraught with challenges. Addressing these issues requires interdisciplinary collaborations and innovative approaches to model development and data integration. As we continue to refine these coupled models, we move closer to more accurate and comprehensive representations of complex coastal systems, ultimately enhancing the ability to manage and respond to coastal hydrological events.
The study’s findings on the variable dissimilarity between the 1D NWM and the 2D SCHISM have implications for the development of the Next-Generation National Water Model. As the hydrological community moves towards more integrated modeling frameworks such as the Community NextGen Water Resources Modeling Framework, the challenges we encountered in reconciling different variable representations become increasingly relevant. The proposed shift from the Earth System Modeling Framework (ESMF) to a Basic Model Interface (BMI) for coastal coupling in the NextGen NWM requires innovative solutions to bridge the gap between inland hydrological models based on hydrofabrics and coastal hydrodynamic models operating on a 2D grid. The experience highlights the need for a sophisticated “mediator” rather than a simple variable-exchange coupler. This mediator must not only facilitate the data exchange but also accurately estimate missing quantities and maintain water and energy flux balances across disparate model domains. The insights gained from the two-way coupling approach can inform the development of such a mediator, potentially improving the Next-Gen NWM’s ability to seamlessly integrate coastal and inland water dynamics. This advancement is important to enhance the model’s predictive capabilities in coastal regions where the accurate representation of the complex interactions between riverine and coastal processes is vital for effective water management and hazard mitigation.
5. Conclusions
This study demonstrates the benefits and challenges of two-way coupling between the NWM and the Semi-implicit Cross-scale Hydroscience Integrated System Model (SCHISM) for coastal hydrological modeling. The approach addressed a gap in the NWM’s capabilities, allowing it to account for complex coastal processes that substantially impact river discharge and storage.
The two-way-coupled model successfully captured key phenomena that the one-way-coupled NWM missed, including tidal influences on river discharge, storm surge effects, flow reversals and backflows, and complex river–river interactions. However, due to the lack of direct discharge observations for a more comprehensive model validation, there was uncertainty regarding the accuracy of the current coupling results. Nevertheless, based on the water-level validation, the coupled model provided a more accurate timing and magnitude of peak discharge as well as an improved representation of water storage and release in coastal floodplains.
The coupling methodology successfully incorporated astronomical tidal and storm surge dynamics into the NWM. The case study showed that these integrated effects were extensively evident throughout the river system, demonstrating the value of this coupled approach for coastal hydrological forecasting.
However, establishing this two-way coupling presented several challenges. A key issue was determining which variable to use for the data exchange between the NWM and the SCHISM. Although the water level was common to both models, the variable dissimilarity made it unsuitable. We instead chose discharge, despite the SCHISM lacking a direct discharge output. This necessitated the development of an integration method using predefined cross-section data to calculate discharge from the SCHISM output.
The introduction of tide and surge signals into the NWM output highlighted the importance of modeling backflows in coastal regions. The two-way-coupled model showed an improvement in representing backflows caused by interactions between inland river systems and coastal processes. However, the Muskingum method used in the NWM for river channel routing has inherent weaknesses in handling backflows, indicating an area for future improvement.
Another challenge was the dissimilarity in the variable representation between the models, particularly in complex coastal environments. This stemmed from fundamental differences in how hydrological and hydraulic models conceptualize and calculate key variables. Addressing this issue would advance coastal hydrodynamic modeling, and represents an important direction for future research.
Despite these challenges, this study represents a step forward in extending the capabilities of large-scale hydrological models like the NWM to capture coastal influences. The improvements in modeling the tidal effects, storm surges, and river–river interactions have real-world implications for flood forecasting, coastal management, and disaster responses.
Looking ahead, there is the potential to build on this study by incorporating additional coastal processes like sediment transport and coastal erosion or adapting the model for different coastal settings. As climate change continues to impact coasts, tools like this are increasingly vital to understand and manage these dynamic environments.
In conclusion, although the two-way coupling approach represents important progress, it also illuminates the path ahead for coastal hydrological modeling. By continuing to refine these models and tackle the challenges of seamless integration, we move closer to a more comprehensive understanding of coastal and riverine systems.
The findings on the variable dissimilarity between the 1D NWM and the 2D SCHISM have potential implications for future coastal–riverine modeling efforts, particularly for the development of the Next-Generation National Water Model. The challenges we encountered underscore the need for innovative approaches in bridging inland and coastal hydrodynamics. As modeling frameworks evolve, this study highlights the importance of developing sophisticated mediators capable of reconciling disparate model domains and variable representations. These advancements are important to improve hydrological predictions in coastal regions, ultimately enhancing water management and hazard mitigation efforts.
Author Contributions
Conceptualization, S.B.; methodology, H.Z. and D.S.; software, H.Z. and D.S.; validation, H.Z. and D.S.; formal analysis, H.Z. and S.B.; investigation, H.Z., D.S. and S.B.; resources, H.Z. and D.S.; data curation, H.Z. and D.S.; writing—original draft preparation, H.Z.; writing—review and editing, S.B. and P.L.; visualization, H.Z.; supervision, S.B. and P.L.; project administration, S.B.; funding acquisition, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Oceanic and Atmospheric Administration (NOAA) awarded to the Cooperative Institute for Research on Hydrology (CIROH) through the NOAA Cooperative Agreement with The University of Alabama, NA22NWS4320003.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to acknowledge high-performance computing support from Cheyenne (doi:10.5065/D6RX99HX) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. Funding for this project was provided by the National Oceanic and Atmospheric Administration (NOAA), awarded to the Cooperative Institute for Research on Hydrology (CIROH) through the NOAA Cooperative Agreement with The University of Alabama, NA22NWS4320003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gochis, D.J.; Barlage, M.; Cabell, R.; Casali, M.; Dugger, A.; FitzGerald, K.; McAllister, M.; McCreight, J.; RafieeiNasab, A.; Read, L.; et al. WRF-Hydro Technical Description (V5.1.1). 2020. Available online: https://ral.ucar.edu/sites/default/files/public/projects/wrf_hydro/technical-description-user-guide/wrf-hydro-v5.1.1-technical-description.pdf (accessed on 3 September 2024).
- Pietrafesa, L.J.; Zhang, H.; Bao, S.; Gayes, P.T.; Hallstrom, J.O. Coastal Flooding and Inundation and Inland Flooding due to Downstream Blocking. J. Mar. Sci. Eng. 2019, 7, 336. [Google Scholar] [CrossRef]
- Zhang, Y.; Baptista, A.M. SELFE: A semi-implicit Eulerian–Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Dresback, K.M.; Fleming, J.G.; Blanton, B.O.; Kaiser, C.; Gourley, J.J.; Tromble, E.M.; Luettich, R.A.; Kolar, R.L.; Hong, Y.; Van Cooten, S.; et al. Skill assessment of a real-time forecast system utilizing a coupled hydrologic and coastal hydrodynamic model during Hurricane Irene (2011). Cont. Shelf Res. 2013, 71, 78–94. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Maitaria, K.; Velissariou, P.; Trimble, B.; Mashriqui, H.; Moghimi, S.; Abdolali, A.; Van der Westhuysen, A.J.; Ma, Z.; Clark, E.P.; et al. New 1D/2D Coupled Modeling Approach for a Riverine-Estuarine System Under Storm Events: Application to Delaware River Basin. J. Geophys. Res. Ocean. 2020, 125, e2019JC015822. [Google Scholar] [CrossRef]
- Hansen, C.; McDonald, S.; Nabors, A.; Shafiei Shiva, J. Using the National Water Model Forecasts to Plan for and Manage Ecological Flow and Low-Flow during Drought. In National Water Center Innovators Program Summer Institute Report; Consortium of Universities for the Advancement of Hydrologic Science, Inc.: Arlington, MA, USA, 2017; p. 66. Available online: https://www.cuahsi.org/uploads/pages/doc/CUAHSI_2017SI_TR14V102_DOI.pdf (accessed on 3 September 2024).
- Johnson, J.M.; Munasinghe, D.; Eyelade, D.; Cohen, S. An integrated evaluation of the national water model (NWM)–Height above nearest drainage (HAND) flood mapping methodology. Nat. Hazards Earth Syst. Sci. 2019, 19, 2405–2420. [Google Scholar] [CrossRef]
- Karki, R.; Krienert, J.M.; Hong, M.; Steward, D.R. Evaluating Baseflow Simulation in the National Water Model: A Case Study in the Northern High Plains Region, USA. JAWRA J. Am. Water Resour. Assoc. 2021, 57, 267–280. [Google Scholar] [CrossRef]
- Rummler, T.; Wagner, A.; Arnault, J.; Kunstmann, H. Lateral terrestrial water fluxes in the LSM of WRF-Hydro: Benefits of a 2D groundwater representation. Hydrol. Process. 2022, 36, e14510. [Google Scholar] [CrossRef]
- Rahman, M.A.; Zhang, Y.; Ghazvinian, M.; Fernando, N.; Schoenbaechler, C.; Gan, Y. Assessment of Relative Accuracy of TxRR and NWM in Simulating Streamflow for a Cluster of Watersheds along the South Texas Coast. Available online: https://www.preprints.org/manuscript/202210.0415 (accessed on 3 September 2024).
- Hughes, M.; Jackson, D.L.; Unruh, D.; Wang, H.; Hobbins, M.; Ogden, F.L.; Cifelli, R.; Cosgrove, B.; DeWitt, D.; Dugger, A.; et al. Evaluation of Retrospective National Water Model Soil Moisture and Streamflow for Drought-Monitoring Applications. J. Geophys. Res. Atmos. 2024, 129, e2023JD038522. [Google Scholar] [CrossRef]
- Duan, Y.; Kumar, S. Predictability of seasonal streamflow and soil moisture in national water model and a humid Alabama–Coosa–Tallapoosa River basin. J. Hydrometeorol. 2020, 21, 1447–1467. [Google Scholar] [CrossRef]
- Cosgrove, B.; Gochis, D.; Flowers, T.; Dugger, A.; Ogden, F.; Graziano, T.; Clark, E.; Cabell, R.; Casiday, N.; Cui, Z.; et al. NOAA’s National Water Model: Advancing operational hydrology through continental-scale modeling. JAWRA J. Am. Water Resour. Assoc. 2024, 60, 247–272. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Yu, H.; Sun, W.; Moghimi, S.; Myers, E.; Nunez, K.; Zhang, R.; Wang, H.; Roland, A.; et al. Simulating compound flooding events in a hurricane. Ocean Dyn. 2020, 70, 621–640. [Google Scholar] [CrossRef]
- Aristizabal, F.; Salas, F.; Petrochenkov, G.; Grout, T.; Avant, B.; Bates, B.; Spies, R.; Chadwick, N.; Wills, Z.; Judge, J. Extending Height Above Nearest Drainage to Model Multiple Fluvial Sources in Flood Inundation Mapping Applications for the U.S. National Water Model. Water Resour. Res. 2023, 59, e2022WR032039. [Google Scholar] [CrossRef]
- Kim, D.; Naliaka, A.; Zhu, Z.; Ogden, F.L.; McMillan, H.K. Experimental Coupling of TOPMODEL with the National Water Model: Effects of Coupling Interface Complexity on Model Performance. JAWRA J. Am. Water Resour. Assoc. 2022, 58, 50–74. [Google Scholar] [CrossRef]
- Deb, M.; Sun, N.; Yang, Z.; Wang, T.; Judi, D.; Xiao, Z.; Wigmosta, M.S. Interacting Effects of Watershed and Coastal Processes on the Evolution of Compound Flooding During Hurricane Irene. Earth’s Future 2023, 11, e2022EF002947. [Google Scholar] [CrossRef]
- Moghimi, S.; van der Westhuysen, A.; Abdolali, A.; Myers, E.; Vinogradov, S.; Ma, Z.; Liu, F.; Mehra, A.; Kurkowski, N. Development of a Flexible Coupling Framework for Coastal Inundation Studies. arXiv 2020, arXiv:2003.12652. [Google Scholar] [CrossRef]
- Hill, C.; DeLuca, C.; Suarez, M.; Da Silva, A. The architecture of the earth system modeling framework. Comput. Sci. Eng. 2004, 6, 18–28. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Stewart, S.R. Hurricane Matthew. 2017. National Hurricane Center. Available online: https://www.nhc.noaa.gov/data/tcr/AL142016_Matthew.pdf (accessed on 3 September 2024).
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.; Iredell, M. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Global Ocean Physics Analysis and Forecast. Available online: https://data.marine.copernicus.eu/product/GLOBAL_ANALYSISFORECAST_PHY_001_024/description (accessed on 11 July 2024).
- Flather, R.A. Practical Aspects of the Use of Numerical Models for Storm Surge Prediction. 1976. Available online: https://nora.nerc.ac.uk/id/eprint/114313/1/14313-01.pdf (accessed on 3 September 2024).
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Bizhanimanzar, M.; Leconte, R.; Nuth, M. Catchment-scale integrated surface water-groundwater hydrologic modelling using conceptual and physically based models: A model comparison study. Water 2020, 12, 363. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types. In Proceedings of the 9th International Congress on Environmental Modelling and Software, Ft. Collins, CO, USA, 24–28 June 2018; 41st Report. Available online: https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=3977&context=iemssconference (accessed on 3 September 2024).
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
Figure 1.
Schematic representation of the two-way coupling between the NWM and the SCHISM. The left side illustrates the NWM to SCHISM coupling at the upstream boundary of the SCHISM domain (blue arrows) where river discharge () was converted to velocity () using the cross-sectional area (). The right side shows the SCHISM to NWM coupling at the red cross-sections along the river channel (red lines) where velocities () were integrated across a cross-section to calculate discharge () using water depths () and segment widths (). The bottom part depicts the interface between the NWM’s 1D channel and the SCHISM’s 2D coastal domain.
Figure 1.
Schematic representation of the two-way coupling between the NWM and the SCHISM. The left side illustrates the NWM to SCHISM coupling at the upstream boundary of the SCHISM domain (blue arrows) where river discharge () was converted to velocity () using the cross-sectional area (). The right side shows the SCHISM to NWM coupling at the red cross-sections along the river channel (red lines) where velocities () were integrated across a cross-section to calculate discharge () using water depths () and segment widths (). The bottom part depicts the interface between the NWM’s 1D channel and the SCHISM’s 2D coastal domain.
Figure 2.
Study area and domains for different model components in this coupled model. The northeastern coast of South Carolina was selected as the domain for the SCHISM. The color in SCHISM doamin represents elevation, with negative values indicating bathymetry. The entire Pee Dee Basin was the domain for the NWM. The bold blue lines delineate the river channel. USGS stations 02135200 and 02110704 were used to provide upstream discharge data. USGS stations 02110802, 021108125, and 02110815 were used to provide water-level data for the model validation.
Figure 2.
Study area and domains for different model components in this coupled model. The northeastern coast of South Carolina was selected as the domain for the SCHISM. The color in SCHISM doamin represents elevation, with negative values indicating bathymetry. The entire Pee Dee Basin was the domain for the NWM. The bold blue lines delineate the river channel. USGS stations 02135200 and 02110704 were used to provide upstream discharge data. USGS stations 02110802, 021108125, and 02110815 were used to provide water-level data for the model validation.
Figure 3.
(a) Water levels near an estuary (from the ROMS); (b) averaged rainfall intensity for the whole Pee Dee Basin (from NLDAS); (c) wind vectors at latitude −79.16 and longitude 33.19, near the estuary (from CFS).
Figure 3.
(a) Water levels near an estuary (from the ROMS); (b) averaged rainfall intensity for the whole Pee Dee Basin (from NLDAS); (c) wind vectors at latitude −79.16 and longitude 33.19, near the estuary (from CFS).
Figure 4.
Validation of coupled modeling results. The left panel shows the comparison of water levels between USGS observations and the SCHISM results. ed lines are the result of the SCHISM driven by NWM-produced discharge; blue lines are the result of the SCHISM driven by USGS-observed discharge from two (Waccamaw and Pee Dee) river inlets; black lines are the water-level observations from USGS gauge stations. The color in SCHISM doamin represents elevation, with negative values indicating bathymetry.
Figure 4.
Validation of coupled modeling results. The left panel shows the comparison of water levels between USGS observations and the SCHISM results. ed lines are the result of the SCHISM driven by NWM-produced discharge; blue lines are the result of the SCHISM driven by USGS-observed discharge from two (Waccamaw and Pee Dee) river inlets; black lines are the water-level observations from USGS gauge stations. The color in SCHISM doamin represents elevation, with negative values indicating bathymetry.
Figure 5.
Coupling model result. In total, 15 points along the river channel were selected as sampling points (the numbers were reach numbers defined in the NWM domain) for the comparison of discharge from “coupling” (red lines on right) and “without coupling” (green lines on right) results. Three points were selected as examples to show the river discharge changes under the influence of importing downstream water-level-change data. The color represents elevation, with negative values indicating bathymetry.
Figure 5.
Coupling model result. In total, 15 points along the river channel were selected as sampling points (the numbers were reach numbers defined in the NWM domain) for the comparison of discharge from “coupling” (red lines on right) and “without coupling” (green lines on right) results. Three points were selected as examples to show the river discharge changes under the influence of importing downstream water-level-change data. The color represents elevation, with negative values indicating bathymetry.
Figure 6.
River–river interactions observed in the SCHISM results (EXP1). Three times were selected to show the flow direction change caused by river–river interactions: (a) 10 October, 12:00 UTC; (b) 11 October, 02:00 UTC; and (c) 11 October, 12:00 UTC. The colors on the arrows indicate water speed from 0–1.6 m/s. The color on background represents elevation, with negative values indicating bathymetry.
Figure 6.
River–river interactions observed in the SCHISM results (EXP1). Three times were selected to show the flow direction change caused by river–river interactions: (a) 10 October, 12:00 UTC; (b) 11 October, 02:00 UTC; and (c) 11 October, 12:00 UTC. The colors on the arrows indicate water speed from 0–1.6 m/s. The color on background represents elevation, with negative values indicating bathymetry.
Figure 7.
Comparisons of water levels from the SCHISM, water levels (head + elevation) from the NWM, and water-level observations from three USGS stations. (a) UGSG 02110802, (b) USGS 021108125, and (c) USGS 02110815. There were significant differences in water-level results between the SCHISM and the NWM.
Figure 7.
Comparisons of water levels from the SCHISM, water levels (head + elevation) from the NWM, and water-level observations from three USGS stations. (a) UGSG 02110802, (b) USGS 021108125, and (c) USGS 02110815. There were significant differences in water-level results between the SCHISM and the NWM.
Table 1.
Model configuration.
Table 1.
Model configuration.
Model
Configuration | NWM | SCHISM | ROMS |
|---|
Spatial
Resolution | Land surface: 1 km. Overland routing: 250 m. Channel: predefined links | ~100 m | 2.70–8.69 km (zonal); 1.83–4.47 km (meridional) |
Temporal
Resolution | 10 s | 20 s | 30 s |
| Forcing Data | North American Land Data Assimilation System (NLDAS) for atmospheric forcing | Climate Forecast System (CFS) for atmospheric forcing | NCEP CFSR and CFSv2. Tides: TPXO9 |
Initial
Conditions | Extracted from operational NWM forecast. | Elevation = 0.1 with spin-ups | Initial: CMEMS GOPR |
Simulation
Period | 28 September–5 November 2016
(5-day spin-up) | 28 September–5 November 2016 (5-day spin-up) | 1 September–30 November 2016 |
Table 2.
Experimental design.
Table 2.
Experimental design.
| Experiment | Coupling Type | NWM | Data Exchange | SCHISM | Upstream BC |
|---|
| EXP1 | Two-way | ✓ | ↔ | ✓ | NWM output |
| EXP2 | No-coupled | ✓ | No | ✓ | USGS observations |
| EXP3 | One-way | ✓ | → | ✓ | NWM output |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).