Simulating the Potential Evapotranspiration of Egypt Using the RegCM4: Sensitivity to the Land Surface and Boundary Layer Parameterizations
Abstract
1. Introduction
- Compare between the BATS and CLM45 land surface model (with respect to the high-resolution ERA5-land based product, hPET [33]).
- Fine-tune the coefficients of the HS equation (using the best land surface scheme) and then compare between the original and calibrated version to check the added value of the fine tuning.
- Assess the sensitivity of the PET to the boundary layer schemes (HOLT and UW) using the calibrated version of the HS to check which scheme is suitable in simulating the PET in comparison with the hPET.
- Compare between the two versions of the calibrated HS equation: (1) temperature-only-based formula and (2) temperature-radiation-based formula (to examine which formula is the best to compute the PET).
- Bias-correct the PET (for each season) using the suitable calibrated HS equation (from point 3) with respect to the hPET.
- Plot the climatological cycle of the PET (before and after applying the bias-correction method) in the validation period.
2. Materials and Methods
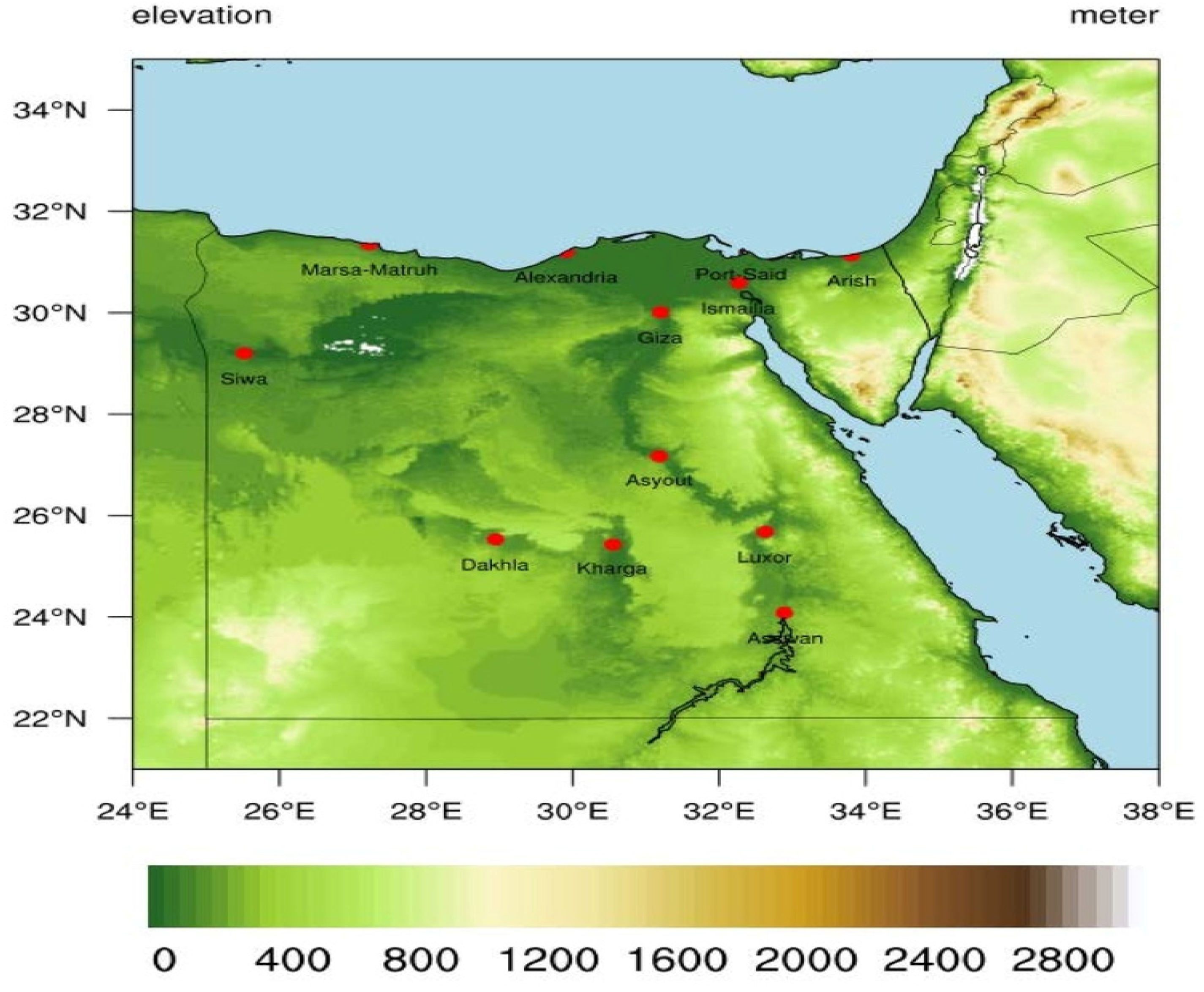
2.1. Study Area
2.2. Model Description
2.3. Experimental Design
2.4. Observational Dataset
3. Results
3.1. Land Surface Parameterization
3.2. Calibrating the HS Equation
3.3. Boundary Layer Parameterization
3.4. Comparison between Two Calibrated Versions of the HS Equation
3.5. Bias-Correcting the PET
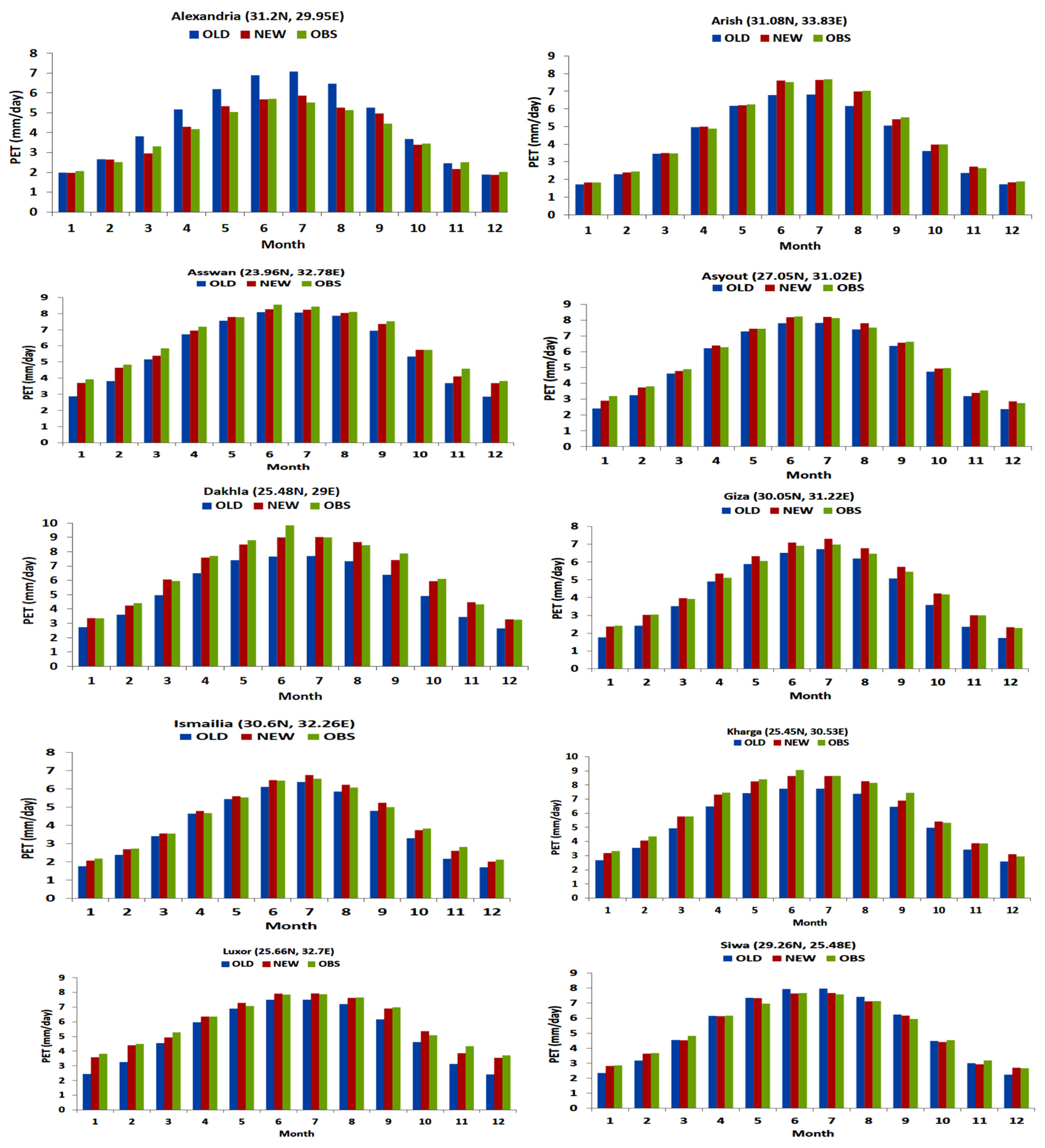
3.6. Climatological Annual Cycle
4. Discussion and Conclusions
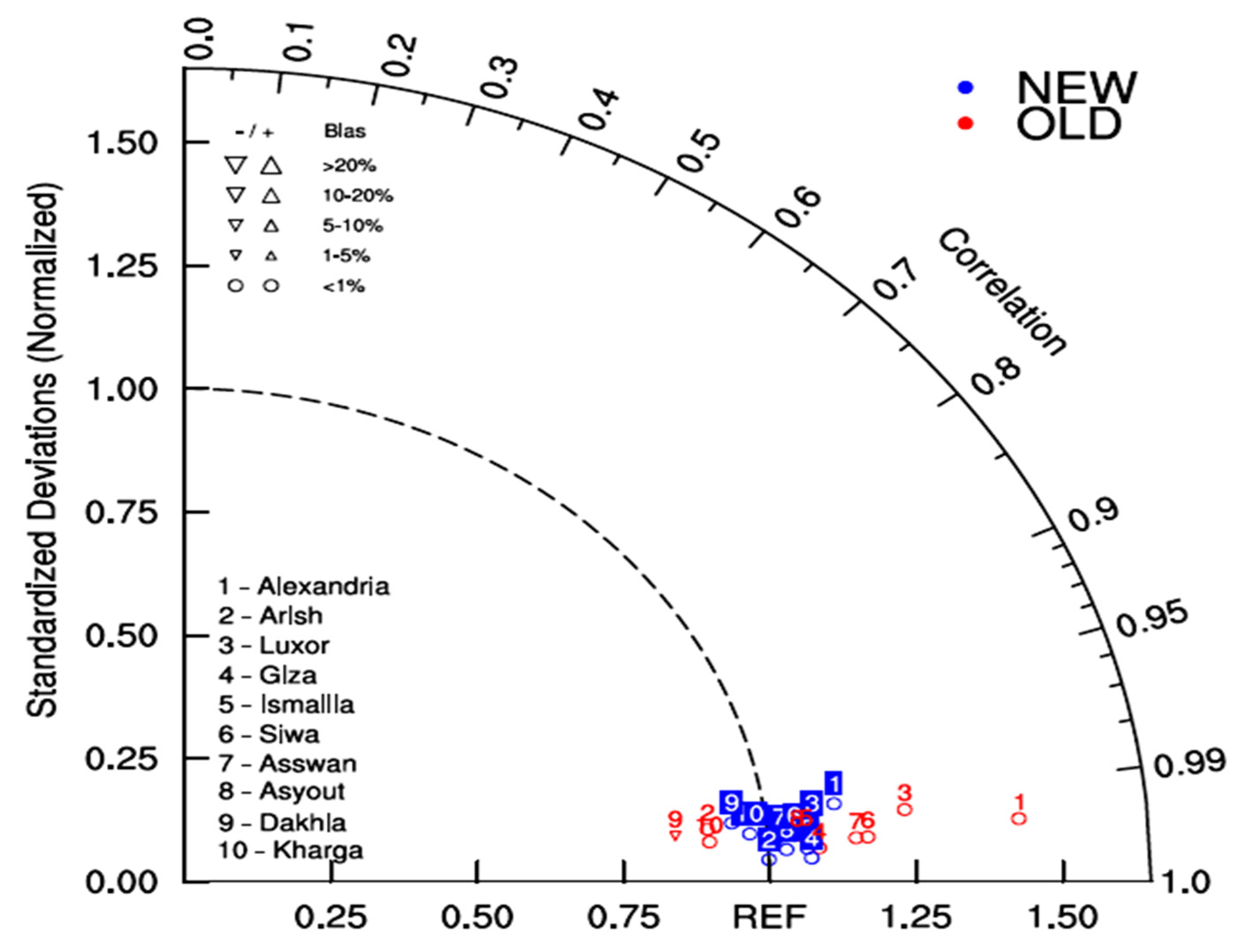
- With respect to the ERA5, the BATS outperformed the CLM45, and the UW was better than the HOLT in all seasons concerning the PET.
- Calibrating the temperature coefficient (of the HS equation) succeeded in reducing the PET bias in comparison with the ERA5.
- Comparison between the two calibrated versions of the HS revealed that the temperature-only version provided a lower PET bias compared to the one noted in the radiation-temperature version.
- The LS method explored its added value in reducing the PET bias either in the evaluation or the validation period.
- Concerning the climatological annual cycle, the calibrated HS equation provided a better performance than the original version (in the ten locations) in comparison with the ERA5.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Currie, D.J. Energy and large-scale patterns of animal and plant species richness. Am. Nat. 1991, 137, 27–49. [Google Scholar] [CrossRef]
- Allen, G.R.; Pereira, S.L.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Report 56; Food and Agricultural Organization of the United Nations (FAO): Rome, Italy, 1998; 300p. [Google Scholar]
- Li, Z.; Yang, Y.; Kan, G.; Hong, Y. Study on the Applicability of the Hargreaves Potential Evapotranspiration Estimation Method in CREST Distributed Hydrological Model (Version 3.0) Applications. Water 2018, 10, 1882. [Google Scholar] [CrossRef]
- Hamed, M.M.; Iqbal, Z.; Nashwan, M.S.; Kineber, A.F.; Shahid, S. Diminishing evapotranspiration paradox and its cause in the Middle East and North Africa. Atmos. Res. 2023, 289, 106760. [Google Scholar] [CrossRef]
- Nooni, I.K.; Hagan, D.F.T.; Wang, G.; Ullah, W.; Lu, J.; Li, S.; Dzakpasu, M.; Prempeh, N.A.; Lim Kam Sian, K.T.C. Future Changes in Simulated Evapotranspiration across Continental Africa Based on CMIP6 CNRM-CM6. Int. J. Environ. Res. Public Health 2021, 18, 6760. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, B.; Feng, X.; Pan, N. Response of Ecohydrological Variables to Meteorological Drought under Climate Change. Remote Sens. 2022, 14, 1920. [Google Scholar] [CrossRef]
- Murat, C.; Hatice, C.; Tefaruk, H.; Kisi, O. Modifying Hargreaves–Samani equation with meteorological variables for estimation of reference evapotranspiration in Turkey. Hydrol. Res. 2017, 48, 480–497. [Google Scholar] [CrossRef]
- Brutsaert, W.; Parlange, M.B. Hydrologic cycle explains the evaporation paradox. Nature 1998, 396, 30. [Google Scholar] [CrossRef]
- Spinoni, J.; Barbosa, P.; Bucchignani, E.; Cassano, J.; Cavazos, T.; Cescatti, A.; Christensen, J.H.; Christensen, O.B.; Coppola, E.; Evans, J.P.; et al. Global exposure of population and land-use to meteorological droughts under different warming levels and SSPs: A CORDEX-based study. Int. J. Climatol. 2021, 41, 6825–6853. [Google Scholar] [CrossRef]
- Raziei, T.; Pereirab, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samni, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrigat. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Rohwer, C. Evaporation from free water surface. USDA Tech. Null. 1931, 217, 1–96. [Google Scholar]
- Mohammadieh, M.; Noori, M.; Helali, J.; Nazari, B.; Sohrabi, T. Evaluation of Hargreaves equation for calculating daily ETo (Case study: North West of Iran). Adv. Nat. Appl. Sci. 2009, 3, 273–279. [Google Scholar]
- Rajabi, A.; Babakhani, Z. The study of potential evapotranspiration in future periods due to climate change in west of Iran. Int. J. Clim. Chang. Strateg. Manag. 2018, 10, 161–177. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Chatterjee, C. Modelling the dynamics of evapotranspiration using Variable Infiltration Capacity model and regionally calibrated Hargreaves approach. Irrig. Sci. 2018, 36, 289–300. [Google Scholar] [CrossRef]
- Swain, R.; Sahoo, B. Improving river water quality monitoring using satellite data products and a genetic algorithm processing approach. Sustain. Water Qual. Ecol. 2017, 9–10, 88–114. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.C.; Allen, R. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid. Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Elagib, N.A.; Musa, A.A. Correcting Hargreaves-Samani formula using geographical coordinates and rainfall over different timescales. Hydrol. Process. 2022, 37, e14790. [Google Scholar] [CrossRef]
- Giménez, P.O.; García-Galiano, S.G. Assessing Regional Climate Models (RCMs) Ensemble-Driven Reference Evapotranspiration over Spain. Water 2018, 10, 1181. [Google Scholar] [CrossRef]
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.B.; Bi, X.; Elguindi, N.; Diro, G.T.; Nair, V.; Giuliani, G.; et al. RegCM4: Model description and preliminary tests over multiple CORDEX domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef]
- Abdel Wahab, M.M.; Essa, Y.H.; Khalil, A.A.; Elfadli, K.; Giulia, P. Water Loss in Egypt Based on the Lake Nasser Evaporation and Agricultural Evapotranspiration. Environ. Asia 2018, 11, 192–204. [Google Scholar] [CrossRef]
- Anwar, S.A.; Lazić, I. Estimating the Potential Evapotranspiration of Egypt Using a Regional Climate Model and a High-Resolution Reanalysis Dataset. Environ. Sci. Proc. 2023, 25, 29. [Google Scholar] [CrossRef]
- Anwar, S.A.; Srivastava, A. On the Sensitivity of Potential Evapotranspiration in Egypt to Different Dynamical Downscaling Options and Boundary Layer Schemes Using a High-Resolution Regional Climate Model. Eng. Proc. 2023, 56, 116. [Google Scholar] [CrossRef]
- Anwar, S.A.; Mostafa, S.M. On the Sensitivity of the Daily Mean Air Temperature of Egypt to Boundary Layer Schemes Using a High-Resolution Regional Climate Model (RegCM4). J. Biomed. Res. Environ. Sci. 2023, 4, 474–484. [Google Scholar] [CrossRef]
- Holtslag, A.A.M.; Boville, B.A. Local versus nonlocal boundary layer diffusion in a global model. J. Clim. 1993, 6, 1825–1842. [Google Scholar] [CrossRef]
- Grenier, H.; Bretherton, C.S. A moist PBL parameterization for large scale models and its application to subtropical cloud topped marine boundary layers. Mon. Weather Rev. 2001, 129, 357–377. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Anwar, S.A.; Mostafa, S.M. Assessment of the Sensitivity of Daily Maximum and Minimum Air Temperatures of Egypt to Soil Moisture Status and Land Surface Parameterization Using RegCM4. Eng. Proc. 2023, 56, 115. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Drewniak, B.; Huang, M.; Koven, C.D.; Levis, S.; Li, F.; Riley, W.J.; Subin, Z.M.; et al. Technical Description of Version 4.5 of the Community Land Model (CLM); NCAR Technical Note NCAR/TN-503+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2013. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version 1e as Coupled to the NCAR Community Climate Model (No. NCAR/TN-387+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 1993. [Google Scholar] [CrossRef]
- Singer, M.; Asfaw, D.; Rosolem, R.; Cuthbert, M.O.; Miralles, D.G.; MacLeod, D.; Michaelides, K. Hourly potential evapotranspiration (hPET) at 0.1degs grid resolution for the global land surface from 1981-present. Sci. Data 2021, 8, 224. [Google Scholar] [CrossRef] [PubMed]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- El Kenawy, A.; Lopez-Moreno, J.I.; Vicente-Serrano, S.M.; Morsi, F. Climatological modeling of monthly air temperature and precipitation in Egypt through GIS techniques. Clim. Res. 2010, 42, 161–176. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Chung, E.-S. High-Resolution Climate Projections for a Densely Populated Mediterranean Region. Sustainability 2020, 12, 3684. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shahid, S. Inter-comparison of Historical Simulation and Future Projection of Rainfall and Temperature by CMIP5 and CMIP6 GCMs Over Egypt. Int. J. Climatol. 2022, 42, 4316–4332. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shiru, M.S.; Shahid, S. Comparison between CMIP5 and CMIP6 Models over MENA Region Using Historical Simulations and Future Projections. Sustainability 2022, 14, 10375. [Google Scholar] [CrossRef]
- Mostafa, S.M.; Anwar, S.A.; Zakey, A.S.; Wahab, M.M.A. Bias-correcting the maximum and minimum air temperatures of Egypt using a high-resolution Regional Climate Model (RegCM4). Eng. Proc. 2023, 31, 73. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Errico, R.M.; Giorgi, F.; Bates, G.T. A regional climate model for the western United States. Clim. Chang. 1989, 15, 383–422. [Google Scholar] [CrossRef]
- Giorgi, F.; Bates, G.T. The climatological skill of a regional model over complex terrain. Mon. Weather Rev. 1989, 117, 2325–2347. [Google Scholar] [CrossRef]
- Giorgi, F. Thirty years of regional climate modeling: Where are we and where are we going? J. Geophys. Res. 2019, 124, 5696–5723. [Google Scholar] [CrossRef]
- Giorgi, F.; Marinucci, M.R.; Bates, G.T. Development of a second generation regional climate model (RegCM2). Part I: Boundary layer and radiative transfer processes. Mon. Weather Rev. 1993, 121, 2794–2813. [Google Scholar] [CrossRef]
- Giorgi, F.; Marinucci, M.R.; Bates, G.T.; DeCanio, G. Development of a second generation regional climate model (RegCM2). Part II: Convective processes and assimilation of lateral boundary conditions. Mon. Wea. Rev. 1993, 121, 2814–2832. [Google Scholar] [CrossRef]
- Pal, J.S.; Giorgi, F.; Bi, X.; Elguindi, N.; Solmon, F.; Gao, X.; Rauscher, S.A.; Francisco, R.; Zakey, A.; Winter, J.; et al. The ICTP RegCM3 and RegCNET: Regional climate modeling for the developing World. Bull. Amer. Meteor. Soc. 2007, 88, 1395–1409. [Google Scholar] [CrossRef]
- Giorgi, F.; Coppola, E.; Giuliani, G.; Ciarlo‘, J.M.; Pichelli, E.; Nogherotto, R.; Raffaele, F.; Malguzzi, P.; Davolio, S.; Stocchi, P.; et al. The Fifth Generation Regional Climate Modeling System, RegCM5: Description and Illustrative Examples at Parameterized Convection and Convection-Permitting Resolutions. J. Geophys. Res. Atmos. 2023, 128, e2022JD038199. [Google Scholar] [CrossRef]
- Coppola, E.; Stocchi, P.; Pichelli, E.; Torres Alavez, J.A.; Glazer, R.; Giuliani, G.; Di Sante, F.; Nogherotto, R.; Giorgi, F. Non-Hydrostatic RegCM4 (RegCM4-NH): Model description and case studies over multiple domains. Geosci. Model. Dev. 2021, 14, 7705–7723. [Google Scholar] [CrossRef]
- Kiehl, J.T.; Hack, J.; Bonan, G.; Boville, B.; Breigleb, B.; Williamson, D.; Rasch, P. Description of the Ncar Community Climate Model (ccm3), National Center for Atmospheric Research Technical Note NCAR/TN-420+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1996; 95p. [Google Scholar]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogenoeus atmoshere: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Emanuel, K.A.; Zivkovic-Rothman, M. Development and evaluation of a convection scheme for use in climate models. J. Atmos. Sci. 1999, 56, 1766–1782. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Steiner, A.L.; Pal, J.S.; Rauscher, S.A.; Bell, J.L.; Diffenbaugh, N.S.; Boone, A.; Sloan, L.C.; Giorgi, F. Land surface coupling in regional climate simulations of the West African monsoon. Clim. Dyn. 2009, 33, 869–892. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Gruber, A.; Scanlon, T.; van der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data. 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Daniel, H. Performance assessment of bias correction methods using observed and regional climate model data in different watersheds, Ethiopia. J. Water Clim. 2023, 14, 2007–2028. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Baker, N.C.; Taylor, P.C. A Framework for Evaluating Climate Model Performance Metrics. J. Clim. 2016, 29, 1773–1782. [Google Scholar] [CrossRef]
- Perez, J.; Menendez, M.; Mendez, F.J.; Losada, I.J. Evaluating the performance of CMIP3 and CMIP5 global climate models over the north-east Atlantic region. Clim. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, G.; Zhang, K.; Bi, J.; Jia, X.; Ding, B.; Zhang, Y.; Shang, S.; Zhao, N.; Qin, W. Evaluation of Evapotranspiration Models Using Different LAI and Meteorological Forcing Data from 1982 to 2017. Remote Sens. 2020, 12, 2473. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model. Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Gleixner, S.; Demissie, T.; Diro, G.T. Did ERA5 improve temperature and precipitation reanalysis over East Africa? Atmosphere 2020, 11, 996. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shahid, S. Performance evaluation of reanalysis products in Egypt using Fuzzy Entropy Time Series Similarity Analysis. Int. J. Climatol. 2021, 41, 5431–5446. [Google Scholar] [CrossRef]
- Gebaly, A.M.; Nashwan, M.S.; Khadr, W.M.; Shahid, S. Future changes in wind energy resources in Egypt under the Paris Climate agreements’ goals. Reg. Environ. Chang. 2023, 23, 63. [Google Scholar] [CrossRef]
- Ayman, M.; Salah, Z.; Tonbol, K.; Shaltout, M. Evaluating ERA5 weather parameters data using remote sensing and in situ data over north red sea. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2023, 48, 77–84. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, S.A.; Olusegun, C.F. Simulating the Potential Evapotranspiration of Egypt Using the RegCM4: Sensitivity to the Land Surface and Boundary Layer Parameterizations. Hydrology 2024, 11, 121. https://doi.org/10.3390/hydrology11080121
Anwar SA, Olusegun CF. Simulating the Potential Evapotranspiration of Egypt Using the RegCM4: Sensitivity to the Land Surface and Boundary Layer Parameterizations. Hydrology. 2024; 11(8):121. https://doi.org/10.3390/hydrology11080121
Chicago/Turabian StyleAnwar, Samy A., and Christiana F. Olusegun. 2024. "Simulating the Potential Evapotranspiration of Egypt Using the RegCM4: Sensitivity to the Land Surface and Boundary Layer Parameterizations" Hydrology 11, no. 8: 121. https://doi.org/10.3390/hydrology11080121
APA StyleAnwar, S. A., & Olusegun, C. F. (2024). Simulating the Potential Evapotranspiration of Egypt Using the RegCM4: Sensitivity to the Land Surface and Boundary Layer Parameterizations. Hydrology, 11(8), 121. https://doi.org/10.3390/hydrology11080121






