Analysis of the Impact of Hydraulic Gates on a Stabilized Tidal Inlet Structure: Mathematical Model and Data Measurements
Abstract
1. Introduction
2. Materials and Methods
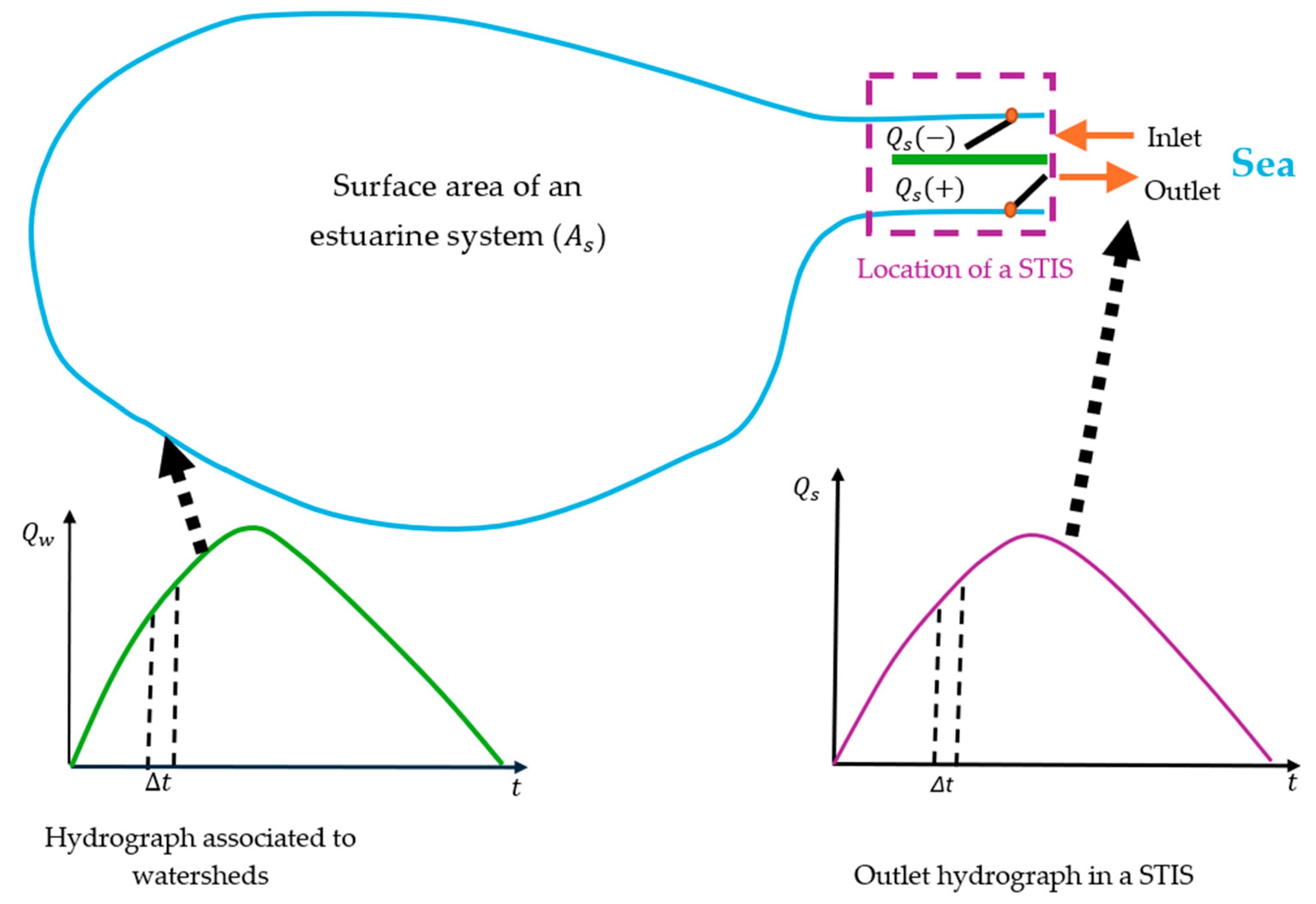
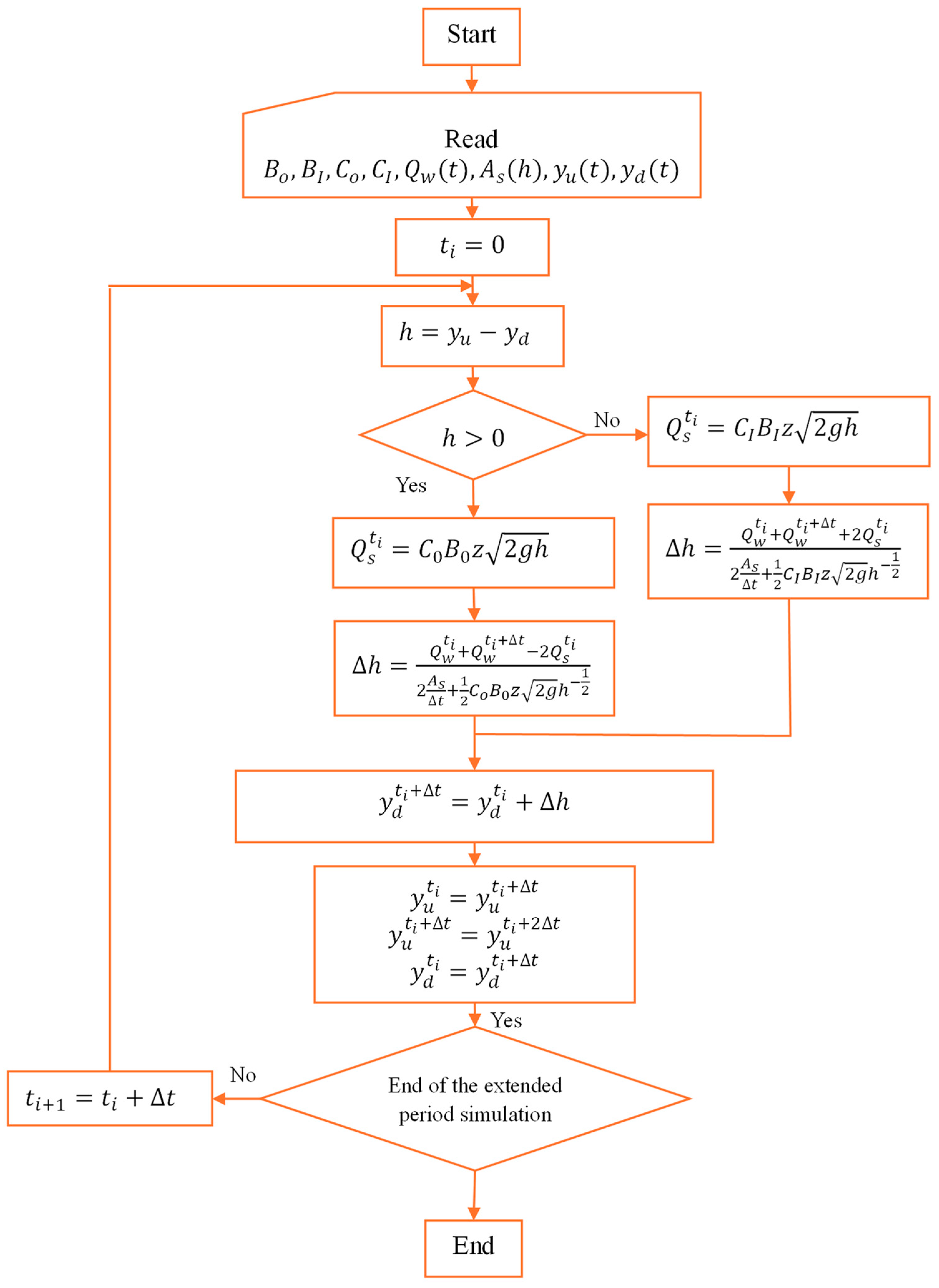
2.1. Mathematical Model
- A water balance suffices to depict the key variables within an estuarine system.
- Evaporation and infiltration processes are neglected during simulations, which is a valid approach, particularly since these present low water volumes compared to the outlet or inlet water volumes of seas or oceans. The water density remains constant, as the numerical value of seawater density fluctuates only after the third decimal point.
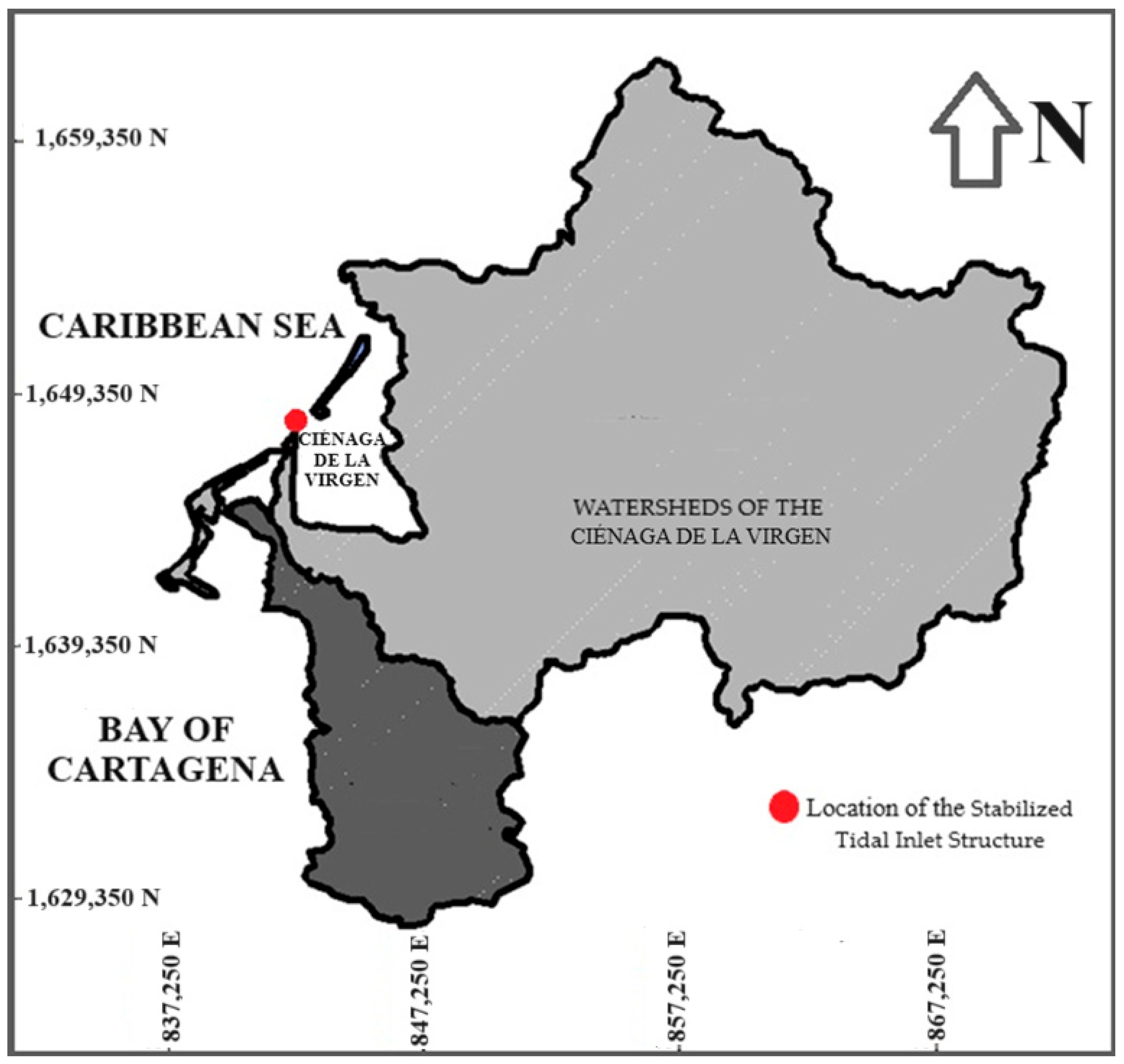
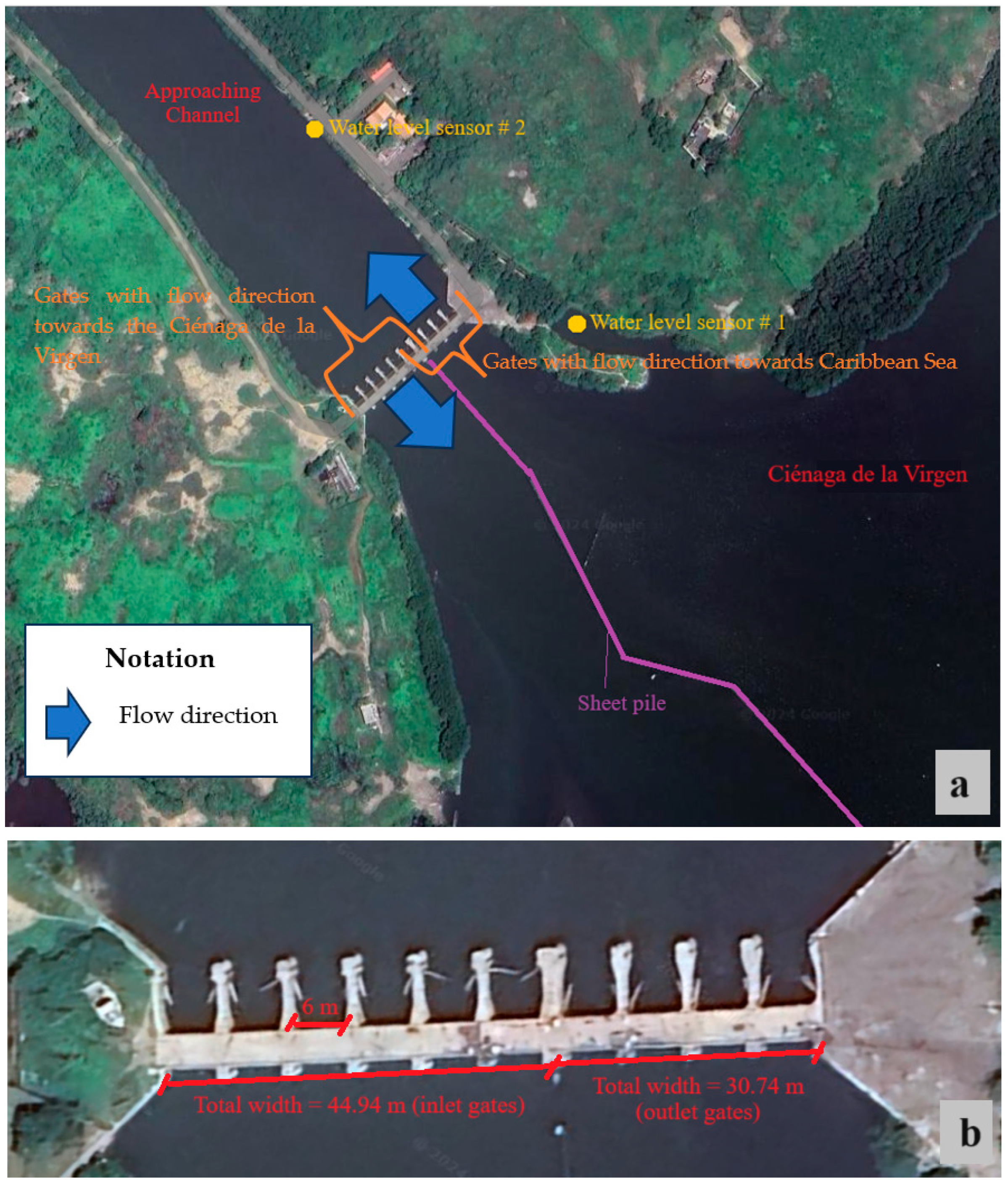
2.2. Case Study and Data
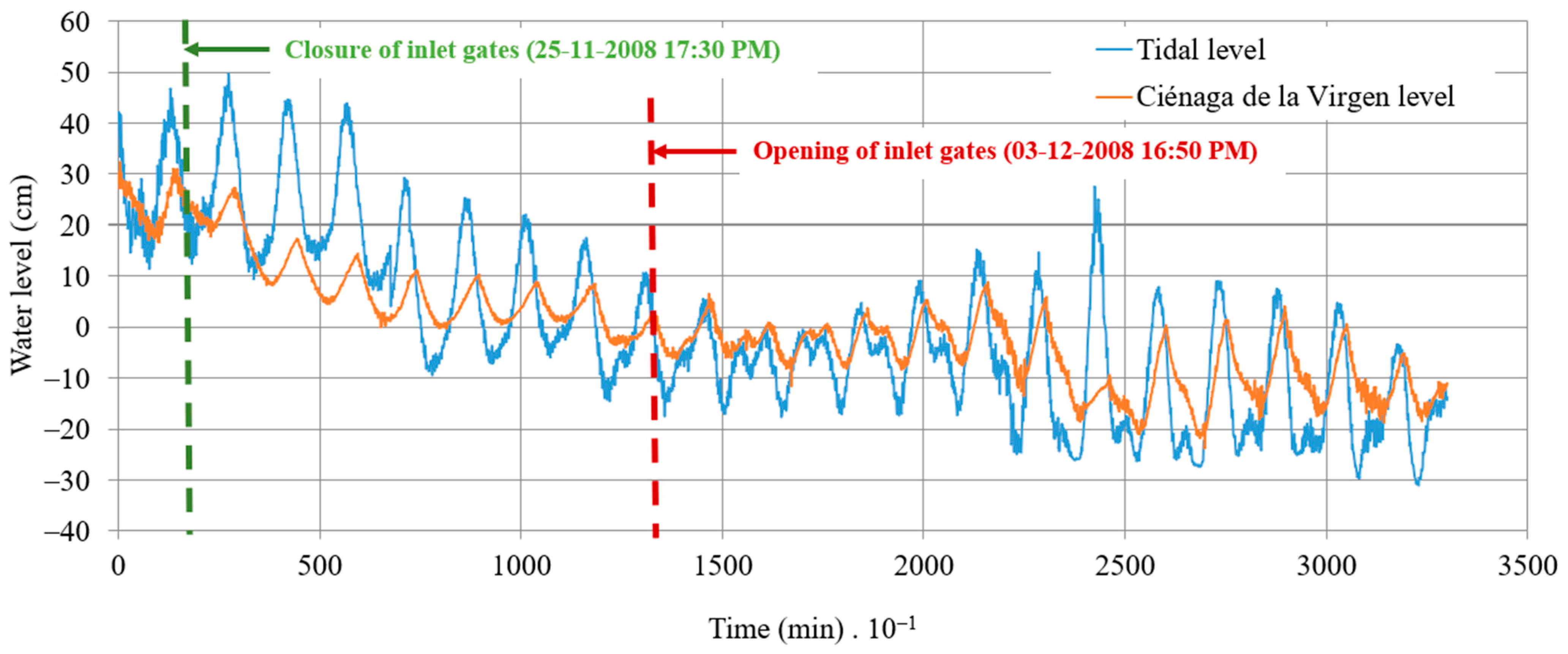
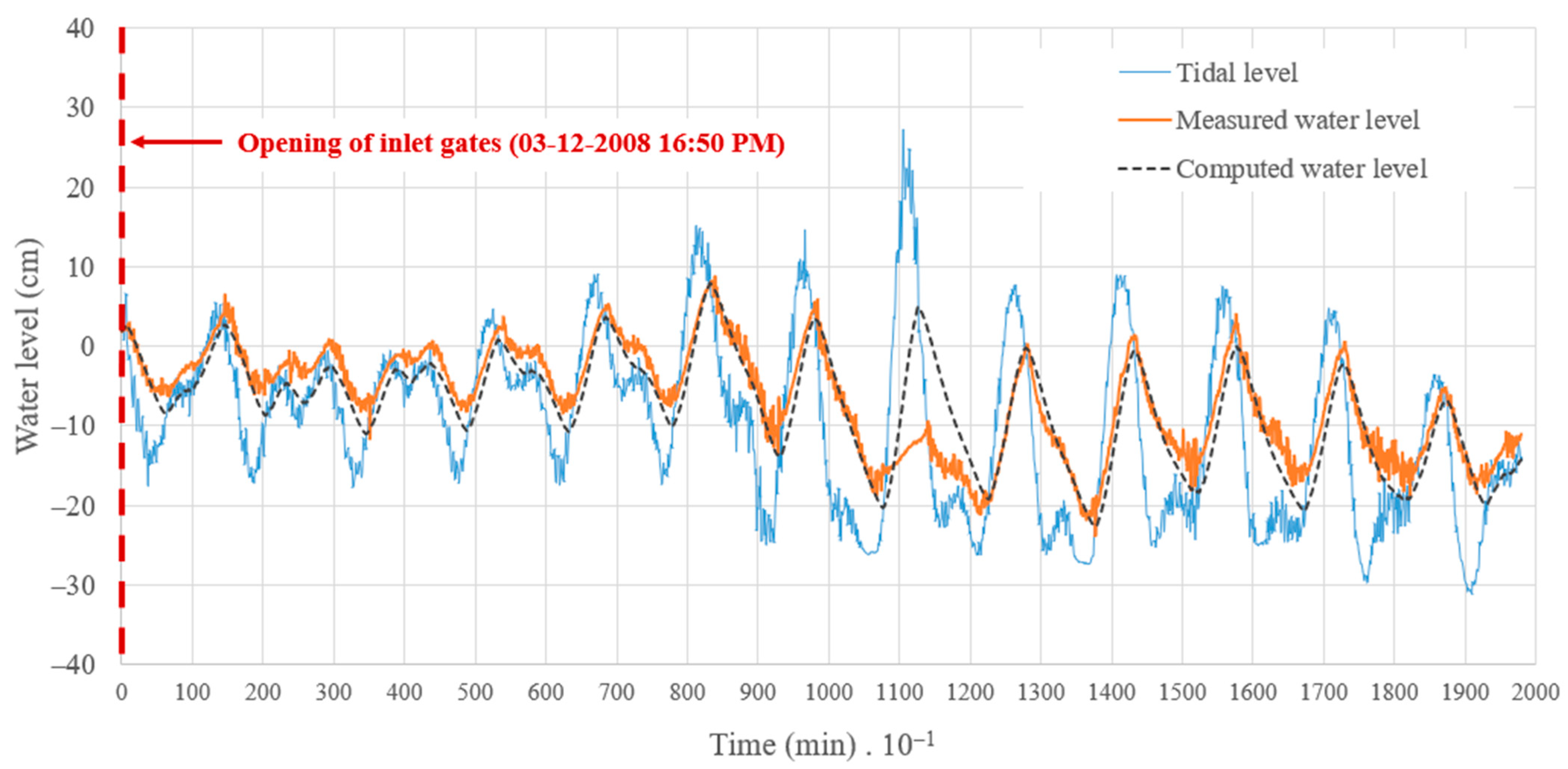
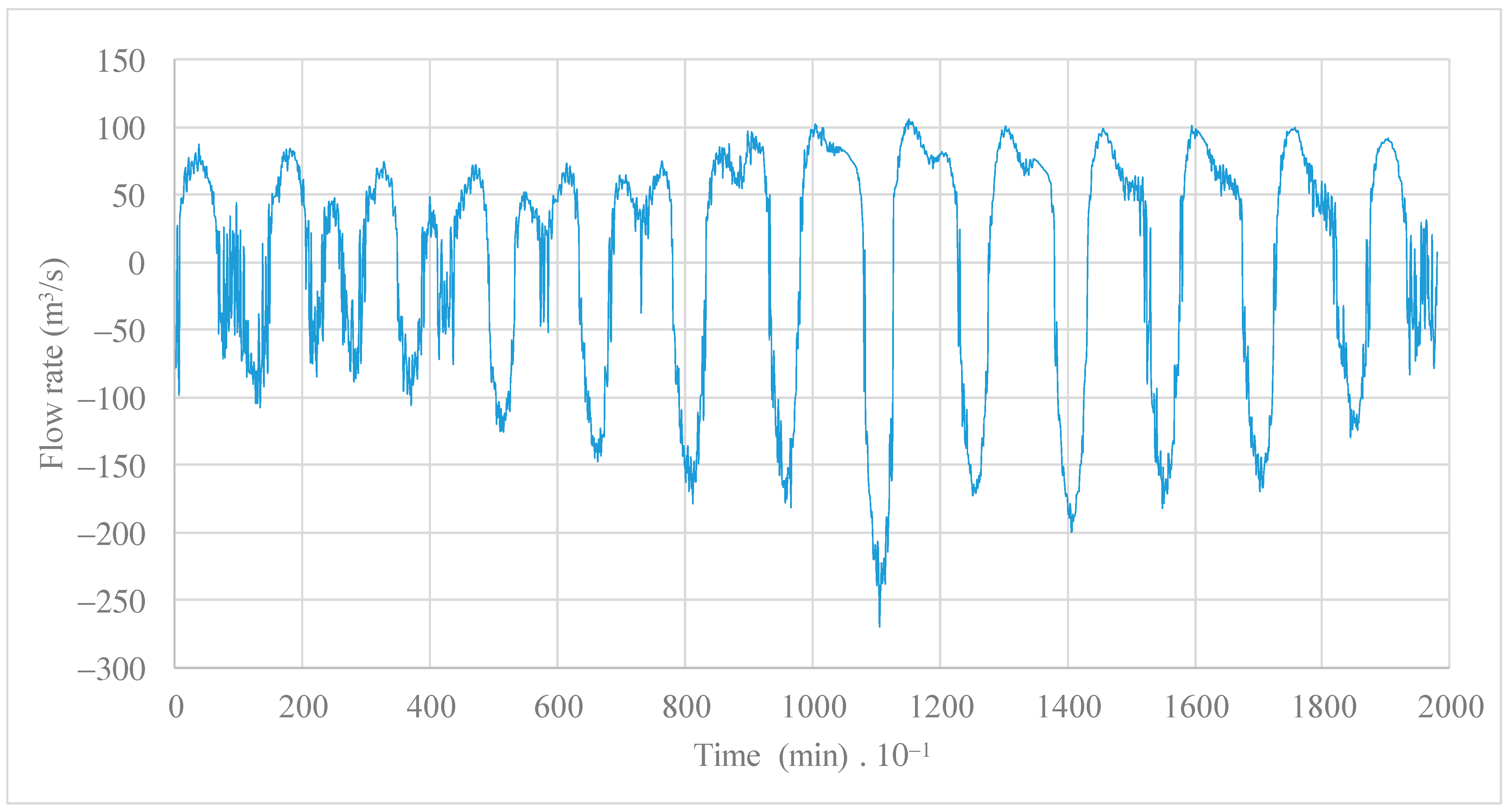
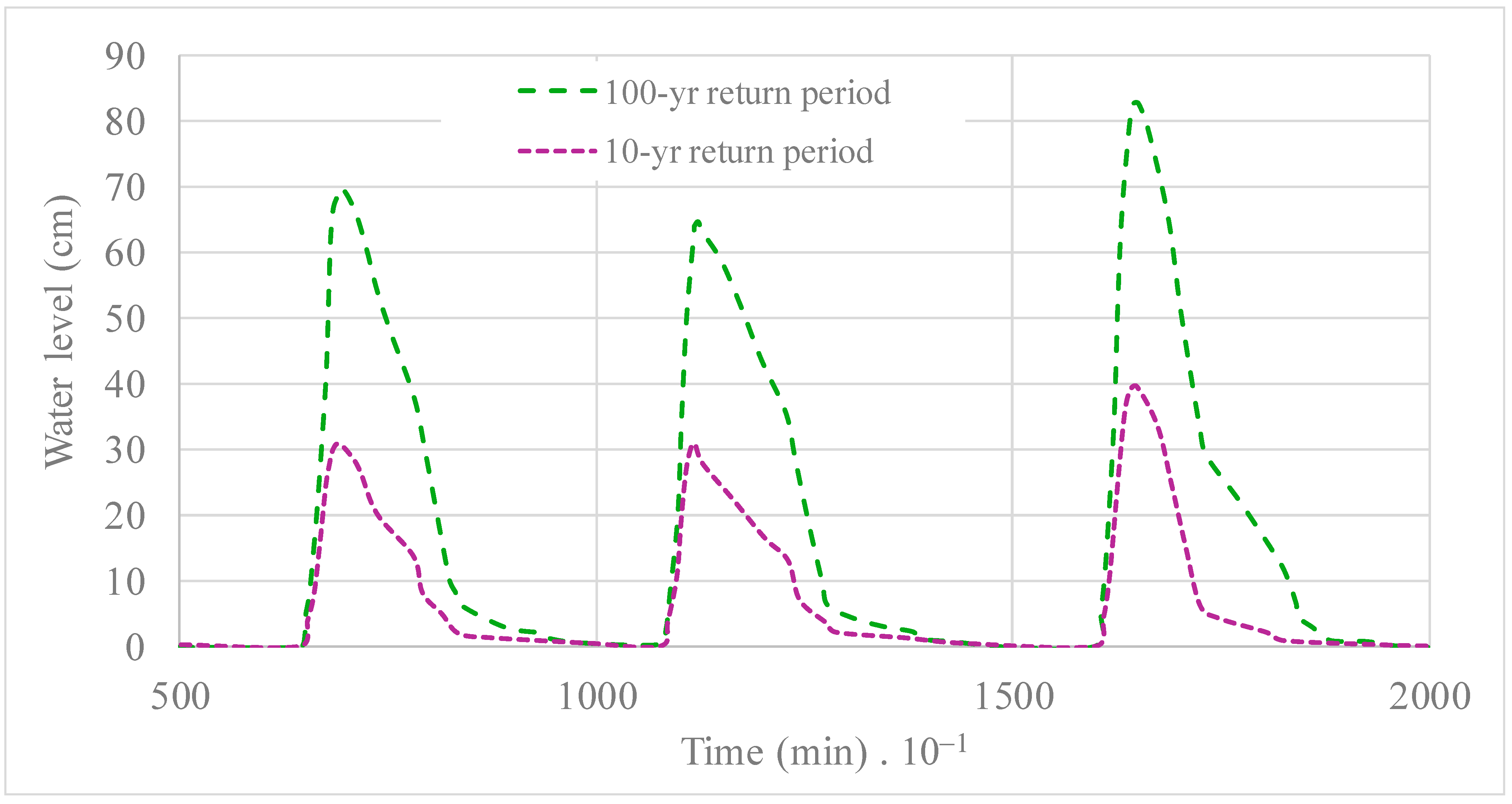
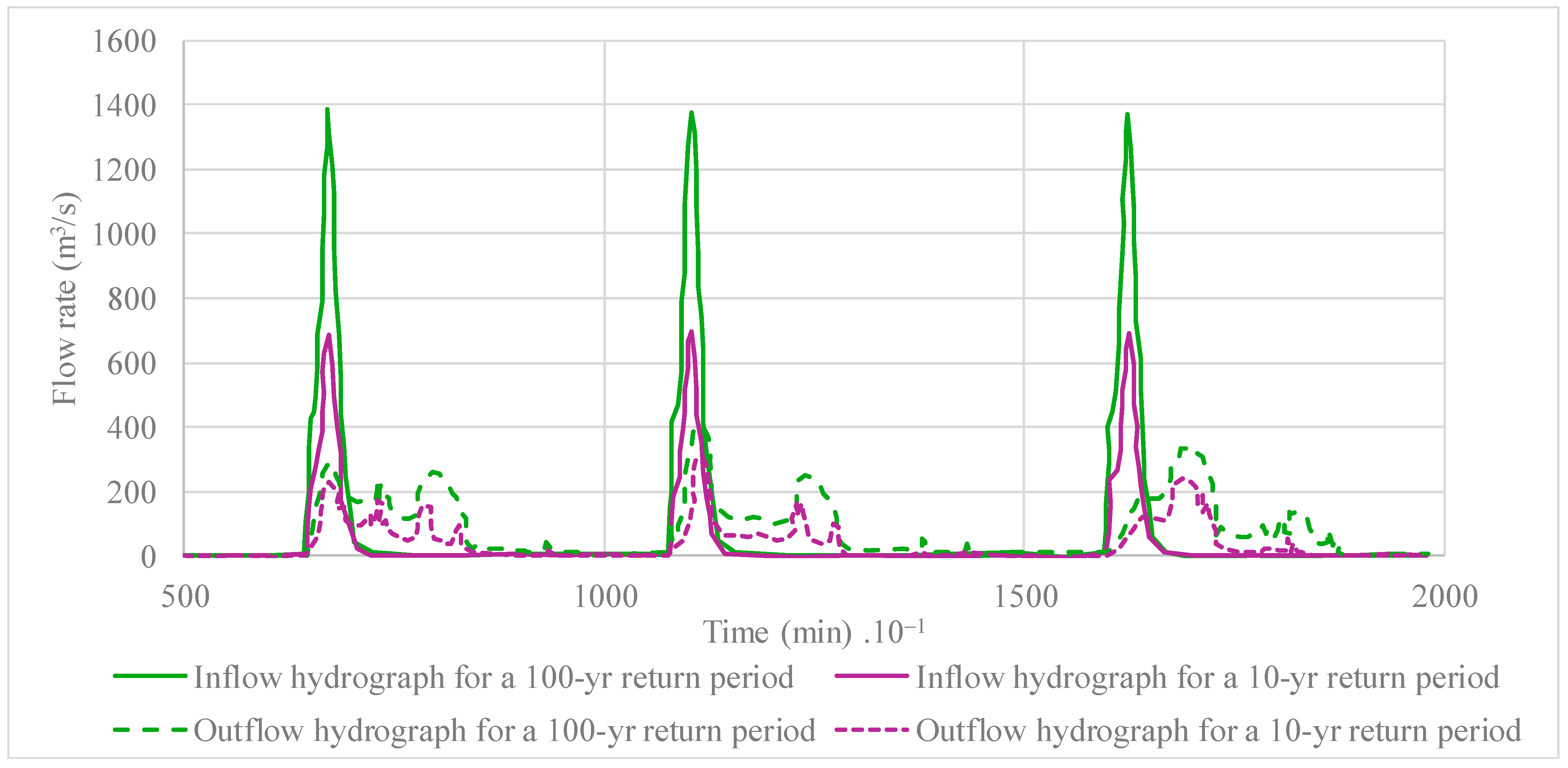
3. Analysis of Results
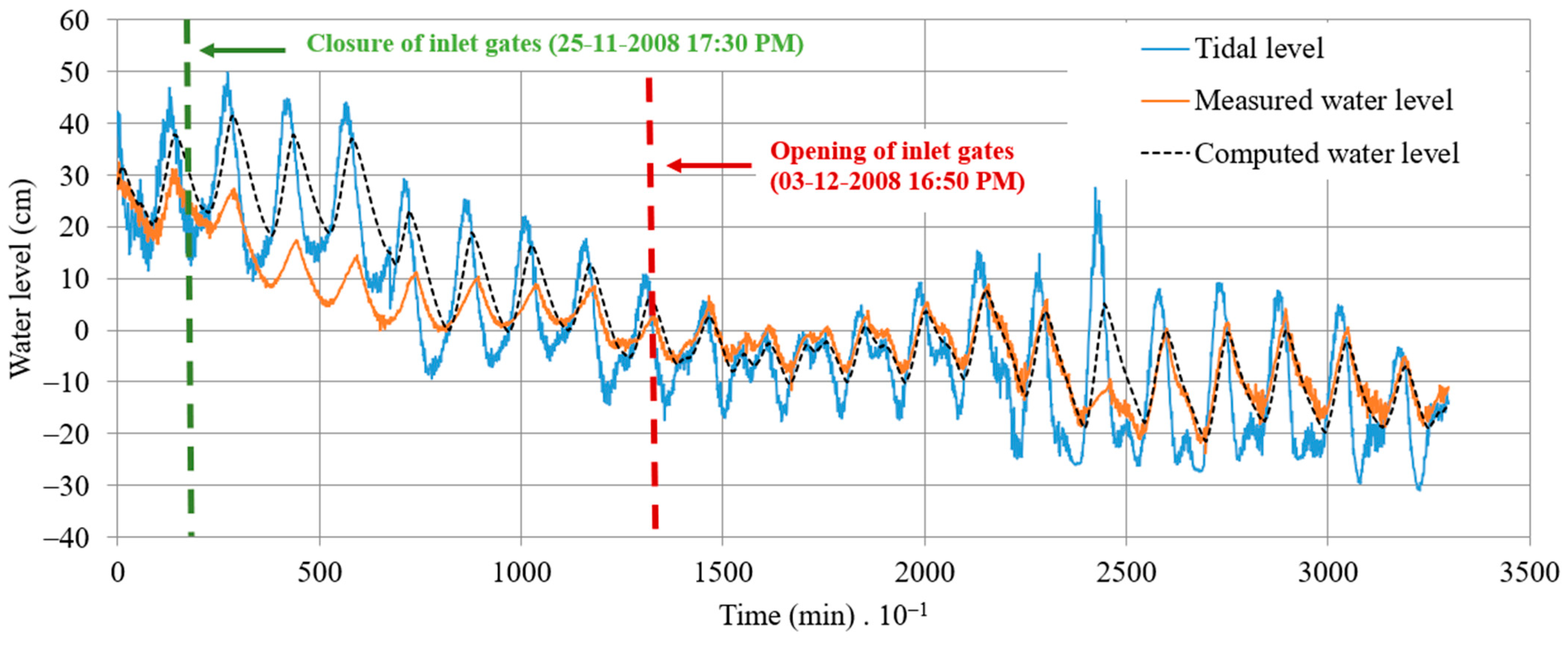
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| surface area of an estuarine system (m2) | |
| B | net width of gates (m) |
| discharge coefficient of a gate (-) | |
| gravitational acceleration (m/s2) | |
| hydraulic head of a gate (m) | |
| flow rate through of a gate (m3/s) | |
| outlet hydrograph in a STIS (m3/s) | |
| hydrograph generated in a watershed of an estuarine system (m3/s) | |
| time (s) | |
| downstream water level (m.a.s.l.) | |
| upstream water level (m.a.s.l.) | |
| average depth of a gate (m) | |
| variation of (m) | |
| time step (s) | |
| variation of stored volume of an estuarine system (m3) | |
| Subscript | |
| 0 | refers to conditions in outlet gates (from an estuarine system towards a sea or ocean) |
| refers to conditions in inlet gates from a sea or ocean towards an estuarine system) | |
References
- Mehta, A.J.; Joshi, P.B. Tidal inlet hydraulics. J. Hydraul. Eng. 1988, 114, 1321–1338. [Google Scholar] [CrossRef]
- Hansen, D.V.; Rattray, M. Gravitational circulation in straits and estuaries. J. Mar. Res. 1965, 23, 104–122. [Google Scholar] [CrossRef]
- Buttolph, A.M.; Reed, C.W.; Kraus, N.C.; Ono, N.; Larson, M.; Camenen, B.; Hanson, H.; Wamsley, T.; Zundel, A.K. Two-Dimensional Depth-Averaged Circulation Model CMS-M2D: Version 3.0, Report 2: Sediment Transport and Morphology Change; ERDC/CHL TR-06, 9; U.S. Army Corps of Engineers: Washington, DC, USA, 2006.
- Provan, M.; Logan, S.; Nistor, I.; Cornett, A.; Drouin, A. Field and numerical investigations of the morpho-hydrodynamic processes of the tidal inlet at Shippagan Gully, New Brunswick, Canada. Coast. Eng. J. 2018, 60, 400–422. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, C.; Vallino, J.; Hopkinson, C.; Beardsley, R.C.; Lin, H.; Lerczak, J. Wetland-estuarine-shelf interactions in the Plum Island Sound and Merrimack River in the Massachusetts coast. J. Geophys. Res. Ocean. 2010, 115, C10. [Google Scholar] [CrossRef]
- Quetzalcóatl, O.; González, M.; Cánovas, V.; Medina, R.; Espejo, A.; Klein, A.; Tessler, M.G.; Almeida, L.R.; Jaramillo, C.; Garnier, R.; et al. SMCε, a coastal modeling system for assessing beach processes and coastal interventions: Application to the Brazilian coast. Environ. Model. Softw. 2019, 116, 131–152. [Google Scholar] [CrossRef]
- Gonzalez, M.; Gutiérrez, O.Q.; Canovas, V.; Kakeh, N.; Medina, R.; Espejo, A.; Méndez, F.; Abascal, A.; Castanedo, S.; Martínez, C.; et al. The new coastal modelling system SMC-BRASIL and its application to the erosional problem in the massaguaçu beach (Sao Paulo, Brazil). Coast. Eng. Proc. 2014, 34, 49. [Google Scholar] [CrossRef]
- Safavi, S.; Saghafian, B.; Hosseini, S.A. Characterizing flow pattern and salinity using the 3D MIKE 3 model: Urmia Lake case study. Arab. J. Geosci. 2020, 13, 115. [Google Scholar] [CrossRef]
- Sivakumar, B.; Puente, C.E.; Maskey, M.L. Complex networks and hydrologic applications. In Advances in Nonlinear Geosciences; Springer: Berlin/Heidelberg, Germany, 2018; pp. 565–586. [Google Scholar] [CrossRef]
- Arrieta, A.; Rejtman, P.; Escorcia, E. Validación de una Nueva Metodología de Simulación Hidrodinamica de Estuarios y Bahías en la Ciénaga de la Virgen de la Ciudad de Cartagena. In Proceedings of the Seminario Internacional La Hidroinformática en la Gestión Integrada de los Recursos Hídricos, Cartagena, Colombia; 2003; pp. 1–4. [Google Scholar]
- Novikov, A.; Bagtzoglou, A.C. Hydrodynamic Model of the Lower Hudson River Estuarine System and its Application for Water Quality Management. Water Resour Manag. 2006, 20, 257–276. [Google Scholar] [CrossRef]
- Hsu, M.; Kuo, A.; Kou, J.; Liu, W. Procedure to calibrate and verify numerical models of estuarine hydrodynamics. J. Hydraul. Eng. 2000, 125, 166–182. [Google Scholar] [CrossRef]
- Levasseur, A.; Shi, L.; Wells, N.; Purdie, D.; Kelly-Gerreyn, B. A three-dimensional hydrodynamic model of estuarine circulation with an application to Southampton Water, UK. Estuar. Coast. Shef Sci. 2007, 73, 753–767. [Google Scholar] [CrossRef]
- Royal Haskoning. Technical Report: Proyecto Bocana Estabilizada en la Ciénaga de la Virgen. Memoria Técnica, Modelación Bidimencional; Royal Haskoning: Cartagena, Colombia, 1996. [Google Scholar]
- Lonin, S.; Yus, T. Water quality model of ecosystem of Cienaga de Tesca coastal lagoon. Ecol. Model. 2001, 144, 279–293. [Google Scholar] [CrossRef]
- El Universal. Emergencias por ‘Iota’ Dejan 155 mil Damnificados en Cartagena. Available online: https://www.eluniversal.com.co/cartagena/emergencias-por-iota-dejan-155-mil-damnificados-en-cartagena-XH3797635 (accessed on 23 February 2024).
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P.; Di Francesco, S.; Abraham, J.P. Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates. Water 2023, 15, 314. [Google Scholar] [CrossRef]
- Lima, M.J.; Barbosa, A.B.; Correia, C.; Matos, A.; Cravo, A. Patterns and Predictors of Phytoplankton Assemblage Structure in a Coastal Lagoon: Species-Specific Analysis Needed to Disentangle Anthropogenic Pressures from Ocean Processes. Water 2023, 15, 4238. [Google Scholar] [CrossRef]
- Weithoff, G.; Beisner, B.E. Measures and Approaches in Trait-Based Phytoplankton Community Ecology—From Freshwater to Marine Ecosystems. Front. Mar. Sci. 2019, 6, 40. [Google Scholar] [CrossRef]
- Law, I.K.; Hii, K.S.; Lau, W.L.S.; Leaw, C.P.; Lim, P.T. Coastal Micro-Phytoplankton Community Changes during the Toxigenic Alexandrium Minutum Blooms in a Semi-Enclosed Tropical Coastal Lagoon (Malaysia, South China Sea). Reg. Stud. Mar. Sci. 2023, 57, 102733. [Google Scholar] [CrossRef]
- Establecimiento Público Ambiental, Distrito de Cartagena de Indias, Colombia. Observatorio Ambiental de Cartagena de Indias. Proyecto Ciénaga de la Virgen. Available online: https://observatorio.epacartagena.gov.co/gestion-ambiental/ecosistemas/proyecto-cienaga-de-la-virgen/cienaga-de-la-virgen/ (accessed on 23 February 2024).
- Global Water. WL16 Water Level Logger. Available online: https://www.ysi.com/wl16 (accessed on 23 February 2024).
- Consorcio Consultores Cartageneros, Alcaldía de Cartagena. Plan Maestro de Drenajes Pluviales de la Ciudad de Cartagena; Distrito de Cartagena de Indias: Cartagena, Colombia, 2008.
- Arrieta-Pastrana, A.; Saba, M.; Alcázar, A.P. Analysis of Climate Variability in a Time Series of Precipitation and Temperature Data: A Case Study in Cartagena de Indias, Colombia. Water 2022, 14, 1378. [Google Scholar] [CrossRef]
- El Universal. Cartagena Sufre por el Paso de la Tormenta Iota por el Caribe. Available online: https://www.eluniversal.com.co/cartagena/cartagena-sufre-por-el-paso-de-la-tormenta-iota-por-el-caribe-HH3797687 (accessed on 23 February 2024).
- Sierra-Sánchez, A.; Coronado-Hernandez, O.E.; Paternina-Verona, D.A.; Gatica, G.; Ramos, H.M. Statistical Analysis to Quantify the Impact of Map Type on Estimating Peak Discharge in Non-Instrumented Basins. Trans. Energy Syst. Eng. Appl. 2023, 4, 1–17. [Google Scholar] [CrossRef]
- Mitu, M.F.; Sofia, G.; Shen, X.; Anagnostou, E.N. Assessing the compound flood risk in coastal areas: Framework formulation and demonstration. J. Hydrol. 2023, 626, 130278. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrieta-Pastrana, A.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S. Analysis of the Impact of Hydraulic Gates on a Stabilized Tidal Inlet Structure: Mathematical Model and Data Measurements. Hydrology 2024, 11, 46. https://doi.org/10.3390/hydrology11040046
Arrieta-Pastrana A, Coronado-Hernández OE, Fuertes-Miquel VS. Analysis of the Impact of Hydraulic Gates on a Stabilized Tidal Inlet Structure: Mathematical Model and Data Measurements. Hydrology. 2024; 11(4):46. https://doi.org/10.3390/hydrology11040046
Chicago/Turabian StyleArrieta-Pastrana, Alfonso, Oscar E. Coronado-Hernández, and Vicente S. Fuertes-Miquel. 2024. "Analysis of the Impact of Hydraulic Gates on a Stabilized Tidal Inlet Structure: Mathematical Model and Data Measurements" Hydrology 11, no. 4: 46. https://doi.org/10.3390/hydrology11040046
APA StyleArrieta-Pastrana, A., Coronado-Hernández, O. E., & Fuertes-Miquel, V. S. (2024). Analysis of the Impact of Hydraulic Gates on a Stabilized Tidal Inlet Structure: Mathematical Model and Data Measurements. Hydrology, 11(4), 46. https://doi.org/10.3390/hydrology11040046






