Hydroclimatic Trends and Streamflow Response to Recent Climate Change: An Application of Discrete Wavelet Transform and Hydrological Modeling in the Passaic River Basin, New Jersey, USA
Abstract
1. Introduction
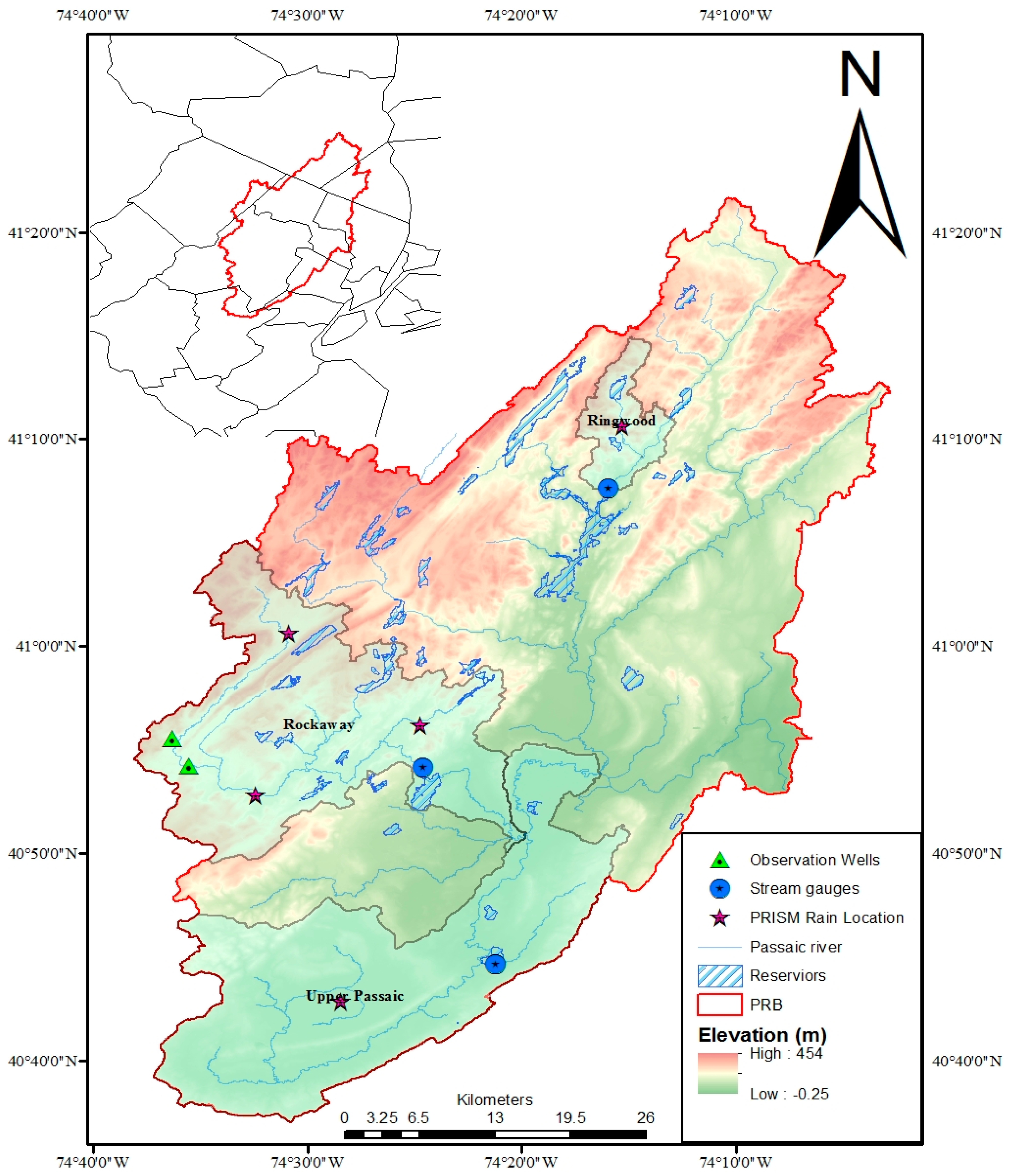
2. Study Area and Data Source
2.1. Study Area
2.2. Hydrometeorological Data
2.3. Land-Use, Soil and Elevation Data
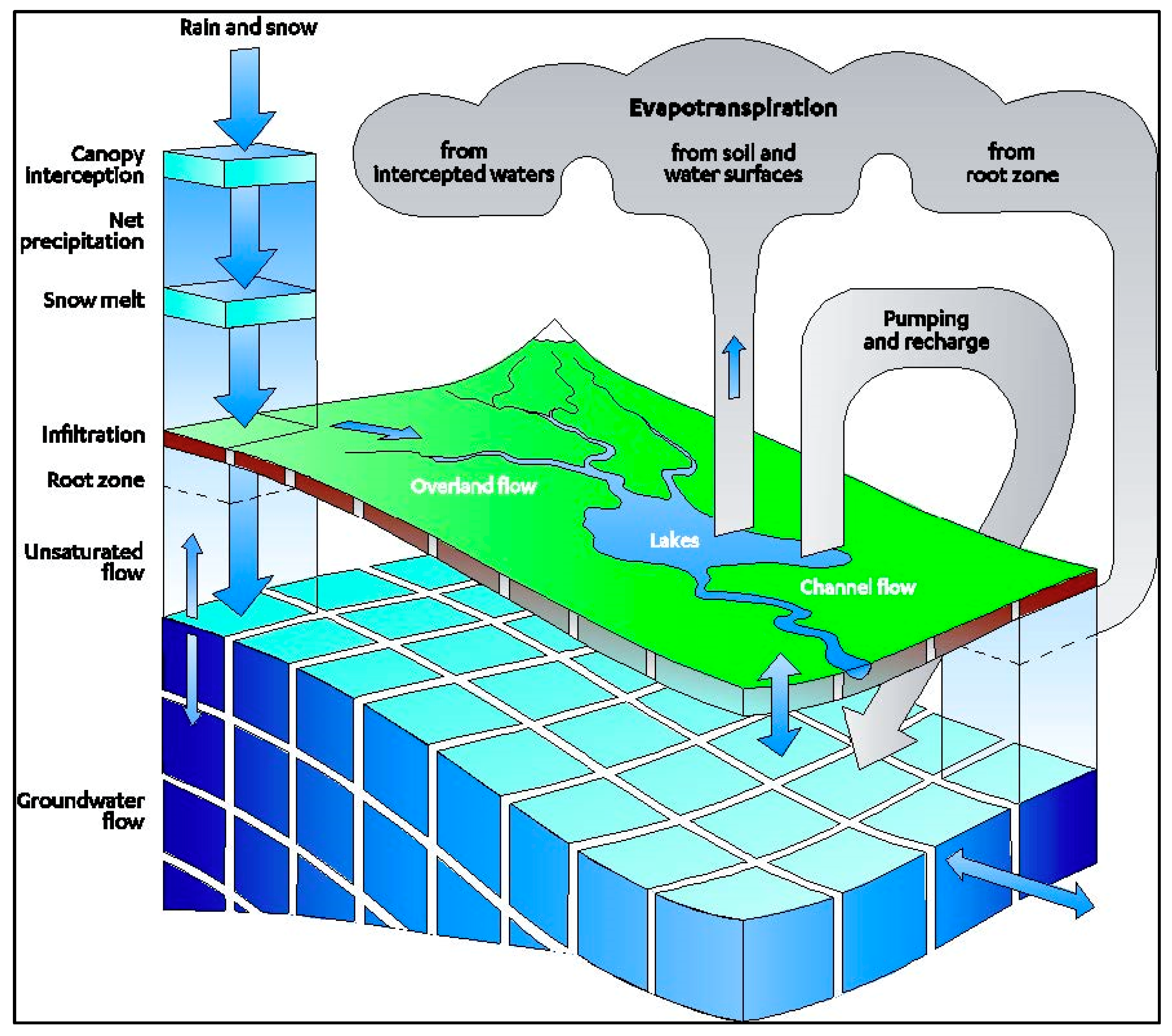
3. Methods
- Seven (7) different hydroclimatic indicator variables used in the trend analysis were derived from temperature, precipitation, and streamflow data series obtained for each subcatchment. They were mean annual Tmin, Tmean, Tmax, Precip, Flow, R10, and CDD spanning the period 1979–2021.
- Each time series was decomposed via the DWT, having selected the Daubechies (db) wavelet, deemed an appropriate mother wavelet in our study context, to split the series into their high frequency detailed (D) and low frequency approximate (A) components.
- The MK Z-values of the original signal and the approximation of each Daubechies (db) wavelet form starting from db4–db10 (e.g., [48]) were computed to determine the wavelet form that gives MK Z-value closer to that of the original signal. This was the optimal trend from the approximation components of each analyzed time series.
- Having selected the optimal monotonic trend, an MK test was subsequently applied to determine the statistical significance of the DWT-based trend.
- A hydrological model for the Rockaway subbasin was developed, calibrated, and validated, and the performance of the model against the observed streamflow and groundwater data was evaluated using standard statistical criterion. The water balance module was run to obtain outputs of water-balance components for the impacts assessment.
- Change point analysis was carried out to divide data into the naturalized or baseline periods, where minimum effects of human activity on streamflow is expected and impacted periods. Subsequently, a climate elasticity exercise was undertaken to explore sensitivities of climate variables to streamflow and corresponding contributions in the Rockaway sub-basin.
3.1. Discrete Wavelet Transform
Time-Series Decomposition via DWT
3.2. Trend and Change-Point Detection Tests
3.3. Hydrological Model Development for the Rockaway River Basin
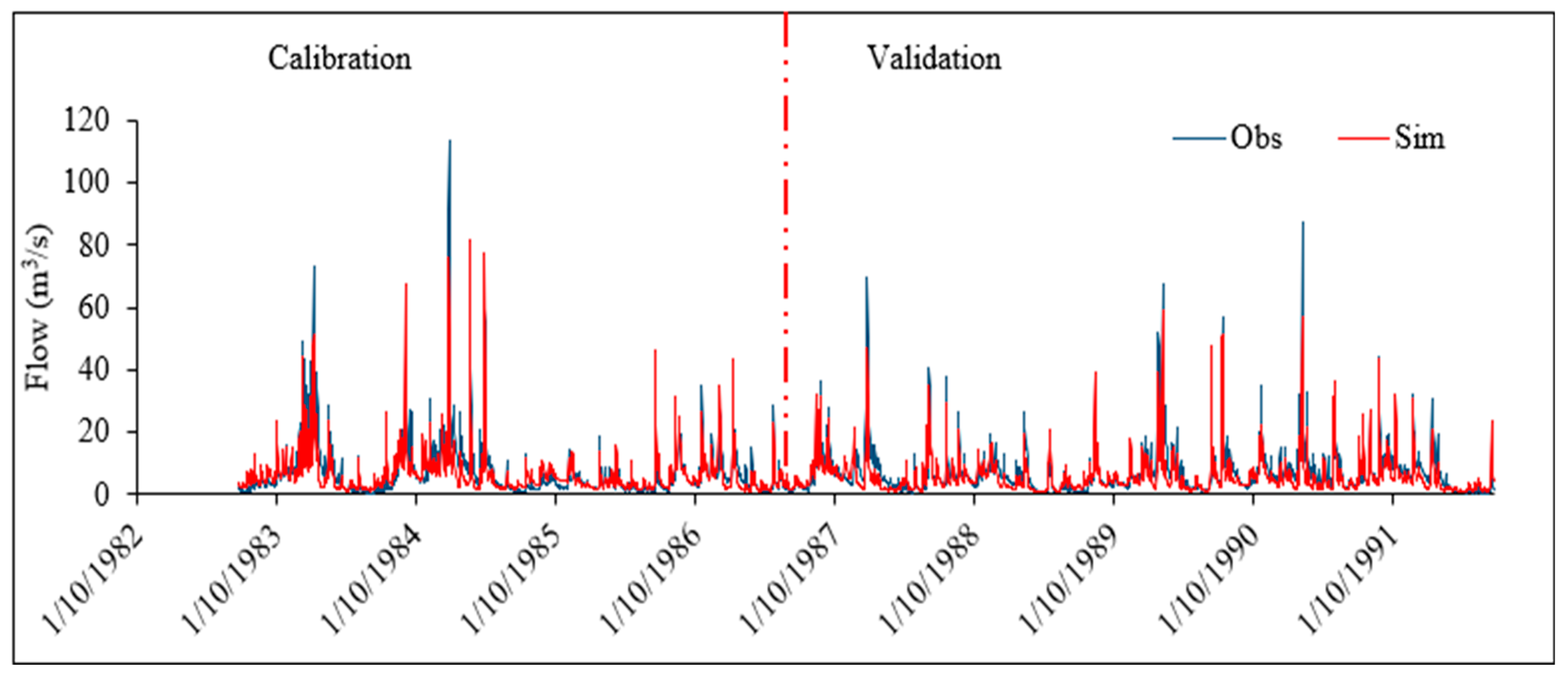
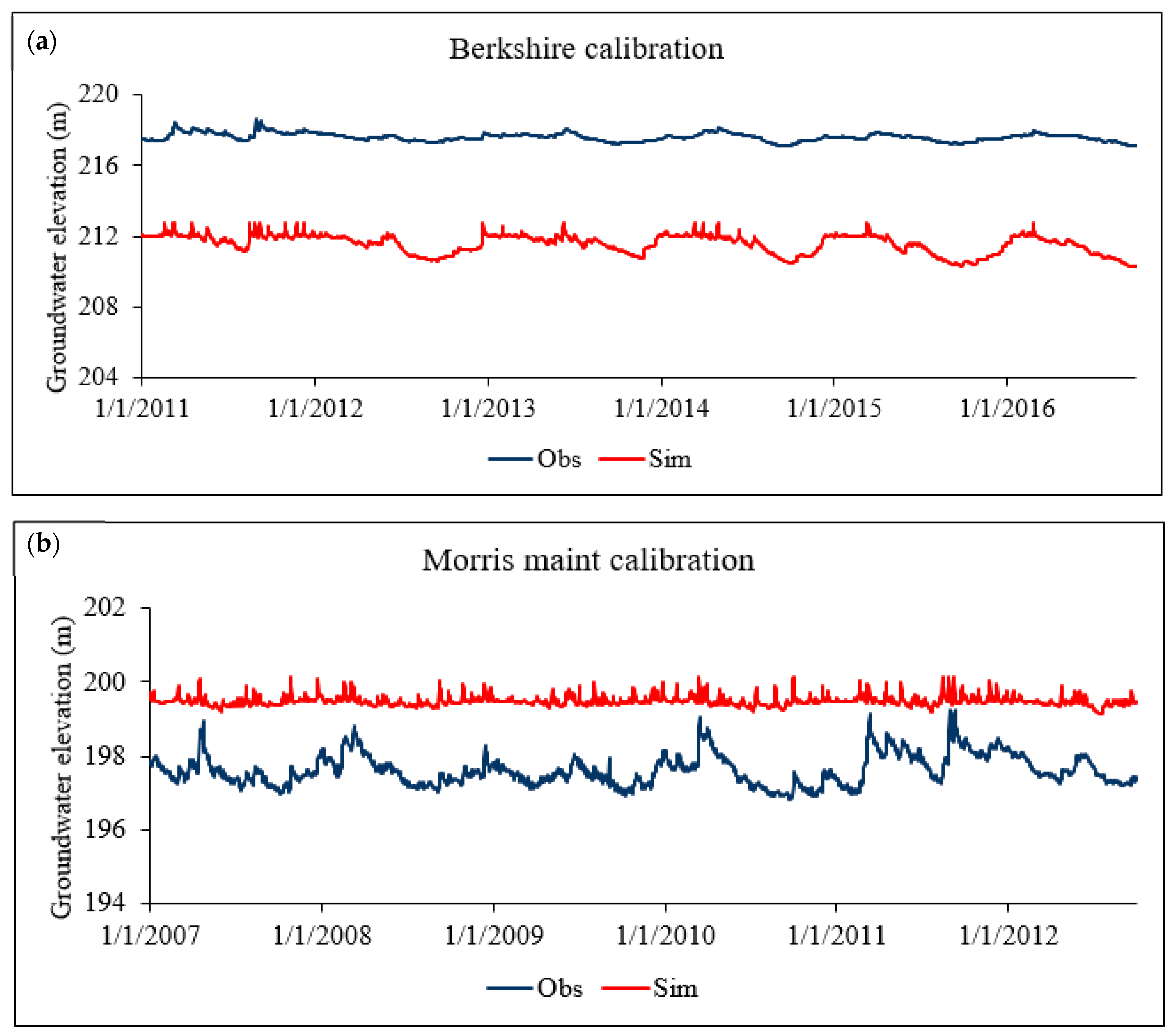
Model Calibration and Validation
3.4. Hydrological Impacts Assessment
4. Results and Discussion
4.1. Decomposition of Time-Series Data via DWT
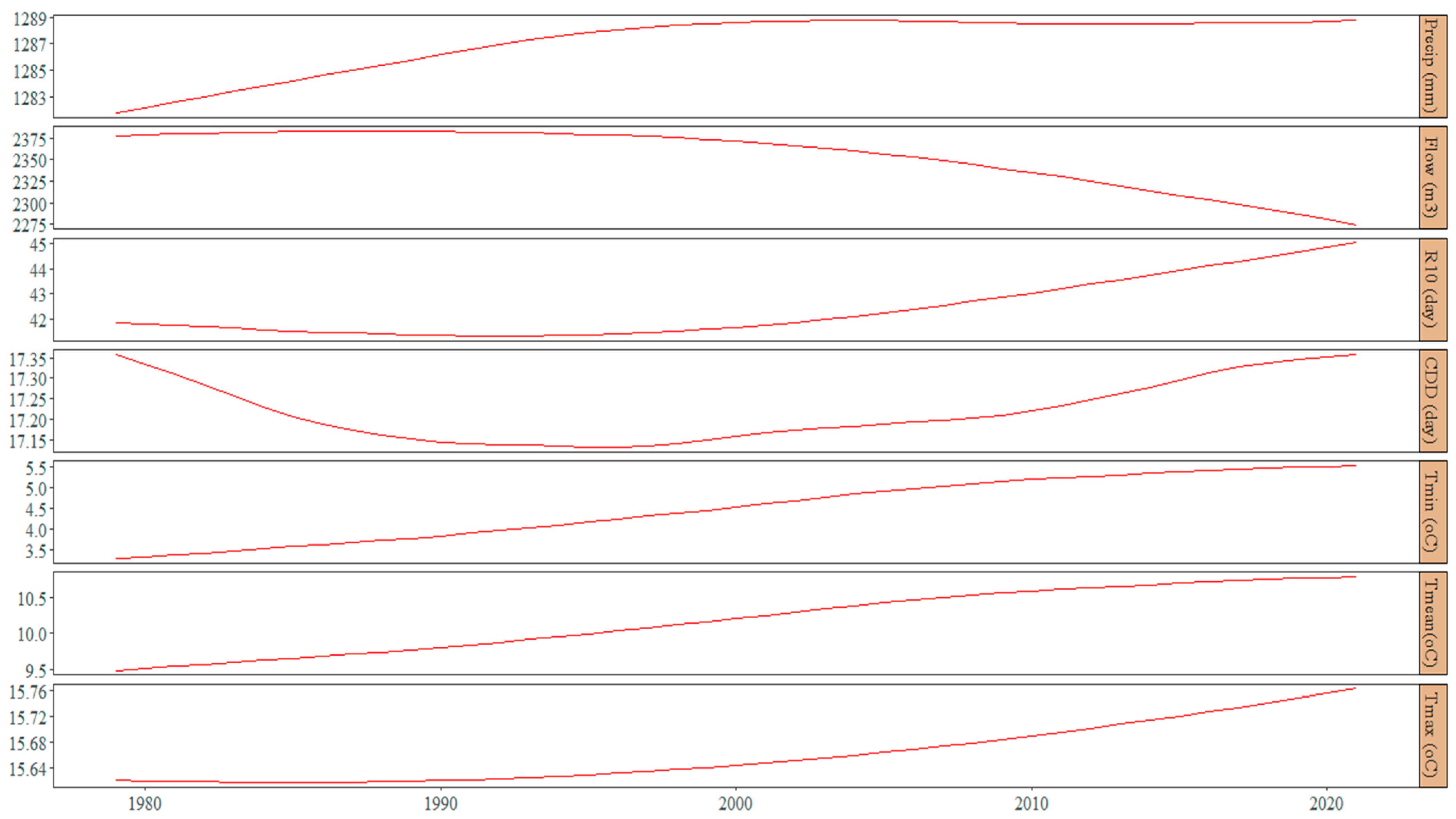
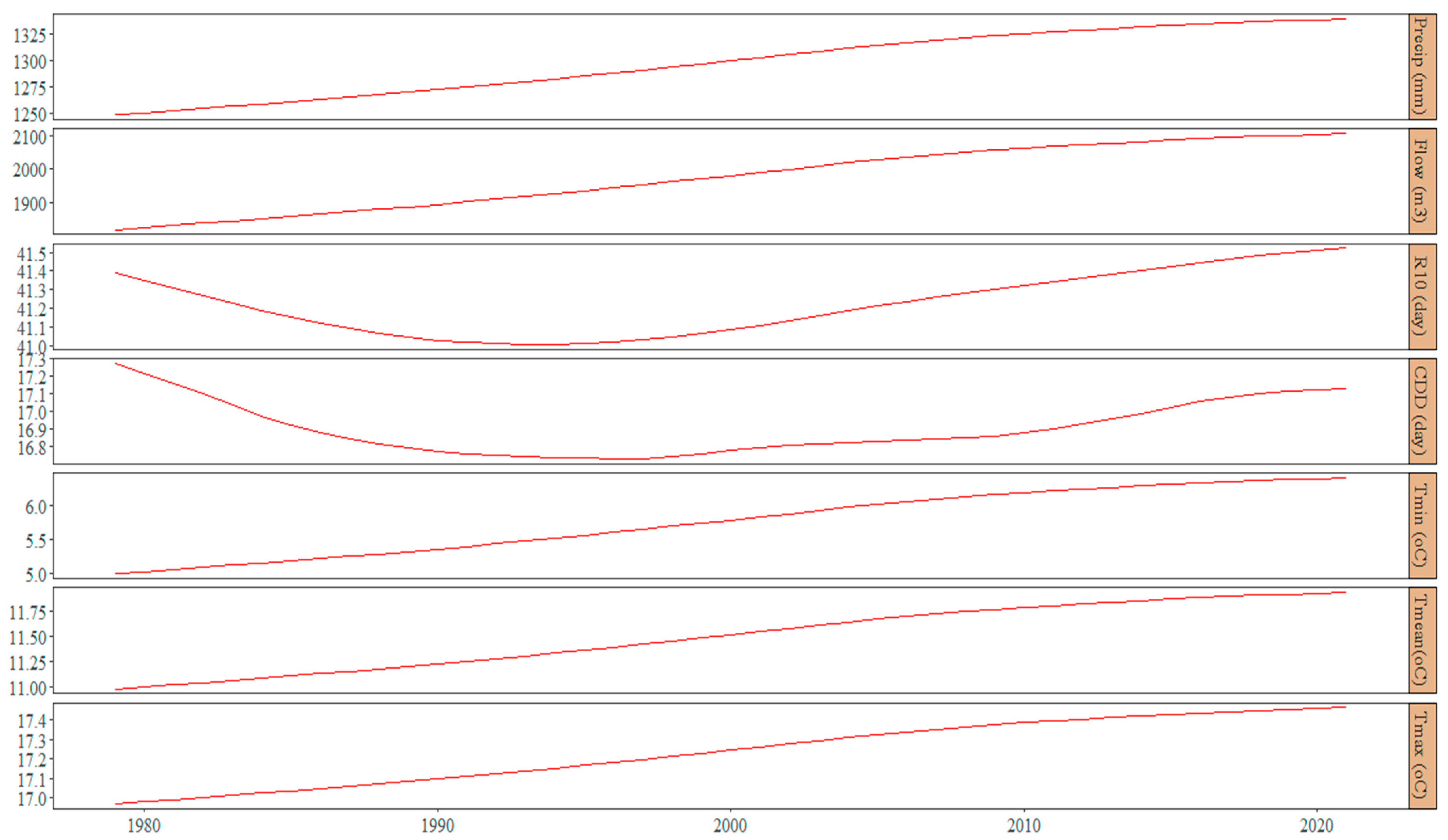
4.1.1. DWT Trend Analysis of Hydroclimatic Indicators
4.1.2. Hydroclimatic Trends in the Ringwood, Rockaway, and Upper Passaic Subcatchments
4.1.3. Comparison of Hydroclimatic Trends by Catchment
4.2. Change Point Analysis and Calibration and Validation of MIKE SHE Model
Change Point Detection
4.3. Calibration and Validation of Rockaway Model
4.3.1. Hydroclimatic Response to Changes Relative to 1982–1991 Baseline, BLP I
4.3.2. Decadal Changes in Hydrometeorological Variables
4.3.3. Hydroclimatic Response to Changes Relative to 1992–2001 Baseline, BLP II
4.3.4. Hydroclimatic Response to Changes Relative to 1982–2001 Baseline, BLP III
5. Summary and Conclusions
- (1)
- Over the period 1979–2021, minimum, mean, and maximum temperatures showed significantly upward trend in all studied subcatchments of the PRB with minimum temperature having the highest rate of change at 0.059 °Cyr−1 in the Rockaway sub-basin. In contrast, maximum temperatures experienced the slowest rate of change at 0.0034 °Cyr−1. Across the PRB, the rate of change in mean temperature ranges from 0.025–0.035 °Cyr−1.
- (2)
- Overall, precipitation showed a significant increasing signal in all analyzed sub-basins with the fastest rate of 0.72 mm/yr in the Ringwood catchment and the slowest rate at 0.13 mm/yr in the Rockaway catchment. This observed long-term increasing trend in precipitation and temperature in the PRB is indicative of a changing climate, consistent with the dominant trends in the broader Northeastern region. Spatially, trends in both precipitation intensity (R10) and consecutive dry days (CDD) were observed to decrease in the uppermost portion of the PRB at the Ringwood catchment but increases towards the south in the Rockaway and Upper Passaic sub-basins. This pattern is also dominant in the wider Northeast, and provide further evidence of the connection between extreme weather events and climate change.
- (3)
- In two out of the three analyzed sub-basins, streamflow displayed significantly downward trends with an increasing trend in the Upper Passaic subcatchment. This is in spite of the increasing trends in both precipitation and temperature in all the three subcatchments. Although it is well established that precipitation amounts and intensity directly affect streamflow [100], the present results rather show that an increase in precipitation does not always lead to an increase in streamflow. From a hydrological modeling standpoint, attempt was therefore made to examine the causes of streamflow in the PRB using the Rockaway subcatchment as a case study.
- (4)
- Decadal changes in climate revealed that the recent decade (2012–2021) was both the warmest and driest period relative to all baseline periods, and compared with the 2001–2011 decade. It showed a mean temperature increase ranging from 1.16 °C in BLP II and 1.29 °C in BLP I. Being the driest period, the recent decade also showed precipitation changing from −1.83% to 6.11% relative to the 1982–1991 and 1992–2001 baselines, respectively. In contrast, the wettest decade was 2002–2011 relative to all baseline periods with precipitation increase ranging from 9.29% in the 1982–1991 baseline to 18.13% in the 1992–2001 baseline.
- (5)
- Relative to the overall baseline period (BLP III), the warmest and the driest decade (2012–2021), having a mean temperature increase of 1.23 °C induced an actual evapotranspiration increase of 5.81% and a marginal precipitation increase of 1.99%, resulting in a 5.97% decrease in streamflow. Similarly, the wettest decade (2002–2011), with mean temperature increase of 0.75 °C relative to the overall baseline period (BPL III), induced an actual evapotranspiration increase of 4.38% and a precipitation of 13.54%, which resulted in a streamflow increase of 9.93%.
- (6)
- Across the three baseline periods, we found that precipitation elasticity to streamflow ranged from 0.96 to 1.35 suggesting that a 10% rise in precipitation will result in between 9.6% to 13.5% increase in streamflow in the study basin. Similarly, evapotranspiration elasticity to streamflow ranged from −2.88 to −0.74 indicating that, a 10% increase in actual ET will lead to between 28.8% to 7.4% decrease in streamflow. The relatively pronounced negative ET elasticity value also reflects the effect of warming climate in the basin. Generally, as temperature increases, ET increases and streamflow decreases. With streamflow showing high sensitivity to actual ET increases more than precipitation, it is safe to conclude that, to a large extent, actual evapotranspiration is more important in the flow dynamics of the PRB in the wake of a warming climate.
- (7)
- The general observation therefore is that in decades where water is available, energy limits actual evapotranspiration which makes streamflow more sensitive to precipitation increase. However, in meteorologically stressed or dry decades, water limits actual ET thereby making streamflow more sensitive to increases in actual evapotranspiration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pumo, D.; Francipane, A.; Cannarozzo, M.; Antinoro, C.; Valerio Noto, L. Monthly Hydrological Indicators to Assess Possible Alterations on Rivers’ Flow Regime. Water Resour. Manag. 2018, 32, 3687–3706. [Google Scholar] [CrossRef]
- Naderi, M.; Sheikh, V.; Bahrehmand, A.; Komaki, C.B.; Ghangermeh, A. Analysis of River Flow Regime Changes Using the Indicators of Hydrologic Alteration (Case Study: Hableroud Watershed). Water Soil. Manag. Model. 2023, 3, 1–19. [Google Scholar] [CrossRef]
- Rasouli, K.; Scharold, K.; Mahmood, T.H.; Glenn, N.F.; Marks, D. Linking Hydrological Variations at Local Scales to Regional Climate Teleconnection Patterns. Hydrol. Process 2020, 34, 5624–5641. [Google Scholar] [CrossRef]
- Khan, F.; Ali, S.; Mayer, C.; Ullah, H.; Muhammad, S. Climate Change and Spatio-Temporal Trend Analysis of Climate Extremes in the Homogeneous Climatic Zones of Pakistan during 1962–2019. PLoS ONE 2022, 17, e0271626. [Google Scholar] [CrossRef]
- Rahaman, M.H.; Saha, T.K.; Masroor, M.; Roshani; Sajjad, H. Trend Analysis and Forecasting of Meteorological Variables in the Lower Thoubal River Watershed, India Using Non-Parametrical Approach and Machine Learning Models. Model. Earth Syst. Environ. 2024, 10, 551–577. [Google Scholar] [CrossRef]
- Banda, V.D.; Dzwairo, R.B.; Singh, S.K.; Kanyerere, T. Trend Analysis of Selected Hydro-Meteorological Variables for the Rietspruit Sub-Basin, South Africa. J. Water Clim. Change 2021, 12, 3099–3123. [Google Scholar] [CrossRef]
- Salaudeen, A.R.; Shahid, S.; Ismail, A.; Adeogun, B.K.; Ajibike, M.A.; Bello, A.A.D.; Salau, O.B.E. Adaptation Measures under the Impacts of Climate and Land-Use/Land-Cover Changes Using HSPF Model Simulation: Application to Gongola River Basin, Nigeria. Sci. Total Environ. 2023, 858, 159874. [Google Scholar] [CrossRef]
- Banda, V.D.; Dzwairo, R.B.; Singh, S.K.; Kanyerere, T. Hydrological Modelling and Climate Adaptation under Changing Climate: A Review with a Focus in Sub-Saharan Africa. Water 2022, 14, 4031. [Google Scholar] [CrossRef]
- Wang, N.; Yang, J.; Zhang, Z.; Xiao, Y.; Wang, H.; He, J.; Yi, L. Analysis of Detailed Lake Variations and Associated Hydrologic Driving Factors in a Semi-Arid Ungauged Closed Watershed. Sustainability 2023, 15, 6535. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S.; Zhu, W. Analysis of Climate Variability, Trends, and Prediction in the Most Active Parts of the Lake Chad Basin, Africa. Sci. Rep. 2019, 9, 6317 . [Google Scholar] [CrossRef]
- Gadedjisso-Tossou, A.; Adjegan, K.I.I.; Kablan, A.K.M. Rainfall and Temperature Trend Analysis by Mann–Kendall Test and Significance for Rainfed Cereal Yields in Northern Togo. Sci 2021, 3, 17. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, F.; Gao, G.; Jim, C.Y.; Leong Tan, M.; Shi, J.; Wang, W.; Zhao, Q. Spatio-Temporal Variability and Trend of Blue-Green Water Resources in the Kaidu River Basin, an Arid Region of China. J. Hydrol. Reg. Stud. 2024, 51, 101640. [Google Scholar] [CrossRef]
- Sanson, A.V.; Van Hoorn, J.; Burke, S.E.L. Responding to the Impacts of the Climate Crisis on Children and Youth. Child. Dev. Perspect. 2019, 13, 201–207. [Google Scholar] [CrossRef]
- Ojala, M.; Cunsolo, A.; Ogunbode, C.A.; Middleton, J. Anxiety, Worry, and Grief in a Time of Environmental and Climate Crisis: A Narrative Review. Annu. Rev. Environ. Resour. 2021, 46, 35–58. [Google Scholar] [CrossRef]
- Campbell, J.L.; Driscoll, C.T.; Pourmokhtarian, A.; Hayhoe, K. Streamflow Responses to Past and Projected Future Changes in Climate at the Hubbard Brook Experimental Forest, New Hampshire, United States. Water Resour. Res. 2011, 47, 2514. [Google Scholar] [CrossRef]
- Sharma, S.; Swayne, D.A.; Obimbo, C. Trend Analysis and Change Point Techniques: A Survey. Energy Ecol. Environ. 2016, 1, 123–130. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Yang, D.; Tong, K.; Hao, Z. Impacts of Recent Climate Change on the Hydrology in the Source Region of the Yellow River Basin. J. Hydrol. Reg. Stud. 2016, 6, 66–81. [Google Scholar] [CrossRef]
- Suhaila, J.; Yusop, Z. Trend Analysis and Change Point Detection of Annual and Seasonal Temperature Series in Peninsular Malaysia. Meteorol. Atmos. Phys. 2018, 130, 565–581. [Google Scholar] [CrossRef]
- Citakoglu, H.; Minarecioglu, N. Trend Analysis and Change Point Determination for Hydro-Meteorological and Groundwater Data of Kizilirmak Basin. Theor. Appl. Clim. 2021, 145, 1275–1292. [Google Scholar] [CrossRef]
- Tekleab, S.; Mohamed, Y.; Uhlenbrook, S. Hydro-Climatic Trends in the Abay/Upper Blue Nile Basin, Ethiopia. Phys. Chem. Earth 2013, 61–62, 32–42. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation Trends over Time Using Mann-Kendall and Spearman’s Rho Tests in Swat River Basin, Pakistan. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Alhaji, U.U.; Yusuf, A.S.; Edet, C.O.; Oche, C.O.; Agbo, E.P. Trend Analysis of Temperature in Gombe State Using Mann Kendall Trend Test. J. Phys. Conf. Ser. 2018, 1734, 012016. [Google Scholar] [CrossRef]
- Basarir, A.; Arman, H.; Hussein, S.; Murad, A.; Aldahan, A.; Al-Abri, M.A. Trend Detection in Annual Temperature and Precipitation Using Mann–Kendall Test—a Case Study to Assess Climate Change in Abu Dhabi, United Arab Emirates. Lect. Notes Civ. Eng. 2018, 7, 3–12. [Google Scholar]
- Bezerra, J.; Júnior, C.; Lucena, R.L. Analysis of Precipitation Using Mann-Kendall and Kruskal-Wallis Non-Parametric Tests. Mercator 2020, 19, 1. [Google Scholar] [CrossRef]
- Seenu, P.Z.; Jayakumar, K.V. Comparative Study of Innovative Trend Analysis Technique with Mann-Kendall Tests for Extreme Rainfall. Arab. J. Geosci. 2021, 14, 1–15. [Google Scholar]
- Sa’adi, Z.; Shahid, S.; Ismail, T.; Chung, E.S.; Wang, X.J. Trend Analysis of the Variations of Ambient Temperature Using Mann-Kendall Test and Sen’s Estimate in Calabar, Southern Nigeria. Meteorol. Atmos. Phys. 2019, 131, 263–277. [Google Scholar] [CrossRef]
- Fatichi, S.; Barbosa, S.M.; Caporali, E.; Silva, M.E. Deterministic versus Stochastic Trends: Detection and Challenges. J. Geophys. Res. Atmos. 2009, 114, 1–11. [Google Scholar] [CrossRef]
- Lutgens, F.K.; Tarbuck, E.J. The Atmosphere: An Introduction to Meteorology; Prentice Hall: Kent, OH, USA, 2010; p. 508. [Google Scholar]
- Sang, Y.F.; Sun, F.; Singh, V.P.; Xie, P.; Sun, J. A Discrete Wavelet Spectrum Approach for Identifying Non-Monotonic Trends in Hydroclimate Data. Hydrol. Earth Syst. Sci. 2018, 22, 757–766. [Google Scholar] [CrossRef]
- Araghi, A.; Mousavi Baygi, M.; Adamowski, J.; Malard, J.; Nalley, D.; Hasheminia, S.M. Using Wavelet Transforms to Estimate Surface Temperature Trends and Dominant Periodicities in Iran Based on Gridded Reanalysis Data. Atmos. Res. 2015, 155, 52–72. [Google Scholar] [CrossRef]
- Hernandez, E.; Weiss, G. A First Course on Wavelets; CRC Press: Boca Raton, FL, USA, 1996; ISBN 9780367802349. [Google Scholar]
- Kirchgässner, G.; Wolters, J. Introduction to Modern Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 9783540732907. [Google Scholar]
- Nalley, D.; Adamowski, J.; Khalil, B. Using Discrete Wavelet Transforms to Analyze Trends in Streamflow and Precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Abebe, S.A.; Qin, T.; Zhang, X.; Yan, D. Wavelet Transform-Based Trend Analysis of Streamflow and Precipitation in Upper Blue Nile River Basin. Reg. Stud. 2022, 44, 2214–5818. [Google Scholar] [CrossRef]
- Nourani, V.; Danandeh Mehr, A.; Azad, N. Trend Analysis of Hydroclimatological Variables in Urmia Lake Basin Using Hybrid Wavelet Mann-Kendall and Şen Tests. Environ. Earth Sci. 2018, 77, 207. [Google Scholar] [CrossRef]
- Das, J.; Mandal, T.; Sakiur Rahman, A.T.M.; Saha, P. Spatio-Temporal Characterization of Rainfall in Bangladesh: An Innovative Trend and Discrete Wavelet Transformation Approaches. Theor. Appl. Clim. 2021, 143, 1557–1579. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, J.; Yu, H.; Liu, D.; Xie, K.; Chen, Y.; Hu, J.; Sun, H.; Xing, F. The Development of a Hybrid Wavelet-ARIMA-LSTM Model for Precipitation Amounts and Drought Analysis. Atmosphere 2021, 12, 74. [Google Scholar] [CrossRef]
- Karbasi, M.; Jamei, M.; Malik, A.; Kisi, O.; Yaseen, Z.M. Multi-Steps Drought Forecasting in Arid and Humid Climate Environments: Development of Integrative Machine Learning Model. Agric. Water Manag. 2023, 281, 108210. [Google Scholar] [CrossRef]
- Labat, D. Recent Advances in Wavelet Analyses: Part 1. A Review of Concepts. J. Hydrol. 2005, 314, 275–288. [Google Scholar] [CrossRef]
- Gardner, R.H.; Urban, D.L. Model Validation and Testing: Past Lessons, Present Concerns, Future Prospects. Models Ecosyst. Sci. 2021, 184–203. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Barford, C.C.; Maayar, M.E.; Wofsy, S.C.; Monson, R.K.; Baldocchi, D.D. A Multiyear Evaluation of a Dynamic Global Vegetation Model at Three AmeriFlux Forest Sites: Vegetation Structure, Phenology, Soil Temperature, and CO2 and H2O Vapor Exchange. Ecol. Model. 2006, 196, 1–31. [Google Scholar] [CrossRef]
- Brydon, N.F. The Passaic River: Past, Present, Future; Rutgers Univ Press: New Brunswick, NJ, USA, 1974; ISBN 9780813507705. [Google Scholar]
- Karmalkar, A.V.; Bradley, R.S. Consequences of Global Warming of 1.5 °C and 2 °C for Regional Temperature and Precipitation Changes in the Contiguous United States. PLoS ONE 2017, 12, e0168697. [Google Scholar] [CrossRef]
- USGCRP. Fourth National Climate Assessment; USGCRP: Washington, DC, USA, 2018. [Google Scholar]
- Campbell, J.L.; Ollinger, S.V.; Flerchinger, G.N.; Wicklein, H.; Hayhoe, K.; Bailey, A.S. Past and Projected Future Changes in Snowpack and Soil Frost at the Hubbard Brook Experimental Forest, New Hampshire, USA. Hydrol. Process 2010, 24, 2465–2480. [Google Scholar] [CrossRef]
- Oteng Mensah, F.; Alo, C.A. Modeling Monthly Actual Evapotranspiration: An Application of Geographically Weighted Regression Technique in the Passaic River Basin. J. Water Clim. Change 2023, 14, 17–37. [Google Scholar] [CrossRef]
- Hickman, R.E.; McHugh, A.R. Methods Used to Reconstruct Historical Daily Streamflows in Northern New Jersey and Southeastern New York, Water Years 1922–2010; US Geological Survey: Reston, VA, USA, 2018. [Google Scholar]
- Adarsh, S.; Janga Reddy, M. Trend Analysis of Rainfall in Four Meteorological Subdivisions of Southern India Using Nonparametric Methods and Discrete Wavelet Transforms. Int. J. Climatol. 2015, 35, 1107–1124. [Google Scholar] [CrossRef]
- Li, M.; Xia, J.; Chen, Z.; Meng, D.; Xu, C. Variation Analysis of Precipitation during Past 286 Years in Beijing Area, China, Using Non-Parametric Test and Wavelet Analysis. Hydrol. Process 2013, 27, 2934–2943. [Google Scholar] [CrossRef]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F. A Wavelet Neural Network Conjunction Model for Groundwater Level Forecasting. J. Hydrol. 2011, 407, 28–40. [Google Scholar] [CrossRef]
- Adamowski, J.F. Development of a Short-Term River Flood Forecasting Method for Snowmelt Driven Floods Based on Wavelet and Cross-Wavelet Analysis. J. Hydrol. 2008, 353, 247–266. [Google Scholar] [CrossRef]
- Chellali, F.; Khellaf, A.; Belouchrani, A. Wavelet Spectral Analysis of the Temperature and Wind Speed Data at Adrar, Algeria. Renew. Energy 2010, 35, 1214–1219. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Trend Detection in Surface Air Temperature in Ontario and Quebec, Canada during 1967-2006 Using the Discrete Wavelet Transform. Atmos. Res. 2013, 132–133, 375–398. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend Analysis in Turkish Precipitation Data. Hydrol. Process 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Partal, T.; Küçük, M. Long-Term Trend Analysis Using Discrete Wavelet Components of Annual Precipitations Measurements in Marmara Region (Turkey). Phys. Chem. Earth 2006, 31, 1189–1200. [Google Scholar] [CrossRef]
- Dong, X.; Nyren, P.; Patton, B.; Nyren, A.; Richardson, J.; Maresca, T. Wavelets for Agriculture and Biology: A Tutorial with Applications and Outlook. Bioscience 2008, 58, 445–453. [Google Scholar] [CrossRef]
- Roushangar, K.; Alizadeh, F. Identifying Complexity of Annual Precipitation Variation in Iran during 1960-2010 Based on Information Theory and Discrete Wavelet Transform. Stoch. Environ. Res. Risk Assess. 2018, 32, 1205–1223. [Google Scholar] [CrossRef]
- Wu, D.Q.; Tan, J.; Guo, F.; Li, H.; Chen, S.; Jiang, S. Multi-Scale Identification of Urban Landscape Structure Based on Two-Dimensional Wavelet Analysis: The Case of Metropolitan Beijing, China. Ecol. Complex. 2020, 43, 100832. [Google Scholar] [CrossRef]
- Turgay, P. Wavelet Transform-Based Analysis of Periodicities and Trends of Sakarya Basin (Turkey) Streamflow Data. River Res. Appl. 2010, 26, 695–711. [Google Scholar] [CrossRef]
- Venkata Ramana, R.; Krishna, B.; Kumar, S.R.; Pandey, N.G. Monthly Rainfall Prediction Using Wavelet Neural Network Analysis. Water Resour. Manag. 2013, 27, 3697–3711. [Google Scholar] [CrossRef]
- Vonesch, C.; Blu, T.; Unser, M. Generalized Daubechies Wavelet Families. IEEE Trans. Signal Process. 2007, 55, 4415–4429. [Google Scholar] [CrossRef]
- Adamowski, K.; Prokoph, A.; Adamowski, J. Development of a New Method of Wavelet Aided Trend Detection and Estimation. Hydrol. Process 2009, 23, 2686–2696. [Google Scholar] [CrossRef]
- Su, H.U.; Quan, L.I.U.; Jingsong, L.I. Alleviating Border Effects in Wavelet Transforms for Nonlinear Time-Varying Signal Analysis. Adv. Electr. Comput. Eng. 2011, 11, 55–60. [Google Scholar] [CrossRef]
- de Artigas, M.Z.; Elias, A.G.; de Campra, P.F. Discrete Wavelet Analysis to Assess Long-Term Trends in Geomagnetic Activity. Phys. Chem. Earth 2006, 31, 77–80. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods. In Public Program Analysis; Springer: Berlin/Heidelberg, Germany, 1948. [Google Scholar]
- Liu, Z.; Menzel, L. Identifying Long-Term Variations in Vegetation and Climatic Variables and Their Scale-Dependent Relationships: A Case Study in Southwest Germany. Glob. Planet. Change 2016, 147, 54–66. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Mcbean, E.; Motiee, H. Assessment of Impacts of Climate Change on Water Resources ? A Case Study of the Great Lakes of North America. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3183–3209. [Google Scholar]
- Hamed, K.H.; Ramachandra Rao, A. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, X.; Mu, X.; Wang, F.; Li, R.; Zhang, X. Analyses Des Tendances et Des Points de Changement Dans Les Débits d’eau et de Sédiments Du Fleuve Jaune de 1950 à 2005. Hydrol. Sci. J. 2010, 55, 275–285. [Google Scholar] [CrossRef]
- Guo, L.P.; Yu, Q.; Gao, P.; Nie, X.F.; Liao, K.T.; Chen, X.L.; Hu, J.M.; Mu, X.M. Trend and Change-Point Analysis of Streamflow and Sediment Discharge of the Gongshui River in China during the Last 60 Years. Water 2018, 10, 1273. [Google Scholar] [CrossRef]
- Sneyers, R. On the Statistical Analysis of Series of Observations; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1990; ISBN 9789263104151. [Google Scholar]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. Appl. Stat. 1979, 28, 126. [Google Scholar] [CrossRef]
- Inclán, C.; Tiao, G.C. Use of Cumulative Sums of Squares for Retrospective Detection of Changes of Variance. J. Am. Stat. Assoc. 1994, 89, 913–923. [Google Scholar] [CrossRef]
- Worsley, K.J. On the Likelihood Ratio Test for a Shift in Location of Normal Populations. J. Am. Stat. Assoc. 1979, 74, 365–367. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Csörgö, M.; Horváth, L. Limit Theorems in Change-Point Analysis; Wiley: Hoboken, NJ, USA, 1997; ISBN 978-0-471-95522-1. [Google Scholar]
- Matteson, D.S.; James, N.A. A Nonparametric Approach for Multiple Change Point Analysis of Multivariate Data. J. Am. Stat. Assoc. 2014, 109, 334–345. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- DHI Mike Zero User’s Guide; MIKE By DHI: Harsholm, Denmark, 2017.
- Refsgaard, J.C. Parameterisation, Calibration and Validation of Distributed Hydrological Models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Butts, M.; von Christierson, B.; Mackay, C.; Machés, D.M.; van Kalken, T.; Rasmussen, M.L. Simulating Flood Behaviour Using an Integrated Surface Water-Groundwater Model; DHI: Hoersholm, Denmark, 2015; Volume 16. [Google Scholar]
- Singh, V.P. (Ed.) Computer Models of Watershed Hydrology; Water Resources Publications: Sacramento, CA, USA, 1995; p. 1130. [Google Scholar]
- Schaake, J.; Waggoner, P. From Climate to Flow. In Climate Change and US Water Resources; John Wiley and Sons Inc.: New York, NY, USA, 1990. [Google Scholar]
- Ma, N.; Szilagyi, J. The CR of Evaporation: A Calibration-Free Diagnostic and Benchmarking Tool for Large-Scale Terrestrial Evapotranspiration Modeling. Water Resour. Res. 2019, 55, 7246–7274. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Q.; Tian, F.; Zhang, Z.; Liu, G. Responses of Natural Runoff to Recent Climatic Variations in the Yellow River Basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 4471–4480. [Google Scholar] [CrossRef]
- Vano, J.A.; Das, T.; Lettenmaier, D.P. Hydrologic Sensitivities of Colorado River Runoff to Changes in Precipitation and Temperature. J. Hydrometeorol. 2012, 13, 932–949. [Google Scholar] [CrossRef]
- Hayhoe, K.; Wake, C.P.; Huntington, T.G.; Luo, L.; Schwartz, M.D.; Sheffield, J.; Wood, E.; Anderson, B.; Bradbury, J.; DeGaetano, A.; et al. Past and Future Changes in Climate and Hydrological Indicators in the US Northeast. Clim. Dyn. 2007, 28, 381–407. [Google Scholar] [CrossRef]
- Lynch, C.; Seth, A.; Thibeault, J. Recent and Projected Annual Cycles of Temperature and Precipitation in the Northeast United States from CMIP5. J. Clim. 2016, 29, 347–365. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.W.; Wolter, K.; Cheng, L. Characterizing Recent Trends in U.S. Heavy Precipitation. J. Clim. 2016, 29, 2313–2332. [Google Scholar] [CrossRef]
- Thibeault, J.M.; Seth, A. Changing Climate Extremes in the Northeast United States: Observations and Projections from CMIP5. Clim. Change 2014, 127, 273–287. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Robeson, S.M.; Knouft, J.H. Impacts of Recent Climate Change on Trends in Baseflow and Stormflow in United States Watersheds. Geophys. Res. Lett. 2016, 43, 5079–5088. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R.; Lo, K.; Lea, D.W.; Medina-Elizade, M. Global Temperature Change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef] [PubMed]
- Ajjur, S.B.; Al-Ghamdi, S.G. Evapotranspiration and Water Availability Response to Climate Change in the Middle East and North Africa. Clim. Change 2021, 166, 28. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. Roots, Storms and Soil Pores: Incorporating Key Ecohydrological Processes into Budyko’s Hydrological Model. J. Hydrol. 2012, 436–437, 35–50. [Google Scholar] [CrossRef]
- Ma, L.; He, C.; Bian, H.; Sheng, L. MIKE SHE Modeling of Ecohydrological Processes: Merits, Applications, and Challenges. Ecol. Eng. 2016, 96, 137–149. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding Predictive Uncertainty in Hydrologic Modeling: The Challenge of Identifying Input and Structural Errors. Water Resour. Res. 2010, 46, 1–22. [Google Scholar] [CrossRef]
- Lan, Y.; Zhao, G.; Zhang, Y.; Wen, J.; Liu, J.; Hu, X. Response of Runoff in the Source Region of the Yellow River to Climate Warming. Quat. Int. 2010, 226, 60–65. [Google Scholar] [CrossRef]


| Drainage Area (sqkm) | Area (% of PRB) | Annual Flow (m3s) | Temperature (°C) | Precipitation (mm) | |
|---|---|---|---|---|---|
| Mean (Min–Max) | |||||
| PRB | 2135 | - | 402,088 (30,968–958,992) | 10.59 | 1281 |
| RA | 300.4 | 14.07 | 2513 (611–4037) | 9.52 | 1296 |
| RW | 46.4 | 2.17 | 337 (122–721) | 9.74 | 1298 |
| UP | 356.3 | 16.67 | 1916 (344–2977) | 11.11 | 1269 |
| Subcatchment | Parameter | Metrics | ||||||
|---|---|---|---|---|---|---|---|---|
| Precip | Flow | R10 | CDD | Tmin | Tmean | Tmax | ||
| Ringwood | Wavelets | db7 | db6 | db8 | db5 | db4 | db4 | db4 |
| RE | 3.75 | 0.03 | 4.86 | 5.72 | 3.93 | 4.48 | 13.46 | |
| MKSL | 871 * | −457 * | −457 * | −877 * | 903 * | 903 * | 903 * | |
| SS | 0.723 | −0.165 | −0.024 | −0.051 | 0.047 | 0.033 | 0.018 | |
| Rockaway | Wavelets | db5 | db6 | db8 | db4 | db4 | db4 | db10 |
| RE | 7.29 | 4.18 | 2.91 | 3.02 | 4.43 | 4.29 | 10.33 | |
| MKSL | 635 * | −745 * | 577 * | 293 * | 903 * | 903 * | 831 * | |
| SS | 0.129 | −2.406 | 0.083 | 0.0042 | 0.059 | 0.035 | 0.0034 | |
| Upper Passaic | Wavelets | db4 | db4 | db7 | db4 | db4 | db4 | db4 |
| RE | 7.49 | 6.32 | 67.10 | 7.79 | 3.21 | 3.79 | 6.86 | |
| MKSL | 903 * | 903 * | 433 * | 213 * | 903 * | 903 * | 903 * | |
| SS | 2.401 | 7.712 | 0.0134 | 0.0062 | 0.0375 | 0.0253 | 0.013 |
| Cumulative Sum Test | Permutation Test | |
|---|---|---|
| Variables | Break Point | Break Point |
| Precipitation | 1980 | 1979 |
| 1990 | 1991 | |
| 2002 | 2003 | |
| 2011 | 2012 | |
| Streamflow | 1980 | 1979 |
| 1990 | 1991 | |
| 2002 | 2003 | |
| 2011 | 2012 |
| Streamflow | Groundwater | |||||
|---|---|---|---|---|---|---|
| Statistics | Calibration | Validation | Full Simulation | Berkshire Obs Well | Morris Obs Well | |
| 1982–1986 | 1987–1991 | 1982–1991 | 2011–2016 | 2007–2012 | ||
| Correlation coefficient (R) | 0.85 | 0.87 | 0.85 | 0.83 | 0.28 | |
| Nash efficiency (R2) | 0.72 | 0.71 | 0.72 | - | - | |
| ME | 0.57 | 1.34 | 0.96 | 6.01 | −1.86 | |
| RMSE | 4.78 | 3.89 | 0.85 | 6.07 | 1.91 | |
| Performance Indicator | Excellent | Good | Fair | Poor |
|---|---|---|---|---|
| Nash-coefficient (NSE) | >0.85 | 0.65–0.85 | 0.5–0.65 | <0.5 |
| Correlation coefficient (R) | >0.95 | 0.85–0.95 | 0.85–0.75 | <0.75 |
| Period | Tmin (°C) | Tmean (°C) | Tmax (°C) | Precip (mm) | Evapo (mm) | Flow (m3) |
|---|---|---|---|---|---|---|
| BLP I: 1982~1991 | 2.76 | 9.27 | 15.78 | 1306 | 805 | 2244 |
| BLP II: 1992~2001 | 2.99 | 9.40 | 15.82 | 1208 | 777 | 1898 |
| BLP III: 1982~2001 | 2.87 | 9.34 | 15.80 | 1257 | 791 | 2071 |
| D III: 2002~2011 | 4.31 | 10.09 | 15.89 | 1427 | 826 | 2277 |
| D IV: 2012~2021 | 5.24 | 10.56 | 15.88 | 1282 | 837 | 1947 |
| D III minus BLP I | 1.55 | 0.82 | 0.11 | 9.29% | 2.58% | 1.46% |
| D IV minus BLP I | 2.49 | 1.29 | 0.11 | −1.83% | 3.98% | −13.22% |
| D III minus BLP II | 1.32 | 0.69 | 0.07 | 18.13% | 6.25% | 19.94% |
| D IV minus BLP II | 2.25 | 1.16 | 0.07 | 6.11% | 7.71% | 2.59% |
| D III minus BLP III | 1.44 | 0.75 | 0.09 | 13.54% | 4.38% | 9.93% |
| D IV minus BLP III | 2.37 | 1.23 | 0.09 | 1.99% | 5.81% | −5.97% |
| Elasticity (ε) | ||||
|---|---|---|---|---|
| Period | Contribution to Q Change | Precip | Evapo | Equation |
| I: 2002~2011 | ||||
| 0.96 | −2.88 | |||
| relative to BLP I | 100% | ~ | ||
| 1.35 | −0.74 | |||
| relative to BLP II | 100% | ~ | ||
| 1.19 | −1.44 | ~ | ||
| relative to BLP III | 55% | −30% | ||
| II: 2012~2021 | ||||
| 0.96 | −2.88 | |||
| relative to BLP I | 13.28% | 86.62% | ||
| 1.35 | −0.74 | |||
| relative to BLP II | 100 | ~ | ||
| 1.19 | −1.44 | |||
| relative to BLP III | ~ | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oteng Mensah, F.; Alo, C.A.; Ophori, D. Hydroclimatic Trends and Streamflow Response to Recent Climate Change: An Application of Discrete Wavelet Transform and Hydrological Modeling in the Passaic River Basin, New Jersey, USA. Hydrology 2024, 11, 43. https://doi.org/10.3390/hydrology11040043
Oteng Mensah F, Alo CA, Ophori D. Hydroclimatic Trends and Streamflow Response to Recent Climate Change: An Application of Discrete Wavelet Transform and Hydrological Modeling in the Passaic River Basin, New Jersey, USA. Hydrology. 2024; 11(4):43. https://doi.org/10.3390/hydrology11040043
Chicago/Turabian StyleOteng Mensah, Felix, Clement Aga Alo, and Duke Ophori. 2024. "Hydroclimatic Trends and Streamflow Response to Recent Climate Change: An Application of Discrete Wavelet Transform and Hydrological Modeling in the Passaic River Basin, New Jersey, USA" Hydrology 11, no. 4: 43. https://doi.org/10.3390/hydrology11040043
APA StyleOteng Mensah, F., Alo, C. A., & Ophori, D. (2024). Hydroclimatic Trends and Streamflow Response to Recent Climate Change: An Application of Discrete Wavelet Transform and Hydrological Modeling in the Passaic River Basin, New Jersey, USA. Hydrology, 11(4), 43. https://doi.org/10.3390/hydrology11040043






