Enhancing Low-Flow Forecasts: A Multi-Model Approach for Rainfall–Runoff Models
Abstract
1. Introduction
2. Materials and Methods
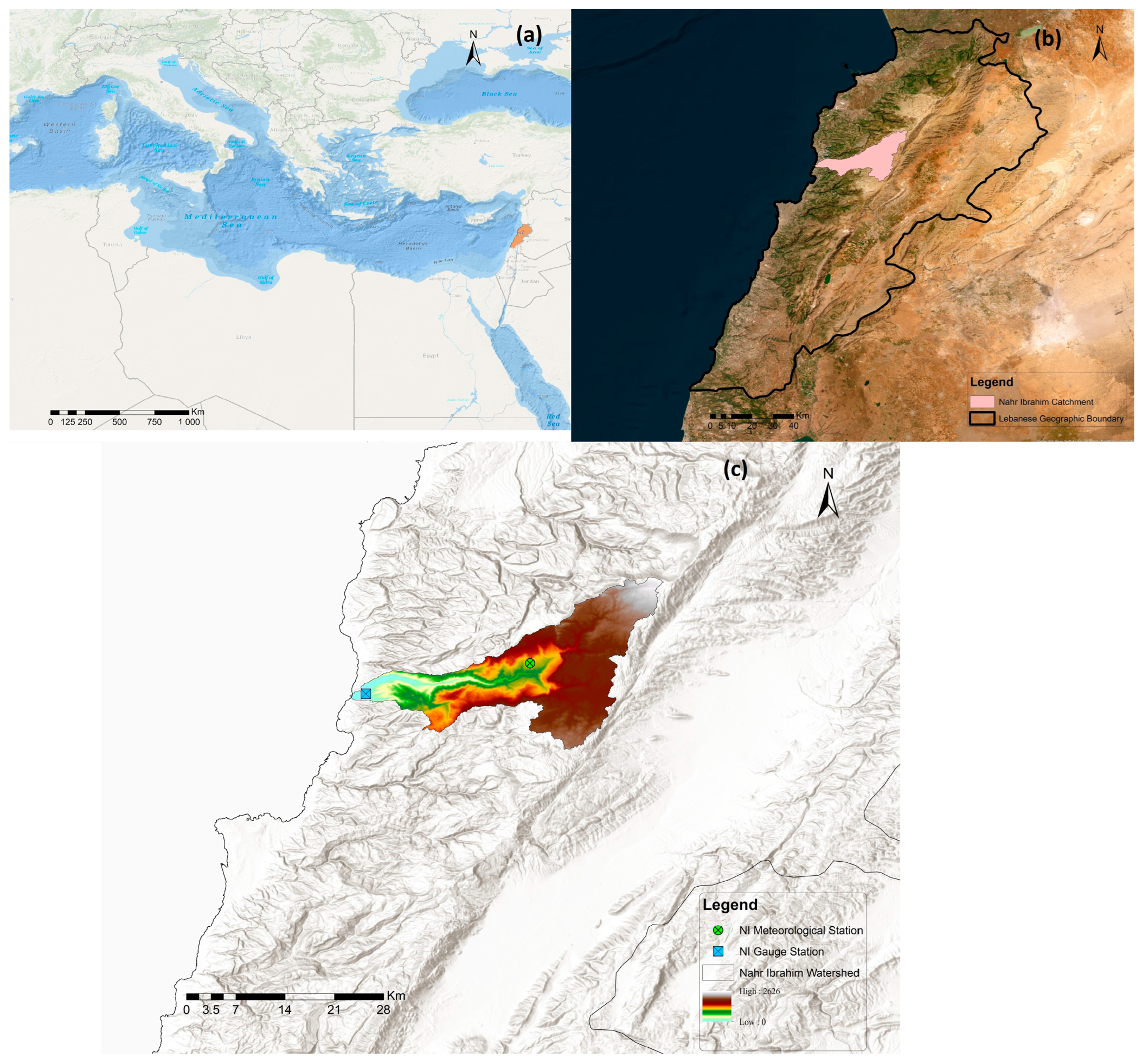
2.1. Study Area
2.2. Hydro-Climatic Data
2.3. Hydrological Models
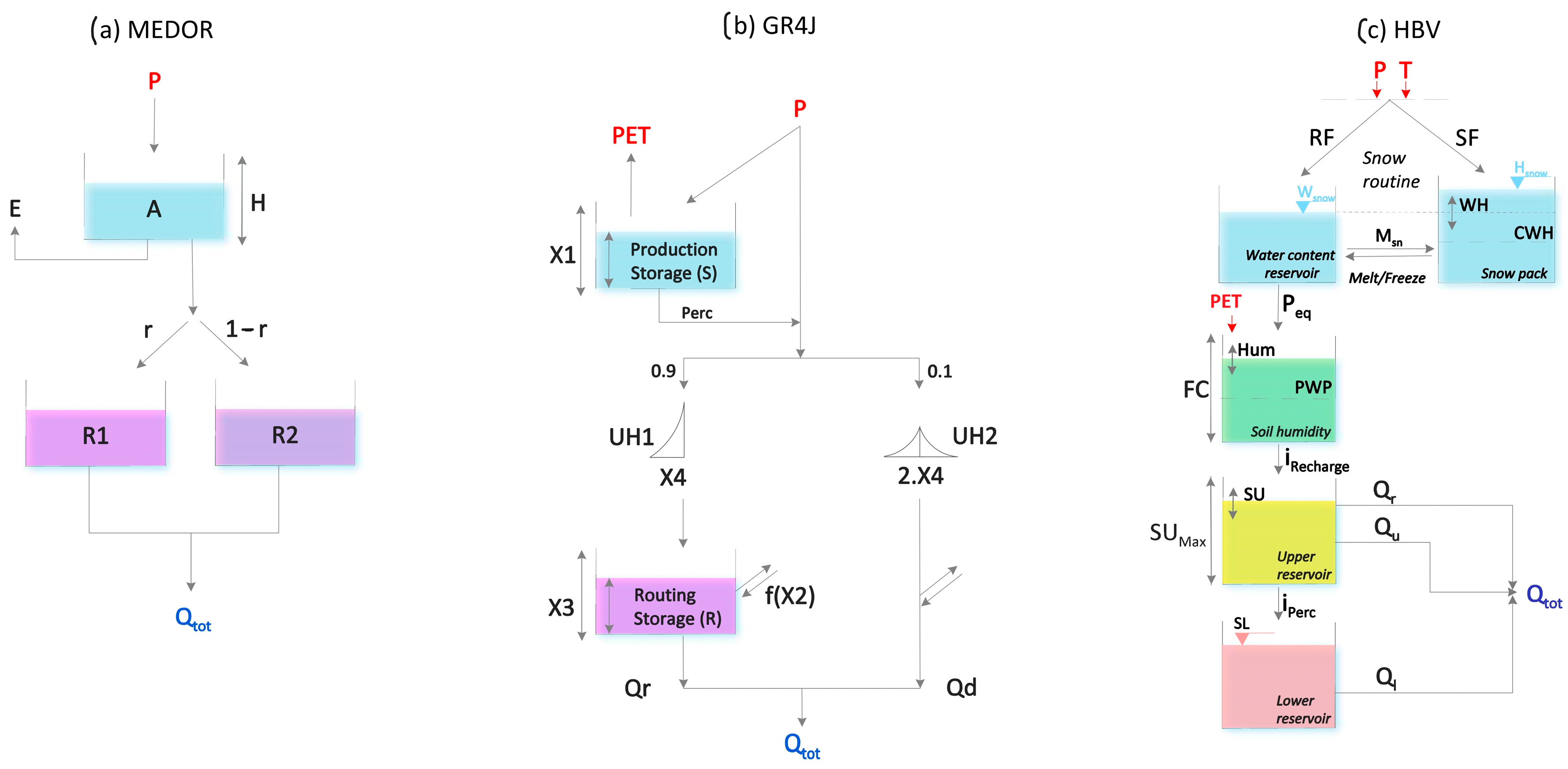
2.3.1. MEDOR
2.3.2. GR4J
2.3.3. HBV
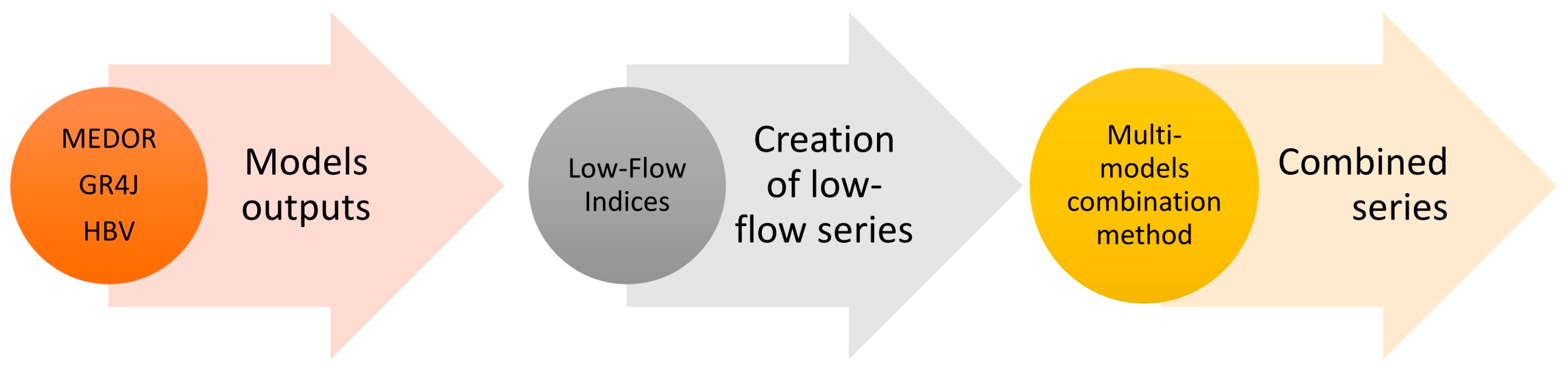
2.4. Methodology
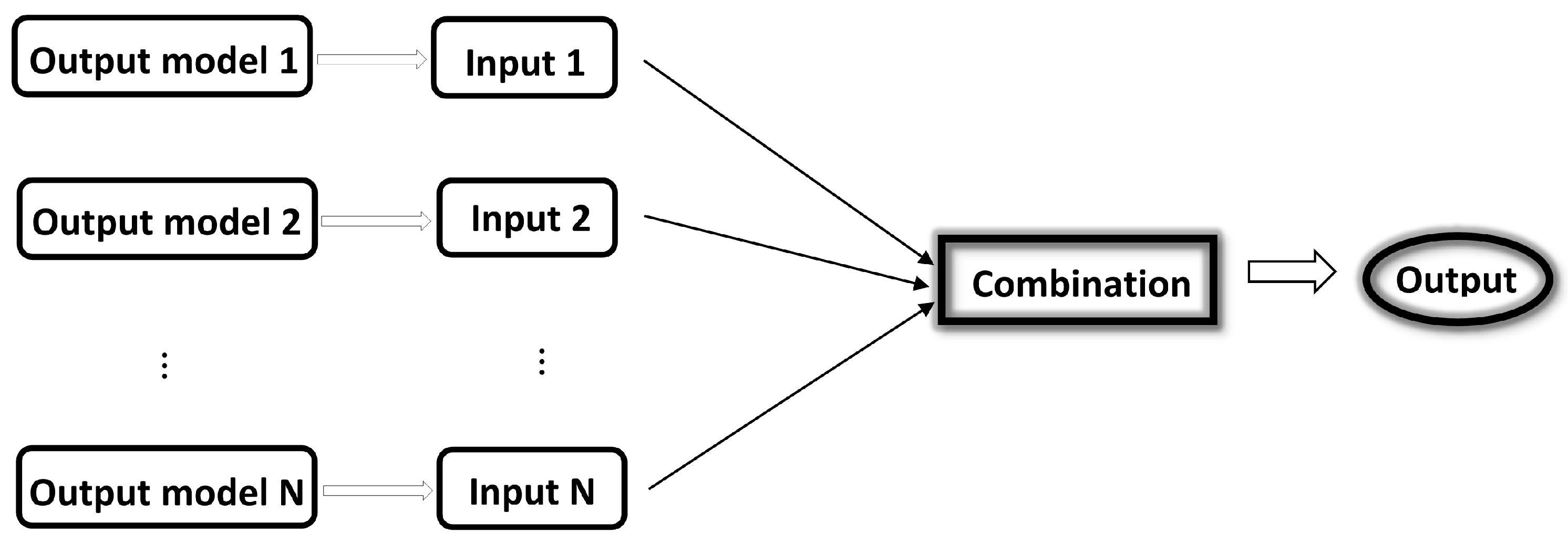
2.5. Multi-Model Approach
2.6. Low-Flow Indices and Series
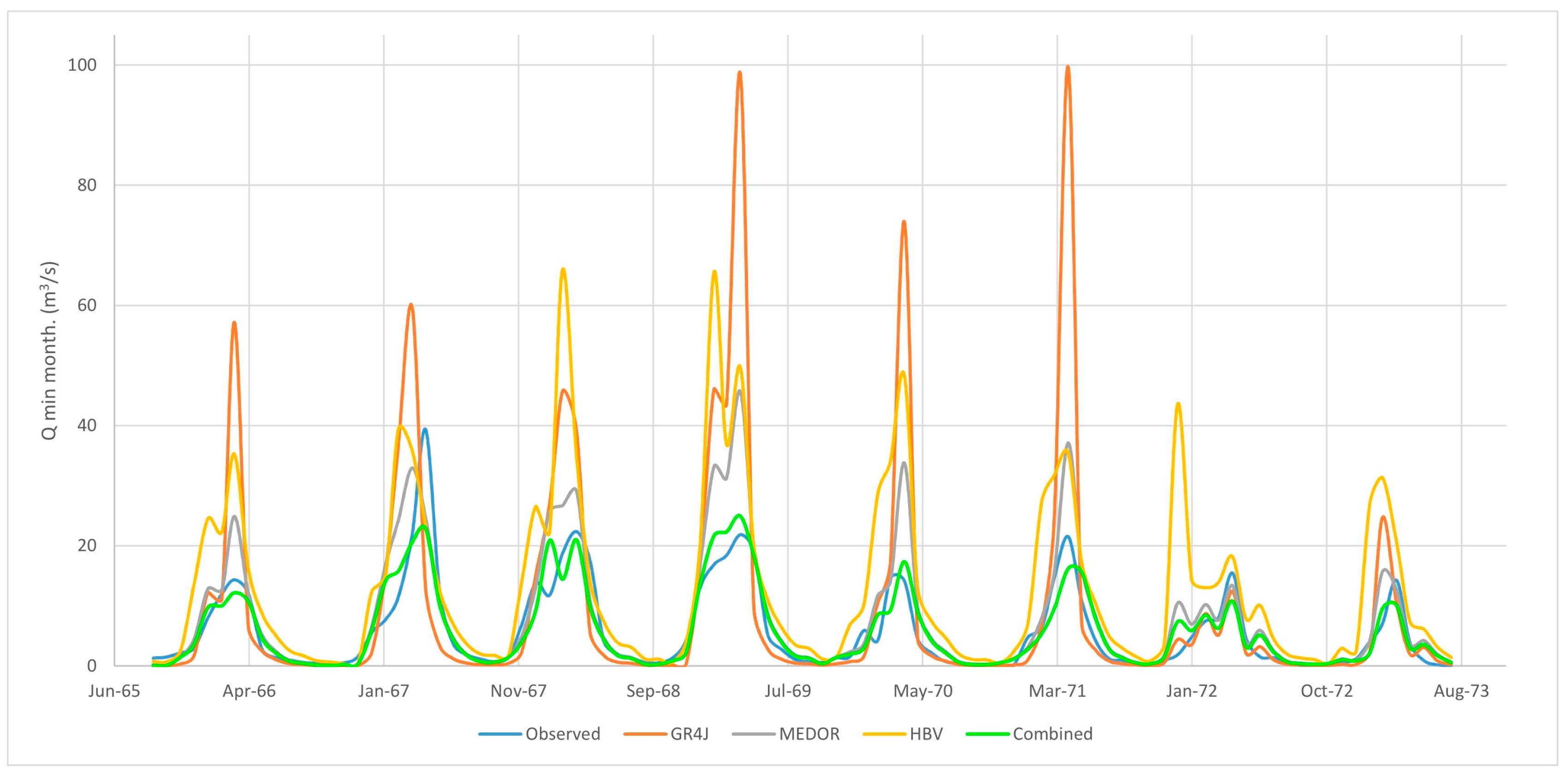
3. Results
3.1. Simple Averages
3.2. Weighted Averages
3.3. Artificial Neural Network
3.4. Genetic Algorithms
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AWG. Working Group on the ‘Anthropocene.’ 2020. Available online: http://quaternary.stratigraphy.org/working-groups/anthropocene/ (accessed on 4 November 2023).
- Steffen, W. Introducing the Anthropocene: The Human Epoch. Ambio 2021, 50, 1784–1787. [Google Scholar] [CrossRef] [PubMed]
- IAHS. Concept Note: IAHS Scientific Decade 2023–2033, HELPING (Hydrology Engaging Local People In One Global World); International Association of Hydrological Sciences: Oxfordshire, UK, 2023. [Google Scholar]
- Bai, M.; Li, Z.; Huo, P.; Wang, J.; Li, Z. Propagation Characteristics from Meteorological Drought to Agricultural Drought over the Heihe River Basin, Northwest China. J. Arid. Land. 2023, 15, 523–544. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Hattermann, F.F. Projection of Low Flow Conditions in Germany under Climate Change by Combining Three RCMs and a Regional Hydrological Model. Acta Geophys. 2013, 61, 151–193. [Google Scholar] [CrossRef]
- Demirel, M.C. Low Flows Mechanisms Forecasts and Climate Change Impacts. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- Collet, L. Capacité à Satisfaire La Demande En Eau Sous Contraintes Climatique et Anthropique Sur Un Bassin Méditerranéen. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 2013. [Google Scholar]
- Portner, H.-O.; Roberts, D.C.; Adams, H.; Adelekan, I.; Adler, C.; Adrian, R.; Aldunce, P.; Ali, E.; Ara Begum, R.; Bednar-Friedl, B.; et al. Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2023; pp. 37–118. [Google Scholar] [CrossRef]
- Milano, M.; Ruelland, D.; Dezetter, A.; Fabre, J.; Ardoin-Bardin, S.; Servat, E. Modeling the Current and Future Capacity of Water Resources to Meet Water Demands in the Ebro Basin. J. Hydrol. 2013, 500, 114–126. [Google Scholar] [CrossRef]
- Hreiche, A. Hydrological Impact Simulations of Climate Change on Lebanese Coastal Rivers. Hydrol. Sci. J. 2007, 52, 1119–1133. [Google Scholar] [CrossRef]
- Goodarzi, M.F. Analysis of Low-Flow Indices in the Era of Climate Change: An Application of CanESM2 Model. In Ecological Footprints of Climate Change; Springer Climate; Chatterjee, U.A., Ed.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Wu, J.; Wang, G.; Chen, X.; Yuan, X.; Yao, H.; Chen, X.; Lan, T.; Zheng, Y.; AghaKouchak, A. Hydrological drought characterization considering onset, maximum streamflow deficit, and termination. Adv. Water Sci. 2024, 184, 104613. [Google Scholar] [CrossRef]
- Cenobio-Cruz, O.; Quintana-Seguí, P.; Barella-Ortiz, A.; Zabaleta, A.; Garrote, L.; Clavera-Gispert, R.; Habets, F.; Beguería, S. Improvement of low flows simulations in the SASER hydrological modeling chain. J. Hydrol. 2023, X18, 100147. [Google Scholar] [CrossRef]
- Yan, H.; Sun, N.; Eldardiry, H.; Thurber, T.B.; Reed, P.M.; Malek, K.; Gupta, R.; Kennedy, D.; Swenson, S.C.; Wang, L.; et al. Characterizing Uncertainty in Community Land Model Version 5 Hydrological Applications in the United States. Sci. Data 2023, 10, 187. [Google Scholar] [CrossRef]
- Veintimilla-Reyes, J.; Cisneros, F.; Vanegas, P. Artificial Neural Networks Applied to Flow Prediction: A Use Case for the Tomebamba River. Procedia Eng. 2016, 162, 153–161. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP Neural Network Algorithm in Traditional Hydrological Model for Flood Forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of Hydrological Model Uncertainties and Advances in Their Analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Montanari, A. Uncertainty of Hydrological Predictions. Treatise on Water Science; Wilderer, P., Ed.; Academic Press: Oxford, UK, 2011; pp. 459–478. [Google Scholar]
- Shrestha, D.L.; Solomatine, D.P. Data-Driven Approaches for Estimating Uncertainty in Rainfall-Runoff Modelling. Int. J. River Basin Manag. IAHS 2008, 6, 109–122. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An Evaluation of the Impact of Model Structure on Hydrological Modelling Uncertainty for Streamflow Simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Doherty, J.; Welter, D. A Short Exploration of Structural Noise. Water Resour. Res. 2010, 46, W05525. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Martel, J.-L.; Brissette, F. Uncertainty of Hydrological Model Components in Climate Change Studies over Two Nordic Quebec Catchments. J. Hydrometeorol. January 2018, 19, 27–46. [Google Scholar] [CrossRef]
- Sheikh, M.R.; Coulibaly, P. Review of recent developments in hydrological forecast merging techniques. Water 2024, 16, 301. [Google Scholar] [CrossRef]
- Farfán, J.F.; Cea, L. Improving the Predictive Skills of Hydrological Models Using a Combinatorial Optimization Algorithm and Artificial Neural Networks. Model. Earth Syst. Environ. 2023, 9, 1103–1118. [Google Scholar] [CrossRef]
- Li, W.; Sankarasubramanian, A.; Ranjithan, R.S.; Sinha, T. Role of Multimodel Combination and Data Assimilation in Improving Streamflow Prediction over Multiple Time Scales. Stoch. Env. Res. Risk Assess. 2016, 30, 2255–2269. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M.; Liang, G. Methods for Combining the Outputs of Different Rainfall Runoff Models. J. Hydrol. 1997, 197, 203–229. [Google Scholar] [CrossRef]
- Velázquez, J.A.; Anctil, F.; Ramos, M.H.; Perrin, C. Can a Multi-Model Approach Improve Hydrological Ensemble Forecasting? A Study on 29 French Catchments Using 16 Hydrological Model Structures. Adv. Geosci. 2011, 29, 33–42. [Google Scholar] [CrossRef]
- Hagedorn, R.; Doblas-Reyes, F.J.; Palmer, T.N. The Rationale behind the Success of Multi-Model Ensembles in Seasonal Forecasting—I. Basic. Concept. Tellus 57A 2005, 57, 219–233. [Google Scholar]
- Moges, E.; Jared, A.; Demissie, Y.; Yan, E.; Mortuza, R.; Mahat, V. Bayesian Augmented L-Moment Approach for Regional Frequency Analysis. In Proceedings of the World Environmental and Water Resources Congress 2018, Minneapolis, Minnesota, 3–7 June 2018; pp. 165–180. [Google Scholar]
- Zhang, L.; Yang, X. Applying a Multi-Model Ensemble Method for Long-Term Runoff Prediction under Climate Change Scenarios for the Yellow River Basin, China. Water 2018, 10, 301. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Gao, X.; Sorooshian, S. Multimodel Combination Techniques for Analysis of Hydrological Simulations: Application to Distributed Model Intercomparison Project Results. J. Hydrometeorol. 2006, 7, 755–768. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F. Multi Model Averaging for Continuous Streamflow Prediction in Ungauged Basins. Hydrol. Sci. J. 2016, 61, 2443–2454. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, R.; Jena, P.P.; Chatterjee, C.; Mishra, A. Identification of the Best Multi-Model Combination for Simulating River Discharge. J. Hydrol. 2015, 525, 313–325. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Ensemble Combination of Seasonal Streamflow Forecasts. J. Hydrol. Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-Model Ensemble Hydrologic Prediction Using Bayesian Model Averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Liu, Z.; Yin, J.; Chen, K.; Wu, X. Uncertainty Analysis of Hydrological Multi-Model Ensembles Based on CBP-BMA Method. Hydrol. Res. 2018, 49, 1636–1651. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather. Rev. Am. Meteorol. Soc. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J.-L. Generating ensemble streamflow forecasts: A review of methods and approaches over the past 40 years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Ahn, K.-H. A Neural Network Ensemble Approach with Jittered Basin Characteristics for Regionalized Low Flow Frequency Analysis. J. Hydrol. 2020, 590, 125501. [Google Scholar] [CrossRef]
- Andraos, C.; Najem, W. Multi-Model Approach for Reducing Uncertainties in Rainfall-Runoff Models. In Advances in Hydroinformatics; Gourbesville, P., Caignaert, G., Eds.; Springer Water; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A. Hydrologic Multi-Model Ensemble Predictions Using Variational Bayesian Deep Learning. J. Hydrol. 2022, 604, 127221. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super Ensemble Learning for Daily Streamflow Forecasting: Large-Scale Demonstration and Comparison with Multiple Machine Learning Algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Lecarpentier, C. L’évapotranspiration Potentielle et Ses Implications Géographiques. Ann. De. Géographie 1975, 464, 385–414. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, I.V. River Flow Forecasting through Conceptual Models. J. Hydrol. 1970, 273, 282–290. [Google Scholar] [CrossRef]
- Hreiche, A. Modélisation Conceptuelle de La Transformation Pluie-Débit Dans Le Contexte Méditerranéen. Ph.D. Thesis, Université Montpellier II et Université Saint-Joseph, Montpellier, France, 2003. [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model—Its Structure and Applications. Smhi Reporis Hydrol. 1992, 4, 443–476. [Google Scholar]
- Li, Z.; Yu, J.; Xu, X.; Sun, W.; Pang, B.; Yue, J. Multi Model Ensemble Hydrological Simulation Using a BP Neural Network for the Upper Yalongjiang River Basin China. Process. Int. Assoc. Hydrol. Sci. 2018, 379, 335–341. [Google Scholar] [CrossRef]
- Ahn, J.B.; Lee, J. A New Multimodel Ensemble Method Using Nonlinear Genetic Algorithm An Application to Boreal Winter Surface Air Temperature and Precipitation Prediction. J. Geophys. Res. Atmos. 2016, 121, 9263–9277. [Google Scholar] [CrossRef]
- Roche, P.A.; Miquel, J.; Gaume, E. Hydrologie Quantitative Processus Modèles et Aide à La Décision; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search Optimization and Machine Learning; The University of Alabama, Addison Wesley Publishing Company, Inc.: Reading, MA, USA, 1989. [Google Scholar]

| GR4J/ Observed | MEDOR/ Observed | HBV/ Observed | Combined Simple/ Observed | Combined with Moving Average/ Observed | Combined with Exponential Smoothing/ Observed | |
|---|---|---|---|---|---|---|
| Q260 | ||||||
| Correlation | 0.26 | 0.38 | 0.32 | 0.35 | 0.40 | 0.39 |
| MSE | 0.81 | 0.55 | 2.15 | 0.56 | 0.41 | 0.30 |
| SSE | 686 | 472 | 1827 | 474 | 347 | 258 |
| Q4m3/s | ||||||
| Correlation | 0.42 | 0.64 | 0.53 | 0.58 | 0.66 | 0.43 |
| MSE | 1.79 | 2.07 | 14.18 | 3.06 | 1.62 | 1.26 |
| SSE | 2460 | 2837 | 19,442 | 4193 | 2216 | 1722 |
| Qmin month | ||||||
| Correlation | 0.69 | 0.86 | 0.74 | 0.79 | 0.87 | 0.02 |
| MSE | 249 | 32 | 158 | 107 | 70 | 73 |
| SSE | 23,977 | 3112 | 15,246 | 10,297 | 6710 | 6957 |
| GR4J/ Observed | MEDOR/ Observed | HBV/ Observed | Combined with ANN/Observed |
|---|---|---|---|
| Q260 | |||
| 0.26 | 0.38 | 0.32 | 0.50 |
| Q4m3/s | |||
| 0.63 | 0.76 | 0.67 | 0.82 |
| Qmin month | |||
| 0.69 | 0.87 | 0.74 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andraos, C. Enhancing Low-Flow Forecasts: A Multi-Model Approach for Rainfall–Runoff Models. Hydrology 2024, 11, 35. https://doi.org/10.3390/hydrology11030035
Andraos C. Enhancing Low-Flow Forecasts: A Multi-Model Approach for Rainfall–Runoff Models. Hydrology. 2024; 11(3):35. https://doi.org/10.3390/hydrology11030035
Chicago/Turabian StyleAndraos, Cynthia. 2024. "Enhancing Low-Flow Forecasts: A Multi-Model Approach for Rainfall–Runoff Models" Hydrology 11, no. 3: 35. https://doi.org/10.3390/hydrology11030035
APA StyleAndraos, C. (2024). Enhancing Low-Flow Forecasts: A Multi-Model Approach for Rainfall–Runoff Models. Hydrology, 11(3), 35. https://doi.org/10.3390/hydrology11030035





