Forecasting Lake Nokoué Water Levels Using Long Short-Term Memory Network
Abstract
1. Introduction
- -
- It is the first attempt to apply artificial intelligence models to a complex water body in order to assess the performance of these models in establishing the nonlinear relationship between input variables and output.
- -
- We also propose and implement a recurrent neural network model to leverage the set of input variables for forecasting the water level of Lake Nokoué.
2. Materials and Methods
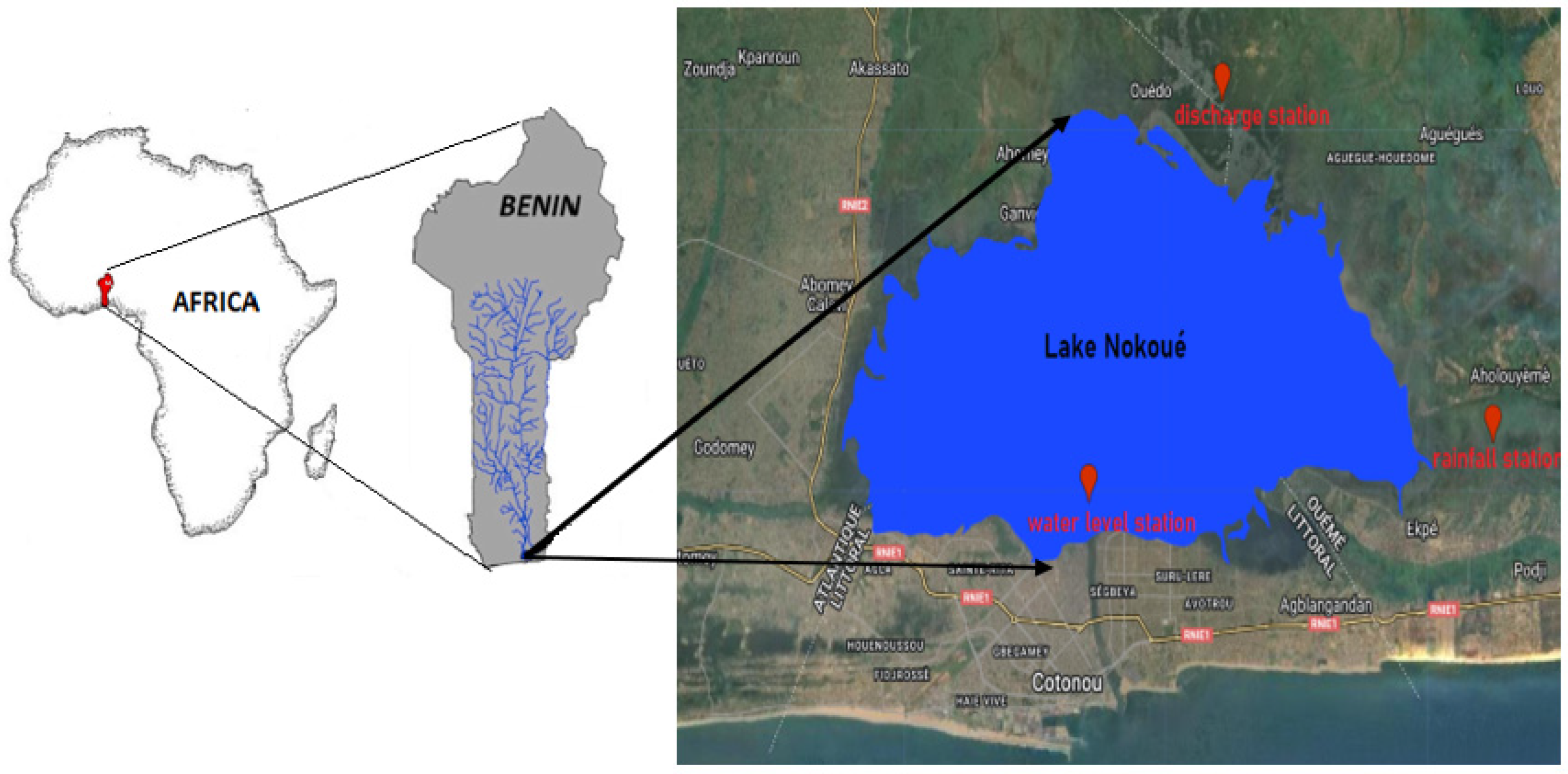
2.1. Study Area
2.2. Data Acquisition
2.3. Data Preprocessing
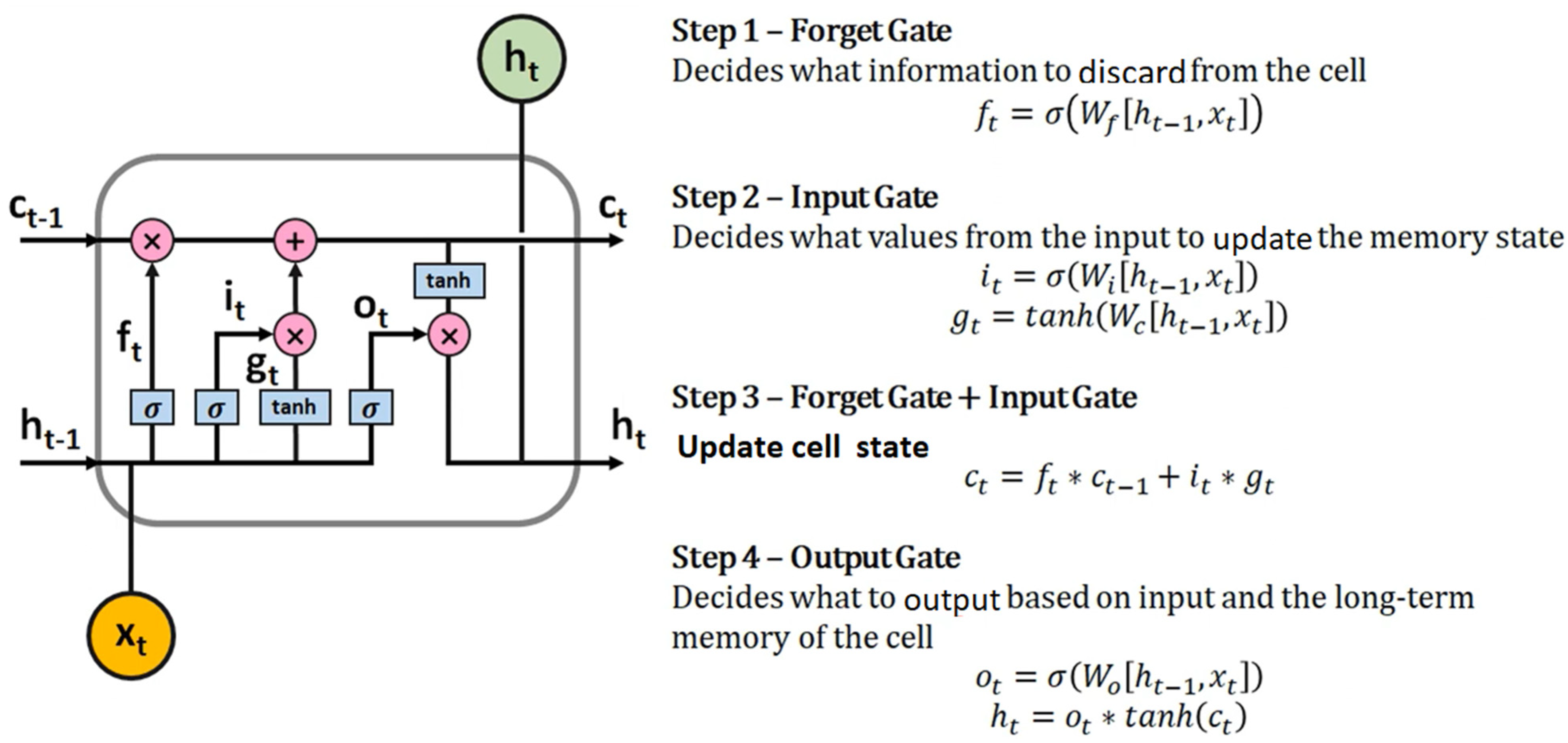
2.4. Structure of the Long Short Term Memory Model
- (a)
- Step 1: the forget gate
- -
- Ft is the value of forget gate at time step t, and the range of Ft is 0–1;
- -
- σ is the sigmoid activation function;
- -
- represent the weight of the forget gate, respectively;
- -
- is the hidden layer output result of the previous time t − 1; and
- -
- is the Current input value at time t.
- (b)
- Step 2: the input gate
- -
- is the value of input gate at time step t, and it is also calculated by the activation function sigmoid, with a value range of 0–1;
- -
- and bi represent the weight and deviation of the input gate, respectively;
- -
- is the cell update candidate; tan h means the hyperbolic tangent function; and
- -
- and bc represent the weight and deviations of the cell, respectively. The purpose of introducing the cell update candidate is to multiply its calculation results by and pass to the cell state as the output of the input gate.
- (c)
- Step 3: Update cell state
- -
- is current cell state at time step t;
- -
- is previous cell output the value of cell state of the previous time t − 1; and
- -
- the updated at time t + 1 will be passed to the next cell as the input.
- (d)
- Step 4: the output gate
- -
- is the value of output gate at time step t;
- -
- represent the weight of the output gate, respectively; and
- -
- is the output result of the hidden layer at time t.
2.5. Long Short-Term Memory Model Configuration
- -
- the part intended for training to recognize the system’s dynamics, which is the most important part (80%);
- -
- the testing part (20%) which prevents overfitting by checking and testing the loss function evolution during training and validation. After the training is stopped and the weights of the interconnections of the most performing model are saved. The validation dataset allows for confirmation of the LSTM model’s performance.
2.6. Model Performance Assessment
3. Results and Discussion
3.1. Variable Selection and Statistics
3.1.1. Selection of the Variables
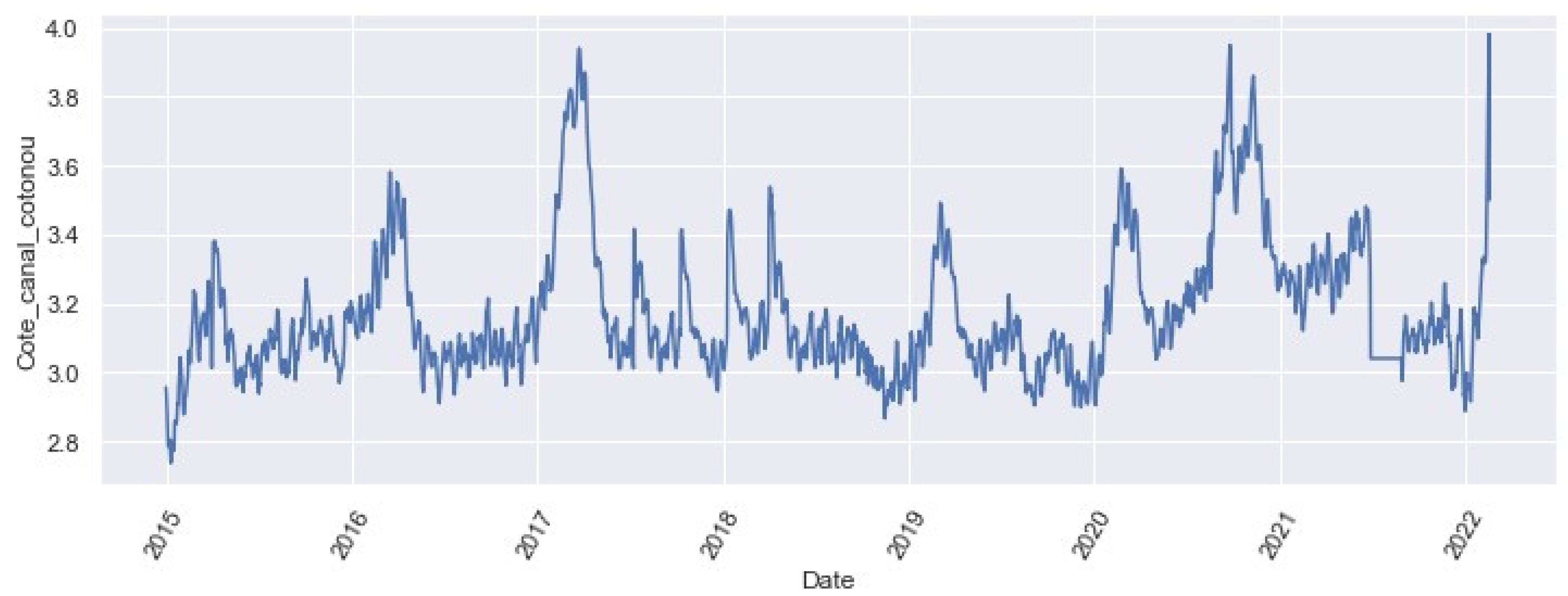
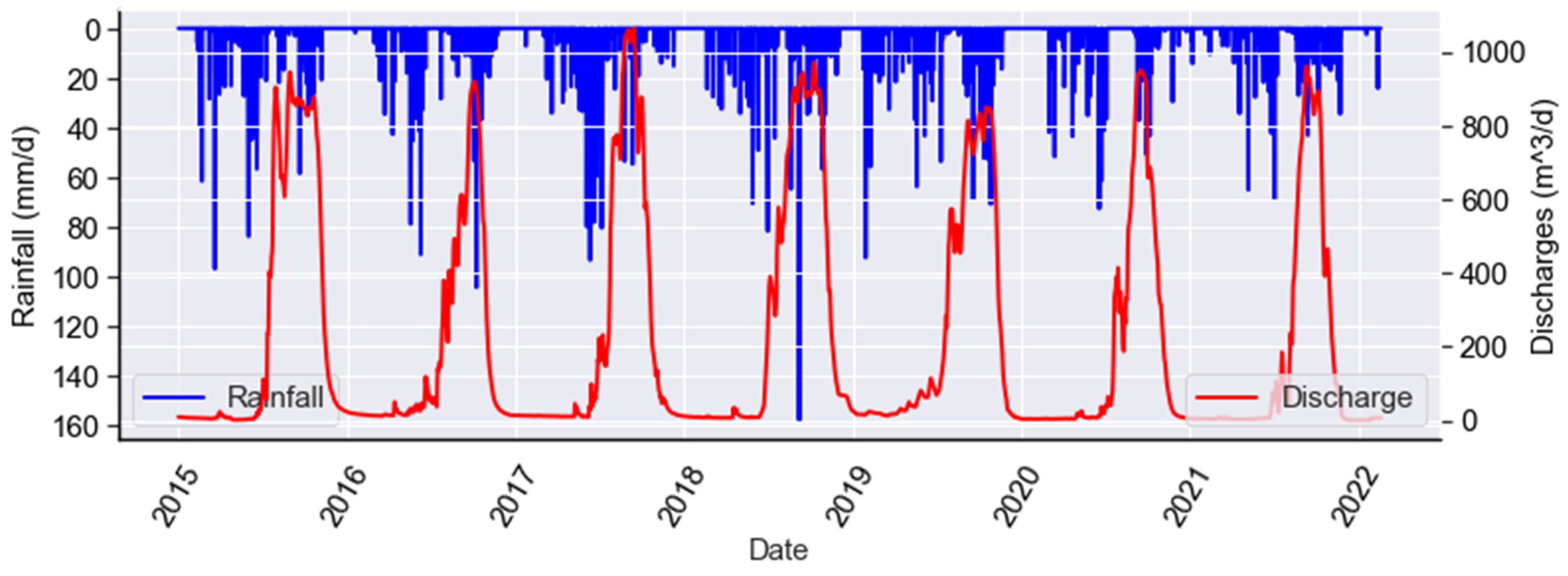
3.1.2. Statistics of the Variable
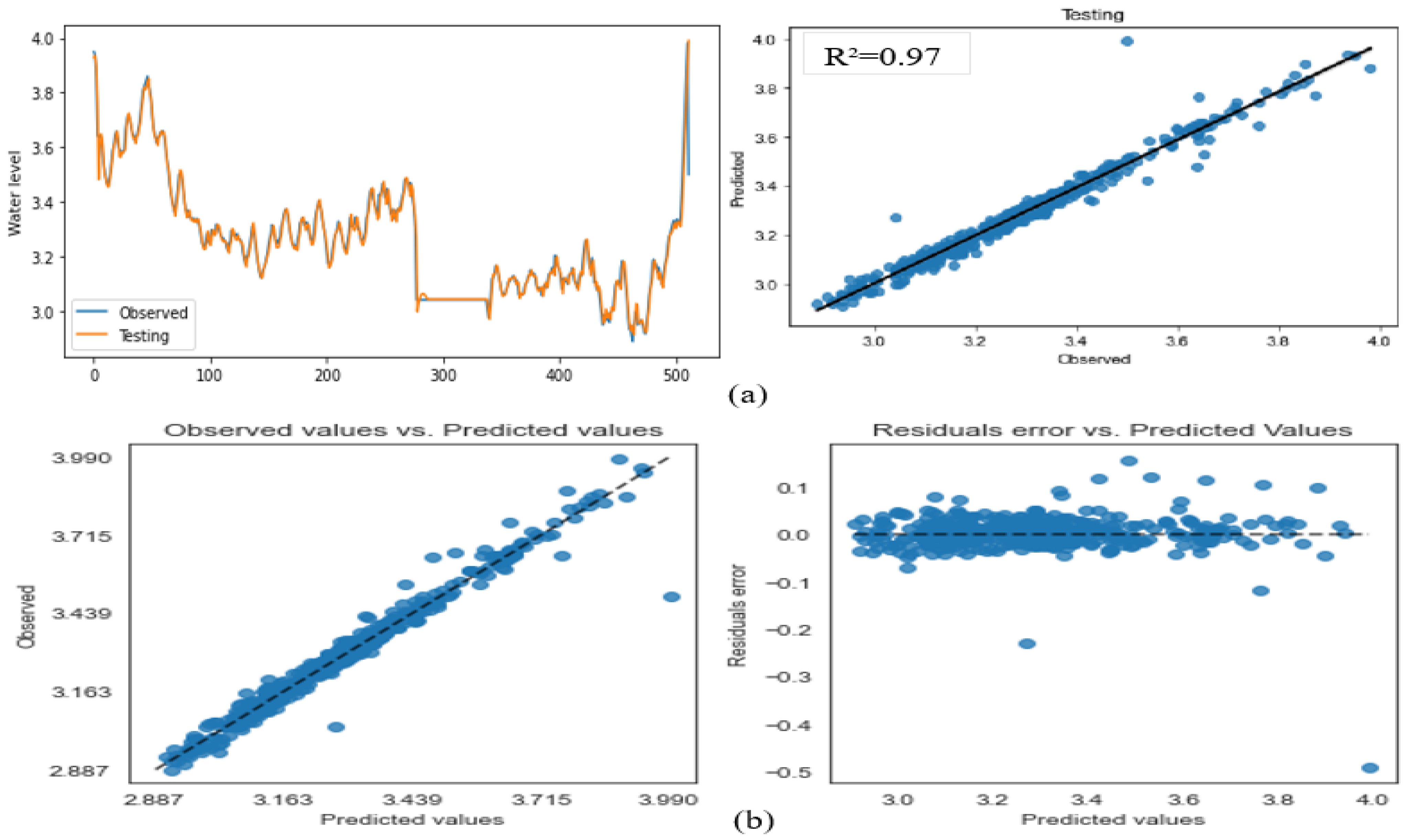
3.2. Model Performance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaigneau, A.; Okpeitcha, O.V.; Morel, Y.; Stieglitz, T.; Assogba, A.; Morgane, B.; Allamel, P.; Honfos, J.; Thierry Derol Awoulmbang, S.; Retif, F.; et al. From seasonal flood pulse to seiche: Multi-frequency water-level fluctuations in a large shallow tropical lagoon (Nokoue Lagoon, Benin). Estuar. Coast. Shelf Sci. 2022, 267, 107–767. [Google Scholar] [CrossRef]
- Ngoc, D.V. Deterministic Hydrological Modeling for Flood Risk Assessment and Climate Change in Large Catchment: Application to Vu Gia Thu Bon Catchment, Vietnam. Ph.D. Thesis, Université Nice Sophia Antipolis, Valbonne, France, 2015. [Google Scholar]
- Rebolho, C. Modélisation conceptuelle de l’aléa inondation à l’échelle du bassin versant. Hydrologie. Ph.D. Thesis, AgroParisTech, Paris, France, 2018. [Google Scholar]
- Golob, R.; Štokelj, T.; Grgič, D. Neural-network-based water inflow forecasting. Control. Eng. Pract. 1998, 6, 37–98. [Google Scholar] [CrossRef]
- Ancona, M.; Corradi, N.; Dellacasa, A.; Delzanno, G.; Dugelay, J.-L.; Federici, B.; Gourbesville, P.; Guerrini, G.; La Caméra, A.; Rosso, P.; et al. On the Design of an Intelligent Sensor Network for Flash Flood Monitoring, Diagnosis and Management in Urban Areas Position Paper. Procedia Comput. Sci. 2014, 32, 941–946. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P. Flood forecasting and error simulation using copula entropy method. In Advances in Streamflow Forecasting; Sharma, P., Machiwal, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 6, pp. 331–368. [Google Scholar]
- Chu, H.; Wu, W.; Wang, Q.J.; Nathan, R.; Wei, J. An ANN-based emulation modeling framework for flood inundation modeling: Application, challenges and future direction. Environ. Model. Softw. 2019, 19, 104–587. [Google Scholar]
- Bornancin Plantier, A. Conception de Modèles de Prévision des Crues Eclair par Apprentissage Artificiel. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2013. [Google Scholar]
- Kharroubi, O.; Blanpain, O.; Masson, E.; Lallahem, S. Application du réseau des neurones artificiels à la prévision des débits horaires: Cas du bassin versant de l’Eure, France. Hydrol. Sci. J. 2016, 61, 541–550. [Google Scholar] [CrossRef]
- Peredo, D.; Ramos, M.-H.; Andréassian, V.; Oudin, L. Investigating hydrological model versatility to simulate extreme flood events. Hydrol. Sci. J. 2022, 67, 628–645. [Google Scholar] [CrossRef]
- Meliho, M.; Khattabi, A.; Driss, Z.; Orlando, C.A. Spatial forecasting of flood susceptible zones in the Ourika watershed of Morocco using machine learning algorithms. Appl. Comput. Inform. 2022, 9. [Google Scholar]
- Noor, F.; Haq, S.; Rakib, M.; Ahmed, T.; Jamal, Z.; Siam, Z.S.; Hasan, R.T.; Adnan, M.S.G.; Dewan, A.; Rahman, R.M. Water Level Forecasting Using Spatiotemporal Attention-Based Long Short-Term Memory Network. Water 2022, 14, 612. [Google Scholar] [CrossRef]
- Alliau, D.; De Saint Seine, J.; Lang, M.; Sauquet, E.; Renard, B. Étude du risque d’inondation d’un site industriel par des crues extrêmes: De l’évaluation des valeurs extrêmes aux incertitudes hydrologiques et hydrauliques. La Houille Blanche 2015, 101, 67–74. [Google Scholar] [CrossRef][Green Version]
- Morel, Y.; Chaigneau, A.; Okpeitcha, V.O.; Stieglitz, T.; Assogba, A.; Duhaut, T.; Rétif, F.; Peugeot, C.; Sohou, Z. Terrestrial or oceanic forcing ? Water level variations in coastal lagoons constrained by river inflow and ocean tides. Adv. Water Resour. 2022, 169, 104–309. [Google Scholar] [CrossRef]
- Fathian, F. Introduction of multiple/multivariate linear and nonlinear time series models in forecasting streamflow process. In Advances in Streamflow Forecasting; Sharma, P., Machiwal, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 3; pp. 87–113. [Google Scholar]
- Wang, L.; Dong, H.; Cao, Y.; Hou, D.; Zhang, G. Real-time water quality detection based on fluctuation feature analysis with the LSTM model. J. Hydroinformatics 2023, 5, 127–305. [Google Scholar] [CrossRef]
- Masselot, P.; Dabo-Niang, S.; Chebana, F.; Ouarda, T.B.M.J. Streamflow forecasting using functional regression. J. Hydrol. 2016, 538, 754–766. [Google Scholar] [CrossRef]
- Luo, X.; Yuan, X.; Zhu, S.; Xu, Z.; Meng, L.; Peng, J. A hybrid support vector regression framework for streamflow forecast. J. Hydrol. 2019, 568, 184–193. [Google Scholar] [CrossRef]
- Douvinet, J.; Serra-Llobet, A.; Radke, J.; Kondolf, M. Quels enseignements tirer des coulées de débris post-incendie survenues le 9 janvier 2018 à Montecito (Californie, USA)? La Houille Blanche 2020, 106, 25–35. [Google Scholar] [CrossRef]
- Lang, M.; Arnaud, P.; Carreau, J.; Deaux, N.; Dezileau, L.; Garavaglia, F.; Latapie, A.; Neppel, L.; Paquet, E.; Renard, B.; et al. Résultats du projet ExtraFlo (ANR 2009-2013) sur l’estimation des pluies et crues extrêmes. La Houille Blanche 2014, 2, 5–13. [Google Scholar] [CrossRef][Green Version]
- Viatgé, J.; Berthet, L.; Marty, R.; Bourgin, F.; Piotte, O.; Ramos, M.-H.; Perrin, C. Vers une production en temps réel d’intervalles prédictifs associés aux prévisions de crue dans Vigicrues en France. La Houille Blanche 2019, 105, 63–71. [Google Scholar] [CrossRef]
- Hosseiny, H. A deep learning model for predicting river flood depth and extent. Environ. Model. Softw. 2021, 145, 105–186. [Google Scholar] [CrossRef]
- Ji, H.; Chen, Y.; Fang, G.; Li, Z.; Duan, W.; Zhang, Q. Adaptability of machine learning methods and hydrological models to discharge simulations in data-sparse glaciated watersheds. J. Arid Land 2021, 13, 549–567. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the forecasting and forecasting of water resources variables: A review of modeling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Tikhamarine, Y.; Souag-Gamane, D.; Kişi, Ö. Hybrid artificial intelligence models for predicting daily runoff. In Advances in Streamflow Forecasting; Sharma, P., Machiwal, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 12; pp. 305–309. [Google Scholar]
- Le Barbé, L.; Alé, G.; Millet, B.; Texier, H.; Borel, Y.; Gualde, R. Les Ressources en eaux Superficielles de la République du Bénin; Orstom: Paris, France, 1993; p. 540. [Google Scholar]
- Mama, D.; Deluchat, V.; Bowen, J.; Chouti, W.; Yao, B.; Gnon, B.; Baudu, M. Caractérisation d’un Système Lagunaire en Zone Tropicale: Cas du lac Nokoué (Bénin). Eur. J. Sci. Res. 2011, 56, 516–528. [Google Scholar]
- Djihouessi, M.B.; Aina, M.P. A review of hydrodynamics and water quality of Lake Nokoué: Current state of knowledge and prospects for further research. Reg. Stud. Mar. Sci. 2018, 17, 2352–4855. [Google Scholar] [CrossRef]
- Texier, H.; Colleuil, B.; Profizi, J.P.; Dossou, C. Le lac Nokoué, Environnement du Domaine Margino-Littoral Sud-Béninois: Bathymétrie, Lithofaciès, Salinité, Mollusque et Peuplements Végétaux; No. 28; 1980; pp. 115–142. [Google Scholar]
- Tore, D.B.; Alamou, A.E.; Obada, E.; Biao, E.I.; Zandagba, E.B.J. Assessment of Intra-Seasonal Variability and Trends of Precipitations in a Climate Change Framework in West Africa. Atmos. Clim. Sci. 2022, 12, 150–171. [Google Scholar] [CrossRef]
- Sedai, A.; Dhakal, R.; Gautam, S.; Dhamala, A.; Bilbao, A.; Wang, Q.; Wigington, A.; Pol, S. Performance Analysis of Statistical, Machine Learning and Deep Learning Models in Long-Term Forecasting of Solar Power Production. Forecasting 2023, 5, 256–284. [Google Scholar] [CrossRef]
- Murray, K.; Rossi, A.; Carraro, D.; Visentin, A. On Forecasting Cryptocurrency Prices: A Comparison of Machine Learning, Deep Learning, and Ensembles. Forecasting 2023, 5, 196–209. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, H.; Huang, J.J.; Tian, S.; Xu, W.; Mai, Y. An ensemble machine learning model for water quality estimation in coastal areas based on remote sensing imagery. J. Environ. Manag. 2022, 323, 116–187. [Google Scholar] [CrossRef]
- Wood, M.; Ogliari, E.; Nespoli, A.; Simpkins, T.; Leva, S. Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting 2023, 5, 297–314. [Google Scholar] [CrossRef]
- Ömer Faruk, D. A hybrid neural network and ARIMA model for water quality time series forecasting. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Sharma, P.; Machiwal, D. Streamflow forecasting: Overview of advances in data-driven techniques. In Advances in Streamflow Forecasting; Sharma, P., Machiwal, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 1; pp. 1–50. [Google Scholar]
- Avahouin, C.N.N.; Vodounon, H.S.T.; Amoussou, E. Variabilité climatique et production halieutique du lac Nokoué dans les Aguégués au Bénin. Ann. UP, Série Sci. Nat. Agron. 2018, 8, 51–61. [Google Scholar]
- Gildas, K.A.; Bernard, A.; Amédée, C.; Abraham, A.; Firminn, A.; Expédit, V. Variabilité Pluvio-Hydrologique et Incidences sur les Eaux de Surface dans la Basse Vallée de l’Ouémé au Sud-Est Bénin. Int. J. Progress. Sci. Technol. (IJPSAT) 2020, 23, 52–65. [Google Scholar]
- Siou, L.K.A.; Johannet, A.; Borrell, V.; Pistre, S. Complexity selection of a neural network model for karst flood forecasting: The case of the Lez Basin (southern France). J. Hydrol. 2011, 403, 367–380. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Qi, H. Snowmelt-driven streamflow forecasting using machine learning techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Luo, B.; Fang, Y.; Wang, H.; Zang, D. Reservoir Inflow Forecasting Using a Hybrid Model based on Deep Learning. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Shanghai, China, 26–28 April 2019; Volume 715, p. 012044. [Google Scholar]



| Statistics | Rainfall | Discharge | Water Level |
|---|---|---|---|
| mean | 3.392 | 219.113 | 3.173 |
| std | 10.852 | 318.670 | 0.195 |
| min | 0.000 | 0.610 | 2.736 |
| 25% | 0.000 | 8.225 | 3.045 |
| 50% | 0.000 | 25.590 | 3.115 |
| 75% | 0.200 | 376.900 | 3.257 |
| max | 158.200 | 1064.000 | 3.981 |
| Forecast Horizon | Training Step | Testing Step | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | NSE | R2 | MAE | RMSE | NSE | R2 | MAE | |
| t + 1 day | 0.03 | 0.98 | 0.98 | 0.02 | 0.04 | 0.97 | 0.97 | 0.03 |
| t + 2 days | 0.03 | 0.98 | 0.98 | 0.02 | 0.04 | 0.97 | 0.97 | 0.03 |
| t + 3 days | 0.03 | 0.98 | 0.98 | 0.02 | 0.04 | 0.97 | 0.97 | 0.02 |
| t + 4 days | 0.03 | 0.94 | 0.98 | 0.02 | 0.03 | 0.96 | 0.97 | 0.02 |
| t + 5 days | 0.03 | 0.98 | 0.98 | 0.02 | 0.03 | 0.97 | 0.97 | 0.02 |
| t + 10 days | 0.03 | 0.92 | 0.97 | 0.02 | 0.04 | 0.90 | 0.96 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabire, N.; Ezin, E.C.; Firmin, A.M. Forecasting Lake Nokoué Water Levels Using Long Short-Term Memory Network. Hydrology 2024, 11, 161. https://doi.org/10.3390/hydrology11100161
Dabire N, Ezin EC, Firmin AM. Forecasting Lake Nokoué Water Levels Using Long Short-Term Memory Network. Hydrology. 2024; 11(10):161. https://doi.org/10.3390/hydrology11100161
Chicago/Turabian StyleDabire, Namwinwelbere, Eugene C. Ezin, and Adandedji M. Firmin. 2024. "Forecasting Lake Nokoué Water Levels Using Long Short-Term Memory Network" Hydrology 11, no. 10: 161. https://doi.org/10.3390/hydrology11100161
APA StyleDabire, N., Ezin, E. C., & Firmin, A. M. (2024). Forecasting Lake Nokoué Water Levels Using Long Short-Term Memory Network. Hydrology, 11(10), 161. https://doi.org/10.3390/hydrology11100161






