Predictive MPC-Based Operation of Urban Drainage Systems Using Input Data-Clustered Artificial Neural Networks Rainfall Forecasting Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Framework of the PR-MPC Operation Model
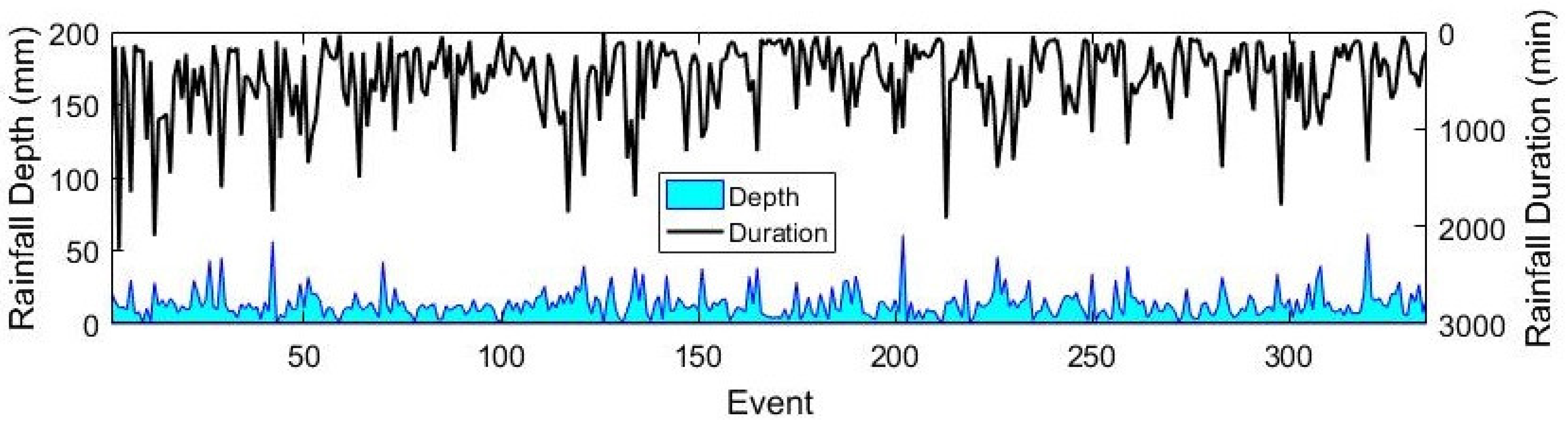
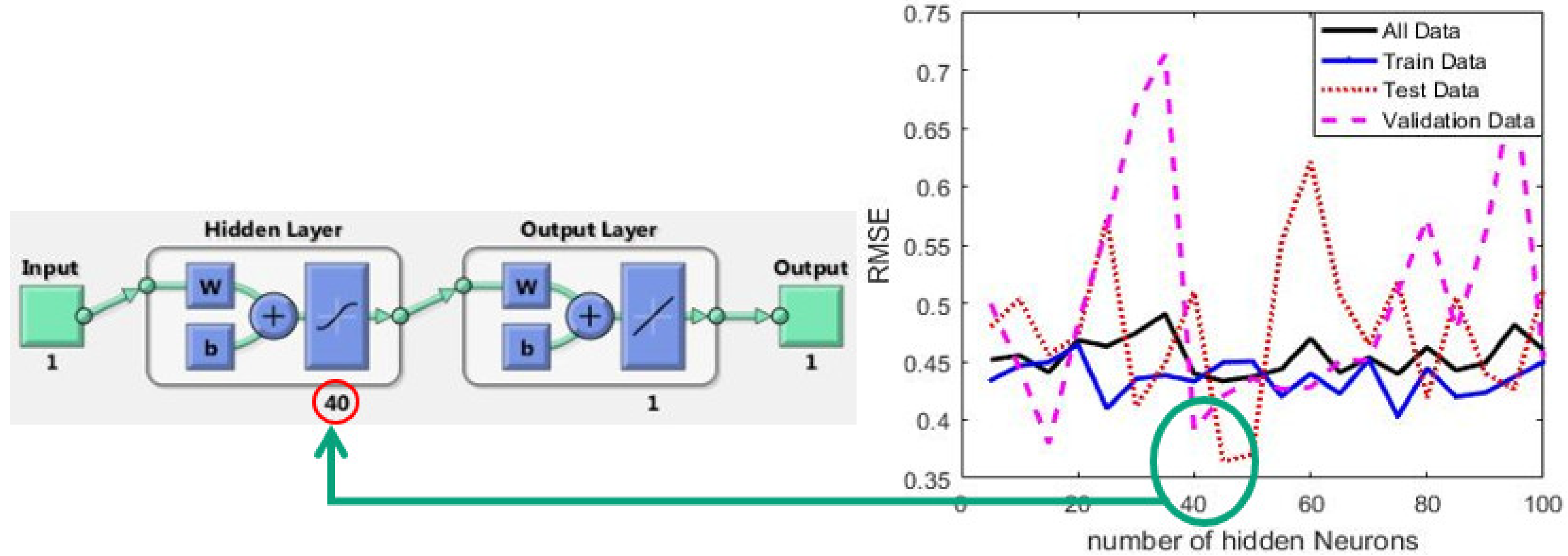
2.2. Short-Term Rainfall Prediction Model
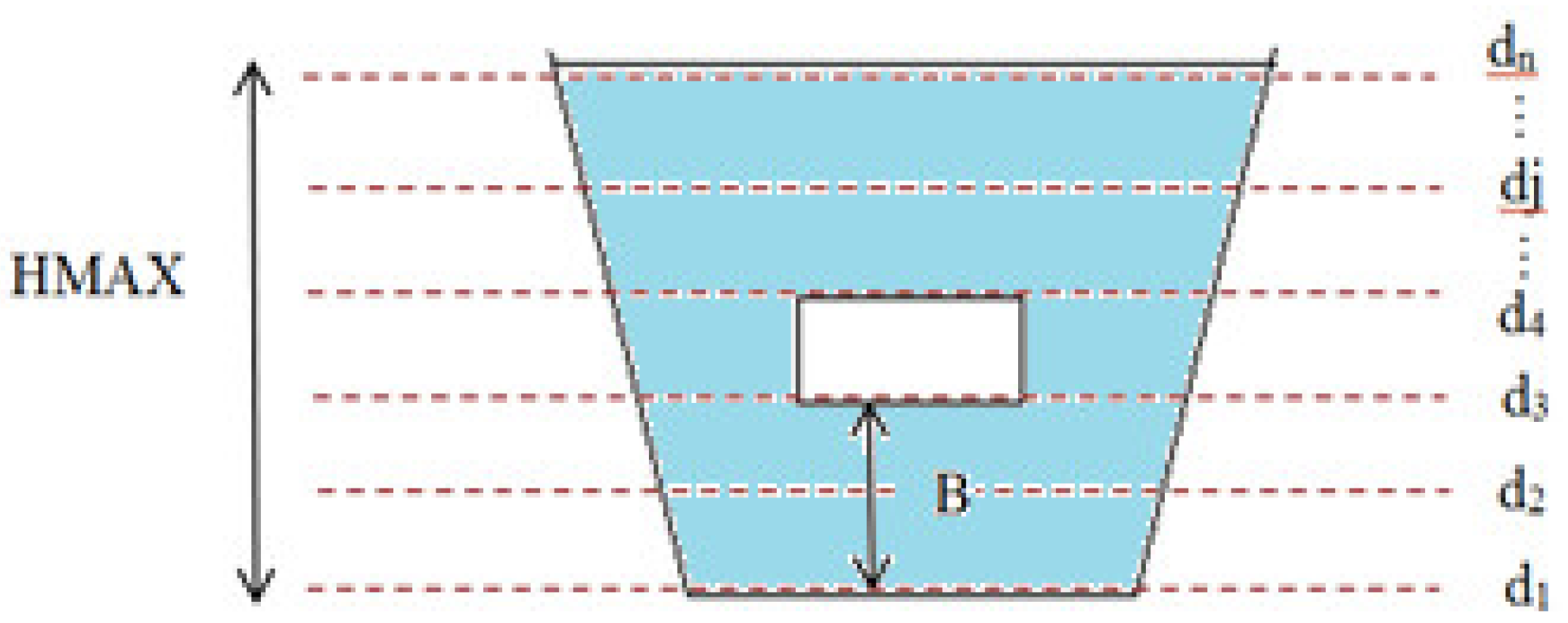
2.3. Model Predictive Control Set-Up for Gate Regulation
2.4. Simulation-Optimization Model
3. Study Area
SWMM Model Inputs
4. Numerical Experiments and Results
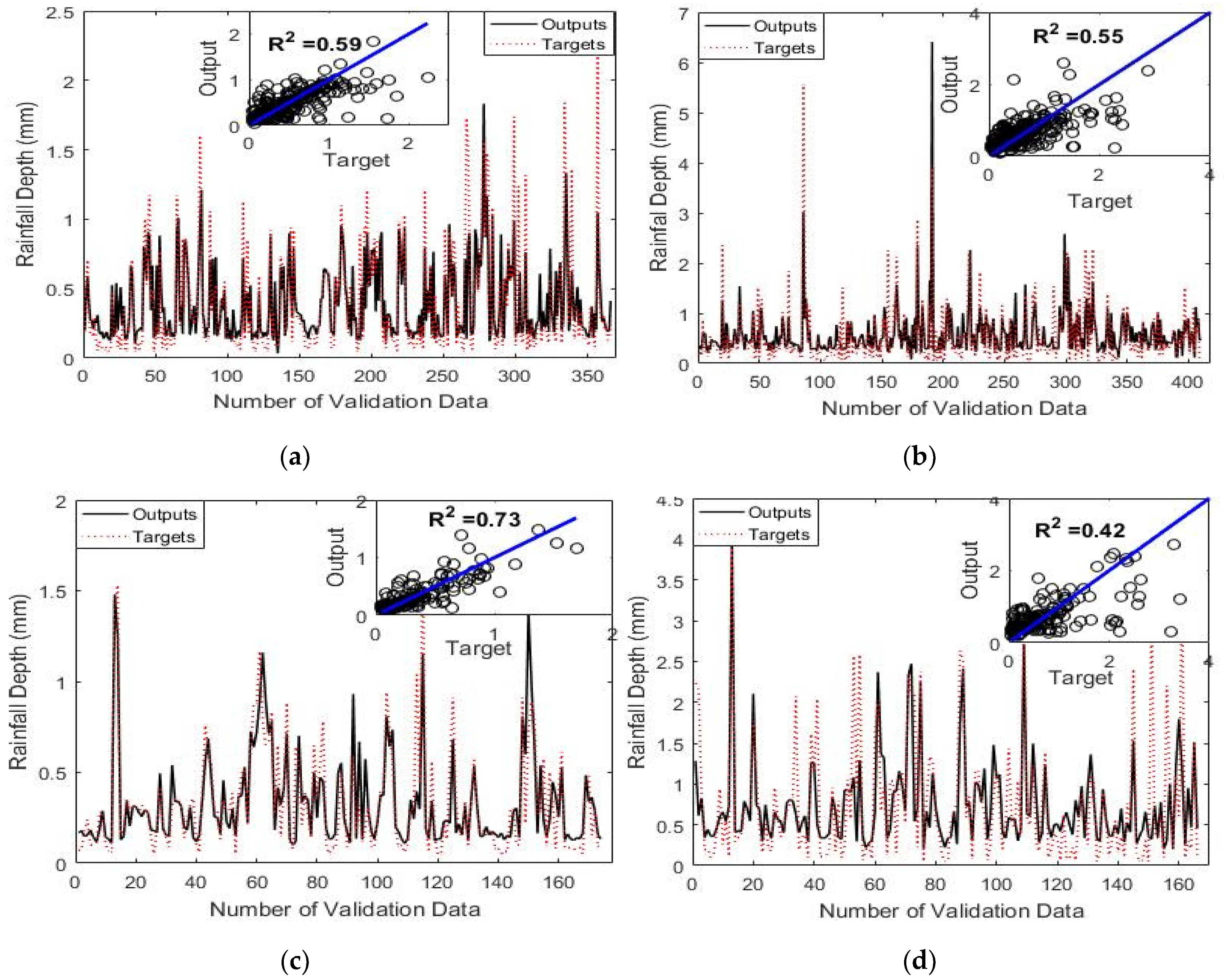
4.1. Results of Short-Term Rainfall Forecasting
4.2. Results of the MPC Framework
5. Final Remarks
6. Conclusions
- Clustering rainfall data as a preprocessing technique not only increased the accuracy of precipitation forecasts but also the performance of the adaptive forecast-based PR-MPC operation model. This suggests that utilizing clustering algorithms can be beneficial in improving forecast precision for flood management.
- The accuracy of ANN forecast models was enhanced by the addition of predictors describing variations in rainfall depth over shorter time intervals than the forecast lead time. This indicates that capturing short-term variations in rainfall depth can contribute to more accurate forecasts.
- The rainfall forecasting module showed a higher impact on the performance of the PR-MPC operation strategy for longer-duration, larger-magnitude rainfall events. This highlights the importance of accurate rainfall forecasts in optimizing flood control operations, particularly for more heavy rainfall events.
- Despite inaccuracies in rainfall forecasts and the ANN model’s uncertainty, the forecast-based adaptive PR-MPC operation model performed 11% better in terms of flood volume reduction than the RE-MPC operation model that did not use rainfall forecasts. This accomplishment was partially attributed to the adaptively updating ANN-based rainfall forecasts and the PR-MPC operating model’s control rules over a dynamic, uncertain decision-making process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | artificial neural networks |
| CTH | control time horizon |
| FAC | forecast accuracy |
| GA | genetic algorithm |
| HM | harmony memory matrix |
| HMCR | harmony memory considering rate |
| HMS | harmony memory size |
| HS | harmony search |
| IFAC | input (rainfall) forecast accuracy |
| IFTH | input (rainfall) forecast time horizon |
| MINLP | mixed-integer nonlinear program |
| MLFNN | Multi-layer Feedforward Neural Network |
| MPC | model predictive control |
| PAR | pitch adjusting rate |
| PR-MPC | predictive MPC |
| PTH | prediction time horizon |
| RE-MPC | reactive MPC |
| RS | repository size |
| RTC | real-time control |
| SWMM | storm water management model |
| Ti | sampling time intervals |
| UDS | urban drainage systems |
References
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Xu, W.; Wang, B. An Optimal Operation Model for Hydropower Stations Considering Inflow Forecasts with Different Lead-Times. Water Resour. Manag. 2018, 33, 173–188. [Google Scholar] [CrossRef]
- Babovic, F.; Mijic, A.; Madani, K. Decision making under deep uncertainty for adapting urban drainage systems to change. Urban Water J. 2018, 15, 552–560. [Google Scholar] [CrossRef]
- Ferdous, R.; Di Baldassarre, G.; Brandimarte, L.; Wesselink, A. The interplay between structural flood protection, population density, and flood mortality along the Jamuna River, Bangladesh. Reg. Environ. Chang. 2020, 20, 5. [Google Scholar] [CrossRef]
- Todeschini, S.; Papiri, S.; Ciaponi, C. Performance of stormwater detention tanks for urban drainage systems in northern Italy. J. Environ. Manag. 2012, 101, 33–45. [Google Scholar] [CrossRef]
- García, L.; Barreiro-Gomez, J.; Escobar, E.; Téllez, D.; Quijano, N.; Ocampo-Martinez, C. Modeling and real-time control of urban drainage systems: A review. Adv. Water Resour. 2015, 85, 120–132. [Google Scholar] [CrossRef]
- Jafari, F.; Mousavi, S.J.; Yazdi, J.; Kim, J.H. Real-Time Operation of Pumping Systems for Urban Flood Mitigation: Single-Period vs. Multi-Period Optimization. Water Resour. Manag. 2018, 32, 4643–4660. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Falk, A.K.V.; Borup, M.; Madsen, H.; Mikkelsen, P.S. Model predictive control of urban drainage systems: A review and perspective towards smart real-time water management. Crit. Rev. Environ. Sci. Technol. 2018, 48, 279–339. [Google Scholar] [CrossRef]
- Mullapudi, A.; Lewis, M.J.; Gruden, C.L.; Kerkez, B. Deep reinforcement learning for the real time control of stormwater systems. Adv. Water Resour. 2020, 140, 103600. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C. Model Predictive Control of Wastewater Systems; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- van der Werf, J.A.; Kapelan, Z.; Langeveld, J. Quantifying the true potential of Real Time Control in urban drainage systems. Urban Water J. 2021, 18, 873–884. [Google Scholar] [CrossRef]
- Hooshyar, M.; Mousavi, S.J.; Mahootchi, M.; Ponnambalam, K. Aggregation–Decomposition-Based Multi-Agent Reinforcement Learning for Multi-Reservoir Operations Optimization. Water 2020, 12, 2688. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Ponnambalam, K.; Celeste, A.B.; Cai, X. Enhancements to explicit stochastic reservoir operation optimization method. Adv. Water Resour. 2022, 169, 104307. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Kerkez, B.; Gruden, C.; Lewis, M.; Montestruque, L.; Quigley, M.; Wong, B.; Bedig, A.; Kertesz, R.; Braun, T.; Cadwalader, O.; et al. Smarter Stormwater Systems. Environ. Sci. Technol. 2016, 50, 7267–7273. [Google Scholar] [CrossRef]
- Beeneken, T.; Erbe, V.; Messmer, A.; Reder, C.; Rohlfing, R.; Scheer, M.; Schuetze, M.; Schumacher, B.; Weilandt, M.; Weyand, M. Real time control (RTC) of urban drainage systems—A discussion of the additional efforts compared to conventionally operated systems. Urban Water J. 2013, 10, 293–299. [Google Scholar] [CrossRef]
- Borsányi, P.; Benedetti, L.; Dirckx, G.; De Keyser, W.; Muschalla, D.; Solvi, A.-M.; Vandenberghe, V.; Weyand, M.; Vanrolleghem, P.A. Modelling real-time control options on virtual sewer systems. J. Environ. Eng. Sci. 2008, 7, 395–410. [Google Scholar] [CrossRef]
- Cembellín, A.; Francisco, M.; Vega, P. Distributed Model Predictive Control Applied to a Sewer System. Processes 2020, 8, 1595. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J.; Hsu, H.-C. Real-Time Reservoir Operation for Flood Control Using Artificial Intelligent Techniques. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 887–902. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Chang, L.-C.; Tsai, M.-J.; Wang, Y.-F.; Chang, F.-J. Auto-control of pumping operations in sewerage systems by rule-based fuzzy neural networks. Hydrol. Earth Syst. Sci. 2011, 15, 185–196. [Google Scholar] [CrossRef]
- Darsono, S.; Labadie, J.W. Neural-optimal control algorithm for real-time regulation of in-line storage in combined sewer systems. Environ. Model. Softw. 2007, 22, 1349–1361. [Google Scholar] [CrossRef]
- Garofalo, G.; Giordano, A.; Piro, P.; Spezzano, G.; Vinci, A. A distributed real-time approach for mitigating CSO and flooding in urban drainage systems. J. Netw. Comput. Appl. 2017, 78, 30–42. [Google Scholar] [CrossRef]
- Hsu, N.-S.; Huang, C.-L.; Wei, C.-C. Intelligent real-time operation of a pumping station for an urban drainage system. J. Hydrol. 2013, 489, 85–97. [Google Scholar] [CrossRef]
- Jafari, F.; Mousavi, S.J.; Yazdi, J.; Kim, J.H. Long-term versus Real-time Optimal Operation for Gate Regulation during Flood in Urban Drainage Systems. Urban Water J. 2018, 15, 750–759. [Google Scholar] [CrossRef]
- Maiolo, M.; Palermo, S.A.; Brusco, A.C.; Pirouz, B.; Turco, M.; Vinci, A.; Spezzano, G.; Piro, P. On the Use of a Real-Time Control Approach for Urban Stormwater Management. Water 2020, 12, 2842. [Google Scholar] [CrossRef]
- Rai, P.K.; Dhanya, C.T.; Chahar, B.R. Flood control in an urban drainage system using a linear controller. Water Pract. Technol. 2017, 12, 942–952. [Google Scholar] [CrossRef]
- Schütze, M.; Campisano, A.; Colas, H.; Schilling, W.; Vanrolleghem, P.A. Real-time control of urban wastewater systems—Where do we stand today? J. Hydrol. 2004, 299, 335–348. [Google Scholar] [CrossRef]
- Sun, C.; Svensen, J.L.; Borup, M.; Puig, V.; Cembrano, G.; Vezzaro, L. An MPC-Enabled SWMM Implementation of the Astlingen RTC Benchmarking Network. Water 2020, 12, 1034. [Google Scholar] [CrossRef]
- Wei, C.-C.; Hsu, N.-S.; Huang, C.-L. Two-Stage Pumping Control Model for Flood Mitigation in Inundated Urban Drainage Basins. Water Resour. Manag. 2013, 28, 425–444. [Google Scholar] [CrossRef]
- Yazdi, J.; Kim, J.H. Intelligent Pump Operation and River Diversion Systems for Urban Storm Management. J. Hydrol. Eng. 2015, 20, 04015031. [Google Scholar] [CrossRef]
- Chiang, P.-K.; Willems, P. Combine Evolutionary Optimization with Model Predictive Control in Real-time Flood Control of a River System. Water Resour. Manag. 2015, 29, 2527–2542. [Google Scholar] [CrossRef]
- Jafari, F.; Mousavi, S.J.; Kim, J.H. Investigation of Rainfall Forecast System Characteristics in Real-Time Optimal Operation of Urban Drainage Systems. Water Resour. Manag. 2020, 34, 1773–1787. [Google Scholar] [CrossRef]
- Pleau, M.; Colas, H.; Lavallée, P.; Pelletier, G.; Bonin, R. Global optimal real-time control of the Quebec urban drainage system. Environ. Model. Softw. 2005, 20, 401–413. [Google Scholar] [CrossRef]
- van Overloop, P.-J.; Weijs, S.; Dijkstra, S. Multiple Model Predictive Control on a drainage canal system. Control Eng. Pract. 2008, 16, 531–540. [Google Scholar] [CrossRef]
- Abraham, A.; Philip, N.S.; Joseph, K.B. Will We Have a Wet Summer? Soft Computing Models for Long Term Rainfall Forecasting. In Proceedings of the 15th European Simulation Multiconference (ESM 2001), Modelling and Simulation, Prague, Czechia, 6–9 June 2001; pp. 1044–1048. [Google Scholar]
- Wahyuni, E.G.; Fauzan LM, F.; Abriyani, F.; Muchlis, N.F.; Ulfa, M. Rainfall Prediction with Backpropagation Method. J. Phys. Conf. Ser. 2018, 983, 012059. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Wood, E.F. Hydrologic Forecasting. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 26. [Google Scholar]
- Luk, K.; Ball, J.; Sharma, A. A study of optimal model lag and spatial inputs to artificial neural network for rainfall forecasting. J. Hydrol. 2000, 227, 56–65. [Google Scholar] [CrossRef]
- Luk, K.C.; Ball, J.; Sharma, A. An application of artificial neural networks for rainfall forecasting. Math. Comput. Model. 2001, 33, 683–693. [Google Scholar] [CrossRef]
- Christodoulou, C.I.; Michaelides, S.C.; Gabella, M.; Pattichis, C.S. Prediction of rainfall rate based on weather radar measurements. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, pp. 1393–1396. [Google Scholar]
- Nasseri, M.; Asghari, K.; Abedini, M. Optimized scenario for rainfall forecasting using genetic algorithm coupled with artificial neural network. Expert Syst. Appl. 2008, 35, 1415–1421. [Google Scholar] [CrossRef]
- Adaryani, F.R.; Mousavi, S.J.; Jafari, F. Short-term rainfall forecasting using machine learning-based approaches of PSO-SVR, LSTM and CNN. J. Hydrol. 2022, 614, 128463. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Reusch, D.B.; Alley, R.B. Automatic Weather Stations and Artificial Neural Networks: Improving the Instrumental Record in West Antarctica. Mon. Weather. Rev. 2002, 130, 3037–3053. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Stanski, H.R.; Wilson, L.; Burrows, W.R. Survey of Common Verification in Meteorology; World Weather Watch Report 358; World Meteorological Organization: Geneva, Switzerland, 1989. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new meta-heuristic algorithm for continuous engineering optimization: Harmony search theory and practice. Comput. Methods Appl. Mech. Eng. 2005, 194, 3902–3933. [Google Scholar] [CrossRef]
- MGCE. Tehran Stormwater Management Master Plan. In Vol 4: Existing Main Drainage Network, Part 2: Hydraulic Modeling and Capacity Assessment, December 2011; MG Consultant Engineers, Technical and development deputy of Tehran municipality: Tehran, Iran, 2011. [Google Scholar]
- Bock, H.H. Clustering Methods: A History of k-Means Algorithms. In Selected Contributions in Data Analysis and Classification; Springer: Berlin/Heidelberg, Germany, 2007; pp. 161–172. [Google Scholar]
- Dirckx, G.; Schütze, M.; Kroll, S.; Thoeye, C.; De Gueldre, G.; Van De Steene, B. RTC versus static solutions to mitigate CSO’s impact. In Proceedings of the 12nd International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011. [Google Scholar]
- Fuchs, L.; Beeneken, T. Development and implementation of a real-time control strategy for the sewer system of the city of Vienna. Water Sci. Technol. 2005, 52, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, L.; Günther, H.; Lindenberg, M. Minimizing the Water Pollution Load by means of Real-Time Control (RTC)-The Dresden exemple. In Proceedings of the 6th International Conference on Urban Drainage Modelling, Dresden, Germany, 15–17 September 2004; pp. 317–325. [Google Scholar]
- Pleau, M.; Fradet, O.; Colas, H.; Marcoux, C. Giving the rivers back to the public. Ten years of real time control in Quebec city. In Proceedings of the NOVATECH 7th International Conference: Sustainable Techniques and Strategies in Urban Waste Water, Lyon, France, 27 June–1 July 2010; Available online: http://documents.irevues.inist.fr/bitstream/handle/2042/35732/31805-055ple.pdf?sequence=1 (accessed on 16 May 2023).



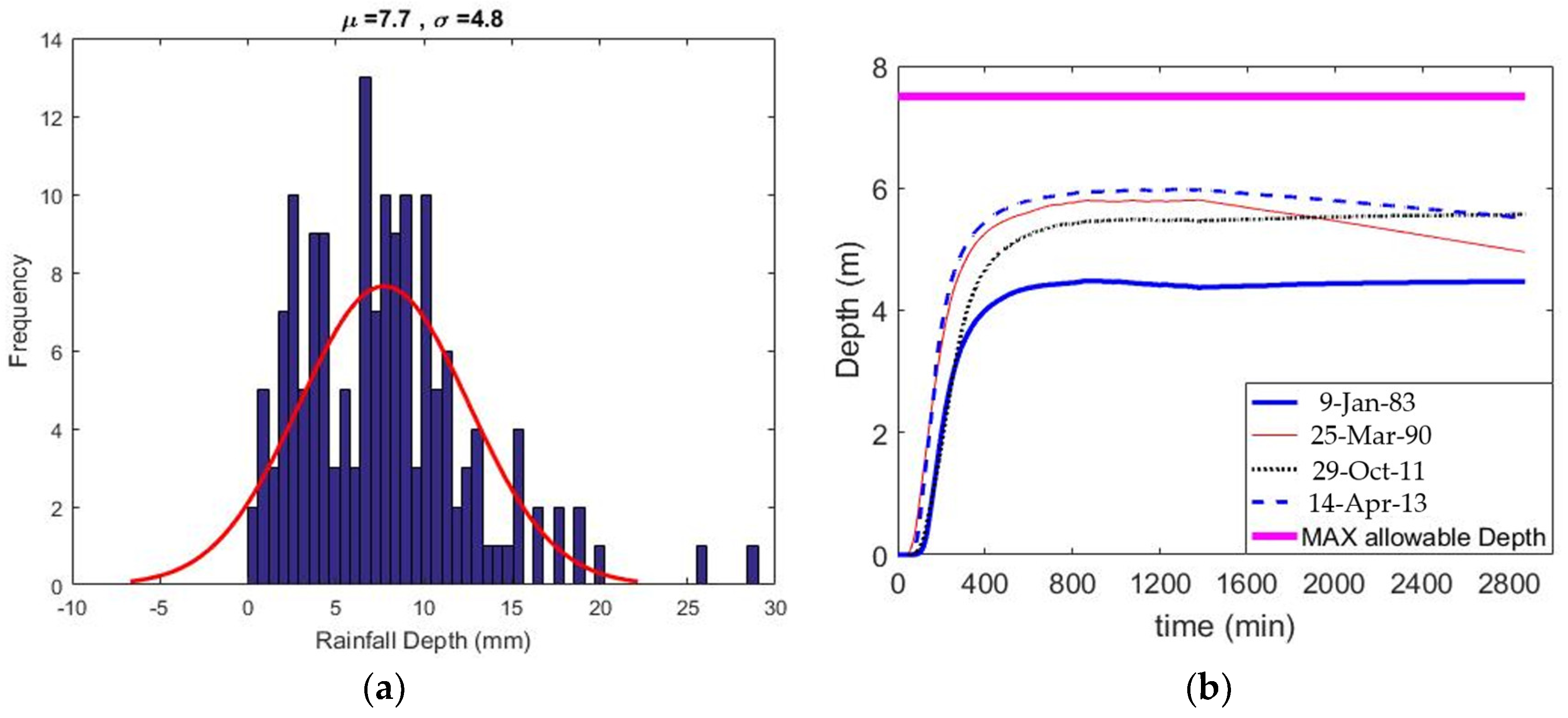
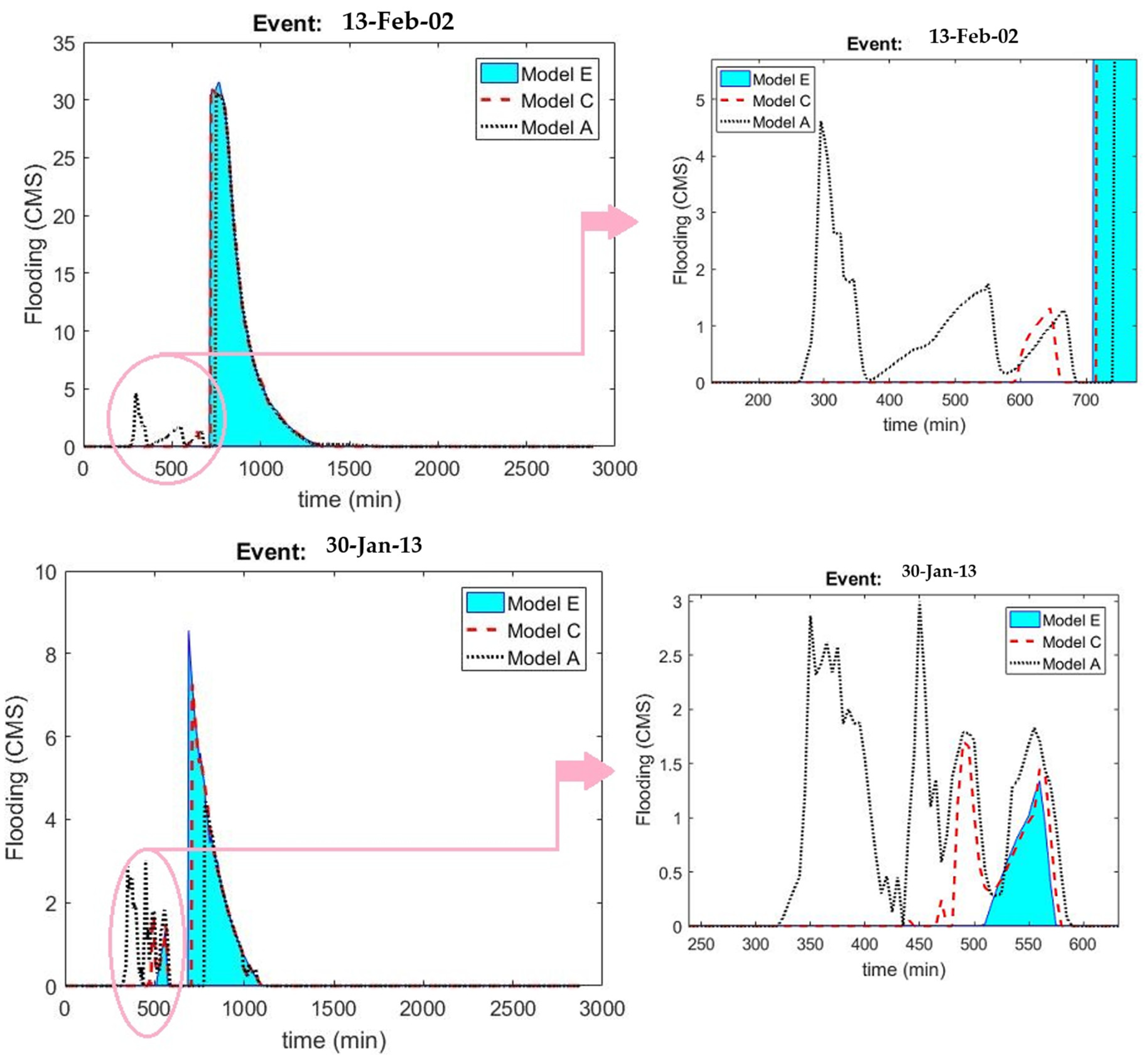

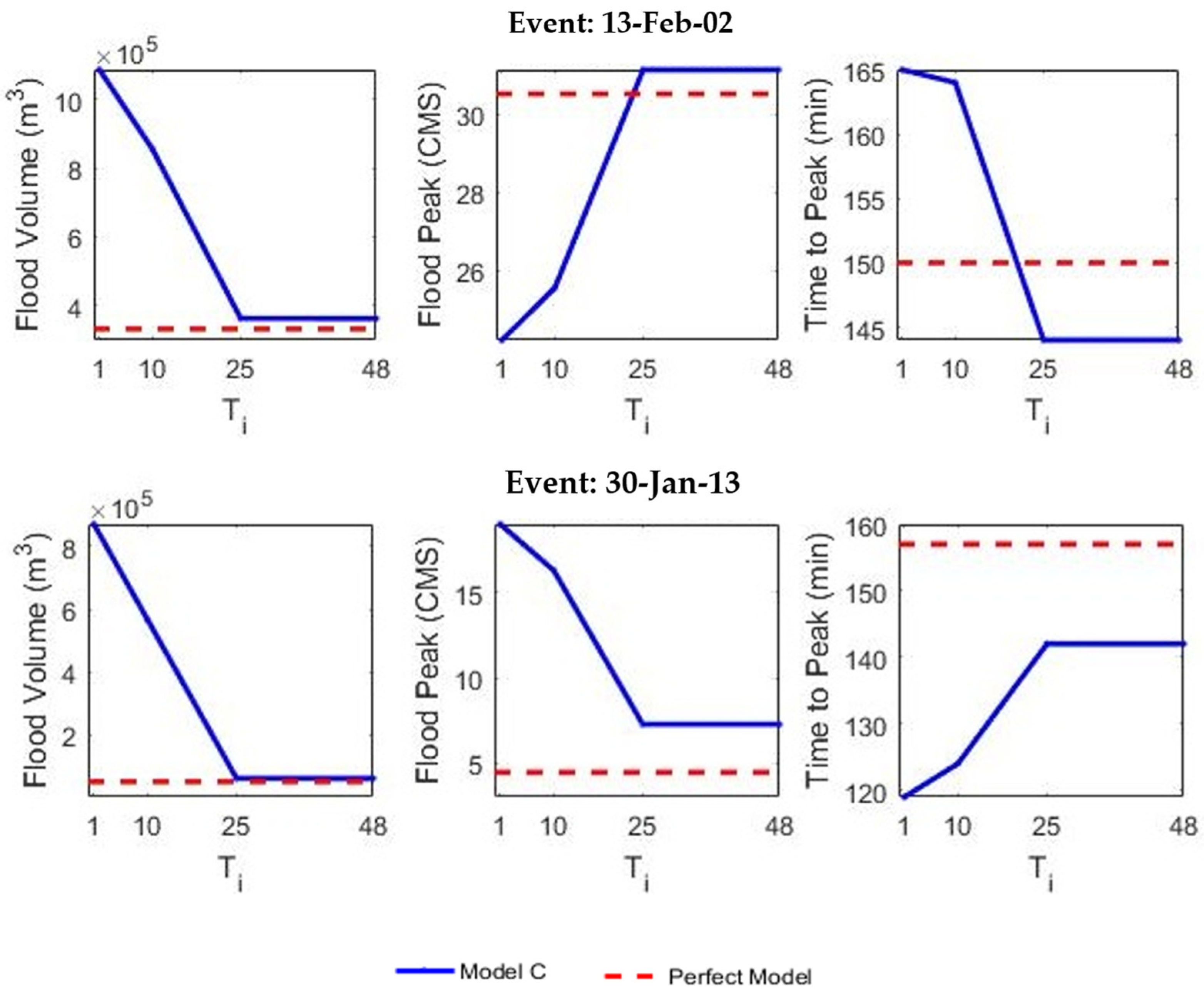
| Event No. | Event | Duration (min) | Depth (mm) |
|---|---|---|---|
| 1 | 9-Jan-83 | 240 | 14.35 |
| 2 | 25-Mar-90 | 270 | 20.29 |
| 3 | 13-Feb-02 | 750 | 26.41 |
| 4 | 29-Oct-11 | 240 | 16.9 |
| 5 | 30-Jan-13 | 450 | 24.1 |
| 6 | 14-Apr-13 | 195 | 18.8 |
| Number of Events Included | Included Events (%) | Number of Data | Average Duration (min) | Average Depth (mm) | Max Depth (mm/15 min) | |
|---|---|---|---|---|---|---|
| All Data | 335 | 100 | 8063 | 487.84 | 13.5 | 10.59 |
| C1 | 52 | 16 | 2576 | 951.9 | 21.2 | 6.3 |
| C2 | 105 | 31 | 2915 | 530.1 | 15.5 | 7.31 |
| C3 | 18 | 5 | 1295 | 1624.2 | 29.1 | 4.57 |
| 160 | 48 | 1277 | 181.4 | 7.7 | 10.59 |
| Scenario | All Data | C1 | C2 | C3 | C4 | |
|---|---|---|---|---|---|---|
| I | Train | 0.41 | 0.49 | 0.44 | 0.55 | 0.28 |
| Test | 0.39 | 0.47 | 0.43 | 0.52 | 0.25 | |
| II | Train | 0.43 | 0.53 | 0.47 | 0.70 | 0.35 |
| Test | 0.42 | 0.51 | 0.46 | 0.68 | 0.31 | |
| III | Train | 0.47 | 0.61 | 0.57 | 0.75 | 0.42 |
| Test | 0.45 | 0.59 | 0.55 | 0.73 | 0.42 |
| Model | Input Forecast Type in Terms of IFAC | IFTH |
|---|---|---|
| A | Perfect (error-free) | Entire rainfall event |
| B | Perfect (error-free) | Two time-steps ahead |
| C | Imperfect use forecasting module | Two time-steps ahead |
| D | Imperfect use forecasting module | One time-step ahead |
| E | Without a forecast module (reactive model) | (reactive model) |
| Model | Event: 13 February 2002 | Event: 30 January 2013 | ||||
|---|---|---|---|---|---|---|
| Flood Reduction Compared with Model E | Flooding | Flood Reduction Compared with Model E | Flooding | |||
| (103 m3) | (103 m3) | |||||
| (%) | (103 m3) | (%) | (103 m3) | |||
| A | 10% | 38.9 | 334.37 | 25% | 17.11 | 52.07 |
| B | 4% | 12.87 | 360.4 | 15% | 10.08 | 59.1 |
| C | 3% | 10.56 | 362.71 | 11% | 7.65 | 61.53 |
| D | 2% | 6.57 | 366.7 | 2% | 1.3 | 67.88 |
| -- | -- | 373.27 | -- | -- | 69.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, F.; Mousavi, S.J.; Ponnambalam, K. Predictive MPC-Based Operation of Urban Drainage Systems Using Input Data-Clustered Artificial Neural Networks Rainfall Forecasting Models. Hydrology 2023, 10, 139. https://doi.org/10.3390/hydrology10070139
Jafari F, Mousavi SJ, Ponnambalam K. Predictive MPC-Based Operation of Urban Drainage Systems Using Input Data-Clustered Artificial Neural Networks Rainfall Forecasting Models. Hydrology. 2023; 10(7):139. https://doi.org/10.3390/hydrology10070139
Chicago/Turabian StyleJafari, Fatemeh, S. Jamshid Mousavi, and Kumaraswamy Ponnambalam. 2023. "Predictive MPC-Based Operation of Urban Drainage Systems Using Input Data-Clustered Artificial Neural Networks Rainfall Forecasting Models" Hydrology 10, no. 7: 139. https://doi.org/10.3390/hydrology10070139
APA StyleJafari, F., Mousavi, S. J., & Ponnambalam, K. (2023). Predictive MPC-Based Operation of Urban Drainage Systems Using Input Data-Clustered Artificial Neural Networks Rainfall Forecasting Models. Hydrology, 10(7), 139. https://doi.org/10.3390/hydrology10070139





