Development of Multi-Inflow Prediction Ensemble Model Based on Auto-Sklearn Using Combined Approach: Case Study of Soyang River Dam
Abstract
1. Introduction
2. Materials and Methods
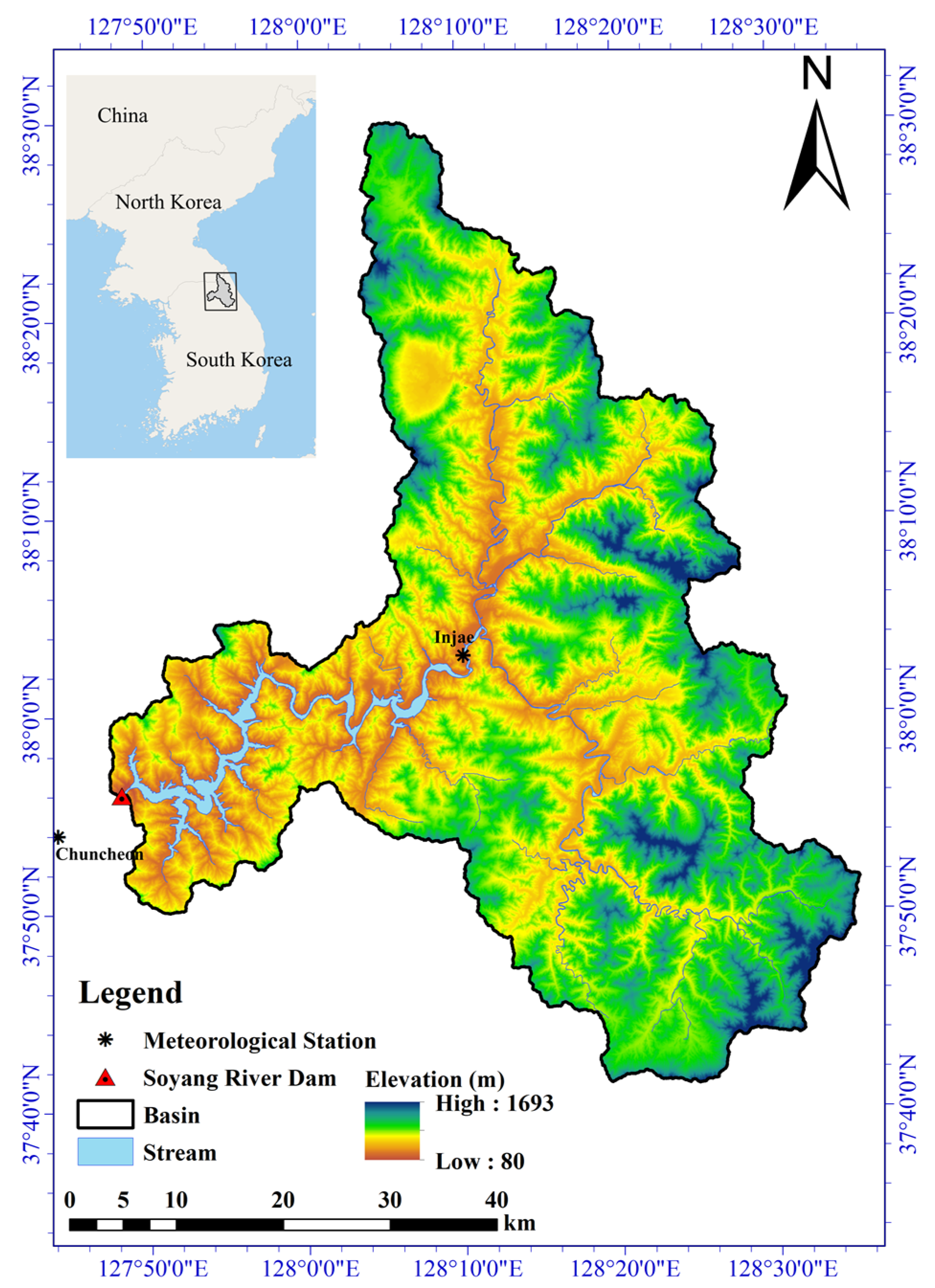
2.1. Description of the Study Area
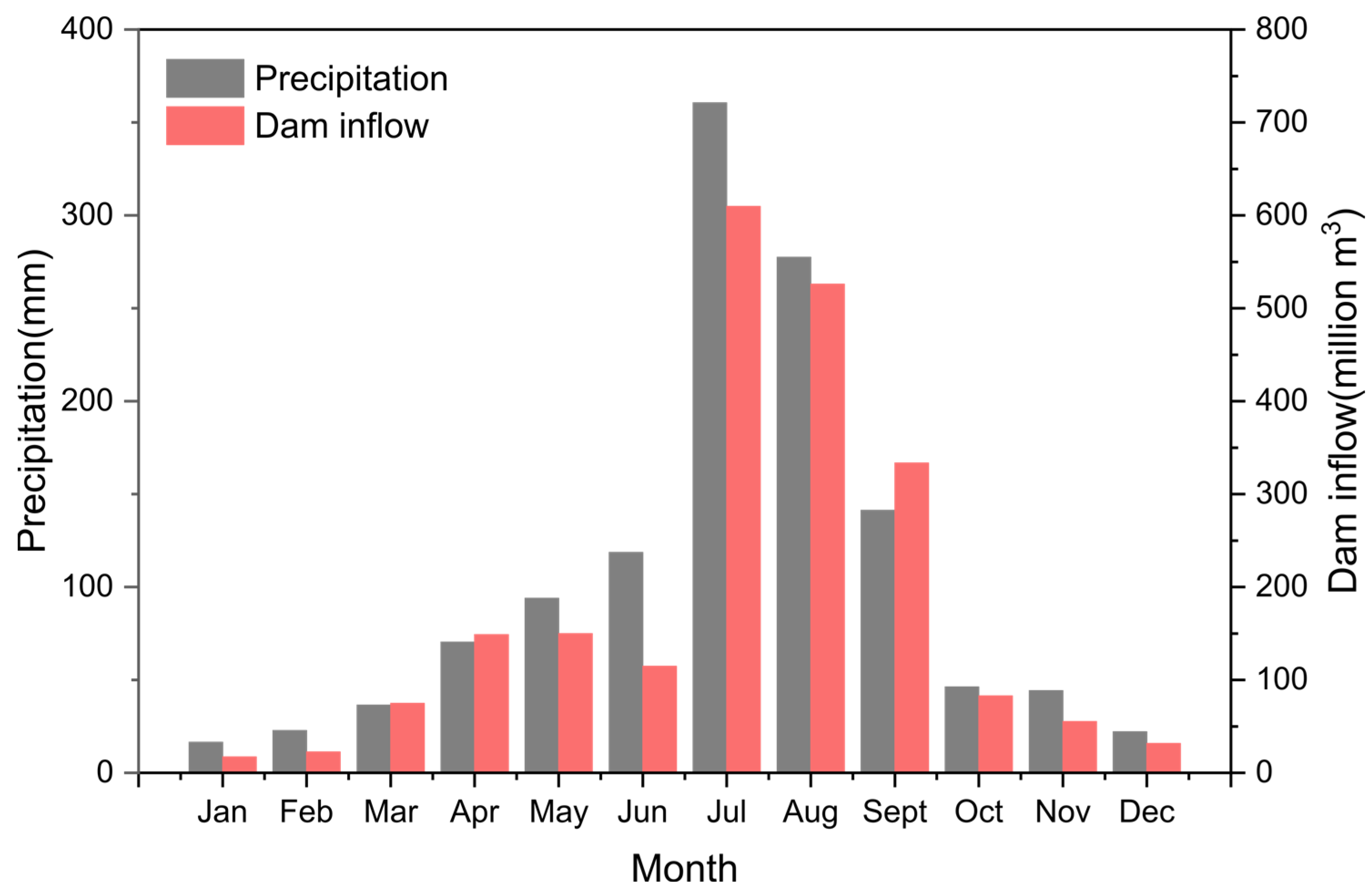
2.2. Data Collection
2.3. Auto-Sklearn
2.4. MPE Model Development Using Split Datasets
2.5. Performance Evaluation Metrics
3. Results and Discussion
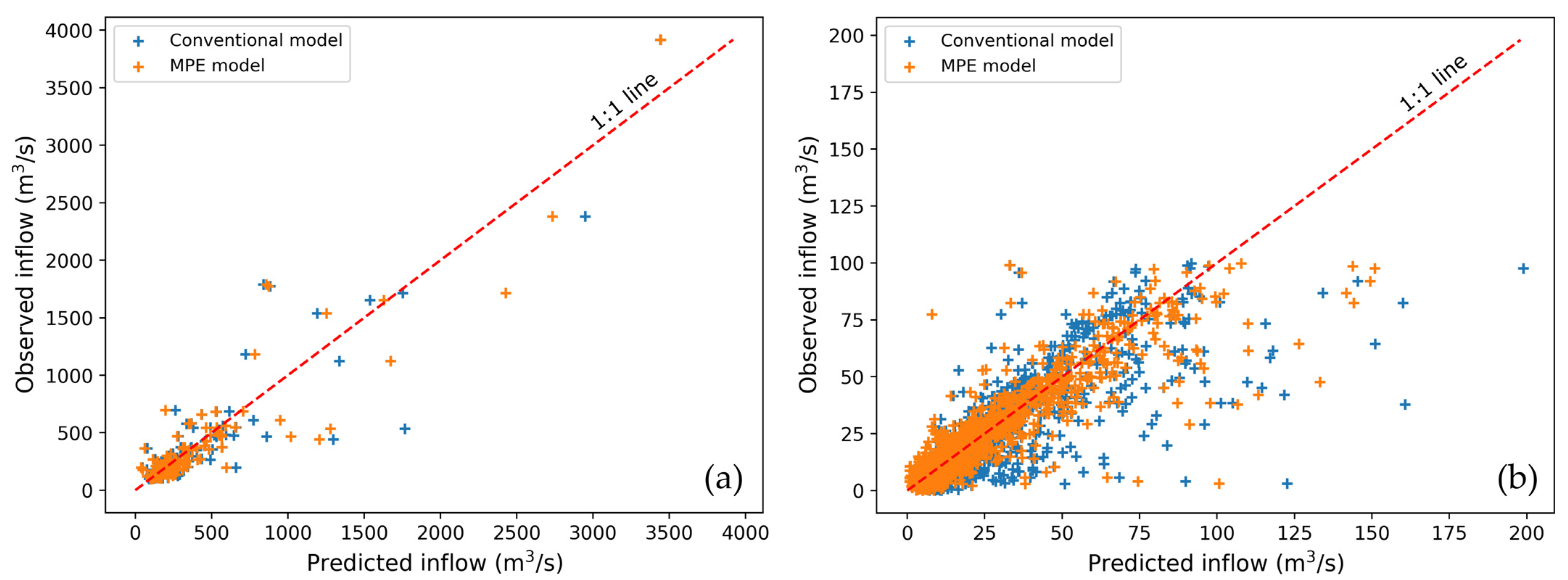
3.1. Ensemble Modeling with Conventional and Combined Approaches for Inflow Prediction
3.2. Comparison of Dam Inflow Prediction Performance
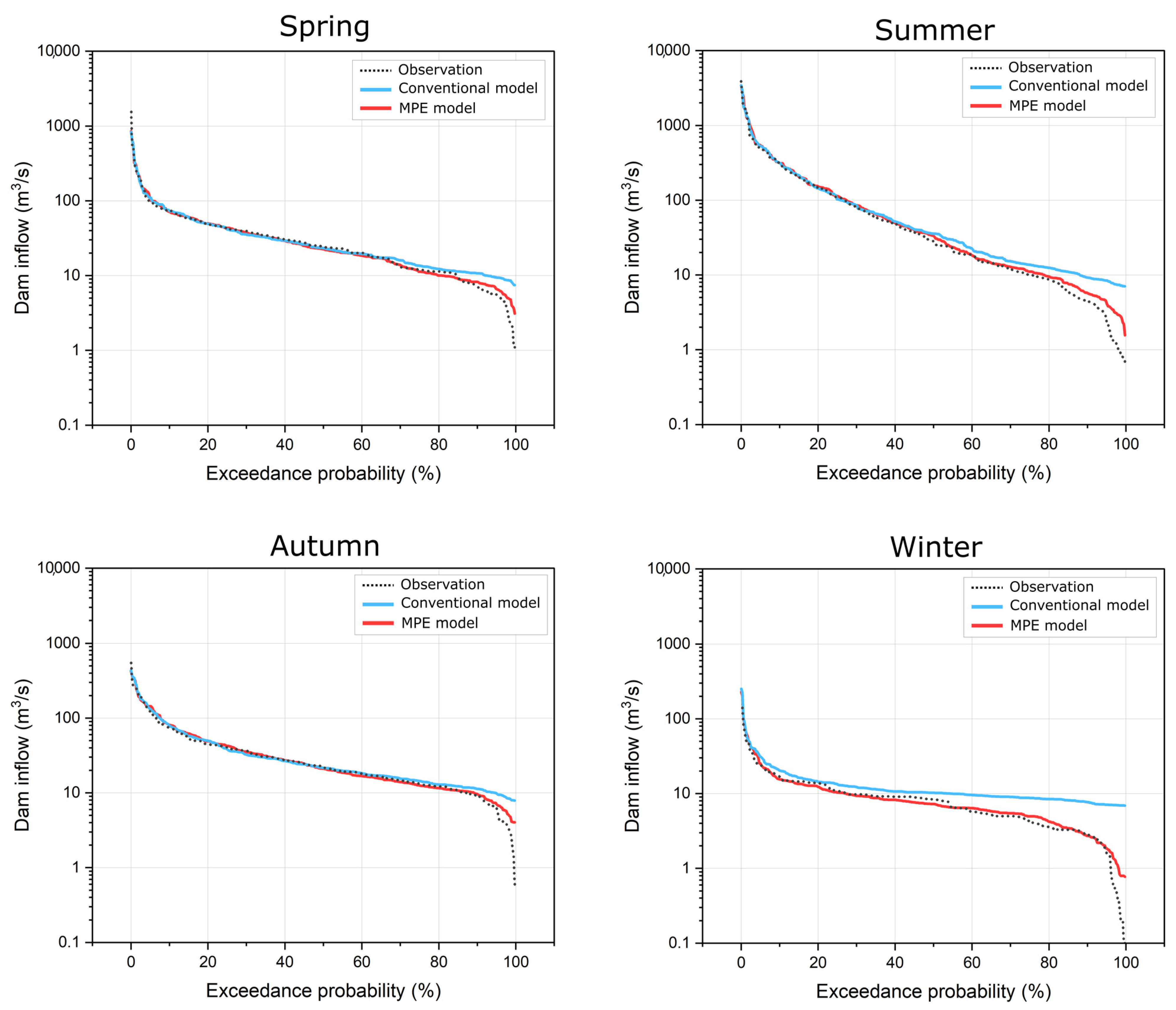
3.3. Comparison of AS-Based Ensemble Models for Dam Inflow Prediction Using FDC Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simonovic, S.P. Bringing Future Climatic Change into Water Resources Management Practice Today. Water Resour. Manag. 2017, 31, 2933–2950. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Sobkowiak, L.; Wang, Z.; Guo, F. Spatial Pattern Characterization and Multivariate Hydrological Frequency Analysis of Extreme Precipitation in the Pearl River Basin, China. Water Resour. Manag. 2012, 26, 3619–3637. [Google Scholar] [CrossRef]
- Samuels, R.; Rimmer, A.; Alpert, P. Effect of Extreme Rainfall Events on the Water Resources of the Jordan River. J. Hydrol. 2009, 375, 513–523. [Google Scholar] [CrossRef]
- Ehsani, N.; Vörösmarty, C.J.; Fekete, B.M.; Stakhiv, E.Z. Reservoir Operations under Climate Change: Storage Capacity Options to Mitigate Risk. J. Hydrol. 2017, 555, 435–446. [Google Scholar] [CrossRef]
- Prasanchum, H.; Kangrang, A. Optimal Reservoir Rule Curves under Climatic and Land Use Changes for Lampao Dam Using Genetic Algorithm. KSCE J. Civ. Eng. 2018, 22, 351–364. [Google Scholar] [CrossRef]
- Naz, B.S.; Kao, S.-C.; Ashfaq, M.; Gao, H.; Rastogi, D.; Gangrade, S. Effects of Climate Change on Streamflow Extremes and Implications for Reservoir Inflow in the United States. J. Hydrol. 2018, 556, 359–370. [Google Scholar] [CrossRef]
- Momiyama, S.; Sagehashi, M.; Akiba, M. Assessment of the Climate Change Risks for Inflow into Sagami Dam Reservoir Using a Hydrological Model. J. Water Clim. Chang. 2020, 11, 367–379. [Google Scholar] [CrossRef]
- Xu, S.; Chen, Y.; Xing, L.; Li, C. Baipenzhu Reservoir Inflow Flood Forecasting Based on a Distributed Hydrological Model. Water 2021, 13, 272. [Google Scholar] [CrossRef]
- Alizadeh, F.; Gharamaleki, A.F.; Jalilzadeh, M.; Akhoundzadeh, A. Prediction of River Stage-Discharge Process Based on a Conceptual Model Using EEMD-WT-LSSVM Approach. Water Resour. 2020, 47, 41–53. [Google Scholar] [CrossRef]
- Shelke, M.; Londhe, S.; Dixit, P.R.; Kolhe, P. Simulation of reservoir inflow using HEC-HMS; 2022. In Proceedings of the HYDRO 2021-International Conference (Hydraulics, Water Resources and Coastal Engineering), Pune, India, 23–25 December 2021. [Google Scholar]
- Wibowo, H.; Ridwansyah, I.; Rahmat, A. Evaluating inflow result from SWAT model at Singkarak Lake under limited data. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 5th Indonesian Society of Limnology (MLI) Congress and International Conference, Online, 2–3 December 2021; IOP Publishing Ltd.: Bristol, UK, 2022; Volume 1062. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Peng, A.; Wang, W.; Li, B.; Huang, X. Quantifying the Uncertainties in Data-Driven Models for Reservoir Inflow Prediction. Water Resour. Manag. 2020, 34, 1479–1493. [Google Scholar] [CrossRef]
- Tran, T.D.; Tran, V.N.; Kim, J. Improving the Accuracy of Dam Inflow Predictions Using a Long Short-Term Memory Network Coupled with Wavelet Transform and Predictor Selection. Mathematics 2021, 9, 551. [Google Scholar] [CrossRef]
- Ahmad, S.K.; Hossain, F. A Generic Data-Driven Technique for Forecasting of Reservoir Inflow: Application for Hydropower Maximization. Environ. Model. Softw. 2019, 119, 147–165. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.-W. Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Herbert, Z.C.; Asghar, Z.; Oroza, C.A. Long-Term Reservoir Inflow Forecasts: Enhanced Water Supply and Inflow Volume Accuracy Using Deep Learning. J. Hydrol. 2021, 601, 126676. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Decomposition Ensemble Model Based on Variational Mode Decomposition and Long Short-Term Memory for Streamflow Forecasting. J. Hydrol. 2020, 585, 124776. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A Physical Process and Machine Learning Combined Hydrological Model for Daily Streamflow Simulations of Large Watersheds with Limited Observation Data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super Ensemble Learning for Daily Streamflow Forecasting: Large-Scale Demonstration and Comparison with Multiple Machine Learning Algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Rajesh, M.; Anishka, S.; Viksit, P.S.; Arohi, S.; Rehana, S. Improving Short-Range Reservoir Inflow Forecasts with Machine Learning Model Combination. Water Resour. Manag. 2023, 37, 75–90. [Google Scholar] [CrossRef]
- Paul, T.; Raghavendra, S.; Ueno, K.; Ni, F.; Shin, H.; Nishino, K.; Shingaki, R. Forecasting of reservoir inflow by the combination of deep learning and conventional machine learning. In Proceedings of the 2021 International Conference on Data Mining Workshops (ICDMW), Auckland, New Zealand, 7–10 December 2021; pp. 558–565. [Google Scholar]
- Rezaie-Balf, M.; Naganna, S.R.; Kisi, O.; El-Shafie, A. Enhancing Streamflow Forecasting Using the Augmenting Ensemble Procedure Coupled Machine Learning Models: Case Study of Aswan High Dam. Hydrol. Sci. J. 2019, 64, 1629–1646. [Google Scholar] [CrossRef]
- Truong, A.; Walters, A.; Goodsitt, J.; Hines, K.; Bruss, C.B.; Farivar, R. Towards automated machine learning: Evaluation and comparison of automl approaches and tools. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1471–1479. [Google Scholar]
- Shi, X.; Wong, Y.D.; Chai, C.; Li, M.Z.-F. An Automated Machine Learning (AutoML) Method of Risk Prediction for Decision-Making of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7145–7154. [Google Scholar] [CrossRef]
- Tsiakmaki, M.; Kostopoulos, G.; Kotsiantis, S.; Ragos, O. Implementing AutoML in Educational Data Mining for Prediction Tasks. Appl. Sci. 2020, 10, 90. [Google Scholar] [CrossRef]
- Babaeian, E.; Paheding, S.; Siddique, N.; Devabhaktuni, V.K.; Tuller, M. Estimation of Root Zone Soil Moisture from Ground and Remotely Sensed Soil Information with Multisensor Data Fusion and Automated Machine Learning. Remote Sens. Environ. 2021, 260, 112434. [Google Scholar] [CrossRef]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Efficient and robust automated machine learning. In Advances in Neural Information Processing Systems 28 (NIPS 2015); Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2015; pp. 2962–2970. [Google Scholar]
- Han, H.; Kim, D.; Wang, W.; Kim, H.S. Dam Inflow Prediction Using Large-Scale Climate Variability and Deep Learning Approach: A Case Study in South Korea. Water Supply 2023, 23, 934–947. [Google Scholar] [CrossRef]
- Hong, J.; Lee, S.; Bae, J.H.; Lee, J.; Park, W.J.; Lee, D.; Kim, J.; Lim, K.J. Development and Evaluation of the Combined Machine Learning Models for the Prediction of Dam Inflow. Water 2020, 12, 2927. [Google Scholar] [CrossRef]
- Moon, G.-H.; Kim, S.-H.; Bae, D.-H. Development and Evaluation of ANFIS-Based Conditional Dam Inflow Prediction Method Using Flow Regime. J. Korea Water Resour. Assoc. 2018, 51, 607–616. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, H.; Lin, Y.; Jin, J.; Liu, W.; An, X. Reservoir Inflow Predicting Model Based on Machine Learning Algorithm via Multi-Model Fusion: A Case Study of Jinshuitan River Basin. IET Cyber-Syst. Robot. 2021, 3, 265–277. [Google Scholar] [CrossRef]
- Choi, H.S.; Kim, J.H.; Lee, E.H.; Yoon, S.-K. Development of a Revised Multi-Layer Perceptron Model for Dam Inflow Prediction. Water 2022, 14, 1878. [Google Scholar] [CrossRef]
- Lee, M.H.; Im, E.S.; Bae, D.H. Future Projection in Inflow of Major Multi-Purpose Dams in South Korea. J. Wetl. Res. 2019, 21, 107–116. [Google Scholar]
- Xu, S.; Qin, M.; Ding, S.; Zhao, Q.; Liu, H.; Li, C.; Yang, X.; Li, Y.; Yang, J.; Ji, X. The Impacts of Climate Variation and Land Use Changes on Streamflow in the Yihe River, China. Water 2019, 11, 887. [Google Scholar] [CrossRef]
- Mao, T.; Wang, G.; Zhang, T. Impacts of Climatic Change on Hydrological Regime in the Three-River Headwaters Region, China, 1960–2009. Water Resour. Manag. 2016, 30, 115–131. [Google Scholar] [CrossRef]
- Feurer, M.; Springenberg, J.; Hutter, F. Initializing Bayesian Hyperparameter Optimization via Meta-Learning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX USA, 25–30 January 2015; Volume 29. [Google Scholar] [CrossRef]
- Pelikan, M.; Goldberg, D.E.; Cantú-Paz, E. BOA: The bayesian optimization algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference GECCO-99, Orlando, FL, USA, 13–17 July 1999; Volume 1, pp. 525–532. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A.; Crew, G.; Ksikes, A. Ensemble Selection from Libraries of Models. In Proceedings of the twenty-first international conference on Machine learning, Banff, AB, Canada, 4–8 July 2004. [Google Scholar]
- Moriasi, D.; Gitau, M.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Motaghian, H.R.; Mohammadi, J. Spatial Estimation of Saturated Hydraulic Conductivity from Terrain Attributes Using Regression, Kriging, and Artificial Neural Networks. Pedosphere 2011, 21, 170–177. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Assessing the Predictive Capability of Randomized Tree-Based Ensembles in Streamflow Modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2669–2684. [Google Scholar] [CrossRef]
- Adnan, R.; Yuan, X.; Kisi, O.; Yuan, Y. Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Am. Sci. Res. J. Eng. Technol. Sci. 2017, 29, 286–294. [Google Scholar]
- Yaghoubi, B.; Hosseini, S.A.; Nazif, S. Monthly Prediction of Streamflow Using Data-Driven Models. J. Earth Syst. Sci. 2019, 128, 141. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial Intelligence Based Models for Stream-Flow Forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Adamowski, J. Using Support Vector Regression to Predict Direct Runoff, Base Flow and Total Flow in a Mountainous Watershed with Limited Data in Uttaranchal, India. Ann. Warsaw Univ. Life Sci. SGGW. L. Reclam. 2013, 45, 71–83. [Google Scholar] [CrossRef]
- Yuan, L.; Forshay, K.J. Enhanced Streamflow Prediction with SWAT Using Support Vector Regression for Spatial Calibration: A Case Study in the Illinois River Watershed, U.S. PLoS ONE 2021, 16, e0248489. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Application of Support Vector Regression for Modeling Low Flow Time Series. KSCE J. Civ. Eng. 2019, 23, 923–934. [Google Scholar] [CrossRef]
- Eldeeb, H.; Matsuk, O.; Maher, M.; Eldallal, A.; Sakr, S. The Impact of Auto-Sklearn’s Learning Settings: Meta-Learning, Ensembling, Time Budget, and Search Space Size. In Proceedings of the EDBT/ICDT Workshops, Nicosia, Cyprus, 23–26 March 2021. [Google Scholar]
- Lundberg, S.; Erion, G.; Lee, S.-I. Consistent Individualized Feature Attribution for Tree Ensembles. ArXiv 2018. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?”: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Shi, M.; Shen, W. Automatic Modeling for Concrete Compressive Strength Prediction Using Auto-Sklearn. Buildings 2022, 12, 1406. [Google Scholar] [CrossRef]
- Tanaka, K.; Monden, A.; Yücel, Z. Prediction of Software Defects Using Automated Machine Learning. In Proceedings of the 2019 20th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Net-working and Parallel/Distributed Computing (SNPD), Toyama, Japan, 8–11 July 2019; pp. 490–494. [Google Scholar]
- Searcy, J.K. Flow-Duration Curves; US Government Printing Office: Washington, DC, USA, 1959. [Google Scholar]
- Yokoo, Y.; Sivapalan, M. Towards Reconstruction of the Flow Duration Curve: Development of a Conceptual Framework with a Physical Basis. Hydrol. Earth Syst. Sci. 2011, 15, 2805–2819. [Google Scholar] [CrossRef]
- Brunner, M.I.; Melsen, L.A.; Newman, A.J.; Wood, A.W.; Clark, M.P. Future Streamflow Regime Changes in the United States: Assessment Using Functional Classification. Hydrol. Earth Syst. Sci. 2020, 24, 3951–3966. [Google Scholar] [CrossRef]
- Chai, Y.; Li, Y.; Yang, Y.; Zhu, B.; Li, S.; Xu, C.; Liu, C. Influence of Climate Variability and Reservoir Operation on Streamflow in the Yangtze River. Sci. Rep. 2019, 9, 5060. [Google Scholar] [CrossRef]






| Model | Input Variables | Target Variable | Period |
|---|---|---|---|
| Training and validation dataset (n =13,148) | It−1, It−2 Pt, Pt−1, Pt−2 | It | 1980–2015 |
| Test dataset (n = 1461) | It−1, It−2 Pt, Pt−1, Pt−2 | It | 2016–2019 |
| Model | Dataset | Weight | Data Preprocessing Method | Feature Preprocessing Method | Hyperparameters | Model Type |
|---|---|---|---|---|---|---|
| Conventional model | All data | 0.20 | encoding = ‘one_hot_encoding’, imputation = ‘mean’, rescaling = ‘standardize’ | extra_trees_preproc_for_regression | activation = ‘relu’, alpha = 6.03 × 10−7 early_stop = ‘valid’, hidden_layer_depth = 3, learning_rate_init = 0.0001, n_iter_no_change = 32, num_nodes_per_layer = 100, solver = ‘adam’ | MLP |
| 0.04 | encoding = ‘one_hot_encoding’, imputation = ‘median’, rescaling = ‘minmax’ | polynomial | activation = ‘relu’, alpha = 6.11 × 10−5, early_stop = ‘valid’, hidden_layer_depth = 3, learning_rate_init = 0.0002, n_iter_no_change = 32, num_nodes_per_layer = 101, solver = ‘adam’ | MLP | ||
| 0.38 | imputation = ‘mean’ | polynomial | n_iter = 300, tol = 0.0091, alpha_1 = 4.70 × 10−5, alpha_2 = 0.0006, lambda_1 = 7.58 × 10−10, lambda_2= 3.92 × 10−8, threshold_lambda= 4052 | ARD regression | ||
| 0.26 | encoding = ‘one_hot_encoding’, imputation = ‘median’, rescaling = ‘standardize’ | polynomial | max_depth = ‘none’, max_leaf_nodes = 28, min_samples_leaf = 6, n_iter_no_change = 5, learning_rate = 0.1329, l2_regularization = 8.22 × 10−10, early_stop = ‘valid’ | GB | ||
| 0.04 | encoding = ‘one_hot_encoding’, imputation = ‘mean’ | polynomial | max_depth = ‘none’, max_leaf_nodes = 31, min_samples_leaf = 25, n_iter_no_change = 7, learning_rate = 0.1239, l2_regularization = 6.08 × 10−10, early_stop = ‘train’ | GB | ||
| 0.08 | encoding = ‘one_hot_encoding’, imputation = ‘median’, rescaling = ‘minmax’ | polynomial | max_depth = ‘none’, max_leaf_nodes = 26, min_samples_leaf = 6, n_iter_no_change = 20, validation_fraction = 0.08, learning_rate = 0.1530, l2_regularization = 0.013, early_stop = ‘valid’ | GB | ||
| MPE model | High-inflow | 0.46 | imputation= ‘most_frequent’, rescaling = ‘minmax’ | polynomial | max_depth = ‘none’, max_features = 0.979, max_leaf_nodes = ‘none’, min_samples_leaf = 1, min_samples_split = 4 | Extra-trees |
| 0.40 | encoding = ‘one_hot_encoding’, imputation = ‘mean’, rescaling = ‘standardize’ | extra_trees_preproc_for_regression | activation = ‘relu’, alpha = 6.03 × 10−7, early_stop = ‘valid’, hidden_layer_depth = 3, learning_rate_init = 0.0001, n_iter_no_change = 32, num_nodes_per_layer = 100, solver = ‘adam’ | MLP | ||
| 0.10 | encoding = ‘one_hot_encoding’, imputation = ‘mean’, rescaling = ‘minmax’ | fast_ica | kernel = ‘rbf’, degree = 3, gamma = 0.201, tol = 0.021, C = 194.03, epsilon = 0.001, max_iter = −1 | SVR | ||
| 0.04 | encoding = ‘one_hot_encoding’, imputation = ‘most_frequent’, rescaling = ‘robust_scaler’ | select_rates_regression | n_iter = 300, tol = 0.0007, alpha_1 = 2.76 × 10−5, alpha_2= 9.50 × 10−7, lambda_1 = 6.51 × 10−9, lambda_2 = 4.24 × 10−7, threshold_lambda = 78,251.5, fit_intercept = ‘ture’ | ARD regression | ||
| Low-inflow | 0.76 | imputation = ‘most_frequent’, rescaling = ‘minmax’ | fast_ica | kernel = ‘rbf’, degree = 2, gamma = 0.032, tol = 0.0034, C = 7277.3, epsilon = 0.001, max_iter = −1 | SVR | |
| 0.06 | encoding = ‘one_hot_encoding’, imputation = ‘median’, rescaling = ‘minmax’ | polynomial | activation = ‘relu’, alpha = 6.11 × 10−5, early_stop = ‘valid’, hidden_layer_depth = 3, learning_rate_init = 0.0003, n_iter_no_change = 32, num_nodes_per_layer = 101, solver = ‘adam’ | MLP | ||
| 0.06 | imputation = ‘mean’ | polynomial | n_iter= 300, tol = 0.0091, alpha_1 = 4.70 × 10−5, alpha_2 = 0.0006, lambda_1 = 7.58 × 10−10, lambda_2 = 3.92 × 10−8, threshold_lambda = 4052, fit_intercept = ‘ture’ | ARD regression | ||
| 0.04 | imputation = ‘mean’, rescaling = ‘power_transformer’ | euclidean | n_estimator = 140, learning_rate = 0.2841, loss = ‘exponential’, max_depth = 8 | Adaboost | ||
| 0.08 | encoding = ‘one_hot_encoding’, imputation = ‘mean’, rescaling = ‘standardize’ | no_preprocessing | max_depth = ‘none’, max_leaf_nodes = 9, min_samples_leaf = 2, n_iter_no_change = 20, learning_rate = 0.0913, l2_regularization = 0.0057, early_stop = ‘train’ | GB |
| Model | Training Period (1985–2015) | Test Period (2016–2019) | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | NSE | RMSE | MAE | R2 | NSE | RMSE | MAE | |
| Conventional model | 0.91 | 0.90 | 70.74 | 19.51 | 0.86 | 0.85 | 67.18 | 17.21 |
| MPE model | 0.95 | 0.94 | 55.48 | 14.01 | 0.88 | 0.87 | 63.93 | 15.29 |
| Period | Model | Inflow Condition | R2 | NSE | RMSE | MAE |
|---|---|---|---|---|---|---|
| Training | Conventional model | ≥100 m3/s | 0.89 | 0.88 | 190.21 | 89.99 |
| <100 m3/s | 0.62 | 0.48 | 16.26 | 8.79 | ||
| MPE model | ≥100 m3/s | 0.93 | 0.93 | 149.76 | 65.65 | |
| <100 m3/s | 0.79 | 0.73 | 11.69 | 6.15 | ||
| Testing | Conventional model | ≥100 m3/s | 0.80 | 0.80 | 210.76 | 103.13 |
| <100 m3/s | 0.64 | 0.53 | 13.91 | 7.92 | ||
| MPE model | ≥100 m3/s | 0.82 | 0.82 | 201.91 | 101.50 | |
| <100 m3/s | 0.78 | 0.72 | 10.84 | 5.95 |
| Model | Metric | High Flow | Moist Conditions | Mid–Range Flow | Dry Conditions | Low Flow |
|---|---|---|---|---|---|---|
| Conventional model | R2 | 0.97 | 0.99 | 0.99 | 0.97 | 0.97 |
| NSE | 0.97 | 0.97 | 0.76 | −0.43 | −19.90 | |
| RMSE | 78.67 | 2.93 | 1.50 | 2.93 | 5.40 | |
| MAE | 28.08 | 2.14 | 1.41 | 2.77 | 5.37 | |
| MPE model | R2 | 0.96 | 1.00 | 0.99 | 0.98 | 0.97 |
| NSE | 0.96 | 0.97 | 0.95 | 0.95 | 0.41 | |
| RMSE | 90.96 | 3.04 | 0.68 | 0.52 | 0.91 | |
| MAE | 34.53 | 2.13 | 0.56 | 0.42 | 0.88 |
| Model | Metric | Spring (Mar–May) | Summer (Jun–Aug) | Autumn (Sep–Nov) | Winter (Dec–Feb) |
|---|---|---|---|---|---|
| Conventional model | R2 | 0.95 | 0.97 | 0.97 | 0.93 |
| NSE | 0.65 | 0.03 | 0.68 | −9.20 | |
| RMSE | 2.76 | 4.54 | 2.38 | 4.80 | |
| MAE | 2.24 | 4.43 | 1.81 | 4.74 | |
| MPE model | R2 | 0.97 | 0.99 | 0.99 | 0.96 |
| NSE | 0.95 | 0.93 | 0.95 | 0.86 | |
| RMSE | 1.02 | 1.26 | 0.98 | 0.55 | |
| MAE | 0.85 | 1.16 | 0.83 | 0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, J.; Bae, J.H.; Lee, G.; Yang, D.; Hong, J.; Lim, K.J. Development of Multi-Inflow Prediction Ensemble Model Based on Auto-Sklearn Using Combined Approach: Case Study of Soyang River Dam. Hydrology 2023, 10, 90. https://doi.org/10.3390/hydrology10040090
Lee S, Kim J, Bae JH, Lee G, Yang D, Hong J, Lim KJ. Development of Multi-Inflow Prediction Ensemble Model Based on Auto-Sklearn Using Combined Approach: Case Study of Soyang River Dam. Hydrology. 2023; 10(4):90. https://doi.org/10.3390/hydrology10040090
Chicago/Turabian StyleLee, Seoro, Jonggun Kim, Joo Hyun Bae, Gwanjae Lee, Dongseok Yang, Jiyeong Hong, and Kyoung Jae Lim. 2023. "Development of Multi-Inflow Prediction Ensemble Model Based on Auto-Sklearn Using Combined Approach: Case Study of Soyang River Dam" Hydrology 10, no. 4: 90. https://doi.org/10.3390/hydrology10040090
APA StyleLee, S., Kim, J., Bae, J. H., Lee, G., Yang, D., Hong, J., & Lim, K. J. (2023). Development of Multi-Inflow Prediction Ensemble Model Based on Auto-Sklearn Using Combined Approach: Case Study of Soyang River Dam. Hydrology, 10(4), 90. https://doi.org/10.3390/hydrology10040090







