Experimental and Artificial Neural Network (ANN) Modeling of Instream Vegetation Hydrodynamic Resistance
Abstract
1. Introduction
2. Materials and Methods
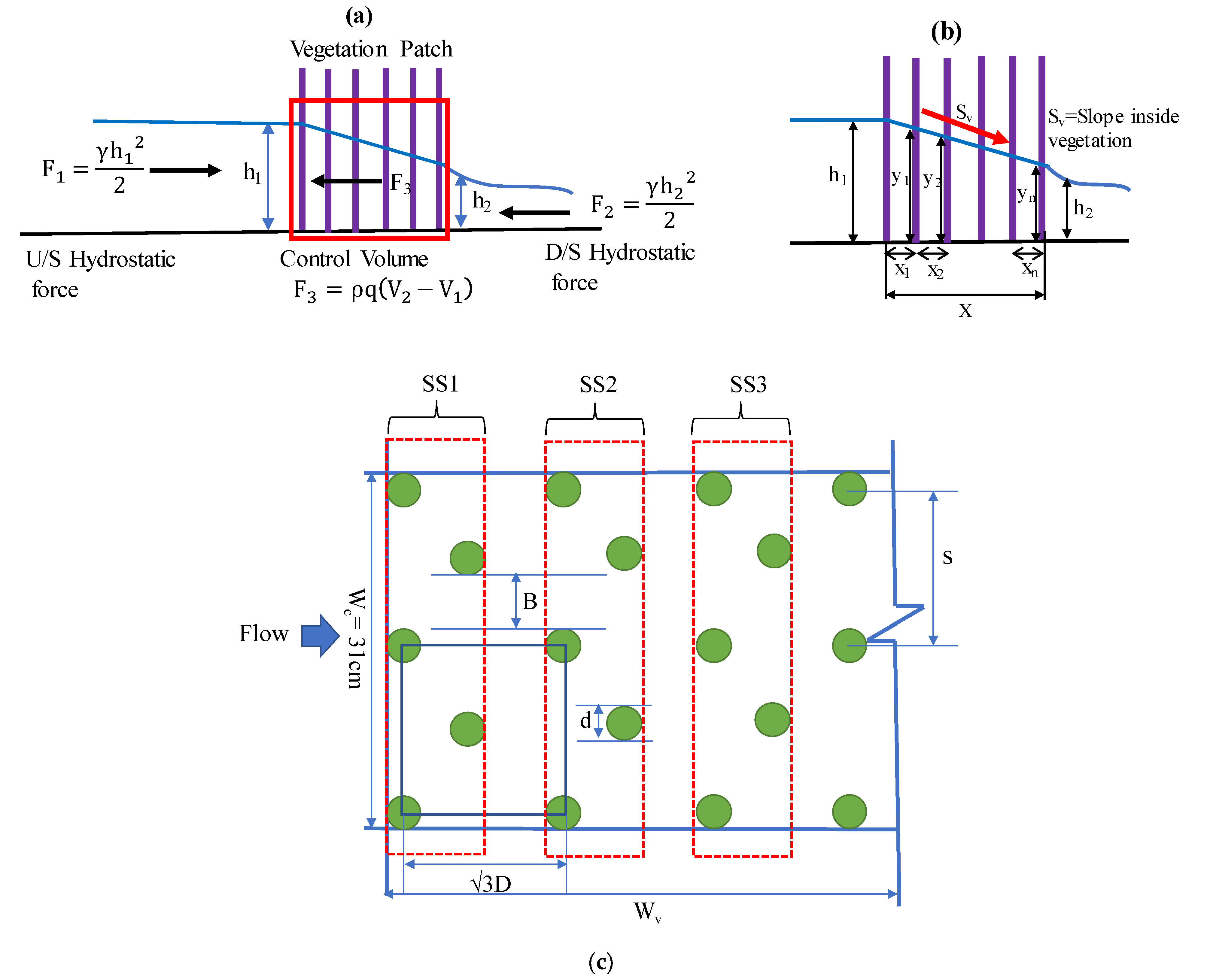
2.1. Flow Resistance of Vegetation
2.2. Dimensional Analysis
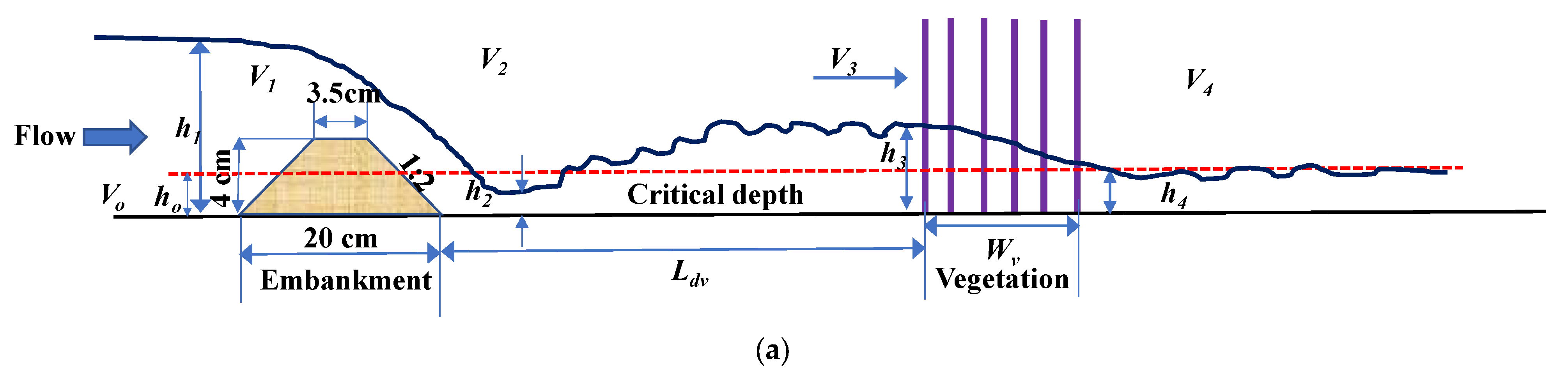
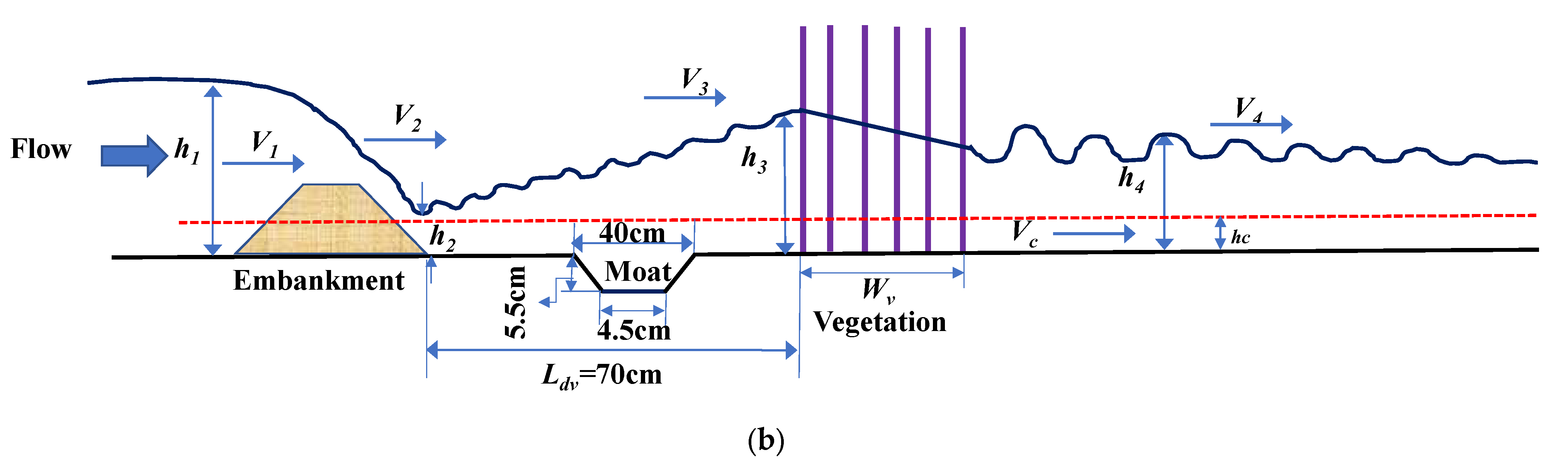
2.3. Flow Conditions
2.4. Vegetation Conditions
2.5. Frontal Area of Trees (Af)
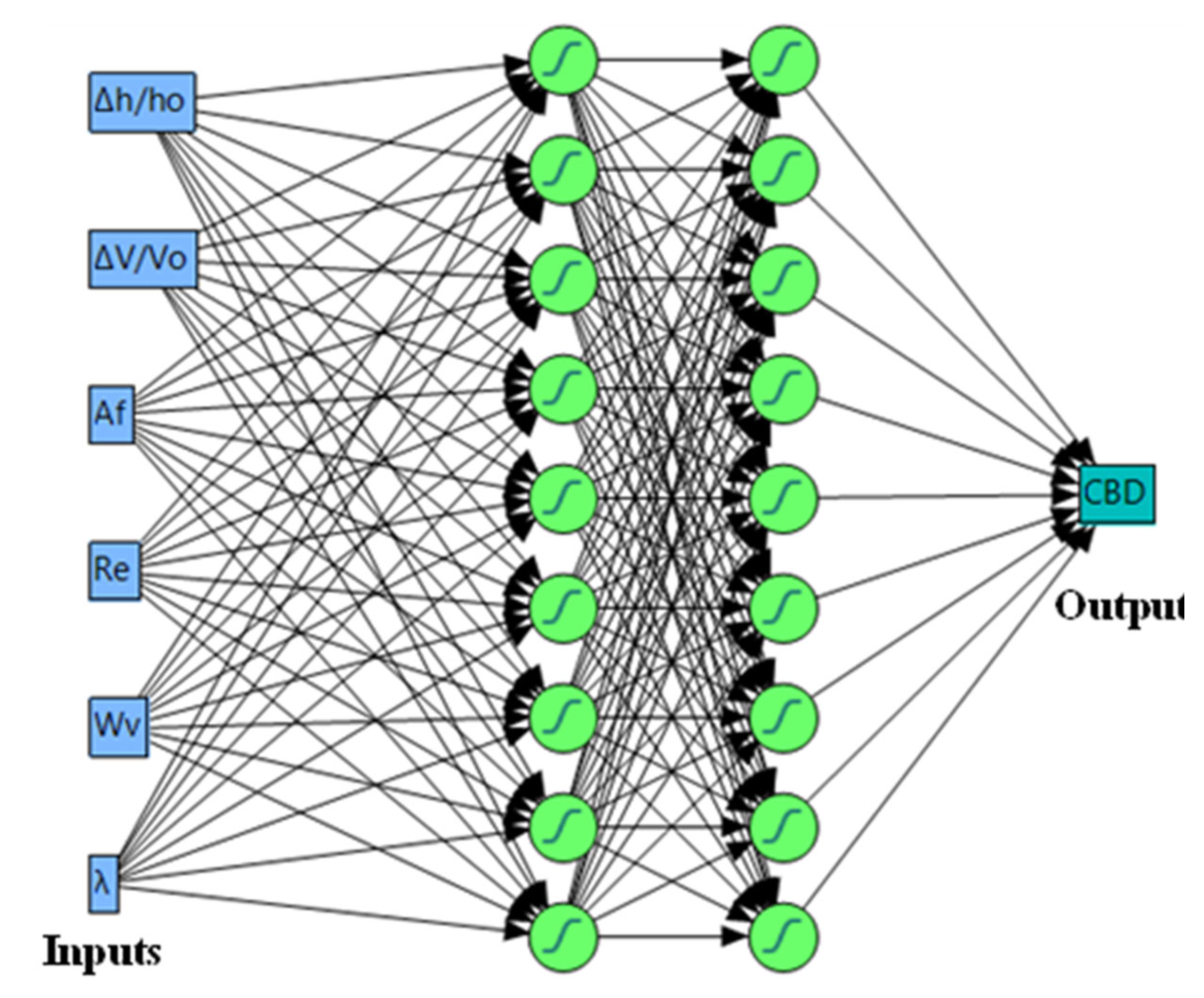
2.6. Artificial Neural Network (ANN)
2.7. Model Performance Evaluation Criteria
3. Results
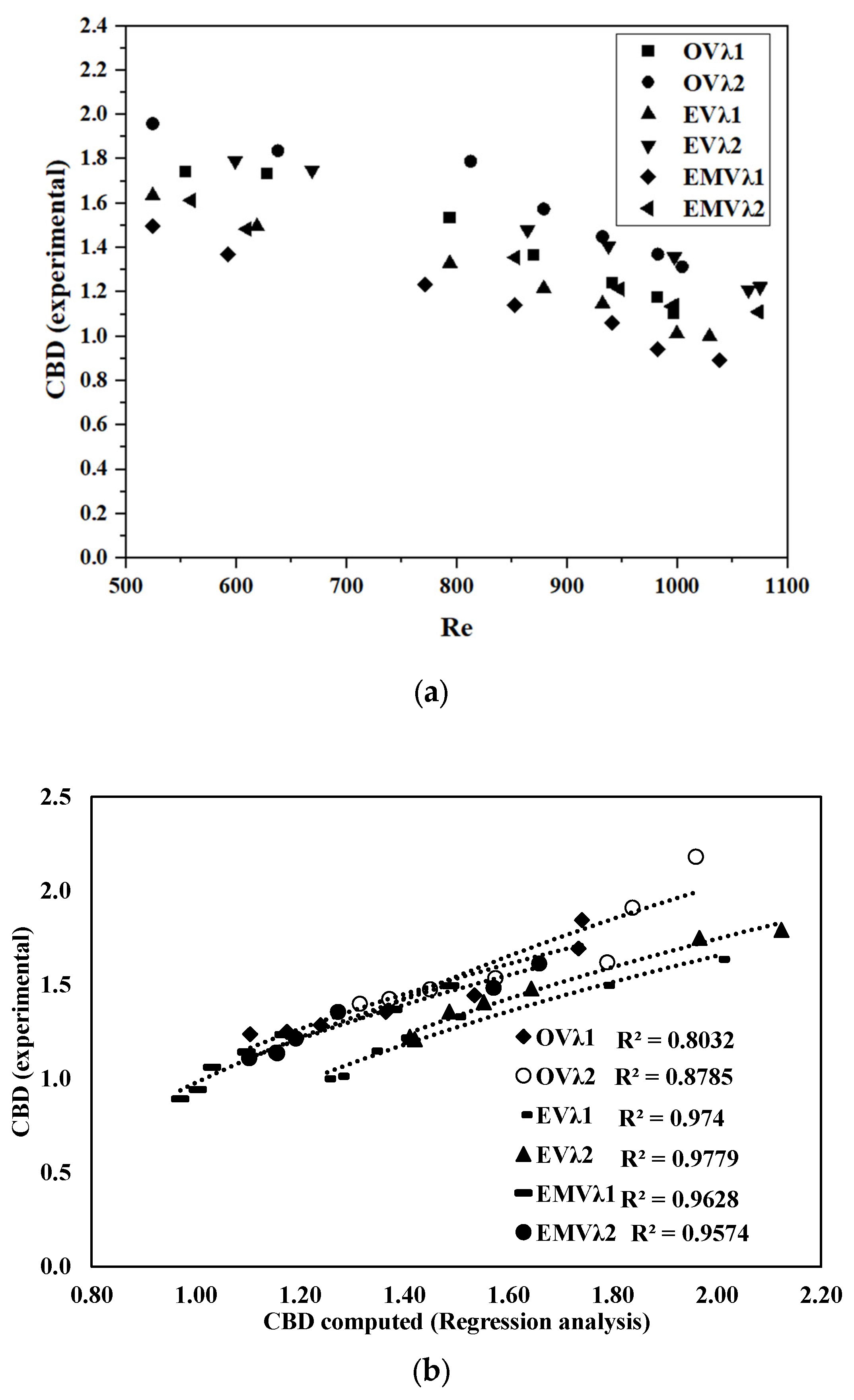
3.1. Experimental Results of Bulk Drag Coefficient (CBD)
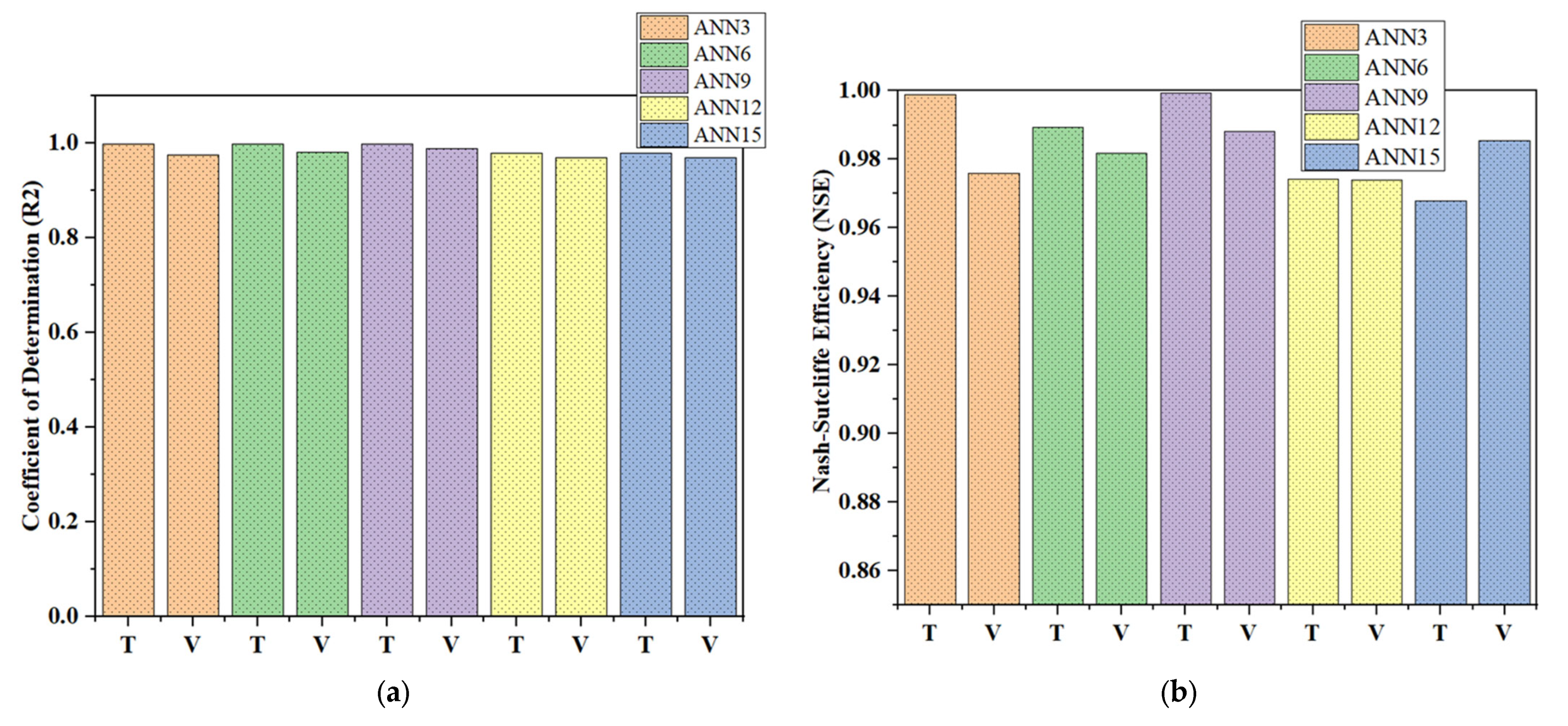
3.2. Computed Results of Bulk Drag Coefficient (CBD) by ANN Model
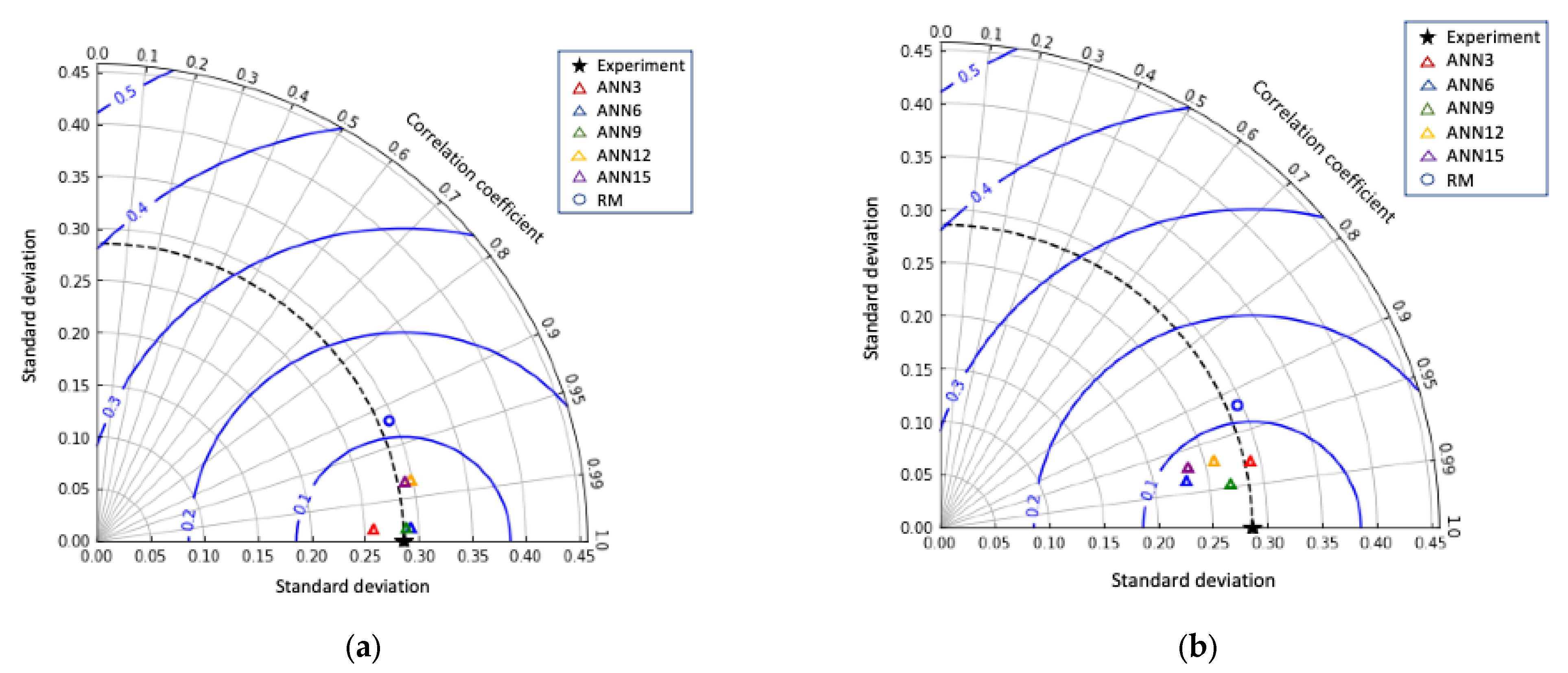
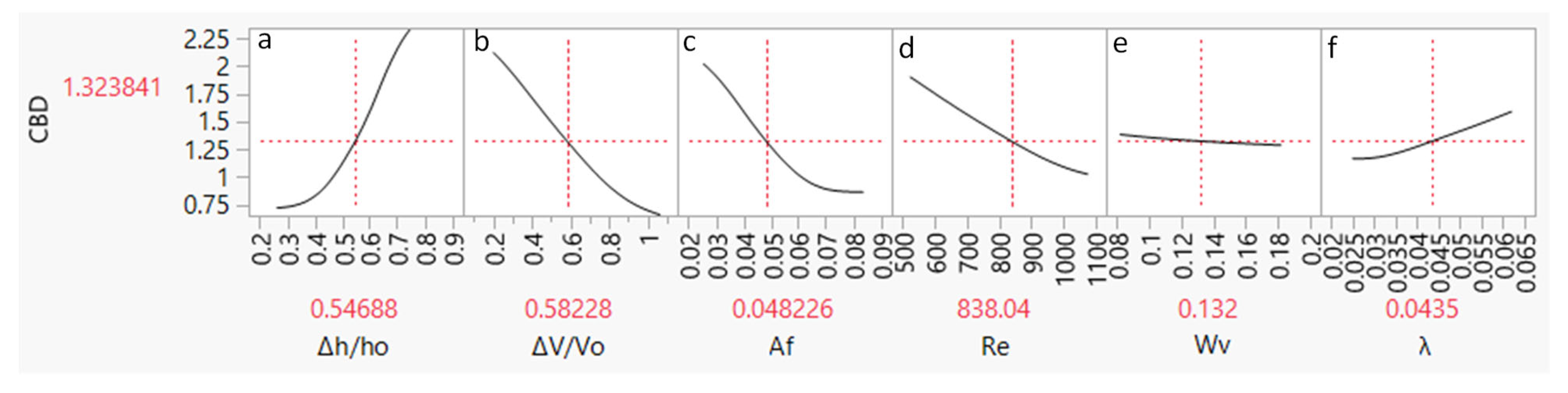
3.3. Prediction Results of CBD against Various Parameters
4. Discussion
5. Conclusions
- The calculated CBD for OVλ1 and OVλ2 showed a direct relationship with vegetation density (λ) and an inverse relationship with Reynolds number (Rd). The calculated ranges of CBD for OVλ1 and OVλ2 were 1.24–1.84 and 1.40–2.18, respectively, with average CBD values of 1.41 and 1.61, respectively.
- The average CBD values for EVλ1 and EVλ2, which represent composite defense cases, were decreased by 10.6% and 11% compared to OVλ1 and OVλ2, respectively. As a result, the calculated average CBD values for EVλ1 and EVλ2 were 1.26 and 1.41, respectively.
- The average CBD values for EMVλ1 and EMVλ2, which also represent composite defense cases, were decreased by 17.73% and 20% compared to OVλ1 and OVλ2, respectively. The calculated average CBD values for EMVλ1 and EMVλ2 were 1.16 and 1.29, respectively.
- The ANN9 model provided the best performance among the five ANN models, with the highest R2 and NSE values and the lowest RMSE, SSE, and MAE values.
- When compared to the prediction of CBD, the ANN9 model outperformed the regression models tested using Taylor’s diagram.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- James, C.S.; Birkhead, A.L.; Jordanova, A.A.; O’sullivan, J.J. Flow resistance of emergent vegetation. J. Hydraul. Res. 2004, 42, 390–398. [Google Scholar] [CrossRef]
- Luhar, M.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 2008, 8, 423–439. [Google Scholar] [CrossRef]
- Cheng, N.; Nguyen, H.T. Hydraulic Radius for Evaluating Resistance Induced by Simulated Emergent Vegetation in Open-Channel Flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Aboueian, J.; Sohankar, A.; Rastan, M.R.; Ghodrat, M. An experimental study on flow over two finite wall-mounted square cylinders in a staggered arrangement. Ocean Eng. 2021, 240, 109954. [Google Scholar] [CrossRef]
- Wang, W.; Peng, W.; Huai, W.; Katul, G.G.; Liu, X. Friction factor for turbulent open channel flow covered by vegetation. Sci. Rep. 2019, 9, 5178. [Google Scholar] [CrossRef]
- Hui, E.Q.; Hu, X.E.; Jiang, C.B.; Zhu, Z.D. A study of drag coefficient related with vegetation based on the flume experiment. J. Hydrodyn. Ser. B 2010, 22, 329–337. [Google Scholar] [CrossRef]
- Yang, S.; Balachandar, R. Determination of Velocity Distribution and Flow Resistance in Vegetated Channel Flows; University of Wollongong Australia: Wollongong, NSW, Australia, 2016; pp. 2211–2218. [Google Scholar]
- Ahmed, A.; Ghumman, A.R. Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System. Water 2019, 11, 1971. [Google Scholar] [CrossRef]
- Farooq, R.; Ahmad, W.; Hashmi, H.N.; Saeed, Z. Computation of Momentum Transfer Coefficient and Conveyance Capacity in Asymmetric Compound Channel. Arab. J. Sci. Eng. 2016, 41, 4225–4234. [Google Scholar] [CrossRef]
- Baptist, M.; Babovic, V.; Rodriguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef]
- Panigrahi, K.; Khatua, K.K. Prediction of velocity distribution in straight channel with rigid vegetation. Aquat. Procedia 2015, 4, 819–825. [Google Scholar] [CrossRef]
- Järvelä, J. Determination of flow resistance of vegetated channel banks and floodplains. In River Flow; Helsinki University of Technology: Espoo, Finland, 2002; pp. 311–318. [Google Scholar]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Cheng, N.-S. Calculation of Drag Coefficient for Arrays of Emergent Circular Cylinders with Pseudofluid Model. J. Hydraul. Eng. 2013, 139, 602–611. [Google Scholar] [CrossRef]
- Huai, W.; Wang, W.; Hu, Y.; Zeng, Y.; Yang, Z. Analytical model of the mean velocity distribution in an open channel with double-layered rigid vegetation. Adv. Water Resour. 2014, 69, 106–113. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Wieselsberger, C. New Data on the Laws of Fluid Resistance; NASA: Washington, DC, USA, 1922.
- Mellado, J.P.; Wang, L.; Peters, N. Gradient trajectory analysis of a scalar field with external intermittency. J. Fluid Mech. 2009, 626, 333–365. [Google Scholar] [CrossRef]
- Su, H.B.; Schmid, H.P.; Vogel, C.S.; Curtis, P.S. Effects of canopy morphology and thermal stability on mean flow and turbulence statistics observed inside a mixed hardwood forest. Agric. For. Meteorol. 2008, 148, 862–882. [Google Scholar] [CrossRef]
- Sonnenwald, F.; Stovin, V.; Guymer, I. Estimating drag coefficient for arrays of rigid cylinders representing emergent vegetation. J. Hydraul. Res. 2018, 57, 591–597. [Google Scholar] [CrossRef]
- Suzuki, T.; Arikawa, T. Numerical Analysis of Bulk Drag Coefficient in Dense Vegetation by Immersed Boundary Method. Coast. Eng. Proc. 2011, 1, 48. [Google Scholar] [CrossRef]
- Thompson, A.M.; Wilson, B.N.; Hansen, B.J. Shear stress partitioning for idealized vegetated surfaces. Trans. ASAE 2004, 47, 701. [Google Scholar] [CrossRef]
- Li, R.M.; Shen, H.W. Effect of tall vegetations on flow and sediment. J. Hydraul. Div. 1973, 99, 793–814. [Google Scholar] [CrossRef]
- Fathi-Maghadam, M.; Kouwen, N. Nonrigid, nonsubmerged, vegetative roughness on floodplains. J. Hydraul. Eng. 1997, 123, 51–57. [Google Scholar] [CrossRef]
- Armanini, A.; Righetti, M.; Grisenti, P. Direct measurement of vegetation resistance in prototype scale. J. Hydraul. Res. 2005, 43, 481–487. [Google Scholar] [CrossRef]
- Wu, F. Characteristics of flow resistance in open channels with non-submerged rigid vegetation. J. Hydrodyn. Ser. B 2008, 20, 239–245. [Google Scholar] [CrossRef]
- Wu, F.-C.; Shen, H.W.; Chou, Y.-J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Muhammad, A.H.; Tanaka, N. Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences 2019, 9, 247. [Google Scholar] [CrossRef]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume experiments on optimal arrangement of hybrid defense system comprising an embankment, moat, and emergent vegetation to mitigate inundating tsunami current. Ocean Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N.; Yagisawa, J.; Achmad, F.N. Tsunami mitigation by combination of coastal vegetation and a backward-facing step. Coast. Eng. J. 2018, 60, 104–125. [Google Scholar] [CrossRef]
- Muhammad, M.M.; Yusof, K.W.; Mustafa, M.R.U.; Zakaria, N.A.; Ghani, A.A. Artificial neural network applications for predicting drag coefficient in flexible vegetated channels. J. Telecommun. Electron. Comput. Eng. 2018, 10, 99–102. [Google Scholar]
- Smith, J.; Eli, R.N. Neural-network models of rainfall-runoff process. J. Water Resour. Plan. Manag. 1995, 121, 499–508. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Nikoofar, B. Forecasting daily lake levels using artificial intelligence approaches. Comput. Geosci. 2012, 41, 169–180. [Google Scholar] [CrossRef]
- Edossa, D.C.; Babel, M.S. Application of ANN-Based Streamflow Forecasting Model for Agricultural Water Management in the Awash River Basin, Ethiopia. Water Resour. Manag. 2011, 25, 1759–1773. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 2017, 17, 1035–1050. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Critical Resistance Affecting Sub- to Super-Critical Transition Flow by Vegetation. J. Earthq. Tsunami 2019, 13, 1950004. [Google Scholar] [CrossRef]
- Anjum, N.; Ghani, U.; Pasha, G.A.; Rashid, M.U.; Latif, A.; Rana, M.Z.Y. Reynolds stress modeling of flow characteristics in a vegetated rectangular open channel. Arab. J. Sci. Eng. 2018, 43, 5551–5558. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Mizuhara, K.; Ashida, M. Drag force on multiple rows of cylinders in an open channel. In Grant-in-Aid Research Project Report; Kyushu University: Fukuoka, Japan, 2000. [Google Scholar]
- Liu, D.; Hession, C. Flow through Rigid Vegetation Hydrodynamics. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2008. [Google Scholar]
- Ferreira, R.M.L.; Ricardo, A.M.; Franca, M.J. Discussion of ‘Laboratory investigation of mean drag in a random array of rigid, emergent cylinders’ by Yukie Tanino and Heidi M. Nepf. J. Hydraul. Eng. 2009, 135, 690–693. [Google Scholar] [CrossRef]
- Tanvir, M.A.; Siddiqui, M.T.; Shah, A.H. Growth and price trend of Eucalyptus camaldulensis in Central Punjab. Int. J. Agric. Biol. 2002, 4, 344–346. [Google Scholar]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Bokaian, A.; Geoola, F. Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 1984, 146, 383–415. [Google Scholar] [CrossRef]
- Khedri, A.; Kalantari, N.; Vadiati, M. Comparison study of artificial intelligence method for short term groundwater level prediction in the northeast Gachsaran unconfined aquifer. Water Sci. Technol. Water Supply 2020, 20, 909–921. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P. ANN and Fuzzy Logic Models for Simulating Event-Based Rainfall-Runoff. J. Hydraul. Eng. 2006, 132, 1321–1330. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Almuhaylan, M.R.; Ghumman, A.R.; Al-Salamah, I.S.; Ahmad, A.; Ghazaw, Y.M.; Haider, H.; Shafiquzzaman, M. Evaluating the impacts of pumping on aquifer depletion in arid regions using MODFLOW, ANFIS and ANN. Water 2020, 12, 2297. [Google Scholar] [CrossRef]
- Iqbal, M.; Naeem, U.A.; Ahmad, A.; Rehman, H.; Ghani, U.; Farid, T. Relating groundwater levels with meteorological parameters using ANN technique. Meas. J. Int. Meas. Confed. 2020, 166, 108163. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö. Artificial Neural Network Models of Daily Pan Evaporation. J. Hydrol. Eng. 2006, 11, 65–70. [Google Scholar] [CrossRef]
- Rauf, A.; Ghumman, A.R. Impact assessment of rainfall-runoffsimulations on the flow duration curve of the Upper Indus river-a comparison of data-driven and hydrologic models. Water 2018, 10, 876. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Pasha, G.A.; Ahmad, A.; Ahmed, A.; Khan, R.A.; Farooq, R. Simulation of Quantity and Quality of Saq Aquifer Using Artificial Intelligence and Hydraulic Models. Adv. Civ. Eng. 2022, 2022, 5910989. [Google Scholar] [CrossRef]
- Samui, T.P.P. Prediction of Rock Strain Using Hybrid Approach of Ann and Optimization Algorithms. Geotech. Geol. Eng. 2022, 40, 4617–4643. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Coscarella, F.; Penna, N.; Ferrante, A.P.; Gualtieri, P.; Gaudio, R. Turbulent flow through random vegetation on a rough bed. Water 2021, 13, 2564. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Tinoco, R.O.; Cowen, E.A. The direct and indirect measurement of boundary stress and drag on individual and complex arrays of elements. Exp. Fluids 2013, 54, 1509. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Liu, X.G.; Zeng, Y.H. Drag coefficient for rigid vegetation in subcritical open channel. Procedia Eng. 2016, 154, 1124–1131. [Google Scholar] [CrossRef]
- Muhammad, M.M.; Yusof, K.W.; Mustafa, M.R.U.; Zakaria, N.A.; Ghani, A.A. Prediction models for flow resistance in flexible vegetated channels. Int. J. River Basin Manag. 2018, 16, 427–437. [Google Scholar] [CrossRef]

| Case ID | Initial Froude (Fro) | Initial Water Depth (ho) [cm] | Density (λ) | Vegetation Width (Wv) [cm] | d | s | Re Range |
|---|---|---|---|---|---|---|---|
| OVλ1 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.025 | 18.4 | 0.3 | 1.25 | 553–996 |
| OVλ2 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.062 | 8.2 | 0.3 | 1.88 | 524–1004 |
| EVλ1 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.025 | 18.4 | 0.3 | 1.25 | 524–1029 |
| EVλ2 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.062 | 8.2 | 0.3 | 1.88 | 599–1064 |
| EMVλ1 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.025 | 18.4 | 0.3 | 1.25 | 524–1037 |
| EMVλ2 | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 4.5, 5.3, 6.8, 7.1, 7.7, 8.2, 8.5 | 0.062 | 8.2 | 0.3 | 1.88 | 559–1073 |
| ANN Model ID | Input Variables | No. of Hidden Layers | No. of Neurons in Each Layer | Output |
|---|---|---|---|---|
| ANN3 | Δh/ho, ΔV/Vo, Af, Re, Wv, λ | 2 | 3 | CBD |
| ANN6 | Δh/ho, ΔV/Vo, Af, Re, Wv, λ | 2 | 6 | CBD |
| ANN9 | Δh/ho, ΔV/Vo, Af, Re, Wv, λ | 2 | 9 | CBD |
| ANN12 | Δh/ho, ΔV/Vo, Af, Re, Wv, λ | 2 | 12 | CBD |
| ANN15 | Δh/ho, ΔV/Vo, Af, Re, Wv, λ | 2 | 15 | CBD |
| Sr. No. | Case Name | Equation Used (Calculated) | Equation Used (Computed) | CBD Range (Calculated) | CBD Range (Computed) | Average CBD (Calculated) | Average CBD (Computed) |
|---|---|---|---|---|---|---|---|
| 1 | OVλ1 | Equation (4) | 1.10–1.74 | 1.24–1.84 | 1.41 | 1.45 | |
| 2 | OV λ2 | Equation (4) | 1.31–1.96 | 1.40–2.18 | 1.61 | 1.65 | |
| 3 | EV λ1 | Equation (4) | 1–1.63 | 1.18–1.80 | 1.26 | 1.41 | |
| 4 | EV λ2 | Equation (4) | 1.2–1.79 | 1.41–2.12 | 1.46 | 1.65 | |
| 5 | EMV λ1 | Equation (4) | 0.9–1.50 | 0.96–1.48 | 1.16 | 1.16 | |
| 6 | EMV λ1 | Equation (4) | 1.11–1.61 | 1.10–1.65 | 1.29 | 1.30 |
| ANN3 | ANN6 | ANN9 | ANN12 | ANN15 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T | V | T | V | T | V | T | V | T | V | |
| R2 | 0.999 | 0.976 | 0.999 | 0.981 | 0.999 | 0.988 | 0.980 | 0.970 | 0.980 | 0.970 |
| RMSE | 0.007 | 0.047 | 0.027 | 0.030 | 0.005 | 0.029 | 0.040 | 0.039 | 0.047 | 0.026 |
| SSE | 0.002 | 0.042 | 0.018 | 0.027 | 0.001 | 0.017 | 0.030 | 0.061 | 0.013 | 0.084 |
| NSE | 0.999 | 0.976 | 0.990 | 0.982 | 1.000 | 0.988 | 0.974 | 0.974 | 0.968 | 0.985 |
| MAE | 0.005 | 0.032 | 0.018 | 0.025 | 0.003 | 0.020 | 0.030 | 0.032 | 0.035 | 0.023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Valyrakis, M.; Ghumman, A.R.; Farooq, R.; Pasha, G.A.; Janjua, S.; Raza, A. Experimental and Artificial Neural Network (ANN) Modeling of Instream Vegetation Hydrodynamic Resistance. Hydrology 2023, 10, 73. https://doi.org/10.3390/hydrology10030073
Ahmed A, Valyrakis M, Ghumman AR, Farooq R, Pasha GA, Janjua S, Raza A. Experimental and Artificial Neural Network (ANN) Modeling of Instream Vegetation Hydrodynamic Resistance. Hydrology. 2023; 10(3):73. https://doi.org/10.3390/hydrology10030073
Chicago/Turabian StyleAhmed, Afzal, Manousos Valyrakis, Abdul Razzaq Ghumman, Rashid Farooq, Ghufran Ahmed Pasha, Shahmir Janjua, and Ali Raza. 2023. "Experimental and Artificial Neural Network (ANN) Modeling of Instream Vegetation Hydrodynamic Resistance" Hydrology 10, no. 3: 73. https://doi.org/10.3390/hydrology10030073
APA StyleAhmed, A., Valyrakis, M., Ghumman, A. R., Farooq, R., Pasha, G. A., Janjua, S., & Raza, A. (2023). Experimental and Artificial Neural Network (ANN) Modeling of Instream Vegetation Hydrodynamic Resistance. Hydrology, 10(3), 73. https://doi.org/10.3390/hydrology10030073








