Assessing Hydrological Simulations with Machine Learning and Statistical Models
Abstract
:1. Introduction
2. Materials and Methods
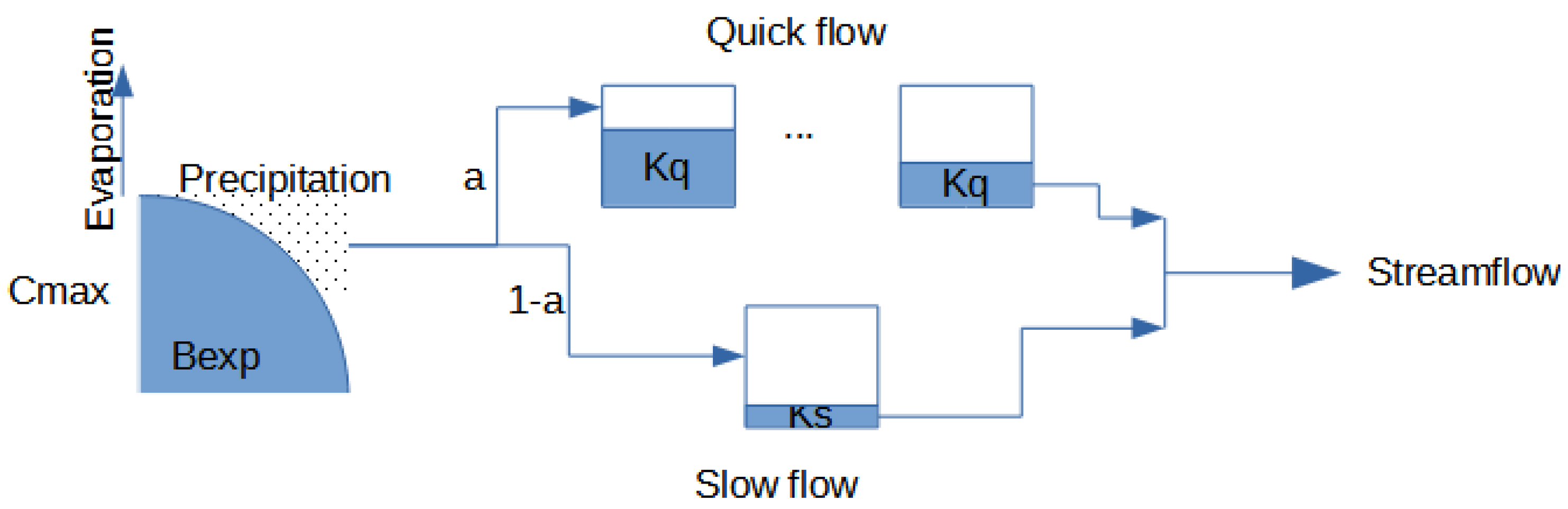
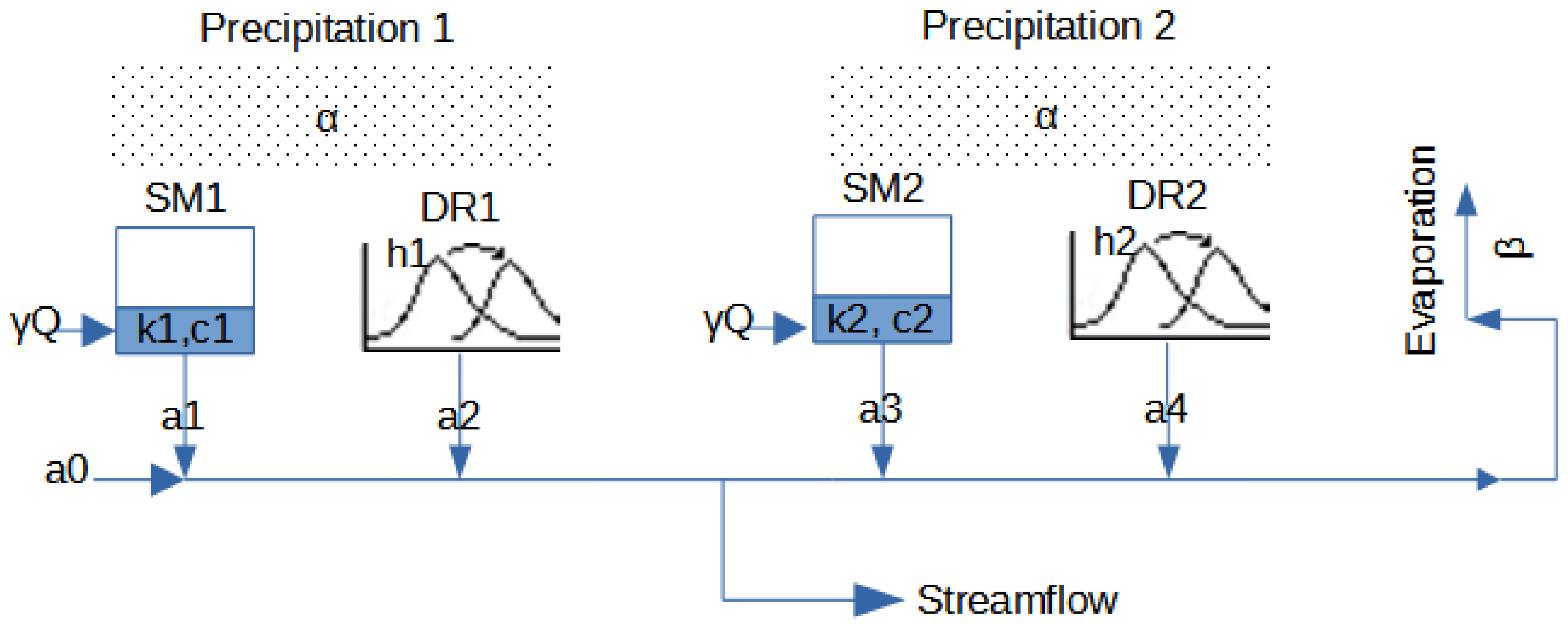
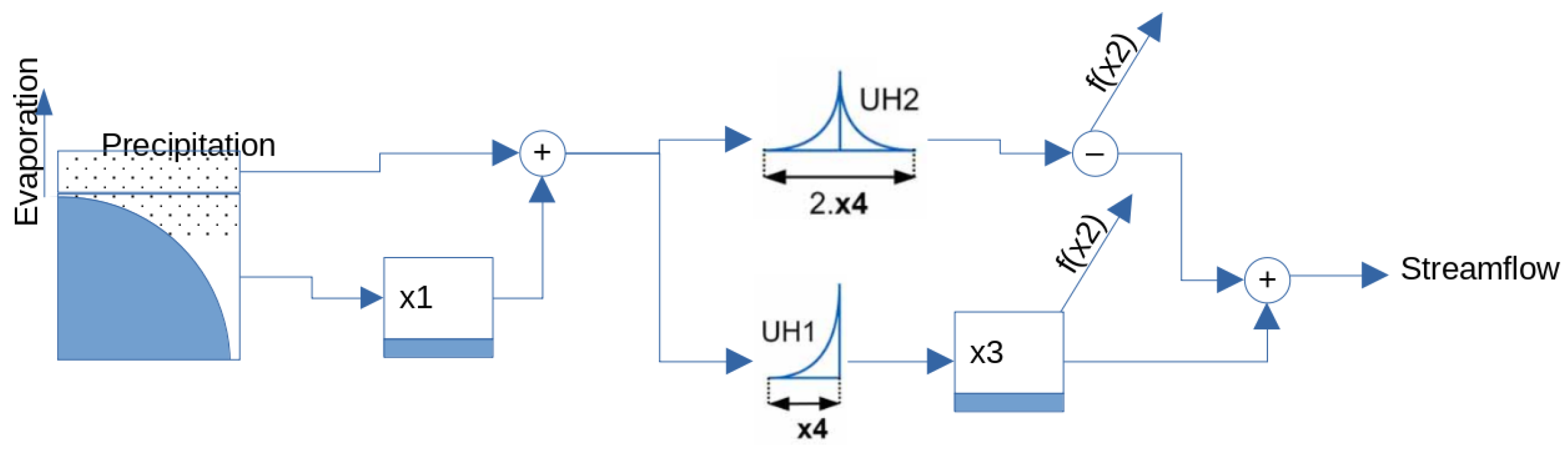
2.1. Hydrological Models
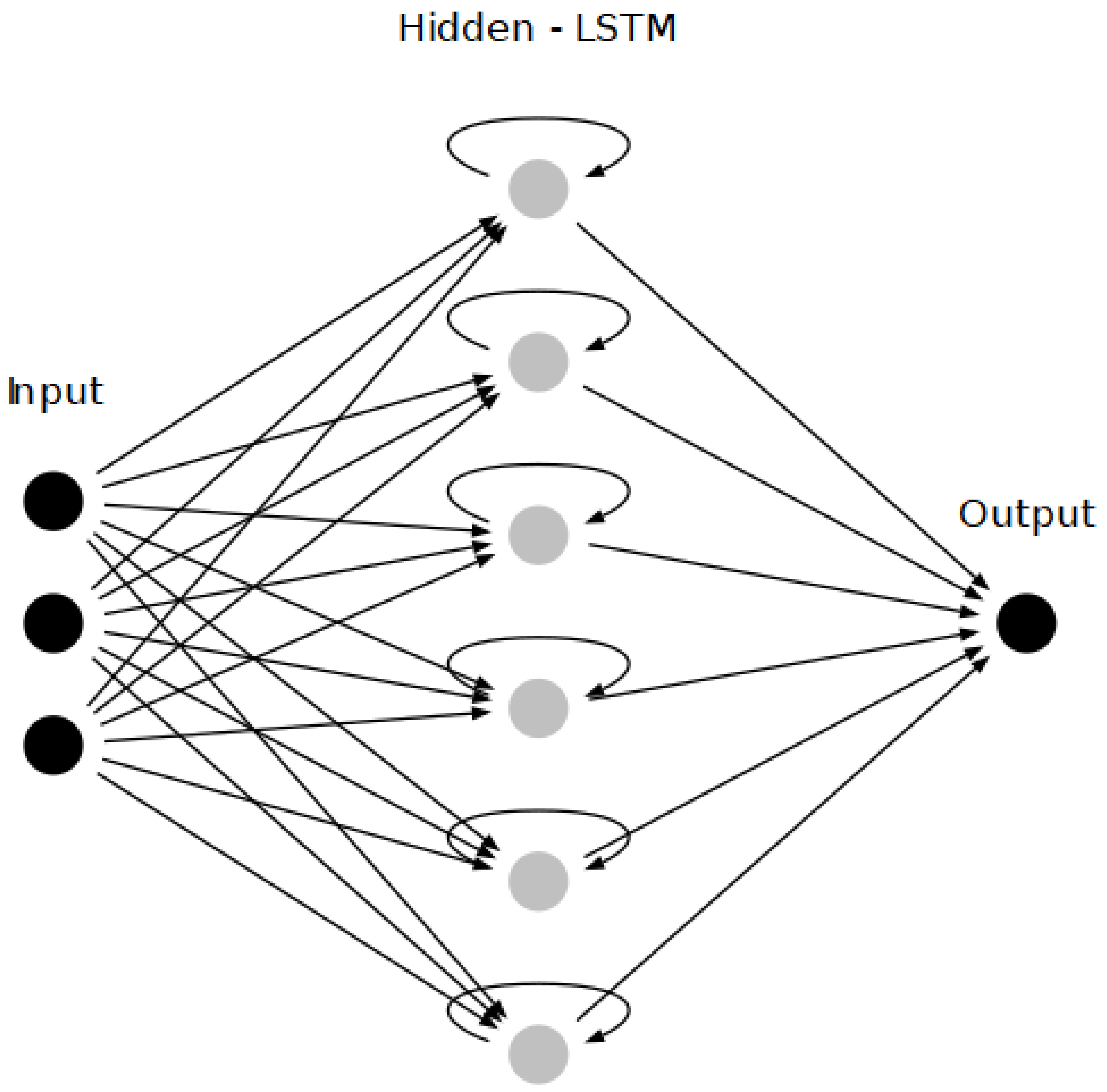
2.2. Recurrent Neural Network
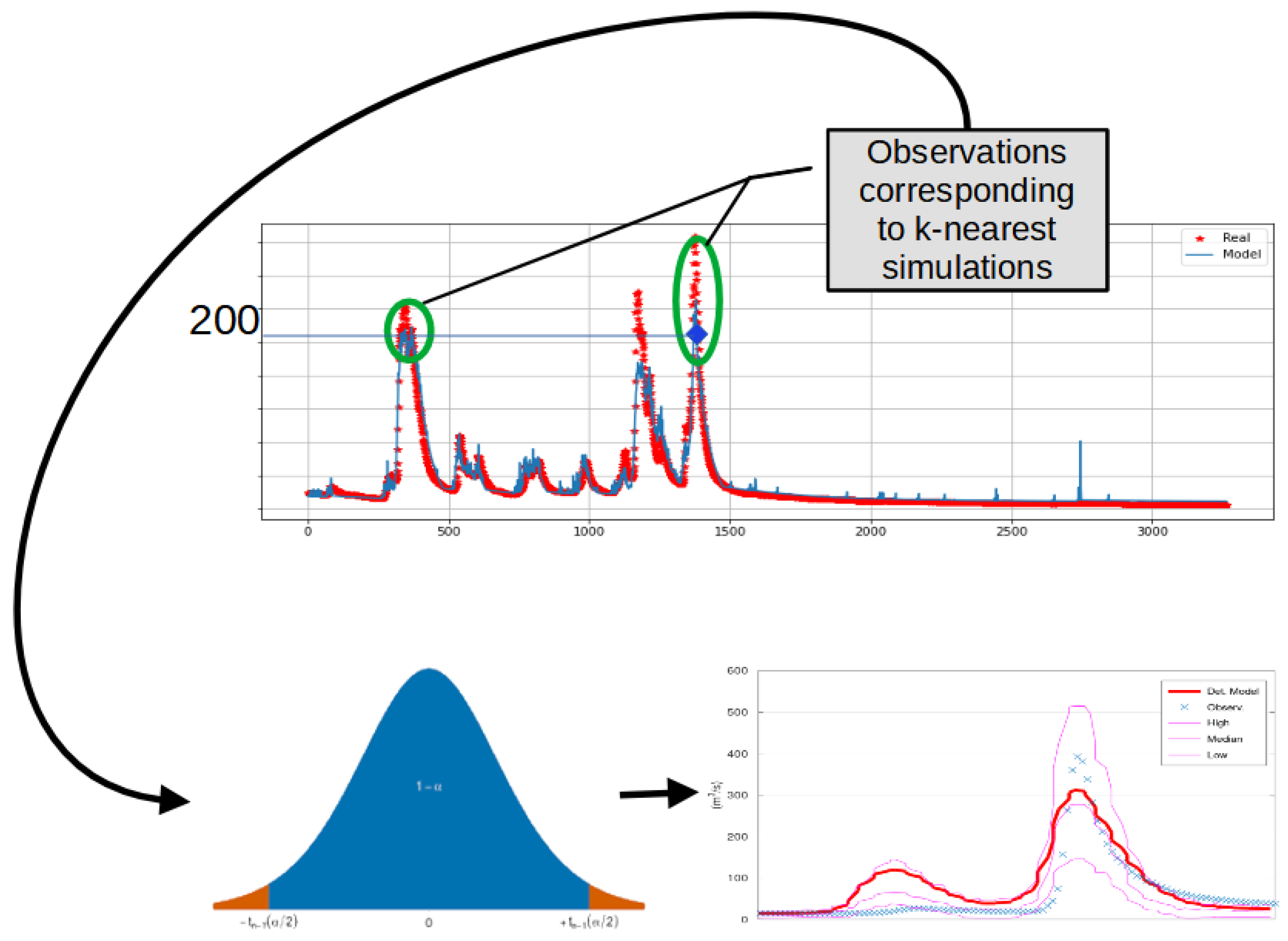
2.3. KNN-Bluecat
2.4. Performance Indicators
2.5. Case Studies
- Arno River at Subbiano, Tuscany, Italy. The catchment of Arno River is 752 km2. The observed data include the mean areal daily rainfall, evapotranspiration, and discharge at the basin exit. The period of the available data starts on 2 January 1992 and ends on 1 January 2014 (8037 time steps). The annual rainfall was 1213 mm/year.
- Sieve River at Fornacina, Tuscany, Italy. The catchment area of Sieve River is 846 km2. The observed data include the mean areal hourly rainfall, evapotranspiration and discharge at the basin exit. The period of the available data starts on 3 June 1992 and ends on 2 January 1997 (36,554 time steps, with a gap in the data from 1 January 1995 to 2 June 1995). The flow regime of Sieve River is intermittent. The annual rainfall was 1190 mm/year.
- Bakas River, tributary of Nedon River, Messenia, Greece. The catchment area of Bakas River is 90 km2. The average annual precipitation depth is 1000 mm. The simulation time step was hourly, with the observations extending from 1 September 2011 01:00 to 1 May 2014 00:00 (23,353 time steps). The annual rainfall was 1393 mm/year.
3. Results
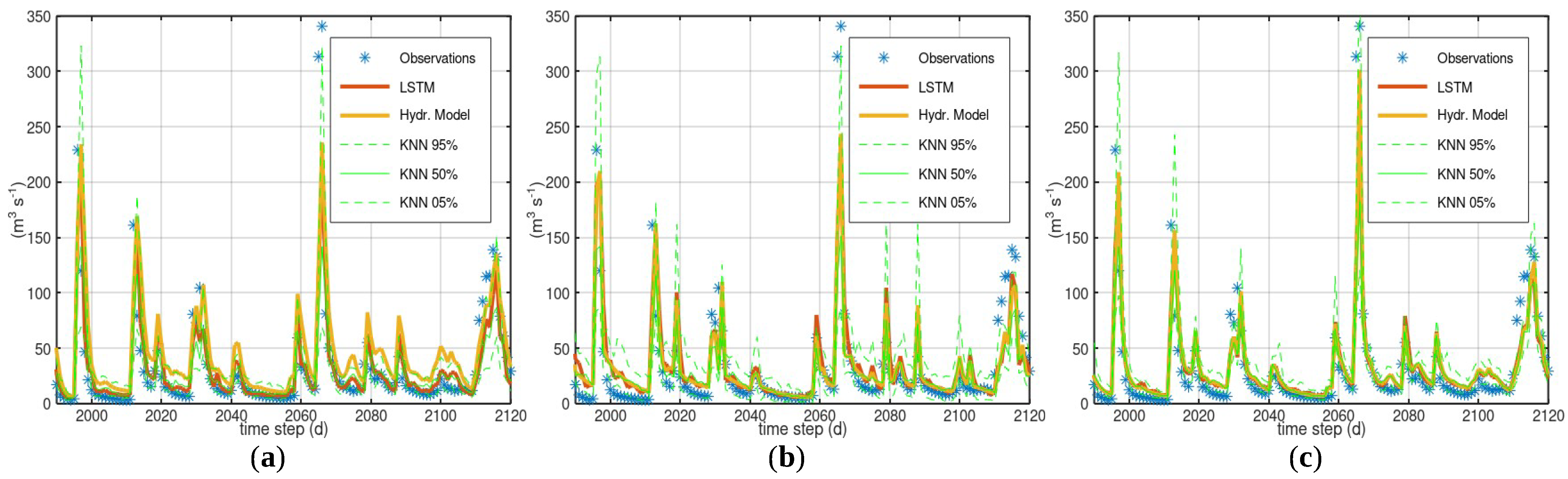
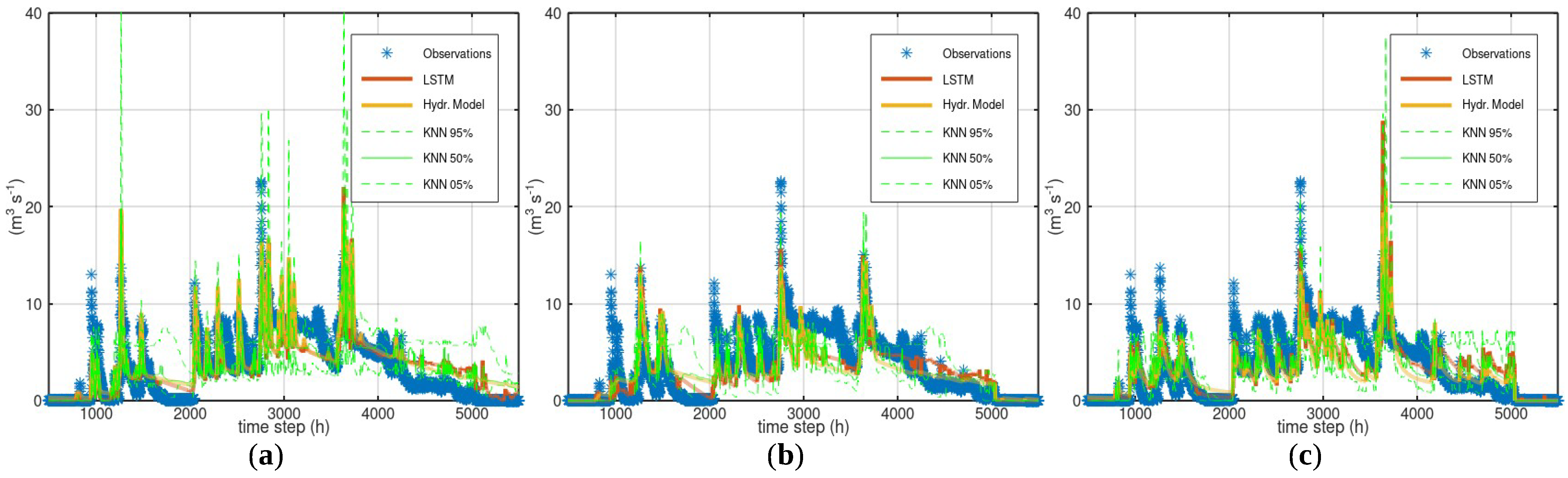
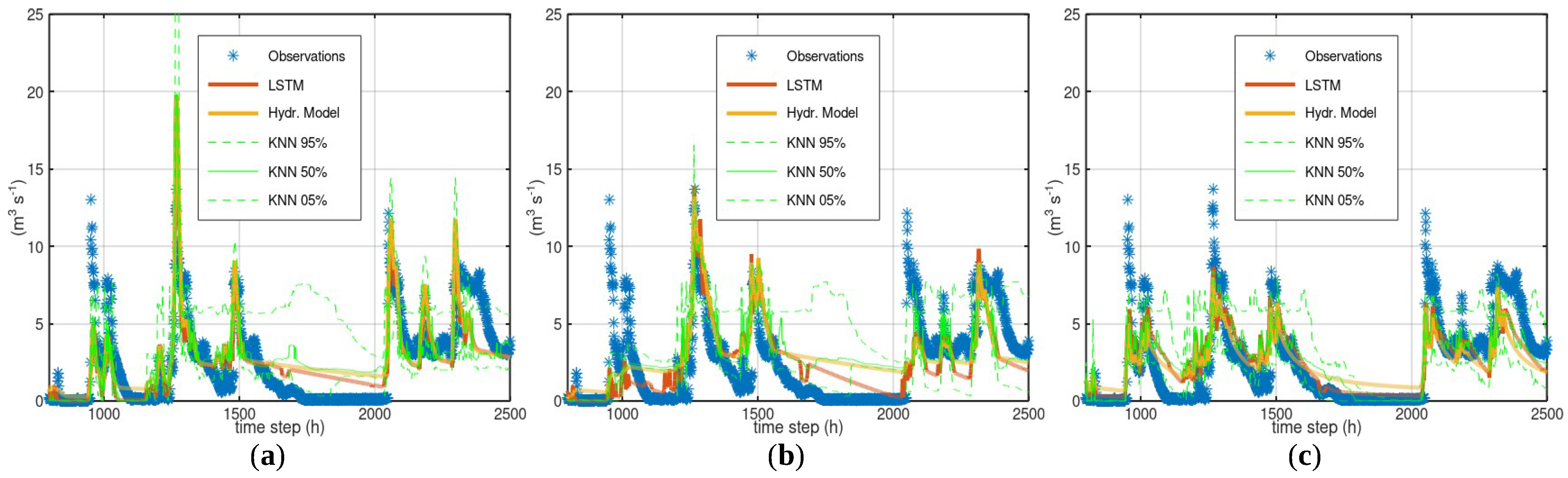
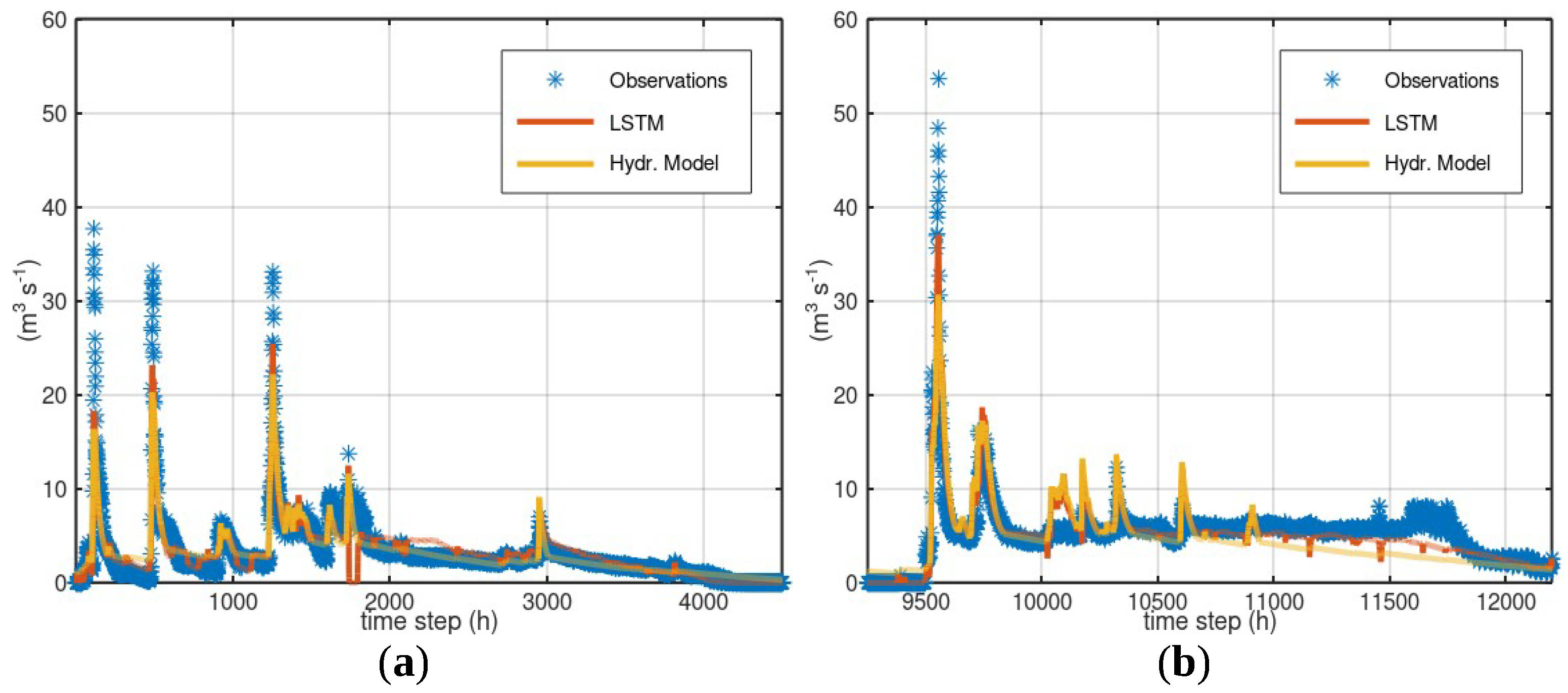
3.1. Case Study—Arno
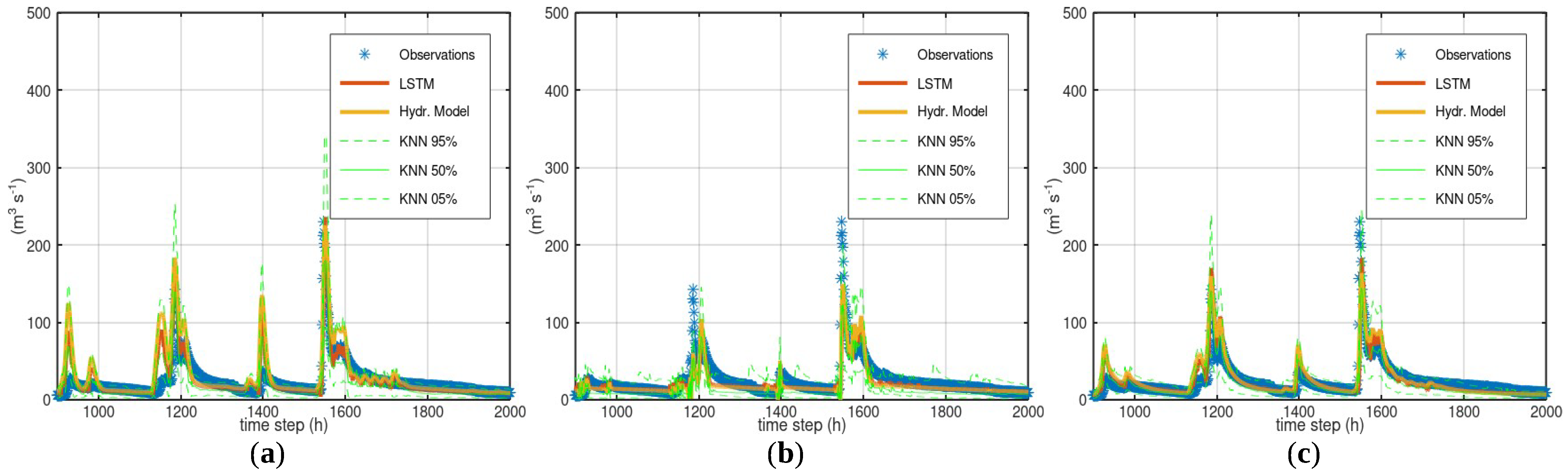
3.2. Case Study—Sieve
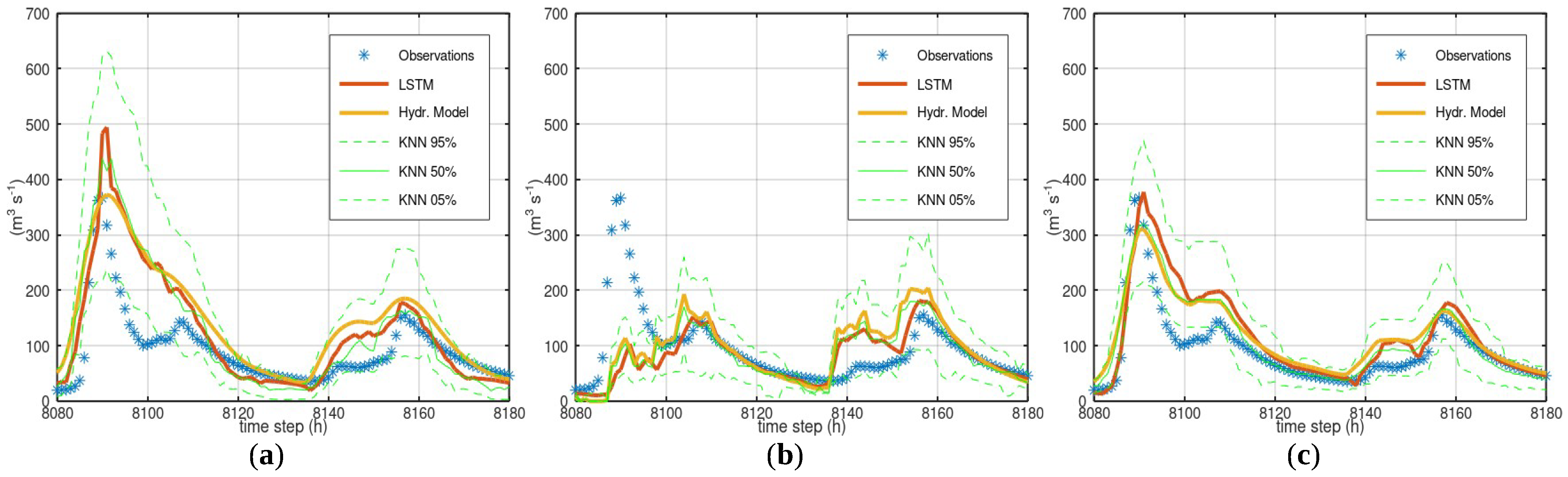
3.3. Case Study—Bakas
4. Discussion
5. Conclusions
- Statistical approaches that estimate the model uncertainty based on observations (e.g., Bluecat or KNN used in this study) can provide, besides an uncertainty analysis, an evaluation of the consistency of the available data, i.e., the plausibility of the observed responses based on the observed stresses. Nevertheless, statistical approaches can underestimate the uncertainty if the assessed hydrological model exhibits conditional systematic errors.
- A simple recurrent neural network such as LSTM can be applied to the model results to detect systematic errors. In these case studies, it was efficient in detecting the systematic overestimations of hydrological models, but less reliable in detecting the failures of hydrological models at high flows. Conditional systematic errors appear to also escape the notice of machine learning approaches.
- A naive combination (mean of the simulated values) of the results of two hydrological models that simulate the same water basin offers the advantage of reducing the effect of the systematic error of the models (especially the conditional systematic error). A recurrent neural network, such as LSTM, can be applied to a naive combination of the models’ results to obtain a good approximation of the best achievable performance with the available data.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CI | Confidence interval |
| GR4J | Géenie Rural à 4 paramètres Journalier |
| HYMOD | Hydrological model |
| KNN | K-nearest neighbours |
| LSTM | Long short-term memory |
| LRHM | Linear regression hydrological modelling |
| ML | Machine learning |
| MSE | Mean squared error |
| PBIAS | Percentage of bias |
| RNN | Recurrent neural network |
References
- Rozos, E.; Dimitriadis, P.; Mazi, K.; Koussis, A.D. A Multilayer Perceptron Model for Stochastic Synthesis. Hydrology 2021, 8, 67. [Google Scholar] [CrossRef]
- Rozos, E.; Leandro, J.; Koutsoyiannis, D. Development of Rating Curves: Machine Learning vs. Statistical Methods. Hydrology 2022, 9, 166. [Google Scholar] [CrossRef]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Hertz, J.; Krogh, A.; Palmer, R.G.; Horner, H. Introduction to the theory of neural computation. Phys. Today 1991, 44, 70. [Google Scholar] [CrossRef]
- Ayzel, G.; Kurochkina, L.; Abramov, D.; Zhuravlev, S. Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks. Hydrology 2021, 8, 6. [Google Scholar] [CrossRef]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking Data-Driven Rainfall-Runoff Models in Great Britain: A comparison of LSTM-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. Discuss. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Jimeno-Sáez, P.; Bueno-Crespo, A.; Pérez-Sánchez, J.; Pulido-Velázquez, D. Coupling machine-learning techniques with SWAT model for instantaneous peak flow prediction. Biosyst. Eng. 2019, 177, 67–77. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Noymanee, J.; Theeramunkong, T. Flood Forecasting with Machine Learning Technique on Hydrological Modeling. Procedia Comput. Sci. 2019, 156, 377–386. [Google Scholar] [CrossRef]
- Althoff, D.; Bazame, H.C.; Nascimento, J.G. Untangling hybrid hydrological models with explainable artificial intelligence. H2Open J. 2021, 4, 13–28. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Bellos, V. Machine Learning in Assessing the Performance of Hydrological Models. Hydrology 2022, 9, 5. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Bluecat: A Local Uncertainty Estimator for Deterministic Simulations and Predictions. Water Resour. Res. 2022, 58, e2021WR031215. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Climate Extrapolations in Hydrology: The Expanded Bluecat Methodology. Hydrology 2022, 9, 86. [Google Scholar] [CrossRef]
- Boyle, D. Multicriteria Calibration of Hydrological Models. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2000. [Google Scholar]
- Rozos, E. A methodology for simple and fast streamflow modelling. Hydrol. Sci. J. 2020, 65, 1084–1095. [Google Scholar] [CrossRef]
- Mullen, K.M.; Ardia, D.; Gil, D.L.; Windover, D.; Cline, J. DEoptim: An R Package for Global Optimization by Differential Evolution. J. Stat. Softw. 2011, 40, 1–26. [Google Scholar] [CrossRef]
- Herath, H.M.V.V.; Chadalawada, J.; Babovic, V. Genetic programming for hydrological applications: To model or forecast that is the question. J. Hydroinf. 2021, 23, 740–763. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Santos, L.; Thirel, G.; Perrin, C. Continuous state-space representation of a bucket-type rainfall-runoff model: A case study with the GR4 model using state-space GR4 (version 1.0). Geosci. Model Dev. 2018, 11, 1591–1605. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Michel, C. Hydrologie Appliquée aux Petits Bassins Versants Ruraux; Cemagref: Antony, France, 1989. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into deep learning. arXiv 2021, arXiv:2106.11342. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:cs.LG/1212.5701. [Google Scholar]
- Jordan, J. Normalizing Your Data (Specifically, Input and Batch Normalization). 2021. Available online: https://www.jeremyjordan.me/batch-normalization/ (accessed on 4 January 2023).
- An Overview of Regularization Techniques in Deep Learning (with Python Code). 2018. Available online: https://www.analyticsvidhya.com/blog/2018/04/fundTamentals-deep-learning-regularization-techniques/ (accessed on 4 January 2023).
- Hashemi, R.; Brigode, P.; Garambois, P.A.; Javelle, P. How can we benefit from regime information to make more effective use of long short-term memory (LSTM) runoff models? Hydrol. Earth Syst. Sci. 2022, 26, 5793–5816. [Google Scholar] [CrossRef]
- Cox, J. Cortexsys 3.1 User Guide. 2022. Available online: https://github.com/rozos/Cortexsys/ (accessed on 4 January 2023).
- Ramsundar, B.; Zadeh, R.B. TensorFlow for Deep Learning: From Linear Regression to Reinforcement Learning; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Rozos, E.; Koutsoyiannis, D.; Montanari, A. KNN vs. Blueca—Machine Learning vs. Classical Statistics. Hydrology 2022, 9, 101. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence a Modern Approach; Pearson Education, Inc.: London, UK, 2010. [Google Scholar]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
| LSTM | Hydrological Model | ||
|---|---|---|---|
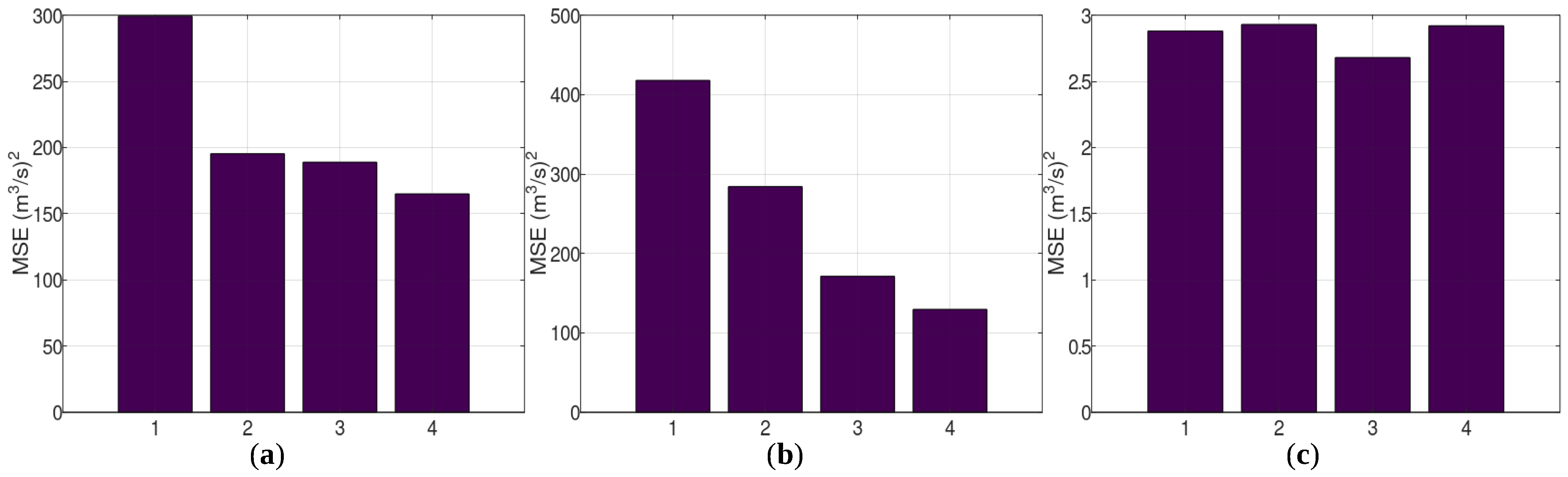
| HYMOD | MSE of training period | 94.58 | 233.77 |
| PBIAS of training period | −3.05% | 33.70% | |
| MSE of test period | 195.36 | 299.25 | |
| PBIAS of test period | 7.72% | 44.19% | |
| LRHM | MSE of training period | 128.80 | 143.59 |
| PBIAS of training period | 1.85% | −2.39% | |
| MSE of test period | 197.69 | 198.25 | |
| PBIAS of test period | 14.30% | 10.03% | |
| GR4J | MSE of training period | 60.25 | 105.12 |
| PBIAS of training period | −0.22% | −3.99% | |
| MSE of test period | 164.99 | 165.56 | |
| PBIAS of test period | 11.07% | 7.75% |
| LSTM | Hydrological Model | ||
|---|---|---|---|
| HYMOD | MSE of training period | 170.07 | 277.45 |
| PBIAS of training period | −3.90% | 30.99% | |
| MSE of test period | 284.21 | 417.89 | |
| PBIAS of test period | 7.50% | 42.12 % | |
| LRHM | MSE of training period | 163.31 | 198.77 |
| PBIAS of training period | 2.42% | 3.64% | |
| MSE of test period | 301.91 | 338.92 | |
| PBIAS of test period | −3.89% | −0.07% | |
| GR4H | MSE of training period | 89.15 | 121.25 |
| PBIAS of training period | −0.73% | 10.55% | |
| MSE of test period | 129.60 | 147.55 | |
| PBIAS of test period | 7.53% | 19.48% |
| LSTM | Hydr. Model | ||
|---|---|---|---|
| HYMOD | MSE of training period | 2.0923 | 2.5895 |
| PBIAS of training period | −6.92% | 2.52% | |
| MSE of test period | 2.9315 | 2.8848 | |
| PBIAS of test period | 5.79% | 20.25% | |
| LRHM | MSE of training period | 1.3191 | 1.9080 |
| PBIAS of training period | −0.15% | 0.39% | |
| MSE of test period | 2.9227 | 3.2485 | |
| PBIAS MSE of test period | −11.13% | −14.14% | |
| GR4H | MSE of training period | 1.5243 | 2.4389 |
| PBIAS of training period | 6.49% | 4.91% | |
| MSE of test period | 3.1121 | 3.2996 | |
| PBIAS MSE of test period | −3.09% | −16.69% |
| Tool | Diagnostic | Interpretation |
|---|---|---|
| KNN-Bluecat | Unusual CI shape and/or width | Inconsistencies in data |
| KNN-Bluecat | Narrow CI width despite large error | Conditional systematic errors |
| KNN-Bluecat | Model simulation far from median | Model bias |
| LSTM | Similar performance of LSTM on multiple hydrological models and on plain model | Best possible performance achieved |
| LSTM | Similar performance of LSTM on multiple hydrological models and on single model, but better than that of plain model | Best achievable performance detected, hydrological model falls short |
| LSTM | Performance of LSTM on multiple hydrological models better than that on single model and plain hydrological model | Best achievable performance not detected, hydrological model falls short |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozos, E. Assessing Hydrological Simulations with Machine Learning and Statistical Models. Hydrology 2023, 10, 49. https://doi.org/10.3390/hydrology10020049
Rozos E. Assessing Hydrological Simulations with Machine Learning and Statistical Models. Hydrology. 2023; 10(2):49. https://doi.org/10.3390/hydrology10020049
Chicago/Turabian StyleRozos, Evangelos. 2023. "Assessing Hydrological Simulations with Machine Learning and Statistical Models" Hydrology 10, no. 2: 49. https://doi.org/10.3390/hydrology10020049
APA StyleRozos, E. (2023). Assessing Hydrological Simulations with Machine Learning and Statistical Models. Hydrology, 10(2), 49. https://doi.org/10.3390/hydrology10020049







