Calibration of Land-Use-Dependent Evaporation Parameters in Distributed Hydrological Models Using MODIS Evaporation Time Series Data
Abstract
:1. Introduction
2. Materials and Methods
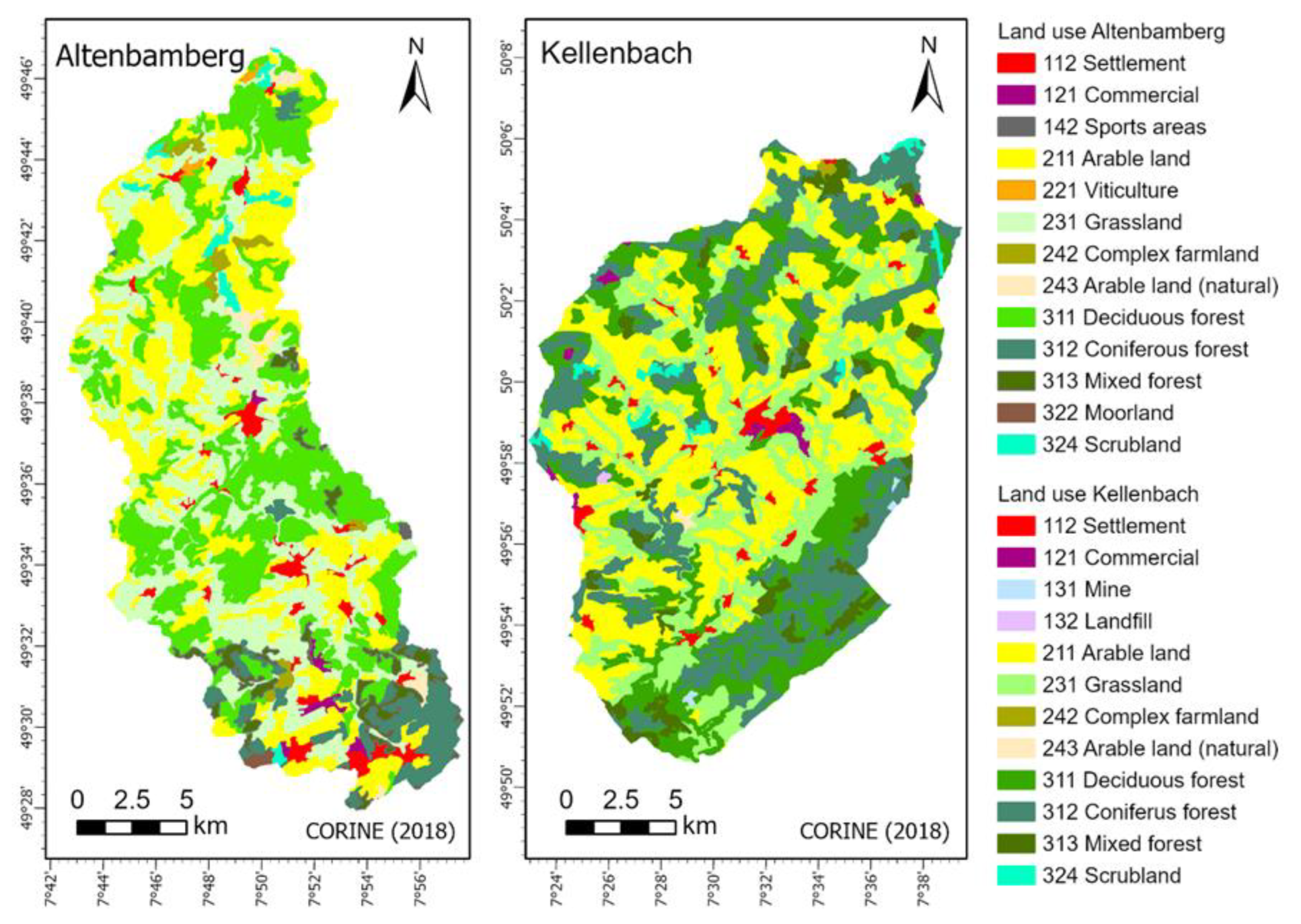
2.1. Study Area
2.2. Model Setup and Parameterization
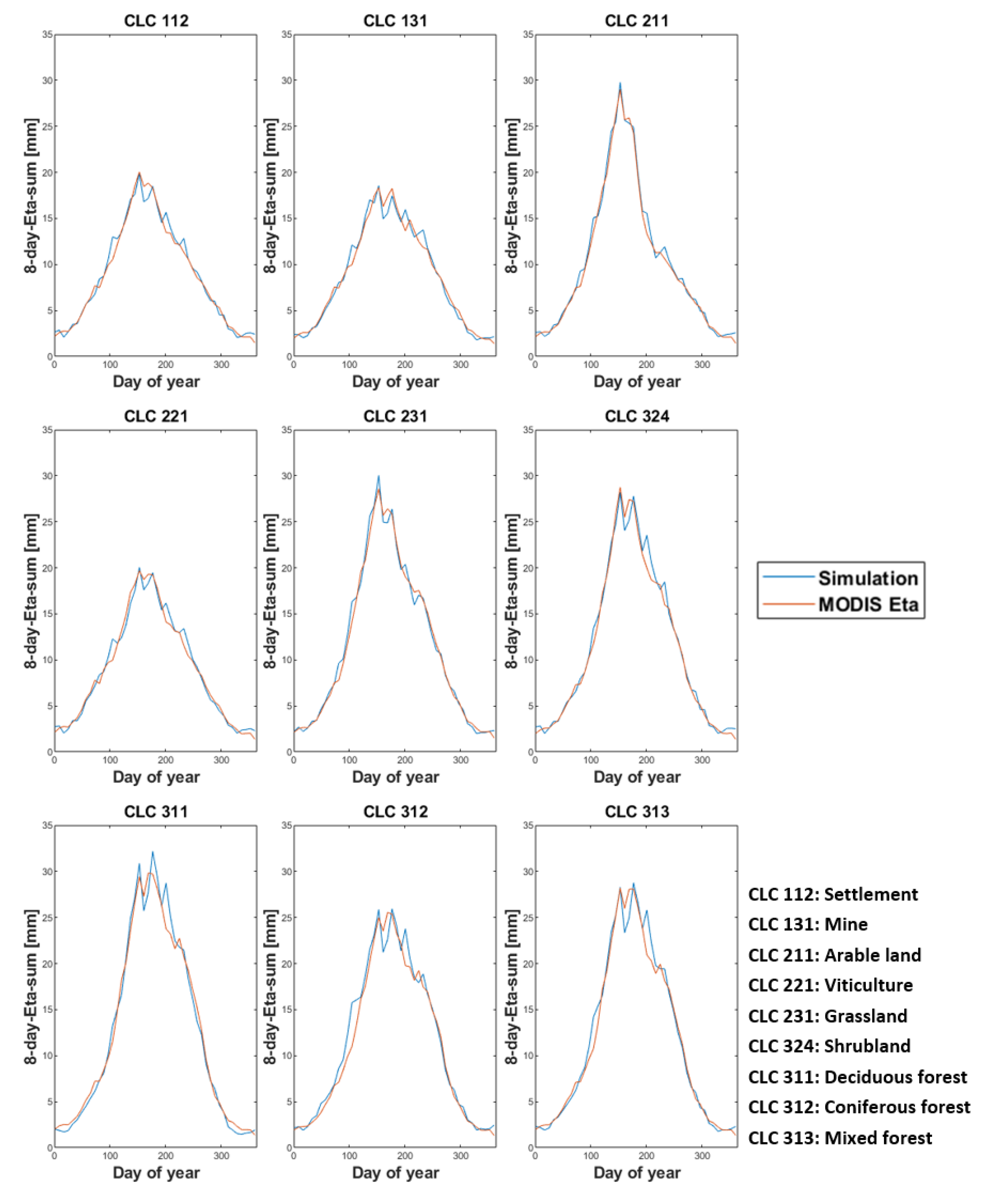
2.3. MODIS ETa (Dataset for Model Calibration)
2.4. Landsat ETa (Dataset for Model Validation)
2.5. Land-Use-Specific Calibration Process Using MODIS Data
- (i)
- Setup of 1D models for land-use-specific calibration:
- (ii)
- Soil parameterization and land-use transformation:
- (iii)
- Manual Calibration of Vegetation Parameters and Phenological Patterns:
2.6. Performance Metrics for Model Analysis
3. Results
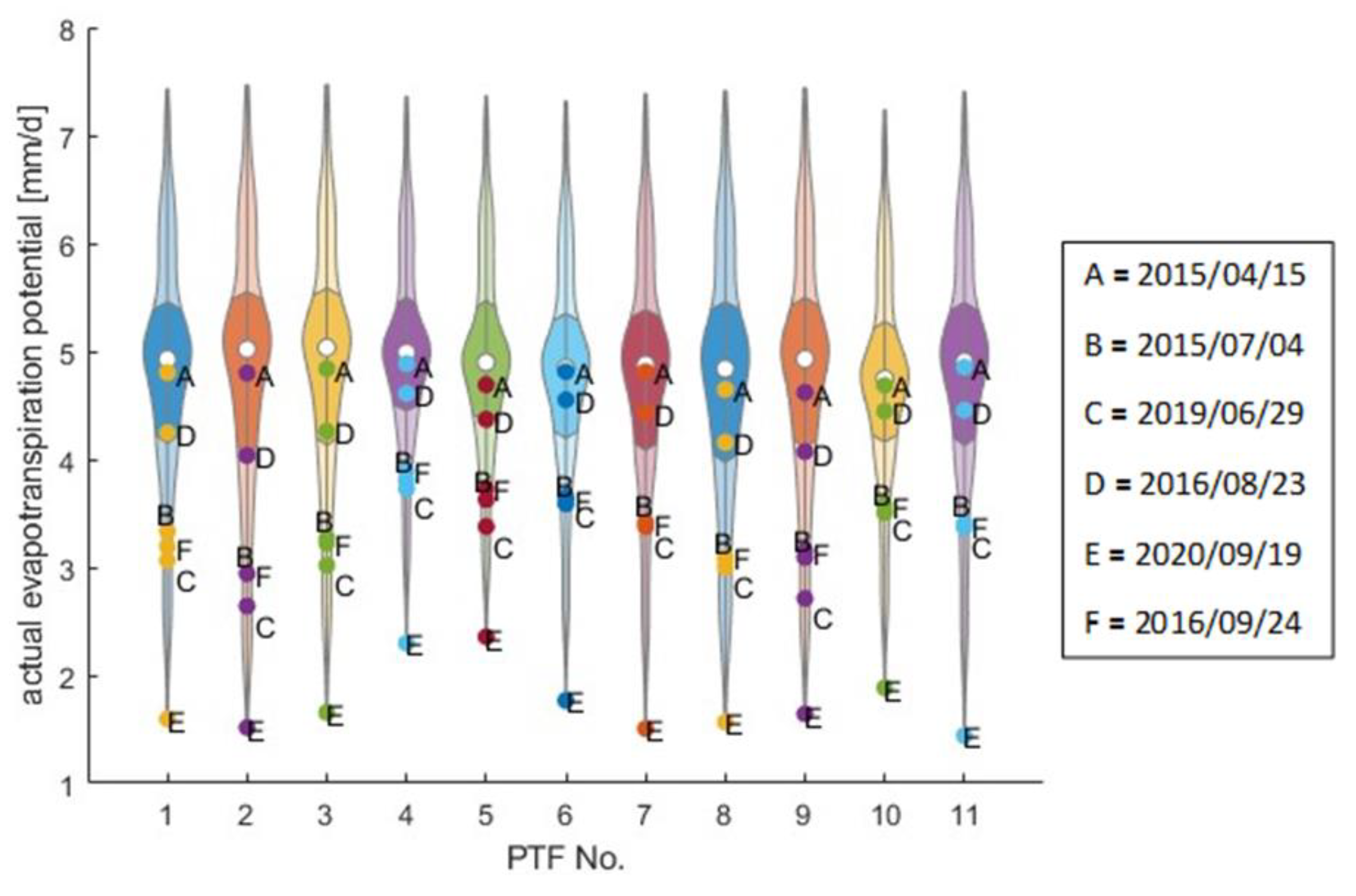
3.1. System State Analysis
3.2. Land-Use-Specific Calibration of Single-Cell Models
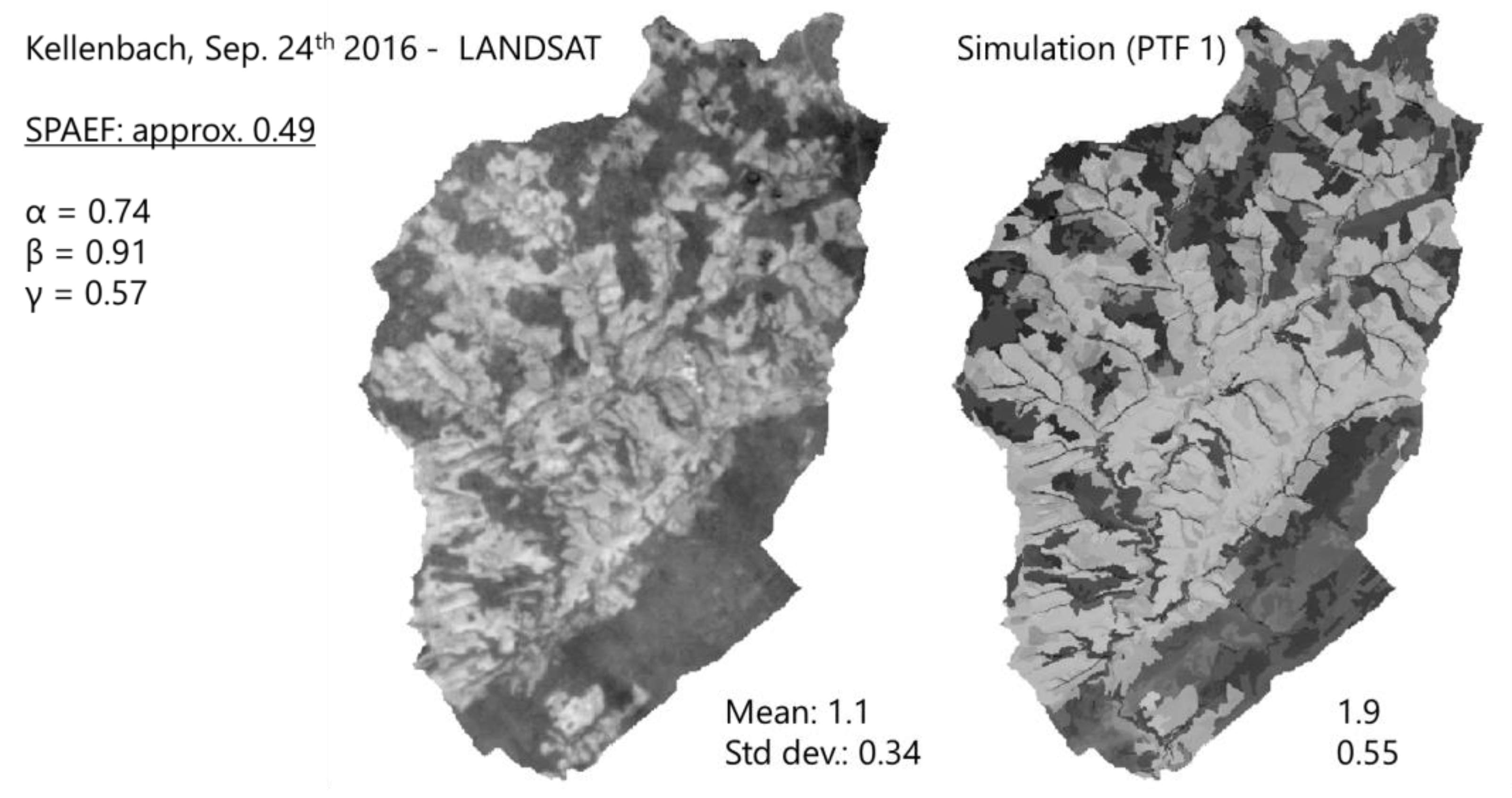
3.3. Spatial Pattern Analysis Based on SPAEF
4. Discussion
5. Conclusions and Outlook
- (1)
- The lack of information on reasonable vegetation parameters for certain land-use types like moorland and industrial areas or land-use classes that only constitute a very small aerial share within the catchments.
- (2)
- Catchment-specific conditions such as elevation, soil moisture states, and harvest times, which influence annual phenological courses and inter-annual shifts in evaporation patterns.
- (3)
- The inherent uncertainty in the MODIS dataset due to the remaining mixed signatures resulting from the rather coarse resolution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 | 0.150 |
| rsc | 100 | 100 | 100 | 110 | 110 | 100 | 150 | 150 | 130 | 100 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 50 | 50 | 50 | 60 | 65 | 65 | 50 | 50 | 50 |
| rs_evaporation | 200 | 200 | 220 | 250 | 200 | 240 | 330 | 360 | 290 | 200 | 200 | 200 |
| LAI | 0.800 | 0.900 | 1.000 | 1.100 | 1.900 | 2.000 | 1.400 | 1.250 | 1.250 | 1.225 | 1.100 | 0.800 |
| z0 | 1.000 | 1.000 | 1.200 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.200 | 1.000 | 1.000 |
| vcf | 0.260 | 0.268 | 0.270 | 0.280 | 0.460 | 0.500 | 0.350 | 0.330 | 0.320 | 0.300 | 0.274 | 0.260 |
| root depth | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 |
| rsc | 100 | 100 | 100 | 100 | 90 | 110 | 135 | 130 | 100 | 100 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 50 | 50 | 55 | 70 | 65 | 50 | 50 | 50 | 50 |
| rs_evaporation | 215 | 215 | 220 | 250 | 190 | 250 | 265 | 260 | 200 | 200 | 200 | 250 |
| LAI | 0.800 | 1.000 | 1.100 | 1.200 | 2.500 | 2.350 | 1.600 | 1.600 | 1.600 | 1.300 | 1.000 | 0.800 |
| z0 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 |
| vcf | 0.260 | 0.270 | 0.270 | 0.270 | 0.500 | 0.500 | 0.450 | 0.450 | 0.450 | 0.400 | 0.350 | 0.260 |
| root depth | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.145 | 0.145 | 0.145 | 0.180 | 0.190 | 0.190 | 0.190 | 0.190 | 0.190 | 0.190 | 0.150 | 0.150 |
| rsc | 100 | 100 | 100 | 110 | 90 | 85 | 135 | 140 | 115 | 100 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 50 | 50 | 45 | 65 | 65 | 50 | 50 | 50 | 50 |
| rs_evaporation | 260 | 250 | 250 | 275 | 265 | 260 | 280 | 290 | 270 | 200 | 220 | 260 |
| LAI | 1.000 | 1.000 | 1.100 | 1.100 | 2.000 | 2.250 | 1.200 | 1.250 | 1.550 | 1.800 | 1.300 | 1.000 |
| z0 | 1.800 | 1.800 | 1.800 | 1.800 | 2.000 | 2.100 | 2.000 | 2.000 | 2.000 | 2.000 | 1.900 | 1.900 |
| vcf | 0.500 | 0.500 | 0.525 | 0.450 | 0.600 | 0.600 | 0.500 | 0.500 | 0.550 | 0.550 | 0.550 | 0.500 |
| root depth | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.193 | 0.193 | 0.197 | 0.197 | 0.197 | 0.197 | 0.197 | 0.197 | 0.193 | 0.193 | 0.193 | 0.193 |
| rsc | 100 | 125 | 125 | 125 | 80 | 80 | 120 | 115 | 100 | 100 | 100 | 100 |
| rs_interception | 50 | 60 | 60 | 60 | 50 | 40 | 50 | 60 | 50 | 50 | 50 | 50 |
| rs_evaporation | 200 | 350 | 350 | 350 | 310 | 260 | 300 | 300 | 200 | 200 | 200 | 200 |
| LAI | 1.900 | 1.900 | 1.900 | 1.900 | 4.000 | 4.000 | 4.000 | 3.500 | 3.500 | 3.250 | 2.000 | 1.600 |
| z0 | 0.100 | 0.100 | 0.130 | 0.200 | 0.500 | 0.500 | 0.200 | 0.200 | 0.200 | 0.150 | 0.130 | 0.100 |
| vcf | 0.750 | 0.750 | 0.750 | 0.750 | 0.950 | 0.950 | 0.750 | 0.700 | 0.750 | 0.750 | 0.750 | 0.750 |
| root depth | 0.400 | 0.400 | 0.400 | 0.400 | 0.450 | 0.450 | 0.450 | 0.400 | 0.400 | 0.400 | 0.400 | 0.400 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.160 | 0.160 | 0.160 | 0.180 | 0.180 | 0.180 | 0.180 | 0.180 | 0.180 | 0.17 | 0.17 | 0.160 |
| rsc | 100 | 100 | 100 | 100 | 100 | 95 | 160 | 160 | 100 | 100 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 60 | 50 | 50 | 60 | 60 | 50 | 50 | 50 | 50 |
| rs_evaporation | 280 | 280 | 300 | 400 | 400 | 400 | 400 | 400 | 380 | 280 | 280 | 290 |
| LAI | 1.000 | 1.000 | 1.300 | 1.800 | 4.000 | 4.200 | 3.200 | 2.900 | 2.400 | 1.800 | 1.000 | 1.000 |
| z0 | 1.000 | 1.000 | 2.000 | 2.500 | 3.500 | 3.500 | 3.200 | 3.000 | 3.000 | 2.500 | 2.000 | 1.000 |
| vcf | 0.400 | 0.400 | 0.500 | 0.550 | 0.850 | 0.900 | 0.800 | 0.750 | 0.700 | 0.650 | 0.500 | 0.400 |
| root depth | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 | 1.300 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.125 | 0.125 | 0.124 | 0.120 | 0.118 | 0.112 | 0.105 | 0.105 | 0.105 | 0.110 | 0.110 | 0.120 |
| rsc | 130 | 130 | 130 | 130 | 110 | 100 | 160 | 160 | 90 | 100 | 100 | 100 |
| rs_interception | 60 | 60 | 60 | 60 | 50 | 50 | 60 | 70 | 45 | 50 | 50 | 50 |
| rs_evaporation | 900 | 900 | 900 | 900 | 800 | 800 | 850 | 900 | 700 | 800 | 800 | 800 |
| LAI | 4.000 | 3.900 | 3.900 | 4.400 | 5.900 | 5.900 | 5.900 | 5.800 | 5.800 | 5.500 | 5.000 | 4.500 |
| z0 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 |
| vcf | 0.700 | 0.700 | 0.710 | 0.740 | 0.830 | 0.850 | 0.830 | 0.820 | 0.820 | 0.750 | 0.750 | 0.700 |
| root depth | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 | 1.500 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.140 | 0.139 | 0.137 | 0.136 | 0.136 | 0.138 | 0.135 | 0.132 | 0.135 | 0.135 | 0.130 | 0.130 |
| rsc | 115 | 115 | 115 | 115 | 105 | 97.5 | 152.5 | 152.5 | 105 | 112.5 | 100 | 100 |
| rs_interception | 55 | 55 | 55 | 60 | 50 | 50 | 60 | 65 | 47.5 | 50 | 50 | 50 |
| rs_evaporation | 590 | 590 | 600 | 650 | 650 | 600 | 620 | 645.5 | 595 | 540 | 540 | 545 |
| LAI | 2.500 | 2.450 | 2.300 | 3.450 | 6.950 | 6.950 | 6.750 | 6.700 | 6.700 | 4.500 | 3.000 | 2.750 |
| z0 | 5.50 | 5.50 | 5.75 | 6.00 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 6.50 | 5.75 | 5.50 |
| vcf | 0.550 | 0.550 | 0.600 | 0.650 | 0.840 | 0.870 | 0.830 | 0.830 | 0.830 | 0.700 | 0.610 | 0.550 |
| root depth | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 | 1.710 |
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Alemayehu, T.; Gupta, H.V.; van Griensven, A.; Bauwens, W. On the Calibration of Spatially Distributed Hydrologic Models for Poorly Gauged Basins: Exploiting Information from Streamflow Signatures and Remote Sensing-Based Evapotranspiration Data. Water 2022, 14, 1252. [Google Scholar] [CrossRef]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; van Beek, L.P.H.; Bierkens, M.F.P.; Blyth, E.; de Roo, A.; Döll, P.; Ek, M.; Famiglietti, J.; et al. Hyperresolution Global Land Surface Modeling: Meeting a Grand Challenge for Monitoring Earth’s Terrestrial Water. Water Resour. Res. 2011, 47, W05301. [Google Scholar] [CrossRef]
- Wu, J.; Lakshmi, V.; Wang, D.; Lin, P.; Pan, M.; Cai, X.; Wood, E.; Zeng, Z. The Reliability of Global Remote Sensing Evapotranspiration Products over Amazon. Remote Sens. 2020, 12, 2211. [Google Scholar] [CrossRef]
- Billah, M.; Goodall, J.; Narayan, U.; Reager, J.; Lakshmi, V.; Famiglietti, J. A Methodology for Evaluating Evapotranspiration Estimates at the Watershed-Scale Using GRACE. J. Hydrol. 2015, 523, 574–586. [Google Scholar] [CrossRef]
- Boegh, E.; Poulsen, R.N.; Butts, M.; Abrahamsen, P.; Dellwik, E.; Hansen, S.; Hasager, C.B.; Ibrom, A.; Loerup, J.-K.; Pilegaard, K.; et al. Remote Sensing Based Evapotranspiration and Runoff Modeling of Agricultural, Forest and Urban Flux Sites in Denmark: From Field to Macro-Scale. J. Hydrol. 2009, 377, 300–316. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Khorrami, B.; Gorjifard, S.; Ali, S.; Feizizadeh, B. Local-Scale Monitoring of Evapotranspiration Based on Downscaled GRACE Observations and Remotely Sensed Data: An Application of Terrestrial Water Balance Approach. Earth Sci. Inform. 2023, 16, 1329–1345. [Google Scholar] [CrossRef]
- Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.; Shang, G.-F. Soil Moisture Retrieval from Remote Sensing Measurements: Current Knowledge and Directions for the Future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R.J. Amazon Forests Maintain Consistent Canopy Structure and Greenness during the Dry Season. Nature 2014, 506, 221–224. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial Water Fluxes Dominated by Transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef]
- Fisher, J.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.; Hook, S.; Baldocchi, D.; Townsend, P.; et al. The Future of Evapotranspiration: Global Requirements for Ecosystem Functioning, Carbon and Climate Feedbacks, Agricultural Management, and Water Resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Rosenzweig, C.; Sellers, P.J. Evapotranspiration Models with Canopy Resistance for Use in Climate Models, a Review. Agric. For. Meteorol. 1991, 54, 373–388. [Google Scholar] [CrossRef]
- Perez, P.; Brau, S.; Castellví, F.; Martínez-Cob, A.; Villalobos, F. A Simple Parameterization of Bulk Canopy Resistance from Climatic Variables for Estimating Hourly Evapotranspiration. Hydrol. Process. 2006, 20, 515–532. [Google Scholar] [CrossRef]
- Kang, M.; Zhang, Z.-Q.; Noormets, A.; Fang, X.; Zha, T.-S.; Zhou, J.; Sun, G.; Mcnulty, S.; Chen, J.-C. Energy Partitioning and Surface Resistance of a Poplar Plantation in Northern China. Biogeosciences 2015, 12, 4245–4259. [Google Scholar] [CrossRef]
- Wilson, M.F.; Henderson-Sellers, A. A Global Archive of Land Cover and Soils Data for Use in General Circulation Climate Models. J. Climatol. 1985, 5, 119–143. [Google Scholar] [CrossRef]
- Kärgel, S.; Förster, M.; Kleinschmit, B. Das Potenzial von Landsat-Zeitreihen für die Analyse Phänologischer Muster bei der Blattentfaltung von Laubwaldvegetation; AGIT: Salzburg, Austria, 2010. [Google Scholar]
- Dai, J.; Zhu, M.; Mao, W.; Liu, R.; Wang, H.; Alatalo, J.; Tao, Z.; Ge, Q. Divergent Changes of the Elevational Synchronicity in Vegetation Spring Phenology in North China from 2001 to 2017 in Connection with Variations in Chilling. Int. J. Climatol. 2021, 41, 6109–6121. [Google Scholar] [CrossRef]
- Hung, C.; Schalge, B.; Baroni, G.; Vereecken, H.; Franssen, H.-J. Assimilation of Groundwater Level and Soil Moisture Data in an Integrated Land Surface-Subsurface Model for Southwestern Germany. Water Resour. Res. 2022, 58, e2021WR031549. [Google Scholar] [CrossRef]
- Sakai, R.K.; Fitzjarrald, D.R.; Moore, K.E. Detecting Leaf Area and Surface Resistance during Transition Seasons. Agric. For. Meteorol. 1997, 84, 273–284. [Google Scholar] [CrossRef]
- Schulla, J. Hydrologische Modellierung von Flussgebieten zur Abschätzung der Folgen von Klimaänderungen. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 1997. [Google Scholar]
- Köppen, W.; Geiger, R. Das Geographische System der Klimate, 1st ed.; Gebrüder Borntraeger: Berlin, Germany, 1936. [Google Scholar]
- Schulla, J. Model Description WaSiM (Water Balance Simulation Model). 2021. Available online: http://www.wasim.ch/en/products/wasim_description.htm (accessed on 5 July 2022).
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.G.; van Genuchten, M.T. Using Pedotransfer Functions to Estimate the van Genuchten-Mualem Soil Hydraulic Properties: A Review. Vadose Zone J. 2010, 9, 795–820. [Google Scholar] [CrossRef]
- Ad-hoc-AG Boden. Bodenkundliche Kartieranleitung. KA5; Schweizerbart Science Publishers: Stuttgart, Germany, 2005; ISBN 978-3-510-95920-4. [Google Scholar]
- Mohajerani, H.; Teschemacher, S.; Casper, M.C. A Comparative Investigation of Various Pedotransfer Functions and Their Impact on Hydrological Simulations. Water 2021, 13, 1401. [Google Scholar] [CrossRef]
- Wösten, J.; Lilly, A.; Nemes, A.; Le Bas, C. Development and Use of a Database of Hydraulic Properties of European Soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Renger, M.; Bohne, K.; Facklam, M.; Harrach, T.; Riek, W.; Schäfer, W.; Wessolek, G.; Zacharias, S. Ergebnisse Und Vorschläge Der DBG-Arbeitsgruppe, Kennwerte Des Bodengefüges. Zur Schätzung Bodenphysikalischer Kennwerte 2009, 40, 4–51. [Google Scholar]
- Weynants, M.; Vereecken, H.; Javaux, M. Revisiting Vereecken Pedotransfer Functions: Introducing a Closed-Form Hydraulic Model. Vadose Zone J. 2009, 8, 86–95. [Google Scholar] [CrossRef]
- Zacharias, S.; Wessolek, G. Excluding Organic Matter Content from Pedotransfer Predictors of Soil Water Retention. Soil Sci. Soc. Am. J. 2007, 71, 43–50. [Google Scholar] [CrossRef]
- Teepe, R.; Dilling, H.; Beese, F. Estimating Water Retention Curves of Forest Soils from Soil Texture and Bulk Density. J. Plant Nutr. Soil Sci. 2003, 166, 111–119. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Weighted Recalibration of the Rosetta Pedotransfer Model with Improved Estimates of Hydraulic Parameter Distributions and Summary Statistics (Rosetta3). J. Hydrol. 2017, 547, 39–53. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a Global Evapotranspiration Algorithm Based on MODIS and Global Meteorology Data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Brust, C.; Kimball, J.; Maneta, M.; Jencso, K.; He, M.; Reichle, R. Using SMAP Level-4 Soil Moisture to Constrain MOD16 Evapotranspiration over the Contiguous USA. Remote Sens. Environ. 2021, 255, 112277. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Cook, M.; Schott, J.; Mandel, J.; Raqueno, N. Development of an Operational Calibration Methodology for the Landsat Thermal Data Archive and Initial Testing of the Atmospheric Compensation Component of a Land Surface Temperature (LST) Product from the Archive. Remote Sens. 2014, 6, 11244–11266. [Google Scholar] [CrossRef]
- Senay, G.; Budde, M.; Verdin, J.; Melesse, A. A Coupled Remote Sensing and Simplified Surface Energy Balance (SSEB) Approach to Estimate Actual Evapotranspiration from Irrigated Fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Gerlach, N. INTERMET–Interpolation Meteorologischer Größen. In Proceedings of the Niederschlags-Abfluss-Modellierung zur Verlängerung des Vorhersagezeitraumes Operationeller Wasserstands-Abflussvorhersagen; Gewaesserkunde, B.F., Veranstaltungen, R.B., Eds.; Bundesanstalt für Gewässerkunde: Koblenz, German; 2006; Volume 3, pp. 5–14. [Google Scholar]
- Senay, G.; Budde, M.; Verdin, J.P. Enhancing the Simplified Surface Energy Balance (SSEB) Approach for Estimating Landscape ET: Validation with the METRIC Model. Agric. Water Manag. 2011, 98, 606–618. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining Satellite Data and Appropriate Objective Functions for Improved Spatial Pattern Performance of a Distributed Hydrologic Model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Rieger, W. Prozessorientierte Modellierung dezentraler Hochwasserschutzmaßnahmen. Ph.D. Thesis, Technische Universität München, München, Germany, 2012. [Google Scholar]
- Teschemacher, S. Gebietsübergreifende Retentionspotenzialanalyse Agrarwirtschaftlicher und Konstruktiver Maßnahmen des Dezentralen Hochwasserrückhalts. Ph.D. Thesis, Technische Universität München, München, Germany, 2021. [Google Scholar]
- Lin, B.-S.; Lei, H.; Hu, M.-C.; Visessri, S.; Hsieh, C.-I. Canopy Resistance and Estimation of Evapotranspiration above a Humid Cypress Forest. Adv. Meteorol. 2020, 2020, 4232138. [Google Scholar] [CrossRef]
- Alemayehu, T.; Griensven, A.; van Senay, G.B.; Bauwens, W. Evapotranspiration Mapping in a Heterogeneous Landscape Using Remote Sensing and Global Weather Datasets: Application to the Mara Basin, East Africa. Remote Sens. 2017, 9, 390. [Google Scholar] [CrossRef]
- Richardson, A.; Hufkens, K.; Milliman, T.; Aubrecht, D.; Chen, M.; Gray, J.; Johnston, M.; Keenan, T.; Klosterman, S.; Kosmala, M.; et al. Tracking Vegetation Phenology across Diverse North American Biomes Using PhenoCam Imagery. Sci. Data 2018, 5, 180028. [Google Scholar] [CrossRef]
- Richardson, A.; Keenan, T.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate Change, Phenology, and Phenological Control of Vegetation Feedbacks to the Climate System. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Tardieu, F.; Simonneau, T. Variability among Species of Stomatal Control under Fluctuating Soil Water Status and Evaporative Demand: Modelling Isohydric and Anisohydric Behaviours. J. Exp. Bot. 1998, 49, 419–432. [Google Scholar] [CrossRef]
- Boegh, E.; Thorsen, M.; Butts, M.B.; Hansen, S.; Christiansen, J.S.; Abrahamsen, P.; Hasager, C.B.; Jensen, N.O.; Van Der Keur, P.; Refsgaard, J.C.; et al. Incorporating Remote Sensing Data in Physically Based Distributed Agro-Hydrological Modelling. J. Hydrol. 2004, 287, 279–299. [Google Scholar] [CrossRef]
- Vereecken, H.; Schnepf, A.; Hopmans, J.; Javaux, M.; Or, D.; Roose, T.; Vanderborght, J.; Young, M.; Amelung, W.; Aitkenhead, M.; et al. Modeling Soil Processes: Review, Key Challenges, and New Perspectives. Vadose Zone J. 2016, 15, 1–57. [Google Scholar] [CrossRef]
- Kutschera, E.; Kim, J.; Pitts, G.; Drapek, R. “What’s Past Is Prologue”: Vegetation Model Calibration with and without Future Climate. Land 2023, 12, 1121. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially Distributed Model Calibration of a Highly Managed Hydrological System Using Remote Sensing-Derived ET Data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Mohajerani, H.; Jackel, M.; Salm, Z.; Schuetz, T.; Casper, M. Spatial Evaluation of a Hydrological Model on Dominant Runoff Generation Processes Using Soil Hydrologic Maps. Hydrology 2023, 10, 55. [Google Scholar] [CrossRef]
- Bundesanstalt für Geowissenschaften und Rohstoffe (BGR) BGR Geoportal-Geoviewer. Bodenarten der Oberböden Deutschlands 1:1.000.000. Available online: https://geoportal.bgr.de/mapapps/resources/apps/geoportal/index.html?lang=de#/geoviewer (accessed on 2 September 2023).
- Dashtaki, S.G.; Homaee, M.; Khodaverdiloo, H. Derivation and Validation of Pedotransfer Functions for Estimating Soil Water Retention Curve Using a Variety of Soil Data. Soil Use Manag. 2010, 26, 68–74. [Google Scholar] [CrossRef]
- Sofia, G.; Ragazzi, F.; Giandon, P.; Dalla Fontana, G. On the Linkage between Runoff Generation, Land Drainage, Soil Properties, and Temporal Patterns of Precipitation in Agricultural Floodplains. Adv. Water Resour. 2019, 124, 120–138. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and Water Flow in Soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]

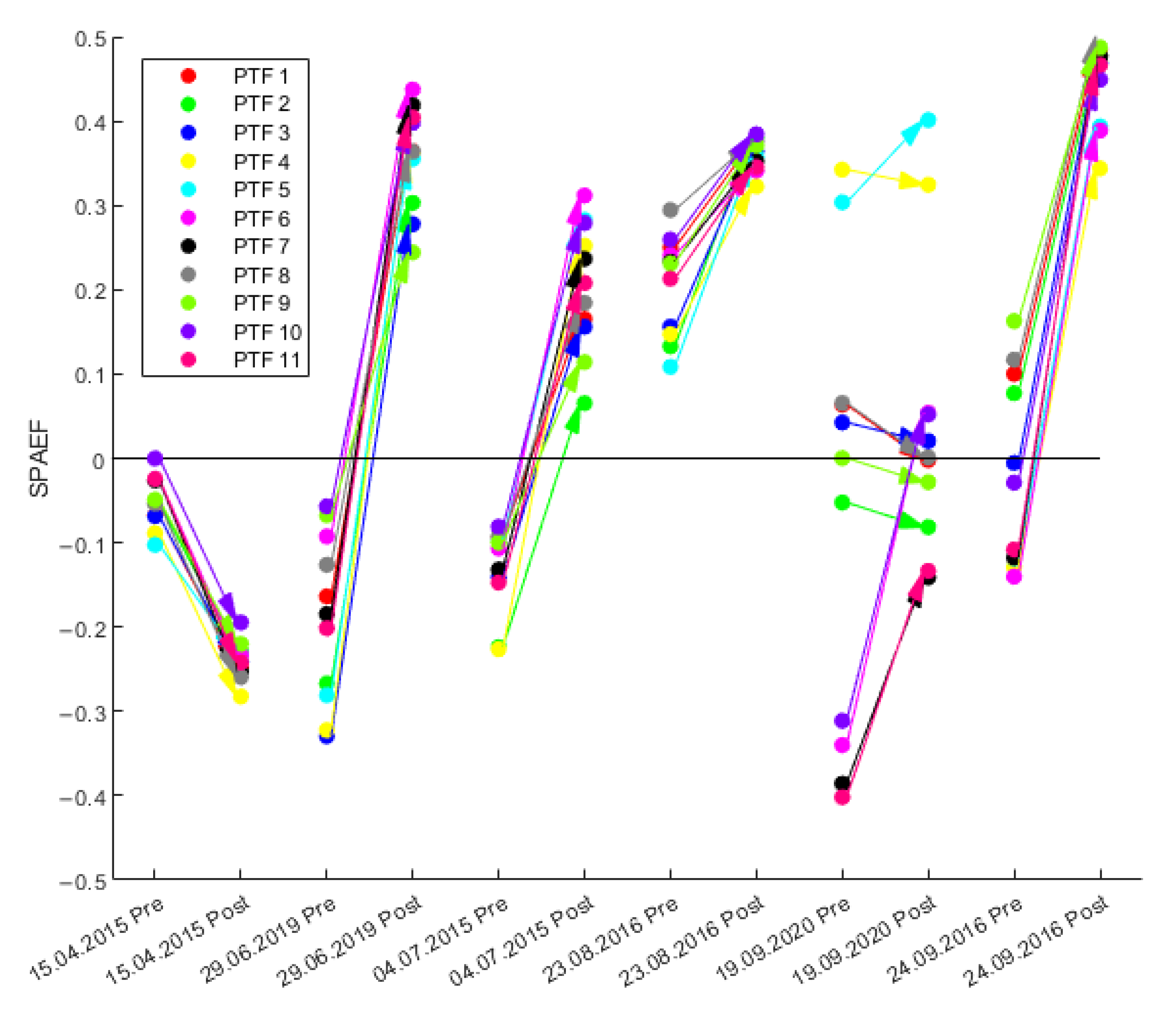
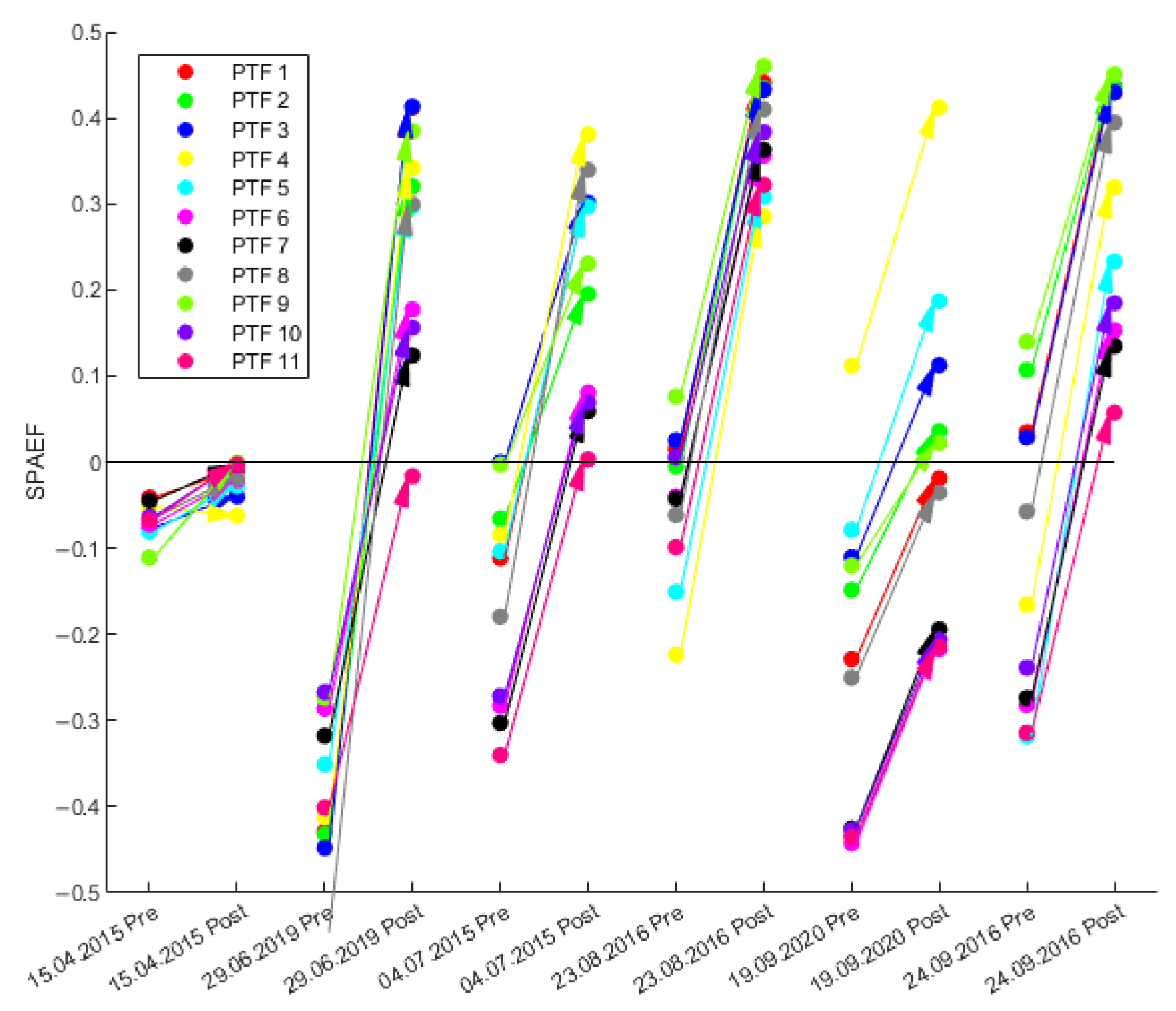
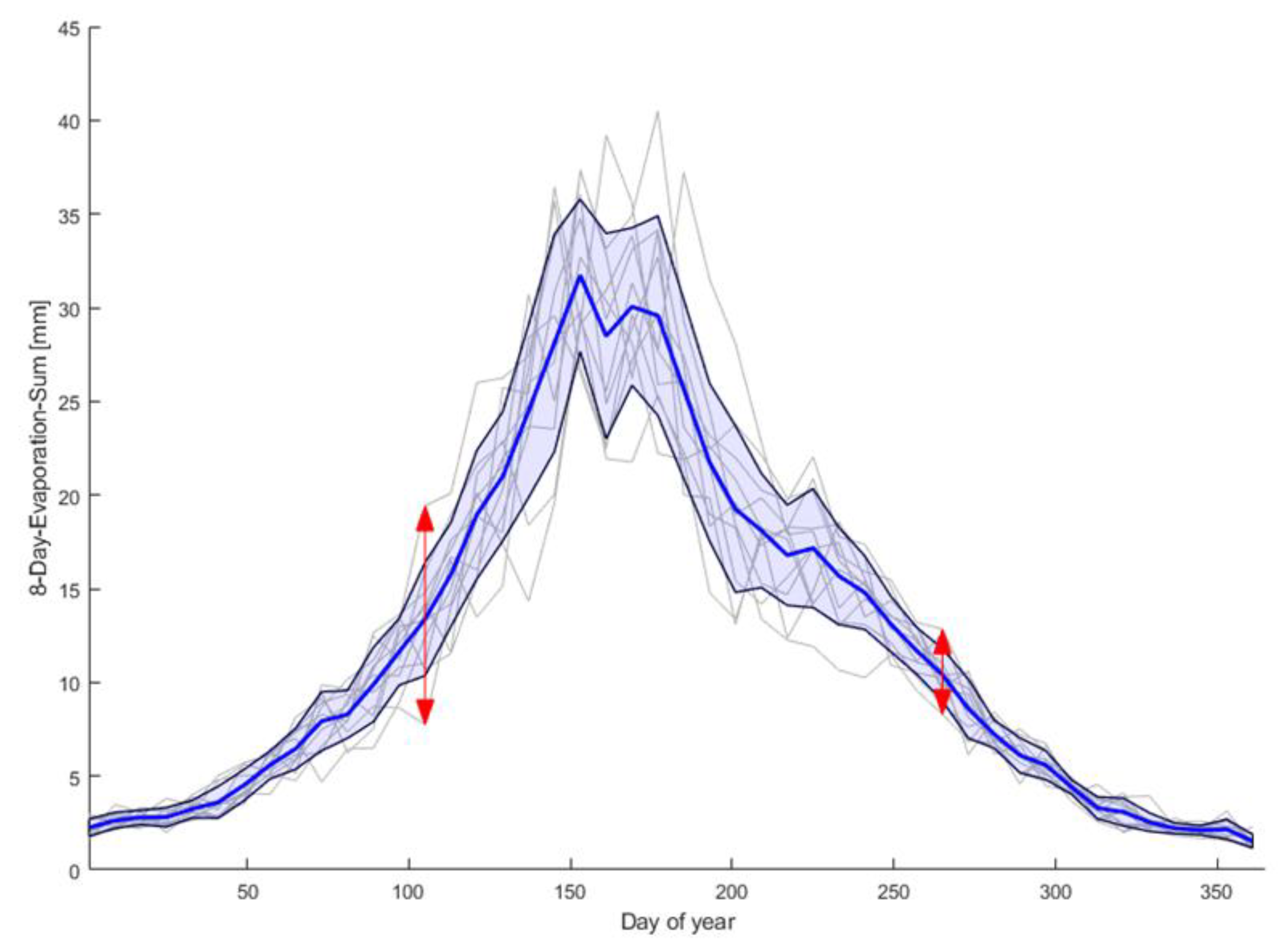
| PTF Combination | van Genuchten Parameters | Soil Hydraulic Conductivity Ksat |
|---|---|---|
| 1 | Wösten et al. (1999) [29] | Ad-Hoc AG Boden (2005) KA5 [27] |
| 2 | Renger et al. (2009) [30] | Ad-Hoc AG Boden (2005) KA5 |
| 3 | Weynants et al. (2009) [31] | Ad-Hoc AG Boden (2005) KA5 |
| 4 | Zacharias and Wessolek (2007) [32] | Ad-Hoc AG Boden (2005) KA5 |
| 5 | Teepe et al. (2003) [33] | Ad-Hoc AG Boden (2005) KA5 |
| 6 | Zhang and Schaap (2017): Rosetta H2w [34] | Ad-Hoc AG Boden (2005) KA5 |
| 7 | Zhang and Schaap (2017): Rosetta H3w [34] | Ad-Hoc AG Boden (2005) KA5 |
| 8 | Wösten et al. (1999) | Wösten et al. (1999) |
| 9 | Renger et al. (2009) | Renger et al. (2009) |
| 10 | Zhang and Schaap (2017): Rosetta H2w | Zhang and Schaap (2017): Rosetta H2w |
| 11 | Zhang and Schaap (2017): Rosetta H3w | Zhang and Schaap (2017): Rosetta H3w |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 258 | 288 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.200 | 0.210 | 0.250 | 0.220 | 0.200 | 0.200 | 0.200 |
| rsc | 100 | 100 | 105 | 105 | 60 | 55 | 110 | 135 | 100 | 100 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| rs_evaporation | 200 | 225 | 240 | 245 | 160 | 150 | 200 | 260 | 205 | 150 | 150 | 180 |
| LAI | 0.900 | 0.900 | 0.900 | 0.900 | 3.800 | 4.900 | 1.700 | 0.900 | 0.900 | 0.900 | 0.900 | 0.900 |
| z0 | 0.500 | 0.500 | 0.500 | 0.500 | 1.000 | 1.000 | 0.900 | 0.400 | 0.500 | 0.500 | 0.500 | 0.50 |
| vcf | 0.500 | 0.500 | 0.500 | 0.500 | 0.600 | 0.660 | 0.450 | 0.300 | 0.500 | 0.500 | 0.500 | 0.50 |
| root depth | 0.400 | 0.400 | 0.400 | 0.400 | 1.100 | 1.200 | 1.000 | 0.400 | 0.400 | 0.400 | 0.400 | 0.40 |
| Julian Days | 15 | 46 | 74 | 105 | 135 | 166 | 196 | 227 | 268 | 298 | 319 | 349 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| albedo | 0.150 | 0.150 | 0.150 | 0.180 | 0.180 | 0.180 | 0.180 | 0.170 | 0.170 | 0.170 | 0.170 | 0.160 |
| rsc | 100 | 100 | 100 | 100 | 100 | 95 | 145 | 145 | 120 | 120 | 100 | 100 |
| rs_interception | 50 | 50 | 50 | 60 | 50 | 50 | 60 | 60 | 50 | 50 | 50 | 50 |
| rs_evaporation | 280 | 280 | 300 | 400 | 400 | 400 | 390 | 390 | 280 | 280 | 280 | 290 |
| LAI | 1.000 | 1.000 | 1.500 | 2.500 | 8.000 | 8.000 | 7.500 | 7.500 | 7.500 | 3.600 | 1.000 | 1.000 |
| z0 | 1.000 | 1.000 | 1.500 | 2.000 | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 3.000 | 1.500 | 1.000 |
| vcf | 0.400 | 0.400 | 0.500 | 0.550 | 0.850 | 0.900 | 0.840 | 0.840 | 0.840 | 0.650 | 0.500 | 0.400 |
| root depth | 2.200 | 2.200 | 2.200 | 2.200 | 2.300 | 2.300 | 2.300 | 2.200 | 2.200 | 2.200 | 2.200 | 2.200 |
| Land Use | PBIAS | RMSE | SKout | |||
|---|---|---|---|---|---|---|
| Before | After cal. | Before | After cal. | Before | After cal. | |
| 112: Settlement | 17.32 | 1.21 | 2.77 | 0.77 | 0.50 | 0.86 |
| 121: Commercial | 17.36 | 1.40 | 2.73 | 0.87 | 0.54 | 0.85 |
| 131: Mine | 4.00 | −0.08 | 1.36 | 0.80 | 0.75 | 0.85 |
| 132: Landfill | 4.35 | 2.73 | 2.41 | 1.14 | 0.64 | 0.83 |
| 142: Sports areas | −15.08 | −4.87 | 3.60 | 1.66 | 0.59 | 0.81 |
| 211: Arable land | −12.60 | 1.86 | 3.55 | 0.73 | 0.55 | 0.91 |
| 221: Viticulture | 50.57 | 0.32 | 5.20 | 0.77 | 0.10 | 0.87 |
| 231: Grassland | −8.23 | 0.79 | 2.89 | 0.77 | 0.66 | 0.91 |
| 242: Complex arable land | −5.39 | 0.82 | 2.47 | 0.81 | 0.69 | 0.90 |
| 243: Arable land (natural) | 20.90 | 1.22 | 4.02 | 1.08 | 0.56 | 0.88 |
| 311: Deciduous forest | 12.84 | −0.11 | 3.00 | 1.20 | 0.69 | 0.88 |
| 312: Coniferous forest | 36.51 | 2.12 | 4.77 | 1.17 | 0.42 | 0.86 |
| 313: Mixed forest | 27.07 | 1.01 | 4.24 | 1.20 | 0.53 | 0.87 |
| 322: Moorland | 26.39 | 9.67 | 3.88 | 1.64 | 0.35 | 0.72 |
| 324: Shrubland | 31.16 | 1.99 | 4.25 | 0.98 | 0.51 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casper, M.C.; Salm, Z.; Gronz, O.; Hutengs, C.; Mohajerani, H.; Vohland, M. Calibration of Land-Use-Dependent Evaporation Parameters in Distributed Hydrological Models Using MODIS Evaporation Time Series Data. Hydrology 2023, 10, 216. https://doi.org/10.3390/hydrology10120216
Casper MC, Salm Z, Gronz O, Hutengs C, Mohajerani H, Vohland M. Calibration of Land-Use-Dependent Evaporation Parameters in Distributed Hydrological Models Using MODIS Evaporation Time Series Data. Hydrology. 2023; 10(12):216. https://doi.org/10.3390/hydrology10120216
Chicago/Turabian StyleCasper, Markus C., Zoé Salm, Oliver Gronz, Christopher Hutengs, Hadis Mohajerani, and Michael Vohland. 2023. "Calibration of Land-Use-Dependent Evaporation Parameters in Distributed Hydrological Models Using MODIS Evaporation Time Series Data" Hydrology 10, no. 12: 216. https://doi.org/10.3390/hydrology10120216
APA StyleCasper, M. C., Salm, Z., Gronz, O., Hutengs, C., Mohajerani, H., & Vohland, M. (2023). Calibration of Land-Use-Dependent Evaporation Parameters in Distributed Hydrological Models Using MODIS Evaporation Time Series Data. Hydrology, 10(12), 216. https://doi.org/10.3390/hydrology10120216









