Simple and Cost-Effective Method for Reliable Indirect Determination of Field Capacity
Abstract
1. Introduction
2. Materials and Methods
2.1. Filter Paper Draining Method
2.2. Data Origin and Processing
2.2.1. Dataset One
2.2.2. Dataset Two
2.2.3. Dataset Three
2.3. Statistical Evaluation and Uncertainty Analysis
3. Results
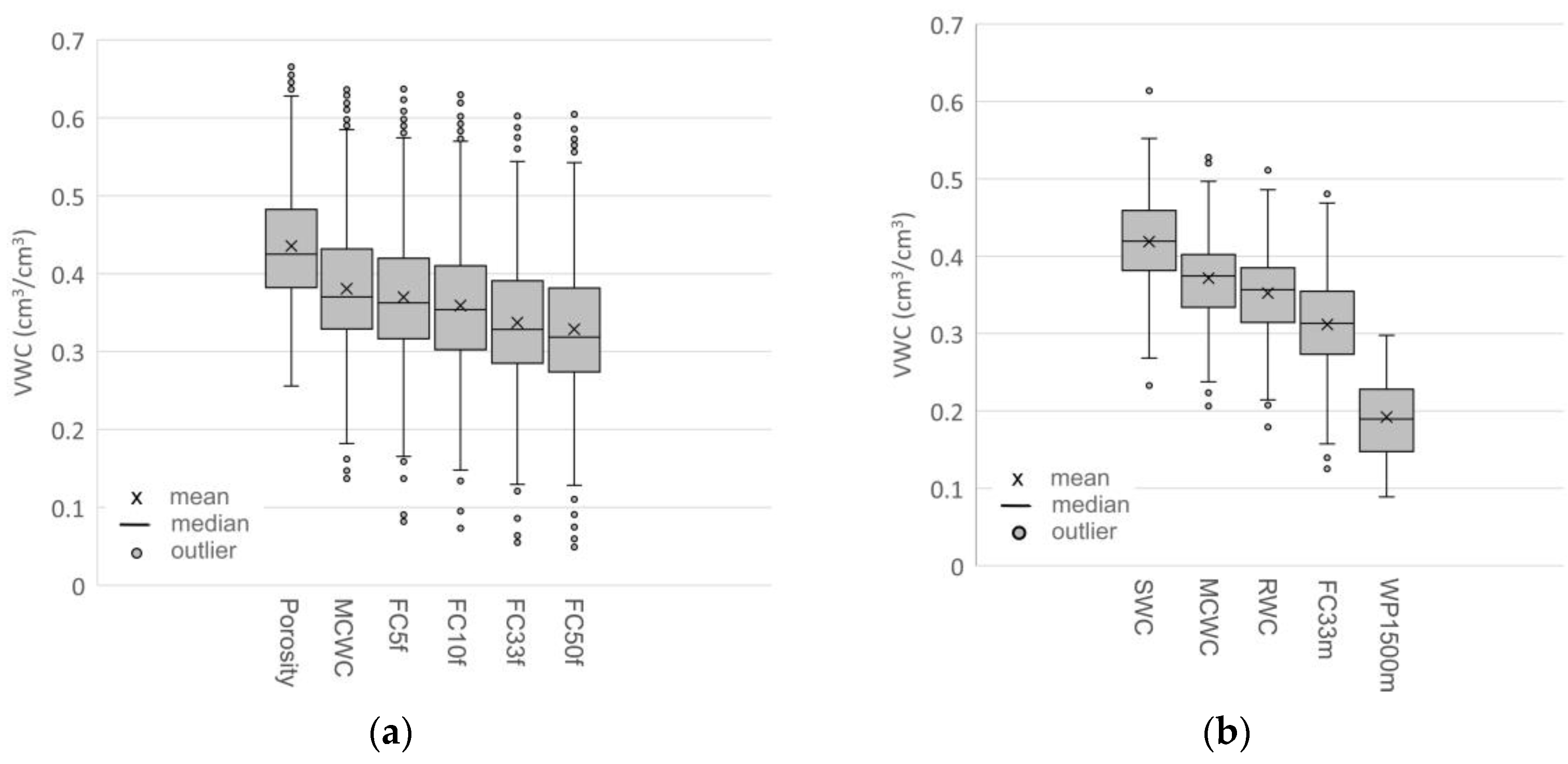
3.1. Descriptive Statistics of Soil Properties in the Datasets
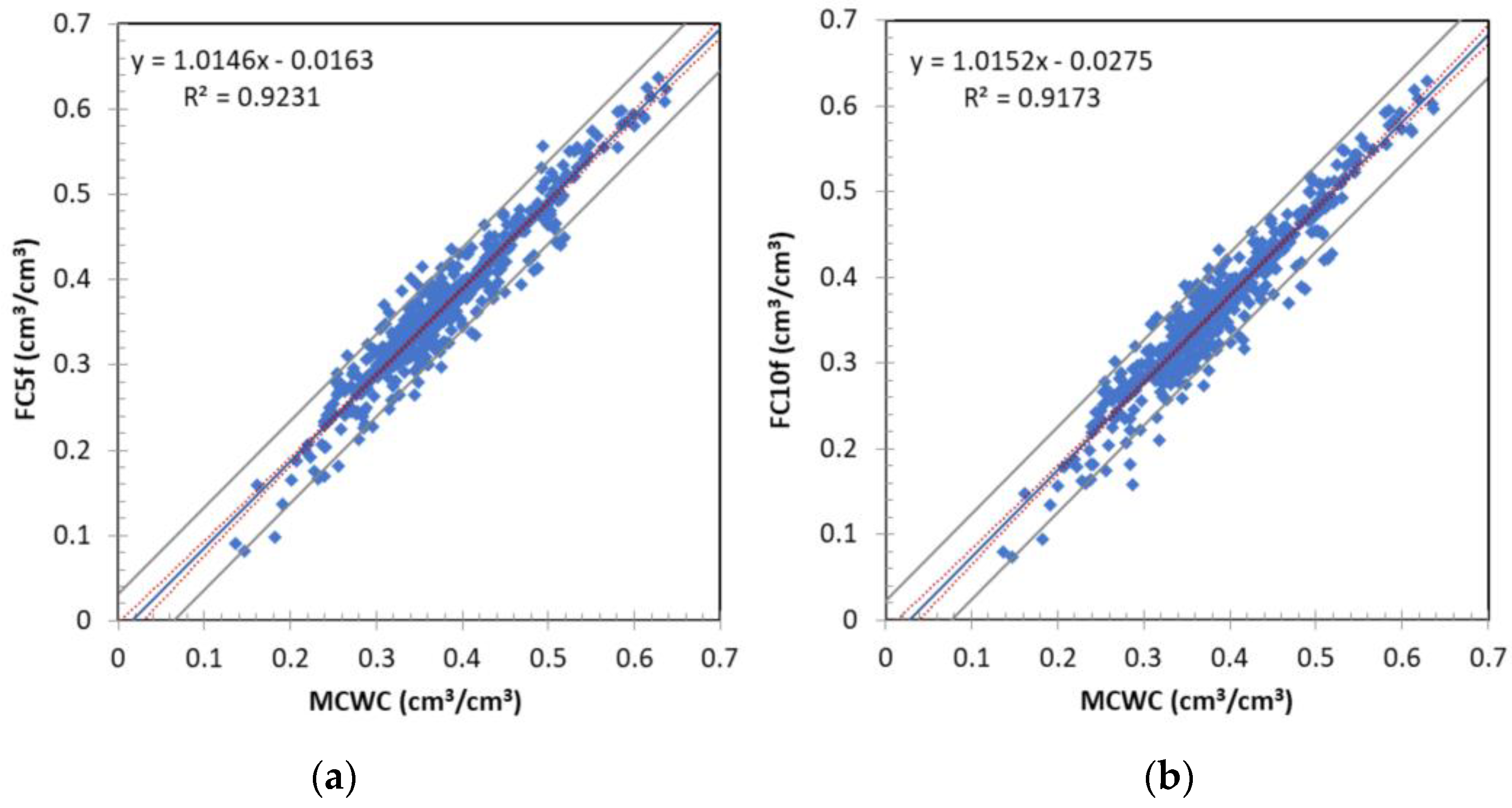
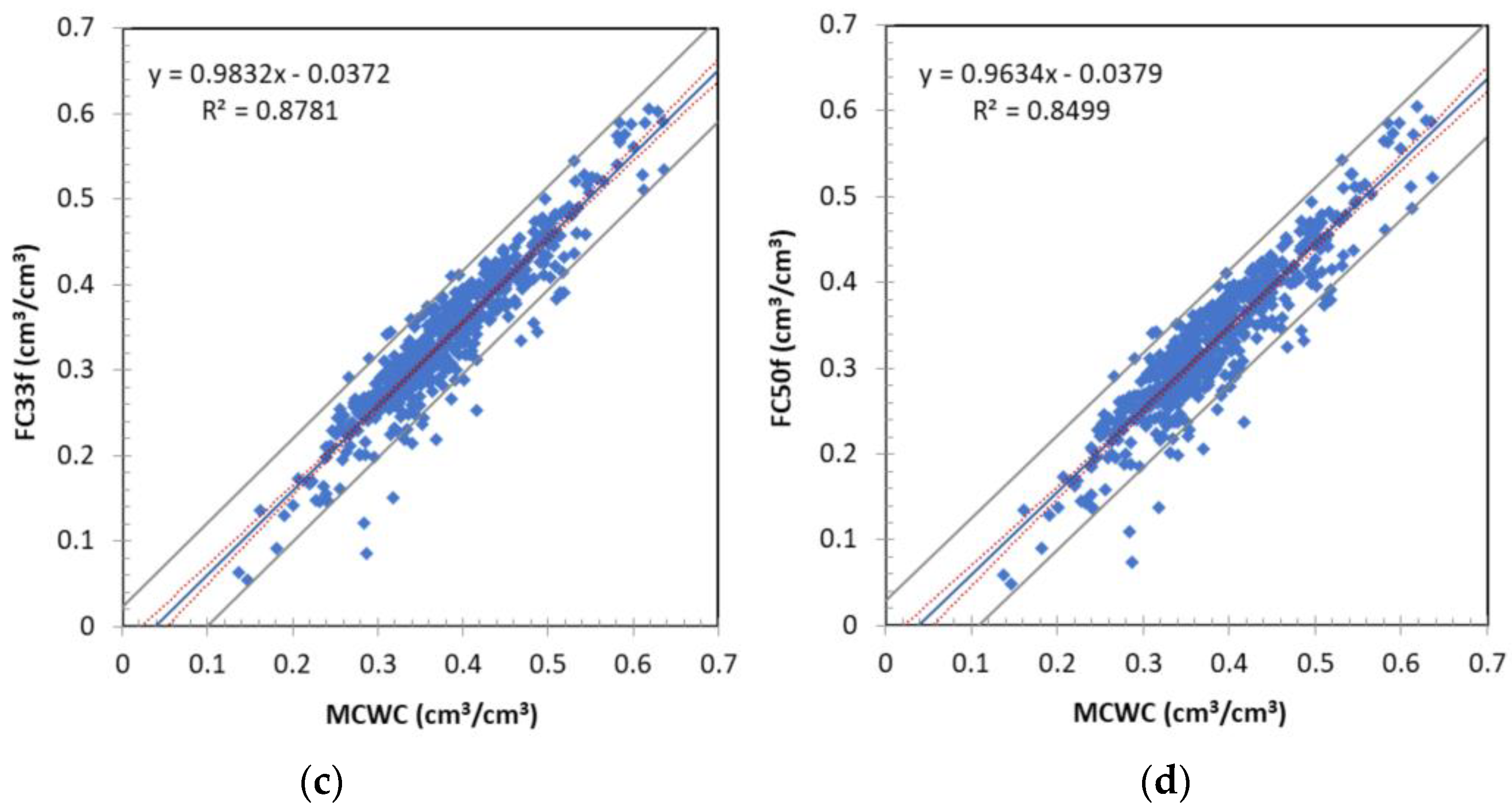
3.2. Predictive Relationships between Soil Moisture Constants and Field Capacity
- Maximum Capillary Water Capacity (Dataset One):
- Retention Water Capacity (Dataset Two):
3.3. Results of Testing the Historical Pedotransfer Functions for Field Capacity Estimation
4. Discussion
5. Conclusions
- FC determined as soil water content of −33 kPa can be effectively approximated using the equation:
- FC determined as soil water content of −5 or −10 kPa can be effectively approximated, respectively, using the equation:
- The use of legacy databases containing MCWC and RWC values together with the equations developed in this study.
- The fast and effective indirect determination of FC in new studies. The potential use of the equations developed in this study out of the Czech Republic should be verified via traditional FC determination.
- The development of similar, site-specific equations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| FC | Field capacity (cm3/cm3 or %) |
| FC5f | Field capacity determined at suction pressure of −5 kPa; letter f indicates fitted value (similarly for suction pressures of −10, −33 and −50 kPa) (cm3/cm3 or %) |
| FC33m | Field capacity determined at suction pressure of −33 kPa; letter m indicates measured value (cm3/cm3 or %) |
| FPSF | Fine particle size fraction (soil particles < 0.01 mm) (%) |
| MCWC | Maximum capillary water capacity (cm3/cm3 or %) |
| PTFs | Pedotransfer functions |
| RWC | Retention water capacity (cm3/cm3 or %) |
| SWRC | Soil water retention curve |
| WP | Permanent wilting point (cm3/cm3 or %) |
References
- Veihmeyer, F.J.; Hendrickson, A.H. Soil moisture conditions in relation to plant growth. Plant Physiol. 1927, 2, 71–82. [Google Scholar] [CrossRef]
- Cassel, D.K.; Nielsen, D.R. Field Capacity and Available Water Capacity. In Methods of Soil Analysis: Part 1. Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; American Society of Agronomy-Soil Science Society of America: Madison, WI, USA, 1986; pp. 901–926. ISBN 0-89118-088-5. [Google Scholar]
- Doležal, F.; Hernandez-Gomis, R.; Matula, S.; Gulamov, M.; Miháliková, M.; Khodjaev, S. Actual evapotranspiration of unirrigated grass in a smart field lysimeter. Vadose Zone J. 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Klute, A. (Ed.) Water Retention: Laboratory methods. In Methods of Soil Analysis: Part 1. Physical and Mineralogical Methods, 2nd ed.; American Society of Agronomy-Soil Science Society of America: Madison, WI, USA, 1986; pp. 635–662. ISBN 0-89118-088-5. [Google Scholar]
- Richards, L.A. A Pressure-membrane Extraction Apparatus for Soil Solution. Soil Sci. 1941, 51, 377–386. [Google Scholar] [CrossRef]
- Gülser, C.; Ekberli, I.; Candemir, F. Spatial variability of soil physical properties in a cultivated field. Eurasian Soil Sci. 2016, 5, 192–200. [Google Scholar] [CrossRef][Green Version]
- Gunarathna, M.H.J.P.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.K.N. Machine Learning Approaches to Develop Pedotransfer Functions for Tropical Sri Lankan Soils. Water 2019, 11, 1940. [Google Scholar] [CrossRef]
- Myeni, L.; Mdlambuzi, T.; Paterson, D.G.; De Nysschen, G.; Moeletsi, M.E. Development and Evaluation of Pedotransfer Functions to Estimate Soil Moisture Content at Field Capacity and Permanent Wilting Point for South African Soils. Water 2021, 13, 2639. [Google Scholar] [CrossRef]
- Schindler, U.; Müller, L. Simplifying the evaporation method for quantifying soil hydraulic properties. J. Plant Nutr. Soil Sci. 2006, 169, 623–629. [Google Scholar] [CrossRef]
- Kutílek, M.; Nielsen, D.R. Soil Hydrology; Catena Verlag: Cremlingen, Germany, 1994. [Google Scholar]
- Vásquez-Nogal, I.; Hernández-Mendoza, C.E.; Cárdenas-Robles, A.I.; Rojas-González, E. Estimating the Soil-Water Retention Curve of Arsenic-Contaminated Soil by Fitting Fuentes’ Model and Their Comparison with the Filter Paper Method. Appl. Sci. 2022, 12, 7793. [Google Scholar] [CrossRef]
- Spasić, M.; Vacek, O.; Vejvodová, K.; Tejnecký, V.; Polák, F.; Borůvka, L.; Drábek, O. Determination of physical properties of undisturbed soil samples according to V. Novák. MethodsX 2023, 10, 102133. [Google Scholar] [CrossRef]
- Drbal, J. Practicum in Soil Amelioration Pedology, 1st ed.; State Pedagogical Publishing House: Prague, Czech Republic, 1971. (In Czech) [Google Scholar]
- Vopravil, J.; Formánek, P.; Khel, T. Comparison of the physical properties of soils belonging to different reference soil groups. Soil Water Res. 2021, 16, 29–38. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Nemes, A.; Roberts, R.T.; Rawls, W.J.; Pachepsky, Y.A.; van Genuchten, M.T. Software to estimate −33 and −1500 kPa soil water retention using the non-parametric k-Nearest Neighbor technique. Version 1.00.02. Environ. Model. Softw. 2008, 23, 254–255. [Google Scholar] [CrossRef]
- Miháliková, M.; Özyazici, M.; Dengiz, O. Mapping Soil Water Retention on Agricultural Lands in Central and Eastern Parts of the Black Sea Region in Turkey. J. Irrig. Drain. Eng. 2016, 142, 05016008. [Google Scholar] [CrossRef]
- Tunçay, T.; Alaboz, P.; Dengiz, O.; Başkan, O. Application of regression kriging and machine learning methods to estimate soil moisture constants in a semi-arid terrestrial area. Comput. Electron. Agric. 2023, 212, 108–118. [Google Scholar] [CrossRef]
- Vlček, V.; Hybler, V. Verification of Appropriateness of Selected Pedotransfer Functions for the Basic Use in Agriculture of the Czech Republic. Acta Univ. Agric. Silvic. Mendel. Brun. 2015, 63, 178. [Google Scholar] [CrossRef]
- Haberle, J.; Duffková, R.; Raimanová, I.; Fučík, P.; Svoboda, P.; Lukas, V.; Kurešová, G. The 13C discrimination of crops identifies soil spatial variability related to water shortage vulnerability. Agronomy 2020, 10, 1691. [Google Scholar] [CrossRef]
- Barradas, J.M.; Matula, S.; Dolezal, F. A decision support system-fertigation simulator (DSS-FS) for design and optimization of sprinkler and drip irrigation systems. Comput. Electron. Agric. 2012, 86, 111–119. [Google Scholar] [CrossRef]
- Miháliková, M.; Matula, S.; Doležal, F. HYPRESCZ—Database of Soil Hydrophysical Properties in the Czech Republic. Soil Water Res. 2013, 8, 34–41. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- van Genuchten, M.V.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying Hydraulic Functions of Unsaturated Soils; EPA/600/2-91/065, R.S.; U.S. Environmental Protection Agency: Ada, OK, USA, 1991; Volume 83.
- Brežný, O. Relationships between soil moisture constants and mechanical-physical properties of soil. Sci. Work. Res. Inst. Irrig. Manag. Bratisl. 1970, 8, 53–80. (In Slovak) [Google Scholar]
- Patil, N.G.; Singh, S.K. Pedotransfer functions for estimating soil hydraulic properties: A review. Pedosphere 2016, 26, 417–430. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mojtahedi, F.F.; Azizi, S.; Mahdi, H.A.; Sujatha, E.R.; Ebid, A.M.; Aneke, F.I. Innovative overview of SWRC application in modeling geotechnical engineering problems. Designs 2022, 6, 69. [Google Scholar] [CrossRef]
- Pospíšilová, L.; Vlček, V.; Hybler, V.; Hábová, M.; Jandák, J. Standard analytical methods and evaluation criteria of soil physical, agrochemical, biological, and hygienic parameters. In Folia Universitatis Agriculturae et Silviculturae Mendelianae Brunensis; Mendelova univerzita v Brně: Brno-sever, Czech Republic, 2016; Volume 9. [Google Scholar]
- Marfo, D.T.; Datta, R.; Vranová, V.; Ekielski, A. Ecotone Dynamics and Stability from Soil Perspective: Forest-Agriculture Land Transition. Agriculture 2019, 9, 228. [Google Scholar] [CrossRef]
- Němeček, J.; Macků, J.; Vokoun, J.; Vavříček, D.; Novák, P. The Taxonomic Classification System of Soils in the Czech Republic; Czech University of Life Sciences Prague: Prague, Czech Republic, 2001; ISBN 80-238-8061-6. (In Czech) [Google Scholar]
- Sládková, J. Conversion of some soil types, subtypes, and varieties between the Taxonomic Classification System of Soils of the Czech Republic and the World Reference Base for Soil Resources. Soil Water Res. 2010, 5, 172–185. [Google Scholar] [CrossRef]
- Litschmann, T.; Doležal, P.; Hausvater, E. A New Approach to Evaluation of Moisture and Temperature Conditions in Potato Growing. In Půdní a Zemědělské Sucho. Sborník Abstraktů z Mezinárodní Konference; Rožnovský, J., Vopravil, J., Eds.; Výzkumný ústav meliorací a ochrany půdy: Kutná Hora, Czech Republic, 2016; pp. 582–592. ISBN 978-80-87361-55-9. [Google Scholar]
- Litschmann, T.; Rožnovský, J.; Salaš, P.; Burgová, J.; Lošák, M.; Vymyslický, T. Stanovení půdních hydrolimitů na písčitých půdách Hodonínska in situ. In Proceedings of the Sborník příspěvků z Conference Hospodaření s Vodou v Krajině, Třeboň, Czech Republic, 9–10 October 2020; pp. 10–17. [Google Scholar]
- Novák, P. Dried-up soils of the Czech Republic and their area assessment. In Proceedings of the Moisture Conditions of the Landscape: Collection of Peer-Reviewed Papers from an International Conference, Mikulov, Czech Republic, 4–5 April 2012; pp. 108–111, ISBN 978-80-86690-78-0. [Google Scholar]
- Haberle, J.; Svoboda, P.; Kohút, M.; Kurešová, G. The comparison of calculated and experimentally determined available water supply in the root zone of selected crops. In Proceedings of the Mendel and Bioclimatology International Conference, Brno, Czech Republic, 3–5 September 2014; Brzezina, J., Hálová, H., Litschmann, T., Rožnovský, J., Středa, T., Středová, H., Eds.; Mendel University in Brno: Brno, Czech Republic, 2016. 1st edition; 478p. ISBN 978-80-7509-397-4. [Google Scholar]
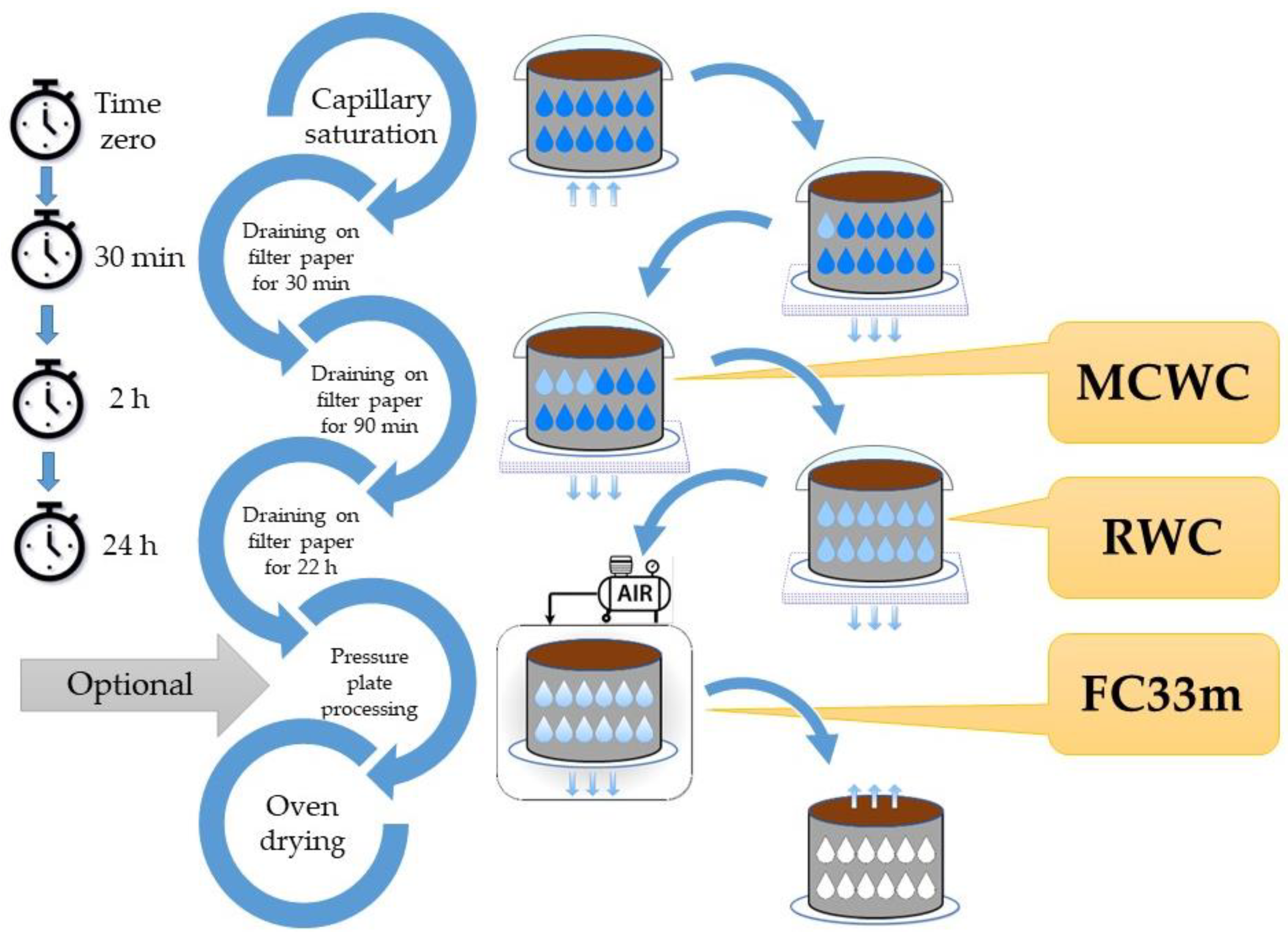

| Dataset One | Dataset Two | Dataset Three | |
|---|---|---|---|
| Origin of data | HYPRESCZ | Measured | HYPRESCZ |
| N. of data | 534 | 207 | 471 |
| Purpose of use | To correlate MCWC with FC5f, FC10f, FC33f and FC50f | To correlate MCWC and RWC with FC33m | To test historical PTFs |
| Availability within the dataset | |||
| MCWC | Yes | Yes | Not relevant |
| RWC | No | Yes | Not relevant |
| FC fitted for −5, −10, −33 and −50 kPa | Yes | No | Yes |
| FC measured for −33 kPa | No | Yes | No |
| FPSF | Not relevant | Not relevant | Yes |
| Variable | Mean | Minimum | Maximum | Lower Quartile | Upper Quartile | SD | CV |
|---|---|---|---|---|---|---|---|
| Clay (%) | 25.4 | 3.4 | 66.9 | 14.9 | 34.1 | 12.5 | 49.0 |
| Silt (%) | 39.3 | 4.2 | 73.0 | 29.3 | 51.2 | 14.6 | 37.1 |
| Sand (%) | 35.3 | 1.0 | 89.8 | 23.6 | 47.6 | 18.1 | 51.3 |
| BD (g/cm3) | 1.499 | 0.800 | 1.920 | 1.380 | 1.660 | 0.215 | 14.4 |
| OM (%) | 1.226 | 0.000 | 14.210 | 0.330 | 1.700 | 1.441 | 117.5 |
| Porosity | 0.4356 | 0.2558 | 0.6656 | 0.3822 | 0.4818 | 0.0773 | 17.8 |
| MCWC (cm3/cm3) | 0.3807 | 0.1370 | 0.6364 | 0.3290 | 0.4315 | 0.0836 | 22.0 |
| FC5f (cm3/cm3) | 0.3700 | 0.0818 | 0.6368 | 0.3166 | 0.4198 | 0.0883 | 23.9 |
| FC10f (cm3/cm3) | 0.3590 | 0.0733 | 0.6296 | 0.3029 | 0.4099 | 0.0886 | 24.7 |
| FC33f (cm3/cm3) | 0.3371 | 0.0548 | 0.6049 | 0.2852 | 0.3907 | 0.0877 | 26.0 |
| FC50f (cm3/cm3) | 0.3288 | 0.0489 | 0.6047 | 0.2738 | 0.3814 | 0.0873 | 26.6 |
| Variable | Mean | Minimum | Maximum | Lower Quartile | Upper Quartile | SD | CV |
|---|---|---|---|---|---|---|---|
| Clay (%) | 18.1 | 3.9 | 50.5 | 11.1 | 23.5 | 8.7 | 48.1 |
| Silt (%) | 39.6 | 4.7 | 70.1 | 27.3 | 51.5 | 15.1 | 38.3 |
| Sand (%) | 42.3 | 4.6 | 91.4 | 26.1 | 59.1 | 20.5 | 48.6 |
| BD (g/cm3) | 1.480 | 1.085 | 1.806 | 1.369 | 1.599 | 0.159 | 10.7 |
| OM (%) | 1.851 | 0.207 | 5.293 | 1.155 | 2.431 | 0.941 | 50.9 |
| SWC (cm3/cm3) | 0.4189 | 0.2330 | 0.6140 | 0.3814 | 0.4590 | 0.0560 | 13.4 |
| MCWC (cm3/cm3) | 0.3715 | 0.2063 | 0.5278 | 0.3339 | 0.4022 | 0.0526 | 14.2 |
| RWC (cm3/cm3) | 0.3525 | 0.1792 | 0.5113 | 0.3145 | 0.3850 | 0.0545 | 15.5 |
| FC33m (cm3/cm3) | 0.3119 | 0.1251 | 0.4805 | 0.2733 | 0.3547 | 0.0617 | 19.8 |
| WP1500m (cm3/cm3) | 0.1749 | 0.0499 | 0.4104 | 0.1265 | 0.2191 | 0.0667 | 38.1 |
| Variable | Mean | Minimum | Maximum | Lower Quartile | Upper Quartile | SD | CV |
|---|---|---|---|---|---|---|---|
| Clay (%) | 15.8 | 0.0 | 42.8 | 8.5 | 19.8 | 10.4 | 65.5 |
| Silt (%) | 29.4 | 1.5 | 70.6 | 16.8 | 40.2 | 15.7 | 53.4 |
| Sand (%) | 54.7 | 3.6 | 98.0 | 37.3 | 71.2 | 23.0 | 42.0 |
| FPSF (%) | 27.2 | 0.4 | 66.0 | 16.8 | 36.2 | 14.1 | 51.9 |
| BD (g/cm3) | 1.504 | 0.991 | 1.870 | 1.400 | 1.620 | 0.161 | 10.7 |
| OM (%) | 1.427 | 0.069 | 12.723 | 0.414 | 2.300 | 1.372 | 96.1 |
| SWC (cm3/cm3) | 0.4019 | 0.2530 | 0.5914 | 0.3631 | 0.4340 | 0.0578 | 14.4 |
| FC33f (cm3/cm3) | 0.2661 | 0.0567 | 0.4537 | 0.2164 | 0.3242 | 7.94 | 29.8 |
| WP1500f (cm3/cm3) | 0.1513 | 0.0157 | 0.3472 | 0.0996 | 0.1956 | 6.82 | 45.1 |
| Correlated Soil Moisture Constants | N | RMSE | MAE | R | R2 | |
|---|---|---|---|---|---|---|
| MCWC | FC5f | 534 | 0.027 | 0.020 | 0.961 | 0.923 |
| FC10f | 534 | 0.033 | 0.026 | 0.958 | 0.917 | |
| FC33f | 534 | 0.053 | 0.045 | 0.937 | 0.878 | |
| FC50f | 534 | 0.062 | 0.052 | 0.922 | 0.850 | |
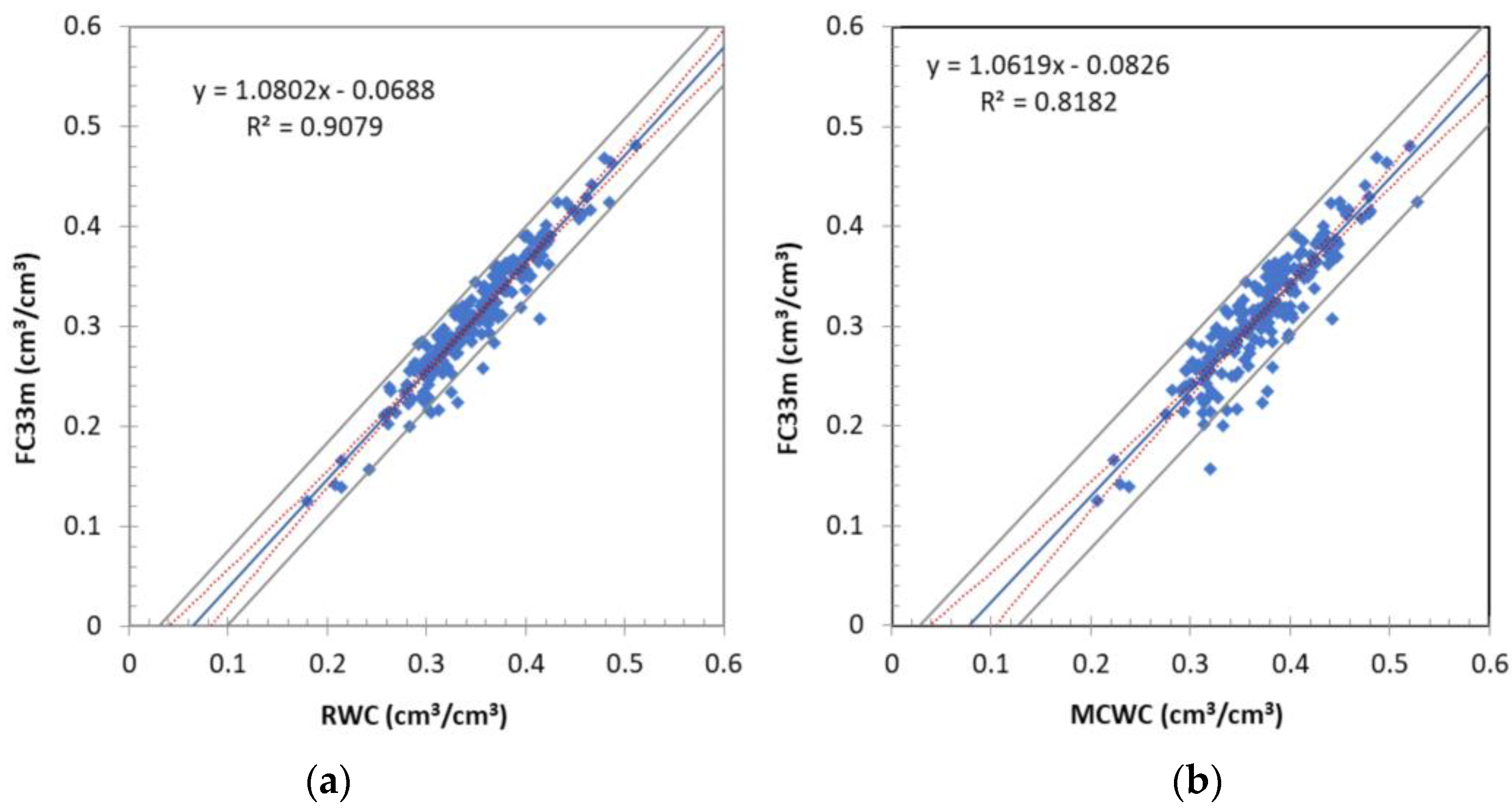
| FC33m | RWC | 207 | 0.045 | 0.041 | 0.953 | 0.908 |
| MCWC | 207 | 0.065 | 0.060 | 0.905 | 0.818 | |
| FC33f | FC by Brežný | 471 | 0.065 | 0.048 | 0.669 | 0.447 |
| FC by Váša | 471 | 0.067 | 0.050 | 0.673 | 0.453 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almaz, C.; Miháliková, M.; Báťková, K.; Vopravil, J.; Matula, S.; Khel, T.; Kara, R.S. Simple and Cost-Effective Method for Reliable Indirect Determination of Field Capacity. Hydrology 2023, 10, 202. https://doi.org/10.3390/hydrology10100202
Almaz C, Miháliková M, Báťková K, Vopravil J, Matula S, Khel T, Kara RS. Simple and Cost-Effective Method for Reliable Indirect Determination of Field Capacity. Hydrology. 2023; 10(10):202. https://doi.org/10.3390/hydrology10100202
Chicago/Turabian StyleAlmaz, Cansu, Markéta Miháliková, Kamila Báťková, Jan Vopravil, Svatopluk Matula, Tomáš Khel, and Recep Serdar Kara. 2023. "Simple and Cost-Effective Method for Reliable Indirect Determination of Field Capacity" Hydrology 10, no. 10: 202. https://doi.org/10.3390/hydrology10100202
APA StyleAlmaz, C., Miháliková, M., Báťková, K., Vopravil, J., Matula, S., Khel, T., & Kara, R. S. (2023). Simple and Cost-Effective Method for Reliable Indirect Determination of Field Capacity. Hydrology, 10(10), 202. https://doi.org/10.3390/hydrology10100202







