Abstract
A method was developed to integrate the truncated power-law distribution of solid volumetric fraction into the widely used Kozeny–Carman (KC)-type equations to assess the potential uncertainty of permeability. The focus was on the heterogeneity of porosity (or solid volumetric fraction) in the KC equation. The truncated power-law distribution simulates a heterogeneous scenario in which the solid volumetric fraction varies over different portions of porous media, which is treated as stationary, so its spatial mean can be replaced by the ensemble mean. The model was first compared with the experimental results of 44 samples from the literature and a recent model of KC equation modification that targets the coefficients in the equation. The effects of the fractal dimension of characteristic length of the solid volumetric fraction on the mean and standard deviation of permeability are calculated and discussed. The comparison demonstrates that the heterogeneous solid volumetric fraction can have similar effects as adjusting the empirical constant in the KC equation. A narrow range smaller than mean ± standard deviation from the model agreed with the experimental data well. Incorporating the truncated power-law distribution into the classical KC model predicts a high mean permeability and uncertainty. Both the mean and standard deviation of the permeability decrease with an increasing fractal dimension.
1. Introduction
The permeability of porous media is a crucial parameter to understand fluid flow in various materials. A widely used equation to predict the permeability of porous media was developed by Kozeny and later modified by Carman, which is now the Kozeny–Carman (KC) equation [1,2,3] for estimating the permeability of porous materials. The KC equation or its variants have been used for many different types of porous materials [4,5,6,7,8,9,10,11,12,13,14,15,16].
The KC equation is a semi-empirical formula involving potentially large uncertainty [10,17,18]. Due to its significance in science and engineering fields, from industrial manufacturing processes to groundwater flows, many semi-empirical corrections and extensions of the KC equation have been developed [12,19,20,21,22,23,24] to improve the prediction of the permeability and/or hydraulic conductivity of various porous materials.
Rodríguez et al. [25] investigated the permeability–porosity relationship for glass and fiber mats. The experimental data were fitted by the Kozeny–Carman equation with two parameters of the Kozeny constant and the exponent of the porosity. Khabbazi et al. [26] employed a lattice Boltzmann (LB) modeling approach to compute the permeability of two periodic porous structures of cylinders and spheres and identified functional forms of the Kozeny–Carman constant by regression analysis. They demonstrated that the algebraic function for the Kozeny–Carman constant produced the most accurate estimation of the KC porosity–permeability relationship. Nomura et al. [27] illustrated that the specific surface area could be derived from the semilog–sigmoid function of particle size distribution. The modified KC equation was then extended in terms of uniformity and sorting coefficients for its use in engineering applications. Safari et al. [28] developed a mathematical equation to modify the porosity–permeability relationship in rocks with ellipsoidal grains and validated it by pore-scale modeling. The results demonstrated that deviations in the sphericity of the grains increased the permeability.
Fractal geometry theory has been used to study physical properties of disordered porous materials in various areas of science and engineering applications [29,30,31,32,33,34,35,36,37]. Bayles et al. [6] applied fractal mathematics to develop a modified KC equation to predict permeability from particle size distribution alone and brought new insight into the dependence of permeability on porosity and tortuosity. Costa [10] applied the classical KC equation and the assumption of fractal pore space geometry to develop the permeability–porosity equation, which contained the two fitting parameters of a Kozeny coefficient and a fractal exponent. Xu and Yu [38] improved the classical KC equation according to the two-dimensional fractal capillary bundle model. The proposed equation was expressed as a function of porosity, fractal dimensions, and maximum pore size, and was found to be more closely related to the microstructures (porosity, maximum pore size, and fractal dimensions) compared to those obtained from the original conventional models. Yu et al. [39] derived the specific surface areas of fractal porous media in two and three dimensions in relation to the fractal dimensions and fundamental microstructural parameters. Xiao et al. [40] developed a fractal solution for the KC constant and the permeability of fibrous porous media and verified the model with the analytical solution, numerical simulation, and experimental data found in the literature. The developed fractal model explicitly related the permeability and the KC constant to the microstructural parameters of the fibrous porous media.
In summary, the KC equation has been widely used to estimate porous media permeability, and many modifications/extensions have been developed for various porous materials. However, effective practical applications of the equation require accurate measurements of the specific surface area, which involve high uncertainty. Many other previous studies mostly focused on the quantification and modification of empirical constants embedded in the KC model, focusing on the fact that the KC constant is not actually a constant but a varying function of microstructural properties. Numerous previous studies of fractal models introduced and applied the fractal dimensions of various porous media properties [41]. The fractal dimensions commonly used in characterizing porous media include those of pore surface [42], pore volume [43], pore tortuosity [44], void [45], fracture surface [46], crack [47], and particle distribution [48], among others. Since porosity is the predominant factor in estimating porous media permeability in many practical applications according to the KC model and its variants, it is logical to investigate the effects of uncertainty related to porosity. As discussed, previous studies treated various variables as fractals, including pore volume, tortuosity, and particle distribution, among others. Because the porosity is complementary to the solid volumetric fraction, as the summation of them is equal to one, the main objective of this study was to investigate the direct impact of the fractal feature of the solid volumetric fraction on porous media permeability.
In the present study, a new approach was developed to treat the total solid volumetric fraction of porous media as a truncated power-law distribution, which was then combined with the KC equation to examine the potential uncertainty in the permeability prediction. While it is natural to assume that the permeability of porous media is related to the porosity, it is not easy to develop the appropriate relationship, since this would require an extensive knowledge of the spatial arrangement of the pore channels and their size distribution in porous media. Therefore, the focus of this study was on the uncertainty from the portion in the KC model that is related to the porosity (or solid volumetric fraction). This type of heterogeneous spatial distribution of the solid volumetric fraction simulates the scenario in which, in part of the porous media, the solid volumetric fraction is higher or lower than the other locations. The porous media are treated as stationary, so the mean of spatial heterogeneity can be replaced by the ensemble mean. The developed model was first compared with a few sets of experimental data and a recent model of KC equation modification that targets the coefficients in the KC-type equation from the literature. Then, the effects of fractal dimension and solid volumetric fraction on the mean and standard deviation are then determined and discussed.
2. Theory and Methods
In the KC model, the hydraulic diameter is related to the porosity and specific surface area, and the permeability is expressed as follows:
where K is the permeability, d is an effective diameter of solid particles, e is the porosity, c is the solid volumetric fraction (= 1 − e), and C is the empirically determined dimensionless constant representing both the flow path tortuosity and the shape factor, as well as many other factors. For random packed beds of spherical particles, the value of C could be approximated as C = 180. The model was originally developed mainly for isotropic, granular porous media of spherical particles at medium porosity and has been expanded and modified in applications to many other different types of porous materials.
Since the focus of the present study was on the effect of heterogeneous solid volumetric fraction (or porosity), a dimensionless permeability k can be defined from normalizing K in Equation (1) by d2/C:
Recently, Ye et al. [12] modified the C coefficient in the KC equation by also considering particle size distribution parameters. In particular, their model also included the uniformity coefficient Cu and the coefficient of curvature Cc to estimate the hydraulic conductivity Ks:
where ρ is the density of water, g is the gravitational acceleration, µ is the dynamic viscosity of water, C2 is an empirical fitting parameter, and d10 is the effective particle size, with 10% of particles being finer by weight. By matching Equation (3) to several experimental datasets compiled in their study, Ye et al. [12] suggested an optimal range for the fitting parameter values of C2 between 1500 and 2500.
The truncated power-law distribution is used to directly describe the spatial heterogeneity of the solid volumetric fraction in porous media. The focus was on the dimensionless permeability k that is only related to the solid volumetric fraction in the general KC equation of permeability. Even with similar particle size distribution statistics, such as Cu and Cc, the porosity (or solid volumetric fraction) can exhibit strong spatial heterogeneity. The effect of this type of heterogeneity on the uncertainty of permeability estimation was the main objective of this study. After the model was developed, we compared the model prediction with Equation (3) and five experimental datasets found from the literature. Ye et al. [12] concluded that by adjusting the fitting parameter C2, Equation (3) could reasonably match the experimental data. In general, there have been many studies to adjust the empirical coefficient in the KC-type models to match experimental results. The goal of this study was to investigate whether strong spatial heterogeneity of solid volumetric fraction represented by a truncated power-law distribution may affect the permeability prediction. In particular, the model was compared with that in Ye et al. [12] in relation to the same sets of experimental data.
With the heterogeneity being taken into account, the solid volumetric fraction c varies spatially and can be assumed to follow the following truncated power-law distribution [49,50,51]:
where ca is the maximum solid volumetric fraction, and D is the fractal dimension of characteristic length of the solid volumetric fraction. In this study, we approximated the solid volumetric fraction as a truncated power-law distribution in which the minimum solid volumetric fraction is c = ci in practical science and engineering problems, which means the range of the solid volumetric fraction in heterogeneous porous media could vary from ci to ca.
To develop analytical solutions of mean dimensionless permeability and its standard deviation, the following parameters related to the truncated power-law distribution parameters of solid volumetric fraction (i.e., D and ca/ci) are first defined in Equation (5) through (7) below. The sole purpose of first defining these parameters is to simplify the mathematical expressions of mean and standard deviation of dimensionless permeability in the subsequent derivations.
With the definition of the parameters in Equations (5)–(7), the probability density function of the truncated power-law distribution of the solid volumetric fraction c can be determined from Equation (4) as:
From the truncated power-law distribution in Equation (8) for the solid volumetric fraction, the mean solid volumetric fraction c* and the ratio of c* over ca in the heterogeneous porous media can then be integrated as, respectively:
The solid volumetric fraction range ratio ca/ci can then be iteratively determined from the constraint specified in Equation (10) with the given values of c*/ca and the fractal dimension D.
After determining the power-law distribution parameters ca/ci and ci, the variance and standard deviation sc of the solid volumetric fraction can be determined as follows, respectively:
In Equation (11), the subscript * denotes the mean operator.
When the truncated power-law distribution of c is given, the mean dimensionless permeability k* and the mean of k2, (k2)*, can be determined from integrating the truncated power-law distribution of the solid volumetric fraction as follows, respectively:
Substituting the expression of the KC equation in Equation (2) and the truncated power-law distribution of the solid volumetric fraction f(c) in Equation (8), integrating and simplifying them, one can obtain the following mean expressions of k* and (k2)*, respectively:
The variance of the dimensionless permeability k can then be determined by the following relationship:
After substituting the expressions in Equations (15) and (16) into Equation (17), one has the following variance s2 and standard deviation s of the dimensionless permeability, respectively:
where A and B in the above equations are related to the various truncated power-law distribution parameters as, respectively:
In the following section, the developed model in the present study is compared with five experimental datasets of saturated hydraulic conductivity Ks found in the literature. In a recent study, Ye et al. [12] compiled several datasets of Ks measurements of sand-gravel mixture, which were listed in their Table 2 [12]. We first compared the present model with these datasets and the modified KC model by Ye et al. [12]. The statistical criteria to quantitatively assess the goodness of fit with the experimental results include the bias (Bias), the root mean square error (RMSE), and the Nash–Sutcliffe model efficiency coefficient (NSE), defined as follows:
In Equations (22) through (24), Ksi and Ksei are the saturated hydraulic conductivity estimated by the model and the observed saturated hydraulic conductivity from experimental data point i with the given porosity, respectively; is the mean of the observed saturated hydraulic conductivity; and M is the total number of data points. The experimental datasets were extracted from Table 2 of Ye et al. [12].
3. Results and Discussion
The comparison with the saturated hydraulic conductivity experimental data that were compiled from five different sources by Ye et al. [12] in the literature is shown in Figure 1. The model results of Ye et al. [12] when the C2 values were 1000, 2000, 3000, and 4000 are also included in Figure 1, which was the same range of C2 in Ye et al. [12] in their trial-and-error process to determine the optimal C2 to best fit the experimental data. Overall, when C2 increased from 1000 to 4000, the modified KC model by Ye et al. [12] evolved from over-prediction to under-prediction, as seen from the scatterplots from Figure 1a–d. The mean saturated hydraulic conductivity by the present model also changed from over-prediction to under-prediction when C2 varied from 1000 to 4000.
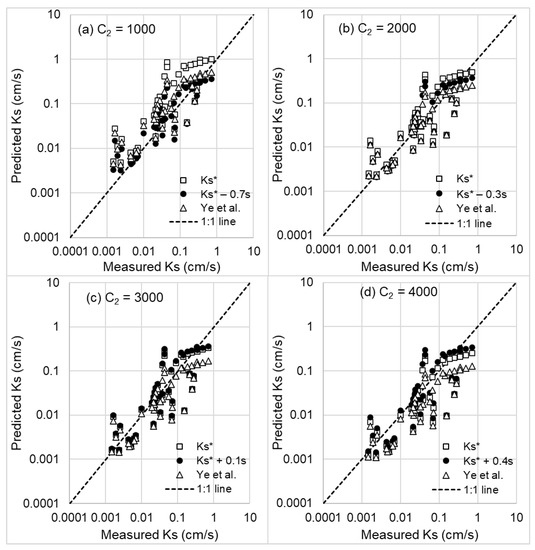
Figure 1.
Comparison with experimental saturated hydraulic conductivity Ks data compiled by Ye et al. [12] from 5 different sources (Zhu [52], Cui [53], Ren et al. [54], Huang et al. [55], and Ye et al. [12]) and listed in their Table 2. The range of C2 presented in (a–d) in this figure is the same as that tried in Ye et al. [12].
For a three-dimensional fractal system, the fractal dimension D is typically from 2 to 3, and the potential range of ca may vary from c* to 1. We used a D value of 2.5 and ca = 0.8 for comparison, as shown in Figure 1. The comparison of statistical measures between the modified KC model by Ye et al. [12] and the present model is shown in Table 1.

Table 1.
Comparison of statistical measures between the modified KC model in [12] and the present model.
Depending on the C2 value, the mean Ks from the truncated power-law distribution may either over-predict or under-predict the experimental results. When C2 is small, the mean Ks needs to be subtracted by a fraction of the standard deviation to best fit the experimental data. On the other hand, if C2 is large, a fraction of the standard deviation needs to be added to the mean Ks to best capture the variation of experimental data. Therefore, if the potential uncertainty due to the heterogeneous solid volumetric fraction is taken into account by adjusting the mean prediction from the present study by the potential uncertainty, the present model can better match the experimental data regardless of the values of C2. Experimental data have significant scatters, which highlight the uncertainty in estimating Ks of porous media. While adjusting the empirical correction factor in Ye et al. [12] can better describe experimental data to a certain extent, the uncertainty could still be very large. The truncated power-law distribution is intended for potential maximum uncertainty. As a result, the standard deviation can be larger than the mean, signifying its significant uncertainty extent.
While the comparison was particularly made against the fitting parameters of the KC model, using the same sets of experimental data, the conclusion should also hold in general cases that strong spatial heterogeneity of solid volumetric fraction could affect the permeability prediction. The uncertainty due to the spatial heterogeneity can also exert similar effects as adjusting empirical constants in the KC equation on predicting the permeability of porous media.
Figure 2 shows the potential range of concentration ca/ci in relation to the porosity at a few values of the fractal dimension D and maximum concentration ca. While there are two parameters in the truncated power-law distribution, the constraint requires D and ca/ci to be related to each other for any given porosity (or solid volumetric fraction). The required range of ca/ci increases dramatically as the porosity e increases, which is due to the required decrease in ci as e increases. Note that a large e value translates into a small c value, as they are simply related by c = 1 − e. If the mean c is small, then the minimum c should be also small enough to bring the overall mean c down to the constrained small c value. For the effect on the dimensionless permeability k, this dramatically increased ca/ci also significantly increases its uncertainty, reflected by its standard deviation. A larger fractal dimension D indicates a narrower range of ca/ci. For a larger D value, the fractal system is more space-filled, which also means the potential range of solid volumetric fraction variability should also be smaller. On the other hand, a larger ca obviously allows a larger range for potential concentration variability, which requires ca/ci to be also larger, as seen in Figure 2.
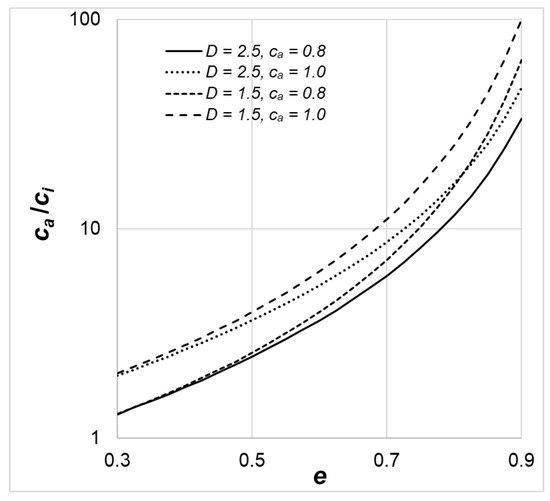
Figure 2.
The ratio of maximum solid volumetric fraction ca over minimum solid volumetric fraction ci (ca/ci) of the truncated power-law distribution in relation to the porosity and fractal parameters.
The influence of porosity on the dimensionless permeability, with a few selected values of the fractal parameters, is shown in Figure 3. When the heterogeneous solid volumetric fraction is incorporated into the widely used KC model, the mean prediction of dimensionless permeability is higher than that predicted by the deterministic KC model. The difference between the predicted mean dimensionless permeability and the deterministic prediction by the KC model increases quickly as the porosity e increases. With the truncated power-law distribution, the low solid volumetric fraction regions are clustered, which means the high porosity regions are also clusters. The KC model indicates that the permeability increases non-linearly but very quickly with increasing porosity; therefore, on the high end of porosity (or the low end of solid volumetric fraction), the dimensionless permeability is significantly higher than that predicted by the deterministic KC equation. For a higher ca and lower D, the mean dimensionless permeability is also higher, as seen in Figure 3.
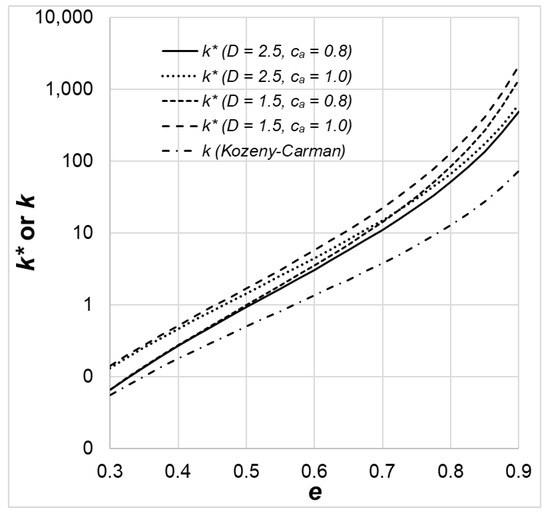
Figure 3.
The mean dimensionless permeability k* versus the porosity e for a few selected values of the fractal parameters. The k result from the KC equation is also plotted for comparison.
The corresponding results of k standard deviation are shown in Figure 4 under the otherwise same conditions as those in Figure 3. The variation of the standard deviation exhibited a similar trend as the dimensionless permeability. The standard deviation also increased significantly with the increase in the porosity. This trend was also reflected by the increase in ca/ci with an increasing e, which meant increasing uncertainty near the high range of porosity. This phenomenon is a general feature of a power-law distribution, in which most of the heterogeneous solid volumetric fraction clusters near its low range. The fractal dimension D also impacts the uncertainty of the dimensionless permeability k. For a smaller fractal dimension D, the heterogeneous solid volumetric fraction is less space-filled, and the range of potential concentration variation is higher, which translates into a lower permeability uncertainty (standard deviation). On the other hand, a high ca means a larger range of solid volumetric fraction, and in turn, indicates a higher permeability standard deviation, as seen in Figure 4.
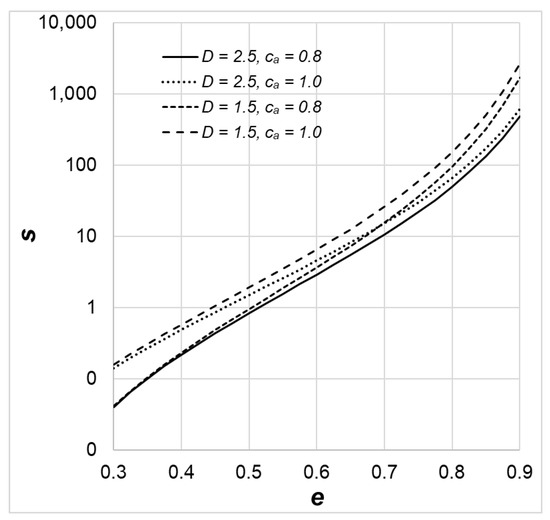
Figure 4.
The standard deviation of dimensionless permeability s as a function of the porosity e for a few selected values of the power-law distribution parameters.
The influence of the fractal dimension D on the dimensionless mean permeability is shown in Figure 5. The corresponding results of the deterministic dimensionless permeability from the classical KC equation are also plotted for comparison, although they did not change with the fractal dimension D (i.e., a horizontal line seen in the figure). The results show that the mean dimensionless permeability decreases with an increasing fractal dimension D. As discussed earlier, the solid volumetric fraction tends to cluster near the low end of its range for a smaller D, which favors a higher porosity in larger regions. Since the permeability increases dramatically with an increase in the porosity, this tendency of clustering near the low end of solid volumetric fraction also enhances the mean dimensionless permeability. In the higher mean porosity case (Figure 5b), the extent of the mean permeability increase with a decreasing fractal dimension D is more significant compared to the case of a lower mean porosity (Figure 5a).
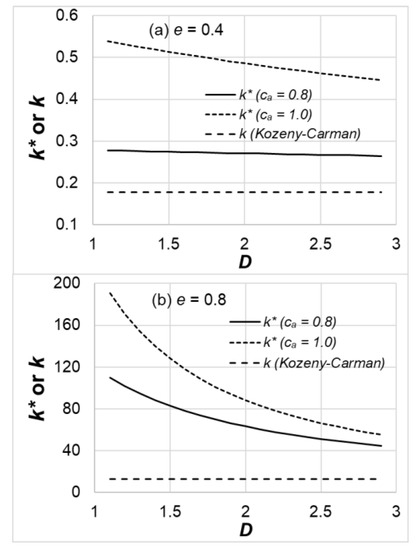
Figure 5.
The influence of fractal dimension D on the mean dimensionless permeability k* for (a) e = 0.4 and (b) e = 0.8. The k result from the KC equation, which is a horizontal line, is also plotted for comparison.
The impact of the fractal dimension D on the standard deviation of the dimensionless permeability is plotted in Figure 6. The standard deviation variation exhibited a similar trend as the mean dimensionless permeability. The standard deviation can be on the same order of magnitude as the mean dimensionless permeability itself, highlighting the significant impact of the heterogeneous solid volumetric fraction on the uncertainty of the dimensionless permeability prediction. Overall, the impact of the fractal dimension D was smaller than that of ca/ci on the dimensionless permeability and its associated standard deviation.
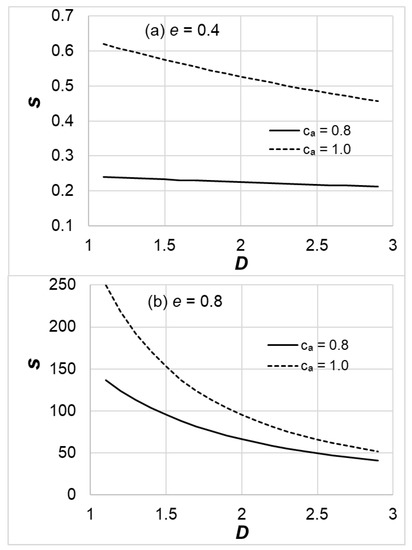
Figure 6.
The influence of the fractal dimension D on the standard deviation of dimensionless permeability s for (a) e = 0.4 and (b) e = 0.8.
In this study, the KC equation was used as a basic model in analyzing uncertainty in the predicted permeability due to the uncertainty in the required input solid volumetric fraction (or the porosity). The KC equation establishes a link between porous media properties and flow resistance in pore channels, which quantitatively expresses the permeability in terms of porosity (or solid volumetric fraction). It should be emphasized, however, that while the KC model has been widely used, it is less satisfactory for porous materials that are cemented or have irregular grain/pore shapes and sizes, as well as for clays [19,56]. The KC equation may also have issues in many practical applications due to the difficulty in determining either the specific surface area or the effective diameter [57]. Other more sophisticated models may perform better than the KC model under certain conditions [58]. No simple universal equations, however, can possibly exist to satisfactorily predict the permeability of all porous media encountered in science and engineering applications, due to the complexity and the large number of parameters involved [10]. It should be, therefore, noted that any limitations inherent in the underlying KC model also apply to the model developed in the present study. In addition, the specific focus in this study was only on the heterogeneity of the solid volumetric fraction. Other potential uncertainties, such as those related to the determination of the specific surface area [59,60,61], which are embedded in the KC model, also affect the predictive uncertainty of porous media permeability. A comprehensive investigation of other types of uncertainty is, however, beyond the scope of this study and warrants further studies in the future.
4. Conclusions
A new approach was developed to incorporate the truncated power-law distribution of the solid volumetric fraction of porous media into the widely used KC model to investigate the potential uncertainty in the permeability prediction of porous media. The truncated power-law distribution is used to describe the potential maximum heterogeneity of porous media. The equations of the mean permeability and its associated standard deviation were developed. The main conclusions can be summarized as follows:
- (1)
- Heterogeneous solid volumetric fraction can have similar effects as adjusting empirical constants embedded in the classical KC equation.
- (2)
- Incorporating the truncated power-law distribution into the classical KC model predicts a higher mean permeability than the deterministic KC equation.
- (3)
- Both the mean and standard deviation of the dimensionless permeability decrease as the fractal dimension D increases.
- (4)
- The increase in both the mean and standard deviation of dimensionless permeability with porosity is more significant when the fractal dimension D is smaller.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| A | parameter in Equation (20) | e | porosity |
| B | parameter in Equation (21) | g | gravitational acceleration (m s−2) |
| C | empirical constant in Equation (1) | K | permeability (m2) |
| C2 | empirical parameter in Equation (3) | Ks | hydraulic conductivity (m s−1 or cm s−1) |
| Cc | coefficient of curvature | k | dimensionless permeability |
| Cu | coefficient of uniformity | k* | mean dimensionless permeability |
| c | solid volumetric fraction (= 1 − e) | s | standard deviation of k |
| cm | maximum solid volumetric fraction | sc | standard deviation of c |
| ci | minimum solid volumetric fraction | T1, T2, T3, T4 | parameters in Equation (6) |
| c* | mean solid volumetric fraction | T5, T6, T7 | parameters in Equation (7) |
| D | fractal dimension | ||
| D1, D2, D3, D4, D5, D6 | parameters in Equation (5) | Greek symbols | |
| d | effective diameter of solid particles (m) | μ | viscosity of water (Pa s m−2) |
| d10 | effective particle size (m) | ρ | density of water (kg m−3) |
References
- Kozeny, J. Ueber kapillare Leitung des Wassers im Boden. Sitz. Akad. Wiss. Wien 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Carman, P.C. Permeability of saturated sands, soils and clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]
- Mcgregor, R.; Peters, R.H. The effect of rate of flow on rate of dyeing I—The diffusional boundary layer in dyeing. J. Soc. Dye. Colour. 1965, 81, 393–400. [Google Scholar] [CrossRef]
- Sangani, A.; Acrivos, A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiph. Flow 1982, 8, 193–206. [Google Scholar] [CrossRef]
- Bayles, G.A.; Klinzing, G.E.; Chiang, S.-H. Fractal mathematics applied to flow in porous systems. Part. Part. Syst. Charact. 1989, 6, 168–175. [Google Scholar] [CrossRef]
- Åström, B.T.; Pipes, R.B.; Advani, S. On flow through aligned fiber beds and its application to composites processing. J. Compos. Mater. 1992, 26, 1351–1373. [Google Scholar] [CrossRef]
- Skartsis, L.; Khomami, B.; Kardos, J.L. Resin flow through fiber beds during composite manufacturing processes. Part II: Numerical and experimental studies of newtonian flow through ideal and actual fiber beds. Polym. Eng. Sci. 1992, 32, 231–239. [Google Scholar] [CrossRef]
- Le Gallo, Y.; Bildstein, O.; Brosse, E. Coupled reaction-flow modeling of diagenetic changes in reservoir permeability, porosity and mineral compositions. J. Hydrol. 1998, 209, 366–388. [Google Scholar] [CrossRef]
- Costa, A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2006, 33, L02318. [Google Scholar] [CrossRef]
- Chen, J.; Tong, H.; Yuan, J.; Fang, Y.; Gu, R. Permeability prediction model modified on Kozeny-Carman for building foundation of clay soil. Buildings 2022, 12, 1798. [Google Scholar] [CrossRef]
- Ye, Y.; Xu, Z.; Zhu, G.; Cao, C. A modification of the Kozeny–Carman equation based on soil particle size distribution. Arab. J. Geosci. 2022, 15, 1079. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny–Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Szabó, N.P.; Kormos, K.; Dobróka, M. Evaluation of hydraulic conductivity in shallow groundwater formations: A comparative study of the Csókás’ and Kozeny–Carman model. Acta Geod. Geophys. 2015, 50, 461–477. [Google Scholar] [CrossRef]
- Zheng, W.; Tannant, D.D. Improved estimate of the effective diameter for use in the Kozeny–Carman equation for permeability prediction. Géotech. Lett. 2017, 7, 1–5. [Google Scholar] [CrossRef]
- Yan, G.; Shi, H.; Ma, Y.; Scheuermann, A.; Li, L. Intrinsic permeabilities of transparent soil under various aqueous environmental conditions. Géotech. Lett. 2022, 12, 225–231. [Google Scholar] [CrossRef]
- Davies, L.; Dollimore, D. Theoretical and experimental values for the parameter k of the Kozeny-Carman equation, as applied to sedimenting suspensions. J. Phys. D Appl. Phys. 1980, 13, 2013–2020. [Google Scholar] [CrossRef]
- Behrang, A.; Mohammadmoradi, P.; Taheri, S.; Kantzas, A. A theoretical study on the permeability of tight media; effects of slippage and condensation. Fuel 2016, 181, 610–617. [Google Scholar] [CrossRef]
- Panda, M.; Lake, W. Estimation of single-phase permeability from parameters of particle-size distribution. AAPG (Am. Assoc. Pet.Geol.) Bull. 1994, 78, 1028–1039. [Google Scholar]
- Yazdchi, Y.; Srivastava, S.; Luding, S. On the validity of the Carman-Kozeny equation in random fibrous media. In Proceedings of the 2nd International Conference on Particle-Based Methods—Fundamentals and Applications (Particles), Barcelona, Spain, 26–28 October 2011; pp. 264–273. [Google Scholar]
- Liu, Y.; Jeng, D.-S. Pore scale study of the influence of particle geometry on soil permeability. Adv. Water Resour. 2019, 129, 232–249. [Google Scholar] [CrossRef]
- Schulz, R.; Ray, N.; Zech, S.; Rupp, A.; Knabner, P. Beyond Kozeny–Carman: Predicting the permeability in porous media. Transp. Porous Media 2019, 130, 487–512. [Google Scholar] [CrossRef]
- Cui, X.; Zhu, C.; Hu, M.; Wang, R.; Liu, H. Permeability of porous media in coral reefs. Bull. Eng. Geol. Environ. 2021, 80, 5111–5126. [Google Scholar] [CrossRef]
- Yan, G.; Ma, Y.; Scheuermann, A.; Li, L. The hydraulic properties of aquabeads considering Forchheimer flow and local heterogeneity. Geotech. Test. J. 2022, 45, 10. [Google Scholar] [CrossRef]
- Rodriguez, E.; Giacomelli, F.; Vazquez, A. Permeability-porosity relationship in RTM for different fiberglass and natural reinforcements. J. Compos. Mater. 2004, 38, 259–268. [Google Scholar] [CrossRef]
- Khabbazi, A.E.; Ellis, J.; Bazylak, A. Developing a new form of the Kozeny–Carman parameter for structured porous media through lattice-Boltzmann modeling. Comput. Fluids 2013, 75, 35–41. [Google Scholar] [CrossRef]
- Nomura, S.; Yamamoto, Y.; Sakaguchi, H. Modified expression of Kozeny–Carman equation based on semilog–sigmoid function. Soils Found. 2018, 58, 1350–1357. [Google Scholar] [CrossRef]
- Safari, M.; Gholami, R.; Jami, M.; Ananthan, M.A.; Rahimi, A.; Khur, W.S. Developing a porosity-permeability relationship for ellipsoidal grains: A correction shape factor for Kozeny-Carman’s equation. J. Pet. Sci. Eng. 2021, 205, 108896. [Google Scholar] [CrossRef]
- Watanabe, K.; Takahashi, H. Fractal geometry characterization of geothermal reservoir fracture networks. J. Geophys. Res. Solid Earth 1995, 100, 521–528. [Google Scholar] [CrossRef]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Zhang, L.-Z. A fractal model for gas permeation through porous membranes. Int. J. Heat Mass Transf. 2008, 51, 5288–5295. [Google Scholar] [CrossRef]
- Andrade, J.; Oliveira, E.A.; Moreira, A.A.; Herrmann, H.J. Fracturing the optimal paths. Phys. Rev. Lett. 2009, 103, 225503. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Luo, L. Fractal characterization of spontaneous co-current imbibition in porous media. Energy Fuels 2010, 24, 1860–1867. [Google Scholar] [CrossRef]
- Li, K. More general capillary pressure and relative permeability models from fractal geometry. J. Contam. Hydrol. 2010, 111, 13–24. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.; Wang, S.; Luo, L. A diffusivity model for gas diffusion through fractal porous media. Chem. Eng. Sci. 2012, 68, 650–655. [Google Scholar] [CrossRef]
- Soto, M.A.; Chang, H.; van Genuchten, M. Fractal-based models for the unsaturated soil hydraulic functions. Geoderma 2017, 306, 144–151. [Google Scholar] [CrossRef]
- Zhu, J. Viscoplastic and pseudoplastic flows through fractal fractures. Int. J. Non-linear Mech. 2022, 145, 104107. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Yu, B.; Cai, J.; Zou, M. On the physical properties of apparent two-phase fractal porous media. Vadose Zone J. 2009, 8, 177–186. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and application of fractal theory in cement-based materials: A Review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Neimark, A. A new approach to the determination of the surface fractal dimension of porous solids. Phys. A Stat. Mech. Its Appl. 1992, 191, 258–262. [Google Scholar] [CrossRef]
- Zarnaghi, V.N.; Fouroghi-Asl, A.; Nourani, V.; Ma, H. On the pore structures of lightweight self-compacting concrete containing silica fume. Constr. Build. Mater. 2018, 193, 557–564. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Tyler, S.W. An explanation of scale-dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, J.; Huang, B. Fractal analysis of effect of air void on freeze–thaw resistance of concrete. Constr. Build. Mater. 2013, 47, 126–130. [Google Scholar] [CrossRef]
- Issa, M.A.; Issa, M.A.; Islam, M.S.; Chudnovsky, A. Fractal dimension—A measure of fracture roughness and toughness of concrete. Eng. Fract. Mech. 2003, 70, 125–137. [Google Scholar] [CrossRef]
- Shang, X.; Yang, J.; Wang, S.; Zhang, M. Fractal analysis of 2D and 3D mesocracks in recycled aggregate concrete using X-ray computed tomography images. J. Clean. Prod. 2021, 304, 127083. [Google Scholar] [CrossRef]
- Moskovits, M. The fractal nature of particle size distributions of grounds clinker. Cem. Concr. Res. 1990, 20, 499–505. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: San Francisco, CA, USA, 1982. [Google Scholar]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Zhu, C. Study on the Coarse-Grained Soil Permeability Characteristic. Master’s Thesis, Northwest Agriculture and Forestry University, Xianyang, China, 2005. [Google Scholar]
- Cui, R.F. Study on Permeability Characteristic of Non-Cohesive Soil and the Mechanism of Seepage-Failure. Master’s Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar]
- Ren, Y.B.; Wang, Y.; Yang, Q. Effects of particle size distribution and shape on permeability of calcareous sand. Rock Soil Mech. 2018, 39, 491–497. [Google Scholar] [CrossRef]
- Huang, B.; Guo, C.; Tang, Y.; Guo, J.; Cao, L. Experimental study on the permeability characteristic of fused quartz sand and mixed oil as a transparent soil. Water 2019, 11, 2514. [Google Scholar] [CrossRef]
- Erol, S.; Fowler, S.J.; Harcouët-Menou, V.; Laenen, B. An analytical model of porosity–permeability for porous and fractured media. Transp. Porous Media 2017, 120, 327–358. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Ghanbarian, B. Applications of critical path analysis to uniform grain packings with narrow conductance distributions: I. Single-phase permeability. Adv. Water Resour. 2020, 137, 103529. [Google Scholar] [CrossRef]
- Arnepalli, D.N.; Shanthakumar, S.; Rao, B.H.; Singh, D.N. Comparison of methods for determining specific-surface area of fine-grained soils. Geotech. Geol. Eng. 2007, 26, 121–132. [Google Scholar] [CrossRef]
- Yukselen, Y.; Kaya, A. Suitability of the methylene blue test for surface area, cation exchange capacity and swell potential determination of clayey soils. Eng. Geol. 2008, 102, 38–45. [Google Scholar] [CrossRef]
- Hong, B.; Li, X.; Wang, L.; Li, L.; Xue, Q.; Meng, J. Using the effective void ratio and specific surface area in the Kozeny–Carman equation to predict the hydraulic conductivity of loess. Water 2019, 12, 24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).