Abstract
Reducing uncertainty in design flood estimates is an essential part of flood risk planning and management. This study presents results from flood frequency estimates and associated uncertainties for five commonly used probability distribution functions, extreme value type 1 (EV1), generalized extreme value (GEV), generalized pareto distribution (GPD), log normal (LN) and log Pearson type 3 (LP3). The study was conducted using Monte Carlo simulation (MCS) and bootstrapping (BS) methods for the 10 river catchments in eastern Australia. The parameters were estimated by applying the method of moments (for LP3, LN, and EV1) and L-moments (for GEV and GPD). Three-parameter distributions (e.g., LP3, GEV, and GPD) demonstrate a consistent estimation of confidence interval (CI), whereas two-parameter distributions show biased estimation. The results of this study also highlight the difficulty in flood frequency analysis, e.g., different probability distributions perform quite differently even in a smaller geographical area.
1. Introduction
Flooding is a common natural disaster that causes loss of human lives and livestock and damages crops and infrastructure. It also causes disruption to transportation routes and other essential services and increases river erosion, resulting in increased sediment and nutrient loads in the flowing water. In Australia, the annual expenditure on infrastructure requiring flood estimation is $1 billion, while the mean annual flood damage is $0.4 billion [1]. Flood damage is remarkably serious in some years in Australia; for example, the widespread floods across Queensland in 2011 claimed over 30 lives and caused over $30 billion in damages [2]. To reduce the overall flood damage, an accurate flood risk assessment is essential, and in this regard, hydrologists use ‘design flood’, which is a flood discharge associated with an average recurrence interval (ARI) or return period [3].
Design flood is used in numerous engineering applications, such as planning and designing bridges, culverts, flood control levees, and drainage pipes. Indeed, reliable design flood estimation provides the basis for sustainable flood management. Among various approaches to design flood estimation, at-site flood frequency analysis is widely used to check the relative accuracy of other flood estimation methods, such as runoff routing and rational methods. At-site flood frequency analysis generally needs a long record of runoff. However, as the recorded streamflow data at most of the gauged stations are considerably shorter than the design ARI, the estimation of design flood needs extrapolation beyond the recorded data. Therefore, the choice of an inappropriate distribution function can lead to substantial bias in estimated floods; in particular, at larger ARIs, it may cause serious implications in practice, either from under- or over-estimation of design floods. For example, an underestimation increases the risk of failure of the infrastructure, while an overestimation increases the capital cost of the infrastructure unnecessarily.
Some of the frequently used probability distributions in flood frequency analysis include log normal (LN), extreme value type 1 (EV1), extreme value type 2 (EV2), log Pearson type 3 (LP3), generalized extreme value (GEV), Weibull, generalized Pareto distribution (GPD), and Wakeby [4,5,6,7]. For the purpose of parameter estimation, L-moments, LH-moments, method of moments (MoM), and maximum likelihood estimation (MLE) methods are generally adopted. The constraint of the MoM is that the higher moments (e.g., coefficient of skewness) are greatly affected by the extreme values (either smaller or larger) in the dataset; however, the L-moments are less impacted by these values [8]. LH-moments give more weight to the larger floods for achieving a relatively better fit to the upper tail of the distribution [9]. Martins and Stedinger [10] stated that MLE is often preferable to the MoM because of its robustness in estimating the distributional parameters by maximising the probability (likelihood) of the sample data [11]. Recently, the Bayesian inference method has become a popular alternative to MoM and MLE since, in this method, the distributional parameters can be described by a distribution function [11]. Recently, Chebana and Ouarda [12] developed a copula-based model to estimate non-stationary multivariate flood quantiles. Based on a survey of 54 agencies in 28 countries, Cunnane [5] noted that LN, P3, EV1, EV2, GEV, and LP3 distributions were recommended for general application in 8, 7, 10, 3, 2, and 7 countries, respectively. Moreover, in the 1970s, LP3 distribution was suggested as the most suitable distribution for New South Wales (NSW) [13] and Queensland (QLD) [14]. Based on the findings of these studies, Australian Rainfall and Runoff (ARR) 1987 (the national guide) suggested LP3 distribution with the MoM for parameter estimation for flood frequency analysis in Australia [15].
In addition to LP3 distribution, Vogel et al. [16] found GEV and Wakeby distributions to provide the best fit to the annual maximum (AM) flood data in winter rainfall-dominated parts of Australia. The suitability of the GEV distribution was further demonstrated by Haddad and Rahman [17] in a flood frequency analysis study using 18 Australian catchments.
Kuczera [18] proposed a flood frequency analysis method based on a Monte Carlo Bayesian framework for computing the expected probability distribution as well as quantile confidence limits for any flood frequency distribution using gauged glow data. He included six commonly used probability distributions in his approach, which is called the FLIKE software. This is the recommended software in the ARR 2019 for flood frequency analysis in Australia [19]. In FLIKE, uncertainty in flood frequency analysis is specified by 90% confidence intervals (CIs) for LP3, EV1, LN, GEV, and GPD distributions.
While there are many studies on flood frequency analysis, studies on uncertainty estimates are still limited in frequency estimates. In this study, uncertainty in flood frequency analysis in Australian catchments was evaluated by two different methods: Monte Carlo simulation technique (MCST) and bootstrapping (BS). In the MCST [20,21], the parameters of a given probability distribution are specified by probability distributions and a correlation matrix. The other approach, BS [22,23,24,25,26,27,28], can be either non-parametric (via resampling with replacement) or parametric (via fitting a parametric distribution to the observed sample and then randomly drawing new samples from this distribution) [29]. Non-parametric BS is applied here. Five different probability distributions are considered in this study, which are LP3, EV1, LN, GEV, and GPD. The parameters are estimated through the MoM (LP3, P3, LN, EV1) and L-moments (GEV and GPD). Finally, these results are compared with the ARR 2019 recommended software, FLIKE.
2. Study Area and Data
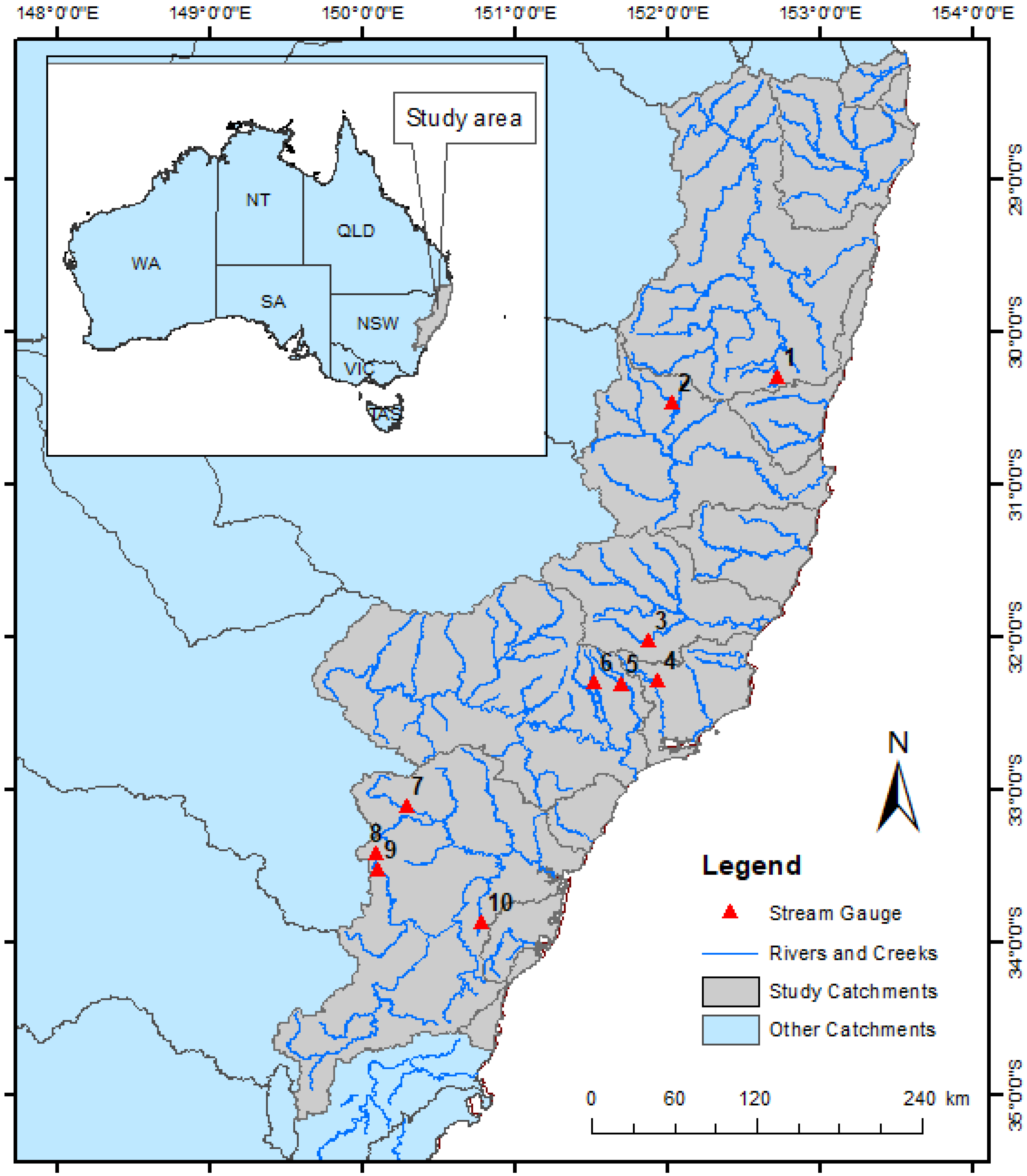
In this study, 10 stream-gauging stations were selected, which are located in New South Wales, Australia (Figure 1). While selecting the stations, a streamflow record length of at least 30 years was considered as a minimum sample size for reasonable estimates in flood frequency analysis [30]. Table 1 presents the details of the 10 stations, including the AM flood record lengths. The record length ranges from 36 to 80 years, with an average value of 51 years. All the sites have AM flood record lengths above the suggested threshold value. The catchment area of the selected stations ranges from 82 to 1010 km2, with an average value of 334.4 km2. The mean streamflow over the 10 stations used in this study varies from 52.09 m3/s (Station ID 212320) to 322.63 m3/s (Station ID 210022). The station ID 208006 has the highest recorded flow, at 2047.85 m3/s. Moreover, the skewness, CV, minimum, and median of flow for each of the 10 stations can be seen from Table 1. It is assumed that AM flood data are not associated with any measurement error, and the data satisfy the assumptions of independence and stationarity. The data is obtained from the Australian Rainfall Runoff Project 5: Regional Flood Methods national database [31]. The selected stations do not have any missing data over the length of the record. Therefore, we preferred the AM method over other approaches, e.g., partial duration series (PDS). This is supported by a study by Nagy et al. [32]. Moreover, all the ten-gauge stations used in this study are located in the East Coast region. It can be noted that Australia’s hydroclimate comprises eight natural resources management (NRM) regions. The East Coast region is defined on its western boundary by the Great Dividing Range and on its eastern boundary by the east Australian coastline [33]. The region contains 5 of the 10 largest urban areas in Australia and is home to around 40% of Australia’s population. The East Coast region ranges from the tropical climate in the north to the temperate climates of the southern New South Wales coast near Wollongong [34]. Most of the precipitation falls in the summer months across both the northern and southern subregions [34]. The difference between winter and summer precipitation is more pronounced in the north than in the south. This is due to the northern subregion having larger tropical influences, such as the monsoon, tropical cyclones, and tropical depressions, and receiving less precipitation associated with fronts during the cooler months [34]. Average annual precipitation is less in the northern subregion than in the southern subregion. Year-to-year precipitation variability in the East Coast region is related to El Niño, La Niña, and the Southern Annular Mode (SAM).
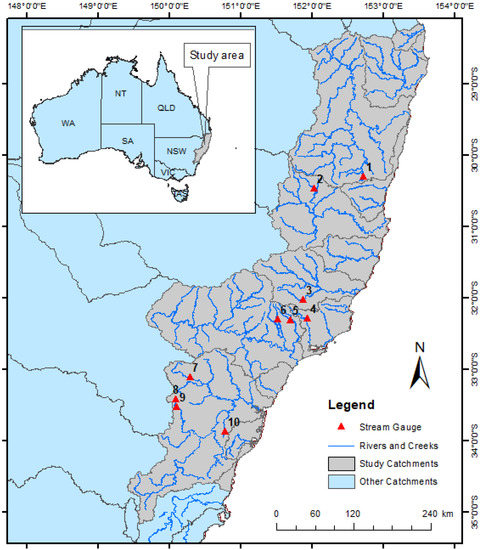
Figure 1.
Study area map showing the location of catchments used for flood frequency and uncertainty estimates.

Table 1.
Physical properties and data length for the selected stream-gauging stations * CV stands for co-efficient of variation.
3. Methodology
In this study, five different probability distributions were adopted: LP3, EV1, LN, GEV, and GPD. Six annual exceedance probabilities (AEPs) were considered, 1 in 2 (50% AEP), 1 in 5 (20% AEP), 1 in 10 (10% AEP), 1 in 20 (5% AEP), 1 in 50 (2% AEP), and 1 in 100 (1% AEP).
The parameters were estimated using the method of moments for the LP3, EV1, and LN distributions. The EV1 and LN have only two parameters; to estimate these, the mean () and standard deviation (σ) values of the sample data were used. The LP3, GEV, and GPD are three-parameter distributions. For LP3, the three parameters were estimated using the sample mean (), standard deviation (σ), and skewness (γ) of the logged AM flood series. For the GEV and GPD distributions, the shape (κ), scale (α), and location (ζ) parameters were estimated by the L-moments technique.
Bootstrapping (BS) and Monte Carlo simulation techniques (MCST) were applied to assess the uncertainty in flood frequency analysis. Finally, the results of these approaches were compared with the FLIKE software, recommended in the ARR 2019.
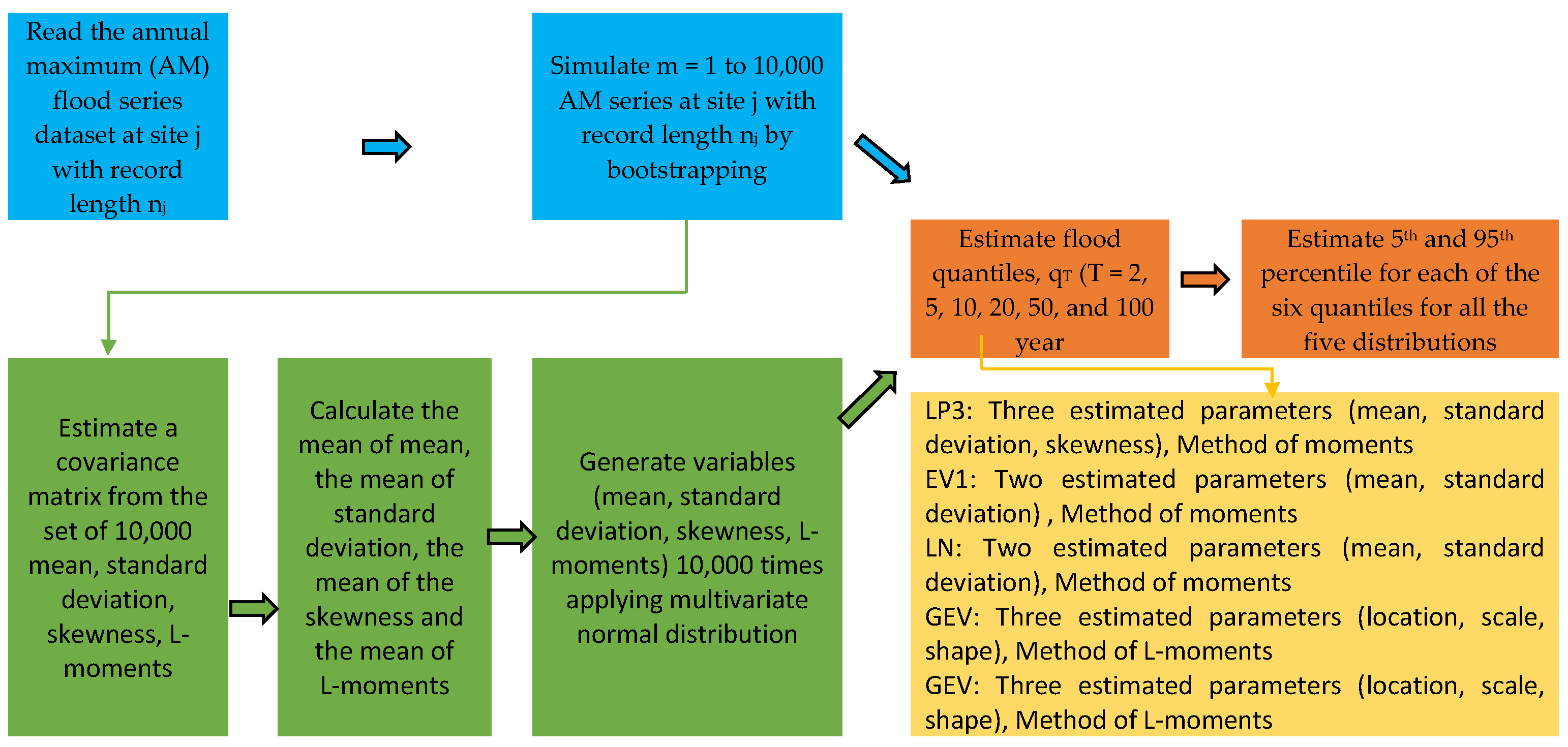
The adopted BS and MCST approaches are summarized below, and the procedure is illustrated in Figure 2:
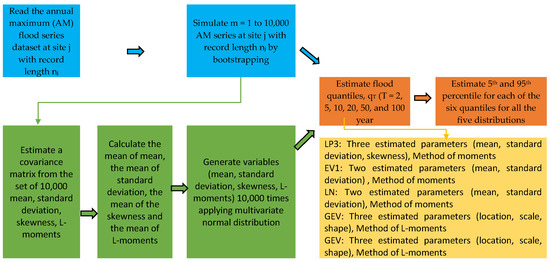
Figure 2.
Computation flowchart of estimating flood quantiles using bootstrapping and Monte Carlo methods.
Step 1. Read the AM flood series dataset at site j with record length nj;
Step 2. Simulate m = 1 to 10,000 AM series at site j with record length nj by bootstrapping (with replacement). For each of the simulated AM series, calculate qT (T = 2, 5, 10, 20, 50, and 100 years) using all five distributions, as presented below:
i. Log Pearson Type 3 (LP3): calculate mean (), standard deviation (σ), skewness of the log of the AM dataset (γ), and the frequency factor, Kp(γ).
where zp is the pth quantile of the standard normal distribution.
Estimate flood quantiles (qT) by
ii. Extreme Value Type 1 (EV1): calculate mean (), standard deviation (σ), and frequency factor (Kp)
Estimate flood quantiles (qT) using Equation (2).
iii. Log normal distribution (LN): calculate mean (), standard deviation (σ), and frequency factor (Kp) as the pth quantile of the standard normal distribution.
Estimate flood quantiles (qT) using Equation (2).
iv. Generalized extreme value distribution (GEV):
the parameters of the GEV distribution in terms of L-moments () are:
Estimate flood quantiles (qT)
v. Generalized Pareto distribution (GPD):
The parameters of the GPD, in terms of L moments (), are:
Estimate flood quantiles (qT)
Step 3. Estimate 5th and 95th percentile for each of the six quantiles from each of the five distributions (BS method).
Step 4. Estimate a covariance matrix from the set of 10,000 mean, standard deviation, skewness, and L-moment (for GEV and GPD only) values based on AM series obtained at Step 2.
Step 5. Calculate the mean of mean, the mean of standard deviation, the mean of the skewness, and the mean of L-moments (GEV and GPD only).
Step 6. Generate variables (mean, standard deviation, skewness, and L-moments (GEV and GPD only)) 10,000 times, applying the multivariate normal distribution.
Step 7. Estimate flood quantiles (qT) for each of the distributions.
Step 8. Estimate 5th and 95th percentile for each of the above quantiles.
We applied three different goodness-of-fit tests to evaluate the merits of the five distributions used in this study with respect to the recorded flood data. The goodness-of-fit tests are chi-square, Kolmogorov–Smirnov and Anderson–Darling test. Except for the chi-square test, the other two tests were non-parametric.
4. Results and Discussion
4.1. Uncertainty Estimates for LP3 Distribution
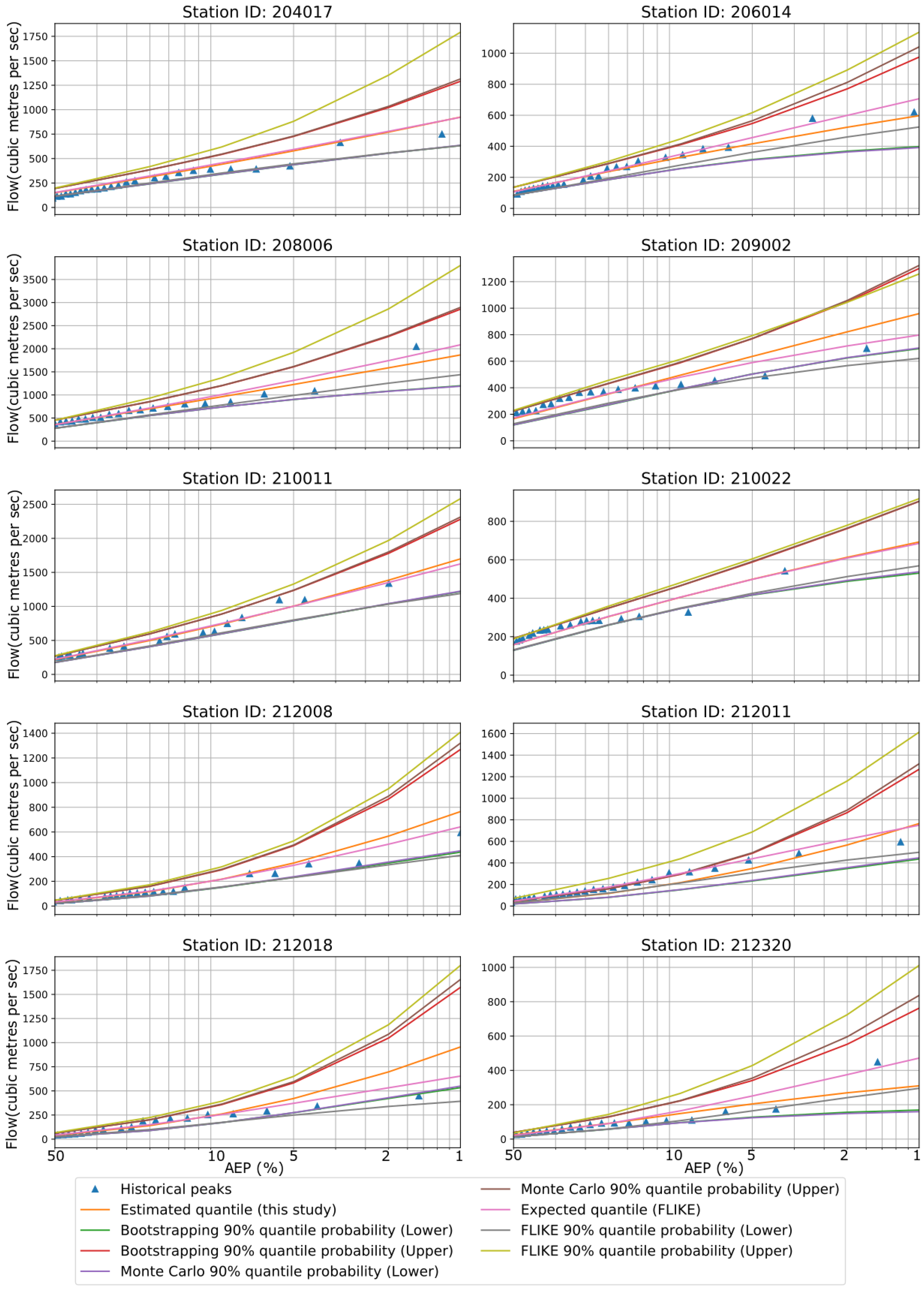
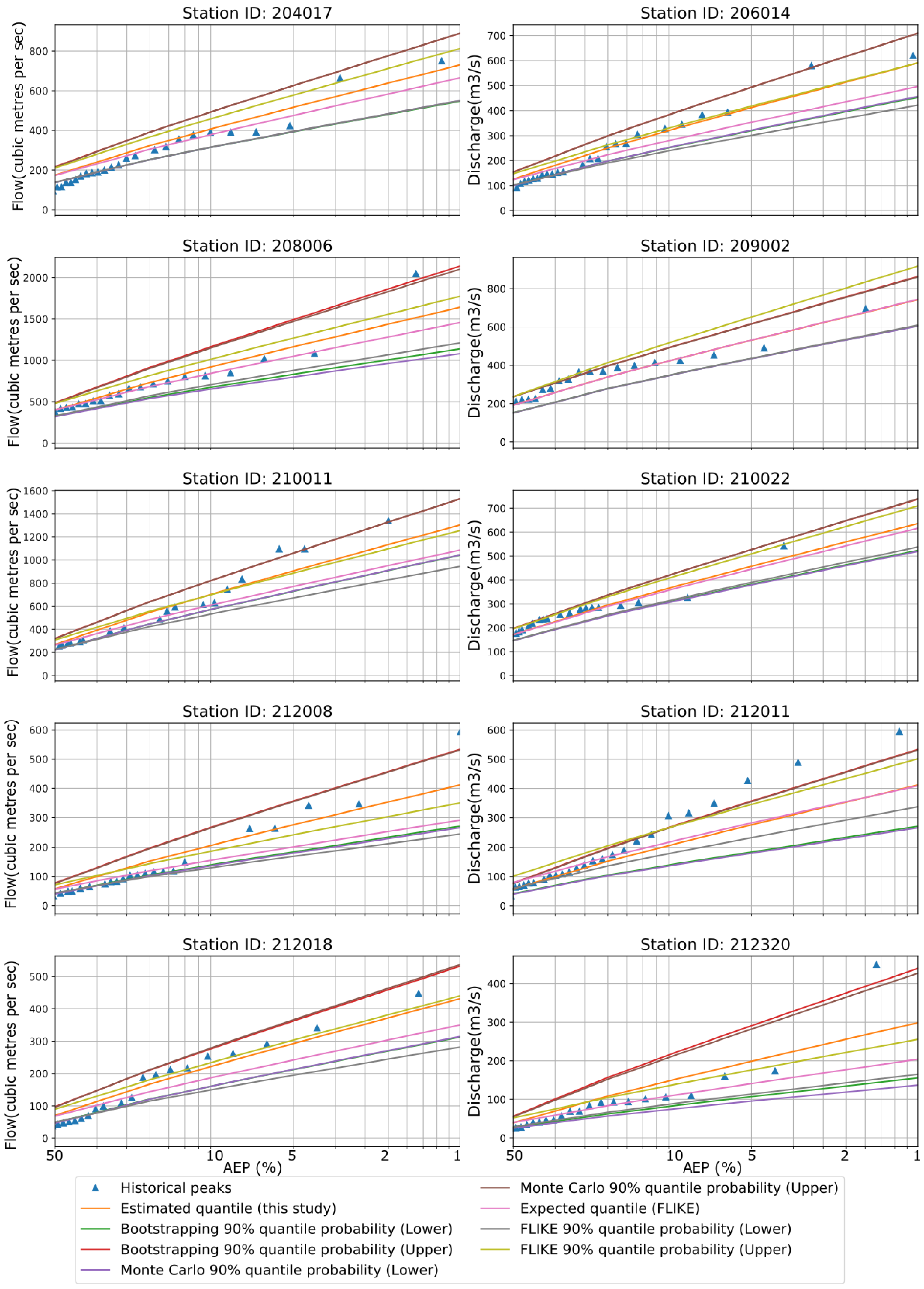
Figure 3 shows an example of flood quantile estimates along with the confidence intervals for the 10 stations. In FLIKE, both the likelihood functions and parameters were evaluated by the Bayesian approach; however, we have estimated the three parameters of the LP3 distribution by the MoM (without the Bayesian approach), and hence some differences in results are expected, as found in this study. Both the BS and MCST were found to result in very similar upper (95%) and lower (5%) confidence limits of flood quantiles for all six AEPs for the 10 stations. For LP3 distribution, the upper limit estimates by FLIKE were generally higher than those by the BS and MCST for most of the stations. In the case of the lower limit, very similar flood quantile estimates were found for most of the stations by all three approaches (BS, MCST, and FLIKE). The historical peaks were contained within the upper and lower bounds of the confidence interval. Both the Kolmogorov–Smirnov test and the Anderson–Darling tests confirmed that LP3 distributions were well fitted to the observed dataset for all 10 stations. LP3 estimated confidence bands from BS, MCST, and FLIKE could be reliably used for the 10 stations.
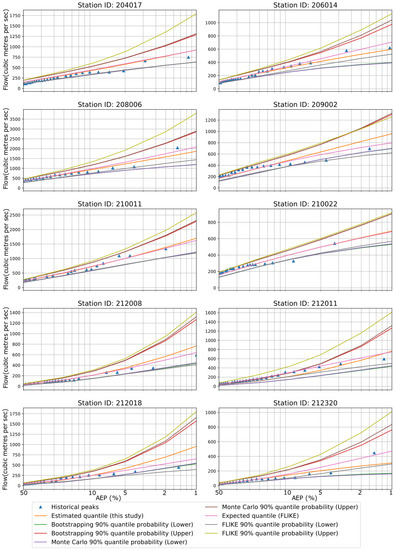
Figure 3.
Flood quantiles from FLIKE and LP3 distribution are presented over various AEPs for all 10 stations. Confidence intervals (CIs) are estimated by FLIKE, BS, and MCST methods. The blue triangle symbolizes historical peak.
4.2. Uncertainty Estimates for GEV Distribution
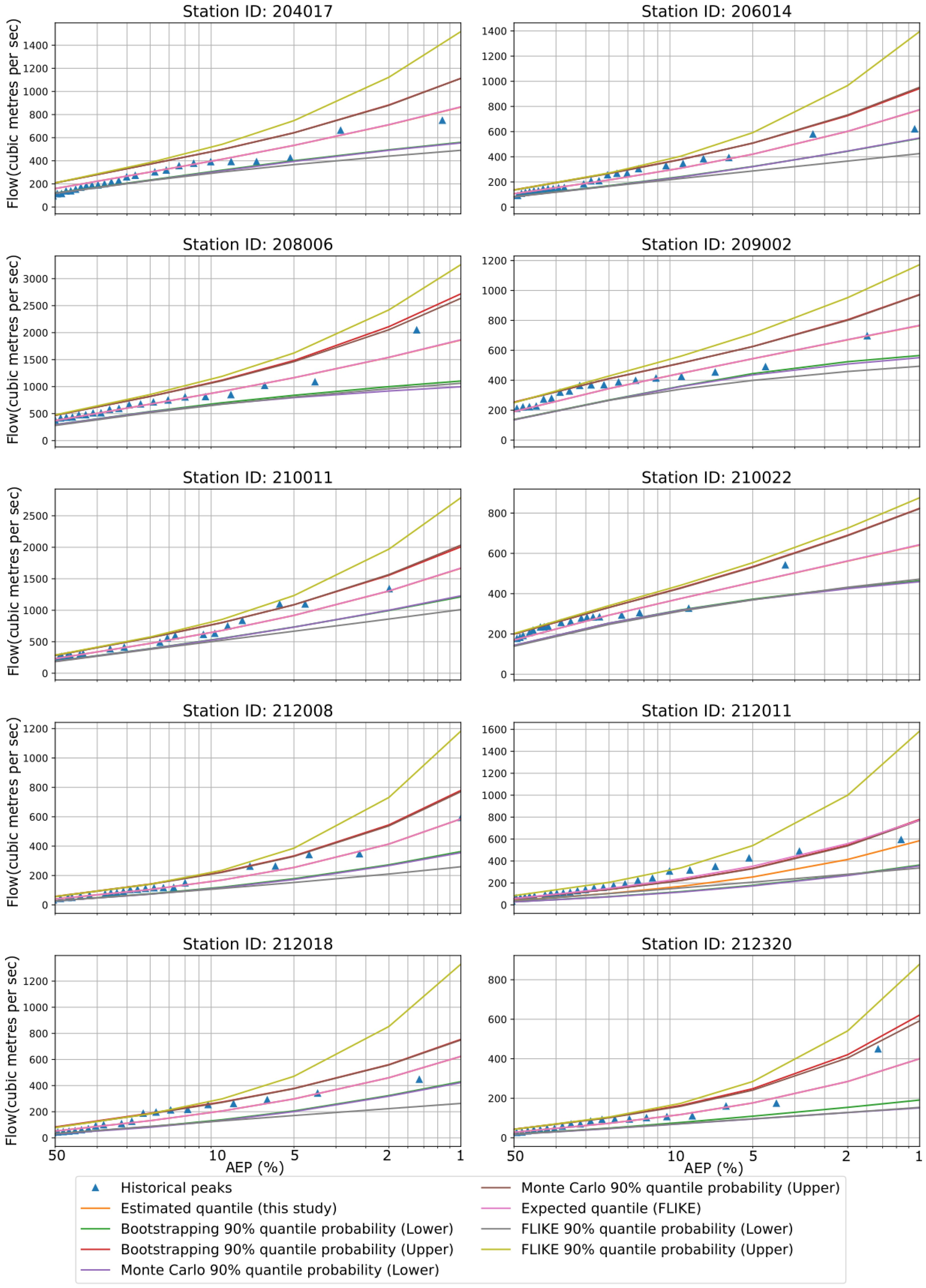
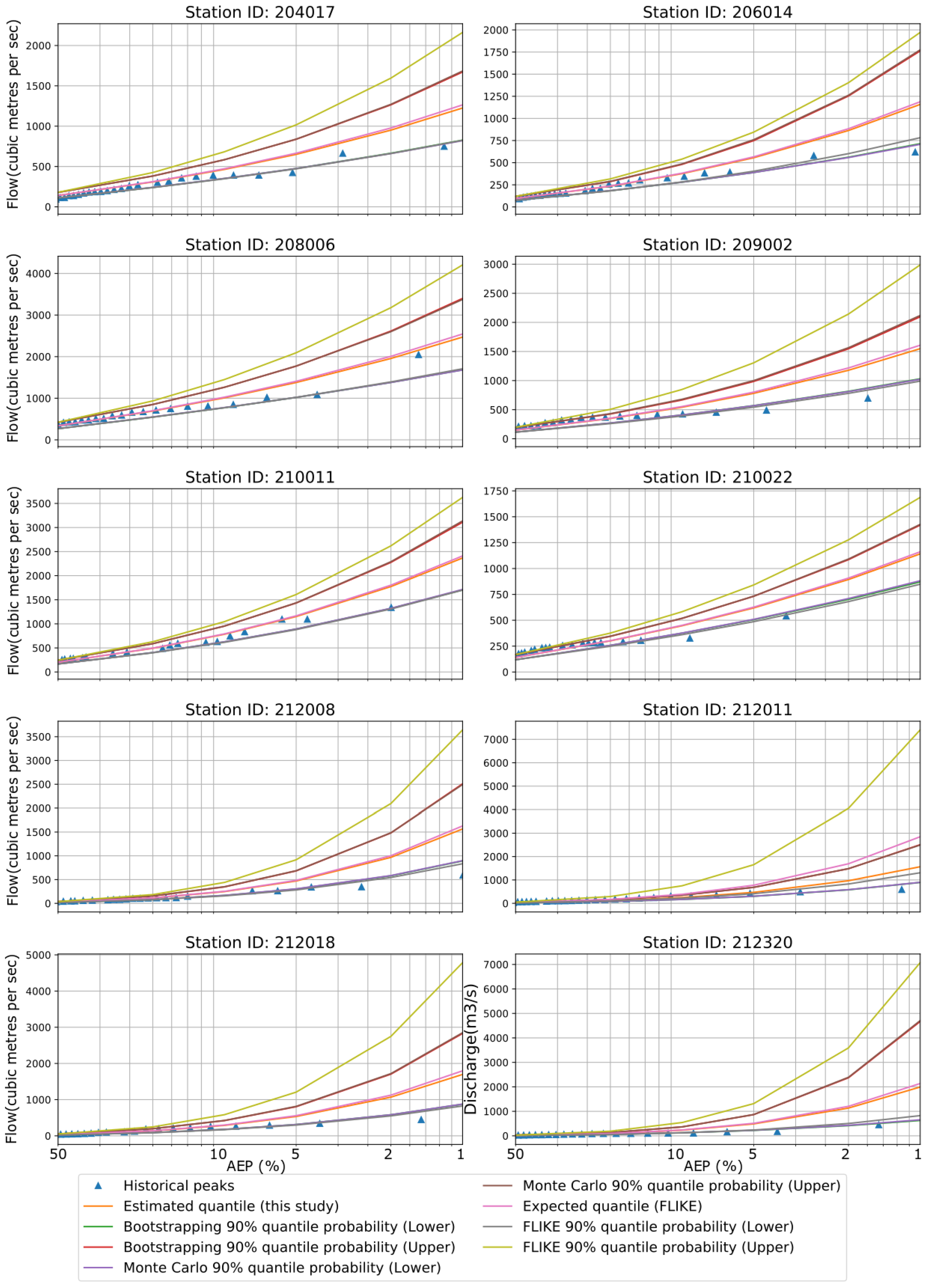
In the case of GEV distribution, the flood quantile estimates (expected values) using MCS and BS were found to be similar to FLIKE results for all 10 stations (Figure 4). However, the upper confidence limit estimates by the FLIKE were found to be generally higher compared with the BS and MCST methods. The lower limits by FLIKE were generally lower compared with the BS and MCST. Hence, the confidence intervals by FLIKE were wider than those of the BS and MCST for the GEV distribution. The historical peaks were within the confidence bounds, though GEV offered a slightly narrower confidence band than LP3. Both distributions, LP3 and GEV, have three parameters. We estimated parameters using the MoM and L-moments for LP3 and GEV, respectively. Both the Kolmogorov–Smirnov and Anderson–Darling tests confirmed that GEV distributions were well fitted to the observed dataset for all 10 stations.
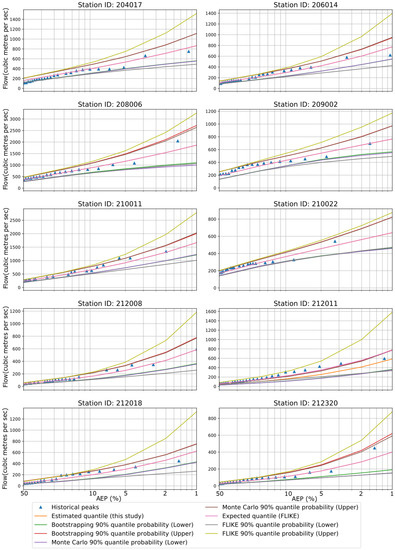
Figure 4.
Flood quantiles from FLIKE and GEV distribution are presented over various AEPs for all 10 stations. CIs are estimated by FLIKE, BS, and MCST. The blue triangle symbolizes historical peak.
4.3. Uncertainty Estimates for EV1 Distribution
For the EVI distribution, the quantile estimates (expected values) by our approach (MCS and BS) showed a wide variation from those of FLIKE for most of the stations (Figure 5). The CIs from FLIKE were found to be narrower than the estimation by the BS and MCST for most of the stations. Moreover, in EV1, the upper limit of FLIKE was lower than that from the BS and MCST for almost all 10 stations, though this was not the case for the LP3 and GEV distributions. For some stations, particularly station ID 212011, few historical peaks were located outside the confidence band. The goodness-of-fit tests, e.g., Kolmogorov–Smirnov and Anderson–Darling showed that EV1 distributions were well fitted to the observed dataset for all 10 stations. However, the skewness was not zero for the selected stations. Therefore, the two-parameter distributions e.g., EV1, may not be a good option.
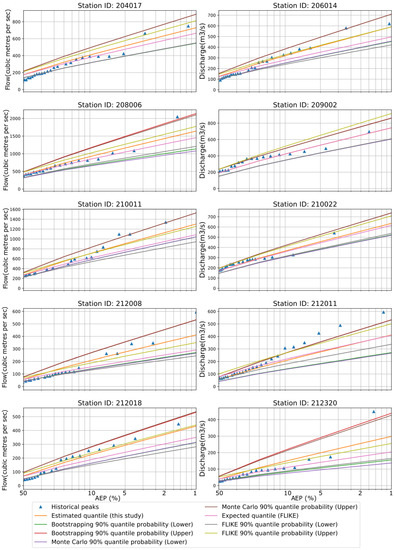
Figure 5.
Flood quantiles from FLIKE and EV1 distribution are presented over various AEPs for all 10 stations. CIs are estimated by FLIKE, BS, and MCST. The blue triangle symbolizes historical peak.
4.4. Uncertainty Estimates for LN Distribution
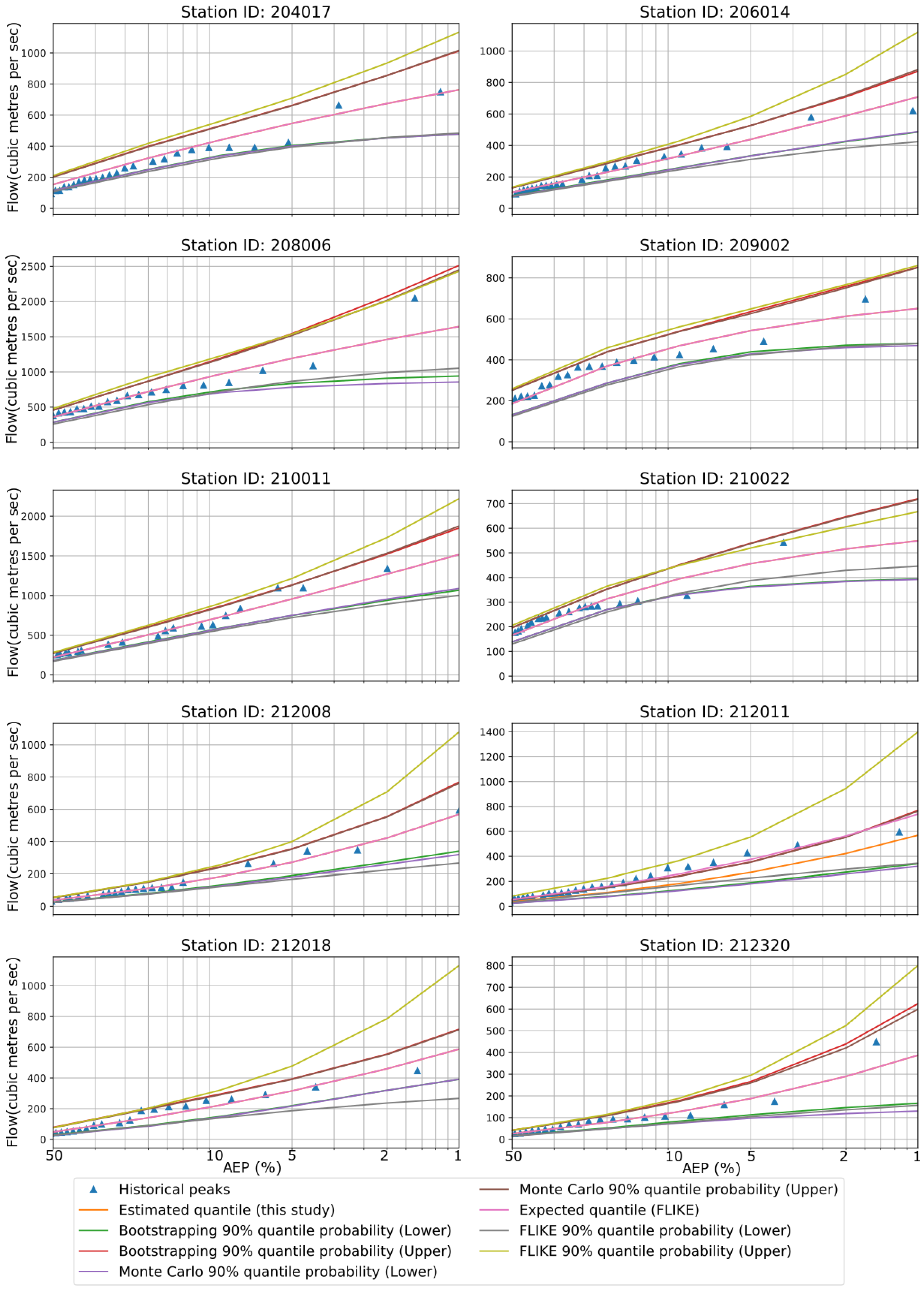
For the LN distribution, our flood quantile estimates (expected values) are very similar to those of FLIKE. The lower limit estimates are very similar for all three approaches (FLIKE, BS and MCST). However, FLIKE provides higher values for the upper limit than the other two methods (Figure 6). The historical peaks locate near the lower limit of CI. The confidence band from LN is even wider than what LP3 distribution offers in this study. The goodness-of-fit test e.g., Kolmogorov-Smirnov and Anderson-Darling test show that LN distribution is well fitted to the observed dataset for all 10 stations. Again, LN is a two-parameter distribution and could be unreliable on some occasions.
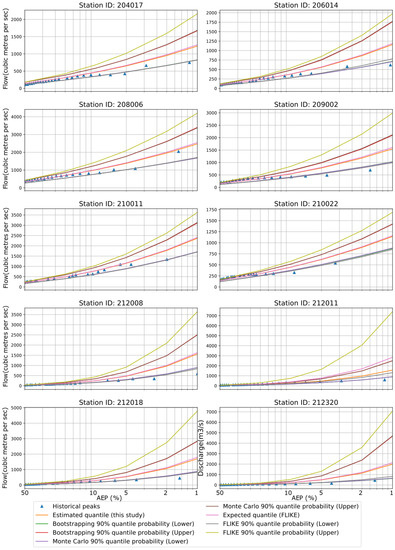
Figure 6.
Flood quantiles from FLIKE and LN distribution are presented over various AEPs for all 10 stations. CIs are estimated by FLIKE, BS and MCST. The blue triangle symbolizes historical peak.
4.5. Uncertainty Estimates for GPD Distribution
For the GPD, the flood quantile estimates (expected values) by FLIKE matched very well with our approach. FLIKE provided higher values for the upper limit of CI for the majority of the stations except station IDs 208006 and 210022. For some of the stations, FLIKE gave a smaller lower limit than the BS or MCST (e.g., station IDs 206014, 212018, and 212008) (Figure 7). The historical peaks were within the upper and lower bounds. Even GPD offered a slightly narrower confidence band than GEV and LP3. GPD is a three-parameter distribution, and we estimated parameters using the L-moments approach. Both the Kolmogorov–Smirnov and Anderson–Darling tests confirm that GEV distributions were well fitted to the observed dataset for all 10 stations.
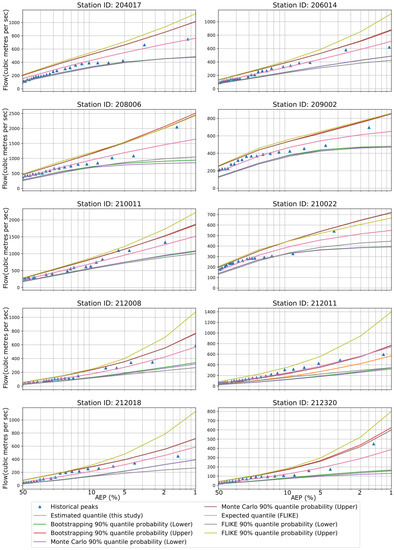
Figure 7.
Flood quantiles from FLIKE and GPD distribution are presented over various AEPs for all 10 stations. CIs are estimated by FLIKE, BS, and MCST. The blue triangle symbolizes historical peak.
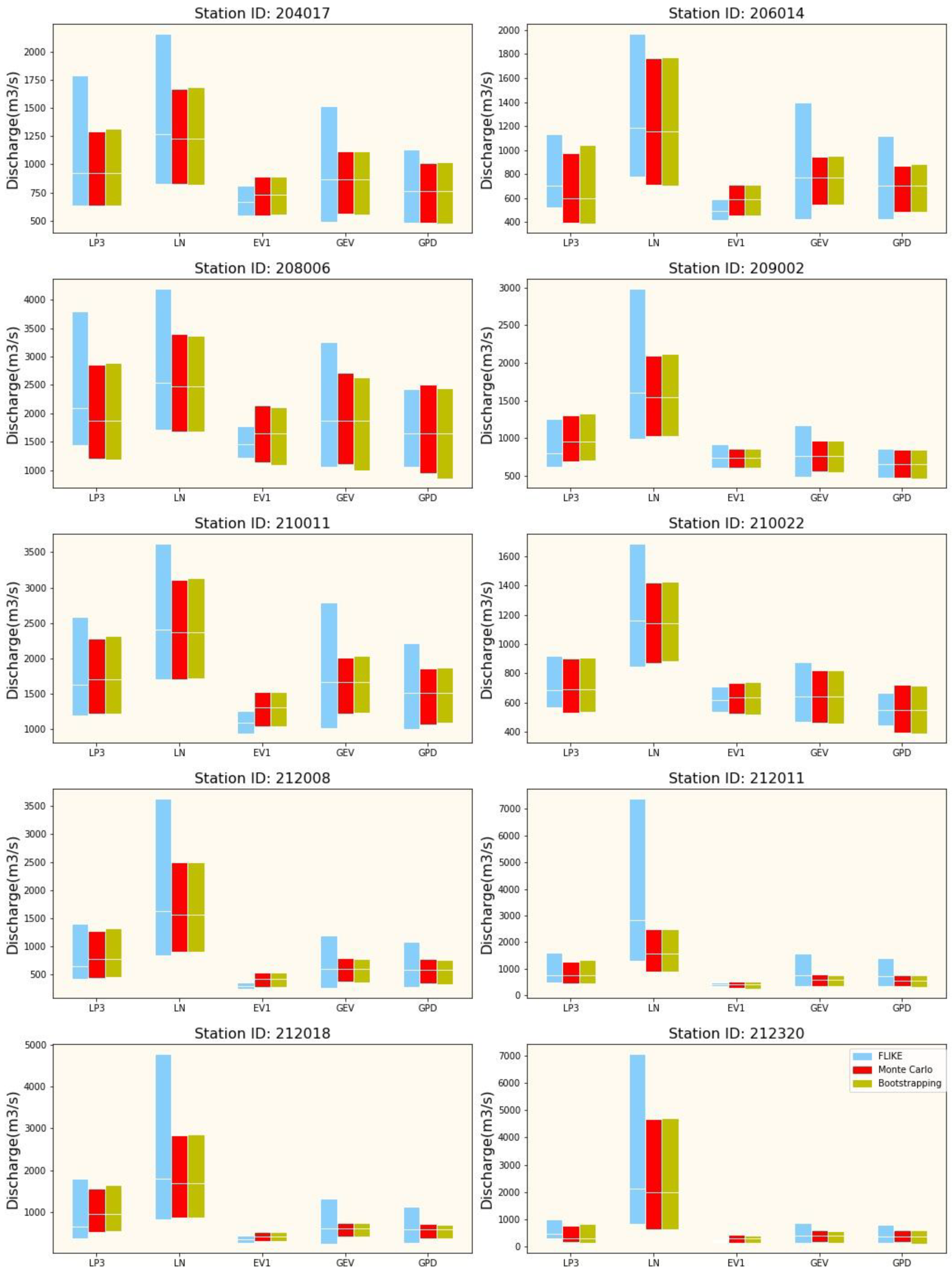
4.6. Uncertainty Estimates for Large Floods (1% AEP)
Figure 8 shows discharges for the confidence band (between 5th and 95th percentile) at 1% AEP using BS, MCST, and FLIKE methods. For all five distributions, the estimations from BS and MCST were very similar, however, different from FLIKE depending on distribution and location. In the case of LP3 distribution, FLIKE had higher values than BS and MCST, except station ID 209002. Moreover, FLIKE had a narrower uncertainty band than the other two approaches only for station ID 210022. Similarly, FLIKE had higher upper limit and wider uncertainty band for GEV and LN over all the stations. Interestingly, this was quite opposite (less magnitude of upper limit and narrower band for FLIKE than BS/MCST) for EV1 distribution. For GPD distribution, FLIKE had a higher estimation of upper limit than BS and MCST for most of the stations. Generally, as AEP reduced, the differences in higher confidence band among the five distributions increased, i.e., the differences were the smallest for 50% AEP and the highest for 1% AEP. It is noteworthy here that LN had much higher estimates of upper confidence limit and much wider band than the other four distributions (an example is shown in Figure 8). On the other hand, it is also observed from Figure 8 that all three approaches (FLIKE, BS, and MCST) had relatively lower magnitude resulting from EV1.

Figure 8.
Flood discharge for upper confidence band at ARI of 100 years (1% AEP) determined from BS, MCST, and FLIKE.
The results highlight several key issues. Firstly, the use of a single flood frequency distribution was not appropriate for the NSW state, as it is dominated by highly variable hydro-meteorological features. Secondly, the use of MCST and BS can provide a quick method of assessing the uncertainty in flood frequency analysis, which may not be obvious from a simple plot of observed AM flood data with the fitted distribution line. Thirdly, the sampling variability in flood frequency analysis was quite high given the wider band of the estimated CIs.
The levels of uncertainty in FFA found in our study are comparable to those of other studies. FLIKE has a similar spread of uncertainty for LP3 and GEV for all 10 stations considered in this study. In the case of MC and BS, most of the stations have wider uncertainty bands in LP3 than GEV. We have applied the MoM and L-moments for LP3 and GEV, respectively. Hu et al. [35] conducted a study for some selected gauging stations in the United States. They showed that GEV distribution combined with the maximum likelihood estimation method is associated with the largest uncertainty, while the LP3 exhibits comparable bias and smaller uncertainty. This doesn’t agree completely with our findings because of using different techniques for estimating LP3 and GEV parameters and different geographical locations.
The record length has a significant impact on estimating FFA and mainly affects the uncertainty of the estimates. For example, a record of around 35 years in the AMS approach is associated with 50% higher uncertainty than the 70-year reference [35]. Gaume [36] noted that a short record length results in significant uncertainty for medium-to-large ARIs in FFA. In another study by St. George and Mudelsee [37] for the Rayado Creek in the USA, omission of the highest flow value resulted in a drop of 45% for a 100-year flood estimate. In the context of regional flood frequency analysis, Rahman et al. [38] showed that for southeast Australia, a 100-year flood estimate is associated with 30 to 60% median error range. From Table 1, station IDs 210011 and 212022 have the highest record of 80 and 71 years, respectively, whereas station ID 209002 has the lowest record of 36 years. To handle uncertainty, we have applied BS and MC in all 10 stations.
5. Conclusions
In this study, uncertainty in flood frequency estimates for 10 gauging stations in New South Wales was examined using the Monte Carlo simulation and bootstrapping methods. We have found that the quantile estimates from our approach notably differ with those from FLIKE (the Australian Rainfall and Runoff recommended method) for most of the stations for LP3 and EV1 distributions. We estimated the parameters using the MoM and L-moments, whereas FLIKE adopted the Bayesian inference method. Moreover, for some of these stations, LN has much higher estimates of the upper confidence limit compared to the other four distributions. This is misleading in some cases. It should be noted here that skewness was not zero for the selected stations; and hence, the use of two-parameter distributions, such as EV1 and LN, may not be appropriate, i.e., these can provide remarkably biased estimations for higher return periods.
A key finding of this study is that in the case of the upper limit of CIs, two-parameter distributions such as LN and EV1 generally provide either over- or under-estimation. However, the three-parameter distributions, such as LP3, GEV, and GPD, provide a consistent estimation of the upper confidence limits. Moreover, L-moments appears to be a robust technique for parameter estimation in this study. Generally, FLIKE provides higher values for the upper limit of CI than BS and MCST for all the distributions except EV1. Furthermore, while all stations are located within a proximity of each other, some of the stations, e.g., 208006 and 210011) have a very high magnitude of upper confidence limits compared to other stations. The results of this study highlight the difficulty in at-site flood frequency analysis (i.e., different probability distributions perform quite differently even in a smaller geographical area). This is primarily due to sampling variability, as the recorded AM flood data are generally of a limited length and differing land characteristics that modify the rainfall into runoff. Results indicate that a single probability distribution for at-site flood frequency analysis is not suitable for the entire region. This is consistent with the recommendation in the most recent version of Australian Rainfall and Runoff. Flood frequency analysis relies on some assumptions, notably the stationarity of data series. However, the stationarity assumption is not always valid for various reasons, such as climate change and human activities [39,40]. Therefore, in future work, it is essential to test the stationarity or develop models that consider the non-stationarity in a new flood risk assessment framework.
Author Contributions
Z.K. analyzed the data and drafted the manuscript; A.R. designed, reviewed/edited the manuscript, and interpreted the results; F.K. reviewed/edited the manuscript and revised the discussion. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://www.bom.gov.au/waterdata/, accessed on 30 October 2022.
Acknowledgments
The authors express their sincere thanks to Muhammad Abdut, who did some initial work.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Charalambous, J.; Rahman, A.; Carroll, D. Application of Monte Carlo Simulation Technique to Design Flood Estimation: A Case Study for North Johnstone River in Queensland, Australia. Water Resour. Manag. 2013, 27, 4099–4111. [Google Scholar] [CrossRef]
- Petherick, A. Calculated Risks. Nat. Clim. Chang. 2011, 1, 188–189. [Google Scholar] [CrossRef]
- Burgan, H.I.; Vaheddoost, B.; Aksoy, H. Frequency Analysis of Monthly Runoff in Intermittent Rivers. In Proceedings of the World Environmental and Water Resources Congress 2017, Sacramento, CA, USA, 21–25 May 2017; pp. 327–334. [Google Scholar] [CrossRef]
- Bobée, B.; Cavadias, G.; Ashkar, F.; Bernier, J.; Rasmussen, P. Towards a Systematic Approach to Comparing Distributions Used in Flood Frequency Analysis. J. Hydrol. 1993, 142, 121–136. [Google Scholar] [CrossRef]
- Cunnane, C. Statistical Distributions for Flood Frequency Analysis; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1989. [Google Scholar]
- Kuriqi, A.; Ardiçlioǧlu, M. Investigation of Hydraulic Regime at Middle Part of the Loire River in Context of Floods and Low Flow Events. Pollack Period. Pollack Period. 2018, 13, 145–156. [Google Scholar] [CrossRef]
- Leščešen, I.; Dolinaj, D. Regional Flood Frequency Analysis of the Pannonian Basin. Water 2019, 11, 193. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Wang, Q.J. LH Moments for Statistical Analysis of Extreme Events. Water Resour. Res. 1997, 33, 2841–2848. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized Maximum-Likelihood Generalized Extreme-Value Quantile Estimators for Hydrologic Data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Selection of the Best Fit Flood Frequency Distribution and Parameter Estimation Procedure: A Case Study for Tasmania in Australia. Stoch. Environ. Res. Risk Assess. 2011, 25, 415–428. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J. Multivariate Non-Stationary Hydrological Frequency Analysis. J. Hydrol. 2021, 593, 125907. [Google Scholar] [CrossRef]
- Conway, K.M. Flood Frequency Analysis of Some NSW Coastal Rivers; The University of New South Wales: Kensington, Australia, 1970. [Google Scholar]
- Kopittke, R.A.; Stewart, B.J.; Tickle, K.S. Frequency analysis of flood data in queensland. In Proceedings of the Hydrological Symposium, Institution of Engineers Australia, National Conference, Sydney, NSW, Australia, 28–30 June 1976; pp. 20–24. [Google Scholar]
- Institution of Engineers Australia. Australian Rainfall and Runoff: A Guide to Flood Estimation; Pilgrim, D.H., Ed.; Institution of Engineers Australia: Barton, Australia, 1987. [Google Scholar]
- Vogel, R.M.; McMahon, T.A.; Chiew, F.H.S. Floodflow Frequency Model Selection in Australia. J. Hydrol. 1993, 146, 421–449. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Investigation on At-Site Flood Frequency Analysis in South-East Australia. J. Inst. Eng. Malays. 2008, 69, 59–64. [Google Scholar]
- Kuczera, G. Comprehensive At-Site Flood Frequency Analysis Using Monte Carlo Bayesian Inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Ball, J.E. Flood Estimation under Changing Climates. In Proceedings of the 19th IAHR-APD Congress, Hanoi, Veitnam, 24 September 2014. [Google Scholar]
- Caballero, W.L.; Rahman, A. Application of Monte Carlo Simulation Technique for Flood Estimation for Two Catchments in New South Wales, Australia. Nat. Hazards 2014, 74, 1475–1488. [Google Scholar] [CrossRef]
- Rahman, A.; Weinmann, E.; Mein, R.G. The Use of Probability-Distributed Initial Losses in Design Flood Estimation. Australas. J. Water Resour. 2002, 6, 17–29. [Google Scholar] [CrossRef]
- Burn, D.H. The Use of Resampling for Estimating Confidence Intervals for Single Site and Pooled Frequency Analysis/Utilisation d’un Rééchantillonnage Pour l’estimation Des Intervalles de Confiance Lors d’analyses Fréquentielles Mono et Multi-Site. Hydrol. Sci. J. 2003, 48, 25–38. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W. Estimating Extremes in Transient Climate Change Simulations. J. Clim. 2005, 18, 1156–1173. [Google Scholar] [CrossRef]
- Paeth, H.; Hense, A. Mean versus Extreme Climate in the Mediterranean Region and Its Sensitivity to Future Global Warming Conditions. Meteorol. Z. 2005, 14, 329–347. [Google Scholar] [CrossRef]
- Rust, H.W.; Kallache, M.; Schellnhuber, H.J.; Kropp, J.P. Confidence Intervals for Flood Return Level Estimates Assuming Long-Range Dependence BT—In Extremis: Disruptive Events and Trends in Climate and Hydrology; Kropp, J., Schellnhuber, H.-J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 60–88. [Google Scholar] [CrossRef]
- Semmler, T.; Jacob, D. Modeling Extreme Precipitation Events—A Climate Change Simulation for Europe. Glob. Planet. Chang. 2004, 44, 119–127. [Google Scholar] [CrossRef]
- Trichakis, I.; Nikolos, I.; Karatzas, G.P. Comparison of Bootstrap Confidence Intervals for an ANN Model of a Karstic Aquifer Response. Hydrol. Process. 2011, 25, 2827–2836. [Google Scholar] [CrossRef]
- Schendel, T.; Thongwichian, R. Flood Frequency Analysis: Confidence Interval Estimation by Test Inversion Bootstrapping. Adv. Water Resour. 2015, 83, 1–9. [Google Scholar] [CrossRef]
- Subramanya, K. Engineering Hydrology; Tata McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Rahman, A.; Haddad, K.; Haque, M.; Kuczera, G.; Weinmann, P. Australian Rainfall and Runoff Project 5: Regional Flood Methods: Stage 3 Report; Commonwealth of Australia (Geoscience Australia): Canberra, Australia, 2015.
- Nagy, B.K.; Mohssen, M.; Hughey, K.F.D. Flood Frequency Analysis for a Braided River Catchment in New Zealand: Comparing Annual Maximum and Partial Duration Series with Varying Record Lengths. J. Hydrol. 2017, 547, 365–374. [Google Scholar] [CrossRef]
- Climate Change in Australia. Available online: https://www.climatechangeinaustralia.gov.au/en/ (accessed on 4 November 2021).
- Matic, V.; Bende-Michl, U.; Hope, P.; Srikanthan, S.; Oke, A.; Khan, Z.; Thomas, S.; Sharples, W.; Kociuba, G.; Peter, J.; et al. East Coast—National Hydrological Projections Assessment Report. Available online: https://awo.bom.gov.au/assets/notes/publications/East_Coast_National_Hydrological_Projections_Assessment_Report.pdf (accessed on 1 December 2022).
- Hu, L.; Nikolopoulos, E.I.; Marra, F.; Anagnostou, E.N. Sensitivity of Flood Frequency Analysis to Data Record, Statistical Model, and Parameter Estimation Methods: An Evaluation over the Contiguous United States. J. Flood Risk Manag. 2020, 13, e12580. [Google Scholar] [CrossRef]
- Gaume, E. Flood Frequency Analysis: The Bayesian Choice. WIREs Water 2018, 5, e1290. [Google Scholar] [CrossRef]
- St. George, S.; Mudelsee, M. The Weight of the Flood-of-Record in Flood Frequency Analysis. J. Flood Risk Manag. 2018, 12, e12512. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, P.E. Regional Flood Methods. In Australian Rainfall & Runoff; Ball, J., Kuczera, G., Lambert, M., Nathan, R., Bill, W., Sharma, A., Bates, B., Finlay, S., Eds.; Institution of Engineers: Barton, Australia, 2019. [Google Scholar]
- Jain, S.; Lall, U. Floods in a Changing Climate: Does the Past Represent the Future? Water Resour. Res. 2001, 37, 3193–3205. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Liu, J. Projected Increases in Intensity and Frequency of Rainfall Extremes through a Regional Climate Modeling Approach. J. Geophys. Res. Atmos. 2014, 119, 213–271, 286. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).