1. Introduction
Streamflow simulation is widely implemented for environmental risk assessment, contaminant fate analysis, soil degradation and erosion and flood forecasting systems all around the world [
1,
2]. Estimated hydrological constants, meteorological data or weather inputs and a physical characterization of the watershed are currently the basis of most streamflow simulation models.
Based on these three input components, the corresponding streamflow of a given watershed or basin can be predicted and, thus, the possible flooding that could occur. These input components can be predicted or measured. Therefore, the streamflow can be simulated within a certain degree of uncertainty. However, there is uncertainty associated with each one of these components [
3,
4,
5,
6]. The total relative uncertainty will be the sum of uncertainty through each of these components and could have values from 0% to over 100% for a particular event [
7,
8].
Meteorological data for a hydrological model is perhaps the most critical parameter to predict streamflow or any other water movement in the internal water cycle of the basin. Examples of these are temperature and precipitation. Temperature is the main driving force of evapotranspiration. On the other hand, precipitation drives infiltration, soil saturation and runoff, subsequently recharging the aquifer and modifying the baseflow volume.
Classical hydrologic simulations [
9,
10,
11] are usually based on historical ground-based measurements that may not be available for a specific area due to the low density of stations, or there might be missing values due to the malfunctioning of the equipment installed in the area. An example of this is the many financial constraints to install, operate, and maintain reliable networks in developing countries or very difficult places for natural reasons, like northern Canada. In order to solve this problem, there are two alternatives that can be considered, namely satellite remote sensing and data assimilation systems. Remote sensing based on satellite retrievals is a very promising technique to retrieve meteorological parameters necessary to run hydrological models [
12,
13,
14]. On the other hand, data assimilation systems (DASs) are a combination of remote sensing products (airborne and satellite observations), ground-based measurements and estimations based on interpolation methods, models and stochastic approximations [
15,
16]. DASs offer the advantage of always providing the best available data, even in places where one or more of the sources are missing.
The Soil and Water Assessment Tool (SWAT), developed by the United States Department of Agriculture (USDA) Agricultural Research Service [
17], was initially created to predict water quality changes as a consequence of watershed anthropogenic practices, with the driving force of the model being the hydrological cycle. Several authors have studied the effects of distributed weather data when implemented in distributed hydrological models, like SWAT, in different watersheds [
18,
19,
20,
21,
22]. However, the simultaneous study of three or more datasets together, analyzing the effects on the calibration process and the final water balance results, has never been attempted before.
The goal of this study is to determine the suitability of available meteorological data for the prediction of streamflow using the SWAT model and discuss the impacts that the use of different available datasets can have in the calibration-validation process. Streamflow simulations using three different weather datasets are compared and analyzed with a baseline scenario defined as the United States Geological Survey (USGS) streamflow from measurement gauges.
2. Study Area
Four watersheds were selected for this study: West Branch Delaware or Cannonsville, West Branch Neversink, Upper Hudson River at Hadley and Aroostook River at Washburn.
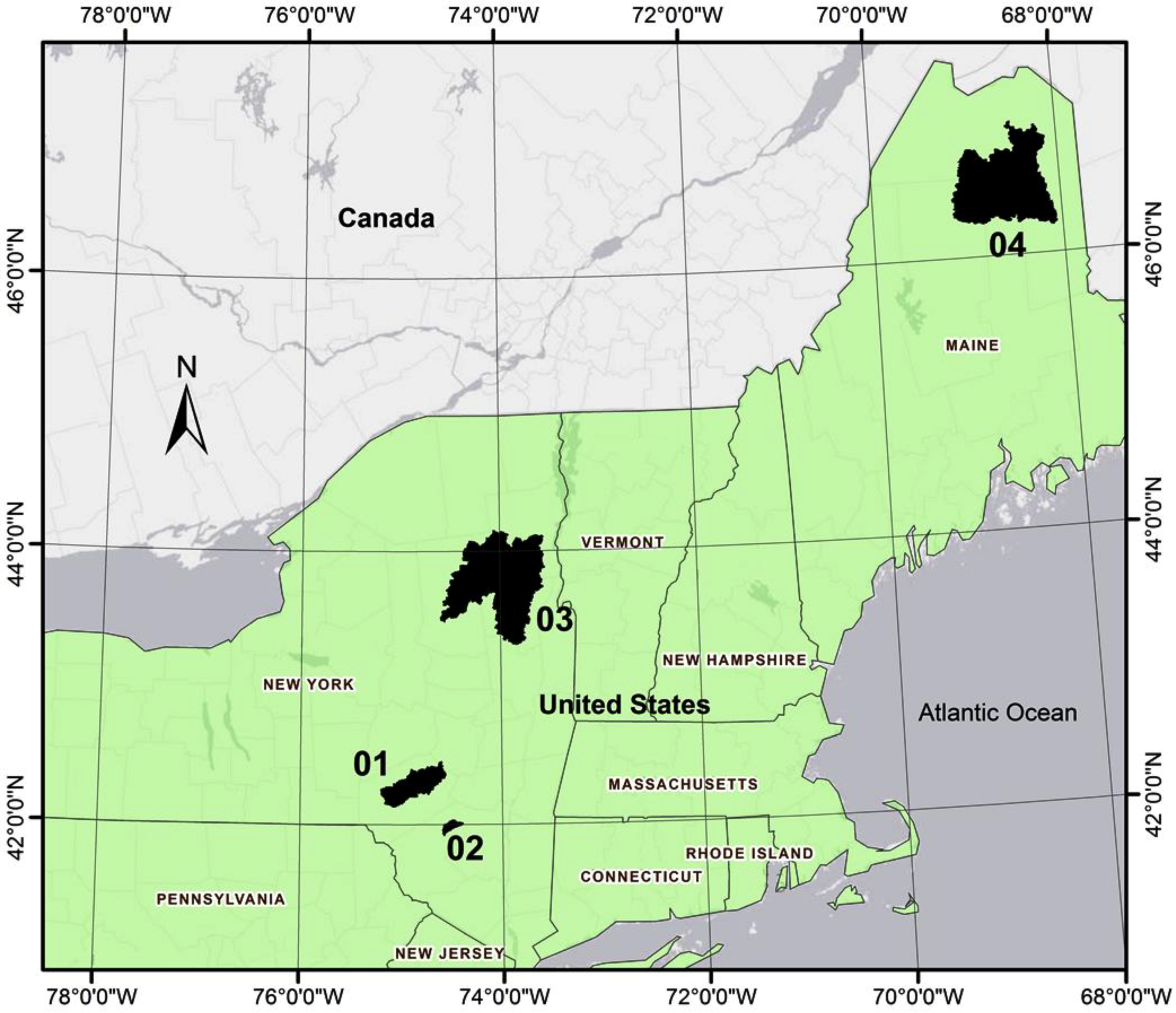
Figure 1 shows the location of the four watersheds, and
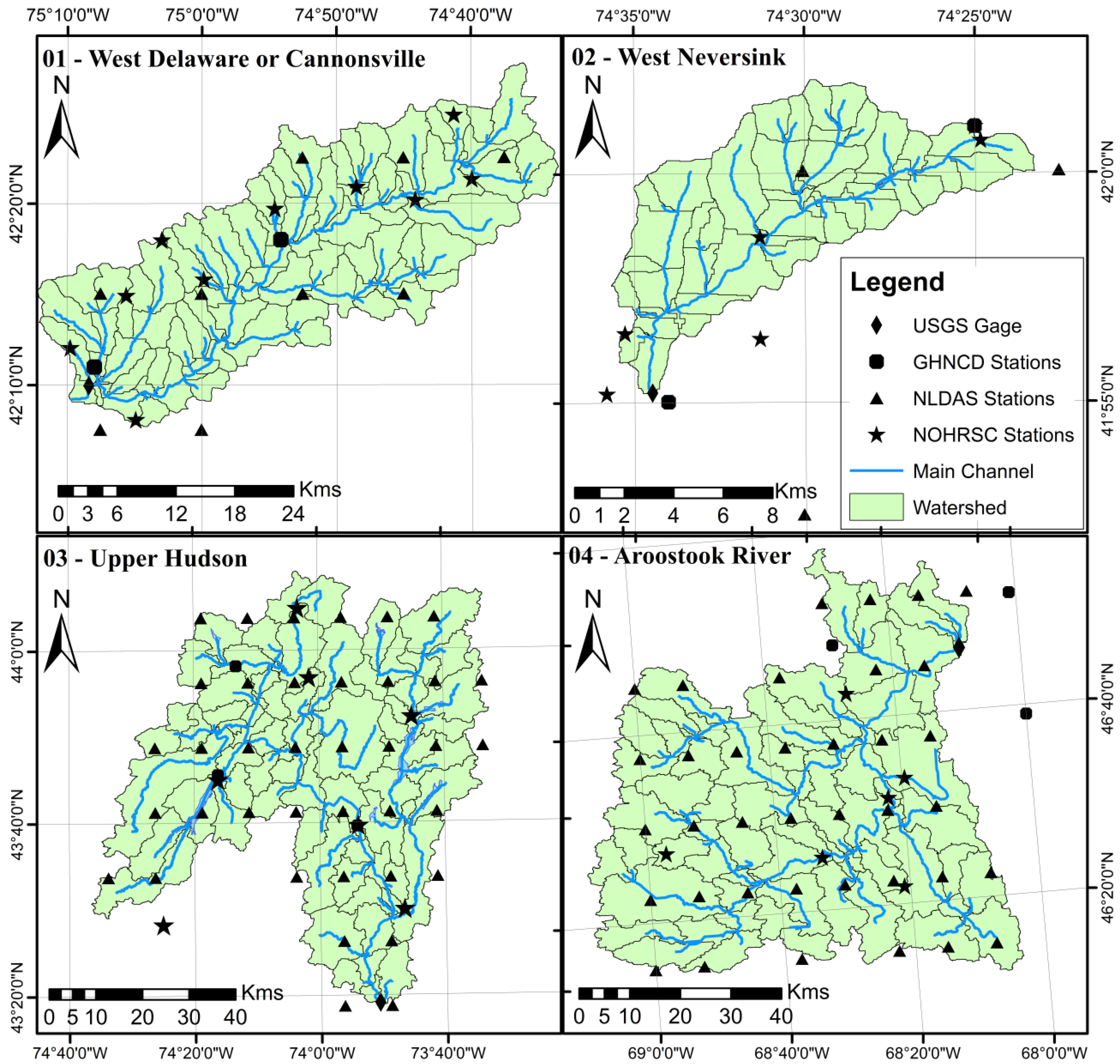
Figure 2 shows the sub-basins distribution within each watershed, the shapes of the watersheds, station locations and USGS observed streamflow gauges located at the outlet of each delineated watershed. For the delineation of the watershed, a 30-meter resolution digital elevation model was used, and 1% of the total area was used as the threshold for delineating the sub-basins within each watershed.
Table 1 shows the name and location of each USGS gauge along with some of the main characteristics of the selected watersheds.
Figure 1.
Location of watersheds. 01, West Delaware or Cannonsville; 02, West Neversink; 03, Upper Hudson; 04, Aroostook River.
Figure 1.
Location of watersheds. 01, West Delaware or Cannonsville; 02, West Neversink; 03, Upper Hudson; 04, Aroostook River.
Figure 2.
Watersheds shapes and locations of meteorological stations and USGS streamflow gauges.
Figure 2.
Watersheds shapes and locations of meteorological stations and USGS streamflow gauges.
Table 1.
Names of the USGS gauges at watersheds outlet, the 8-digit Hydrologic Unit Code (HUC08 code), and summary of watersheds characteristics: area; maximum and minimum elevation; average (Avg.) slope; hydrologic length in kilometers; elongation factor; average (Avg.) observed flow and flow standard deviation (SD); number of sub-basins considered in simulation; and number of weather stations considered in the simulation for each scenario.
Table 1.
Names of the USGS gauges at watersheds outlet, the 8-digit Hydrologic Unit Code (HUC08 code), and summary of watersheds characteristics: area; maximum and minimum elevation; average (Avg.) slope; hydrologic length in kilometers; elongation factor; average (Avg.) observed flow and flow standard deviation (SD); number of sub-basins considered in simulation; and number of weather stations considered in the simulation for each scenario.
| Watersheds’ Properties |
|---|
| Name | HUC08 No. | Area | Elevation (m) | Slope | Length | Elongation Factor | Flow (mm/d) | Sub-Basins | Number of Stations |
|---|
| (km2) | Max | Min | Avg. | (km) | Avg. | SD | GHCN | NLDAS | NOHRSC |
|---|
| W. Branch Delaware | 02040101 | 849.9 | 1018 | 358 | 32.8% | 57.64 | 0.256 | 2.25 | 2.93 | 117 | 2 | 9 | 10 |
| W. Branch Neversink | 02040104 | 86.5 | 1120 | 624 | 42.6% | 18.13 | 0.263 | 3.71 | 5.39 | 48 | 1 | 3 | 6 |
| Hudson at Hadley | 02020001 | 4260 | 913 | 186 | 31.7% | 94.69 | 0.475 | 2.06 | 2.04 | 75 | 3 | 34 | 7 |
| Aroostook at Washburn | 01010004 | 4234 | 674 | 160 | 10.7% | 92.70 | 0.493 | 1.98 | 2.72 | 74 | 2 | 37 | 6 |
These watersheds were selected because they represent a wide range of hydrological behavior in which the integrated effect of watershed shape, size, slope, land use and storage characteristics could be analyzed in relation to the hydrological response to a given precipitation event. Watershed selection covered average slopes from 10% to 40%, a watershed size from 80 to 4000 km2 and shapes that vary from elongated to concentrated.
3. Datasets
The digital elevation model (DEM) was downloaded from the National Elevation Dataset. A mosaic from multiple raster datasets was created and merged into a single raster dataset. Land cover/use is described by the National Land Cover Dataset Version 2006, an interpretation of Landsat remote sensing imagery to define a set of distinct land cover types. Soil data was obtained from United States Department of Agriculture (USDA) Soil Data Mart, from which the Soil Survey Geographic (SSURGO) database was used, because it provides the most detailed level of soil information.
This study makes use of three different climate datasets as weather inputs into the SWAT model in order to identify differences between the results obtained from the simulations with specific meteorological data. In the first place, the National Climatic Data Center’s Global Historical Climatology Network (GHCN-D) is a dependency from the National Oceanic Atmospheric Administration (NOAA) and compiles one of the largest ground stations global datasets, including most of the United States’ network.
The National Land Data Assimilation System (NLDAS) is a consistent global mosaic over land of meteorological forcing weather parameters, such as solar radiation, wind, temperature, precipitation and humidity. These data are the result of processing, quality controlling and spatial and temporal downscaling products from remote sensing, ground-based measurements and simulated data. The National Land Data Assimilation System (NLDAS) has coverage over the continental United States. The spatial resolution of this gridded dataset is 1/8th degree, and the temporal resolution is hourly [
23].
The National Operational Hydrological Remote Sensing Center’s Interactive Snow Information (NOHRSC-ISI) is a product similar to NLDAS, as it ingests daily ground-based, airborne and satellite observations. Even though NOHRSC-ISI’s priority is snow observation and snowpack characteristics estimation, forcing weather data is also collected and publicly available on NOHRSC-ISI’s website. NOHRSC-ISI output products are distributed in a variety of interactive maps, time-series and gridded formats [
24]. NOHRSC-ISI reports around 125,000 observation points for snow depth and/or snow water equivalent, and for each of these points, meteorological data is derived from the 13-km resolution rapid refresh numeric weather model. All weather datasets along with the watershed’s physical description datasets are referenced in
Table 2.
Table 2.
Datasets references and description.
Table 2.
Datasets references and description.
| No. | Data Type | Source/Authors | Name | Version/Release Date | Web Access | Date Accessed |
|---|
| 1 | Weather Data 1 | National Climatic Data Center from NESDIS. | GHCN-D dataset | Ver. 02/2006 | [25] | May 2013 |
| 2 | Weather Data 2 | Hydrological Sciences Laboratory at NASA/Goddard Space Flight Center (GSFC/HSL) | NLDAS Forcing Data L4 Hourly 0.125 x 0.125 degree | Ver. 01/2009 | [26] | May 2013 |
| 3 | Weather Data 3 | National Operational Hydrologic Remote Sensing Center’s Interactive Snow Information | NOHRSC-ISI weather data | No Ver./2004 | [27] | Jun 2013 |
| 4 | Soil data | Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture | Soil Survey Geographic (SSURGO) Database | No Ver./2004 | [28] | Feb 2013 |
| 5 | Elevation Data | Gesch, Dean, 2007, The National Elevation Dataset | 1-ArcSec Resolution Digital Elevation Model | 1-ArcSec Resolution DEM/1997 | [29] | Feb 2013 |
| 6 | Land Cover/Use | Joyce Fry, George Xian, Suming Jin, Jon Dewitz, Collin Homer, Limin Yang, Christopher Barnes, Nathaniel Herold, James D. Wickham. | National Land Cover Database (NLCD) | 2006/2009 | [30] | Feb 2013 |
| 7 | Streamflow | United States Geological Survey | The USGS National Water Information System (NWIS) | 2001 | [31] | May 2013 |
4. Methodology
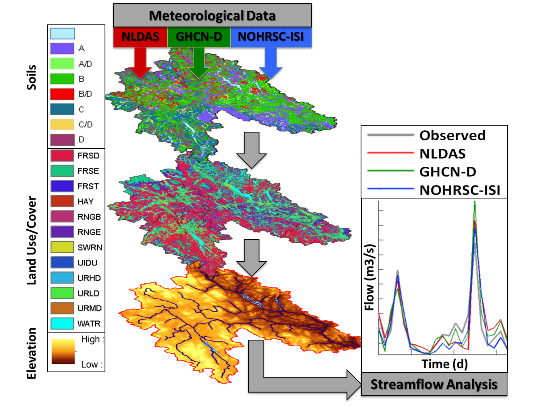
In order to predict the streamflow using SWAT, it is necessary to collect a large number of input parameters and datasets. The SWAT model requires three components: (1) the physical description of the watershed; (2) weather data to force the hydrological cycle components inside the basin; and (3) hydrological parameters.
The physical description of the basin is achieved by incorporating the soil, land use/cover and elevation data at a pixel base to each sub-basin of the watershed. This process (described below) is helped by ArcSWAT 2012 (an ArcMap10 GIS interface). It consists basically of the spatial processing of shape, vector and raster files to describe the variability of land use/cover, elevation, slope and soil properties. The meteorological data input is what defined the three simulations scenarios. Three different sources of meteorological data were used as inputs to the model to produce simulated streamflow and later compared to observed streamflow data for performance assessment.
The most complicated step or component is the right selection and adjustment of the parameters that controls the hydrological response of the watershed or hydrological parameters. Using the ArcSWAT 2012 interface, an approximation can be obtained. However, a manual local sensitivity analysis of hydrological parameters was performed in order to identify which of them should be selected for the calibration process. Local sensitivity analysis has the main disadvantage of missing the synergic effect that two or more parameters can have when changed simultaneously. Yet, this methodology can still provide a very good idea of which parameters should be assessed to improve the model performance in a particular basin [
32]. After the local manual sensitivity analysis, calibration was performed. This process implies a large number for the model’s executions, and the objective is to minimize the error between the simulated and the observed streamflow without compromising the realistic value of the parameters being calibrated. The specifics of the calibration process are explained in
Section 4.2.
4.1. SWAT Model Description and Setup
The SWAT model was first published in 1993 as a comprehensive hydrological model, is GIS based and capable of simulating runoff and contaminant movement through a watershed [
33]. This model considers the spatial distribution of the watershed characteristics by implementing the hydrological response unit (HRU) into the calculations [
34]. The driving force of the contamination movement in the model is the water cycle throughout the basin. The model’s hydrology has been improved considerably during its historical upgrades and versions [
32,
35]. The SWAT model has great potential, because it is computationally efficient, capable of continuous simulations over long time periods and a very comprehensive model capable of simulating several hydrologic processes, such as surface runoff, infiltration, evapotranspiration, lateral flow, return flow and recharge by seepage [
17,
32].
There are three basic ways for the SWAT model to convert precipitation or snowmelt into river discharge: surface runoff, lateral flow and shallow aquifer return flow (baseflow). The land phase of the SWAT model is based on the water balance. The technical report TR-406 [
36] from the USDA has a very detailed description of how all of the components of the water balance equation are calculated for each time step. SWAT allows weather inputs in a daily time step, and specifically, for precipitation, it allows hourly, too. Depending on the time step of the precipitation input, the infiltration and, thus, the surface runoff for each hydrological response unit is calculated by either the Green and Ampt method (1911) for hourly calculations or a modified Soil Conservation Service Curve Number (SCS-CN) procedure (1972) for daily calculations. This experiment used the SCS Curve number method and, thus, a daily time step calculation, because GHCN-D is daily data, and it was decided to keep the same time step for all scenarios to use the same infiltration method.
Instead of assuming a soil moisture condition, the SWAT model estimates soil moisture on each time step based on calculations that depend on the soil profile water content (variable curve number (CN) method) [
37]. Thus, a CN value for each sub-basin and time step (day) is calculated. The peak of the hydrograph for any given event is calculated based on the modified rational method, and the lag of the peak or the rising time of the hydrograph is calculated using an exponential decay based on available water in each time step. There are several algorithms that can be used for the calculation of the potential evapotranspiration integrated in the SWAT model, and the algorithm used in these simulations was the Penman/Monteith method.
The groundwater movement of the model is also governed by the shallow aquifer mass balance. Additionally, optionally, the SWAT model allows input files that describe the operation of reservoirs (if any exist); the file contains the daily, monthly, yearly or targeted release flow information. The Hudson River watershed contains three main reservoirs, namely Schroon, Brant and Lewey. For all three of them, daily outflow data were used as the inputs to describe the routing behavior of the lakes.
The velocity of the water on the river channel is controlled by Manning’s roughness coefficient CH_N2, and the losses associated with river bed infiltration (tloss) are assumed proportional to the wet perimeter of the channel’s section, the travel time and the channel bed transmissibility coefficient (CH_K2).
4.2. Watershed Characterization and Model Calibration
In the United States, it is possible to access very accurate and up-to-date physical characterization databases for almost the entire territory. On the contrary, in the rest of the world, it can be difficult to find these databases for a particular area. However, in situ or remote surveys can always be used to reduce the absence of information about watershed characterization parameters.
In the SWAT model, the physical characterization of the watershed is achieved by describing the soil types, elevation, slope, and land use/cover of the basin’s area. The land and water management description, such as agriculture and irrigation practices can be optionally used as an input, but it was not considered in this study. The ArcSWAT 2012 (a GIS interface for the SWAT model) can be used to generate the input files that physically describe the basin in the model. This interface reads the information on the USGS’ digital elevation model (DEM) raster data, USGS’ land use/cover raster data and USDA’s SSURGO soil data shape file.
The DEM is used to delineate the basin, reaches and sub-basins and to account for slope variability. Land use/cover and soil variability is extracted from their corresponding files by sub-basin. This information is finally used to describe the sub-basin’s variability in slope, land use and soils using an approach based on the proportionality of hydrologic response units (HRUs) within each sub-basin.
From the HRU analysis, ArcSWAT’s interface produces a parameterization of the model. A systematic process can be used for a better estimation of hydrological parameters, such as the curve number (CN2), baseflow alpha factor (ALPHA_BF), baseflow alpha factor for bank storage (ALPHA_BNK), groundwater delay factor (GW_DELAY), groundwater minimum depth for baseflow to occur (GWQMN), ground water capillarity factor (GW_REVAP), soil evaporation factor (ESCO), Manning’s coefficient for the main channel (CH_N2), hydraulic conductivity for main channel (CH_K2) and plant evaporation coefficient (EPCO) [
10,
38]. This estimation can be first approximated by experience (expert knowledge) or obtained from the ArcSWAT interface, with subsequent calibration performed for further adjustments.
The sensitivity analysis and calibration procedures are iterative and can be long and tedious. However, this is the best way to describe the spatially variable process of runoff through a variable medium, such as soil. Although the results from these processes might not be strictly a physical representation of the watershed hydrology, it has been demonstrated that these procedures are powerful tools to improve and adjust the simulation results [
32,
39].
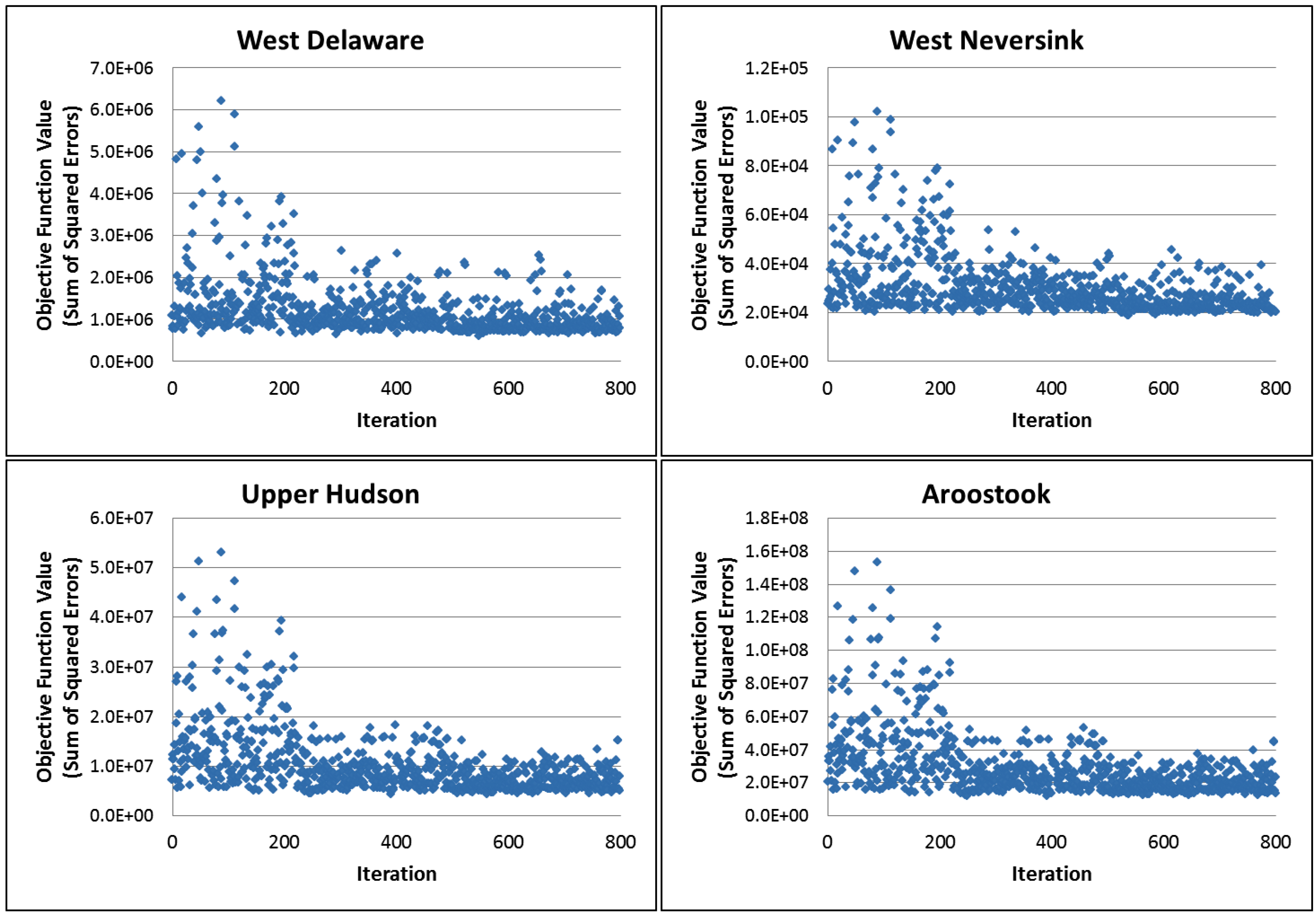
After the initial model setup and execution, calibration was implemented to adjust the hydrological parameters described above. To facilitate the calibration procedures, the SWAT-Calibration and Uncertainty Procedures (SWAT-CUP calibration tool) was implemented. SWAT-CUP is a freeware available for this purpose, and it has been demonstrated to be practical and efficient. The calibration was performed using this tool under the parameter solution calibration scheme (Parasol method) to calibrate the 10 selected hydrological parameters simultaneously. The USGS’ observed streamflow data (for the same period) located at the outlet of each watershed was used as the observed variable or ground truth. Different arrangements were used to optimize the time of calibration. It was observed that the number of iterations required for achieving the best possible simulation oscillated between 300 and 500 (
Figure 3). Consequently, the number of trials for each scenario was set to 800 in order to consider as many combinations as possible.
Figure 3.
Convergence plot of the calibration process for all four watersheds.
Figure 3.
Convergence plot of the calibration process for all four watersheds.
The meteorological parameters were downloaded from the three different sources (NOHRSC-ISI, NLDAS and GHCN-D) for the same time period. The time period selected was from January 2007, to August 2011, for calibration and September 2011, to December 2012, for the validation period. This was considered a relevant time frame, because complete and reliable data were available from all of the different data sources and the selected basins. Furthermore, it is important to analyze the short-term hydrologic response of the watershed, which can be accomplished using the information of a specific rainfall event.
4.3. Multi-Annual Validation
The objective of this research is to study the capabilities of the model in the short term (e.g., 1 year performance). However, it is also of great importance to study the efficiency of the model throughout a multi-annual time frame, because it is understood that the results for a 1-year validation period could be a coincidence of the hydro-climatology of that specific year.
In order to measure the multi-annual efficiency, a timeframe larger than one year is needed. To obtain this multi-annual timeframe, the same calibration scheme described above was used. However, the warmup period was set to 2003–2004, the calibration period was set to 2005–2008 and the validation period was set to 2009–2012. The rest of the calibration parameters and setup remained as explained before. This calibration scheme is commonly known as split-sample calibration [
39,
40].
This was considered necessary because of several reasons. Increasing the size of the sample can provide more reliable statistics (e.g., percentage of peaks detected). For multi-seasonal analysis and multi-annual analysis, as implied by the name, more than one year of validation data is needed. Lastly, the use of a multi-annual validation period will strengthen the conclusions of this manuscript, because the statistical analysis will not be biased by the hydro-climatic conditions of a single year.
4.4. Statistical Analysis
The R
2 value is a commonly used statistical measure of how close the observed data (USGS streamflow measurement or baseline) are to the simulated data (SWAT simulated streamflow). This test is also known as the coefficient of determination [
41,
42].
The root mean square error (RMSE) is an index used to measure the error in models results [
42,
43]. It can immediately tell how large the difference is between the measured and the simulated values over the studied period (theoretically, the larger the RMSE, the larger the uncertainty).
For daily streamflow, big variations could be expected between two consecutives observations or a relatively large standard deviation. Thus, the use of the RMSE-observations standard deviation ratio (RSR) is recommended by some authors [
42,
44]. The RSR is a standardized RMSE by using the standard deviation of the observed streamflow hydrograph.
The main objective of this work is to assess the models capabilities of simulating the hydrological response and water balance of the watershed for the given scenarios. Consequently, two measurements were implemented, namely the total volume difference percentage between the observed and the simulated streamflow and the percentage of peaks detected by the model.
For peak detection assessment, an event was defined as any streamflow measurement that was above a threshold. The threshold was defined as three times the average flow for the two smallest watersheds and two times the average flow for the two biggest watersheds. Finally, the number of events during the validation period for both observed and simulated streamflow was manually counted. If the observed and simulated peak flow were observed on the same day, it was considered a timely detection.
Since all water movement inside a watershed is mostly driven by precipitation, to avoid the possible bias that could generate these differences between scenarios, two ratios were used for comparison purposes: total water yield over precipitation ratio (TWY/PCP) [
45] and the shallow aquifer flow (return flow) over total water yield (TWY/SAF) [
46]. Total water yield is the total amount of water that comes out of the basin as streamflow, and the shallow aquifer flow is the part of the streamflow that is due to return flow or groundwater returning to the main channel as baseflow. The SWAT model includes these values as output, and for the reference or observed values, the USGS’s ratio [
45] and the baseflow ratio from the separation algorithm proposed by Arnold and Allen 1999 [
46] were used. These ratios allow assessing the general water balance of the simulations without being biased by the input differences of each scenario. Finally, the statistic
t-test was used to assess if the difference between each scenario and the USGS measurement was significant or not.
A satisfactory simulation or good fit is considered for [
42]: correlation coefficient values above 0.60 for daily values and over 0.70 for monthly observations. The RMSE should be less than half of standard deviation or the RSR less than 0.50 for monthly values. The total relative volume differences should be less than 10%. Finally, the
t-stat critical value for a monthly time step is ±2.18 and for a daily time step is ±1.97.
Equations (1)–(6) are used for the statistical analysis performed in this experiment, where Y
n,obs is the observed variable,
is the average observed variable, Y
n,sim is the simulated variable,
is the average simulated variable, n is the number of observations, StdDev is the standard deviation, R
2 is the correlational coefficient, RMSE is the root mean square error, RSR is the standardized RMSE, %Vol.Dif. is the difference in the percentage of total yielded volume of water, Vol
obs is the observed volume of yielded water for a given day and Vol
sim is the simulated volume of yielded water for a given day. N is the total number of observations/simulations, and n is the sum counter.
5. Results and Discussion
Each model’s run, based on the three meteorological data used, was called the scenario. The streamflow hydrograph that resulted from each modeling scenario was compared with the observed streamflow obtained from USGS’s station installed at the outlet of the watershed and shown for monthly and daily time scales. The streamflow hydrograph is the basis for the hydrologic analysis of high intensity rainfall events that are able to generate flooding conditions in a given watershed. This information is also essential in the understanding and evaluation of the hydrologic regime and response of a watershed during an extreme event.
5.1. Monthly Scale Results Analysis
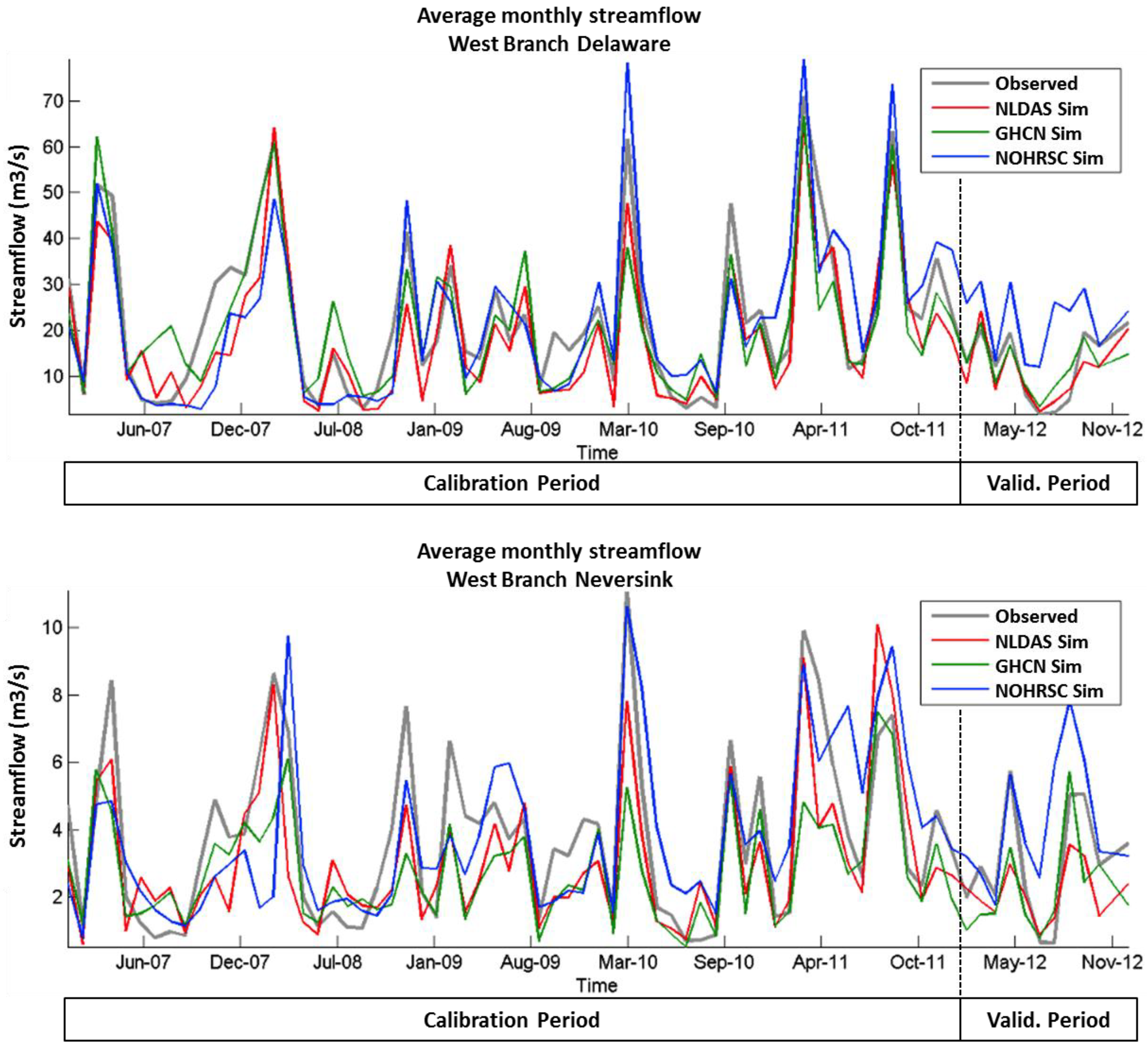
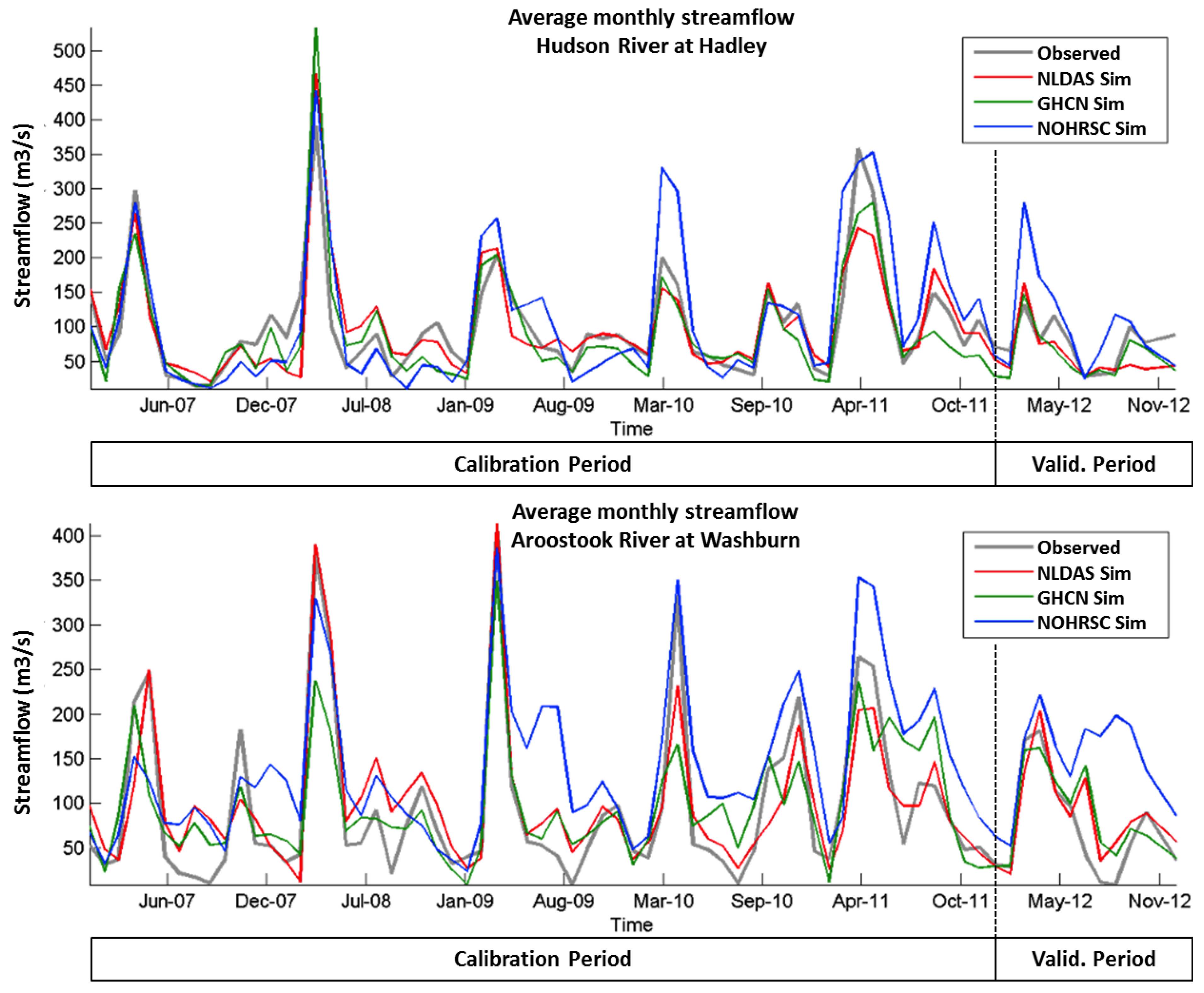
A good fit for the streamflow simulation is observed using the three different meteorological datasets (NOHRSC-ISI, GHCN-D and NLDAS) at monthly scale (See
Figure 4 and
Figure 5). Generally, NOHRSC-ISI scenario overestimated streamflow, while GHCN and NLDAS were both closer to each other and to the observed monthly means.
Figure 4.
Monthly flow from the three scenarios compared with the USGS measured at West Branch Delaware (Cannonsville) and West Branch Neversink. Calibration and Validation (Valid.) Periods.
Figure 4.
Monthly flow from the three scenarios compared with the USGS measured at West Branch Delaware (Cannonsville) and West Branch Neversink. Calibration and Validation (Valid.) Periods.
Figure 5.
Monthly flow from the three scenarios compared with the USGS measured at Hudson River and Aroostook River. Calibration and Validation (Valid.) Periods.
Figure 5.
Monthly flow from the three scenarios compared with the USGS measured at Hudson River and Aroostook River. Calibration and Validation (Valid.) Periods.
The statistics in
Table 3 shows that the variability of the streamflow at a monthly time scale is better explained by the NLDAS scenario (better R
2 values obtained), which implies that the model’s hydrological response is improved by using NLDAS meteorological data. The RMSE and RSR values also showed that the NLDAS scenario is closer to the observed monthly streamflow, implying that the approach for hydrological simulation using NLDAS meteorological data is plausible. Finally, the
t-test values showed that the difference of the means between the observed and simulated streamflow was not significant in any of the scenarios, meaning that all of the simulations were reasonably good at this time scale.
Table 3.
Single-year validation period statistics for monthly and daily simulated streamflow for each scenario and watershed. Shaded values are the best for each efficiency measure. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data. RSR, RMSE-observations standard deviation ratio; %Vol.Dif., the difference in the percentage of total yielded volume of water.
Table 3.
Single-year validation period statistics for monthly and daily simulated streamflow for each scenario and watershed. Shaded values are the best for each efficiency measure. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data. RSR, RMSE-observations standard deviation ratio; %Vol.Dif., the difference in the percentage of total yielded volume of water.
| Time Step and Period | Stats | West Branch Delaware | West Branch Neversink | Upper Hudson | Aroostook River |
|---|
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 |
|---|
| MONTHLY Validation Period | R2 | 0.77 | 0.80 | 0.38 | 0.54 | 0.79 | 0.31 | 0.52 | 0.58 | 0.49 | 0.60 | 0.77 | 0.56 |
| RMSE | 3.81 | 3.80 | 12.19 | 1.37 | 1.27 | 1.91 | 32.22 | 31.01 | 57.58 | 46.19 | 33.62 | 90.25 |
| RSR | 0.48 | 0.48 | 1.53 | 0.83 | 0.77 | 1.15 | 1.01 | 0.97 | 1.80 | 0.66 | 0.48 | 1.29 |
| t-test | 0.09 | 0.53 | −3.07 | 1.36 | 1.56 | −1.54 | 1.90 | 0.86 | −1.99 | −0.64 | −0.20 | −3.43 |
| DAILY Validation Period | R2 | 0.58 | 0.64 | 0.39 | 0.15 | 0.67 | 0.55 | 0.49 | 0.51 | 0.45 | 0.39 | 0.42 | 0.23 |
| RMSE | 7.94 | 7.69 | 15.21 | 4.55 | 3.09 | 3.26 | 45.95 | 44.40 | 71.01 | 73.41 | 70.68 | 110.59 |
| RSR | 0.65 | 0.63 | 1.24 | 1.00 | 0.68 | 0.72 | 0.85 | 0.82 | 1.31 | 0.80 | 0.77 | 1.21 |
| t-test | 0.33 | 1.84 | −10.56 | 2.87 | 3.16 | −3.50 | 7.59 | 3.41 | −8.34 | −2.03 | −2.14 | 12.02 |
| %Vol.Dif. | −2% | −12% | 75% | −19% | −11% | 35% | −27% | −1.5% | 39% | 18% | 13% | 98% |
5.2. Annual Water Balance and Flow Partition
A direct method to see the impact of each scenario in the performance of the model is to analyze the water balance of the watershed annually. The simple observation of the annual average of precipitation, evaporation, runoff and infiltration can offer a very good idea of the impact of each scenario on the model. In most cases, all values were close to each other, meaning that all three scenarios’ setup achieved similar results (
Table 4). However, there are some exceptions that should be further analyzed.
Table 4.
Before double line: average annual water balance for each watershed and scenario over the validation period. After double line: Simulated and Observed (Obs.) total water yield over precipitation ratio and shallow aquifer flow over total water yield ratio for the same period. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data.
Table 4.
Before double line: average annual water balance for each watershed and scenario over the validation period. After double line: Simulated and Observed (Obs.) total water yield over precipitation ratio and shallow aquifer flow over total water yield ratio for the same period. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data.
| Watershed’s Summary for the Validation Period (Values in mm/y and °C) | West Branch Delaware | West Branch Neversink | Upper Hudson | Aroostook River |
|---|
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 |
|---|
| Precipitation (PCP) | 1,133.0 | 1,073.6 | 1,492.2 | 1,352.7 | 1,312.2 | 1,905.5 | 1,015.9 | 1,006.4 | 1,362.1 | 978.7 | 1,022.4 | 1,470.8 |
| Temperature | 8.5 | 9.2 | 9.1 | 6.3 | 10.2 | 8.6 | 6.3 | 8.3 | 8.3 | 6.1 | 6.3 | 5.8 |
| Snow fall | 164.6 | 137.0 | 212.8 | 192.1 | 158.0 | 294.7 | 232.6 | 207.9 | 299.3 | 239.7 | 258.2 | 427.7 |
| Snow melt | 126.2 | 112.0 | 170.2 | 171.1 | 148.5 | 240.7 | 176.5 | 155.0 | 264.2 | 255.5 | 230.0 | 335.8 |
| Surface Runoff | 479.0 | 293.8 | 692.4 | 682.0 | 756.4 | 1,457.7 | 262.1 | 282.4 | 406.4 | 614.4 | 464.9 | 1,048.4 |
| Shall. aquifer flow (SAF) | 53.5 | 192.3 | 211.5 | 100.6 | 32.0 | 11.8 | 148.0 | 133.1 | 318.0 | 6.9 | 64.6 | 1.1 |
| Deep aquifer recharge | 6.3 | 12.2 | 15.8 | 5.3 | 4.1 | 0.7 | 9.3 | 10.4 | 20.5 | 0.4 | 5.5 | 0.2 |
| Total aquifer recharge | 126.3 | 243.8 | 316.4 | 106.8 | 82.8 | 13.7 | 185.2 | 207.2 | 409.0 | 7.5 | 109.3 | 3.3 |
| Total water yield (TWY) | 532.5 | 486.1 | 903.8 | 782.6 | 788.4 | 1,469.6 | 410.1 | 415.6 | 724.4 | 621.2 | 529.5 | 1,049.4 |
| Evapotranspiration | 533.6 | 521.2 | 467.8 | 557.8 | 497.6 | 390.4 | 536.9 | 529.0 | 502.1 | 368.0 | 445.2 | 325.8 |
| Potential Evapotranspiration | 793.5 | 752.4 | 577.6 | 1,016.0 | 957.3 | 698.4 | 892.1 | 843.4 | 701.5 | 911.0 | 803.9 | 692.4 |
| Simulated TWY/PCP = | 0.47 | 0.45 | 0.61 | 0.58 | 0.60 | 0.77 | 0.40 | 0.41 | 0.53 | 0.63 | 0.52 | 0.71 |
| Obs. TWY/PCP (2012) = | 0.44 | 0.82 | 0.55 | 0.55 |
| Simulated SAF / TWY = | 0.10 | 0.40 | 0.23 | 0.13 | 0.04 | 0.01 | 0.36 | 0.32 | 0.44 | 0.01 | 0.12 | 0.00 |
| Obs. SAF/TWY (2012) = | 0.47–0.69 | 0.44–0.65 | 0.58–0.78 | 0.46–0.69 |
The NOHRSC-ISI precipitation values were greater in all four watersheds, which explains the larger water yield and snow fall/melt values and, consequently, the volume difference (%Vol.Dif.) result for that scenario (
Table 3). This overestimation can be also observed at monthly and daily scales.
The total water yield over precipitation ratio in the simulations was generally in agreement for the West Branch Neversink and Aroostook watersheds. On the other hand, the Upper Hudson and the West Delaware basins were in the low side of the observed range. In the case of the Upper Hudson, this could be explained by the effect of reservoir operation. Because this effect was taken into account, it was not considered as a problem in the simulation results. However, there are no reservoirs in the West Branch Delaware. Therefore, the difference could be explained by higher evapotranspiration values, but since no observed values were available for comparison, further studies should be made to assess this discrepancy.
The partition of the flow (surface runoff and groundwater) is one of the most important parts of the simulation; the reason why is that it is important to assess the behavior of the model in this matter. The shallow aquifer flow over total water yield ratio was only within the observed range for the NLDAS scenario of the West Delaware and the NOHRSC scenario of the Hudson River. The other scenarios and watersheds were completely out of the observed range, indicating that further adjustments have to be made to the parameters controlling the flow partition in the model.
In the West Delaware watershed, the final values of the calibration parameters (
Table 5) show that the curve number (CN2) value directly influences the amount of runoff, along with the groundwater delay (GW_DELAY). Both parameters affect the amount of water leaving the shallow aquifer, as they control the infiltration rate and the detention time. The NLDAS scenario showed lower values for the two same parameters compared to the other two scenarios (NOHRSC and GHCN) of the West Delaware basin. This setup will give a different flow partition (producing more return flow and less direct runoff) without altering the total water yield (
Table 4).
Table 5.
Final parameter solution after calibration. The calibration method (Calib. Method) is the name as the calibration method used in the SWAT-CUP tool. The parameters are described in
Section 4.2. Min and Max refer to the maximum and minimum value of the parameter for calibration. In the type column, “RC” means that the parameter was changed proportionally to the original value and “Subst.” means that the parameter was substituted by a value in the selected range in the next step of calibration. Curve number (CN2), baseflow alpha factor (ALPHA_BF), baseflow alpha factor for bank storage (ALPHA_BNK), groundwater delay factor (GW_DELAY), groundwater minimum depth for baseflow to occur (GWQMN), ground water capillarity factor (GW_REVAP), soil evaporation factor (ESCO), plant evaporation coefficient (EPCO), Manning’s coefficient for the main channel (CH_N2) and hydraulic conductivity for main channel (CH_K2).
Table 5.
Final parameter solution after calibration. The calibration method (Calib. Method) is the name as the calibration method used in the SWAT-CUP tool. The parameters are described in Section 4.2. Min and Max refer to the maximum and minimum value of the parameter for calibration. In the type column, “RC” means that the parameter was changed proportionally to the original value and “Subst.” means that the parameter was substituted by a value in the selected range in the next step of calibration. Curve number (CN2), baseflow alpha factor (ALPHA_BF), baseflow alpha factor for bank storage (ALPHA_BNK), groundwater delay factor (GW_DELAY), groundwater minimum depth for baseflow to occur (GWQMN), ground water capillarity factor (GW_REVAP), soil evaporation factor (ESCO), plant evaporation coefficient (EPCO), Manning’s coefficient for the main channel (CH_N2) and hydraulic conductivity for main channel (CH_K2).
| Parameters for Calibration | West Branch Delaware | West Branch Neversink |
|---|
| Calib. Method: Parameter Solution |
|---|
| Name | Min | Max | Units | Type | GHCN | NLDAS | NOHRSC | GHCN | NLDAS | NOHRSC |
| CN2 | −0.4 | 0.4 | - | RC | 0.10 | −0.15 | 0.06 | −0.01 | 0.11 | 0.30 |
| ALPHA_BF | 0.0 | 1.0 | days | S | 0.09 | 0.07 | 0.07 | 0.04 | 0.05 | 0.03 |
| GW_DELAY | 10.0 | 450.0 | days | S | 179 | 12 | 124 | 322 | 421 | 220 |
| GWQMN | 0.0 | 2.0 | mm | S | 1.41 | 1.20 | 1.05 | 0.15 | 1.34 | 0.76 |
| GW_REVAP | 0.0 | 0.2 | - | S | 0.14 | 0.07 | 0.17 | 0.01 | 0.13 | 0.09 |
| ESCO | 0.8 | 1.0 | - | S | 0.90 | 0.89 | 0.87 | 0.93 | 1.00 | 0.89 |
| EPCO | 0.8 | 1.0 | - | S | 0.89 | 0.89 | 0.91 | 0.81 | 0.87 | 0.87 |
| CH_N2 | 0.0 | 0.3 | - | S | 0.06 | 0.06 | 0.05 | 0.12 | 0.09 | 0.12 |
| CH_K2 | 5.0 | 130.0 | mm/h | S | 130 | 127 | 114 | 59 | 124 | 105 |
| ALPHA_BNK | 0.0 | 1.0 | days | S | 0.51 | 0.84 | 0.33 | 0.22 | 0.28 | 0.16 |
| | Upper Hudson | Caribou |
| |
| Name | Min | Max | Unds. | Type | GHCN | NLDAS | NOHRSC | GHCN | NLDAS | NOHRSC |
| CN2 | −0.4 | 0.4 | - | RC | −0.26 | −0.22 | 0.40 | 0.23 | 0.11 | 0.40 |
| ALPHA_BF | 0.0 | 1.0 | days | S | 0.04 | 0.06 | 0.05 | 0.04 | 0.02 | 0.04 |
| GW_DELAY | 10.0 | 450.0 | days | S | 10 | 95 | 10 | 263 | 148 | 107 |
| GWQMN | 0.0 | 2.0 | mm | S | 0.89 | 0.28 | 2.00 | 0.63 | 0.95 | 1.16 |
| GW_REVAP | 0.0 | 0.2 | - | S | 0.10 | 0.06 | 0.16 | 0.08 | 0.10 | 0.08 |
| ESCO | 0.8 | 1.0 | - | S | 0.98 | 0.89 | 0.86 | 0.85 | 0.87 | 0.90 |
| EPCO | 0.8 | 1.0 | - | S | 0.95 | 0.80 | 0.88 | 0.89 | 0.87 | 0.83 |
| CH_N2 | 0.0 | 0.3 | - | S | 0.12 | 0.15 | 0.24 | 0.21 | 0.28 | 0.30 |
| CH_K2 | 5.0 | 130.0 | mm/h | S | 93 | 78 | 130 | 114 | 130 | 128 |
| ALPHA_BNK | 0.0 | 1.0 | days | S | 0.57 | 0.38 | 0.71 | 0.24 | 0.00 | 0.18 |
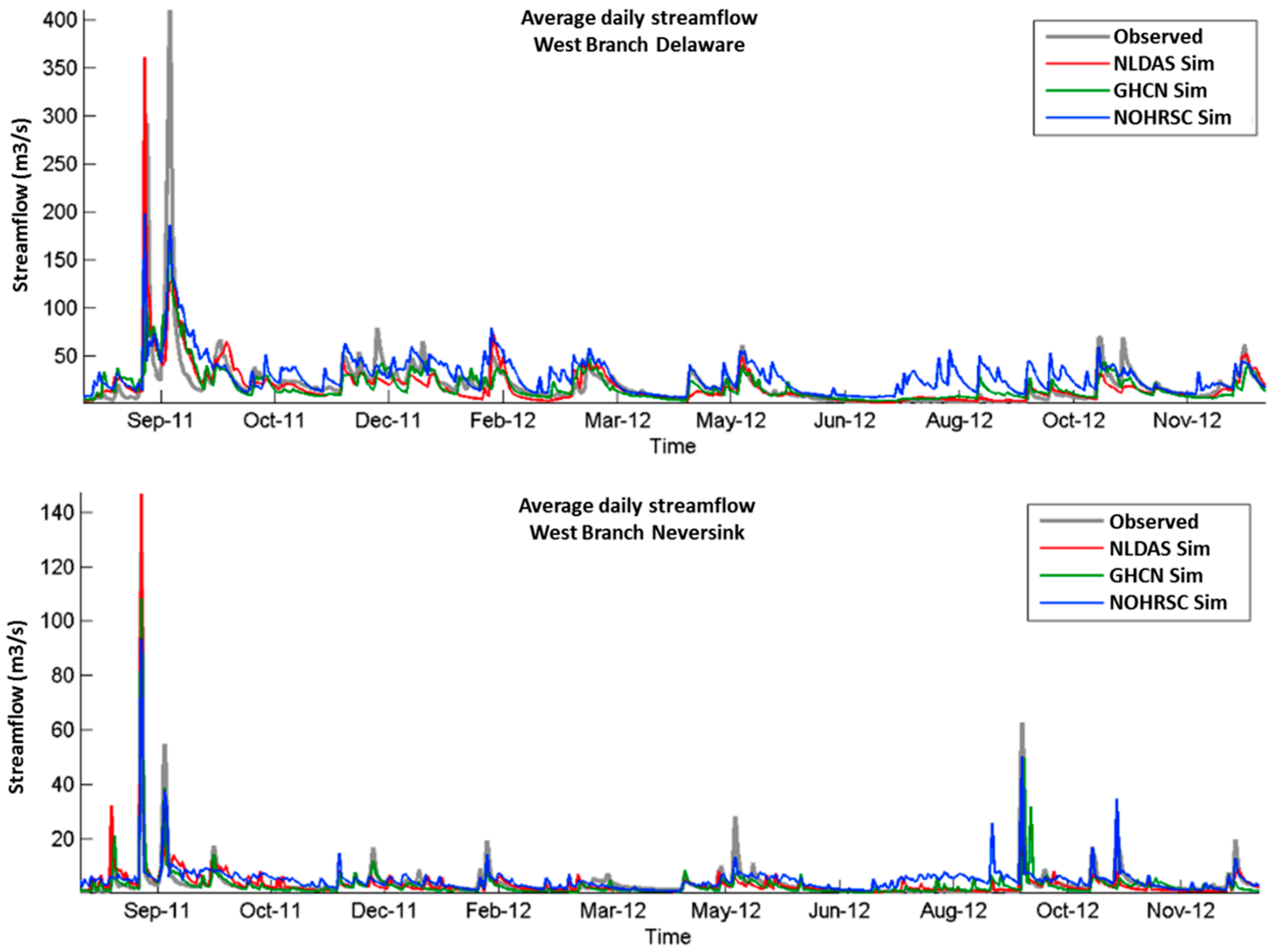
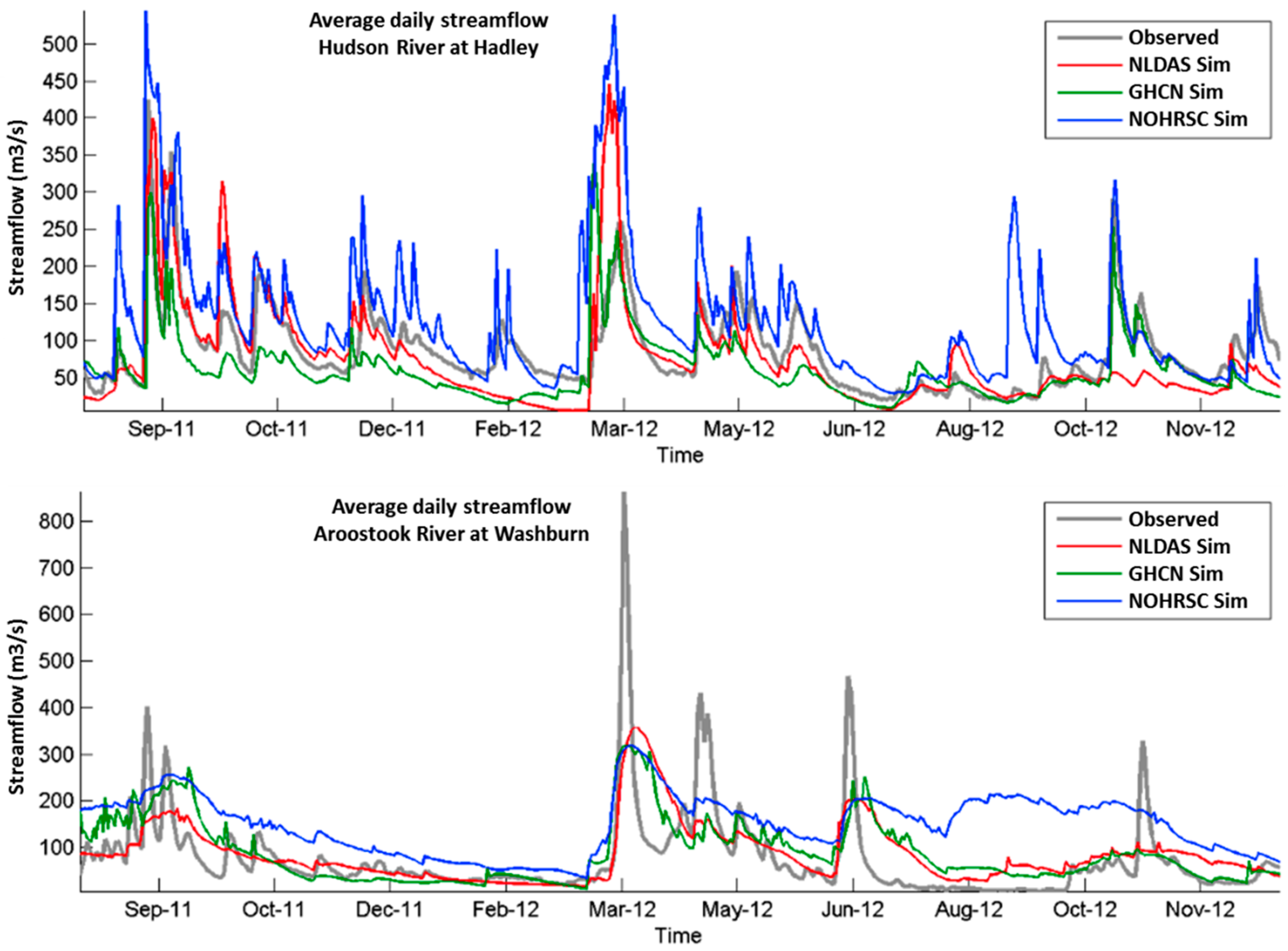
5.3. Daily Scale Results Analysis
Figure 6 and
Figure 7 show the daily streamflow hydrograph for each watershed and scenario. Both figures show that all cases have good agreement with USGS observed streamflow. Some overestimation by the NOHRSC scenario can be seen in all of the watersheds with more noticeable instances for the Aroostook and Hudson rivers (
Figure 7). Like the monthly scale, the NLDAS scenario had the highest correlation coefficient, thus showing the best representation of the variability of daily streamflow, too. The RSR values also showed better agreement for the NLDAS scenario, making it the closest fit for these two statistical measures (
Table 3). However, when comparing the
t-stat test, only the West Delaware (Cannonsville) watershed showed non-significant mean differences for the same NLDAS scenario. Even though, based on the other statistics, NLDAS was the best scenario, further improvements should be made to achieve better streamflow simulation at the daily scale.
Figure 6.
Daily streamflow from the three scenarios compared with the USGS measured at West Branch Delaware and West Branch Neversink for the validation period.
Figure 6.
Daily streamflow from the three scenarios compared with the USGS measured at West Branch Delaware and West Branch Neversink for the validation period.
Based on the complete daily statistics of
Table 3, the only scenario that captured the optimum parameter solution was the NLDAS scenario in the West Delaware watershed. Still, information from all other scenarios could be obtained to find the optimal solution in the other watersheds: in the West Delaware basin, the GHCN scenario had the minimum %Vol.Dif., and thus, NLDAS precipitation could be adjusted based on GHCN’s to see if further improvements could be made locally; the parameter solution for the NOHRSC scenario on the Hudson River Basin was the best approach, because this scenario obtained a TWY/PCP ratio closer to the observed; thus, it should be the reference for further parameter value refinement; lastly, the NLDAS scenarios for calibration generally showed more sensitivity for groundwater parameters than the NOHRSC scenarios, and this last one more than the GHCN scenarios, demonstrating that the distributed data is a better approach for groundwater parameter calibration.
Figure 7.
Daily streamflow from the three scenarios compared with the USGS measured at the Hudson River and Aroostook River for the validation period.
Figure 7.
Daily streamflow from the three scenarios compared with the USGS measured at the Hudson River and Aroostook River for the validation period.
5.4. Multi-Annual Validation
It was explained before that the objective of this research is to study a short-term simulation period (e.g., one year). However, it was also explained that single-year validation period results could be the consequence of the specific climatology of that year. As a consequence, a multi-annual validation period was considered necessary to avoid this possible bias in the findings of this manuscript.
A split-sample calibration scheme was implemented to generate a multi-annual validation period. The parameter solution obtained from this calibration was very similar to the one in the forward calibration scheme. Some differences were observed for the optimum value of the calibrated parameters, but all of them were within the values shown in
Table 5, ±15% around them. The results from this calibration were used to analyze discrete event detection, multi-seasonal statistics and multi-annual statistics.
5.4.1. Discrete Events Analysis
The most responsive simulation in terms of peak detection was obtained for the NLDAS scenario, followed by NOHRSC-ISI.
Table 6 shows the fraction of observed hydrograph peaks that were also hydrograph peaks in the simulated streamflow and the fraction of peaks that were detected on the day they occurred. NLDAS was considered to be the meteorological data source that provided the most accurate streamflow hydrograph firstly, because the statistical analysis shown before, and, secondly, because the main hydrograph portions (rising limb, crest segment which includes peak flow rate and recession limb) turned out to be very similar to those found in the observed streamflow hydrograph. This is crucial, since coincidence in these inflection points of the streamflow hydrograph means that, using the SWAT model combined with distributed weather data, it is possible to better understand changes in the streamflow contributions.
Table 6.
Statistics for the detection of peak events over the validation period (2009–2012) from the split-sample scheme. A detection is when peaks are in both (simulated and observed streamflow); a timely detected peak is when observed and simulated streamflow peak are in the same day; flow threshold is the threshold over which a peak is considered.
Table 6.
Statistics for the detection of peak events over the validation period (2009–2012) from the split-sample scheme. A detection is when peaks are in both (simulated and observed streamflow); a timely detected peak is when observed and simulated streamflow peak are in the same day; flow threshold is the threshold over which a peak is considered.
| Event Accuracy | West Branch Delaware | West Branch Neversink |
| Obs. | GHCN | NLDAS | NOHRSC | Obs. | GHCN | NLDAS | NOHRSC |
| Detection | 22 | 23% | 32% | 27% | 28 | 20% | 16% | 28% |
| Timely Detected Peaks | 18% | 14% | 14% | 16% | 16% | 28% |
| Flow (Q) Threshold | Q > 70 m3/s | Q > 15 m3/s |
| Event Accuracy | Upper Hudson | Aroostook River |
| Obs. | GHCN | NLDAS | NOHRSC | Obs. | GHCN | NLDAS | NOHRSC |
| Detection | 19 | 74% | 89% | 89% | 22 | 23% | 32% | 27% |
| Timely Detected Peaks | 21% | 21% | 32% | 18% | 14% | 14% |
| Flow (Q) Threshold | Q > 200 m3/s | Q > 200 m3/s |
5.4.2. Seasonal Analysis
The SWAT model runoff production, like several other hydrological models, is based on two processes, namely precipitation and snow melt. Thus, it is also of interest to see how good is the performance of the model in both periods, under snow presence and without snow presence, on the watershed (
Table 7). The RSR values for the simulated daily streamflow for all watersheds and scenarios improved in most of the cases from snow periods to no-snow periods. The root mean square error (RMSE) for all scenarios was relatively higher for the months of March and April. The relative error for each scenario was large in some cases and not constant throughout the simulation period, showing relative error values from 1% up to 97%. Several reasons could be the cause of this, like errors in the snowmelt amount calculations or bad timing of the snowmelt/accumulation process, but this issue will be addressed in future studies.
5.4.3. Multi-Annual Statistical Analysis
Extending the validation period to four years (e.g., 2009–2012) can confirm that the observations and analysis made before are still valid for different climatological conditions and not only for the ones observed in that specific year (2012).
Table 8 shows the daily statistics for the four-year validation period (2009–2012) obtained from the split-sample calibration scheme. The results were very similar to those obtained with the forward calibration scheme. The NLDAS dataset was the best approach for calibration and achieved the best results for streamflow simulation. This scenario explained the variability of streamflow (higher R
2 values), the magnitude of the events (lower RMSE and RSR values) and the watersheds water yield (lower %Vol.Dif. values) better.
Table 7.
RMSE and RSR comparison for the snow-influenced streamflow (December to April) and no snow-influenced streamflow (May to October) periods. All tested watersheds and over the validation period (2009–2012) from the split-sample scheme.
Table 7.
RMSE and RSR comparison for the snow-influenced streamflow (December to April) and no snow-influenced streamflow (May to October) periods. All tested watersheds and over the validation period (2009–2012) from the split-sample scheme.
| | West Branch Delaware | West Branch Neversink | Upper Hudson | Aroostook River | |
|---|
| Dec–Apr | May–Oct | Dec–Apr | May–Oct | Dec–Apr | May–Oct | Dec–Apr | May–Oct |
|---|
| GHCN | 21.64 | 11.65 | 1.32 | 1.35 | 65.57 | 40.06 | 97.65 | 60.23 | RMSE |
| NLDAS | 18.66 | 10.60 | 1.86 | 1.02 | 77.61 | 44.22 | 99.42 | 99.42 |
| NOHRSC | 22.93 | 22.93 | 1.53 | 0.23 | 107.13 | 63.88 | 95.79 | 106.47 |
| GHCN | 0.73 | 0.35 | 0.19 | 0.18 | 0.64 | 0.52 | 0.66 | 0.75 | RSR |
| NLDAS | 0.63 | 0.32 | 0.27 | 0.14 | 0.76 | 0.57 | 0.68 | 0.55 |
| NOHRSC | 0.77 | 0.47 | 0.22 | 0.03 | 1.05 | 0.83 | 0.65 | 1.33 |
Table 8.
Multi-annual daily statistics for streamflow for each scenario and watershed for the split-sample scheme validation period (2009–2012). Notes: critical value for the t-test for a daily time step is ±1.67. Shaded values are the best for each efficiency measure. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data.
Table 8.
Multi-annual daily statistics for streamflow for each scenario and watershed for the split-sample scheme validation period (2009–2012). Notes: critical value for the t-test for a daily time step is ±1.67. Shaded values are the best for each efficiency measure. S1 is the scenario with GHCN-D data; S2 is the scenario with NLDAS data; and S3 is the scenario with NOHRSC-ISI data.
| Time Step | Stats | West Branch Delaware | West Branch Neversink | Upper Hudson | Aroostook River |
|---|
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 |
|---|
| DAILY Validation Period | R2 | 0.58 | 0.59 | 0.47 | 0.52 | 0.66 | 0.58 | 0.58 | 0.58 | 0.44 | 0.49 | 0.54 | 0.48 |
| RMSE | 19.3 | 19.3 | 22.1 | 4.4 | 3.7 | 4.1 | 65.7 | 65.6 | 97.7 | 82.3 | 77.9 | 105.7 |
| RSR | 0.65 | 0.65 | 0.74 | 0.71 | 0.61 | 0.66 | 0.67 | 0.67 | 1.00 | 0.72 | 0.68 | 0.93 |
| t-test | 0.30 | 1.40 | −2.98 | 4.58 | 3.04 | −3.98 | 4.77 | 1.25 | −7.59 | −1.86 | −0.56 | −16.7 |
| %Vol.Dif. | −1.2% | −6.1% | 12.3% | −27% | −18% | 24% | −17% | −4.8% | 34% | 7.2% | 2.2% | 69% |
It is also of great importance to notice that the results did not show any correlation between the characteristics of the watersheds (slope, elongation and length) used in this experiment and the performance of the model. Even though different watershed characteristics were used (
Table 2), none of them seemed to affect the performance of the model. However, based on the
t-test and %Vol.Dif., better efficiency of the model was observed using the NLDAS dataset on larger watersheds (Upper Hudson and Aroostook River) than in smaller watersheds (W Branch Neversink). The first observation can be explained because the watershed characteristics are taken into account within the model’s inputs. The second observation can be explained because NLDAS is a distributed dataset, and thus, it can better represent the weather spatial variability within a larger watershed. However, it fails to have enough precision at smaller scales. Future work will also concentrate on studying these two observations further and their explanations.
6. Conclusions
Three different meteorological data sources were used as the inputs into the SWAT hydrological model to simulate four different watersheds’ streamflow. Each watershed was calibrated from 2007 to 2011 and validated on 2012. It was demonstrated that different meteorological datasets can produce different hydrological responses for a given watershed. Consequently, the use of different meteorological datasets for calibration and validation of the model could be recommended to improve the simulation.
Simulations with NLDAS and NOHRSC-ISI data were shown to be the more responsive when compared to the other scenarios. This was expected, because both meteorological datasets had better coverage of the watersheds’ area. Therefore, the representation of the spatial variability of precipitation and temperature over the watershed was better in these two scenarios. Based on the R2, RMSE and RSR values, the simulation scenario with the NLDAS dataset can achieve an overall better agreement with the measured streamflow, but some issues should be further assessed: the performance differences from snow season to no-snow season and the results derived from the t-test at a daily time scale. Uncertainty associated with the snow sub-routines for accumulation and melting processes could be the reason for the discrepancies in the snow-influenced periods and should be studied further. The calibration process can be improved further based on the results of each watershed’s scenario; NLDAS in some cases presented lower precipitation values than the other two datasets, and most of the time, NOHRSC presented higher precipitation and temperature values; subsequently, one dataset can be statistically corrected with the aid of the other dataset (if necessary).
Based on the findings, there is no relationship between the characteristics of the watershed and the results obtained from the model’s output. The streamflow simulation results are more impacted by the weather inputs and the calibration parameters than by the physical characteristics of the watersheds. The reason for this is that the watershed characteristics, such as land cover, soil properties, slope and elevation differences, are already taken into account by the model as input data.
The scenarios fail to capture, for the different watersheds, either the spatial variability (GHCN-D) or the events’ magnitudes (NLDAS and NOHRSC-ISI). As a consequence, the merging of datasets can help minimize the uncertainty. Using two calibration scenarios (e.g., NLDAS and GHCN) and comparing the optimum parameter solutions from each scenario can give a better idea of which parameter set is the best.
Improvement of the model’s results can be accomplished by taking into account more stations. Analyzing the R2 values for each scenario, the NOHRSC-ISI and NLDAS spatially distributed forcing weather datasets showed more consistency over time and seasons than the GHCN-D weather dataset. Gridded data from assimilation systems or remote sensing datasets should be used whenever possible, but should be analyzed for bias and accuracy on each site.
Acknowledgement
This study was supported and monitored by the National Oceanic and Atmospheric Administration (NOAA) under Center of Remote Sensing Science and Technology (CREST) Grant No. NA11SEC4810004. The statements contained within the research article are not the opinions of the funding agency nor the U.S. government, but reflect the author’s opinions. A special thanks to Isabel Perez, Don Pierson, Elliot Schneiderman and Mark Zion for their contributions and ideas. Finally, thank you very much to the anonymous reviewers, whose contributions were of great importance to the improvement of the manuscript.
Author Contributions
Jose Alberto Infante Corona was responsible for data analysis, writing the manuscript and communicating with the journal. Tarendra Lakhankar, Soni Pradhanang and Reza Khanbilvardi were responsible for supervising the experiments, the structure of the manuscript and providing key components for discussion on the results and conclusions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leon, A.S.; Kanashiro, E.A.; Valverde, R.; Sridhar, V. Dynamic framework for intelligent control of river flooding: Case study. J. Water Resour. Plan. Manag. 2012, 140, 258–268. [Google Scholar] [CrossRef]
- Werner, M.; Schellekens, J.; Gijsbers, P.; Van Dijk, M.; Van den Akker, O.; Heynert, K. The Delft-FEWS flow forecasting system. Environ. Model. Softw. 2013, 40, 65–77. [Google Scholar] [CrossRef]
- Hora, S.C. Aleatory and epistemic uncertainty in probability elicitation with an example from hazardous waste management. Reliab. Eng. Syst. Saf. 1996, 54, 217–223. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Kavetski, D.; Franks, S.W.; Kuczera, G. Confronting Input Uncertainty in Environmental Modelling, in Calibration of Watershed Models; Duan, Q., Gupta, H.V., Sorooshian, S., Rousseau, A.N., Turcotte, R., Eds.; American Geophysical Union: Washington, D.C., USA, 2003. [Google Scholar]
- Yen, H.; Wang, X.; Fontane, D.G.; Harmel, R.D.; Arabi, M. A framework for propagation of uncertainty contributed by parameterization, input data, model structure, and calibration/validation data in watershed modeling. Environ. Model. Softw. 2014, 54, 211–221. [Google Scholar] [CrossRef]
- Harmel, R.D.; Cooper, R.J.; Slade, R.M.; Haney, R.L.; Arnold, J.G. Cumulative uncertainty in measured streamflow and water quality data for small watersheds. ASABE 2006, 49, 689–701. [Google Scholar] [CrossRef]
- Daren Harmel, R.; Smith, P.K. Consideration of measurement uncertainty in the evaluation of goodness-of-fit in hydrologic and water quality modeling. J. Hydrol. 2007, 337, 326–336. [Google Scholar]
- Bedient, P.B.; Huber, W.C.; Vieux, B.E. Hydrology and Floodplain Analysis, 5th ed.; Stark, H., Ed.; Prentice Hall: Cranbury, NJ, USA, 2012; p. 800. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Beven, K. Robert E. Horton’s perceptual model of infiltration processes. Hydrol. Process. 2004, 18, 3447–3460. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res.: Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Mishra, A.K. Effect of rain gauge density over the accuracy of rainfall: A case study over Bangalore, India. Springerplus 2013, 2, 311. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Liston, G.E.; Hiemstra, C.A. A simple data assimilation system for complex snow distributions (SnowAssim). J. Hydrometeorol. 2008, 9, 989–1004. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. ASABE 2012, 55, 1491–1508. [Google Scholar]
- Arsenault, R.; Brissette, F. Determining the optimal spatial distribution of weather station networks for hydrological modeling purposes using RCM datasets: An experimental approach. J. Hydrometeorol. 2014, 15, 517–526. [Google Scholar] [CrossRef]
- Cole, S.J.; Moore, R.J. Distributed hydrological modelling using weather radar in gauged and ungauged basins. Adv. Water Resour. 2009, 32, 1107–1120. [Google Scholar] [CrossRef]
- Méndez-Antonio, B.; Caetano, E.; Soto-Cortés, G.; Rivera-Trejo, F.G.; Carvajal Rodríguez, R.A.; Watts, C. Weather radar data and distributed hydrological modelling: An application for Mexico Valley. Open J. Mod. Hydrol. 2013, 3, 79–88. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Tolson, B.A. Progress in integrating remote sensing data and hydrologic modeling. Prog. Phys. Geogr. 2014, 38, 464–498. [Google Scholar] [CrossRef]
- Zhu, D.; Xuan, Y.; Cluckie, I. Hydrological appraisal of operational weather radar rainfall estimates in the context of different modelling structures. Hydrol. Earth Syst. Sci. 2014, 18, 257–272. [Google Scholar] [CrossRef]
- Rui, H. Readme Document for North America Land Data Assimilation System Phase 2 (NLDAS-2) Products; Goddard Earth Sciences Data and Information Services: Greenbelt, ML, USA, 2013.
- Carroll, T.R. Operational remote sensing of snow water equivalent and soil moisture in the United States using natural terrestrial gamma radiation. IAHS 1987, 166, 213–223. [Google Scholar]
- National Climatic Data Center from NESDIS GHCN-D Dataset. Available online: http://gis.ghcn.noaa.gov/map/viewer/#app=cdo (accessed on 15 May 2013).
- Hydrological Sciences Laboratory at NASA/Goddard Space Flight Center (GSFC/HSL). NLDAS Forcing Data L4 Hourly 0.125 × 0.125 degree. Available online: http://disc.sci.gsfc.nasa.gov/hydrology/data-holdings (accessed on 15 May 2013).
- National Operational Hydrologic Remote Sensing Center. Interactive Snow Information NOHRSC-ISI Weather Data. Available online: http://www.nohrsc.noaa.gov/interactive/html/map.html (accessed on 10 June 2013).
- Reybold, W.U.; TeSelle, G.W. Soil geographic data bases. J. Soil Water Conserv. 1989, 44, 28–29. [Google Scholar]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The national elevation dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–32. [Google Scholar]
- Fry, J.A.; Coan, M.J.; Homer, C.G.; Meyer, D.K.; Wickham, J.D. National land cover database (NLCD). Available online: http://viewer.nationalmap.gov/viewer (accessed on 15 February 2013).
- United States Geological Survey. The USGS National Water Information System (NWIS). Available online: http://waterdata.usgs.gov/nwis (accessed on 15 May 2013).
- Williams, J.R.; Arnold, J.G.; Kiniry, J.R.; Gassman, P.W.; Green, C.H. History of model development at Temple, Texas. Hydrol. Sci. J. 2008, 53, 948–960. [Google Scholar] [CrossRef]
- Engel, B.A.; Srinivasan, R.; Arnold, J.G.; Rewerts, C.; Brown, S.J. Nonpoint source (NPS) pollution modeling using models integrated with geographic information systems (GIS). Water Sci. Technol. 1993, 28, 685–690. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Allen, P.M. Continental scale simulation of the hydrologic balance. Am. Water Resour. Assoc. 2000, 35, 1037–1051. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assesment tool: Historical development, applications, and future research directions. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011; p. 647. [Google Scholar]
- Kannan, N.; Santhi, C.; Williams, J.R.; Arnold, J.G. Development of a continuous soil moisture accounting procedure for curve number methodology and its behaviour with different evapotranspiration methods. Hydrol. Process. 2008, 22, 2114–2121. [Google Scholar] [CrossRef]
- Anderton, S.; Latron, J.; Gallart, F. Sensitivity analysis and multi-response, multi-criteria evaluation of a physically based distributed model. Hydrol. Process. 2002, 16, 333–353. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parametrisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Shirmohammadi, A.; Chu, T.W. Evaluation of the SWAT model’s hydrology component in the Piedmont physiographic region of Maryland. ASAE 2004, 47, 1057–1073. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. ASAE 2007, 50, 885–900. [Google Scholar]
- Vazquez-Amábile, G.G.; Engel, B.A. Use of SWAT to compute groundwater table depth and streamflow in the Muscatatuck River watershed. ASAE 2005, 48, 991–1003. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrologic modeling of the Iroquois River watershed using HSPF and SWAT. Am. Water Resour. Assoc. 2005, 41, 361–375. [Google Scholar] [CrossRef]
- Church, M.R.; Bishop, G.D.; Cassell, D.L. Maps of regional evapotranspiration and runoff/precipitation ratios in the northeast United States. J. Hydrol. 1995, 168, 283–298. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).