Numerical Simulation of the Isoparaffins Dehydrogenation Process in Fluidized Bed Reactor: From Laboratory to Industry
Abstract
1. Introduction
2. Materials and Methods
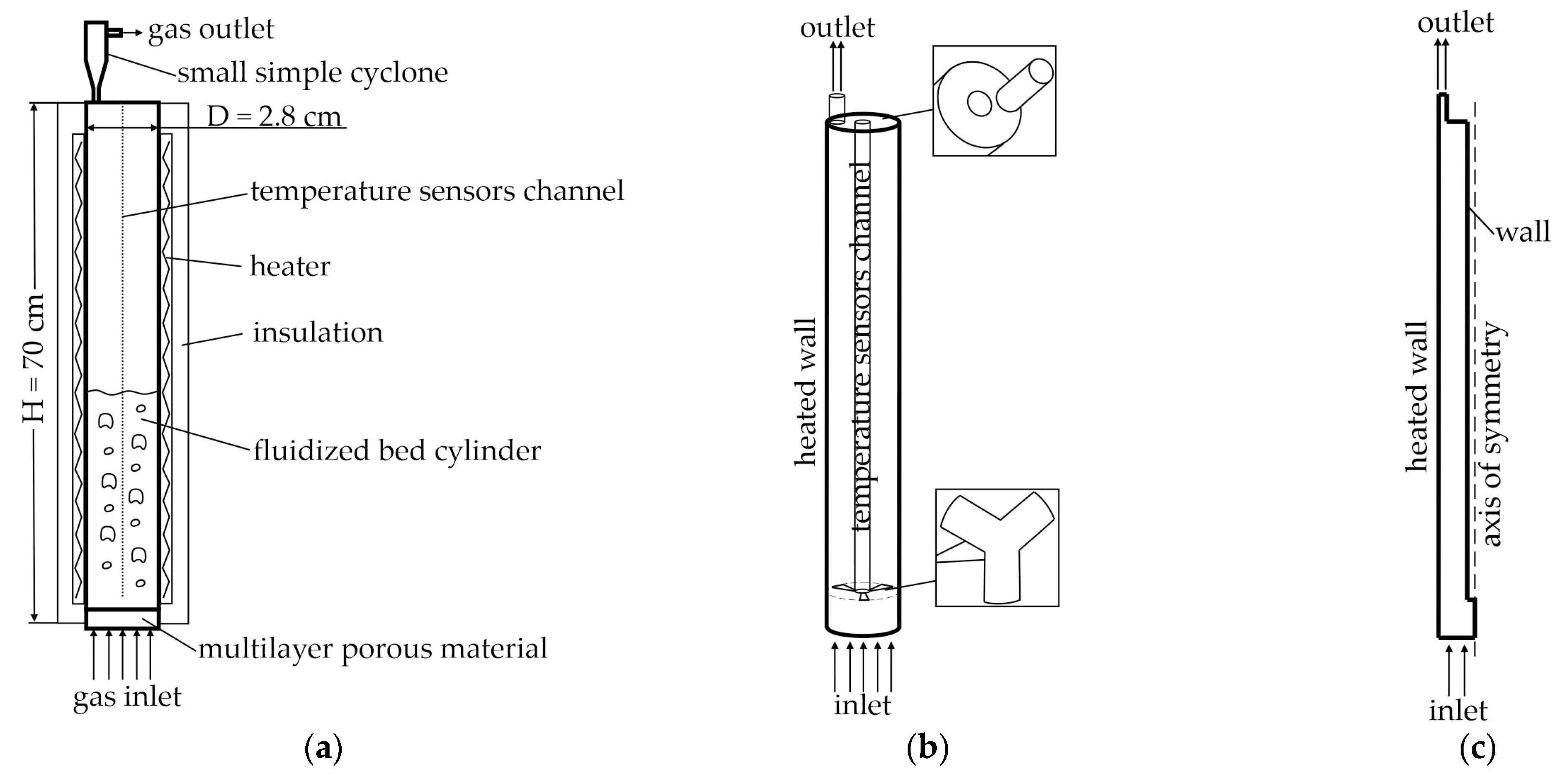
2.1. Laboratory Reactor
2.2. Industrial Reactor
2.3. CFD-Simulation Model
2.3.1. Fluidize Bed Hydrodynamic Model
2.3.2. Fluidize Bed Heat Transfer Model
2.3.3. Chemical Reaction Model
2.3.4. Particle Mean Diameter
2.3.5. Boundary and Initial Conditions
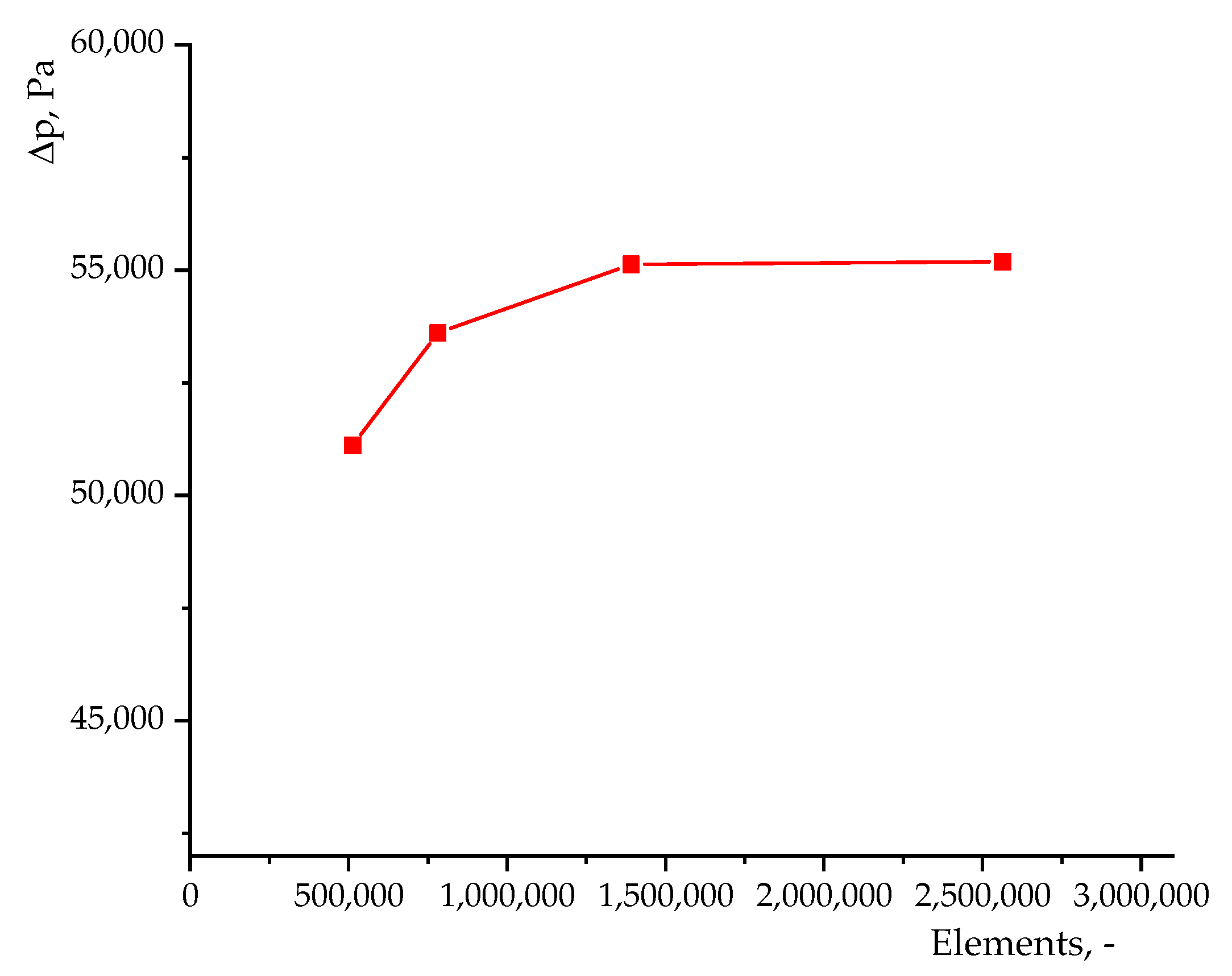
2.3.6. Mesh and Time Step
3. Results
3.1. Laboratory Reactor Simulation
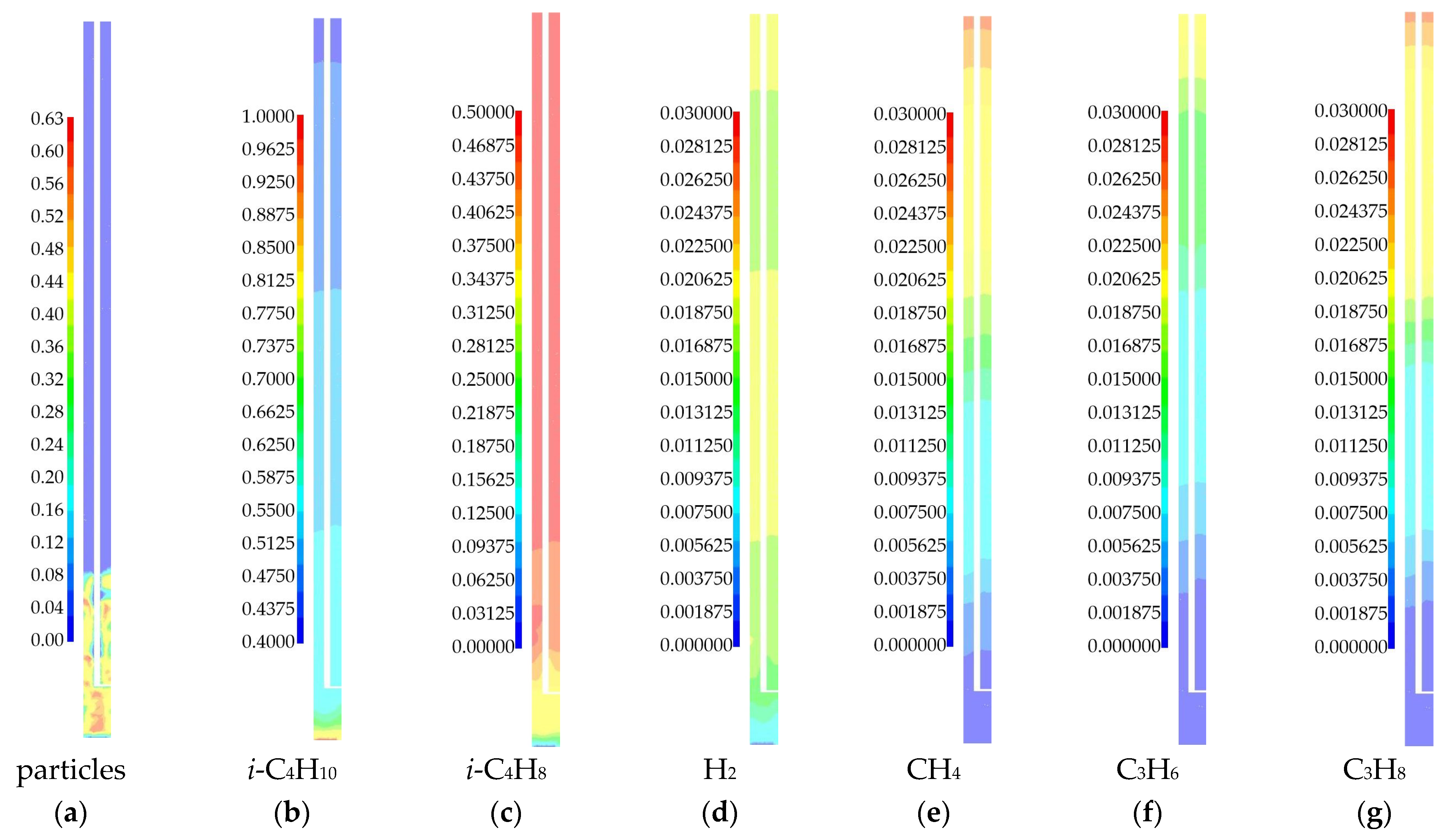
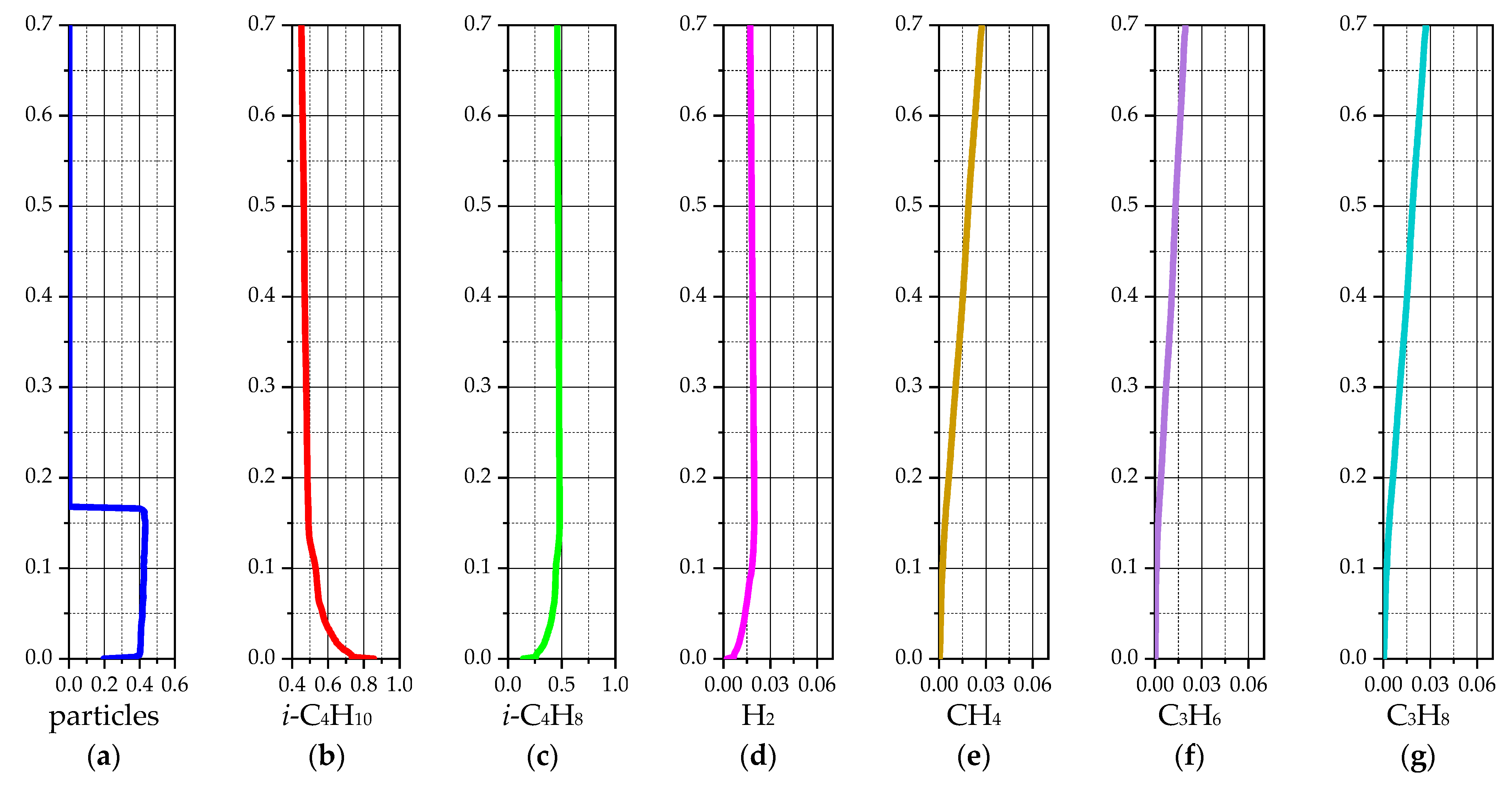
3.1.1. 3D Simulation
3.1.2. 2D-Axisymmetric Simulation
3.2. Industrial Reactor Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| A | heat exchange surface area |
| coefficient of the gas–solid contact area | |
| pre-exponential factor | |
| CD | drag coefficient |
| Cfr | friction coefficient |
| species concentration in the mixture | |
| Cp | heat capacity |
| D | particle diameter |
| d | particle diameter |
| D32 | Sauter mean diameter |
| mass diffusion coefficients | |
| thermal diffusion coefficients | |
| activation energy | |
| es | coefficient of recovery |
| distribution density function | |
| g | gravitation |
| h | enthalpy |
| hgs | heat transfer coefficient |
| unit tensor | |
| diffusion flux | |
| K | coefficient of interaction between phases |
| reaction rate constant | |
| granule energy diffusion coefficient | |
| molecular weight | |
| number of reactions | |
| NC | Courant number |
| Nu | Nusselt number |
| Pr | Prandtl number |
| pressure | |
| ps | pressure of solid phase granules |
| species formation source | |
| Re | Reynolds number |
| Schmidt number | |
| T | temperature |
| t | time |
| velocity | |
| species mass fraction | |
| Greek symbols | |
| volume fraction | |
| particle collisions energy dissipation | |
| exponent for the reactant | |
| solid granule temperature | |
| radial distribution coefficient | |
| the thermal conductivity coefficient | |
| bulk viscosity | |
| shear viscosity | |
| density | |
| stress tensor | |
| energy exchange | |
| Subscripts | |
| g | gas phase |
| s | solid phase |
References
- Kunii, D.; Levenspiel, O. Fluidization engineering. In Butterworth-Heinemann; Butterworth-Heinemann: Oxford, UK, 1991; p. 491. [Google Scholar]
- Grace, J.R.; Bi, X.; Ellis, N. Essentials of Fluidization Technology; Grace, J.R., Bi, X., Ellis, N., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2020; p. 611. [Google Scholar]
- Sadeghbeigi, R. Fluid Catalytic Cracking Handbook: An Expert Guide to the Practical Operation, Design, and Optimization of FCC Units; Butterworth-Heinemann: Oxford, UK, 2020; p. 352. [Google Scholar]
- de Lasa, H. Chemical Reactor Design and Technology: Overview of the New Developments of Energy and Petrochemical Reactor Technologies. Projections for the 90’s; de Lasa, H., Ed.; University of Porto: Porto, Portugal, 2012; p. 850. [Google Scholar]
- Basu, P. Combustion and Gasification in Fluidized Beds; CRC Press: Boca Raton, FL, USA, 2006; p. 496. [Google Scholar]
- Bai, P.; Etim, U.J.; Yan, Z.; Mintova, S.; Zhang, Z.; Zhong, Z.; Gao, X. Fluid catalytic cracking technology: Current status and recent discoveries on catalyst contamination. Catal. Rev. 2019, 61, 333–405. [Google Scholar] [CrossRef]
- Özkaya, B.; Kaksonen, A.H.; Sahinkaya, E.; Puhakka, J.A. Fluidized bed bioreactor for multiple environmental engineering solutions. Water Res. 2019, 150, 452–465. [Google Scholar] [CrossRef]
- Hanchate, N.; Ramani, S.; Mathpati, C.S.; Dalvi, V.H. Biomass gasification using dual fluidized bed gasification systems: A review. J. Clean. Prod. 2021, 280, 123148. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, T.; Hou, B.; Yang, H.; Hu, N.; Zhang, M. A comprehensive review of biomass gasification characteristics in fluidized bed reactors: Progress, challenges, and future directions. Fluids 2025, 10, 147. [Google Scholar] [CrossRef]
- Menéndez, M.; Herguido, J.; Bérard, A.; Patience, G.S. Experimental methods in chemical engineering: Reactors-fluidized beds. Can. J. Chem. Eng. 2019, 97, 2383–2394. [Google Scholar] [CrossRef]
- Chen, J.; Kemoun, A.; Al-Dahhan, M.H.; Dudukovi´c, M.P.; Lee, D.J.; Fan, L.-S. Comparative hydrodynamics study in a bubble column using computer-automated radioactive particle tracking (CARPT)/computed tomography (CT) and particle image velocimetry (PIV). Chem. Eng. Sci. 1999, 54, 2199–2207. [Google Scholar] [CrossRef]
- Jin, H.; Yang, S.; Guo, Z.; Guangxiang, H.; Tong, Z. The axial distribution of holdups in an industrial-scale bubble column with evaluated pressure using gamma ray attenuation approach. Chem. Eng. J. 2005, 115, 45–50. [Google Scholar] [CrossRef]
- Patel, A.K.; Waje, S.S.; Thorat, B.N.; Mujumdar, A.S. Tomographic diagnosis of gas maldistribution in gas–solid fluidized beds. Powder Technol. 2008, 185, 239–250. [Google Scholar] [CrossRef]
- Heindel, T.J.; Gray, J.N.; Jensen, T.C. An X-ray system for visualizing fluid flows. Flow Meas. Instrum. 2008, 19, 67–78. [Google Scholar] [CrossRef]
- Wang, F.; Marashdeh, Q.; Wang, A.; Fan, L.-S. Electrical capacitance volume tomography imaging of three-dimensional flow structures and solids concentration distributions in a riser and a bend of a gas–solid circulating fluidized bed. Ind. Eng. Chem. Res. 2012, 51, 10968–10976. [Google Scholar] [CrossRef]
- Mandal, D.; Sharma, V.K.; Pant, H.J.; Sathiyamoorthy, D.; Vinjamur, M. Quality of fluidization in gas–solid unary and packed fluidized beds: An experimental study using gamma ray transmission technique. Powder Technol. 2012, 226, 91–98. [Google Scholar] [CrossRef]
- Escudero, D.R.; Heindel, T.J. Acoustic fluidized bed hydrodynamics characterization using X-ray computed tomography. Chem. Eng. J. 2014, 243, 411–420. [Google Scholar] [CrossRef]
- Kingston, T.A.; Geick, T.A.; Robinson, T.R.; Heindel, T.J. Characterizing 3D granular flow structures in a double screw mixer using X-ray particle tracking velocimetry. Powder Technol. 2015, 278, 211–222. [Google Scholar] [CrossRef]
- Errigo, M.; Lettieri, P.; Materazzi, M. X-ray imaging techniques for gas–solid fluidized beds: A technical review. Particuology 2005, 101, 67–89. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C.; Tao, Y. Computational Fluid Dynamics: A Practical Approach; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Zhao, Z.; Zhou, L.; Bai, L.; Wang, B.; Agarwal, R. Recent advances and perspectives of CFD–DEM simulation in fluidized bed. Arch. Comput. Methods Eng. 2024, 31, 871–918. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. A comparison of two-fluid model, dense discrete particle model and CFD-DEM method for modeling impinging gas–solid flows. Powder Technol. 2014, 254, 94–102. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Wu, Y.; Liu, D.; Hu, J.; Ma, J.; Chen, X. Comparative study of two fluid model and dense discrete phase model for simulations of gas–solid hydrodynamics in circulating fluidized beds. Particuology 2021, 55, 108–117. [Google Scholar] [CrossRef]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2020, 215, 115428. [Google Scholar] [CrossRef]
- Alobaid, F.; Almohammed, N.; Farid, M.M.; May, J.; Rößger, P.; Richter, A.; Epple, B. Progress in CFD simulations of fluidized beds for chemical and energy process engineering. Prog. Energy Combust. Sci. 2022, 91, 100930. [Google Scholar] [CrossRef]
- Wang, S.; Hu, C.; Luo, K.; Yu, J.; Fan, J. Multi-scale numerical simulation of fluidized beds: Model applicability assessment. Particuology 2023, 80, 11–41. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Zhou, G.; Xie, J.; Zhang, H. CFD simulation of dense particulate reaction system: Approaches, recent advances and applications. Chem. Eng. Sci. 2016, 140, 16–43. [Google Scholar] [CrossRef]
- Akbari, V.; Borhani, T.N.G.; Shamiri, A.; Shafeeyan, M.S. Computational fluid dynamics modeling of gas-solid fluidized bed reactor: Influence of numerical and operating parameters. Exp. Comput. Multiph. Flow 2024, 6, 85–125. [Google Scholar] [CrossRef]
- Qi, W.; Lan, P.; Yang, J.; Chen, Y.; Zhang, Y.; Wang, G.; Peng, F.; Hong, J. Multi-U-Style micro-channel in liquid cooling plate for thermal management of power batteries. Appl. Therm. Eng. 2024, 256, 123984. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Song, Y.; Qi, W.; Guo, Q.; Li, X.; Kong, L.; Chen, J. Real-time global optimal energy management strategy for connected PHEVs based on traffic flow information. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20032–20042. [Google Scholar] [CrossRef]
- Gosavi, A.A.; Nandgude, T.D.; Mishra, R.K.; Puri, D.B. Exploring the Potential of Artificial Intelligence as a Facilitating Tool for Formulation Development in Fluidized Bed Processor: A Comprehensive Review. AAPS PharmSciTech 2024, 25, 111. [Google Scholar] [CrossRef]
- Alotaibi, F.N.; Berrouk, A.S.; Salim, I.M. Scaling up dry methane reforming: Integrating computational fluid dynamics and machine learning for enhanced hydrogen production in industrial-scale fluidized bed reactors. Fuel 2024, 376, 132673. [Google Scholar] [CrossRef]
- Schneiderbauer, S.; Puttinger, S.; Pirker, S.; Aguayo, P.; Kanellopoulos, V. CFD modeling and simulation of industrial scale olefin polymerization fluidized bed reactors. Chem. Eng. J. 2015, 264, 99–112. [Google Scholar] [CrossRef]
- Schneiderbauer, S.; Pirker, S.; Puttinger, S.; Aguayo, P.; Touloupidis, V.; Joaristi, A.M. A Lagrangian-Eulerian hybrid model for the simulation of poly-disperse fluidized beds: Application to industrial-scale olefin polymerization. Powder Technol. 2017, 316, 697–710. [Google Scholar] [CrossRef]
- Shah, S.; Myöhänen, K.; Kallio, S.; Hyppänen, T. CFD simulations of gas–solid flow in an industrial-scale circulating fluidized bed furnace using subgrid-scale drag models. Particuology 2015, 18, 66–75. [Google Scholar] [CrossRef]
- Solov’ev, S.A.; Egorov, A.G.; Lamberov, A.A.; Egorova, S.R.; Kataev, A.N. Effect of the design of a feedstock injection device in a fluidized bed reactor on the efficiency of the reaction, using the dehydrogenation of iso-paraffins in a fluidized chromia-alumina catalyst bed as an example. Catal. Ind. 2016, 8, 48–55. [Google Scholar] [CrossRef]
- Soloveva, O.V.; Solovev, S.A.; Egorova, S.R.; Lamberov, A.A.; Antipin, A.V.; Shamsutdinov, E.V. CFD modeling a fluidized bed large scale reactor with various internal elements near the heated particles feeder. Chem. Eng. Res. Des. 2018, 138, 212–228. [Google Scholar] [CrossRef]
- Dash, S.; Mohanty, S.; Mishra, B.K. CFD modelling and simulation of an industrial scale continuous fluidized bed roaster. Adv. Powder Technol. 2020, 31, 658–669. [Google Scholar] [CrossRef]
- Lin, R.; Wang, S.; Tao, Y.; Feng, X.; Zhang, H. Numerical Simulation and Optimization of Industrial-Scale Fluidized Bed Reactor Coupling Biomass Catalytic Pyrolysis Kinetics. Energies 2025, 18, 3601. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, B.; Wang, W.; Liu, M.; Lu, C.; Ye, M. CFD simulation of an industrial MTO fluidized bed by coupling a population balance model of coke content. Chem. Eng. J. 2022, 446, 136849. [Google Scholar] [CrossRef]
- Han, C.; Xu, Y.; Lu, B.; Wang, W. Two-Phase and Three-Phase Modeling of an Industrial Fluidized Bed for Maximizing Iso-Paraffins. Chem. Ing. Tech. 2023, 95, 97–106. [Google Scholar] [CrossRef]
- Sun, H.; Yang, S.; Bao, G.; Luo, K.; Hu, J.; Wang, H. CFD investigation of the complex multiphase flow of biomass gasification in industrial-scale dual fluidized bed reactor. Chem. Eng. J. 2023, 457, 141312. [Google Scholar] [CrossRef]
- Sun, H.; Bao, G.; Yang, S.; Hu, J.; Wang, H. Numerical investigation on the influence of immersed tube bundles on biomass gasification in industrial-scale dual fluidized bed gasifier. Fuel 2024, 357, 129742. [Google Scholar] [CrossRef]
- Singh, V.; Nemalipuri, P.; Das, H.C.; Vitankar, V. An Eulerian-Eulerian multifluid simulation for co-combustion of coal and sawdust in industrial scale circulating fluidized bed boiler. Clean. Energy Syst. 2025, 10, 100169. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, W.; Du, X.; Pan, M.; Yu, H.; Gao, F.; Wu, F.; Hong, Y.; Wang, Y.; Zhou, M.; et al. Enhancing the desulfurization performance of industrial scale circulating fluidized bed flue gas desulfurization process using turbulent ring. Appl. Therm. Eng. 2025, 272, 126339. [Google Scholar] [CrossRef]
- Sanfilippo, D.; Miracca, I. Dehydrogenation of paraffins: Synergies between catalyst design and reactor engineering. Catal. Today 2006, 111, 133–139. [Google Scholar] [CrossRef]
- Sanfilippo, D. Dehydrogenations in fluidized bed: Catalysis and reactor engineering. Catal. Today 2011, 178, 142–150. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, L.; Berrouk, A.S. Exergy analysis of propane dehydrogenation in a fluidized bed reactor: Experiment and MP-PIC simulation. Energy Convers. Manag. 2019, 202, 112213. [Google Scholar] [CrossRef]
- Airaksinen, S.M.; Harlin, M.E.; Krause, A.O.I. Kinetic modeling of dehydrogenation of isobutane on chromia/alumina catalyst. Ind. Eng. Chem. Res. 2002, 41, 5619–5626. [Google Scholar] [CrossRef]
- Pakhomov, N.A.; Parakhin, O.A.; Nemykina, E.I.; Danilevich, V.V.; Chernov, M.P.; Pecherichenko, V.A. Microspherical chromium oxide/alumina catalyst KDM for fluidized-bed isobutane dehydrogenation: Development and industrial application experience. Catal. Ind. 2012, 4, 298–307. [Google Scholar] [CrossRef]
- Ma, Z.; Mo, Y.; Li, J.; An, C.; Liu, X. Optimization of PtSnK/Al2O3 isobutane dehydrogenation catalyst prepared by an impregnation-reduction method. J. Nat. Gas Sci. Eng. 2015, 27, 1035–1042. [Google Scholar] [CrossRef]
- Matveyeva, A.N.; Omarov, S.O.; Sladkovskiy, D.A.; Murzin, D.Y. Experimental studies and kinetic regularities of isobutane dehydrogenation over Ga2O3/Al2O3. Chem. Eng. J. 2019, 372, 1194–1204. [Google Scholar] [CrossRef]
- Matveyeva, A.N.; Wärnå, J.; Pakhomov, N.A.; Murzin, D.Y. Kinetic modeling of isobutane dehydrogenation over Ga2O3/Al2O3 catalyst. Chem. Eng. J. 2020, 381, 122741. [Google Scholar] [CrossRef]
- Matveyeva, A.N.; Zaitseva, N.A.; Mäki-Arvela, P.; Aho, A.; Bachina, A.K.; Fedorov, S.P.; Murzin, D.Y.; Pakhomov, N.A. Fluidized-bed isobutane dehydrogenation over alumina-supported Ga2O3 and Ga2O3/Al2O3 catalysts. Ind. Eng. Chem. Res. 2018, 57, 927–938. [Google Scholar] [CrossRef]
- Utemov, A.V.; Matveeva, A.N.; Sladkovskaya, E.V.; Murzin, D.Y.; Sladkovskii, D.A. Integration of Turboexpanders into Reactor Blocks of the Dehydrogenation of Processes of Light Alkanes. Theor. Found. Chem. Eng. 2024, 58, 1619–1629. [Google Scholar] [CrossRef]
- Vernikovskaya, N.V.; Savin, I.G.; Kashkin, V.N.; Pakhomov, N.A.; Ermakova, A.; Molchanov, V.V.; Nemykina, E.L.; Parahin, O.A. Dehydrogenation of propane-isobutane mixture in a fluidized bed reactor over Cr2O3/Al2O3 catalyst: Experimental studies and mathematical modelling. Chem. Eng. J. 2011, 176, 158–164. [Google Scholar] [CrossRef]
- Azimi, S.S.; Kalbasi, M. Three-phase modeling of dehydrogenation of isobutane to isobutene in a fluidized bed reactor: Effect of operating conditions on the energy consumption. Energy 2018, 149, 250–261. [Google Scholar] [CrossRef]
- Egorova, S.R.; Bekmukhamedov, G.E.; Lamberov, A.A. Effect of High-Temperature Treatment on the Properties of an Alumina–Chromium Catalyst for the Dehydrogenation of Lower Paraffins. Kinet. Catal. 2013, 54, 49–58. [Google Scholar] [CrossRef]
- Bekmukhamedov, G.E.; Egorova, S.R.; Lamberov, A.A. Effect of the Nature of Silicon Oxide Structures on the Activity of an Alumina–Chromium Catalyst in the Reaction of iso-Butane Dehydrogenation. Catal. Ind. 2014, 6, 44–52. [Google Scholar] [CrossRef]
- Bekmukhamedov, G.E.; Mukhamed’yarova, A.N.; Egorova, S.R.; Lamberov, A.A. Modification by SiO2 of Alumina Support for Light Alkane Dehydrogenation Catalysts. Catalysts 2016, 6, 162. [Google Scholar] [CrossRef]
- Lamberov, A.A.; Egorova, S.R.; Gilmanov KhKh Kataev, A.N.; Bekmukhamedov, G.E. Pilot Tests of the Microspherical Aluminochromium KDI-M Catalyst for iso-Butane Dehydrogenation. Catal. Ind. 2017, 9, 17–22. [Google Scholar] [CrossRef]
- Egorova, S.R.; Tuktarov, R.R.; Boretskaya, A.V.; Laskin, A.I.; Gizyatullov, R.N.; Lamberov, A.A. Stabilizing effect of α-Cr2O3 on highly active phases and catalytic performance of a chromium alumina catalyst in the process of isobutane dehydrogenation. Mol. Catal. 2021, 509, 111610. [Google Scholar] [CrossRef]
- Solovev, S.A.; Soloveva, O.V.; Bekmukhamedov, G.E.; Egorova, S.R.; Lamberov, A.A. CFD-Simulation of isobutane dehydrogenation for a fluidized bed reactor. ChemEngineering 2022, 6, 98. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Ogawa, S.; Umemura, A.; Oshima, N. On the equation of fully fluidized granular materials. J. Appl. Math. Phys. 1980, 31, 483–493. [Google Scholar] [CrossRef]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J. Kinetic theories for granular flow: Inelastic particles in couette flow and slightlyinelastic particles in a general flow field. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Syamlal, M. The Particle-Particle Drag Term in a Multiparticle Model of Fluidization; DOE/MC/21353-2373, NTIS/DE87006500; National Technical Information Service: Springfield, VA, USA, 1987.
- Gunn, D.J. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Wang, D.; Fan, L.-S. Particle characterization and behavior relevant to fluidized bed combustion and gasification systems. In Fluidized Bed Technologies for Near-Zero Emission Combustion and Gasification; Elsevier: Cambridge, UK, 2013; pp. 42–76. [Google Scholar]
- Yates, J.G.; Newton, D. Fine particle effects in a fluidized-bed reactor. Chem. Eng. Sci. 1986, 41, 801–806. [Google Scholar] [CrossRef]
- Kono, H.O.; Ells, T.S.; Chiba, S.; Suzuki, M.; Morimoto, E. Quantitative criteria for emulsion phase characterization and for the transition between particulate and bubbling fluidization. Powder Technol. 1987, 52, 69–76. [Google Scholar] [CrossRef]
- Grace, J.R.; Sun, G. Influence of particle size distribution on the performance of fluidized bed reactors. Can. J. Chem. Eng. 1991, 69, 1126–1134. [Google Scholar] [CrossRef]
- van Ommen, J.R.; Nijenhuis, J.; van den Bleek, C.M.; Coppens, M. Four ways to introduce structure in fluidized bed reactors. Ind. Eng. Chem. Res. 2007, 46, 4236–4244. [Google Scholar] [CrossRef]
- Khoe, G.K.; Ip, T.L.; Grace, J.R. Rheological and fluidization behavior of powders of different particle size distribution. Powder Technol. 1991, 66, 127–141. [Google Scholar] [CrossRef]
- Saayman, J.; Ellis, N.; Nicol, W. Fluidization of high-density particles: The influence of fines on reactor performance. Powder Technol. 2013, 245, 48–55. [Google Scholar] [CrossRef]
- Beetstra, R.; Nijenhuis, J.; Ellis, N.; van Ommen, J.R. The influence of the particle size distribution on fluidized bed hydrodynamics using high throughput experimentation. AIChE J. 2009, 55, 2013–2023. [Google Scholar] [CrossRef]
- Brouwer, G.C.; Wagner, E.C.; van Ommen, J.R.; Mudde, R.F. Effects of pressure and fines content on bubble diameter in a fluidized bed studied using fast X-ray tomography. Chem. Eng. J. 2012, 207–208, 711–717. [Google Scholar] [CrossRef]
- Gu, Y.; Ozel, A.; Sundaresan, S. Numerical studies of the effects of fines on fluidization. AIChE J. 2016, 62, 2271–2281. [Google Scholar] [CrossRef]
- Solovev, S.A.; Soloveva, O.V. Study of the influence of the mean particle diameter choice and the fractions number on the quality of fluidized bed numerical simulation. Processes 2024, 12, 2528. [Google Scholar] [CrossRef]
- Gobin, A.; Neau, H.; Simonin, O.; Llinas, J.; Reiling, V.; Selo, J. Numerical simulations of a gas-phase polymerization reactor. In Proceedings of European Congress on Computational Methods in Applied Sciences and Engineering, Wales, UK, 4–7 September 2001. [Google Scholar]
- Cornelissen, J.T.; Taghipour, F.; Escudie, R.; Ellis, N.; Grace, J.R. CFD modelling of a liquid–solid fluidized bed. Chem. Eng. Sci. 2007, 62, 6334–6348. [Google Scholar] [CrossRef]
- Soloveva, O.V.; Solovyev, S.A. Investigation of the influence of heated catalyst feeding system on the intensity of temperature-dependent chemical reaction in the fluidized bed apparatus. IOP Conf. Ser. Mater. Sci. Eng. 2016, 158, 012086. [Google Scholar] [CrossRef]
- Solovev, S.A.; Soloveva, O.V.; Antipin, A.V.; Shamsutdinov, E.V. Investigation of internal elements impaction on particles circulation in a fluidized bed reactor. IOP Conf. Ser. J. Phys. 2018, 944, 012114. [Google Scholar] [CrossRef]



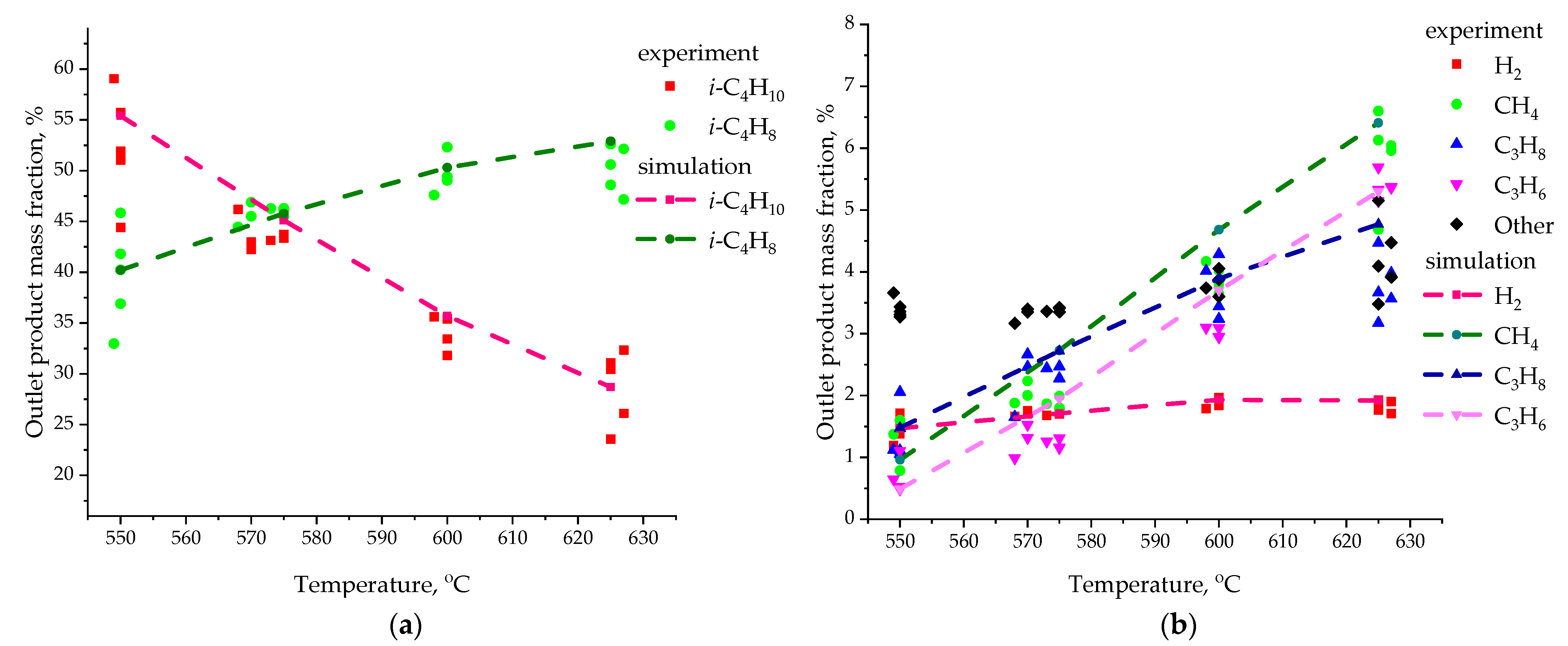

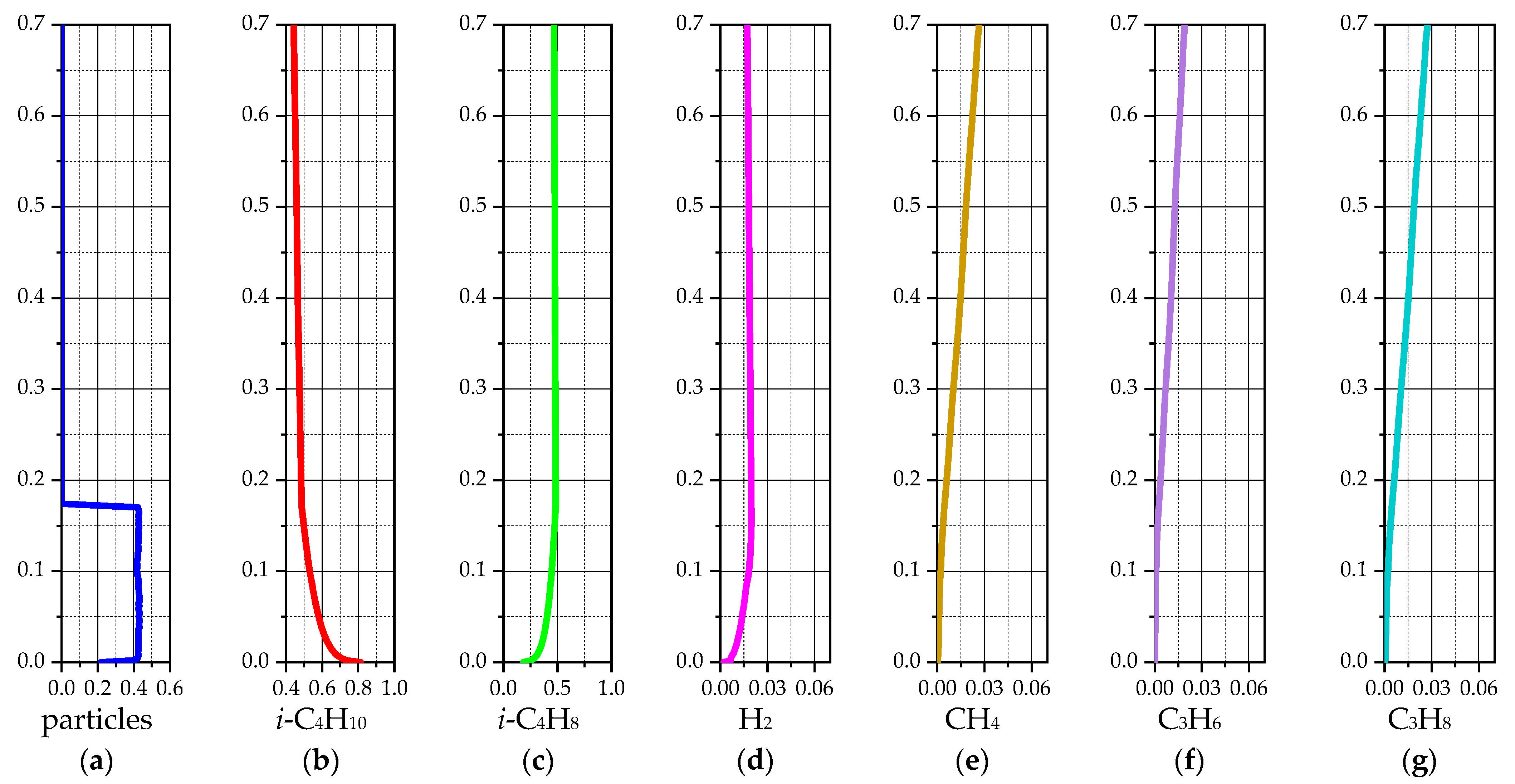
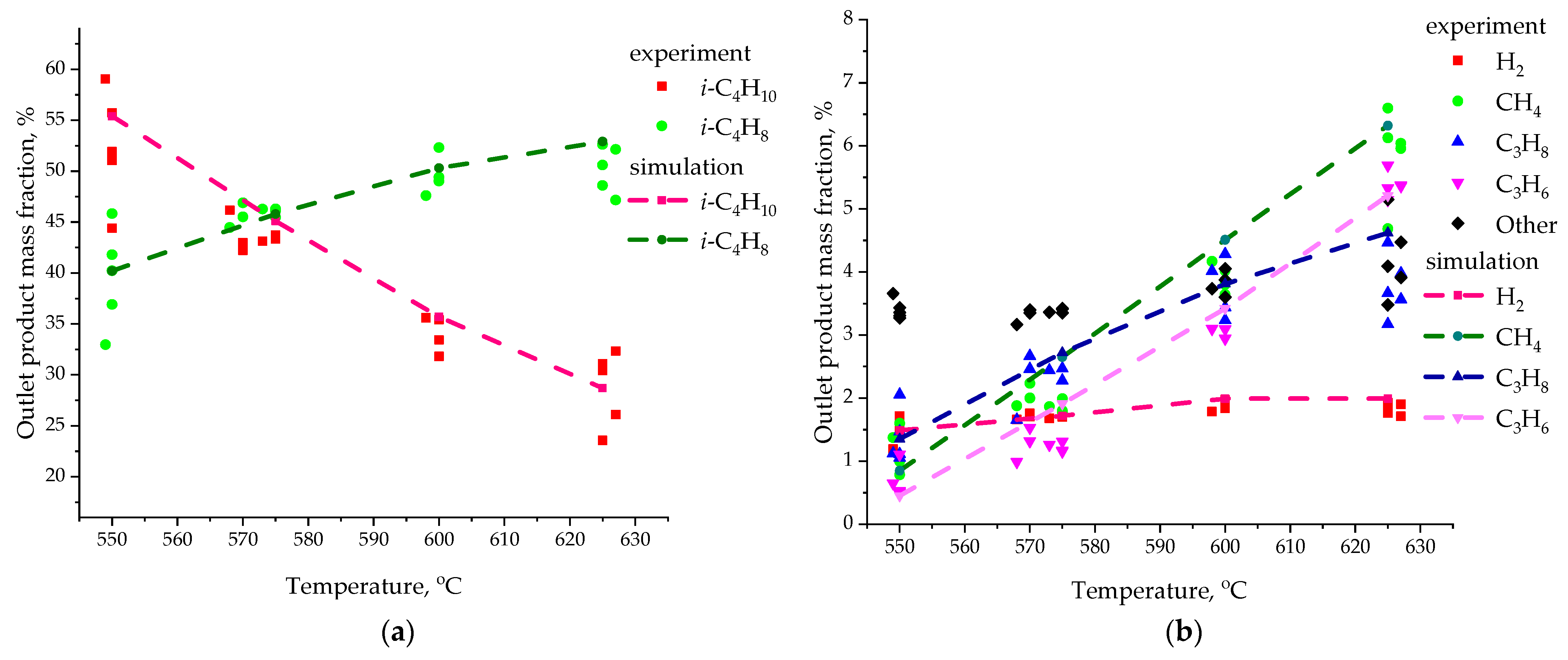
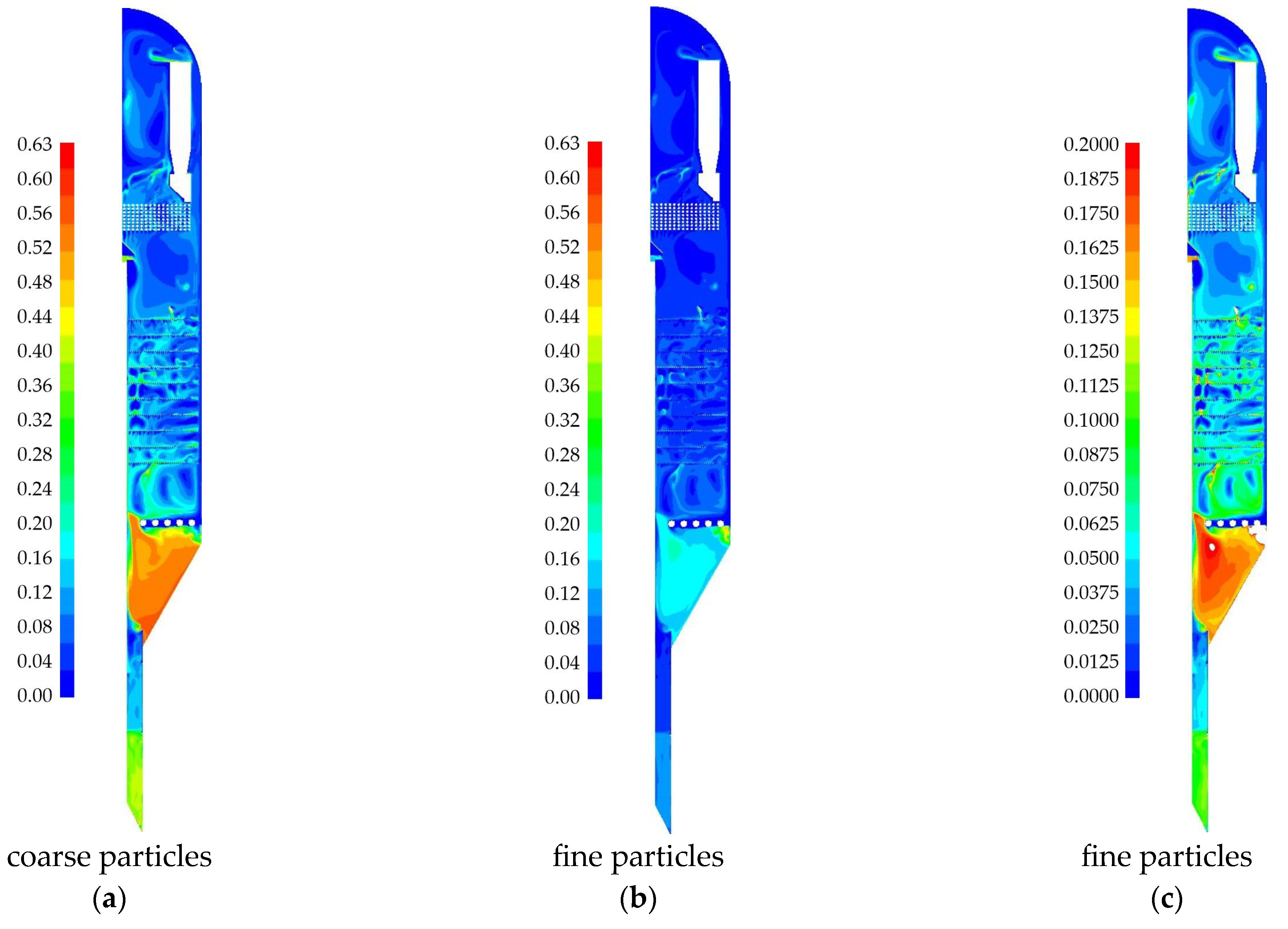
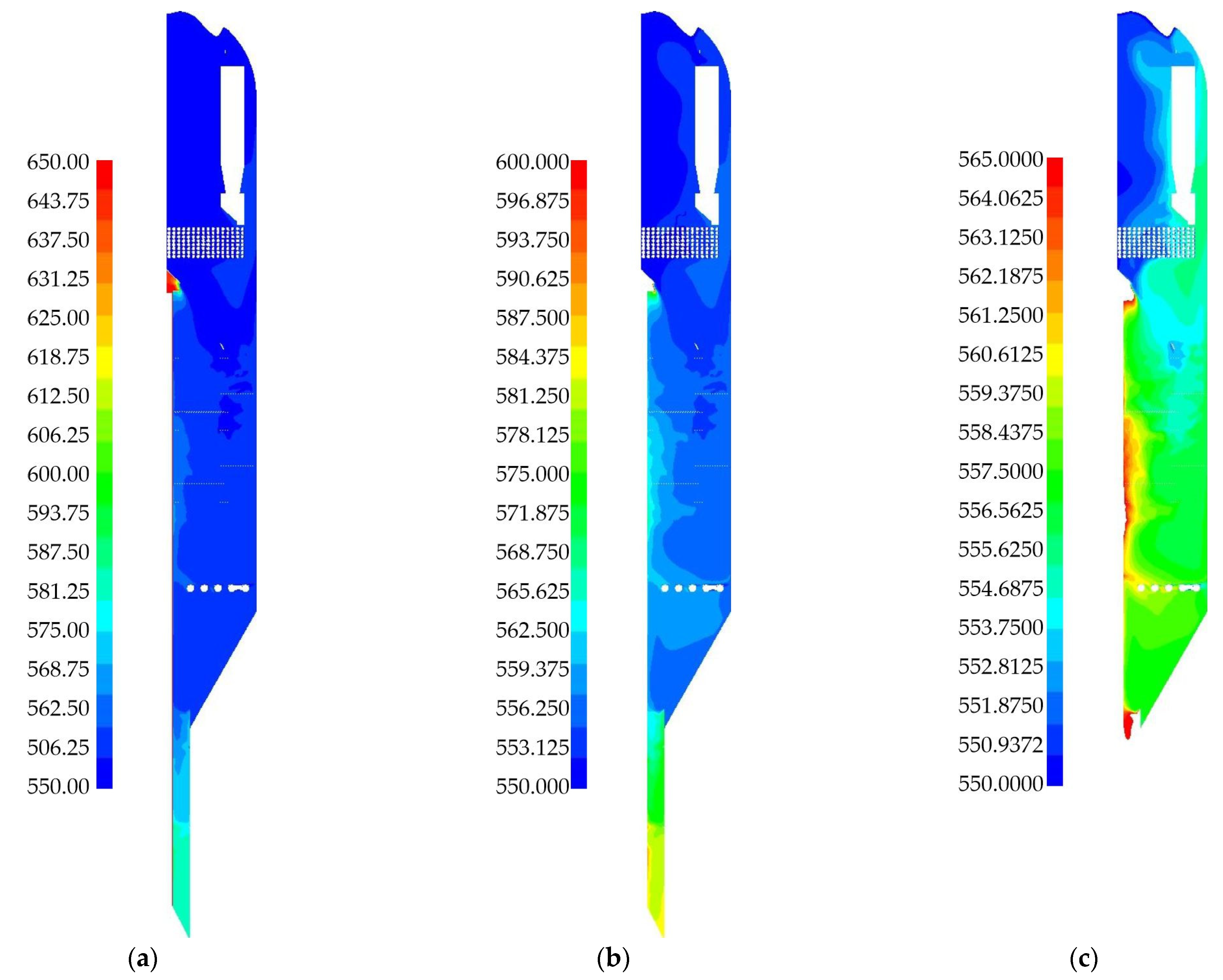

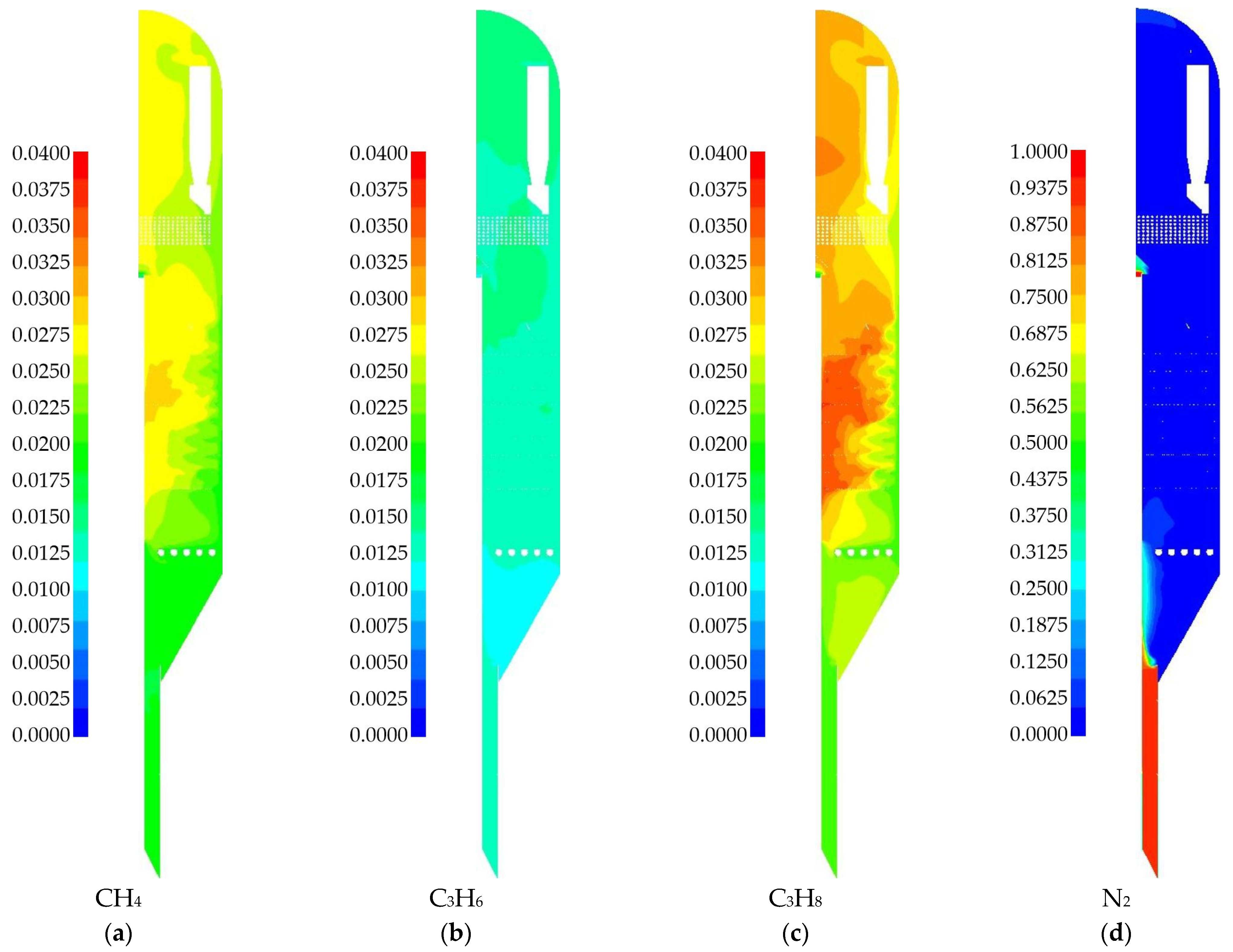
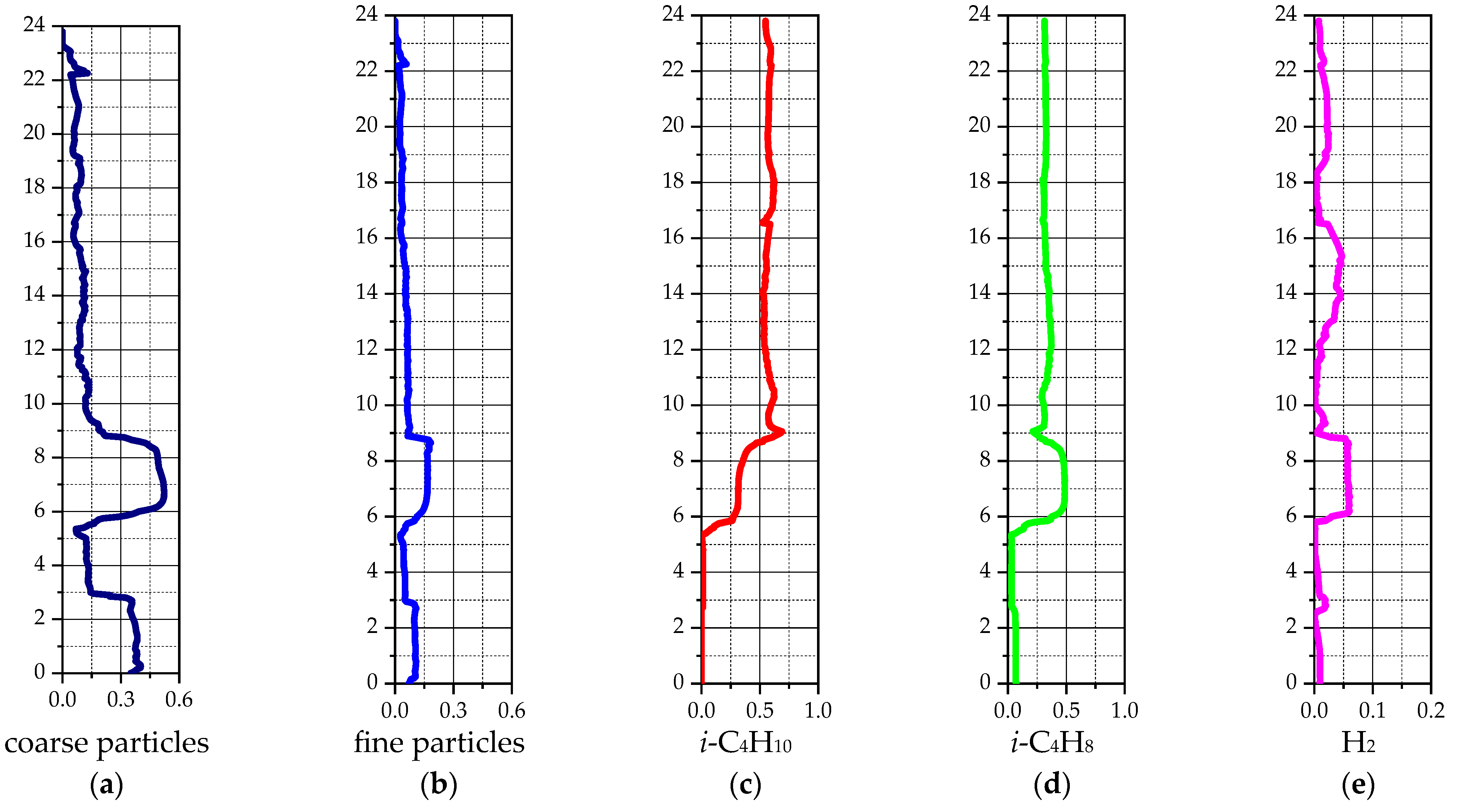
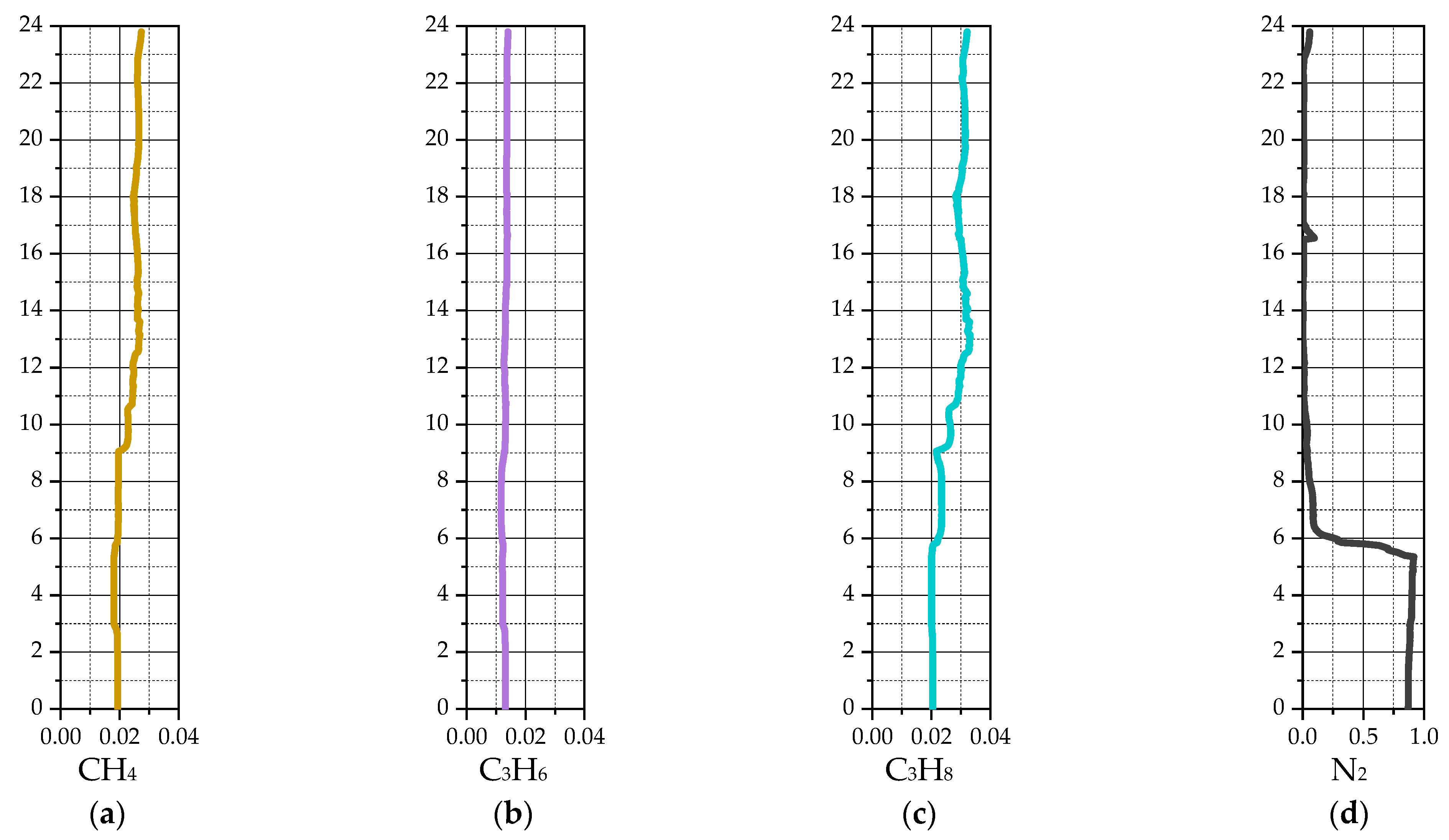

| Species | i-C4H10 | i-C4H8 | H2 | CH4 | C3H6 | C3H8 | - |
|---|---|---|---|---|---|---|---|
| wt.% | 40.329 | 46.104 | 1.707 | 3.064 | 2.708 | 2.428 | - |
| Species | CO + CO2 | n-C4H10 | C2H6 | C4H8 | n-C4H8 | C5 fractions | C2H4 |
| wt.% | 1.365 | 0.656 | 0.612 | 0.581 | 0.197 | 0.161 | 0.084 |
| Reaction | , kJ/mol | |
|---|---|---|
| Isobutane dehydrogenation (19) | 1.5 × 109 | 117 |
| Thermal cracking (20) | 2.0 × 109 | 120 |
| Propylene hydrogenation (21) | 1.8 × 109 | 121 |
| Laboratory Reactor | Industrial Reactor | |
|---|---|---|
| Gas | species mixture: | species mixture: |
| i-C4H10 | i-C4H10 | |
| i-C4H8 | i-C4H8 | |
| H2 | H2 | |
| CH4 | CH4 | |
| C3H6 | C3H6 | |
| C3H8 | C3H8 | |
| - | N2 | |
| Mass-flow rate i-C4H10, kg/s | 1.32 × 10−5 | 8.05 |
| Mass-flow rate N2, kg/s | - | 0.11 |
| Supply gas temperature, °C | 550 575 600 625 | 550 |
| Catalyst | spherical particle model, one fraction | spherical particle model, two fractions |
| Mean diameter, µm | 84 | 40 (30%) 100 (70%) |
| Mass-flow rate of particles, kg/s | - | 33.3348 |
| Supply particles temperature, °C | - | 650 |
| Temperature, °C | Species, Name | Average Value Y3D, wt.% | Average Value Y2D, wt.% | |Y3D–Y3D|, wt.% | |Y3D–Y3D|/Y3D, wt.%/wt.% |
|---|---|---|---|---|---|
| 550 | i-C4H10 | 55.40 | 55.04 | 0.36 | 0.006498 |
| i-C4H8 | 40.20 | 40.82 | 0.62 | 0.015423 | |
| H2 | 1.47 | 1.49 | 0.02 | 0.013605 | |
| CH4 | 0.96 | 0.85 | 0.11 | 0.114583 | |
| C3H6 | 0.49 | 0.45 | 0.04 | 0.081633 | |
| C3H8 | 1.48 | 1.35 | 0.13 | 0.087838 | |
| 575 | i-C4H10 | 45.10 | 44.10 | 1.00 | 0.022173 |
| i-C4H8 | 45.79 | 46.91 | 1.12 | 0.024459 | |
| H2 | 1.71 | 1.72 | 0.01 | 0.005848 | |
| CH4 | 2.73 | 2.65 | 0.08 | 0.029304 | |
| C3H6 | 1.95 | 1.91 | 0.04 | 0.020513 | |
| C3H8 | 2.72 | 2.71 | 0.01 | 0.003676 | |
| 600 | i-C4H10 | 35.70 | 34.98 | 0.72 | 0.020168 |
| i-C4H8 | 50.30 | 51.29 | 0.99 | 0.019682 | |
| H2 | 1.93 | 1.99 | 0.06 | 0.031088 | |
| CH4 | 4.68 | 4.51 | 0.17 | 0.036325 | |
| C3H6 | 3.50 | 3.42 | 0.08 | 0.022857 | |
| C3H8 | 3.89 | 3.81 | 0.08 | 0.020566 | |
| 625 | i-C4H10 | 28.70 | 28.36 | 0.34 | 0.011847 |
| i-C4H8 | 52.90 | 53.50 | 0.60 | 0.011342 | |
| H2 | 1.92 | 1.99 | 0.07 | 0.036458 | |
| CH4 | 6.41 | 6.32 | 0.09 | 0.014041 | |
| C3H6 | 5.30 | 5.21 | 0.09 | 0.016981 | |
| C3H8 | 4.77 | 4.62 | 0.15 | 0.031447 |
| - | Temperature, °C | ||||
|---|---|---|---|---|---|
| - | 550 | 575 | 600 | 625 | 550–650 |
| Species, Name | Laboratory Reactor, wt.% | Industrial Reactor, wt.% | |||
| i-C4H10 | 55.04 | 44.10 | 34.98 | 28.36 | 59.15 |
| i-C4H8 | 40.82 | 46.91 | 51.29 | 53.50 | 31.88 |
| H2 | 1.49 | 1.72 | 1.99 | 1.99 | 1.35 |
| CH4 | 0.85 | 2.65 | 4.51 | 6.32 | 2.61 |
| C3H6 | 0.45 | 1.91 | 3.42 | 5.21 | 1.24 |
| C3H8 | 1.35 | 2.71 | 3.81 | 4.62 | 3.07 |
| N2 | - | - | - | - | 0.7 |
| - | Temperature, °C | ||||
|---|---|---|---|---|---|
| - | 550 | 575 | 600 | 625 | 550–650 |
| - | Laboratory Reactor | Industrial Reactor | |||
| Average temperature, °C | 549.92 | 574.86 | 599.80 | 624.76 | 557.13 |
| Maximum temperature, °C | 552.72 | 578.46 | 605.57 | 631.53 | 650.00 |
| Minimum temperature, °C | 548.79 | 573.04 | 596.94 | 619.48 | 549.34 |
| Maximum temperature difference, °C | 3.93 | 5.42 | 8.63 | 12.05 | 100.66 |
| Heat source | Reactor wall | Supply of heated catalyst | |||
| - | Laboratory Reactor | Industrial Reactor |
|---|---|---|
| Calculated average velocity based on determined gas flow rate, m/s | 0.016 | 0.376 |
| Calculated average time of gas movement in a reactor, s | 43.75 | 36.197 |
| Fluidization regime | bubbling | turbulent |
| Average height of catalyst particle bed, m | 0.169 | the whole reactor |
| Calculated average time of gas movement in the catalyst bed, s | 10.563 | 36.197 |
| Average velocity from CFD solution, m/s | 0.0301 | 0.201 |
| Maximum velocity from CFD solution, m/s | 0.367 | 7.157 |
| Minimum velocity from CFD solution, m/s | 0.000065 | 0.00024 |
| Average time of gas movement in a catalyst bed from a CFD solution, s | 5.615 | 67.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solovev, S.A.; Soloveva, O.V. Numerical Simulation of the Isoparaffins Dehydrogenation Process in Fluidized Bed Reactor: From Laboratory to Industry. ChemEngineering 2025, 9, 129. https://doi.org/10.3390/chemengineering9060129
Solovev SA, Soloveva OV. Numerical Simulation of the Isoparaffins Dehydrogenation Process in Fluidized Bed Reactor: From Laboratory to Industry. ChemEngineering. 2025; 9(6):129. https://doi.org/10.3390/chemengineering9060129
Chicago/Turabian StyleSolovev, Sergei A., and Olga V. Soloveva. 2025. "Numerical Simulation of the Isoparaffins Dehydrogenation Process in Fluidized Bed Reactor: From Laboratory to Industry" ChemEngineering 9, no. 6: 129. https://doi.org/10.3390/chemengineering9060129
APA StyleSolovev, S. A., & Soloveva, O. V. (2025). Numerical Simulation of the Isoparaffins Dehydrogenation Process in Fluidized Bed Reactor: From Laboratory to Industry. ChemEngineering, 9(6), 129. https://doi.org/10.3390/chemengineering9060129








