Mathematical Modeling and Design of a Cooling Crystallizer Incorporating Experimental Data for Crystallization Kinetics
Abstract
1. Introduction
2. Materials and Methods
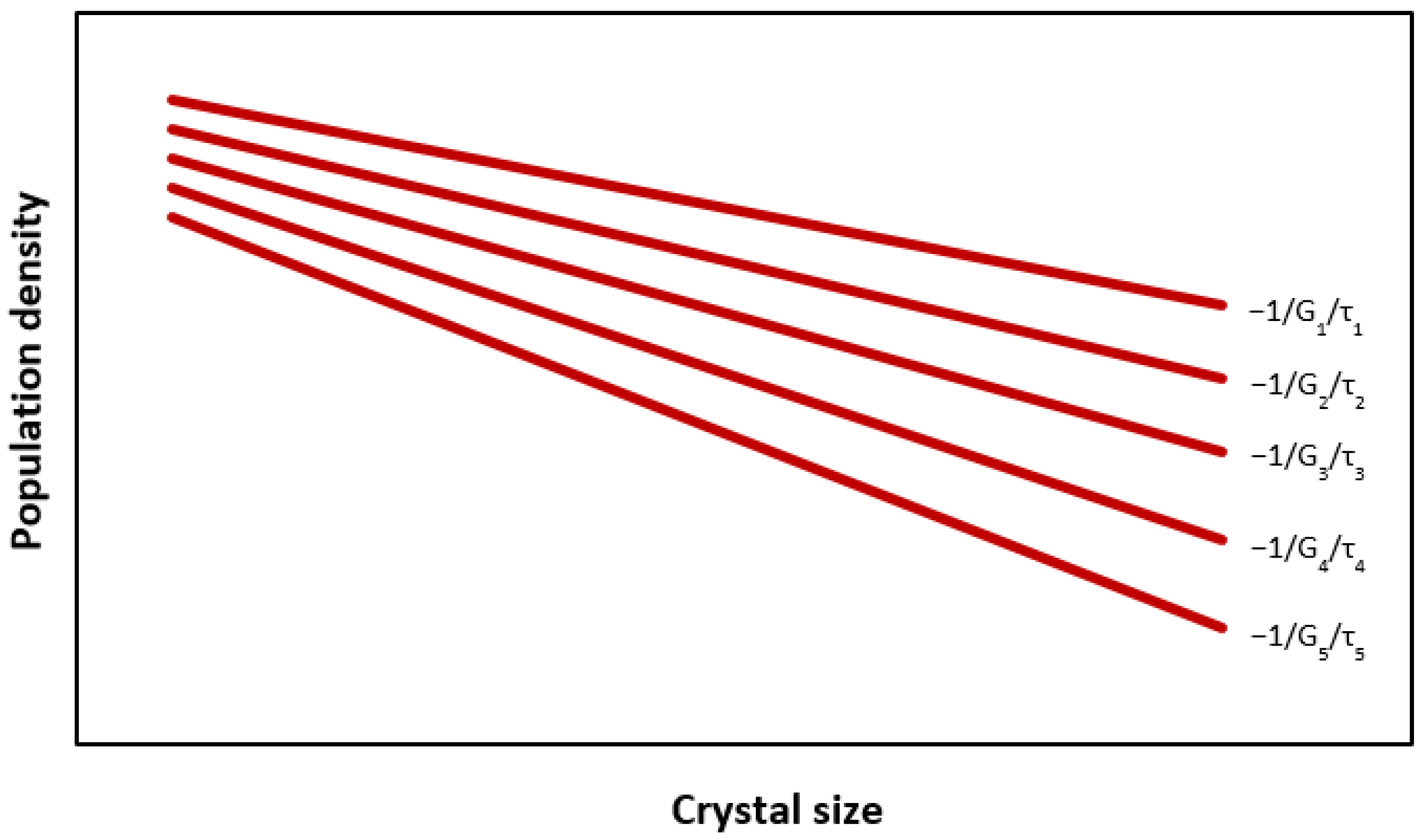
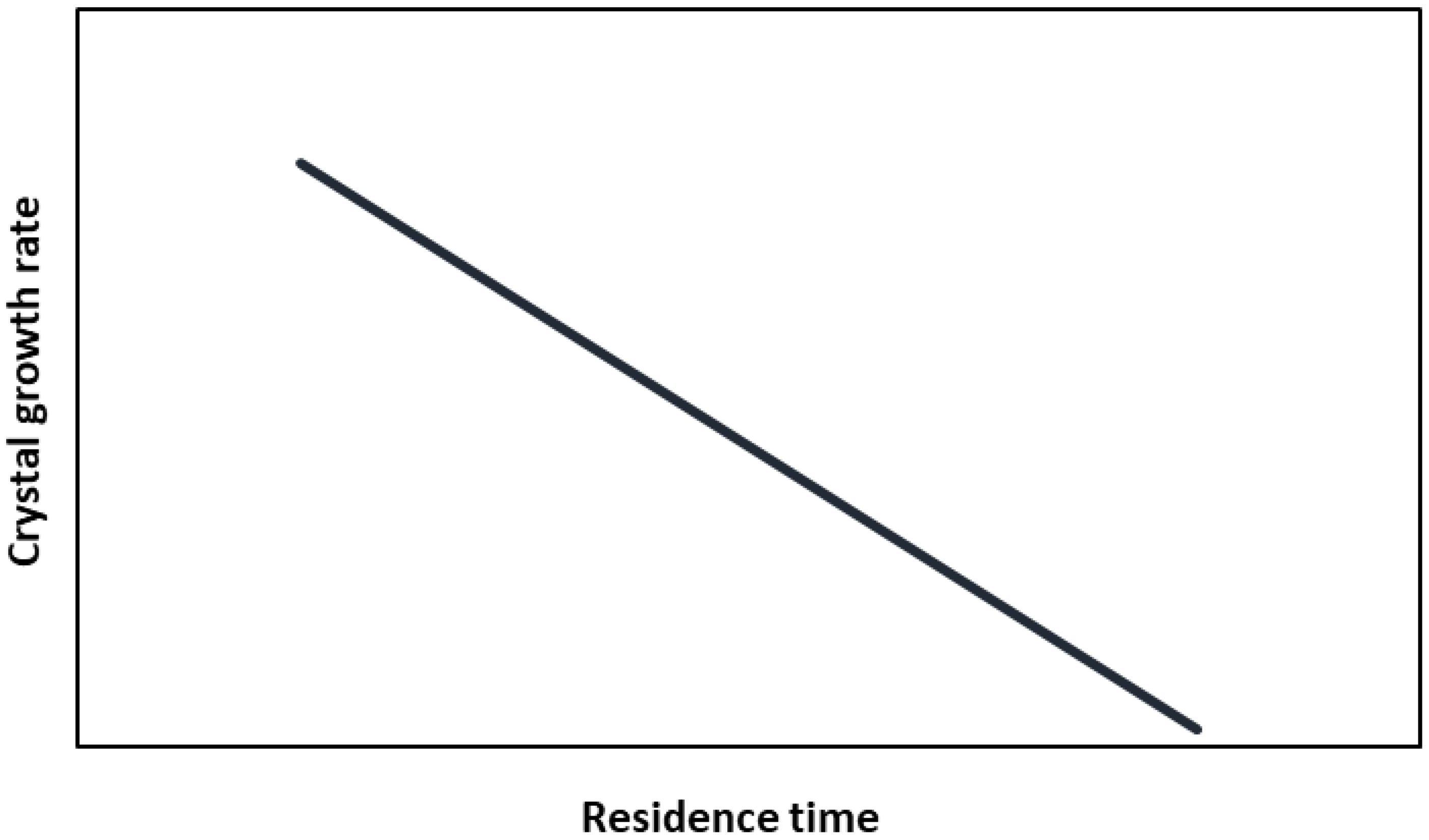
2.1. Crystal Growth Rate—Residence Time Relationship
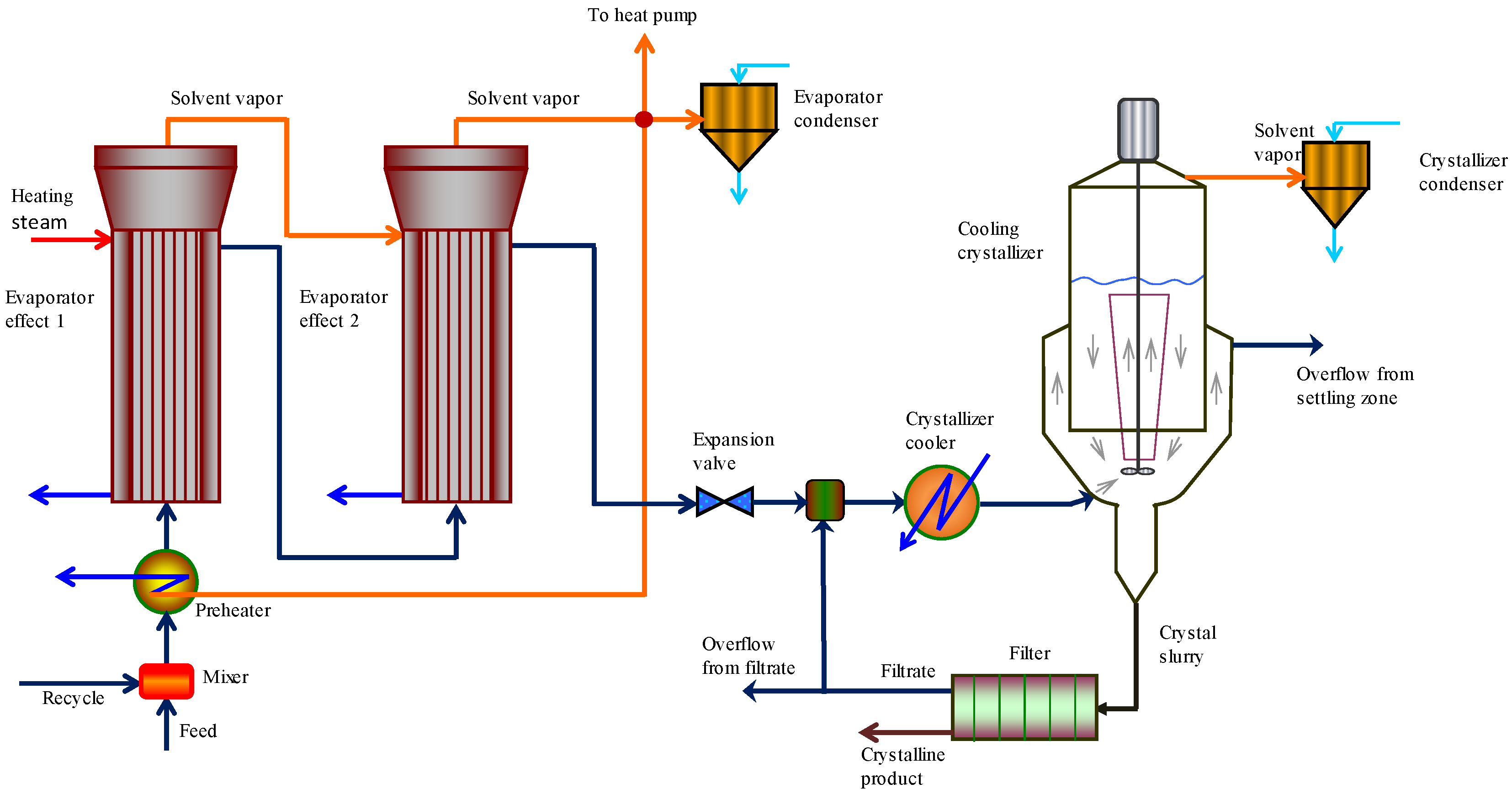
2.2. Crystallization Unit Flow Sheet Development
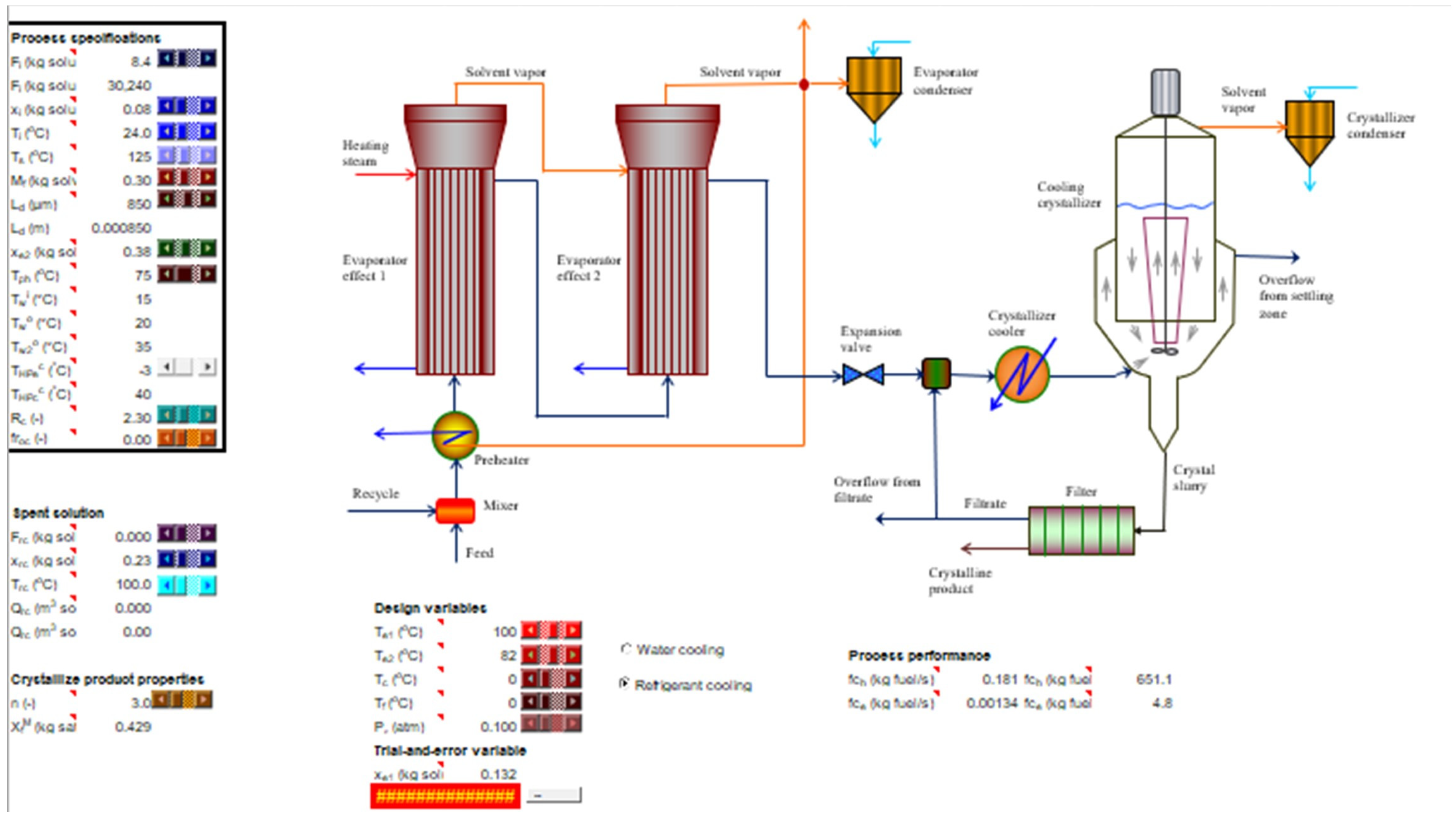
2.3. Case Study
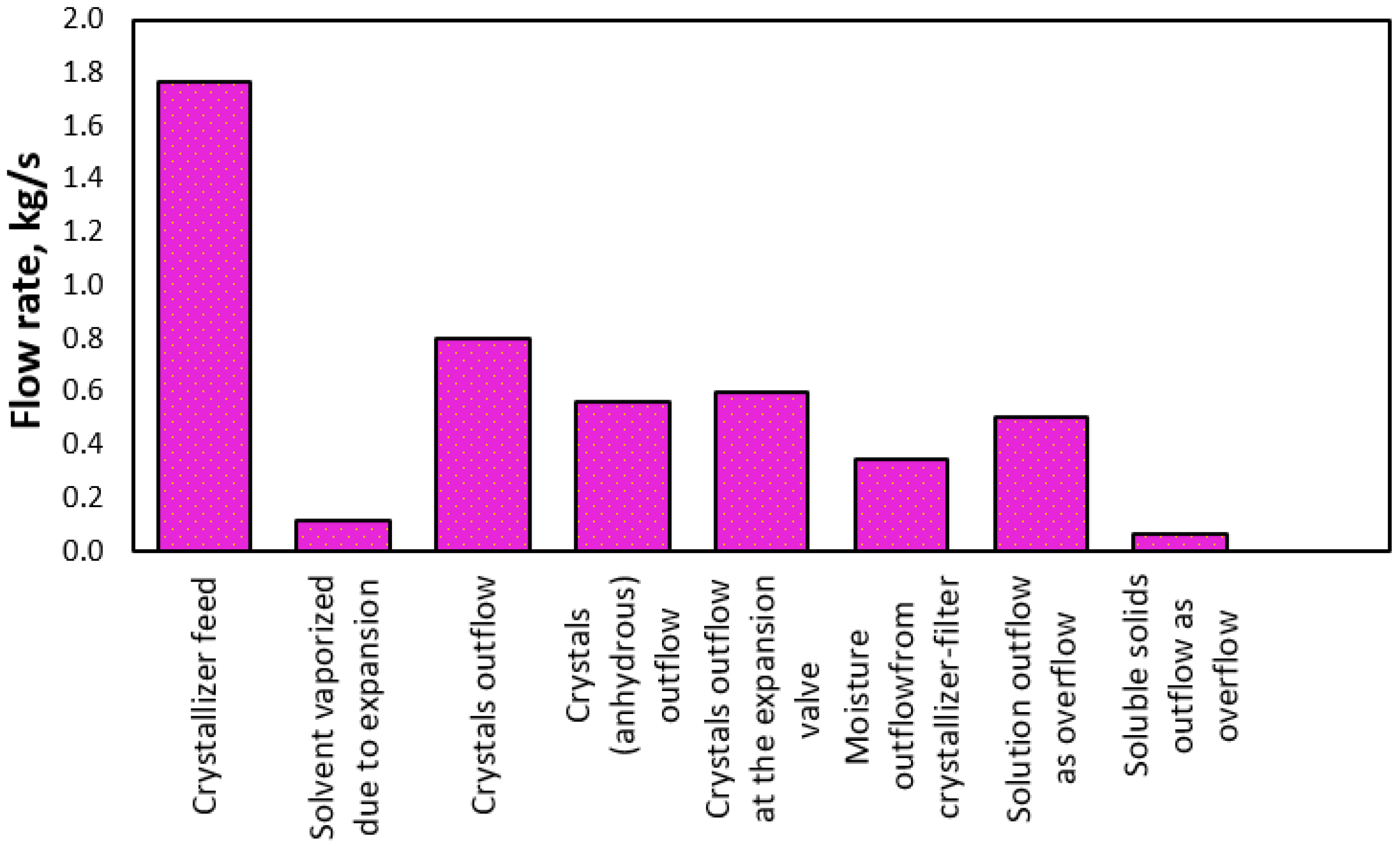
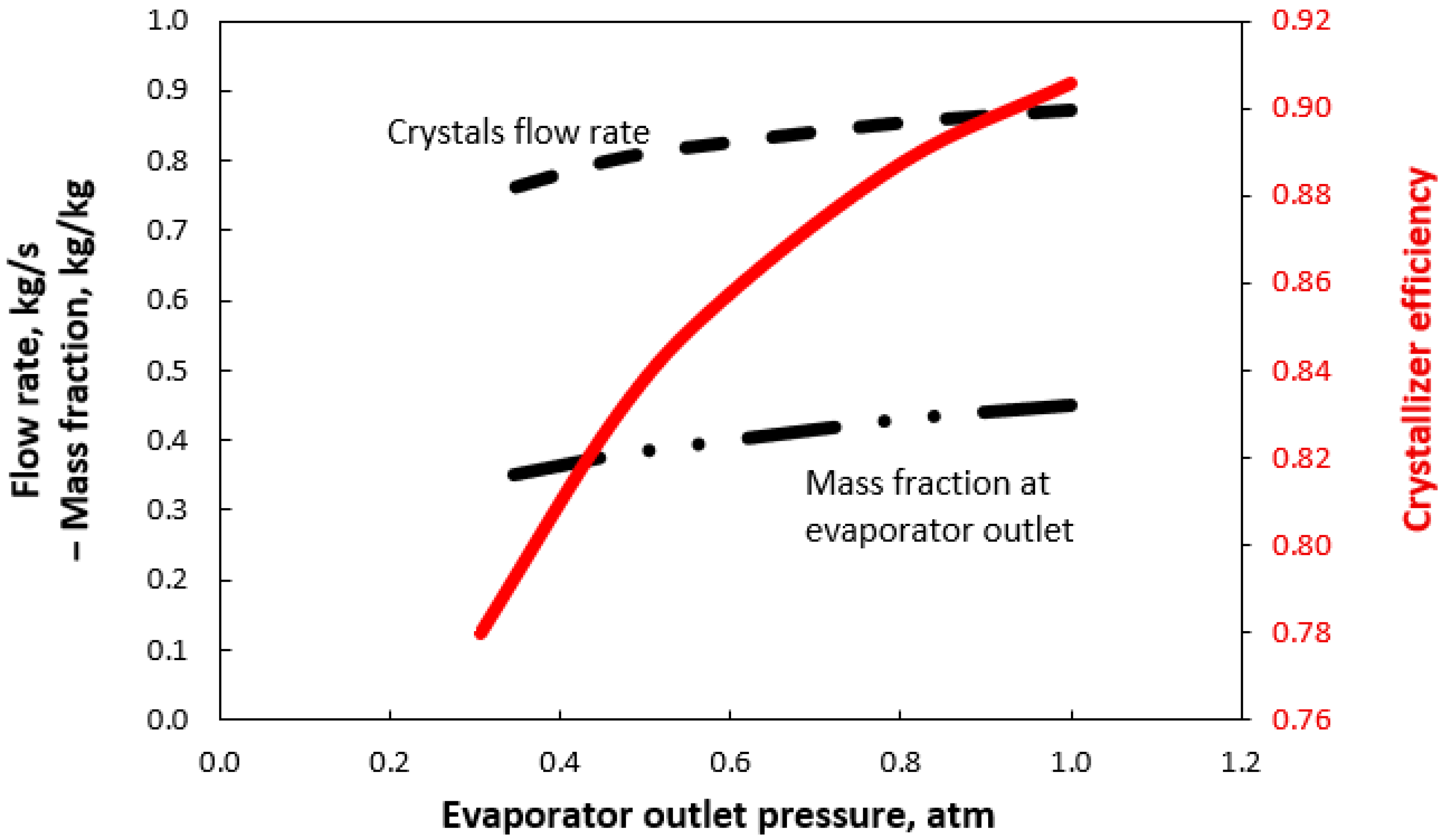
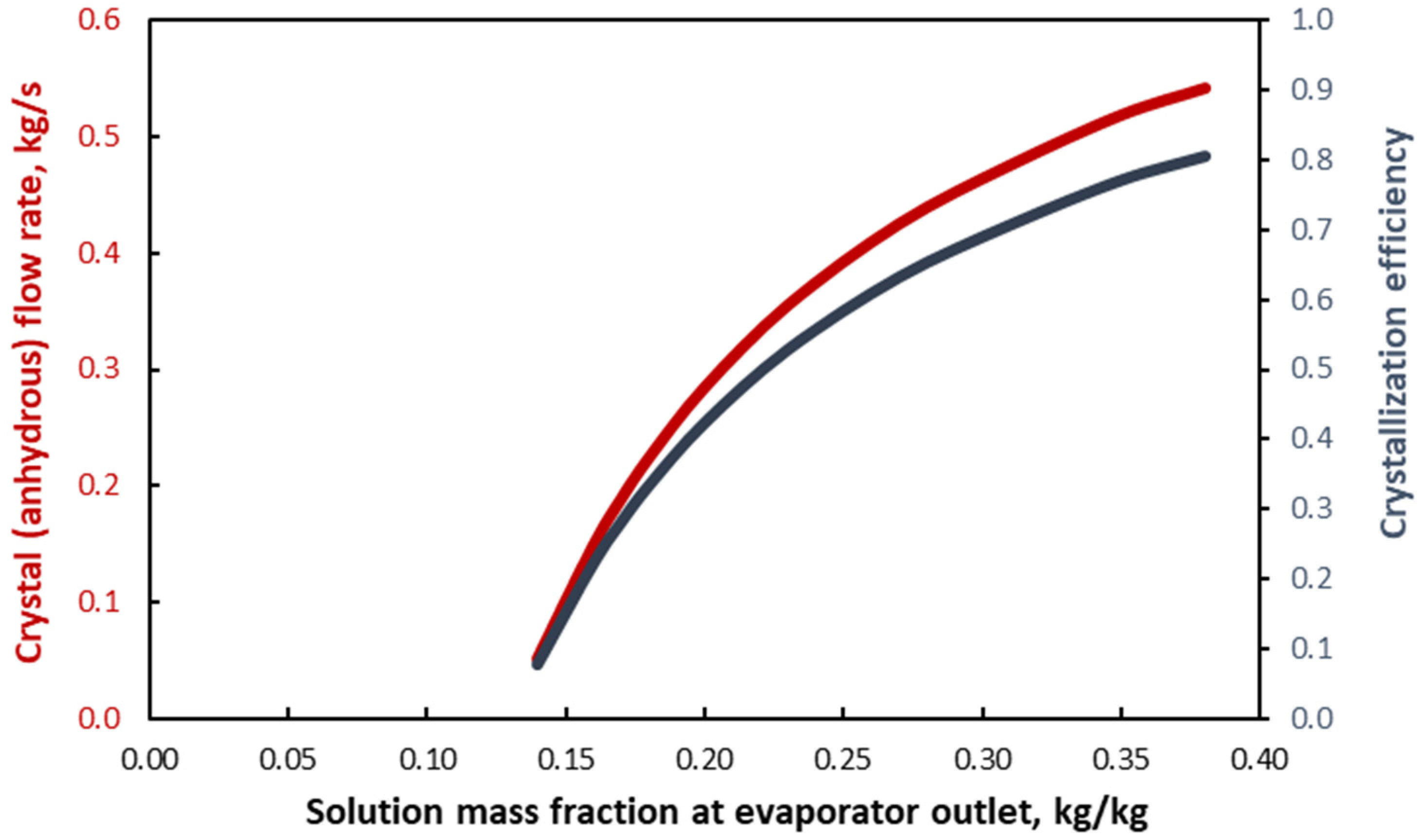
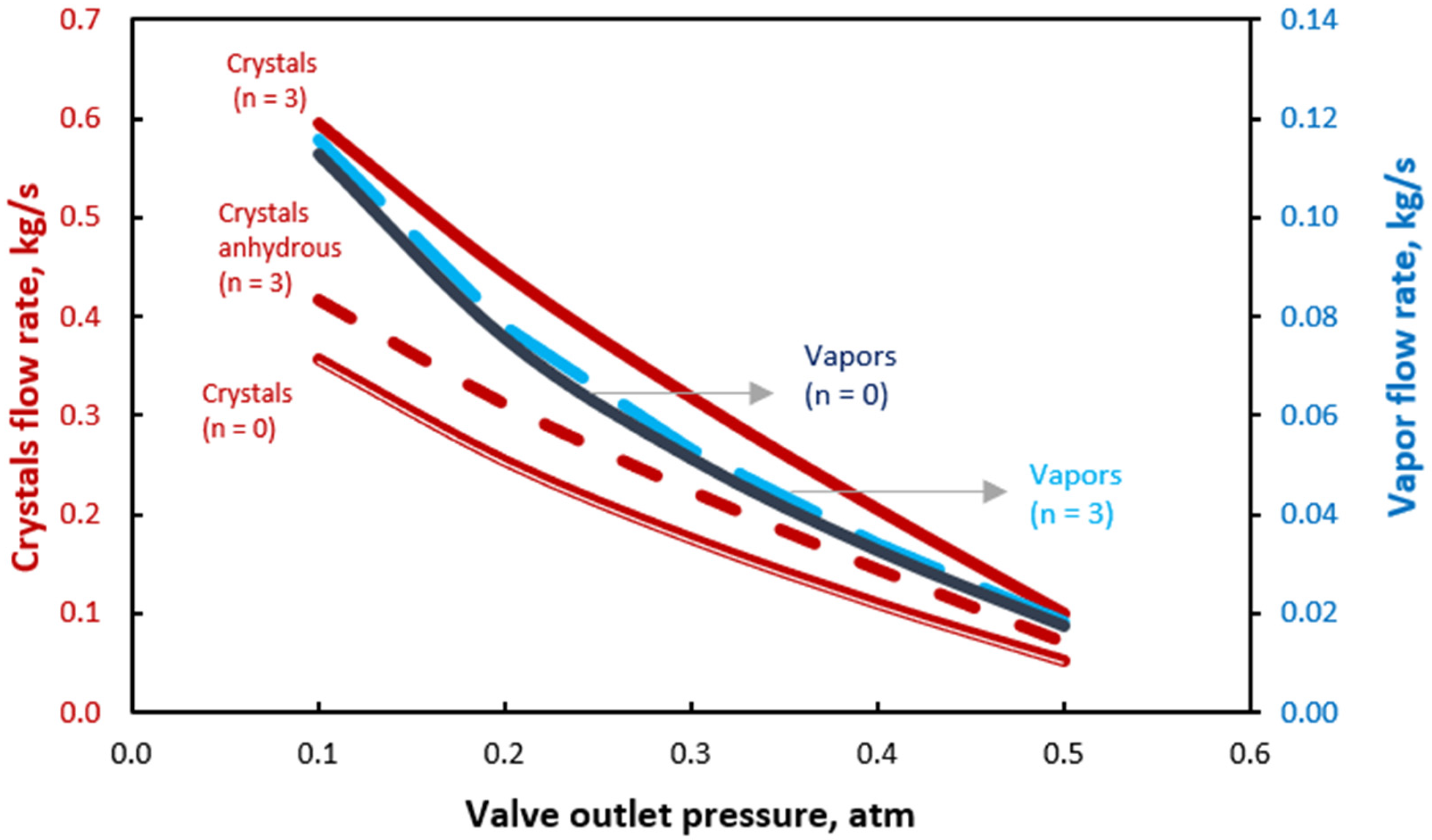
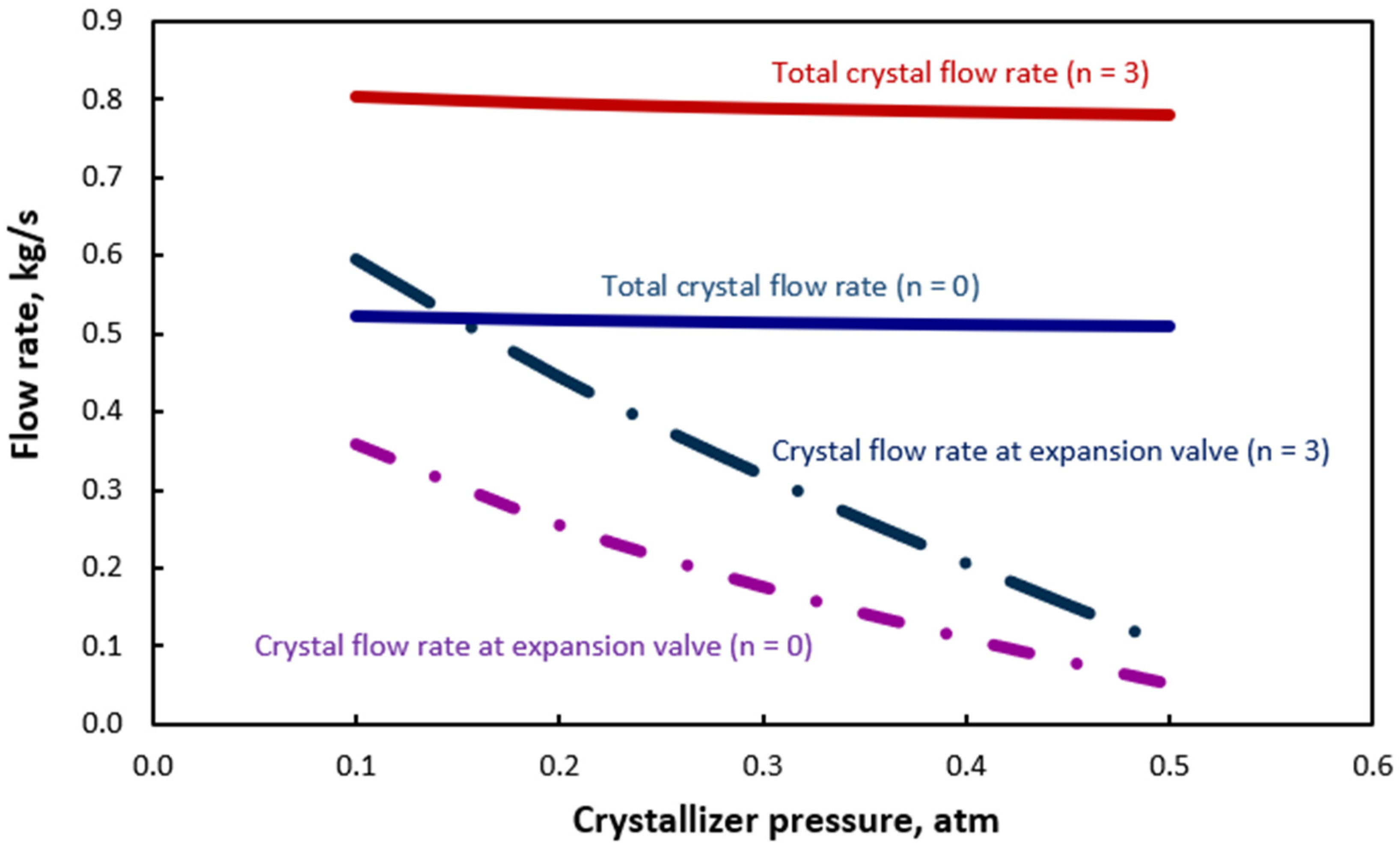
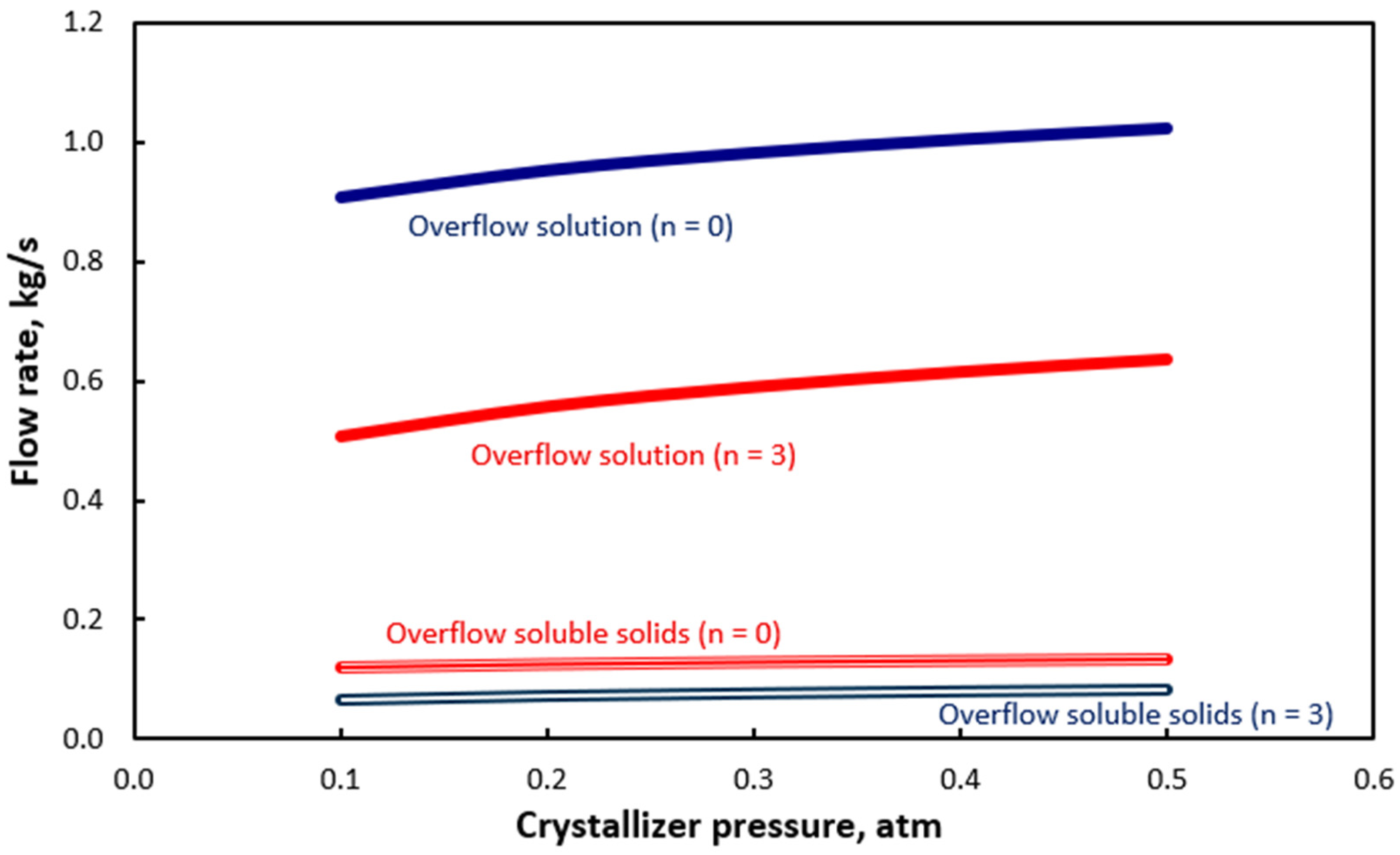
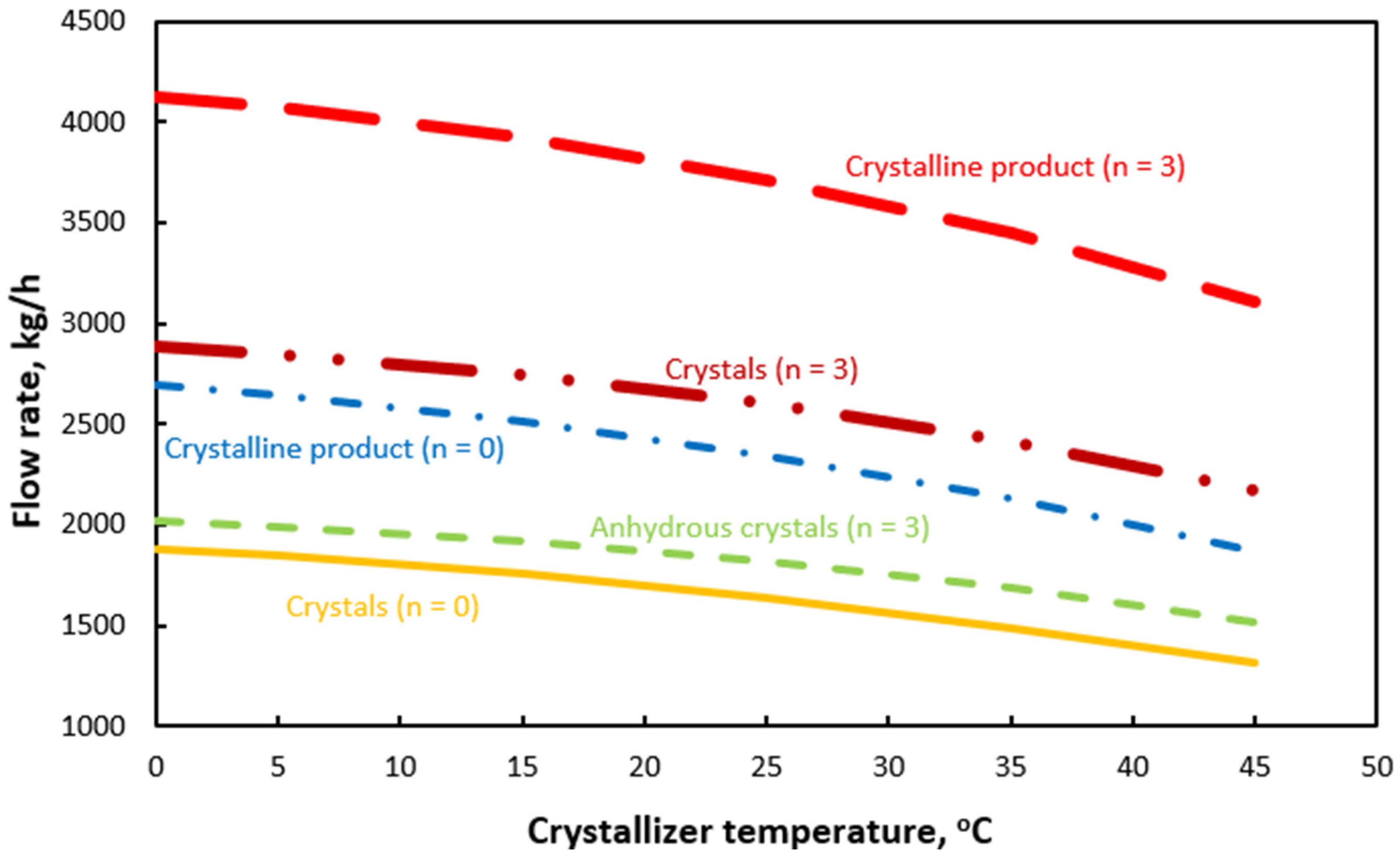
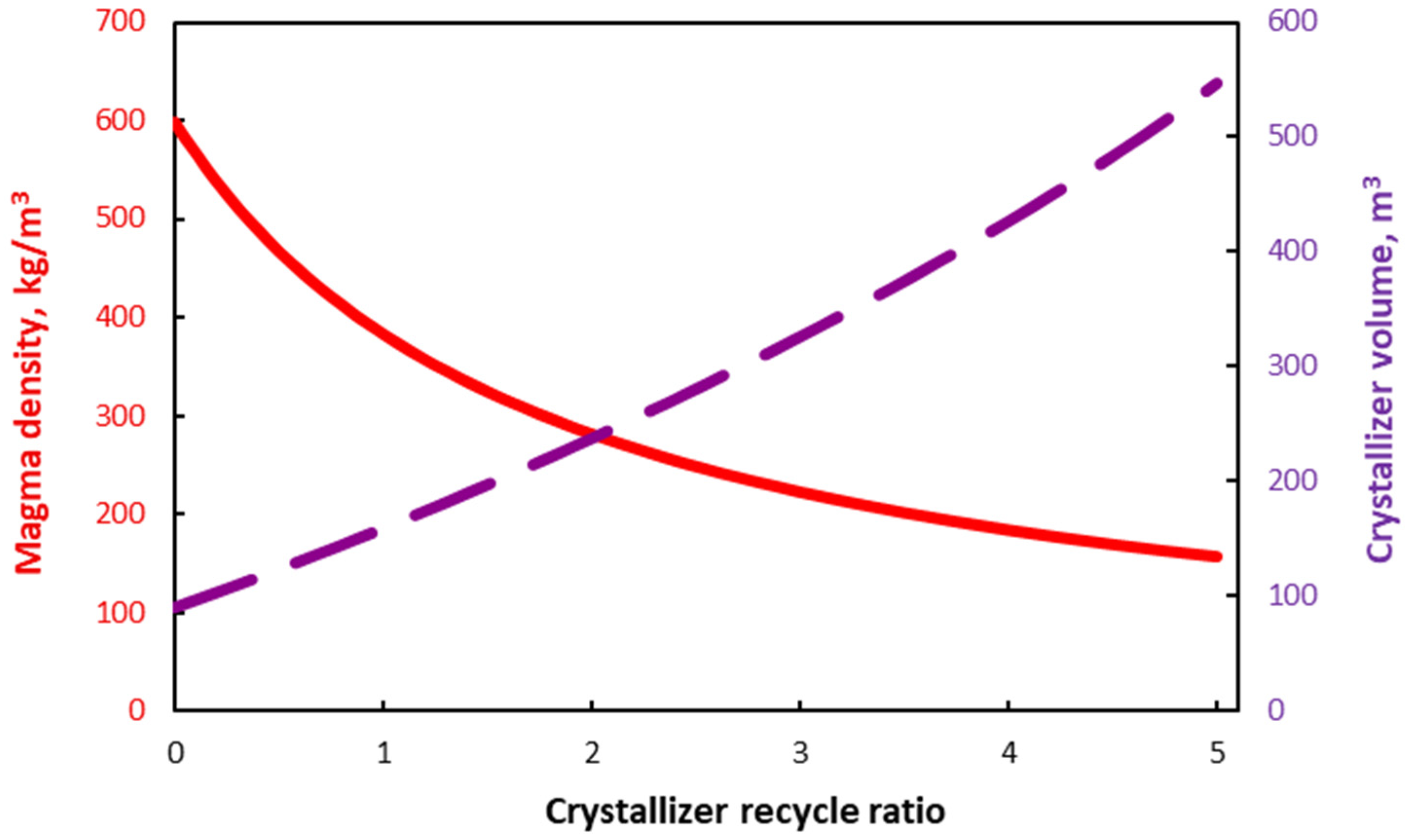
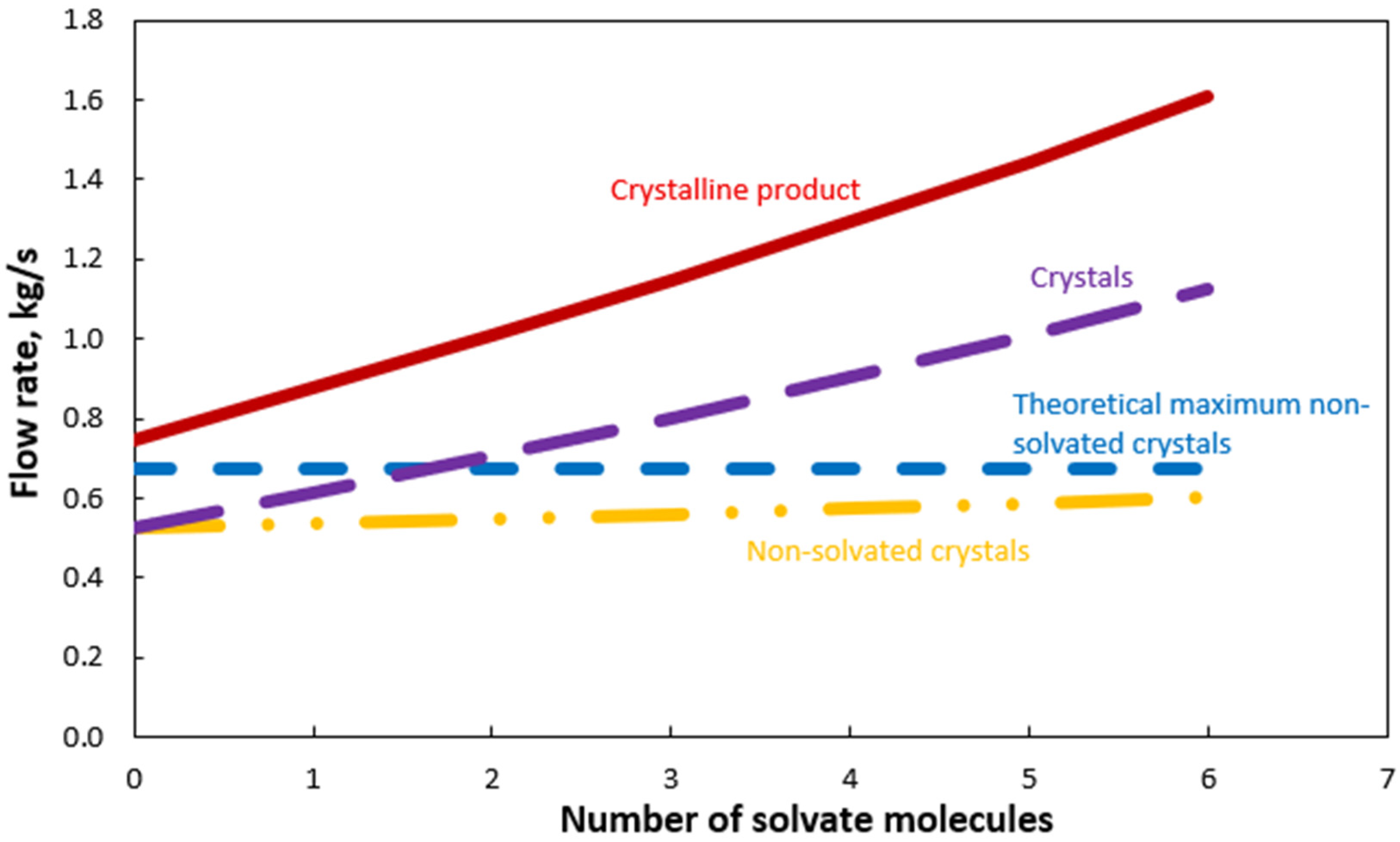
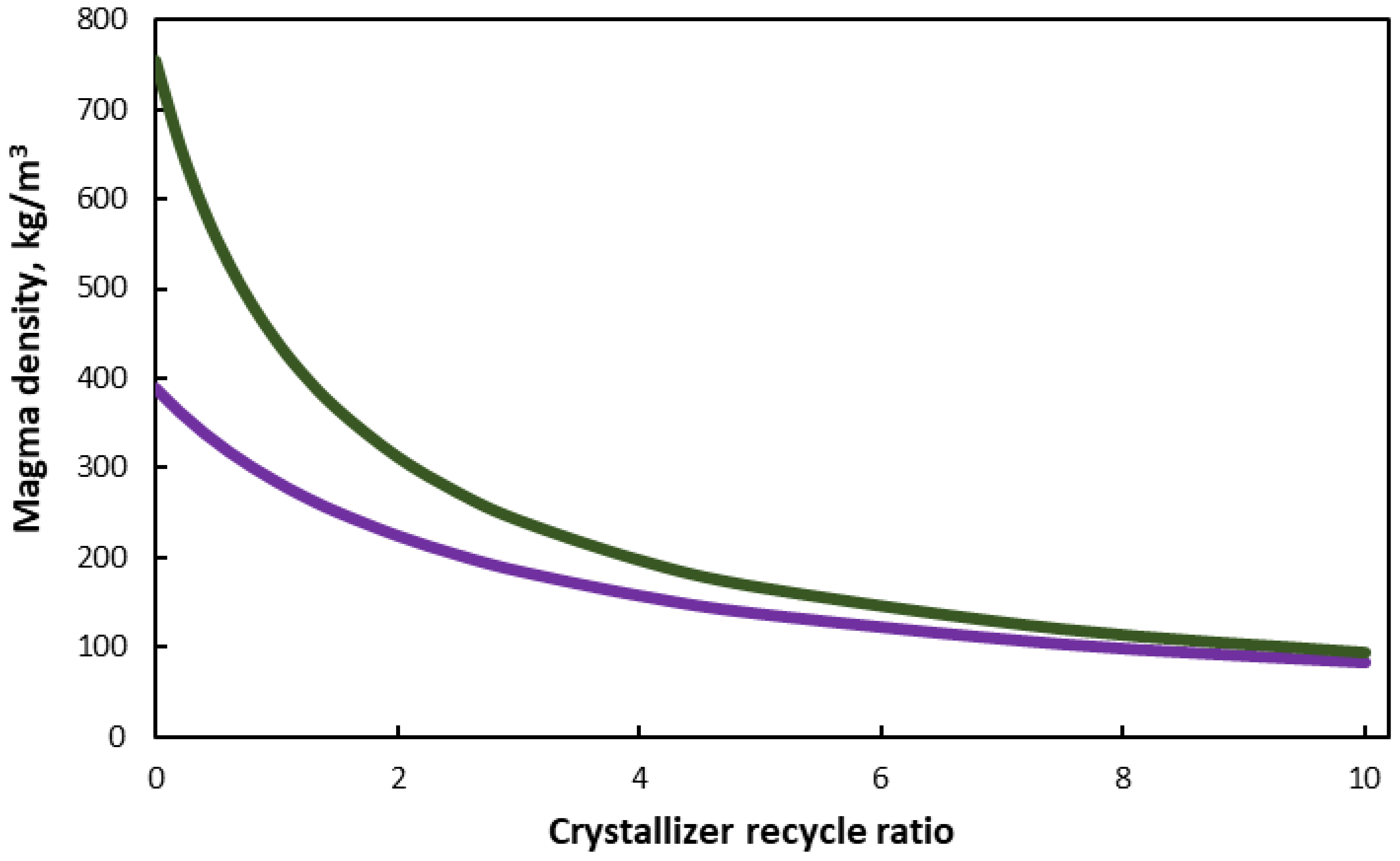
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Nomenclature
| (m2) | Evaporator first effect heat transfer area | |
| (m2) | Evaporator second effect heat transfer area | |
| (–) | Antoine constant for solvent (water) | |
| (–) | Boiling point elevation constant | |
| (–) | Solubility—temperature constant | |
| (m2) | Crystallizer cross sectional surface area based on maximum allowable vapor velocity | |
| (m2) | Cross sectional surface area of liquid-vapor separator of evaporator first effect | |
| (m2) | Cross sectional surface area of liquid-vapor separator of evaporator second effect | |
| (–) | Crystal growth rate—residence time constant | |
| (m2) | Heat transfer area of crystallizer heat pump condenser | |
| (m2) | Heat transfer area of crystallizer heat pump evaporator | |
| (m2) | Preheater heat transfer area | |
| (–) | Overall heat transfer coefficient constant | |
| (–) | Latent heat of vaporization—temperature constant for solvent (water) | |
| (m2) | Crystallizer heat exchanger surface area for water cooling | |
| (# nuclei/m3/s) | Nucleation rate per unit magma (solution) volume | |
| (–) | Antoine constant for solvent (water) | |
| (–) | Boiling point elevation constant | |
| (–) | Solubility—temperature constant | |
| (–) | Crystal growth rate—residence time constant | |
| (°C) | Evaporator first effect boiling point elevation | |
| (°C) | Evaporator second effect boiling point elevation | |
| (–) | Overall heat transfer coefficient constant | |
| (–) | Latent heat of vaporization—temperature constant for solvent (water) | |
| (–) | Antoine constant for solvent (water) | |
| (–) | Solubility—temperature constant | |
| (–) | Crystallizer heat pump coefficient of performance | |
| (kJ/kg/°C) | Specific heat capacity of crystallizer feed solution (downstream mixing of valve outlet solution and recycling solution) | |
| (kJ/kg/°C) | Solution specific heat capacity at expansion valve outlet | |
| (kJ/kg/°C) | Solution specific heat capacity at evaporator first effect | |
| (kJ/kg/°C) | Solution specific heat capacity at evaporator second effect | |
| (kJ/kg/°C) | Feed solution specific heat capacity | |
| (kJ/kg/°C) | Solution specific heat capacity at mixer outlet | |
| (kJ/kg/°C) | Solution specific heat capacity in the crystallizer | |
| (kJ/kg/°C) | Crystallizer heat pump fluid heat capacity | |
| (kJ/kg/°C) | Recycling solution specific heat capacity | |
| (kJ/kg/°C) | Solute heat capacity | |
| (kJ/kg/°C) | Liquid solvent (water) heat capacity | |
| (–) | Constant for maximum allowable vapor velocity | |
| (–) | Latent heat of vaporization—temperature constant for solvent (water) | |
| (m) | Crystallizer diameter | |
| (m) | Crystallizer diameter based on magma holdup volume | |
| (m) | Crystallizer diameter based on maximum vapor velocity | |
| (m) | Cross sectional diameter of liquid-vapor separator of evaporator first effect | |
| (m) | Cross sectional diameter of liquid-vapor separator of evaporator second effect | |
| (kW) | Crystallizer heat pump compressor electrical power | |
| (kg fuel/s) | Total fuel consumption | |
| (kg solvent vapor/s) | Vapor flow rate to evaporator condenser | |
| (kg magma/s) | Outlet magma flow rate from the crystallizer (feed to its filter) | |
| (kg fuel/s) | Fuel consumption for electricity generation | |
| (kg fuel/s) | Fuel consumption for heating steam generation | |
| (kg solution–magma/s) | Crystallizer total inlet solution and crystals flow rate downstream expansion (excluding vapor flow rate) | |
| (kg solution/s) | Crystallizer total inlet solution flow rate (solution flow rate at crystallizer mixer) | |
| (kg solvent/s) | Crystallizer total inlet solvent flow rate downstream expansion | |
| (kg soluble solids/s) | Crystallizer total inlet soluble solid flow rate downstream expansion | |
| (kg crystals anhydrous/s) | Anhydrous crystals or anhydrous part of solvated crystals outlet flow rate | |
| (kg crystalline product/s) | Outlet flow rate of crystalline product, including its moisture, at filter outlet | |
| (kg vapor/s) | Vapor flow rate to evaporator condenser | |
| (kg solution/s) | Solution flow rate at mixer outlet | |
| (kg solution/s) | Crystallizer total inlet solution flow rate upstream expansion valve | |
| (kg crystals/s) | Crystals (hydrated) outlet flow rate | |
| (kg crystals anhydrous/s) | Theoretical maximum anhydrous crystalline product flow rate | |
| (kg solution/s) | Overflow flow rate from filtrate stream | |
| (kg solvent/s) | Solvent flow rate exiting crystallizer as overflow (at liquid state) | |
| (kg soluble solids/s) | Soluble solids flow rate exiting crystallizer as overflow | |
| (kg solution/s) | Solution flow rate exiting crystallizer as overflow | |
| (kg solution/s) | Overflow flow rate from the calming zone | |
| (kg solvent/s) | Solvent flow rate at the evaporator first effect outlet | |
| (kg soluble solids/s) | Soluble solids flow rate at the evaporator first effect outlet | |
| (kg solvent/s) | Solvent flow rate at the evaporator second effect outlet | |
| (kg soluble solids/s) | Soluble solids flow rate at the evaporator second effect outlet | |
| (kg solution/s) | Solution flow rate at the expansion valve outlet | |
| (kg crystals/s) | Crystals flow rate at the expansion valve | |
| (kg solvent/s) | Solvent flow rate at the expansion valve outlet | |
| (kg solvent/s) | Hydrated solvent flow rate at the expansion valve outlet | |
| (kg soluble solids/s) | Soluble solids flow rate at the expansion valve outlet | |
| (kg solution/s) | Feed solution flow rate | |
| (kg solvent/s) | Solvent flow rate in the feed stream | |
| (kg soluble solids/s) | Soluble solids flow rate in the feed stream | |
| (kg solution/s) | Moisture flow rate exiting crystallizer (including its filter) | |
| (kg solution/s) | Filtrate flow rate | |
| (kg solution/s) | Evaporator first effect outlet solution flow rate | |
| (kg solution/s) | Evaporator second effect outlet solution flow rate | |
| (kg solvent/s) | Moisture solvent flow rate exiting crystallizer (including its filter) | |
| (kg solvent/s) | Solvent flow rate in the mixer outlet | |
| (kg soluble solids/s) | Moisture soluble solids flow rate exiting crystallizer (including its filter) | |
| (kg soluble solids/s) | Soluble solids flow rate in the mixer outlet | |
| (kg solution/s) | Recycling solution flow rate | |
| (–) | Fraction overflow flow rate from the calming zone | |
| (kg steam/s) | Vapor flow rate to evaporator preheater | |
| (kg refrigerant/s) | Crystallizer heat pump fluid flow rate | |
| () | Hydrated solvent flow rate exiting crystallizer | |
| (–) | Vessel increase factor | |
| (kg vapor/s) | Evaporator first effect vapor flow rate | |
| (kg vapor/s) | Evaporator second effect vapor flow rate | |
| (kg vapor/s) | Evaporator total vapor flow rate | |
| (kg cooling water/s) | Cooling water flow rate to evaporator condenser | |
| (m/s) | Crystal (linear) growth rate | |
| (m/s) | Reference crystal linear growth rate | |
| (kW) | Enthalpy of solution overflows crystallizer | |
| (kW) | Latent heat of crystallization | |
| (kW) | Solution/magma enthalpy at crystallizer mixer outlet | |
| (kW) | Crystalline product enthalpy | |
| (–) | Exponent of the kinetic equation | |
| (–) | Exponent of the kinetic equation | |
| (–) | Crystal volume shape factor | |
| (μm) | Dominant size of crystalline product | |
| (kg moisture/kg slurry) | Crystalline product moisture content (wet basis) | |
| (kg moisture/kg slurry) | Crystalline product moisture content at the filter outlet (wet basis) | |
| (kg crystals) | Crystals mass in the crystallizer | |
| (kg solution) | Magma solution mass in the crystallizer | |
| (kg magma) | Magma mass in the crystallizer | |
| (kg soluble solids) | Soluble solids mass in the crystallizer | |
| (kg solvent) | Solvent mass in the crystallizer | |
| (kg heating steam/s) | Heating steam flow rate | |
| (kg solvent/mol anhydrous crystal) | Mass of solvent per molecular mass of anhydrous crystal | |
| (kg crystals/m3 magma) | Magma density | |
| (kg crystals/m3 magma) | Reference magma density | |
| (kg/mol) | Anhydrous solid molecular weight | |
| (kg/mol) | Solvent molecular weight | |
| (–) | Number of hydrate molecules per solid molecule | |
| (# crystals/s) | Crystal number production rate | |
| (–) | Crystallization recovery (efficiency) | |
| (–) | Electrical efficiency | |
| (–) | Thermal efficiency | |
| (# nuclei/m4) | Population density of nuclei (number density) | |
| (atm) | Crystallizer pressure | |
| (atm) | Evaporator first effect pressure | |
| (atm) | Evaporator second effect pressure | |
| (atm) | Heating steam pressure | |
| (kW) | Crystallizer heat duty | |
| (kW) | Evaporator condenser heat duty | |
| (m3 solution–magma/s) | Solution/magma volumetric feed flow rate to the crystallizer (excluding vapors) | |
| (kW) | Crystallizer heat pump condenser heat duty | |
| (m3 solution/s) | Total crystallizer feed solution volumetric rate | |
| (m3 magma/s) | Outlet magma volumetric flow rate from the crystallizer | |
| (m3 solution/s) | Overflow volumetric flow rate from filtrate stream | |
| (m3 solution/s) | Overflow volumetric flow rate from the calming (settling) zone | |
| (m3 crystals/s) | Crystals volumetric flow rate | |
| (m3 crystals/s) | Crystals volumetric flow rate at the expansion valve outlet | |
| (kW) | Crystallizer heat pump evaporator heat duty | |
| (kW) | Evaporator first effect heat duty | |
| (kW) | Evaporator second effect heat duty | |
| (kW) | Evaporator condenser heat duty | |
| (m3 solution/s) | Solution volumetric flow rate at the expansion valve outlet | |
| (m3 vapor/s) | Volumetric flow rate of solvent vaporized due to expansion in the crystallizer | |
| (m3 solution/s) | Filtrate volumetric flow rate | |
| (m3 solution/s) | Feed solution volumetric flow rate | |
| (m3 solution/s) | Evaporator first effect outlet solution volumetric flow rate | |
| (m3 solution/s) | Evaporator second effect outlet solution volumetric flow rate | |
| (m3 solution/s) | Solution volumetric flow rate at mixer outlet | |
| (kW) | Preheater heat duty | |
| (m3 solution/s) | Recycling solution volumetric flow rate | |
| (m3 vapor/s) | Evaporator first effect vapor volumetric flow rate | |
| (m3 vapor/s) | Evaporator second effect vapor volumetric flow rate | |
| (–) | Ratio of recycling solution flow rate to crystalline product flow rate (crystallizer recycle) | |
| (kg (hydrated) crystals/kg anhydrous crystals) | Ratio of molecular masses (weights) of hydrated to anhydrous crystals | |
| (J/mol/°C) | Universal ideal gas constant | |
| (–) | Height-to-diameter vessel ratio | |
| (–) | Evaporator steam economy | |
| (°C) | Crystallizer temperature | |
| (°C) | Solvent boiling temperature at crystallizer pressure | |
| (°C) | Feed solution/magma temperature at expansion valve outlet (crystallizer mixer inlet) | |
| (°C) | Evaporator first effect temperature | |
| (°C) | Solution boiling point temperature at evaporator first effect | |
| (°C) | Evaporator seond effect temperature | |
| (°C) | Solution boiling point temperature at evaporator second effect | |
| (°C) | Crystallizer heat pump condenser temperature | |
| (°C) | Crystallizer heat pump evaporator temperature | |
| (°C) | Feed solution temperature | |
| (°C) | Solution temperature at mixer outlet | |
| (°C) | Feed outlet temperature from preheater | |
| (°C) | Heating steam temperature | |
| (°C) | Cooling water inlet temperature | |
| (°C) | Cooling water outlet temperature for crystallizer | |
| (°C) | Cooling water outlet temperature for coolers | |
| (W/m2/°C) | Evaporator first effect overall heat transfer coefficient | |
| (W/m2/°C) | Evaporator second effect overall heat transfer coefficient | |
| (kW/m2/°C) | Preheater overall heat transfer coefficient | |
| (kW/m2/°C) | Crystallizer overall heat transfer coefficient for heat pump condenser (rwc: refrigerant water cooling) | |
| (kW/m2/°C) | Crystallizer overall heat transfer coefficient for heat pump evaporator (rsc: refrigerant solution condenser) | |
| (kW/m2/°C) | Crystallizer overall heat transfer coefficient for water cooling | |
| (m/s) | Maximum allowable vapor velocity at evaporator first effect | |
| (m/s) | Maximum allowable vapor velocity at evaporator second effect | |
| (kg solvent vapor/s) | Flow rate of solvent vaporized due to expansion in the crystallizer | |
| (m3) | Crystallizer volume | |
| (m3 solvent) | Solvent volume in the crystallizer | |
| (m3 solution) | Solution (mother liquor) volume in the crystallizer | |
| (kg vapor/kg solvent/s) | Solvent removed by evaporation per unit mass of feed solvent | |
| (m3) | Magma holdup volume (magma volume in the crystallizer) | |
| Soluble solids volume in the crystallizer | ||
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at crystallizer temperature | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at crystallizer temperature | |
| kg moisture/kg dry solids (crystals) | Solubility (mass ratio at equilibrium) at crystallizer temperature | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at boiling temperature of the solvent at crystallizer pressure | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at boiling temperature of the solvent at crystallizer pressure | |
| (kg soluble solids/kg solution) | Soluble solids mass fraction of crystallizer feed solution (solution exiting crystallizer mixer) | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at crystallizer mixer temperature | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at filter working temperature | |
| (kg soluble solids/kg solution) | Solution mass fraction at evaporator first effect | |
| (kg soluble solids/kg solution) | Solution mass fraction at evaporator second effect | |
| (kg soluble solids/kg solvent) | Solution mass ratio at evaporator first effect outlet | |
| (kg soluble solids/kg solvent) | Solution mass ratio at evaporator second effect outlet | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at expansion valve outlet | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at expansion valve outlet | |
| (kg soluble solids/kg solution) | Feed solution mass fraction of crystallizing material | |
| (kg soluble solids/kg solvent) | Feed solution mass ratio | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at feed temperature | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at solvent boiling point in the feed | |
| (kg soluble solids/kg solution) | Solution mass fraction at mixer outlet | |
| (kg soluble solids/kg solvent) | Solution mass ratio at mixer outlet | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) at mixer temperature | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) at mixer temperature | |
| (kg soluble solids/kg solvent) | Solubility (mass ratio at equilibrium) of recycling solution | |
| (kg soluble solids/kg solution) | Solubility (mass fraction) of recycling solution | |
| (kJ/kg crystals) | Latent heat of crystallization | |
| (kJ/kg fuel) | Fuel calorific value | |
| (kJ/kg) | Latent heat of vaporization of water at its boiling temperature at crystallizer pressure | |
| (kJ/kg) | Latent heat of vaporization of solvent (water) at evaporator first effect temperature | |
| (kJ/kg) | Latent heat of vaporization of solvent (water) at evaporator second effect temperature | |
| (kJ/kg fluid) | Latent heat of vaporization of crystallizer heat pump fluid | |
| (°C) | Logarithmic mean temperature difference at crystallizer heat pump condenser | |
| (°C) | Logarithmic mean temperature difference at crystallizer heat pump evaporator | |
| (°C) | Preheater logarithmic mean temperature difference | |
| (°C) | Crystallizer heat exchanger logarithmic mean temperature for water cooling | |
| (°C) | Latent heat of vaporization of water at heating steam temperature | |
| (kg solution/m3) | Density of feed solution to crystallizer at crystallizer mixer outlet | |
| (kg vapor/m3) | Solvent vapor density at crystallizer | |
| (kg solution/m3) | Evaporator first effect solution density | |
| (kg solution/m3) | Evaporator second effect solution density | |
| (kg vapor/m3) | Solvent vapor density at evaporator first effect | |
| (kg vapor/m3) | Solvent vapor density at evaporator second effect | |
| (kg solution/m3) | Solution density at expansion valve outlet | |
| (kg solution/m3) | Feed solution density | |
| (kg solution/m3) | Solution density at mixer outlet | |
| (kg solid/m3) | Solids density | |
| (kg solvent/m3) | Solvent density | |
| (s) | Product retention time |
References
- Zokić, I.; Prlić Kardum, J. Crystallization Behavior of Ceritinib: Characterization and Optimization Strategies. ChemEngineering 2023, 7, 84. [Google Scholar] [CrossRef]
- Boonkerd, S.; Wantha, L. Antisolvent Crystallization of Papain. ChemEngineering 2024, 8, 4. [Google Scholar] [CrossRef]
- Nazarchuk, E.V.; Charkin, D.O.; Siidra, O.I. Successive Crystallization of Organically Templated Uranyl Sulfates: Synthesis and Crystal Structures of [Pyh](H3o)[(Uo2)3(So4)4(H2o)2], [Pyh]2[(Uo2)6(So4)7(H2o)], and [Pyh]2[(Uo2)2(So4)3]. ChemEngineering 2021, 5, 5. [Google Scholar] [CrossRef]
- Chen, P.-C.; Jhuang, J.-H.; Tseng, C.-E.; Lin, Z.-Y. Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer. Crystals 2024, 14, 1021. [Google Scholar] [CrossRef]
- Höving, S.; Bolien, P.; Siebers, P.; Kockmann, N. Simplified Approach to Characterize the Cooling Crystallization in a Modular Mini-Plant. Crystals 2023, 13, 147. [Google Scholar] [CrossRef]
- Kufner, A.C.; Rix, M.; Wohlgemuth, K. Modeling of Continuous Slug Flow Cooling Crystallization towards Pharmaceutical Applications. Processes 2023, 11, 2637. [Google Scholar] [CrossRef]
- Nandan, N.; Parambil, J.V. Cooling Crystallization of Paracetamol in a Slug-Flow Crystallizer with Silicone Oil as Continuous Phase. Crystals 2023, 13, 1094. [Google Scholar] [CrossRef]
- Panagopoulos, A. Zero Liquid Discharge (ZLD) and Minimal Liquid Discharge (MLD) Technologies for Sustainable Wastewater Management and Valorization. In Smart Waste and Wastewater Management by Biotechnological Approaches; Yatoo, A.M., Sillanpää, M., Eds.; Springer Nature: Singapore, 2025; pp. 307–320. ISBN 978-981-97-8673-2. [Google Scholar]
- Panagopoulos, A.; Michailidis, P. Membrane Technologies for Sustainable Wastewater Treatment: Advances, Challenges, and Applications in Zero Liquid Discharge (ZLD) and Minimal Liquid Discharge (MLD) Systems. Membranes 2025, 15, 64. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, P. Designing Heat-Set Gels for Crystallizing APIs at Different Temperatures: A Crystal Engineering Approach. ChemEngineering 2022, 6, 65. [Google Scholar] [CrossRef]
- Kufner, A.C.; Westkämper, N.; Bettin, H.; Wohlgemuth, K. Prediction of Particle Suspension State for Various Particle Shapes Used in Slug Flow Crystallization. ChemEngineering 2023, 7, 34. [Google Scholar] [CrossRef]
- Chianese, A.; Fasoli, U.; Prati Gaglia, M.P. Design of a Continuous Crystallizer by Evaporation as Unit Operation. Cryst. Res. Technol. 1984, 19, 7. [Google Scholar] [CrossRef]
- Al-Harahsheh, A.M. A Heat Pump in a Countercurrent Crystallization Process. Appl. Therm. Eng. 2005, 25, 545–555. [Google Scholar] [CrossRef]
- Al-Anber, Z.A. Heat Saving In Evaporative Crystallization By Introducing A Heat Pump. J. Chem. Technol. Metall. 2013, 48, 277–288. [Google Scholar] [CrossRef]
- Pu, S.; Hadinoto, K. Comparative Evaluations of Bulk Seeded Protein Crystallization in Batch versus Continuous Slug Flow Crystallizers. Chem. Eng. Res. Des. 2021, 171, 139–149. [Google Scholar] [CrossRef]
- Pascual, G.K.; Donnellan, P.; Glennon, B.; Wood, B.; Jones, R.C. Design and Optimization of the Single-Stage Continuous Mixed Suspension-Mixed Product Removal Crystallization of 2-Chloro- N-(4-Methylphenyl)Propenamide. ACS Omega 2022, 7, 13676–13686. [Google Scholar] [CrossRef] [PubMed]
- Nassif, L. Accelerating Treatment of Radioactive Waste by Evaporative Fractional Crystallization; Georgia Institute of Technology: Atlanta, GA, USA, 2008. [Google Scholar]
- Liu, J.; Benyahia, B. Optimal Start-up Strategies of a Combined Cooling and Antisolvent Multistage Continuous Crystallization Process. Comput. Chem. Eng. 2022, 159, 107671. [Google Scholar] [CrossRef]
- Wankat, P.C. Rate-Controlled Separations; Chapman and Hall: London, UK, 1994. [Google Scholar]
- Lewis, A.E.; Seckler, M.M.; Kramer, H.; Van Rosmalen, G. Industrial Crystallization: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Seader, J.D.; Henley, E.J.; Roper, D.K. Separation Process Principles: Chemical and Biochemical Operations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Maroulis, Z.B.; Saravacos, G.D. Food Process Design; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Saravacos, G.D.; Maroulis, Z.B. Transport Properties of Foods; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Souders, M.; Brown, G.G. Design of Fractionating Columns: I. Entrainment and Capacity. Ind. Eng. Chem. 1934, 26, 98–103. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Grossmann, I.E.; Westerberg, A.W.; Biegler, L.T. Others Retrofit Design of Processes; Carnegie Mellon University: Pittsburgh, PA, USA, 1987. [Google Scholar]






| Equation | No |
|---|---|
| Feed | |
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| Unit mixer | |
| (5) | |
| (6) | |
| (7) | |
| (8) | |
| (9) | |
| (10) | |
| (11) | |
| 2-effect forward feed evaporator | |
| (12) | |
| (13) | |
| (14) | |
| (15) | |
| (16) | |
| (17) | |
| (18) | |
| (19) | |
| (20) | |
| (21) | |
| (22) | |
| (23) | |
| (24) | |
| (25) | |
| (26) | |
| (27) | |
| (28) | |
| (29) | |
| (30) | |
| (31) | |
| (32) | |
| (33) | |
| (34) | |
| (35) | |
| (36) | |
| (37) | |
| (38) | |
| (39) | |
| (40) | |
| (41) | |
| Evaporator preheater | |
| (42) | |
| (43) | |
| (44) | |
| (45) | |
| (46) | |
| Evaporator condenser | |
| (47) | |
| (48) | |
| Expansion valve | |
| (49) | |
| (50) | |
| (51) | |
| (52) | |
| (53) | |
| (54) | |
| (55) | |
| (56) | |
| (57) | |
| (58) | |
| (59) | |
| (60) | |
| (61) | |
| (62) | |
| Cooling crystallizer | |
| (63) | |
| (64) | |
| (65) | |
| (66) | |
| (67) | |
| (68) | |
| (69) | |
| (70) | |
| (71) | |
| (72) | |
| (73) | |
| (74) | |
| (75) | |
| (76) | |
| (77) | |
| (78) | |
| (79) | |
| (80) | |
| (81) | |
| (82) | |
| (83) | |
| (84) | |
| (85) | |
| (86) | |
| (87) | |
| (88) | |
| (89) | |
| (90) | |
| (91) | |
| (92) | |
| (93) | |
| (94) | |
| (95) | |
| Crystallizer condenser | |
| (96) | |
| (97) | |
| Crystallizer cooling | |
| (98) | |
| (99) | |
| (100) | |
| (101) | |
| (102) | |
| Cooling with water | |
| (103) | |
| (104) | |
| (105) | |
| Cooling with a refrigeration cycle | |
| (106) | |
| (107) | |
| (108) | |
| (109) | |
| (110) | |
| (111) | |
| (112) | |
| (113) | |
| Crystallizer content | |
| (114) | |
| (115) | |
| (116) | |
| (117) | |
| (118) | |
| (119) | |
| (120) | |
| (121) | |
| (122) | |
| (123) | |
| Crystallization kinetics | |
| (124) | |
| (125) | |
| (126) | |
| (127) | |
| (128) | |
| (129) | |
| (130) | |
| (131) | |
| Crystallizer sizing | |
| (132) | |
| (133) | |
| (134) | |
| (135) | |
| (136) | |
| (137) | |
| (138) | |
| Crystallization parameters | |
| (139) | |
| (140) | |
| Operating pressure | |
| (141) | |
| (142) | |
| (143) | |
| (144) | |
| Overall heat transfer coefficient | |
| (145) | |
| (146) | |
| (147) | |
| (148) | |
| (149) | |
| Solubility | |
| (150) | |
| (151) | |
| (152) | |
| (153) | |
| (154) | |
| (155) | |
| (156) | |
| (157) | |
| (158) | |
| (159) | |
| (160) | |
| (161) | |
| Solubility at boiling temperature of solution | |
| (162) | |
| (163) | |
| (164) | |
| (165) | |
| (166) | |
| (167) | |
| (168) | |
| (169) | |
| Moisture content | |
| (170) | |
| Thermophysical properties | |
| Specific heat capacity | |
| (171) | |
| (172) | |
| (173) | |
| (174) | |
| (175) | |
| (176) | |
| (177) | |
| Latent heat of vaporization | |
| (178) | |
| (179) | |
| (180) | |
| (181) | |
| Boiling point rise | |
| (182) | |
| (183) | |
| Solution—vapor density | |
| (184) | |
| (185) | |
| (186) | |
| (187) | |
| (188) | |
| (189) | |
| (190) | |
| (191) | |
| (192) | |
| (193) | |
| Statistical analysis of product crystals | |
| (194) | |
| (195) | |
| (196) | |
| (197) | |
| (198) | |
| (199) | |
| (200) | |
| (201) | |
| (202) | |
| (203) | |
| (204) | |
| (205) | |
| (206) | |
| (207) | |
| (208) | |
| (209) | |
| (210) | |
| Crystallization unit efficiency | |
| (211) | |
| (212) | |
| (213) | |
| (214) |
| Process Specifications | ||
|---|---|---|
| Feed pressure | Pi (atm) | 1.0 |
| Feed solution flow rate | Fi (kg solution/s) | 8.4 |
| Feed solution mass fraction | xi (kg soluble solids/kg solution) | 0.08 |
| Feed solution temperature | Ti (°C) | 24.0 |
| Heating steam temperature | Ts (°C) | 125 |
| Crystalline product moisture content (wet basis) | Mc (kg solution/kg crystalline slurry) | 0.30 |
| Dominant size of crystalline product | Ld (μm) | 850 |
| Solution mass fraction at evaporator final effect outlet | xe2 (kg soluble solids/kg solution) | 0.38 |
| Feed outlet temperature from preheater | Tph (°C) | 75 |
| Cooling water inlet temperature | Twi (°C) | 15 |
| Design variables | ||
| First effect evaporator temperature | Te1 (°C) | 100 |
| Second effect evaporator temperature | Te2 (°C) | 82 |
| Crystallizer temperature | Tc (°C) | 0 |
| Filter working temperature | Tf (°C) | 0 |
| Crystallizer pressure | Pc (atm) | 0.10 |
| Ratio of recycling solution flow rate to crystalline product flow rate (crystallizer recycle) | Rc (-) | 2.30 |
| Fraction overflow flow rate from the settling zone | froc (-) | 0.00 |
| Cooling water outlet temperature for crystallizer | Two (°C) | 20 |
| Cooling water outlet temperature for coolers | Tw2o (°C) | 35 |
| Crystallizer heat pump evaporator temperature | THPec (°C) | −3 |
| Crystallizer heat pump condenser temperature | THPcc (°C) | 40 |
| Trial-and-error variable | ||
| Solution mass fraction at evaporator first effect outlet | xe1 (kg soluble solids/kg solution) | 0.132 |
| Technical data | ||
| Solubility—temperature constant | aCT (-) | 0.0043 |
| Solubility—temperature constant | bCT (-) | 0.1665 |
| Solubility—temperature constant | cCT (-) | 15.117 |
| Heat of vaporization—temperature constant for water | Aw (-) | 2491.5 |
| Heat of vaporization—temperature constant for water | Bw (-) | −2.048 |
| Heat of vaporization—temperature constant for water | Cw (-) | −0.0032 |
| Antoine constant for water | Aant (-) | 8.07131 |
| Antoine constant for water | Bant (-) | 1730.63 |
| Antoine constant for water | Cant (-) | 233.426 |
| Overall heat transfer coefficient constant for solution | Ueo (W/m2/°C) | 1000 |
| Overall heat transfer coefficient constant for solution | aU (-) | 4 |
| Overall heat transfer coefficient constant for solution | bU (-) | 1.2 |
| Overall heat transfer coefficient for crystallizer heat pump condenser | Urco (W/m2/°C) | 700 |
| Overall heat transfer coefficient constant for water cooling | Uwco (W/m2/°C) | 500 |
| Anhydrous solid molecular weight | MWs (kg/mol) | 0.125 |
| Solvent molecular weight | MWsl (kg/mol) | 0.018 |
| Boiling point elevation constant | abpr (-) | 15 |
| Boiling point elevation constant | bbpr (-) | 10 |
| Specific heat of crystallization | ΔHcr (kJ/kg crystals) | 30 |
| Latent heat of vaporization of heat pump fluid | ΔHrc (kJ/kg) | 1250 |
| Liquid solvent heat capacity | Cpw (kJ/kg/°C) | 4.18 |
| Vapor solvent heat capacity | Cpv (kJ/kg/°C) | 1.88 |
| Solute heat capacity | Cps (kJ/kg/°C) | 2.4 |
| Crystallizer heat pump fluid heat capacity | Cprc (kJ/kg/°C) | 1.20 |
| Solvent density | ρw (kg/m3) | 1000 |
| Crystal density | ρs (kg/m3) | 1850 |
| Fuel calorific value | ΔHf (kJ/kg) | 50,000 |
| Thermal efficiency | nh (-) | 0.92 |
| Electrical efficiency | ne (-) | 0.63 |
| Crystal growth rate—residence time constant | aGτ (-) | −2.48 × 10−12 |
| Crystal growth rate—residence time constant | bGτ (-) | 7.22 × 10−9 |
| Reference magma density | MTref (kg/m3) | 280 |
| Exponent of the crystallization kinetic equation | i (-) | 3.5 |
| Exponent of the crystallization kinetic equation | j (-) | 0 |
| Universal ideal gas constant | Rg (J/mol/°C) | 8.314 |
| Constant for maximum allowable vapor velocity | Cv (m/s) | 0.0244 |
| Vessel increase factor | fv (-) | 1.4 |
| Height-to-diameter vessel ratio | RHD (-) | 1.54 |
| Crystal volume shape factor | kv (-) | 0.627 |
| Number of hydrate molecules per solid molecule | n (-) | 3.0 |
| Process Variables | ||
|---|---|---|
| Preheater heat duty | Qph (kW) | 1729.7 |
| Evaporator first effect outlet solution flow rate | FL1 (kg solution/s) | 5.110 |
| Evaporator first effect vapor flow rate | FV1 (kg solvent/s) | 3.290 |
| Evaporator second effect outlet solution flow rate | FL2 (kg solution/s) | 1.768 |
| Evaporator second effect vapor flow rate | FV2 (kg solvent/s) | 3.342 |
| Evaporator first effect heat duty | Qe1 (kW) | 8319.3 |
| Evaporator second effect heat duty | Qe2 (kW) | 7418.0 |
| Heating steam flow rate | ms (kg heating steam/s) | 3.807 |
| Evaporator condenser heat duty | Qce (kW) | 5962.7 |
| Flow rate of solvent vaporized due to expansion in the crystallizer | V (kg solvent/s) | 0.116 |
| Crystals flow rate at the expansion valve | Fcrexp (kg crystals/s) | 0.596 |
| Anhydrous crystals flow rate at the expansion valve | Fcraexp (kg anhydrous crystals/s) | 0.416 |
| Magma density | MT (kg crystals/m3 magma) | 260.7 |
| Theoretical maximum anhydrous crystal flow rate | Fcramax (kg crystals/s) | 0.672 |
| Crystals (anhydrous) outlet flow rate | Fcra (kg crystals (anhydrous)/s) | 0.560 |
| Crystals (hydrated) outlet flow rate | Fcr (kg crystals/s) | 0.802 |
| Hydrated solvent flow rate exiting crystallizer | Fslh (kg solvent/s) | 0.242 |
| Moisture flow rate exiting crystallizer (including its filter) | FfM (kg moisture/s) | 0.344 |
| Moisture-soluble solids flow rate exiting the crystallizer (including its filter) | FMss (kg soluble solids/s) | 0.045 |
| Moisture solvent flow rate exiting the crystallizer (including its filter) | FMsl (kg solvent/s) | 0.299 |
| Outlet flow rate of crystalline product, including its moisture, at filter outlet | FcrMf (kg crystalline product/s) | 1.146 |
| Solution flow rate exiting crystallizer as overflow | Fcost (kg solution/s) | 0.506 |
| Recycling solution flow rate | Fr (kg solution/s) | 1.846 |
| Filtrate flow rate | Ffl (kg solution/s) | 2.352 |
| Crystallizer total inlet solution flow rate prior to expansion | Fcti (kg solution/s) | 3.614 |
| Crystallizer total inlet solution and crystal flow rate following expansion (excluding vapor flow rate) | Fci (kg solution-magma/s) | 3.498 |
| Crystallizer total inlet solution flow rate (solution flow rate at crystallizer mixer) | FcL (kg solution/s) | 2.902 |
| Feed solution/magma temperature at expansion valve outlet (crystallizer mixer inlet) | Tcm (°C) | 46.1 |
| Solution/magma temperature at crystallizer mixer outlet | TLc (°C) | 19.6 |
| Outlet magma flow rate from the crystallizer (feed to its filter) | Fcmo (kg magma/s) | 3.498 |
| Outlet magma volumetric flow rate from the crystallizer | Qcmo (m3 magma/s) | 3.078 × 10−3 |
| Crystallization recovery (efficiency) | ncr (-) | 0.834 |
| Solution/magma enthalpy at crystallizer mixer outlet | Hcm (kW) | 248.7 |
| Enthalpy of solution overflows crystallizer | Hco (kW) | 0.0 |
| Crystalline product enthalpy | HcrM (kW) | 0.0 |
| Heat of crystallization | Hcr (kW) | 6.2 |
| Crystallizer heat pump evaporator heat duty | QeHPc (kW) | 254.9 |
| Heat pump fluid flow rate | FrHPc (kg fluid/s) | 0.213 |
| Crystallizer heat pump condenser heat duty | QcHPc (kW) | 297.3 |
| Heat pump compressor electrical power | Ecc (kW) | 42.3 |
| Product retention time | τp (h) | 16.98 |
| Crystal growth rate | G (m/s) | 4.64 × 10−9 |
| Crystallizer volume | Vc (m3) | 263.4 |
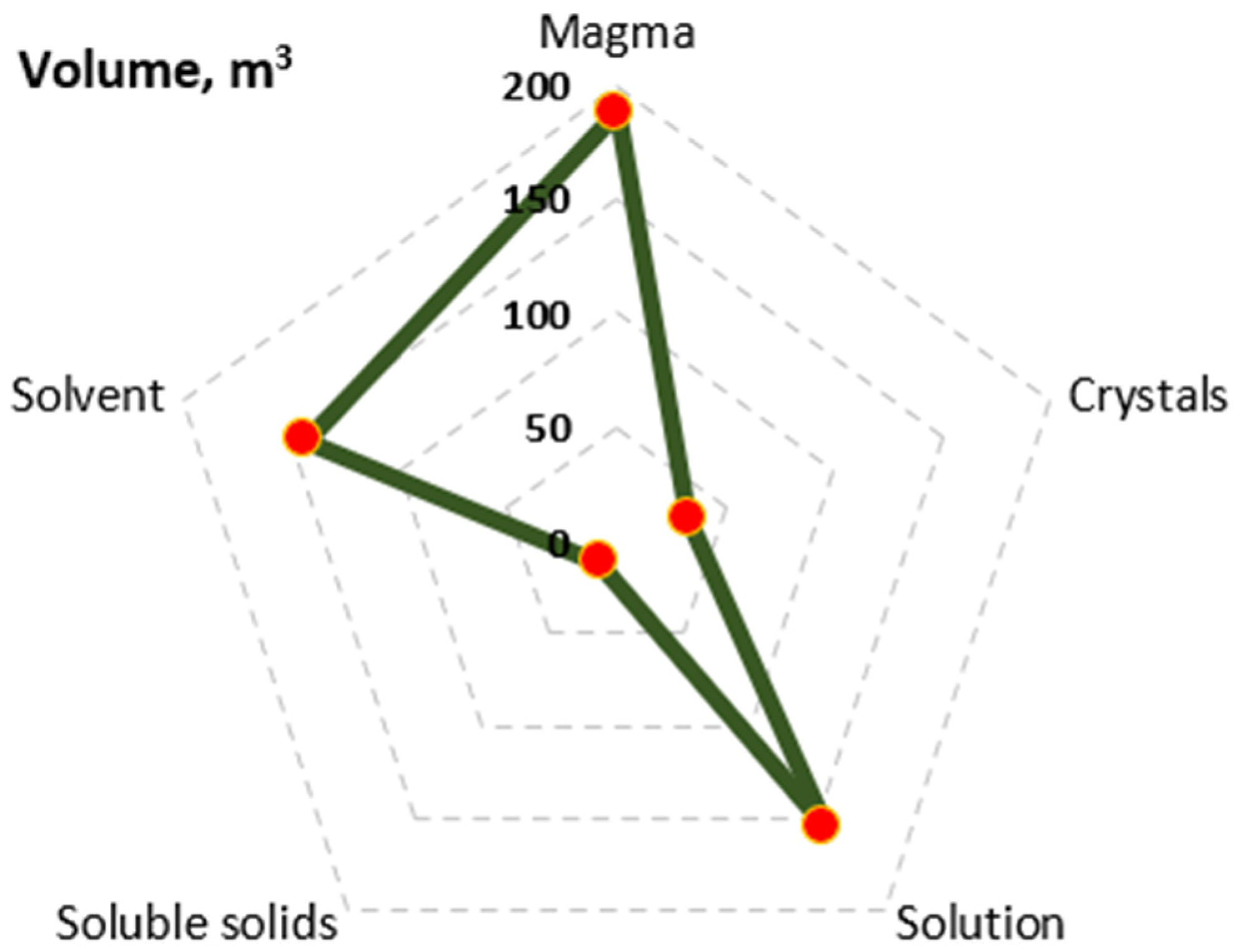
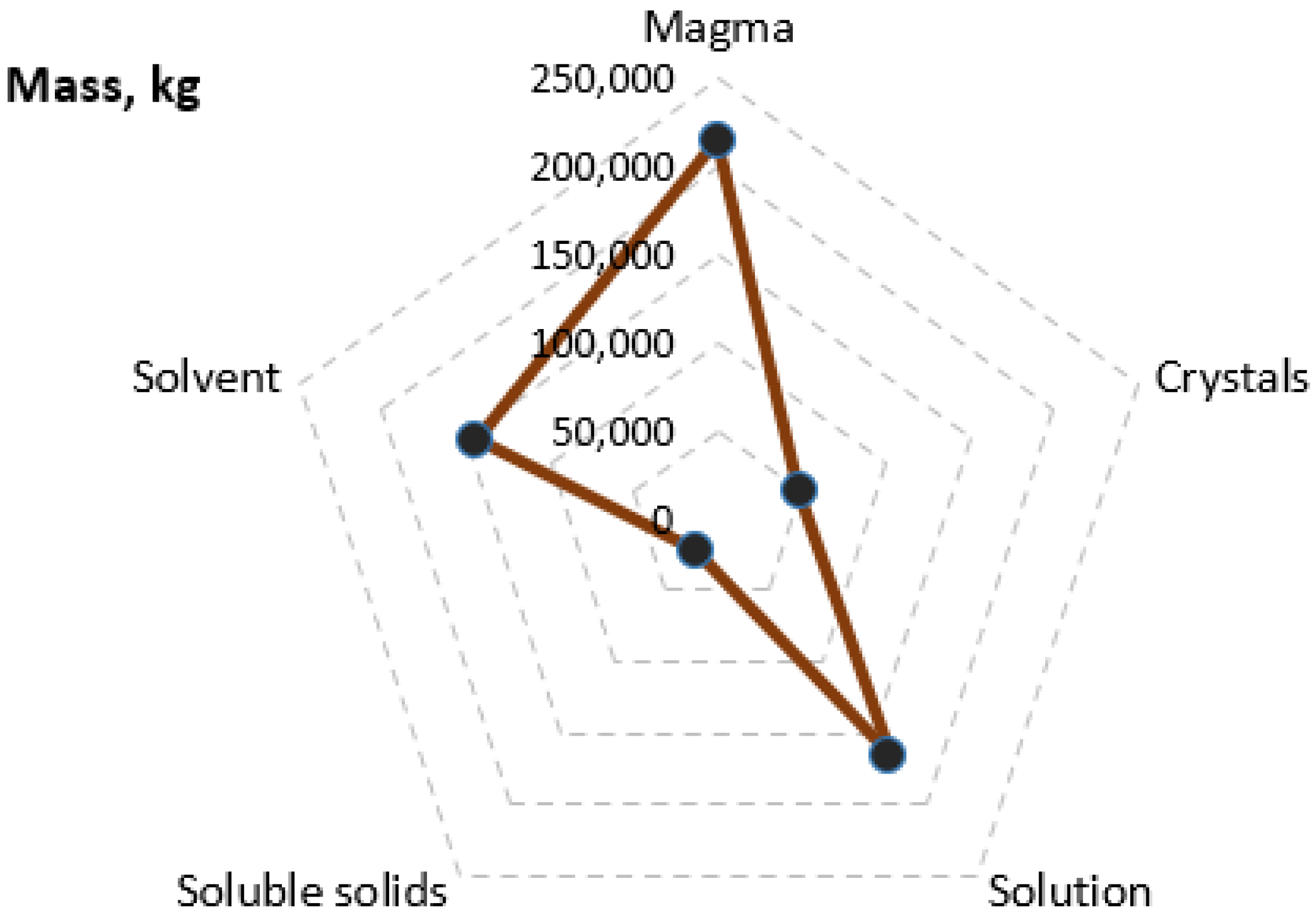
| Solvent (kg/s) | Soluble Solids (kg/s) | Crystals (kg/s) | Solvent Hydrated (kg/s) | Vapor (kg/s) | ||
|---|---|---|---|---|---|---|
| Feed | 1 | 7.728 | 0.672 | |||
| Evaporator first effect | 2 | 4.438 | 0.672 | 3.290 | ||
| Evaporator second effect | 3 | 1.096 | 0.672 | 3.342 | ||
| Expansion valve | 4 | 0.809 | 0.259 | 0.592 | 0.179 | 0.108 |
| Crystallizer outlet | 5 | 0.746 | 0.113 | 0.801 | 0.242 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michailidis, P.A.; Panagopoulos, A. Mathematical Modeling and Design of a Cooling Crystallizer Incorporating Experimental Data for Crystallization Kinetics. ChemEngineering 2025, 9, 97. https://doi.org/10.3390/chemengineering9050097
Michailidis PA, Panagopoulos A. Mathematical Modeling and Design of a Cooling Crystallizer Incorporating Experimental Data for Crystallization Kinetics. ChemEngineering. 2025; 9(5):97. https://doi.org/10.3390/chemengineering9050097
Chicago/Turabian StyleMichailidis, Panagiotis A., and Argyris Panagopoulos. 2025. "Mathematical Modeling and Design of a Cooling Crystallizer Incorporating Experimental Data for Crystallization Kinetics" ChemEngineering 9, no. 5: 97. https://doi.org/10.3390/chemengineering9050097
APA StyleMichailidis, P. A., & Panagopoulos, A. (2025). Mathematical Modeling and Design of a Cooling Crystallizer Incorporating Experimental Data for Crystallization Kinetics. ChemEngineering, 9(5), 97. https://doi.org/10.3390/chemengineering9050097









